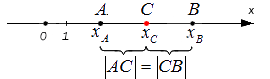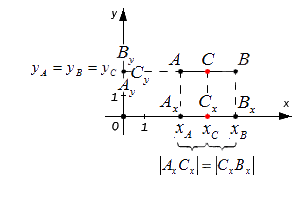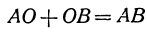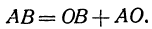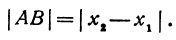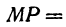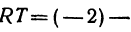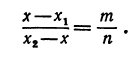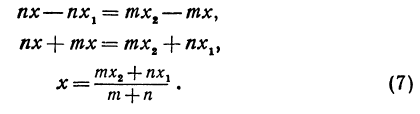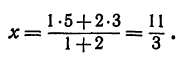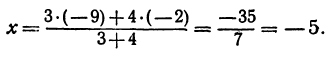Нахождение координат середины отрезка: примеры, решения
В статье ниже будут освещены вопросы нахождения координат середины отрезка при наличии в качестве исходных данных координат его крайних точек. Но, прежде чем приступить к изучению вопроса, введем ряд определений.
Отрезок – прямая линия, соединяющая две произвольные точки, называемые концами отрезка. В качестве примера пусть это будут точки A и B и соответственно отрезок A B .
Если отрезок A B продолжить в обе стороны от точек A и B , мы получим прямую A B . Тогда отрезок A B – часть полученной прямой, ограниченный точками A и B . Отрезок A B объединяет точки A и B , являющиеся его концами, а также множество точек, лежащих между. Если, к примеру, взять любую произвольную точку K , лежащую между точками A и B , можно сказать, что точка K лежит на отрезке A B .
Длина отрезка – расстояние между концами отрезка при заданном масштабе (отрезке единичной длины). Длину отрезка A B обозначим следующим образом: A B .
Середина отрезка – точка, лежащая на отрезке и равноудаленная от его концов. Если середину отрезка A B обозначить точкой C , то верным будет равенство: A C = C B
И далее мы рассмотрим, как же определять координаты середины отрезка (точки C ) при заданных координатах концов отрезка ( A и B ), расположенных на координатной прямой или в прямоугольной системе координат.
Середина отрезка на координатной прямой
Исходные данные: координатная прямая O x и несовпадающие точки на ней: A и B . Этим точкам соответствуют действительные числа x A и x B . Точка C – середина отрезка A B : необходимо определить координату x C .
Поскольку точка C является серединой отрезка А В , верным будет являться равенство: | А С | = | С В | . Расстояние между точками определяется модулем разницы их координат, т.е.
| А С | = | С В | ⇔ x C – x A = x B – x C
Тогда возможно два равенства: x C – x A = x B – x C и x C – x A = – ( x B – x C )
Из первого равенства выведем формулу для координаты точки C : x C = x A + x B 2 (полусумма координат концов отрезка).
Из второго равенста получим: x A = x B , что невозможно, т.к. в исходных данных – несовпадающие точки. Таким образом, формула для определения координат середины отрезка A B с концами A ( x A ) и B ( x B ):
Полученная формула будет основой для определения координат середины отрезка на плоскости или в пространстве.
Середина отрезка на плоскости
Исходные данные: прямоугольная система координат на плоскости О x y , две произвольные несовпадающие точки с заданными координатами A x A , y A и B x B , y B . Точка C – середина отрезка A B . Необходимо определить координаты x C и y C для точки C .
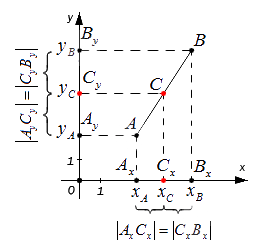
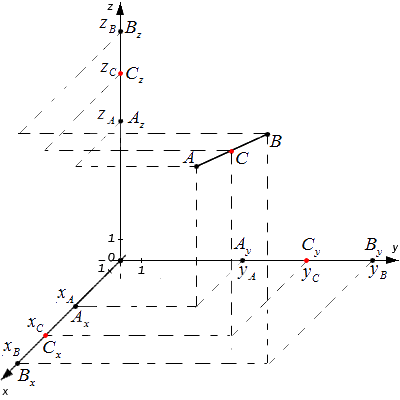
Возьмем для анализа случай, когда точки A и B не совпадают и не лежат на одной координатной прямой или прямой, перпендикулярной одной из осей. A x , A y ; B x , B y и C x , C y – проекции точек A , B и C на оси координат (прямые О х и О y ).
Согласно построению прямые A A x , B B x , C C x параллельны; прямые также параллельны между собой. Совокупно с этим по теореме Фалеса из равенства А С = С В следуют равенства: А x С x = С x В x и А y С y = С y В y , и они в свою очередь свидетельствуют о том, что точка С x – середина отрезка А x В x , а С y – середина отрезка А y В y . И тогда, опираясь на полученную ранее формулу, получим:
x C = x A + x B 2 и y C = y A + y B 2
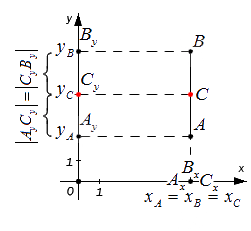
Этими же формулами можно воспользоваться в случае, когда точки A и B лежат на одной координатной прямой или прямой, перпендикулярной одной из осей. Проводить детальный анализ этого случая не будем, рассмотрим его лишь графически:
Резюмируя все выше сказанное, координаты середины отрезка A B на плоскости с координатами концов A ( x A , y A ) и B ( x B , y B ) определяются как:
( x A + x B 2 , y A + y B 2 )
Середина отрезка в пространстве
Исходные данные: система координат О x y z и две произвольные точки с заданными координатами A ( x A , y A , z A ) и B ( x B , y B , z B ) . Необходимо определить координаты точки C , являющейся серединой отрезка A B .
A x , A y , A z ; B x , B y , B z и C x , C y , C z – проекции всех заданных точек на оси системы координат.
Согласно теореме Фалеса верны равенства: A x C x = C x B x , A y C y = C y B y , A z C z = C z B z
Следовательно, точки C x , C y , C z являются серединами отрезков A x B x , A y B y , A z B z соответственно. Тогда, для определения координат середины отрезка в пространстве верны формулы:
x C = x A + x B 2 , y c = y A + y B 2 , z c = z A + Z B 2
Полученные формулы применимы также в случаях, когда точки A и B лежат на одной из координатных прямых; на прямой, перпендикулярной одной из осей; в одной координатной плоскости или плоскости, перпендикулярной одной из координатных плоскостей.
Определение координат середины отрезка через координаты радиус-векторов его концов
Формулу для нахождения координат середины отрезка также можно вывести согласно алгебраическому толкованию векторов.
Исходные данные: прямоугольная декартова система координат O x y , точки с заданными координатами A ( x A , y A ) и B ( x B , x B ) . Точка C – середина отрезка A B .
Согласно геометрическому определению действий над векторами верным будет равенство: O C → = 1 2 · O A → + O B → . Точка C в данном случае – точка пересечения диагоналей параллелограмма, построенного на основе векторов O A → и O B → , т.е. точка середины диагоналей.Координаты радиус-вектора точки равны координатам точки, тогда верны равенства: O A → = ( x A , y A ) , O B → = ( x B , y B ) . Выполним некоторые операции над векторами в координатах и получим:
O C → = 1 2 · O A → + O B → = x A + x B 2 , y A + y B 2
Следовательно, точка C имеет координаты:
x A + x B 2 , y A + y B 2
По аналогии определяется формула для нахождения координат середины отрезка в пространстве:
C ( x A + x B 2 , y A + y B 2 , z A + z B 2 )
Примеры решения задач на нахождение координат середины отрезка
Среди задач, предполагающих использование полученных выше формул, встречаются, как и те, в которых напрямую стоит вопрос рассчитать координаты середины отрезка, так и такие, что предполагают приведение заданных условий к этому вопросу: зачастую используется термин «медиана», ставится целью нахождение координат одного из концов отрезка, а также распространены задачи на симметрию, решение которых в общем также не должно вызывать затруднений после изучения настоящей темы. Рассмотрим характерные примеры.
Исходные данные: на плоскости – точки с заданными координатами А ( – 7 , 3 ) и В ( 2 , 4 ) . Необходимо найти координаты середины отрезка А В .
Решение
Обозначим середину отрезка A B точкой C . Координаты ее буду определяться как полусумма координат концов отрезка, т.е. точек A и B .
x C = x A + x B 2 = – 7 + 2 2 = – 5 2 y C = y A + y B 2 = 3 + 4 2 = 7 2
Ответ: координаты середины отрезка А В – 5 2 , 7 2 .
Исходные данные: известны координаты треугольника А В С : А ( – 1 , 0 ) , В ( 3 , 2 ) , С ( 9 , – 8 ) . Необходимо найти длину медианы А М .
Решение
- По условию задачи A M – медиана, а значит M является точкой середины отрезка B C . В первую очередь найдем координаты середины отрезка B C , т.е. точки M :
x M = x B + x C 2 = 3 + 9 2 = 6 y M = y B + y C 2 = 2 + ( – 8 ) 2 = – 3
- Поскольку теперь нам известны координаты обоих концов медианы (точки A и М ), можем воспользоваться формулой для определения расстояния между точками и посчитать длину медианы А М :
A M = ( 6 – ( – 1 ) ) 2 + ( – 3 – 0 ) 2 = 58
Ответ: 58
Исходные данные: в прямоугольной системе координат трехмерного пространства задан параллелепипед A B C D A 1 B 1 C 1 D 1 . Заданы координаты точки C 1 ( 1 , 1 , 0 ) , а также определена точка M , являющаяся серединой диагонали B D 1 и имеющая координаты M ( 4 , 2 , – 4 ) . Необходимо рассчитать координаты точки А .
Решение
Диагонали параллелепипеда имеют пересечение в одной точке, которая при этом является серединой всех диагоналей. Исходя из этого утверждения, можно иметь в виду, что известная по условиям задачи точка М является серединой отрезка А С 1 . Опираясь на формулу для нахождения координат середины отрезка в пространстве, найдем координаты точки А : x M = x A + x C 1 2 ⇒ x A = 2 · x M – x C 1 = 2 · 4 – 1 + 7 y M = y A + y C 1 2 ⇒ y A = 2 · y M – y C 1 = 2 · 2 – 1 = 3 z M = z A + z C 1 2 ⇒ z A = 2 · z M – z C 1 = 2 · ( – 4 ) – 0 = – 8
Ответ: координаты точки А ( 7 , 3 , – 8 ) .
Векторы в пространстве и метод координат
Существует два способа решения задач по стереометрии
Первый — классический — требует отличного знания аксиом и теорем стереометрии, логики, умения построить чертеж и свести объемную задачу к планиметрической. Способ хорош тем, что развивает мозги и пространственное воображение.
Другой метод — применение векторов и координат. Это простые формулы, алгоритмы и правила. Он очень удобен, особенно когда времени до экзамена мало, а решить задачу хочется.
Если вы освоили векторы на плоскости и действия с ними — то и с векторами в пространстве разберетесь. Многие понятия окажутся знакомыми.
Система координат в пространстве
Выберем начало координат. Проведем три взаимно перпендикулярные оси X, Y и Z. Зададим удобный масштаб.
Получилась система координат в трехмерном пространстве. Теперь каждая его точка характеризуется тремя числами — координатами по X, Y и Z. Например, запись M(−1; 3; 2) означает, что координата точки M по X (абсцисса) равна −1, координата по Y (ордината) равна 3, а координата по Z (аппликата) равна 2.
Векторы в пространстве определяются так же, как и на плоскости. Это направленные отрезки, имеющие начало и конец. Только в пространстве вектор задается тремя координатами x, y и z:
Как найти координаты вектора? Как и на плоскости — из координаты конца вычитаем координату начала.

Длина вектора в пространстве – это расстояние между точками A и B. Находится как корень квадратный из суммы квадратов координат вектора.
Пусть точка M – середина отрезка AB. Ее координаты находятся по формуле:
Для сложения векторов применяем уже знакомые правило треугольника и правило параллелограмма
Сумма векторов, их разность, произведение вектора на число и скалярное произведение векторов определяются так же, как и на плоскости. Только координат не две, а три. Возьмем векторы и
.
Произведение вектора на число:
Скалярное произведение векторов:
Косинус угла между векторами:
Последняя формула удобна для нахождения угла между прямыми в пространстве. Особенно если эти прямые – скрещиваются. Напомним, что так называются прямые, которые не параллельны и не пересекаются. Они лежат в параллельных плоскостях.
1. В кубе ABCDA1B1C1D1 точки E и K — середины ребер соответственно A1B1 и B1C1. Найдите косинус угла между прямыми AE и BK.
Если вам достался куб — значит, повезло. Он отлично вписывается в прямоугольную систему координат. Строим чертеж:
Длина ребра куба не дана. Какой бы она ни была, угол между AE и BK от нее не зависит. Поэтому возьмем единичный куб, все ребра которого равны 1.
Прямые AE и BK — скрещиваются. Найдем угол между векторами и
. Для этого нужны их координаты.
Запишем координаты векторов:
и найдем косинус угла между векторами и
:
2. В правильной четырехугольной пирамиде SABCD, все ребра которой равны 1, точки E, K — середины ребер SB и SC соответственно. Найдите косинус угла между прямыми AE и BK.
Лучше всего выбрать начало координат в центре основания пирамиды, а оси X и Y сделать параллельными сторонам основания.
Координаты точек A, B и C найти легко:
Из прямоугольного треугольника AOS найдем
Координаты вершины пирамиды:
Точка E — середина SB, а K — середина SC. Воспользуемся формулой для координат середины отрезка и найдем координаты точек E и K.
Найдем координаты векторов и
и угол между ними:
Покажем теперь, как вписать систему координат в треугольную призму:
3. В правильной треугольной призме ABCA1B1C1, все ребра которой равны 1, точка D — середина ребра A1B1. Найдите косинус угла между прямыми AD и BC1
Пусть точка A — начало координат. Возьмем ось X параллельно стороне BC, а ось Y перпендикулярно ей. Другими словами, на оси Y будет лежать отрезок AH, являющийся высотой треугольника ABC. Нарисуем отдельно нижнее основание призмы.
Запишем координаты точек:
Точка D — середина A1B1. Значит, пользуемся формулами для координат середины
отрезка.
Найдем координаты векторов и
, а затем угол между ними:
Смотрите, как легко с помощью векторов и координат найти угол между прямыми. А если требуется найти угол между плоскостями или между прямой и плоскостью? Для решения подобных задач нам понадобится уравнение плоскости в пространстве.
Плоскость в пространстве задается уравнением:
Здесь числа A, B и C — координаты вектора, перпендикулярного этой плоскости. Его называют нормалью к плоскости.
Вместо x, y и z можно подставить в уравнение координаты любой точки, принадлежащей данной плоскости. Получится верное равенство.
Плоскость в пространстве можно провести через любые три точки, не лежащие на одной прямой. Поэтому для того, чтобы написать уравнение плоскости, берем координаты трех принадлежащих ей точек. Подставляем их по очереди в уравнение плоскости. Решаем полученную систему.
Покажем, как это делается.
Напишем уравнение плоскости, проходящей через точки M (1; 0; 1), N (2; −2; 0) и K (4; 1; 2).
Уравнение плоскости выглядит так:
Подставим в него по очереди координаты точек M, N и K.
То есть A + C + D = 0.
Аналогично для точки K:
Получили систему из трех уравнений:
В ней четыре неизвестных: A, B, C и D. Поэтому одну из них мы выберем сами, а другие выразим через нее. Правило простое — вместо одной из переменных можно взять любое число, не равное нулю.
Пусть, например, D = −2. Тогда:
Выразим C и B через A и подставим в третье уравнение:
Решив систему, получим:
Уравнение плоскости MNK имеет вид:
Умножим обе части уравнения на −3. Тогда коэффициенты станут целыми:
Вектор — это нормаль к плоскости MNK.
Уравнение плоскости, проходящей через заданную точку имеет вид:
Угол между плоскостями равен углу между нормалями к этим плоскостям:
Не правда ли, знакомая формула? Скалярное произведение нормалей поделили на произведение их длин.
Заметим, что при пересечении двух плоскостей вообще-то образуется четыре угла.
Мы берем меньший из них. Поэтому в формуле стоит модуль скалярного произведения — чтобы косинус угла был неотрицателен.
4. В кубе ABCDA1B1C1D1 точки E и F — середины ребер соответственно A1B1 и A1D1. Найдите тангенс угла между плоскостями AEF и BDD1.
Строим чертеж. Видно, что плоскости AEF и BDD1 пересекаются где-то вне куба. В классическом решении пришлось бы строить линию их пересечения. Но векторно-координатный метод значительно всё упрощает. Не будем ломать голову над тем, по какой прямой пересекаются плоскости. Просто отметим координаты нужных нам точек и найдем угол между нормалями к плоскостям AEF и BDD1.
Сначала — нормаль к плоскости BDD1. Конечно, мы можем подставить координаты точек B, D и D1 в уравнение плоскости и найти коэффициенты, которые и будут координатами вектора нормали. А можем сделать хитрее — увидеть нужную нормаль прямо на чертеже. Ведь плоскость BDD1 — это диагональное сечение куба. Вектор перпендикулярен этой плоскости.
Итак, первый вектор нормали у нас уже есть:
Напишем уравнение плоскости AEF.
Берем уравнение плоскости и по очереди подставляем в него, вместо x, y и z, соответствующие координаты точек A, E и F.
Пусть С = -1. Тогда A = B = 2.
Уравнение плоскости AEF:
Нормаль к плоскости AEF:
Найдем угол между плоскостями:
5. Основание прямой четырехугольной призмы BCDA1B1C1D1 — прямоугольник ABCD, в котором AB = 5, AD = √33. Найдите тангенс угла между плоскостью грани AA1D1D и плоскостью, проходящей через середину ребра CD перпендикулярно прямой B1D, если расстояние между прямыми A1C1 и BD равно √3.
Эта задача наглядно показывает, насколько векторный метод проще классического. Попробуйте, для разнообразия, построить необходимые сечения и провести все доказательства — как это делается в «классике» 🙂
Строим чертеж. Прямую четырехугольную призму можно по-другому назвать “параллелепипед”.
Замечаем, что длина и ширина параллелепипеда у нас есть, а вот высота — вроде не дана. Как же ее найти?
«Расстояние между прямыми A1C1 и BD равно √3». Прямые A1C1 и BD скрещиваются. Одна из них — диагональ верхнего основания, другая — диагональ нижнего. Вспомним, что расстояние между скрещивающимися прямыми равно длине их общего перпендикуляра. Общий перпендикуляр к A1C1 и BD — это, очевидно, OO1, где O — точка пересечения диагоналей нижнего основания, O1 — точка пересечения диагоналей верхнего. А отрезок OO1 и равен высоте параллелепипеда.
Плоскость AA1 D1 D — это задняя грань призмы на нашем чертеже. Нормаль к ней — это любой вектор, перпендикулярный задней грани, например, вектор или, еще проще, вектор
.
Осталась еще «плоскость, проходящая через середину ребра CD перпендикулярно прямой B1D». Но позвольте, если плоскость перпендикулярна прямой B1D — значит, B1D и есть нормаль к этой плоскости! Координаты точек B1 и D известны:
Координаты вектора — тоже:
Находим угол между плоскостями, равный углу между нормалями к ним:
Зная косинус угла, находим его тангенс по формуле
Получим:
Ответ:
Угол между прямой m и плоскостью α тоже вычисляется с помощью скалярного произведения векторов.
Пусть — вектор, лежащий на прямой m (или параллельный ей),
— нормаль к плоскости α.
Находим синус угла между прямой m и плоскостью α по формуле:
6. В кубе ABCDA1B1C1D1 точка E — середина ребра A1B1. Найдите синус угла между прямой AE и плоскостью BDD1.
Как всегда, рисуем чертеж и выбираем систему координат
Находим координаты вектора .
Нужно ли нам уравнение плоскости BDD1? В общем-то, без него можно обойтись. Ведь эта плоскость является диагональным сечением куба, а значит, нормалью к ней будет любой вектор, ей перпендикулярный. Например, вектор .
Найдем угол между прямой и плоскостью:
Ответ:
Расстояние от точки M с координатами x0, y0 и z0 до плоскости α, заданной уравнением Ax + By + Cz + D = 0, можно найти по формуле:
7. В основании прямоугольного параллелепипеда BCDA1B1C1D1 лежит прямоугольник ABCD со сторонами AB = , AD =
. Высота параллелепипеда AA1 =
. Найдите расстояние от точки A до плоскости A1DB.
Построим чертеж и выпишем координаты точек:
Запишем уравнение плоскости A1DB. Вы помните, как это делается — по очереди подставляем координаты точек A1, D и B в уравнение Ax + Be + Cz + D
Решим эту систему. Выберем
Тогда
Уравнение плоскости A1DB имеет вид:
Дальше все просто. Находим расстояние от точки A до плоскости A1DB:
В некоторых задачах по стереометрии требуется найти расстояние от прямой до параллельной ей плоскости. В этом случае можно выбрать любую точку, принадлежащую данной прямой.
Как найти конец вектора зная координаты начала и середины
Найти координаты конца B отрезка, если другой конец отрезка – точка A(-5, -7), а середина отрезка – C(-9, -12).
(1)
координаты середины отрезка обозначены через x и y. По условию задачи x = -9; y = -12. Координаты одного конца отрезка точки A в этих формулах x1 = -5; y1 = -7. Координаты точки B (другого конца отрезка) – величины неизвестные, которые мы обозначим через x2 и y2. Тогда по формулам (1) для определения этих неизвестных получаем два уравнения:
[spoiler title=”источники:”]
http://ege-study.ru/ru/ege/materialy/matematika/vektory-v-prostranstve-i-metod-koordinat/
http://www.pm298.ru/reshenie/fha0774.php
[/spoiler]
На произвольную ось. Проекции отрезка на оси координат.
Длина и полярный угол отрезка. Расстояние
Между двумя точками

отрезок называется направленным, если
указано, какая из ограничивающих его
точек считается началом, какая — концом.
Направленный отрезок, имеющий точку
А своим
началом и точку В
концом (черт. 3),
обозначается символом АВ
(т. е. так же, как отрезок
оси; см. § 1). Длина направленного отрезка
АВ (при
заданном масштабе) обозначается символом
| АВ|
(или АВ;
см. сноску на стр. 13).
Проекцией отрезка АВ
на ось и
называется число,
равное величине отрезка A1В1
оси и,
где точка A1
является проекцией
на ось и точки
А, а
В1
— проекцией
Черт. 3. точки В.
Проекция отрезка АВ
на ось и
обозначается символом
приАВ.
Если на плоскости
задана система декартовых прямоугольных
координат, то проекция отрезка на ось
Ох обозначается
символом X,
его проекция на ось
Оу — символом
Y.
Если известны координаты
точек M1
(x1,
у1)
и М2(x2;
у2),
то проекции X
и Y
на оси координат направленного отрезка
М1М2
могут быть вычислены по формулам
X = х2
— x1
Y = y2
— y1
Таким образом, чтобы найти проекции
направленного отрезка на оси координат,
нужно от координат его конца отнять
соответствующие координаты начала.
Угол ,
на который нужно повернуть положительную
полуось Ох так,
чтобы её направление совпало с направлением
отрезка M1M2,
называется полярным
углом отрезка M1M2,
Угол
понимается, как в тригонометрии.
Соответственно этому
имеет бесконечно много возможных
значений, которые отличаются друг от
друга на величину вида ± 2п
(где п
— целое положительное
число). Главным значением полярного
угла называется то из его значений,
которое удовлетворяет неравенствам —
<
.
Формулы
X = d*cos , Y
= d* sin
,
выражают проекции произвольного отрезка
на координатные оси через его длину и
полярный угол. Отсюда же вытекают формулы
d =
и
cos
=
, sin
=
,
которые выражают длину и полярный угол
отрезка через его проекции на оси
координат.
Если на плоскости даны две
точки M1
(х1,
у1)
и M2
(х2,
у2),
то расстояние d
между ними определяется
формулой
d =
.
44. Вычислить проекцию отрезка
на ось и, если
даны его длина d и
угол
наклона к оси:
l) d = 6,
=
;2) d
= 6,
=
;
3) d
= 7,
=
;
4) d
= 5,
= 0; 5)
d = 5,
= ;
6) d = 4,
= —
.
45. Построить на чертеже отрезки, исходящие
из начала координат, зная их проекции
на координатные оси:
1) Х =
3, Y
= 2; 2) Х =
2, Y =
— 5; 3) Х
= — 5, Y
= 0; 4) Х
= — 2, Y
= 3;
5) Х = 0, Y
= 3; 6) Х
= — 5, Y
= — 1.
46. Построить на чертеже
отрезки, имеющие началом точку M(2;
—1), зная их проекции на координатные
оси:
а) Х = 4, Y =
3; б) Х = 2, Y = 0; в) Х = — 3,
Y = 1; г) Х
= — 4, Y
= — 2;
д) Х = 0, Y
= —3; е) X =
1, Y
== —3.
47. Даны точки M1(1;
—2), M1
(2; 1), M2
(5; 0), M3
(—1; 4) и M4(0;
—3).
Найти проекции на координатные оси
следующих отрезков:
1) M1M2,
2) M3M23)M4M5,
4) M5M3.
48. Даны проекции отрезка
М1М2
на оси координат Х=
5, Y
= — 4; зная, что его
начало в точке M1(—2;
3), найти координаты его конца.
49. Даны проекции отрезка АВ
на оси координат Х=
4, Y
= — 5; зная, что его
конец в точке В(1;
—3), найти координаты его начала.
50. Построить на чертеже
отрезки, исходящие из начала координат,
зная длину d и
полярный угол
каждого из них:
l) d
= 5,
=
;
2)d =
3,
=
;
3) d
= 4,
= —;
4) d
= 3,
= —.
51. Построить на чертеже
отрезки, имеющие началом точку М
(2; 3), зная длину и
полярный угол каждого из них:
1) d
= 2,
= —;
2)d
= 1,
=
;
3)d =
5,
= —
(координаты точки М
— декартовы).
52. Вычислить
проекции на координатные оси отрезка,
зная длину d и
полярный угол
каждого из них:
l) d
= 12,
=
;
2)d = 6,
= —;
3)
d =
2, e = —.
53. Даны проекции отрезков на координатные
оси:
1) Х
= 3, Y
= —4; 2) Х
=12, Y
=5; 3) Х
= —8, Y
= 6.
Вычислить длину каждого из них.
54. Даны проекции отрезков на координатные
оси:
1) X
= 1, Y
=
;
2)X
= 3,Y =
—3;
3)Х
= — 2,Y =
2.
Вычислить длину d
и полярный угол
каждого из них.
55. Даны точки
М1(2;
—3), М2(1;
—4), М3(—1;
—7) и М4(—4;
8).
Вычислить длину и полярный
угол следующих отрезков:
1) M1M2,
2) M1M3
3) M2M4,
4) M4M3.
56. Длина d
отрезка равна 5, его
проекция на ось абсцисс равна 4. Найти
проекцию этого отрезка на ось ординат
при условии, что он образует с осью
ординат: а) острый угол, б) тупой угол.
57. Длина отрезка MN
равна 13; его начало в
точке М (3;—2),
проекция на ось абсцисс равна — 12. Найти
координаты конца этого отрезка при
условии, что он образует с осью ординат:
а) острый угол, б) тупой угол.
58. Длина отрезка MN
равна 17, его конец в
точке N (—7; 3),
проекция на ось ординат равна 15. Найти
координаты начала этого отрезка при
условии, что он образует с осью абсцисс:
а) острый угол, б) тупой угол.
59. Зная проекции отрезка на
координатные оси Х =
1, Y = —,
найти его проекцию на ось, которая
составляет с осьюОх
угол
= —
.
60. Даны
две точки M1(1;
—5) и M
2(4; —1). Найти проекцию
отрезка M1M2
на ось, которая
составляет с осью Ох
угол
= —
.
61. Даны две точки Р(—5;
2) и Q(3; 1). Найти проекцию отрезка PQ
на ось, которая
составляет с осью Ох
угол
= arctg
.
62. Даны две точки М1(2;
—2) и М2(7;
—3). Найти проекцию
отрезка М1М2
на ось, проходящую
через точки А (5;
— 4), В(—
7; 1) и направленную: 1) от
А к
В,
2) от В
к А.
63. Даны точки А
(0; 0), В(3;
—4), С(—3;
4), D(—
2; 2) и E(10;
—3). Определить расстояние d
между точками: 1) А
и В;
2) В
и С; 3)
А и
С;
4) С и D; 5)
А и
D; 6)
D и
Е.
64. Даны две смежные вершины
квадрата А(3;
—7) и В(—1;4).
Вычислить его площадь.
65. Даны две противоположные
вершины квадрата Р(3;
5) и Q(l; —3). Вычислить
его площадь.
66. Вычислить площадь
правильного треугольника, две вершины
которого суть А(—3;
2) и В(1;
6).
67. Даны три вершины А(3;
—7), В(5;
—7), С(—2;
5) параллелограмма ABCD,
четвёртая вершина
которого D противоположна
В. Определить длину диагоналей этого
параллелограмма.
68. Сторона ромба равна 5,
две его противоположные вершины суть
точкиР(4; 9)
и Q(—2;
1). Вычислить площадь этого ромба.
69. Сторона ромба равна 5,
две его противоположные вершины суть
точки Р(3; —4) и Q(l; 2). Вычислить длину
высоты этого ромба.
70. Доказать, что точки A(3;
—5), В(—2;
—7) и С(18;
1) лежат на одной прямой.
71. Доказать, что треугольник
с вершинами А1(1;
1), А2(2;
3) и А3(5;
—1) прямоугольный.
72. Доказать, что точки А(2;
2), В(—1;
6), С(—5; 3) и D(—2; —1)
являются вершинами квадрата.
73. Определить, есть ли среди
внутренних углов треугольника с вершинами
M1(1;
1), М2(0;
2) и M
3(2; —1) тупой угол.
74. Доказать, что все внутренние
углы треугольника с вершинами М(—1;
3), N(1;
2) и Р(0;
4) острые.
75. Вершины треугольника
суть точки А (5;
0), В(0; 1)
и С(3; 3). Вычислить его внутренние углы.
76. Вершины треугольника
суть точки А(—
;
1)В(0; 2)
и С(—2;
2). Вычислить его внешний угол при вершинеА.
77. На оси абсцисс найти такую
точку М, расстояние
которой до точки N (2;
—3) равнялось бы 5.
78. На оси ординат найти такую
точку М, расстояние
которой до точки N(—8;
13) равнялось бы 17.
79. Даны две точки М(2;
2) и N(5;
—2); на оси абсцисс
найти такую точку Р,
чтобы угол MPN
был прямым.
80. Через точку А
(4; 2) проведена
окружность, касающаяся обеих координатных
осей. Определить её центр С
и радиус R.
81. Через точку М1(1;
—2) проведена окружность
радиуса 5, касающаяся оси Ох.
Определить центр С
окружности.
82. Определить координаты
точки М2,
симметричной точке М1(1;
2) относительно прямой,
проходящей через точки А(1;
0) и В(-1;
-2).
83. Даны две противоположные
вершины квадрата А
(3; 0) и С(—4;
1). Найти две его другие вершины.
84. Даны две смежные вершины
квадрата А(2;
— 1) и В(— 1;
3). Определить две его другие вершины.
85. Даны вершины треугольника
М1(—3;
6), М
2(9; —10) и М3(—5;
4). Определить центр С
и радиус R
описанного около
этого треугольника круга.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Найти координаты конца отрезка, если известны координаты начала, его длина и угол наклона можно по формулам:
Где:
x, y – координаты конца отрезка,
x0, y0 – координаты начала отрезка,
α – угол наклона в радианах (относительно горизонта),
Z – длина отрезка.
1
Расчёт в JS
Пример расчета координат и построении линии в canvas:
var x0 = 250; // Начальная точка x
var y0 = 400; // Начальная точка y
var z = 400; // Длина отрезка
var deg = -60; // Угол наклона, градусы
var x = Math.round(x0 + Math.cos(deg * Math.PI / 180) * z);
var y = Math.round(y0 + Math.sin(deg * Math.PI / 180) * z);
// Рисование линии
var canvas = document.getElementById('canvas');
var ctx = canvas.getContext('2d');
ctx.beginPath();
ctx.lineWidth = 2;
ctx.strokeStyle = 'red';
ctx.moveTo(x0, y0);
ctx.lineTo(x, y);
ctx.stroke();JS
2
Расчёт в PHP
Пример вывода линии в библиотеки GD:
$x0 = 250; // Начальная точка x
$y0 = 400; // Начальная точка y
$z = 400; // Длина отрезка
$deg = -60; // Угол наклона, градусы
$x = round($x0 + cos(deg2rad($deg)) * $z);
$y = round($y0 + sin(deg2rad($deg)) * $z);
// Рисование линии
$img = imagecreate(800, 800);
$bg = imagecolorallocate($img, 0, 0, 0);
imagesetthickness($img, 2);
imageline($img, $x0, $y0, $x, $y, 0x000000);
imagepng($im);
imagedestroy($im);PHP
3
Онлайн расчет
Координаты на прямой:
Если на прямой задано направление, то такую прямую называют направленной, а выбранное направление—положительным. Например, на горизонтальной прямой можно отметить направление вправо, тогда будем говорить, что направленная прямая имеет положительное направление вправо. Можно с таким же правом считать положительным и направление влево. Направление прямой будем указывать стрелкой (рис. 1).
Выберем на направленной прямой точку, которую назовем началом отсчета или началом координат, и будем обозначать ее буквой О. Кроме того, выберем отрезок, длину которого будем считать единицей длины. Этот отрезок назовем единицей масштаба.
Определение: Прямая линия, на которой указаны: начало отсчета, единица масштаба и направление отсчета, называется осью координат.
Рассмотрим отрезок, расположенный на оси координат. Если одну из точек, ограничивающих отрезок, назовем началом отрезка, а другую—его концом, то отрезок будем называть направленным отрезком. Направленный отрезок обозначают двумя буквами, например: АВ, СМ, КР, причем на первом месте ставят букву, обозначающую начало, на втором— букву, обозначающую конец. Таким образом, запись АВ показывает, что начало отрезка есть точка А, а конец — точка В. Направление отрезка считается от начала к концу.
Если направление отрезка совпадает с направлением оси, то отрезок называют положительно направленным: если же его направление противоположно направлению оси, то—отрицательно направленным. Таким образом, отрезки АВ и ВА имеют противоположные направления. Это записывают так:
Отметим, что положительный отрезок может находиться в любом месте координатной оси, только его направление должно совпадать с направлением оси.
Сложение направленных отрезков производится по следующему правилу: Для того чтобы сложить два направленных отрезка, нужно к концу первого приложить начало второго; тогда отрезок, имеющий началом начало первого отрезка и концом конец второго, называют суммой двух направленных отрезков.
Из этого определения вытекает, что сумма отрезков АВ и ВС равна отрезку АС при любом расположении точек А, В, С, т. е. всегда:
(рис. 2 и 3).
Координатным отрезком точки А называется направленный отрезок, имеющий начало в точке О (т. е. в начале координат), а концом — рассматриваемую точку А.
Всякий направленный отрезок, лежащий на оси, можно выразить через координатные отрезки его начала и конца. В самом деле, рассмотрим направленный отрезок АВ. На основании равенства (2) можно написать
(здесь вместо точки В поставлена точка О, а вместо точки С точка В) или
Отрезок ОВ есть координатный отрезок (его начало есть точка О), но отрезок АО не является координатным, посколькуего начало не является началом координат. Но в силу равенства (1)
поэтому можно написать
Получен следующий результат:
Направленный отрезок равен разности координатного отрезка его конца и координатного отрезка его начала.
Это верно для любого отрезка, лежащего на координатной оси. Теперь дадим одно из самых важных определений:
Координатой точки на координатной оси называется число, равное по абсолютной величине длине координатного отрезка этой точки и по знаку совпадающее со знаком координатного отрезка.
Точку А, имеющую координатной число 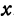
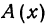
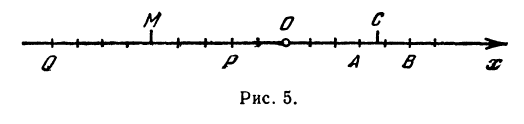
Указанные на рис. 4 точки имеют следующие координаты: 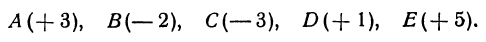
Если даны точки 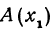
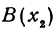
т. е. направленный отрезок равен разности координат его конца и начала. Отсюда сразу получаем, что длина отрезка равна абсолютной величине разности координат его конца и начала.
Длину отрезка будем обозначать, пользуясь знаком | |, т. е. знаком абсолютной величины. Таким образом, длина отрезка АВ будет записываться так:
- Заказать решение задач по высшей математике
Пример:
Если даны точки 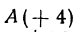
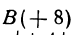
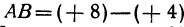
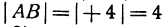
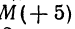
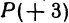
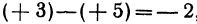
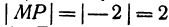
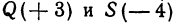
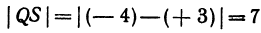
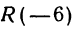
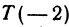
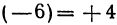
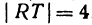
Пример:
Начало отрезка АВ находится в точке 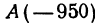
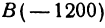
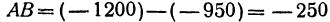
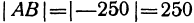
Пример:
На координатной оси даны две точки: 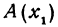
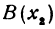
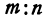
Обозначая координату искомой точки С через 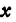
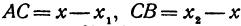
Решая последнее уравнение относительно 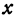
Это и есть координата искомой точки.
Пример:
Найти точку С, делящую отрезок АВ в отношении 1:2, если даны начало отрезка 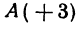
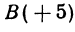
Решение:
Здесь 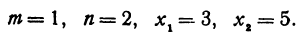
Пример:
Найти точку 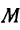
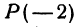
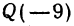
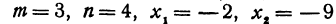
Решение:
Если 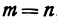
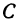
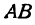
Таким образом, координата точки, делящей отрезок пополам, равна средней арифметической координат его начала и конца.
Пример:
Найдем середину отрезка, заключенного между точками 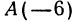
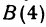
Решение:
Применяя формулу (8), получим, 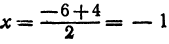
- Координаты на плоскости
- Линейная функция
- Квадратичная функция
- Тригонометрические функции
- Элементы матричного анализа
- Уравнение линии
- Функции нескольких переменных
- Комплексные числ
Как найти конец координат отрезка?
К примеру, есть ёж, который находится в координате (300,500)
Тут ёж начинает двигаться в направление со случайным углом. В данном случае он начал двигаться под углом 163 градуса относительно верхней оси ординат. (игрек)
Мы знаем что ёж прошел расстояние, равное 120. В какую точку он пришел? Нужны сами координаты. Как посчитать, какая формула, помогите как-нибудь, заранее спасибо!
-
Вопрос заданболее трёх лет назад
-
533 просмотра
len = 120;
f = degreesToRadian(163);
x0 = 300;
y0 = 500;
x = x0 + cos(f) * len;
y =y0 + sin(f) * len;
Пригласить эксперта
h=120*sin(163) – это высота
w = sqrt(h** + 120**) – длина
(300+w, 500+h) – новые координаты!
Геометрия 6-й класс, прямоугольный треугольник (ссылка просто так не вставлялась) –
https://www.fxyz.ru/формулы_по_геометрии/плоские_фигуры/треугольник/решение_прямоугольного_треугольника/-
Показать ещё
Загружается…
18 мая 2023, в 17:43
3000 руб./за проект
18 мая 2023, в 17:40
2000 руб./за проект
18 мая 2023, в 17:26
1500 руб./за проект