Содержание:
- Критические точки и экстремумы функции
- Теорема Ферма (Необходимое условие существовании экстремумов)
- Достаточное условие существования экстремума
- Задача пример №117
- Задача пример №118
- Задача пример №119
- Задача пример №120
- Задача пример №121
Критические точки и экстремумы функции
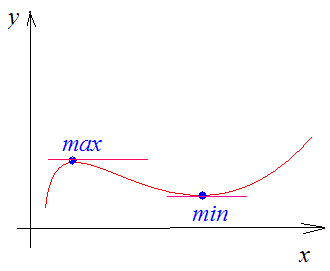
В некоторых точках из области определения производная функции может быть равна нулю или вообще может не существовать. Такие точки из области определения называются критическими точками функции. Покажем критические точки на графике заданной функции.
1. Для значений 


2. В точках 
3. Для рассматриваемой нами функции критические точки 

По графику видно, что в точках внутреннего экстремума 

Теорема Ферма (Необходимое условие существовании экстремумов)
Во внутренних точках экстремума производная либо равна нулю, либо не существует.
Примечание. Точка, в которой производная равна нулю, может и не быть точкой экстремума. Например, в точке 

На отрезке непрерывности функция может иметь несколько критических точек, точек максимума и минимума. Существование экстремума в точке зависит от значения функции в данной точке и в точках, близких к данной, т.е. имеет смысл локального (местного) значения. Поэтому иногда используют термин локальный максимум и локальный минимум.

Достаточное условие существования экстремума
Пусть функция 



1 ) 


2) 


3) 


Чтобы найти наибольшее (абсолютный максимум) или наименьшее (абсолютный минимум) значение функции, имеющей конечное число критических точек на отрезке, надо найти значение функции во всех критических точках и на концах отрезка, а затем из полученных значений выбрать наибольшее или наименьшее.
Соответствующие наибольшее и наименьшее значения функции 



Ниже представлены примеры определения максимума и минимума в соответствии со знаком производной первого порядка.
Задача пример №117
Для функции 
Решение:
Для решения задания сначала надо найти критические точки. Для данной функции этими точками являются точки (стационарные), в которых производная равна нулю.
1. Производная функции:
2. Критические точки функции:
3. Точки 

Проверим знак 



Интервал 
Знак 

При 

При 

4. Используя полученные для функции 

Задача пример №118
Найдите наибольшее и наименьшее значение функции 
Решение:
Сначала найдем критические точки. Так как 



Из этих значений наименьшее – 4, наибольшее 12. Таким образом:
Задача пример №119
Найдите экстремумы функции 
Решение:
1. Производная функции:
2. Критические точки: 
3. Интервалы, на которые критические точки делят область определения функции:
Проверим знак 
Для промежутка 
Для промежутка (0; 1,5) возьмем
Для промежутка 
Интервал
Пробные точки
Знак 

Используя полученную для функции 



• Функция 

• Точка 

• Функция 
• Функция 

•
Задача пример №120
Найдите экстремумы функции
Решение:
1. Производная
2. Критические точки: для этого надо решить уравнение 



3. Промежутки, на которые критическая точка делит область определения функции: 
Определим знак 
Для 


Интервал 
Знак 
Возрастание-убывание
• Функция 

• Функция 

•
Задача пример №121
По графику функции производной 
Решение:
Производная 







Эта лекция взята из раздела решения задач по математике, там вы найдёте другие лекци по всем темам математики:
Другие темы которые вам помогут понять математику:
|
|
|
|
Лекции:
- Экстремумы функции двух переменных. Производная по направлению
- Доказательство неравенств
- Системы уравнений
- Максимальные и минимальные значения функции
- Действия с корнями
- Отрицательное биномиальное распределение
- Длина дуги кривой
- Вычислить несобственный интеграл
- Градиент функции: пример решения
- Интеграл натурального логарифма
Критические точки – это точки в которых производная функции равна нулю или не существует. Если производная равна 0 то функция в этой точке принимает локальный минимум или максимум. На графике в таких точках функция имеет горизонтальную асимптоту, то есть касательная параллельна оси Ох.
Такие точки называют стационарными. Если видите на графике непрерывной функции «горб» или «яму» помните, что максимум или минимум достигается в критической точке. Рассмотрим для примера следующее задание.
Пример 1. Найти критические точки функции y=2x^3-3x^2+5 .
Решение. Алгоритм нахождения критических точек следующий:
Итак функция имеет две критические точки.
Далее, если нужно провести исследование функции то определяем знак производной слева и справа от критической точки. Если производная при переходе через критическую точку меняет знак с «-» на «+», то функция принимает локальный минимум. Если с «+» на «-» должны локальный максимум.
Второй тип критических точек это нули знаменателя дробных и иррациональных функций
Функции с логарифмами и тригонометрические, которые не определены в этих точках
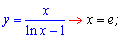
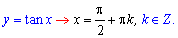
Третий тип критических точек имеют кусочно-непрерывные функции и модули.
Например любая модуль-функция имеет минимум или максимум в точке излома.
Например модуль y = | x -5 | в точке x = 5 имеет минимум (критическую точку).
Производная в ней не существует, а справа и слева принимает значение 1 и -1 соответственно.
Попробуйте определить критические точки функций
1) 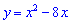
2) 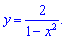
3) 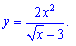
4) 
5)
Если в ответе у Вы получите значение
1) x=4;
2) x=-1;x=1;
3) x=9;
4) x=Pi*k;
5) x=1.
то Вы уже знаете как найти критические точки и сможете справиться с простой контрольной или тестами.
| bold{mathrm{Basic}} | bold{alphabetagamma} | bold{mathrm{ABGamma}} | bold{sincos} | bold{gedivrightarrow} | bold{overline{x}spacemathbb{C}forall} | bold{sumspaceintspaceproduct} | bold{begin{pmatrix}square&square\square&squareend{pmatrix}} | bold{H_{2}O} | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Подпишитесь, чтобы подтвердить свой ответ
Подписаться
Войдите, чтобы сохранять заметки
Войти
Номер Строки
Примеры
-
критические:точки:y=frac{x^2+x+1}{x}
-
критические:точки:f(x)=x^3
-
критические:точки:f(x)=ln (x-5)
-
критические:точки:f(x)=frac{1}{x^2}
-
критические:точки:y=frac{x}{x^2-6x+8}
-
критические:точки:f(x)=sqrt{x+3}
-
критические:точки:f(x)=cos(2x+5)
-
критические:точки:f(x)=sin(3x)
- Показать больше
Описание
Пошаговый поиск критических и стационарных точек функций
function-critical-points-calculator
ru
Блог-сообщения, имеющие отношение к Symbolab
Functions
A function basically relates an input to an output, there’s an input, a relationship and an output. For every input…
Read More
Введите Задачу
Сохранить в блокнот!
Войти
Экстремумы функции
Необходимое условие экстремума функции одной переменной
Достаточное условие экстремума функции одной переменной
Если в точке x * выполняется условие:
Пример №1 . Найти наибольшее и наименьшее значения функции: 
Решение.
Критическая точка одна x1 = 2 (f’(x)=0). Эта точка принадлежит отрезку [1;3]. (Точка x=0 не является критической, так как 0∉[1;3]).
Вычисляем значения функции на концах отрезка и в критической точке.
f(1)=9, f(2)= 5 /2, f(3)=3 8 /81
Ответ: fmin= 5 /2 при x=2; fmax=9 при x=1
Пример №2 . С помощью производных высших порядков найти экстремум функции y=x-2sin(x) .
Решение.
Находим производную функции: y’=1-2cos(x) . Найдем критические точки: 1-cos(x)=2, cos(x)=½, x=± π /3+2πk, k∈Z. Находим y’’=2sin(x), вычисляем 

Пример №3 . Исследовать на экстремум фцнкцию в окрестностях точки x=0.
Решение. Здесь необходимо найти экстремумы функции. Если экстремум x=0 , то выяснить его тип (минимум или максимум). Если среди найденных точек нет x = 0, то вычислить значение функции f(x=0).
Следует обратить внимание, что когда производная с каждой стороны от данной точки не меняет своего знака, не исчерпываются возможные ситуации даже для дифференцируемых функций: может случиться, что для сколь угодно малой окрестности по одну из сторон от точки x0 или по обе стороны производная меняет знак. В этих точках приходится применять другие методы для исследования функций на экстремум.
Пример №4 . Разбить число 49 на два слагаемых, произведение которых будет наибольшим.
Решение. Обозначим x – первое слагаемое. Тогда (49-x) – второе слагаемое.
Произведение будет максимальным: x·(49-x) → max
или
49x – x 2
Как найти критические точки функции по уравнению
Учасники групи мають 10% знижку при замовленні робіт, і ще багато бонусів!
Контакты
Администратор, решение задач
Роман
Tel. +380685083397
[email protected]
skype, facebook:
roman.yukhym
Решение задач
Андрей
facebook:
dniprovets25
Построение графиков функций
О чем эта статья:
11 класс, ЕГЭ/ОГЭ
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Понятие функции
Функция — это зависимость y от x, где x является переменной или аргументом функции, а y — зависимой переменной или значением функции.
Задать функцию значит определить правило, в соответствии с которым по значениям независимой переменной можно найти соответствующие ее значения. Вот, какими способами ее можно задать:
- Табличный способ — помогает быстро определить конкретные значения без дополнительных измерений или вычислений.
- Графический способ — наглядно.
- Аналитический способ — через формулы. Компактно, и можно посчитать функцию при произвольном значении аргумента из области определения.
- Словесный способ.
Область определения — множество х, то есть область допустимых значений выражения, которое записано в формуле.
Например, для функции вида область определения выглядит так
- х ≠ 0, потому что на ноль делить нельзя. Записать можно так: D (y): х ≠ 0.
Область значений — множество у, то есть это значения, которые может принимать функция.
Например, естественная область значений функции y = x² — это все числа больше либо равные нулю. Можно записать вот так: Е (у): у ≥ 0.
Понятие графика функции
Графиком функции y = f(x) называется множество точек (x; y), координаты которых связаны соотношением y = f(x). Само равенство y = f(x) называется уравнением данного графика.
График функции — это множество точек (x; y), где x — это аргумент, а y — значение функции, которое соответствует данному аргументу.
Проще говоря, график функции показывает множество всех точек, координаты которых можно найти, просто подставив в функцию любые числа вместо x.
Для примера возьмём самую простую функцию, в которой аргумент равен значению функции, то есть y = x.
В этом случае нам не придётся вычислять для каждого аргумента значение функции, так как они равны, поэтому у всех точек нашего графика абсцисса будет равна ординате.
Отметим любые три точки на координатной плоскости, например: L (-2; -2), M (0; 0) и N (1; 1).
Если мы последовательно от наименьшего значения аргумента к большему соединим отмеченные точки, то у нас получится прямая линия. Значит графиком функции y = x является прямая. На графике это выглядит так:
Надпись на чертеже y = x — это уравнение графика. Ставить надпись с уравнением на чертеже удобно, чтобы не запутаться в решении задач.
Важно отметить, что прямая линия бесконечна в обе стороны. Хоть мы и называем часть прямой графиком функции, на самом деле на чертеже изображена только малая часть графика.
Исследование функции
Важные точки графика функции y = f(x):
- стационарные и критические точки;
- точки экстремума;
- нули функции;
- точки разрыва функции.
Стационарные точки — точки, в которых производная функции f(x) равна нулю.
Критические точки — точки, в которых производная функции f(x) равна нулю либо не существует. Стационарные точки являются подмножеством множества критических точек.
Экстремум в математике — максимальное или минимальное значение функции на заданном множестве. Точка, в которой достигается экстремум, называется точкой экстремума. Соответственно, если достигается минимум — точка экстремума называется точкой минимума, а если максимум — точкой максимума.
Нули функции — это значения аргумента, при которых функция равна нулю.
Асимптота — прямая, которая обладает таким свойством, что расстояние от точки графика функции до этой прямой стремится к нулю при неограниченном удалении точки графика от начала координат. По способам их отыскания выделяют три вида асимптот: вертикальные, горизонтальные, наклонные.
Функция непрерывна в точке k, если предел функции в данной точке равен значению функции в этой точке:
Если функция f(x) не является непрерывной в точке x = a, то говорят, что f(x) имеет разрыв в этой точке.
Если нам нужно построить график незнакомой функции, когда заранее невозможно представить вид графика, полезно применять схему исследования свойств функции. Она поможет составить представление о графике и приступить к построению по точкам.
Схема построения графика функции:
- Найти область определения функции.
- Найти область допустимых значений функции.
- Проверить не является ли функция четной или нечетной.
- Проверить не является ли функция периодической.
- Найти нули функции.
- Найти промежутки знакопостоянства функции, то есть промежутки, на которых она строго положительна или строго отрицательна.
- Найти асимптоты графика функции.
- Найти производную функции.
- Найти критические точки в промежутках возрастания и убывания функции.
- На основании проведенного исследования построить график функции.
У нас есть отличные курсы по математике для учеников с 1 по 11 классы!
Построение графика функции
Чтобы понять, как строить графики функций, потренируемся на примерах.
Задача 1. Построим график функции
Упростим формулу функции:
при х ≠ -1.
График функции — прямая y = x – 1 с выколотой точкой M (-1; -2).
Задача 2. Построим график функции
Выделим в формуле функции целую часть:
График функции — гипербола, сдвинутая на 3 вправо по x и на 2 вверх по y и растянутая в 10 раз по сравнению с графиком функции
Выделение целой части — полезный прием, который применяется в решении неравенств, построении графиков и оценке целых величин.
Задача 3. По виду графика определить знаки коэффициентов общего вида функции y = ax2 + bx + c.
Вспомним, как параметры a, b и c определяют положение параболы.
Ветви вниз, следовательно, a 0.
Точка пересечения с осью Oy — c = 0.
Координата вершины , т.к. неизвестное число при делении на положительное дает отрицательный результат, то это число отрицательное, следовательно, b > 0.
Ветви вниз, следовательно, a 0.
Координата вершины , т.к. неизвестное число при делении на отрицательное дает в результате положительное, то это число отрицательное, следовательно, b
Как видим, k = 3 > 0 и угол наклона к оси Ox острый, b = -1 — смещение по оси Oy.
k = -1 > 0 и b = 2 можно сделать аналогичные выводы, как и в первом пункте.
k = 2 > 0 — угол наклона к оси Ox острый, B = 0 — график проходит через начало координат.
k = 0 — константная функция, прямая проходит через точку b = -1 и параллельно оси Ox.
Задача 5. Построить график функции
Это дробно-рациональная функция. Область определения функции D(y): x ≠ 4; x ≠ 0.
Нули функции: 3, 2, 6.
Промежутки знакопостоянства функции определим с помощью метода интервалов.
Вертикальные асимптоты: x = 0, x = 4.
Если x стремится к бесконечности, то у стремится к 1. Значит, y = 1 — горизонтальная асимптота.
Вот так выглядит график:
Задача 6. Построить графики функций:
б)
г)
д)
Когда сложная функция получена из простейшей через несколько преобразований, то преобразования графиков можно выполнить в порядке арифметических действий с аргументом.
а)
Преобразование в одно действие типа f(x) + a.
Сдвигаем график вверх на 1:
б)
Преобразование в одно действие типа f(x – a).
Сдвигаем график вправо на 1:
В этом примере два преобразования, выполним их в порядке действий: сначала действия в скобках f(x – a), затем сложение f(x) + a.
Сдвигаем график вправо на 1:
Сдвигаем график вверх на 2:
г)
Преобразование в одно действие типа
Растягиваем график в 2 раза от оси ординат вдоль оси абсцисс:
д)
Мы видим три преобразования вида f(ax), f (x + a), -f(x).
Чтобы выполнить преобразования, посмотрим на порядок действий: сначала умножаем, затем складываем, а уже потом меняем знак. Чтобы применить умножение ко всему аргументу модуля в целом, вынесем двойку за скобки в модуле.
Сжимаем график в два раза вдоль оси абсцисс:
Сдвигаем график влево на 1/2 вдоль оси абсцисс:
Отражаем график симметрично относительно оси абсцисс:
[spoiler title=”источники:”]
http://yukhym.com/ru/issledovanie-funktsii/kriticheskie-tochki-na-grafike-funktsii.html
http://skysmart.ru/articles/mathematic/postroenie-grafikov-funkcij
[/spoiler]
Что такое экстремум функции и каково необходимое условие экстремума?
Экстремумом функции называется максимум и минимум функции.
Необходимое условие максимума и минимума (экстремума) функции следующее: если функция f(x) имеет экстремум в точке х = а, то в этой точке производная либо равна нулю, либо бесконечна, либо не существует.
Это условие необходимое, но не достаточное. Производная в точке х = а может обращаться в нуль, в бесконечность или не существовать без того, чтобы функция имела экстремум в этой точке.
Каково достаточное условие экстремума функции (максимума или минимума)?
Первое условие:
Если в достаточной близости от точки х = а производная f?(x) положительна слева от а и отрицательна справа от а, то в самой точке х = а функция f(x) имеет максимум при условии, что функция f(x) здесь непрерывна.
Если в достаточной близости от точки х = а производная f?(x) отрицательна слева от а и положительна справа от а, то в самой точке х = а функция f(x) имеет минимум при условии, что функция f(x) здесь непрерывна.
Вместо этого можно воспользоваться вторым достаточным условием экстремума функции:
Пусть в точке х = а первая производная f?(x) обращается в нуль; если при этом вторая производная f??(а) отрицательна, то функция f(x) имеет в точке x = a максимум, если положительна – то минимум.
О случае f??(а) = 0 можно прочитать в Справочнике по высшей математике М.Я. Выгодского.
Что такое критическая точка функции и как её найти?
Это значение аргумента функции, при котором функция имеет экстремум (т.е. максимум или минимум). Чтобы его найти, нужно найти производную функции f?(x) и, приравняв её к нулю, решить уравнение f?(x) = 0. Корни этого уравнения, а также те точки, в которых не существует производная данной функции, являются критическими точками, т. е. значениями аргумента, при которых может быть экстремум. Их можно легко определить, взглянув на график производной: нас интересуют те значения аргумента, при которых график функции пересекает ось абсцисс (ось Ох) и те, при которых график терпит разрывы.
Для примера найдём экстремум параболы.
Функция y(x) = 3x2 + 2x – 50.
Производная функции: y?(x) = 6x + 2
Решаем уравнение: y?(x) = 0
6х + 2 = 0, 6х = -2, х=-2/6 = -1/3
В данном случае критическая точка – это х0=-1/3. Именно при этом значении аргумента функция имеет экстремум. Чтобы его найти, подставляем в выражение для функции вместо «х» найдённое число:
y0 = 3*(-1/3)2 + 2*(-1/3) – 50 = 3*1/9 – 2/3 – 50 = 1/3 – 2/3 – 50 = -1/3 – 50 = -50,333.
Как определить максимум и минимум функции, т.е. её наибольшее и наименьшее значения?
Если знак производной при переходе через критическую точку х0 меняется с «плюса» на «минус», то х0 есть точка максимума; если же знак производной меняется с минуса на плюс, то х0 есть точка минимума; если знак не меняется, то в точке х0 ни максимума, ни минимума нет.
Для рассмотренного примера:
Берём произвольное значение аргумента слева от критической точки: х = -1
При х = -1 значение производной будет у?(-1) = 6*(-1) + 2 = -6 + 2 = -4 (т.е. знак – «минус»).
Теперь берём произвольное значение аргумента справа от критической точки: х = 1
При х = 1 значение производной будет у(1) = 6*1 + 2 = 6 + 2 = 8 (т.е. знак – «плюс»).
Как видим, производная при переходе через критическую точку поменяла знак с минуса на плюс. Значит, при критическом значении х0 мы имеем точку минимума.
Наибольшее и наименьшее значение функции на интервале (на отрезке) находят по такой же процедуре, только с учетом того, что, возможно, не все критические точки будут лежать внутри указанного интервала. Те критические точки, которые находятся за пределом интервала, нужно исключить из рассмотрения. Если внутри интервала находится только одна критическая точка – в ней будет либо максимум, либо минимум. В этом случае для определения наибольшего и наименьшего значений функции учитываем также значения функции на концах интервала.
Например, найдём наибольшее и наименьшее значения функции
y(x) = 3sin(x) — 0,5х
на интервалах:
а) [-9; 9]
б) [-6; -3]
Итак, производная функции —
y?(x) = 3cos(x) — 0,5
Решаем уравнение 3cos(x) — 0,5 = 0
3cos(x) = 0,5
cos(x) = 0,5/3 = 0,16667
х = ±arccos(0,16667) + 2πk.
Находим критические точки на интервале [-9; 9]:
х = arccos(0,16667) — 2π*2 = -11,163 (не входит в интервал)
х = –arccos(0,16667) — 2π*1 = -7,687
х = arccos(0,16667) — 2π*1 = -4,88
х = –arccos(0,16667) + 2π*0 = -1,403
х = arccos(0,16667) + 2π*0 = 1,403
х = –arccos(0,16667) + 2π*1 = 4,88
х = arccos(0,16667) + 2π*1 = 7,687
х = –arccos(0,16667) + 2π*2 = 11,163 (не входит в интервал)
Находим значения функции при критических значениях аргумента:
y(-7,687) = 3cos(-7,687) — 0,5 = 0,885
y(-4,88) = 3cos(-4,88) — 0,5 = 5,398
y(-1,403) = 3cos(-1,403) — 0,5 = -2,256
y(1,403) = 3cos(1,403) — 0,5 = 2,256
y(4,88) = 3cos(4,88) — 0,5 = -5,398
y(7,687) = 3cos(7,687) — 0,5 = -0,885
Видно, что на интервале [-9; 9] наибольшее значение функция имеет при x = -4,88:
x = -4,88, у = 5,398,
а наименьшее – при х = 4,88:
x = 4,88, у = -5,398.
На интервале [-6; -3] мы имеем только одну критическую точку: х = -4,88. Значение функции при х = -4,88 равно у = 5,398.
Находим значение функции на концах интервала:
y(-6) = 3cos(-6) — 0,5 = 3,838
y(-3) = 3cos(-3) — 0,5 = 1,077
На интервале [-6; -3] имеем наибольшее значение функции
у = 5,398 при x = -4,88
наименьшее значение —
у = 1,077 при x = -3
Как найти точки перегиба графика функции и определить стороны выпуклости и вогнутости?
Чтобы найти все точки перегиба линии y = f(x), надо найти вторую производную, приравнять её к нулю (решить уравнение) и испытать все те значения х, для которых вторая производная равна нулю, бесконечна или не существует. Если при переходе через одно из этих значений вторая производная меняет знак, то график функции имеет в этой точке перегиб. Если же не меняет, то перегиба нет.
Корни уравнения f ? (x) = 0, а также возможные точки разрыва функции и второй производной разбивают область определения функции на ряд интервалов. Выпуклость на каждом их интервалов определяется знаком второй производной. Если вторая производная в точке на исследуемом интервале положительна, то линия y = f(x) обращена здесь вогнутостью кверху, а если отрицательна – то книзу.
Как найти экстремумы функции двух переменных?
Чтобы найти экстремумы функции f(x,y), дифференцируемой в области её задания, нужно:
1) найти критические точки, а для этого — решить систему уравнений
fх? (x,y) = 0, fу? (x,y) = 0
2) для каждой критической точки Р0(a;b) исследовать, остается ли неизменным знак разности
f(x,y) – f(a,b)
для всех точек (х;у), достаточно близких к Р0. Если разность сохраняет положительный знак, то в точке Р0 имеем минимум, если отрицательный – то максимум. Если разность не сохраняет знака, то в точке Р0 экстремума нет.
Аналогично определяют экстремумы функции при большем числе аргументов.
Источники:
- Выгодский М.Я. Справочник по высшей математике
- Черненко В.Д. Высшая математика в примерах и задачах. В 3-х томах. Том 1.