Содержание
- Как найти координаты луны
- Что такое координаты луны?
- Как найти экваториальные координаты луны?
- Как найти горизонтальные координаты луны?
- Заключение
- Как найти координаты луны: полезные советы для лунных и любознательных путешественников
- Что такое координаты луны?
- Как найти координаты луны
- Как использовать координаты луны
- Общий итог
- Как найти координаты луны
- Что такое координаты луны
- Как найти координаты луны
- Как использовать координаты луны
- Итог
Как найти координаты луны

Луна – это небесное тело, которое всегда было объектом внимания для астрономов и любителей космоса. Несмотря на то, что луна находится ближе к Земле, чем любая другая планета или звезда, найти ее координаты может быть сложной задачей для тех, кто не имеет достаточно знаний и опыта в этой области. В этой статье мы расскажем, как найти координаты луны без проблем.
Что такое координаты луны?
Координаты луны – это два числовых значения, которые показывают точное местонахождение луны на небесной сфере. Важно понимать, что координаты луны меняются в зависимости от времени и местоположения наблюдателя. Наиболее часто используются две системы координат: экваториальные и горизонтальные.
Как найти экваториальные координаты луны?
Экваториальные координаты луны определяются относительно экватора Земли и точки весеннего равноденствия. Для их нахождения необходимо знать точное время и место наблюдения, а также скорректировать его с учетом местного времени и времени универсального координированного времени (UTC).
Один из лучших способов для нахождения экваториальных координат луны – это использование астрономического программного обеспечения. Такие программы могут определить экваториальные координаты луны, а также предоставить информацию о ее фазе, размере и текущем состоянии. Некоторые из самых популярных программ, которые могут помочь вам найти экваториальные координаты луны – это «Stellarium», «Cartes du Ciel», «SkySafari» и «Celestia».
Как найти горизонтальные координаты луны?
Горизонтальные координаты луны определяются относительно места наблюдения и могут быть найдены с помощью компаса и небесной карты. Для нахождения горизонтальных координат луны вам необходимо сначала узнать грубые координаты луны (например, с помощью астрономической программы), а затем откорректировать их в зависимости от местоположения наблюдателя.
Для начала необходимо найти север и юг, используя компас. Затем нужно определить азимут, на который смотрит наблюдатель, и отметить его на небесной карте. Если вас интересует лунный диск, вы можете использовать лунный калькулятор для того, чтобы вычислить его положение на небосводе. Следующим шагом будет нахождение угла высоты луны. Для этого нужно знать высоту наблюдателя над уровнем моря и откорректировать угол высоты луны соответственно.
Заключение

Как вы можете видеть, найти координаты луны может оказаться сложным. Но с помощью современных инструментов, таких как астрономические программы и лунный калькулятор, это может быть значительно облегчено. Важно помнить, что для того, чтобы найти точные координаты луны, необходимо учитывать время и место наблюдения, а также проводить все необходимые корректировки.
Как найти координаты луны: полезные советы для лунных и любознательных путешественников

Луна — это одно из самых близких к Земле небесных тел, которое привлекает внимание своей красотой и мистической притягательной силой. Но несмотря на некоторые общеизвестные факты о Луне, многие люди не знают, как найти ее координаты и отслеживать ее движение. В этой статье мы расскажем о том, как найти координаты луны и как использовать эту информацию для изучения нашего соседнего космического объекта.
Что такое координаты луны?
Координаты Луны — это ее местоположение на небесной сфере в определенный момент времени. Эти координаты задаются двумя углами: прямым восхождением (RA) и склонением (Dec). Прямое восхождение — это угол между линией места и звездой на экваторе, который проходит через небесный полюс. Склонение — это угол между звездой и плоскостью экватора. Когда мы знаем прямое восхождение и склонение Луны, мы можем точно определить ее местоположение на небесной сфере.
Как найти координаты луны
Для того, чтобы найти координаты Луны, необходимо выполнить несколько простых шагов.
- Установите время: Прежде всего, нужно установить точное время, в котором вы хотите найти координаты луны. Это может быть любое время в прошлом, настоящем или будущем.
- Определите местоположение: Чтобы найти координаты Луны, необходимо знать свое местоположение на земле. Для этого можно использовать приложение или карту, которая поможет определить широту и долготу.
- Выберите метод: Существует много различных методов для определения координат Луны. Вы можете использовать компьютерную программу, такую как Stellarium, или инструменты, такие как астрологические таблицы, чтобы вычислить координаты Луны для выбранного времени.
- Вычислите координаты: Запустите программу или используйте астрологические таблицы для вычисления координат Луны для выбранного времени. Запишите значения RA и Dec.
Как использовать координаты луны

Координаты Луны могут быть использованы для различных целей, таких как изучение Луны, путешествия к ней или просто увлечение астрономией.
- Изучение Луны: Координаты Луны могут помочь вам найти определенные небесные объекты, такие как кратеры, долины или ратравы, на ее поверхности. Используйте эти координаты, чтобы заснять Луну через телескоп или наблюдать ее через бинокль.
- Планирование путешествия к Луне: Если вы планируете путешествие на Луну, вы можете использовать координаты, чтобы определить место, где вы находитесь на Луне и каково ваше местоположение относительно других космических объектов.
- Увлечение астрономией: Если вы интересуетесь астрономией и любите наблюдать за звездами, планетами и космосом в целом, координаты Луны могут помочь вам найти ее на небосводе и следить за ее движением относительно других объектов.
Общий итог
Теперь вы знаете, как найти координаты Луны и как использовать эту информацию для изучения нашего соседнего космического объекта. Используйте эту информацию, чтобы наблюдать за Луной, путешествовать к ней или просто удовлетворить свое любопытство с помощью астрономии.
«Луна — мир внутри мира, вечное очарование, бессмертный величайший объект созерцания.» — Сенека
Как найти координаты луны
Наблюдение за луной всегда было одним из самых интересных занятий для любителей астрономии. Но чтобы наблюдать за луной, нужно знать ее координаты. В этой статье мы расскажем, как найти координаты луны.
Что такое координаты луны

Координаты луны — это ее положение на небесной сфере. Координаты луны задаются двумя углами: прямым восхождением (RA) и склонением (Dec). Прямое восхождение — это астрономическая координата, которая показывает, на какой долготе луна находится на небесной сфере в данный момент времени. Склонение — это координата, показывающая, на какой широте луна находится в данный момент времени.
Как найти координаты луны
Существует несколько способов, как найти координаты луны. Рассмотрим наиболее распространенные из них:
- С помощью астрономических таблиц. Астрономические таблицы содержат информацию о положении луны на небесной сфере в различные моменты времени. Наиболее популярными астрономическими таблицами являются астрономический календарь и таблицы эфемерид. Используя данные таблицы, вы можете найти координаты луны в нужный вам момент времени.
- С помощью астрономических программ. Существует множество астрономических программ, которые могут помочь вам найти координаты луны. Некоторые из них, такие как Stellarium и Sky Chart, являются бесплатными и доступны для загрузки в Интернете. Вы можете использовать эти программы для наблюдения за луной и определения ее координат в режиме реального времени.
- С помощью телескопа. Если у вас есть телескоп, вы можете использовать его для наблюдения за луной и определения ее координат. Смотрите в прибор и записывайте координаты луны в момент наблюдения.
Как использовать координаты луны
Когда вы найдете координаты луны, вы можете использовать их для запланирования наблюдения за луной или для прогнозирования ее положения на небесной сфере в будущем. Вы также можете использовать информацию о координатах луны для более точного определения ее расстояния от Земли.
Координаты луны могут быть полезны не только для астрономов-любителей, но и для профессиональных астрономов и космонавтов, которые могут использовать эти данные для планирования космических миссий и исследований.
Итог

Координаты луны — это важный параметр, который позволяет наблюдать за луной и планировать космические миссии. Найти координаты луны можно с помощью астрономических таблиц, программ и телескопов. Помните, что за любым наблюдением за небесными телами нужно следить правилами безопасности и использовать только профессиональные инструменты.
- Печать
Страницы: [1] Вниз
A A A A

Тема: Как посчитать координаты Луны? (Прочитано 768 раз)
0 Пользователей и 1 Гость просматривают эту тему.
Казалось бы – совершенно разжеванная тема, однако, беру я libnova и пытаюсь с ее помощью определить, где же находится Луна.
Она выдает мне экваториальные координаты, совершенно отличающиеся от координат, которые я вижу в стеллариуме и разнообразных веб-сервисах с эфемеридами (ошибка больше, чем полградуса!).
Ковыряться в недрах стеллариума никакого желания нет: уж очень там много исходников.
Собственно вопрос: какую же взять библиотеку (в SOFA частично вычисляются координаты Луны, но функции, чтобы получить ее геоцентрические экваториальные координаты, нет), чтобы с точностью хотя бы в 5..10” определить расстояние от избранного объекта на небе до Луны?
Язык – C, система – Gentoo Linux.

Записан

Записан
モ – mo
(ошибка больше, чем полградуса!).
А реальные координаты наблюдателя по времени – точно учитываются?
Геоцентрических координат недостаточно, мы же крутимся по поверхности Земли а не просто смотрим на Луну из центра.

Записан
• С14 HD [0.96] + HS F/1.9 @ CGE Pro
• С8 HD [0.93] + HS F/2.1 @ NexStarSE
• TS 152/900 @ MiniTowerII
Sun Hα Moon ⭐AstroSeeing Bot
Ну так горизонтальный параллакс Луны этот самый градус и даёт!

Записан
У природы нет плохой погоды, у неё просто на нас аллергия.
Учение без размышления бесполезно, но и размышление без учения опасно /Конфуций/
Слово есть поступок. /Л. Толстой/
А реальные координаты наблюдателя по времени – точно учитываются?
Да, координаты не хуже секунды, время – доли миллисекунд.
Ну так горизонтальный параллакс Луны этот самый градус и даёт!
Ну и как тогда считать и кому верить?
Ведь в стеллариуме-то как-то рассчитывают это все с хорошей точностью…

Записан
Информация из StarCalc
»Луна08.10.2020 0:30:57
Экват. координаты (на текущую эпоху):
Геоцентр.: Alp: 5ч 19м 38.1с Del: +22° 58' 43"
Топоцентр.: Alp: 5ч 21м 39.5с Del: +22° 19' 2"
r=395839 км; Угловой размер: 30.19'
Возраст: 20.2 дней.; Фаза: 0.71
Восход: 21ч 1м
Кульминация: 5ч 32м
Заход: 14ч 50м
58.00N, 27.55E
GMT+3

Записан
У природы нет плохой погоды, у неё просто на нас аллергия.
Учение без размышления бесполезно, но и размышление без учения опасно /Конфуций/
Слово есть поступок. /Л. Толстой/
Вот, что сейчас пишет libnova:
./lunarСтеллариум пишет: 5:47:02, +23:06:44
JD 2459130.970771
lunar x 17833.446078 y 396102.605968 z 3351.711822
lunar long 87.422154 lat 0.484319
lunar RA 5:48.721563 Dec 23:53.741074
lunar az: 143.952048, lunar z: -13.684787
lunar distance km 396523.279634
lunar disk 0.655078
lunar phase 71.931376
lunar bright limb 88.724931
Даже для наших будущих роботов с поляной в полтора градуса это – критично! Эдак можно и Луну цепануть…

Записан
Судя по том, что libnova не учитывает положение на Земле, она выдают геоцентрику.
Сделайте 3° от Луны и не ходите на те площадки…

Записан
У природы нет плохой погоды, у неё просто на нас аллергия.
Учение без размышления бесполезно, но и размышление без учения опасно /Конфуций/
Слово есть поступок. /Л. Толстой/
Сделайте 3° от Луны и не ходите на те площадки…
Хотелось бы, все-таки, иметь более точные данные…
Народ же считает каким-то образом покрытия Луной всяких звезд и планет? Неужто они для этого сторонние сервисы используют?
Да и в том же стеллариуме нормально все считается.
Задача – совершенно избитая. И явно должно быть ее вменяемое решение, а не примерный алгоритм 1967 года…

Записан
http://thaec.rascanu.de/ пример программы на C++. Использует библиотеки calceph и iau sofa. Можно использоваать разные эфемериды: epm, inpop, jpl. Обеспечивает максимальную точность.
./thaecC
Searching for IERS files...
deltat.preds found (0.008808 days old)
UP: 0 of 0 DOWN: 0 of 0
UP: 0 of 0 DOWN: 0 of 0
tai-utc.dat found (0.008576 days old)
UP: 0 of 0 DOWN: 0 of 0
UP: 0 of 0 DOWN: 0 of 0
finals2000A.data found (4.560266 days old)
finals2000A.daily found (0.610162 days old)
eopc04_IAU2000.62-now found (4.706539 days old)
TTBIPM.act found (0.007905 days old)
Searching for Ephemeris files...
inpop13c_TDB_m100_p100_tt.dat found (0.008322 days old)
local: 13.10.2020 10:59:33
UT1: 13.10.2020 07:59:33
TT(=TDT): 13.10.2020 08:00:45.034539 (TT-UT1: 72.034539s)
TT(BIPMxx): 13.10.2020 08:00:45.034567 (TT-UT1: 72.034567s)
TCG: 13.10.2020 08:00:45.997480
TDB: 13.10.2020 08:00:45.032892 (TDB-TT: -1.674827ms)
TCB: 13.10.2020 08:01:06.455733
JD (TT): 2459135.833855
MJD (UTC): 59135.333021
ERA: 09h 27m 51.940927s
CIP @ GCRS: X=409.367088" Y=0.715809" dX=0.000000" dY=0.000000"
CIO @ GCRS: s=-3.086146mas
CIP @ ITRS: x=0.000000" y=0.000000"
TIO @ ITRS: s'=-0.009768mas
Geocenter BCRS: x=+0.9304498 y=+0.3213587 z=+0.1393991
Observer BCRS: x=+0.9304260 y=+0.3213721 z=+0.1394317
Sun: (8.297237 light-minutes)
BCRS: RA: 09.070365 dec: +17.341363, x=-0.0060884 y=+0.0058682 z=+0.0026405
CIRS: RA: 13.241198 dec: -07.986488
obs: RA: 13.239649 dec: -07.946887, Az: 129.10525 Alt: +18.622129
Moon: (1.212628 light-seconds)
BCRS: RA: 01.276646 dec: +08.111339, x=+0.9282903 y=+0.3223512 z=+0.1400525
CIRS: RA: 10.358721 dec: +14.698996
obs: RA: 10.358651 dec: +14.710114, Az: 172.12908 Alt: +54.386306
В исходнике можно пути поменять на ftp://cddis.gsfc.nasa.gov/pub/products/iers/, чтобы скачивались свежие данные. А то по приведённым там ссылкам глухо всё.
« Последнее редактирование: 13 Окт 2020 [11:48:39] от gasha »

Записан
БПЦ 15х50, Nikon Aculon 7×50, Celestron Advanced VX 8″ N, Sky-Watcher BK 909AZ3, ТАЛ-65, Таир-3ФС, Canon EOS 60D, Sony Alpha NEX-3.
@gasha , спасибо!
Буду ковырять, как руки дойдут до этого.

Записан
- Печать
Страницы: [1] Вверх
- Астрофорум – астрономический портал »
- Практическая астрономия »
- Астрономия и компьютеры (Модератор: Ed_Vazhorov) »
- Как посчитать координаты Луны?
Луна сейчас: фаза, освещенность, координаты, знак зодиака, либрация. Расчет онлайн JS
Фаза Луны сейчас,
астрономические характеристики лунных фаз
и положения Луны в пространстве онлайн
Луна переходит из одной фазы в следующую в среднем за семь с небольшим суток, вот, почему в неделе именно семь дней – это наследие первых лунных календарей! Правда, первые составители календарей воспринимали фазовые изменения Луны как данность природы, не вдаваясь в объяснения причин наблюдаемого…
Содержание:
- Фаза Луны сейчас
- Фазовые состояния Луны
- Либрация Луны
- О Луне и фазах Луны в словаре В.Даля
Фаза Луны сейчас – виджет Java Script

5%
17.05.2023 15:00
Убывающая
4 четверть
Овен
Сейчас 15:00, 17 мая 2023 года
Среда
Фаза Луны: Убывающая в последней четверти
Международное название фазы: Waning crescent
Русский народный титул фазы: Старый месяц
(ветхий месяц, ущербный серп, убыль)
Освещенность Луны: 5%
Возраст Луны: 27 дней 7 часов 47 минут
Расстояние до Луны: 378003 км, средняя Луна
Знак зодиака: Луна в знаке Овен, λ: 29°43’
Созвездие: Луна видна в созвездии Рыбы
Ожидаемое новолуние: 19 мая 2023 18:52
Ближайшее полнолуние: 4 июня 2023 06:41
Обновить Часы Мини Виджет Машина времени Стоп
Вы можете открыть виджет «Фаза Луны сейчас» в отдельном окне о виджете*
Календарь лунных фаз на весь 2023 год на странице Фазы Луны и затмения 2023
Небесные координаты Луны сейчас:
Экваториальная система координат
Прямое восхождение Луны α: 1ч 51м
Склонение Луны δ: 11° 00’
Эклиптическая система координат
Эклиптическая долгота λ: 29° 43’
Эклиптическая широта Луны β: -0° 23’
Селенографические параметры Луны в текущий момент:
Либрация Луны по долготе L: 4° 35’
Либрация Луны по широте B: 0° 24’
Доля освещенной поверхности Луны: 5.3%
Показатель фазы Луны (коэффициент фазы): 0,92
Координаты точки над которой Солнце в зените –
подсолнечная точка Луны:
долгота лунной подсолнечной точки: 211° 11’
широта лунной подсолнечной точки: 0° 36’
Долгота точки пересечения линии терминатора и экватора: -59° 48’.
Описание фазовых состояний Луны
Первые древние лунные календари основывались на наблюдениях за перемещением по поверхности Луны границы света и тени, называемой терминатором. При этом выделялись четыре довльно четко фиксирующиеся визуально состояния, называемые точками фазовых переходов Луны – новолуние, начало месяца; первая четверть; полнолуние и последняя четверть, также имеют собственные названия и переходные стадии лунных фаз:
Таблица 1. Фазы Луны. характеристики фазовых состояний от новолуния до новолуния
| Фазовые состояния (стадии) Луны | Вид Луны | Освещенность и конфигурация | Период видимости | Время кульминации | Восход и заход Луны |
|---|---|---|---|---|---|
| Новолуние
Народное::Новая Луна, межлуние; рождение луны; безлунные ночи. Международное: |
 |
0-1% – видимая сторона Луны полностью в тени
Солнце, Луна и Земля выстроились в одну линию |
Из-за близости Солнца, видна только при затмениях | Полдень | Луна восходит и заходит вместе с Солнцем |
| Растущая Луна в первой четверти
Народное: Молодой Месяц, Новик, народившийся Месяц, остророгий Месяц, ранний серп Международное |
 |
Освещена правая сторона лунного диска от 1 до 49%
Лучи: Земля-Луна и Земля-Солнце образуют острый угол |
От познего утра до раннего вечера | Вторая половина дня | Луна восходит вслед за солнцем с нарастающим опозданием |
| Первая четверть
Народное: Половина Луны, молодая Половинка, Краюшка Международное: |
 |
Освещена правая половина лунного диска (от 49 до 51%) Лучи: Земля-Луна и Земля-Солнце образуют прямой угол |
От полудня до полуночи | Ранний вечер | Восход Луны – ровно в полдень, заход Луны – в полночь |
| Растущая Луна вo второй четверти
Народное: Полнеющая Луна, полный месяц, Луна на сносях Международное: |
 |
Растущая с правой стороны освещенная область (от 51 до 99% видимой площади Луны) Лучи: Земля-Луна и Земля-Солнце образуют тупой угол |
Со второй половины дня до поздней ночи | Начало ночи, летом поздний вечер | Луна восходит во второй половине дня, заходит во второй половине ночи |
| Полнолуние
Народное: Полная Луна, круглолицая Луна, круглая Луна Международное: |
 |
Полностью освещенный видимый круг Луны (освещенность между 100 и 99%)
Солнце, Земля и Луна на одной линии |
Видна всю ночь (от захода до восхода Солнца) |
Полночь | Луна восходит во время захода Солнца и заходит с его восходом |
| Убывающая Луна в третьей четверти
Народное: Ущербная Луна, Луна в убытке, пузатый месяц на убыли Международное: Waning gibbous |
 |
С левой стороны Солнце освещает от 99 до 51% видимой площади Луны
Лучи: Земля-Солнце и Земля-Луна образуют тупой угол |
Видна с позднего вечера до раннего утра | Во второй половине ночи | Луна восходит вечером с нарастающим опозданием, заходит утром. |
| Третья четверть
Народное: Последняя четверть, старшая Половинка Международное: Third quarter |
 |
Освещена ровно половина круга Луны с левой стороны (50 ± 1%) Лучи: Земля-Солнце и Земля-Луна образуют прямой угол |
Луну можно наблюдать после полуночи и утром | Раннее утро | Восход Луны – ровно в полночь, заход Луны – в полдень |
| Убывающая Луна в последней четверти
Народное: Старый месяц, ветхий месяц, ущербный серп, убыль Международное: |
 |
Освещена левая сторона лунного диска от 49 до 1%
Лучи: Земля-Солнце и Земля-Луна образуют острый угол |
Луна видна со второй половины ночи до второй половины дня | Утро | Луна восходит во второй половине ночи, заходит во второй половине дня |
Народные названия фаз Луны взяты из словаря Даля**, а так же из обиходной речи севера Нижегородской области.
Эта коллекция пополняемая, полагаю, всем будут интересны сообщения о других народных названиях лунных фаз (форум – зеленый флажок слева).
Либрация Луны
Теоретически, из утверждения, что Луна повернута к Земле одной стороной, следует, что мы, находясь на земле, можем увидеть не более 50% ее поверхности. Благодаря либрации (видимому с Земли покачиванию Луны) мы можем взглянуть на ее полюса, и чуть-чуть подглядеть за тем, что там творится с ее обратной стороны, в целом взгляду становится доступно 60% ее поверхности!

На видеоизображении слева представлены результаты численного моделирования либрационного движения Луны. Смоделировано кажущееся движение Луны, которое может видеть наблюдатель с поверхности Земли (чтобы увеличить изображение, кликните по нему – откроется новое окно [2,5 Мб]).
Как видно из рисунка, это довольно сложное колебательно-вращательное движение определяемое тремя составляющими: наклон лунной оси + орбитальное движение Луны + вращение Земли. Вследствие либрации для земного наблюдателя на лунном диске будет неподвижной только точка зенита земли, точка над которой земля видна в зените (голубой круг в центре лунного диска), а сама поверхность луны находится в непрерывном движении (параметры либрации луны, как раз и примерно соответствуют селенографическим координатам точки зенита Земли). Сиреневый непрерывно движущийся крестик – это “Пуп Луны”, точка пересечения нулевого меридиана и экватора с координатами (0°, 0°). Круиз “крестика” вокруг “кружочка” в реальности длится целый лунный месяц!
Либрация по широте
Благодаря либрации по широте мы имеем возможность по очереди рассматривать, то южный, то северный полюс Луны – при либрационном движении Луна как бы то наклоняется к нам, то “пытается посмотреть выше” (рис. 1). Либрация по широте происходит вследствие наклона оси вращения Луны к плоскости ее орбиты, на который еще накладывается и наклон самой орбиты к плоскости эклиптики. Суммарная максимальная амплитуда A может достигать 6,68° ( A = 5,145°+1,5424°)***, в момент, когда Луна находится в точке перигея орбиты при минимальном расстоянии до Земли.
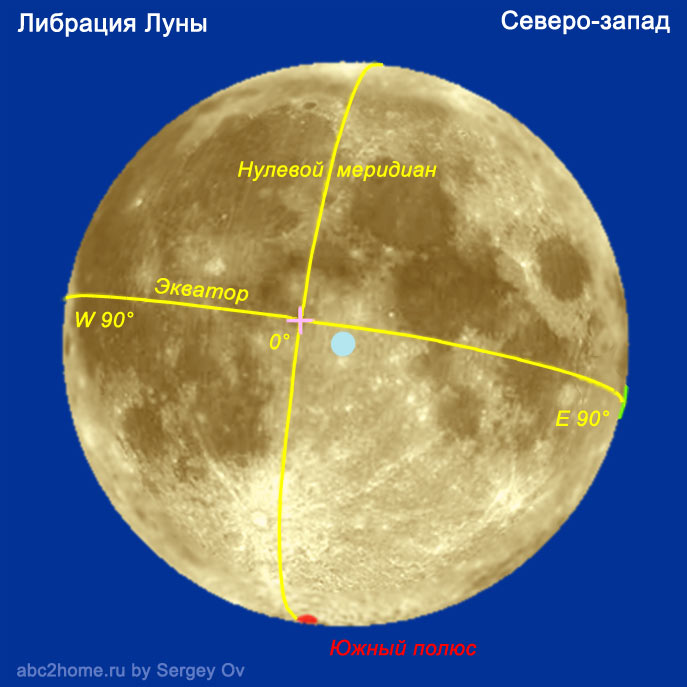
Либрация Луны, отклонение на юго-восток
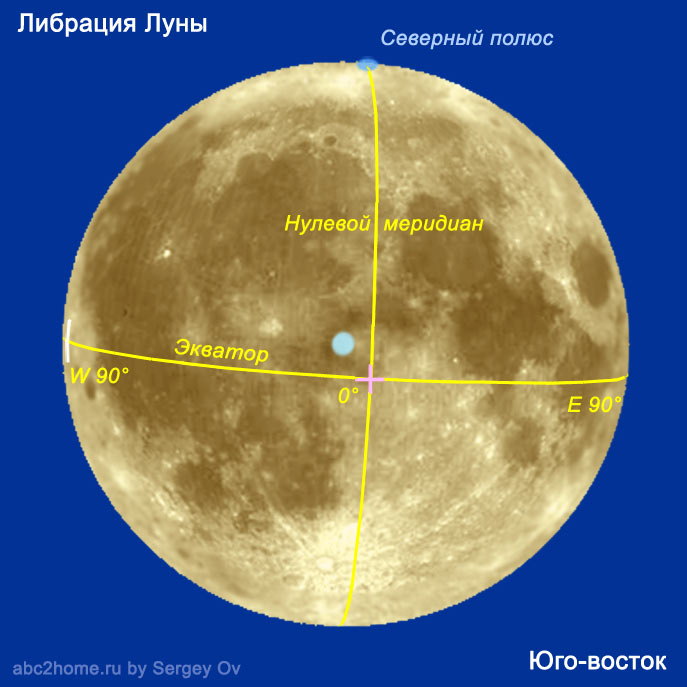
Рис.1. Либрация Луны. Представлен либрационный ракурс Луны, при котором видны лунный Южный полюс и восточная часть обратной строны Луны (зеленая вертикальная линия).
При подведении курсора появляется рисунок с ракурсом, при котором виден Северный полюс Луны и ее обратая западная сторона (за белой вертикальной полудугой). Голубой круг обозначает точку на поверхности Луны из которой Земля видна в зените. Сиреневый крест – это своего рода селенографический “Пуп Луны”, точка с координатами (0°, 0°). (Традиционо, в обиходе принято считать “Пупом Луны” кратер Тихо (ввиду визуального сходства), а у нас на рисунке настоящий селенографический Пуп!)
Либрация по долготе
Либрация по долготе позволяет нам заглянуть на обратную сторону Луны с запада и востока, правда, совсем на чуть-чуть с каждой стороны (рис. 1). Оптическая составляющая либрации по долготе складывается результате двух явлений: неравномерности орбитального движения Луны и параллакса, вызванного суточным вращением Земли.
При орбитальном движении Луна, то ускоряется и достигает максимальной скорости в перигее 1,052 км/с
***, то замедляется до минимума в апогее – 0,995 км/с, в то время как скорость вращения вокруг своей оси неизменна. Получается, что в перигее Луна “не успевает повернуться к нам своим центром” и вынуждена показать часть своей обратной стороны с востока, в апогее, наоборот, она как бы вращается быстрее, “торопится”, показывая обратную сторону с запада. Максимальная амплитуда таких отклонений может достигать 7,9°.
Параллактическая составляющая либрации возникает вследствие того, что Луну и Землю по отношению к друг другу совершенно нельзя представлять точечными телами. Радиус Земли (6371 км) значимо сравним с расстоянием до Луны – 384400 км!
Наблюдатель, находящийся на экваторе, в момент восхода Луны смотрит на нее как бы находясь сбоку на один градус ( для супер Луны: Arcsin(6371/356400)/π*180 = 1,02°).
Не правда ли, интересное явление? – Оказывается, жители Москвы и жители Владивостока, глядя на Луну в один и тот же момент, видят ее по-разному!
Sergey Ov (Seosnews9)
О Луне и фазах луны в Толковом словаре живого великорусского языка В.И.Даля
Луна ж. спутник земли, небесное тело, которое ходит вкруг земли; месяц; | иногда принимается за меру времени в четыре недели. На луне Каин убивает Авеля; брат закалывает брата вилами. Ясная, круторогая луна зимой к стуже, летом к ведру. Красноватый круг около луны, скоро пропадающий, к ведру. Два таких круга, или один тусклый, к морозу; красный, к ветру; перерванный, к снегу. | Костр. зарево, зарница, всякий отдаленный или слабый блеск на небе. | Луна, в знач. зык, звук, гул, голк, см. дунуть. | лунка или ямка. Лунный, к луне относящ. Лунная ночь, – свет. Лунный месяц, синодический, лунация ж. 29 дней 12 часов 44 минут 3 секунды, полное обращение луны, от новолуния до новолуния. Лунный год, двенадцать таких месяцев. | ….
Серп … – …Луна серпом, узкой вырезкой, полоской, серповидно, -образно
Полный Полнолунье ср. пора, когда луна в противостоянии с солнцем, когда земля наша стоит промеж солнца и луны, которая посему и бывает освещена во весь круг свой, во всю половину;
/ самый вид сполна освещенного месяца. После полнолуния идет ущерб, убыль, ветух, месяц на ветху; затем последня четверть; там новолуние, вовсе темный, невидимый месяц; там первая четверть, молодой месяц, нарожденный, молодик, новец; затем перекрой, прибыль, прибылой, и снова полнолунье./
Луна выглядит как полная 3 дня – в день астрономического полнолуния, за день до полнолуния и день после.
Месяц Когда месяц родится вниз рогами (на юг), то зимой будет теплый, летом жаркий; вверх (на север), зимой холодный, летом ветряный; рога кверху, но нижний крутой, верхний отлогий, то первая половина месяца зимой холодная, летом ветряная: если же верхний рог круче, нижний отложе, то та же примета на вторую половину месяца.
Крутые рога месяца – к ведру; пологие – к ненастью; тусклый месяц – к мокрети; ясный, к суху; в синеве – к дождю; в красне – к ветру; с ушами – к морозу.
Молодой месяц обмывается (о перемене погоды в новолунье). Богоявленье под полный месяц – к большому разливу (перм.). Если месяц в три дня обглядится, то весь будет ведрый, а когда три дня дождя, то весь ненастный (вор.). Ветхий месяц Бог на звезды крошит. На месяце видно, как Каин Авеля вилами убил (как брат брата вилами заколол), пятна на луне. Месяц умылся, т. е. дождь на молодник.
Месяц народился, молодой, новый месяц, когда серп луны покажется после новолуния, на первую четверть; месяц на ущербе, старый, ветхий месяц, последняя четверть, убыль.
Над бабушкиной избушкой хлеба краюшка? – месяц. Кто глядит на месяц (на погоду, в хозяйстве), в деже не месит. На месяц смотреть (угадывать погоду) – ни жать, ни молотить. На месяц смотреть – в закромы заглядывать (пусто). Светит, да не греет (месяц), только напрасно у Бога хлеба ест. Как месяц ни свети, а все не солнышко. Как молодой месяц: покажется, да опять и спрячется. Что это за месяц – когда светит, а когда нет! Месяц на небе, а число в святцах. Пропал как молодой месяц. Грело б красное солнышко, а месяц – как себе знает. Светило б солнце, а месяц даром. Светил бы мне ясный месяц, а по частым звездам колом бью. И месяц светит, когда солнца нет.
Русский месяц подождет (потому что отстал, по старому счисленью).
Всю ночь собака на месяц пролаяла, а месяц того и не знает.
Еще какого захотела (жениха), во лбу месяц, а в затылке ясны звезды?
Кругло, а не месяц; зелено, а не дуброва; с хвостом, а не мышь? (репа).
Месяц, месяц, где ты был? – В лесу. – Что ты делал? – Лыки драл. – Куда клал? – Под колоду. – Кто взял? – Родион. – Поди вон! конанье.
Под светлым месяцем, под белыми облаками, под чистыми звездами и пр. сказочн. Месячный, к месяцу относящийся, длящийся целый месяц или бывающий ежемесячно. Месячный свет, лунный свет.
Луна – астрономические характеристики
Характеристики движения Луны как твердого тела:
Луна является единственным естественным спутником Земли и обращается вокруг нее по эллиптической орбите, с параметрами:
– большая полуось: 384 399 км (0,00257 а. е.);
– эксцентриситет
0,05490;
– наклонение (к эклиптике)
5,145° (min 4.99°, max 5.30°);
– период обращения линии апсид: 8,8504 лет;
– период обращения восходящего узла: 18,5996 лет;
– орбитальная скорость: средняя 1,023 км/с (min 0,995 км/с, max 1,052 км/с);
– сидерический период обращения (по звездам) 27,321582 дн. (27 дн. 07 ч 43 мин 06 сек)
– синодический период обращения (по Солнцу) 29,530588 дн. ( 29 дн. 12 ч 44 мин 00 сек)
Расстояние от Земли до Луны: общепринятое среднее 384400 км:
– в перигее: среднее 363104 км (min 356400 км, max 370400 км);
– в апогее: среднее
405696 км (min 404000 км, max 406700 км)
Период собственного обращения Луны: 27,321661 дн. (27 дн. 07 ч 43 мин 12 сек).
Наклон лунной оси:
–
к плоскости орбиты: 6,687°,
–
к плоскости эклиптики: 1.5424°.
Вращательная скорость поверхности Луны на экваторе: 4,627 м/с.
Характеристики Луны как астрономического объекта:
– средний радиус Луны: 1737,10 км (0,273 земных);
– полярное сжатие 0,00125 (экваториальный радиус 1738,14 км, полярный 1735,97 км);
– окружность экватора 10917 км;
– площадь поверхности Луны 3,793·107 км² (0,074 от площади Земли);
– оценочный объём Луны 2,1958·1010 км³ (0,020 от объема Земли):
– масса Луны: 7,3477·1022 кг (0,0123 от массы Земли);
– средняя плотность: 3,3464 г/см³;
– ускорение свободного падения на экваторе: 1,62 м/с² (0,165 g);
–
первая космическая скорость: 1,68 км/с;
– вторая космическая скорость: 2,38 км/с;
– альбедо Луны 0,12;
– средняя температура поверхности: -53 °C [220 К] (min -233°C, max +123°С).
Видимая звёздная величина от -2,5 до – 12,9 (-12,74 средняя при полной Луне).
О браузерном виджете «Фаза Луны сейчас»
Браузерный виджет «Фаза Луны сейчас» создан на основе Java Script, все выводимые виджетом параметры рассчитываются на стороне пользователя непосредственно в браузере, на основе исходного времени, предоставляемого устройством.
Предлагаются три варианта виджета “Фото Луны” – мини, “Фото Луны + информер” – виджет и “Фото Луны + информер + селенографические параметры” – макси.
Если не нажимать кнопку “Обновить”, то виджет может работать в режиме оффлайн. Используя, браузерные регулировки масштаба “Ctrl +” и “Ctrl -” можно произвольным образом менять масштаб отрисовки виджета, увеличивая или уменьшая его до нужных размеров.
При включении режимов “Часы” и “Машина времени” необходимо помнить, что хотя при этом не расходуется интернет трафик, браузерные онлайн расчеты параметров и фаз Луны расходуют энергетические ресурсы вашего устройства, поэтому не следует надолго включать эти режимы на устройствах с автономным питанием.
● Главная
![]() Лунный календарь
Лунный календарь
✔ Фаза Луны сейчас
Астрономические данные спутника Земли – Луны
| Наименование населенного пункта |
| Местное время в виде ДД/ММ/ГГГГ/ЧЧ/ММ/СС |
| В населенном пункте |
| На заданную дату и местное время |
| Спутник Земли – Луна имеет характеристики |
| Расстояние от Земли до Луны (км) |
| Фаза Луны |
| Азимут ( в градусах) |
| Высота над горизонтом (в градусах) |
| Экваториальная система координат |
| Склонение |
| Прямое восхождение |
| Эклиптическая система координат |
| Широта |
| Долгота |
| Топоцентрическая система координат |
| Склонение |
| Прямое восхождение |
ЛУНА. Общие характеристики
Бот рассчитывает следующие параметры этой планеты:
– Склонение
– Прямое восхождение
– Экваториальные координаты
– Гелиоцентрические координаты
– Фазу
– Азимут и высоту
– Расстояние до Земли
Рассмотрим немного систему координат что бы было понятно о чем собственно идет речь
Горизонтальные координаты
Горизонтальные координаты объекта на небе — азимут и высота — измеряются относительно плоскости горизонта наблюдателя (смртим ниже приведенный рисунок). Предположим, что наблюдатель находится в точке О; тогда его горизонт — это круг NESW , где буквы означают соответственно
север (N), восток (E), юг (S), запад (W)
. Заметим, что направление на север означает направление не на магнитный северный полюс, а на Северный полюс, определяемый осью вращения Земли. Представьте себе, что звезды расположены на поверхности полусферы, в центре которой находится наблюдатель, как показано на рисунке. Сфера, частью которой является эта полусфера, называется небесной. Точка прямо над головой наблюдателя называется зенитом ,(противоположная точка на сфере – под ногами наблюдателя – надир) направление OZ определяется отвесной линией в точке наблюдения. Рассмотрим теперь светило X и мысленно проведем большой круг (т. е. круг на поверхности сферы, центр которого совпадает с центром сферы) через точки Z и X, он пересечет горизонт в точке В.
Высота светила над горизонтом а — это угол с вершиной в точке О, опирающийся на дугу ХВ. Азимут А — это угол с вершиной О, опирающийся на дугу NB. Таким образом, высота определяет в градусах «насколько высоко» (высота под горизонтом считается отрицательной), а азимут — «как далеко в сторону» от направления на север расположена звезда; азимут тоже измеряется в градусах.
Угол А возрастает от О до 360° по мере поворота в направлении север—восток— юг—запад. В точке севера азимут равен 0°, в точке юга 180° и т. д.
Экваториальные координаты
Как подсказывает название, экваториальные координаты отсчитываются относительно плоскости земного экватора (см рисунок). Наблюдатель находится в точке О, плоскость, содержащая круг NESW, как обычно, является горизонтом, а точка Z — зенитом.
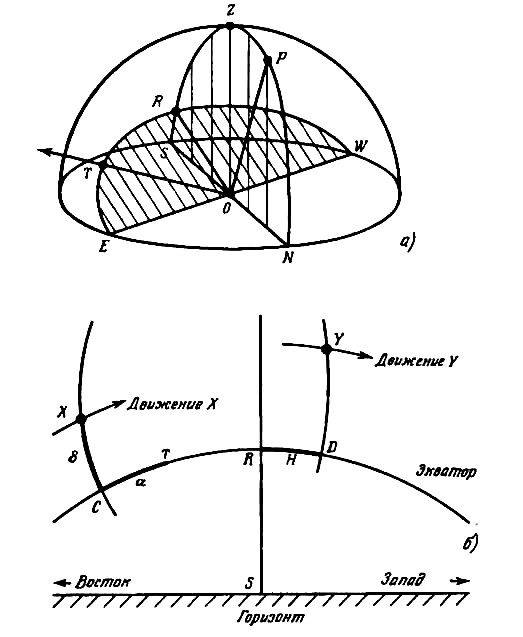
Рис 6. Экваториальные координаты: а на небесной сфере; b при наблюдении с Земли.
Представьте себе, что наш рисунок изображает вид на Землю с очень большого расстояния. Планета вместе с расположенным на ней наблюдателем превращается в точку в центре рисунка, а плоскость экватора может быть продолжена до пересечения с небесной сферой по большому кругу E♈RW. Эта плоскость называется экваториальной, она наклонена к плоскости горизонта под углом (90° – ϕ), где ϕ— географическая широта наблюдателя. Например, для наблюдателя на северной широте 52° этот угол равен 38°. Перпендикулярно экваториальной плоскости вдоль прямой ОР проходит ось вращения Земли, которая пересекает небесную сферу в точке Р — северном полюсе мира, или просто Северном полюсе. Поскольку именно вокруг этой прямой вращается Земля, нам кажется, что все звезды описывают круги по небу вокруг точки Р. Рис. 6, b показывает, что видит наблюдатель О, глядящий на небо. Помимо точки юга S на горизонте на рисунке показана также воображаемая линия экватора C♈RD.Дуга, идущая книзу через точки R и S, является частью большого круга NPZRS, показанного на рис. 6, а. Дуга ХС — это часть другого большого круга, не отмеченного на рис. 6, а, проходящего через точки Р, X и С. Рассмотрим звезду, находящуюся в точке X.Дуга ХС или угол с центром в О, опирающийся на эту дугу, называется склонением δ точки X и определяет, «насколько высоко» или «насколько на север» от плоскости экватора расположена звезда. Другая координата, определяющая «как далеко в сторону», отсчитывается от определенной точки на небе, обозначаемой символом ♈. Это точка весеннего равноденствия, ее положение определяется пересечением плоскостей земного экватора и эклиптики — орбиты Земли вокруг Солнца. Однако сейчас это определение нам не понадобится. Следует только помнить, что положение точки ♈ остается неизменным по отношению к звездам и что именно от нее мы отсчитываем вторую координату. Эта координата называется прямым восхождением а и определяется величиной угла с центром в О, опирающегося на дугу ♈С. С течением времени звезда X постепенно перемещается на запад вдоль круга с центром в точке Р, совершая один оборот за 24 ч по звездному времени . Поскольку плоскость этого круга параллельна плоскости экватора, склонение остается неизменным. Более того, поскольку точка ♈ занимает фиксированное положение на небе, то она должна смещаться вдоль экватора с точно такой же угловой скоростью, что и звезда X по своему кругу. Следовательно, прямое восхождение звезды X также не изменяется. Таким образом, α и δ оказываются идеальными координатами для описания положения звезд и других «неподвижных» небесных тел.
Помимо прямого восхождения существует и другая величина, называемая часовым углом Н, для описания, «насколько далеко в сторону» расположена точка (см. рис. 6, б). Для звезды Y эта величина измеряется углом с центром в О, опирающимся на дугу RD, и определяет, как далеко звезда ушла вдоль экватора от точки R на юге; другими словами, Н — мера времени, протекающего с момента пересечения звездой меридиана. Величина Н равномерно возрастает со временем и обращается в нуль, когда звезда пересекает большой круг NPZRS (см. рис. 6, а). Этот круг называется меридианом, а пересечение его звездой — ее кульминацией или прохождением через меридиан. Высота небесного тела в этот момент максимальна, а азимут равен 180° (при условии, что склонение звезды меньше географической широты).
Склонение измеряется в градусах и считается положительным к северу и отрицательным к югу от экватора. Часовой угол и прямое восхождение тоже могут быть измерены в градусах, они изменяются от 0 до 360°. Угол а измеряется так, что увеличивается на восток от точки ♈, а в самой точке ♈ принимает значение 0. (Отметим, что это направление противоположно тому, в котором отсчитывается величина Н). Однако более распространенным является измерение этих величин в часах, минутах и секундах от 0 до 24 ч. Один полный оборот (360°) соответствует 24 ч звездного времени, т. е. 1 ч соответствует 15°. Утверждения «прямое восхождение звезды X равно 90°» и «прямое восхождение звезды X равно 6h»полностью эквивалентны. Для перехода от одних единиц к другим достаточно просто разделить или умножить соответствующие значения на 15.
Удобство измерения прямого восхождения в часовой мере определяется тем, что в момент кульминации местное звездное время равно прямому восхождению.
Фаза планеты
Фаза планеты измеряется отношением площади освещенной части видимого диска ко всей его площади. Угол между направлением с планеты на Солнце и Землю называется фазовым углом. При фазовом угле ф = 180° (планета находится между Солнцем и Землей) фаза равна нулю, так как половина планеты, обращенная к Земле, не освещена совсем (Для Луны этот момент называется новолунием).
При фазовом угле ф = 0 (Земля и Солнце находятся по одну сторону от планеты) фаза равна 1, видимый диск планеты освещен полностью (Для Луны этот момент называется полнолунием). В общем случае связь между фазой Ф и фазовым углом ф определяется формулой
Фазовый угол для нижней планеты изменяется от 0° (верхнее соединение) до 180° (нижнее соединение) и, следовательно, ее фазы изменяются от нуля до единицы
Для верхних планет фазовый угол никогда не превышает той максимальной величины, которая достигается в моменты квадратур (т. е. когда Земля видна с планеты в наибольшем удалении от Солнца).
Для Марса эта величина составляет не более 48°,3, для Юпитера 11°, для всех остальных планет — меньше 11°.
Поэтому для Марса фаза всегда не меньше 0,84, а для других верхних планет она всегда очень близка к единице.
Синтаксис
Для тех, кто использует XMPP клиент: astroda <город>;<дата>
Датой может быть дата, выраженная в формате ДД.ММ.ГГГГ.ЧЧ.мм.сс
где ДД -дата, ММ – месяц, ГГГГ-год,мм-минута, сс- секунда
а городом – населенный пункт в любой точке мира.
Система небесных координат используется в астрономии для описания положения светил на небе или точек на воображаемой небесной сфере. Координаты светил или точек задаются двумя угловыми величинами (или дугами), однозначно определяющими положение объектов на небесной сфере. Таким образом, система небесных координат является сферической системой координат, в которой третья координата — расстояние — часто неизвестна и не играет роли.
Системы небесных координат отличаются друг от друга выбором основной плоскости (см. Фундаментальная плоскость) и началом отсчёта. В зависимости от стоя́щей задачи, может быть более удобным использовать ту или иную систему. Наиболее часто используются горизонтальная и экваториальная системы координат. Реже — эклиптическая, галактическая и другие.
Горизонтальная топоцентрическая система координат[править | править код]
В этой системе центр помещается в месте нахождения наблюдателя на поверхности Земли, основной плоскостью является плоскость математического горизонта. Одной координатой при этом является либо высота светила h, либо его зенитное расстояние z. Другой координатой является азимут A. Вследствие того что горизонтальная система координат всегда топоцентрическая (наблюдатель всегда находится на поверхности Земли, либо на некотором возвышении) слово «топоцентрическая» обычно опускается.
Высотой h светила называется дуга вертикального круга от математического горизонта до светила, или угол между плоскостью математического горизонта и направлением на светило. Высоты отсчитываются в пределах от 0° до +90° к зениту и от 0° до −90° к надиру.
Зенитным расстоянием z светила называется дуга вертикального круга от зенита до светила, или угол между отвесной линией и направлением на светило. Зенитные расстояния отсчитываются в пределах от 0° до 180° от зенита к надиру.
Азимутом A светила называется дуга математического горизонта от точки юга до вертикального круга светила, или угол между полуденной линией и линией пересечения плоскости математического горизонта с плоскостью вертикального круга светила. Азимуты отсчитываются в сторону суточного вращения небесной сферы, то есть к западу от точки юга, в пределах от 0° до 360°. Иногда азимуты отсчитываются от 0° до +180° к западу и от 0° до −180° к востоку. (В геодезии и навигации азимуты отсчитываются от точки севера.)
Изменения координат при вращении небесной сферы[править | править код]
Высота h, зенитное расстояние z, азимут A и часовой угол t светил постоянно изменяются вследствие вращения небесной сферы, так как отсчитываются от точек, не связанных с этим вращением. Склонение δ, полярное расстояние p и прямое восхождение α светил при вращении небесной сферы не изменяются, но они могут меняться из-за движений светил, не связанных с суточным вращением.
Первая экваториальная система координат[править | править код]
В этой системе основной плоскостью является плоскость небесного экватора. Одной координатой при этом является склонение δ (реже — полярное расстояние p). Другой координатой — часовой угол t.
Склонением δ светила называется дуга круга склонения от небесного экватора до светила, или угол между плоскостью небесного экватора и направлением на светило. Склонения отсчитываются в пределах от 0° до +90° к северному полюсу мира и от 0° до −90° к южному полюсу мира.
Полярным расстоянием p светила называется дуга круга склонения от северного полюса мира до светила, или угол между осью мира и направлением на светило. Полярные расстояния отсчитываются в пределах от 0° до 180° от северного полюса мира к южному.
Часовым углом t светила называется дуга небесного экватора от верхней точки небесного экватора (то есть точки пересечения небесного экватора с верхней частью небесного меридиана) до круга склонения светила, или двугранный угол между плоскостями небесного меридиана и круга склонения светила. Часовые углы отсчитываются в сторону суточного вращения небесной сферы, то есть к западу от верхней точки небесного экватора, в пределах от 0° до 360° (в градусной мере) или от 0h до 24h (в часовой мере). Иногда часовые углы отсчитываются от 0° до +180° (от 0h до +12h) к западу и от 0° до −180° (от 0h до −12h) к востоку.
Вторая экваториальная система координат[править | править код]

Использование экваториальной системы координат.
В этой системе, как и в первой экваториальной, основной плоскостью является плоскость небесного экватора, а одной координатой — склонение δ (реже — полярное расстояние p). Другой координатой является прямое восхождение α.
Прямым восхождением (RA, α) светила называется дуга небесного экватора от точки весеннего равноденствия до круга склонения светила, или угол между направлением на точку весеннего равноденствия и плоскостью круга склонения светила. Прямые восхождения отсчитываются в сторону, противоположную суточному вращению небесной сферы, в пределах от 0° до 360° (в градусной мере) или от 0h до 24h (в часовой мере).
RA — астрономический эквивалент земной долготы. И RA и долгота измеряют угол восток-запад вдоль экватора; обе меры берут отсчёт от нулевого пункта на экваторе. Для долготы, нулевой пункт — нулевой меридиан; для RA нулевой отметкой является место на небе, где Солнце пересекает небесный экватор, в направлении с юга на север (в весеннее равноденствие).
Склонение (δ) в астрономии — одна из двух координат экваториальной системы координат. Равняется угловому расстоянию на небесной сфере от плоскости небесного экватора до светила и обычно выражается в градусах, минутах и секундах дуги. Склонение положительно к северу от небесного экватора и отрицательно к югу.
- Объект на небесном экваторе имеет склонение 0°
- Склонение северного полюса небесной сферы равно +90°
- Склонение южного −90°
У склонения всегда указывается знак, даже если склонение положительно.
Склонение небесного объекта, проходящего через зенит, равно широте наблюдателя (если считать северную широту со знаком +, а южную отрицательной). В северном полушарии Земли для заданной широты φ небесные объекты со склонением δ > +90° − φ не заходят за горизонт, поэтому называются незаходящими. Если же склонение объекта δ < −90° + φ, то объект называется невосходящим, а значит он ненаблюдаем на широте φ.[1]
Эклиптическая система координат[править | править код]
В этой системе основной плоскостью является плоскость эклиптики. Одной координатой при этом является эклиптическая широта β, а другой — эклиптическая долгота λ.
Эклиптической широтой β светила называется дуга круга широты от эклиптики до светила, или угол между плоскостью эклиптики и направлением на светило. Эклиптические широты отсчитываются в пределах от 0° до +90° к северному полюсу эклиптики и от 0° до −90° к южному полюсу эклиптики.
Эклиптической долготой λ светила называется дуга эклиптики от точки весеннего равноденствия до круга широты светила, или угол между направлением на точку весеннего равноденствия и плоскостью круга широты светила. Эклиптические долготы отсчитываются в сторону видимого годового движения Солнца по эклиптике, то есть с запада к востоку от точки весеннего равноденствия в пределах от 0° до 360°.
Галактическая система координат[править | править код]
В этой системе основной плоскостью является плоскость нашей Галактики. Одной координатой при этом является галактическая широта b, а другой — галактическая долгота l.
Галактической широтой b светила называется дуга круга галактической широты от эклиптики до светила, или угол между плоскостью галактического экватора и направлением на светило.
Галактические широты отсчитываются в пределах от 0° до +90° к северному галактическому полюсу и от 0° до −90° к южному галактическому полюсу.
Галактической долготой l светила называется дуга галактического экватора от точки начала отсчёта C до круга галактической широты светила, или угол между направлением на точку начала отсчёта C и плоскостью круга галактической широты светила. Галактические долготы отсчитываются против часовой стрелки, если смотреть с северного галактического полюса, то есть к востоку от точки начала отсчёта C в пределах от 0° до 360°.
Точка начала отсчёта C находится вблизи направления на галактический центр, но не совпадает с ним, поскольку последний, вследствие небольшой приподнятости Солнечной системы над плоскостью галактического диска, лежит примерно на 1° к югу от галактического экватора. Точку начала отсчёта C выбирают таким образом, чтобы точка пересечения галактического и небесного экваторов с прямым восхождением 280° имела галактическую долготу 32,93192° (на эпоху 2000).
Координаты точки начала отсчёта C на эпоху 2000 в экваториальной системе координат составляют:


История и применение[править | править код]
Небесные координаты употреблялись уже в глубокой древности. Описание некоторых систем содержится в трудах древнегреческого геометра Евклида (около 300 до н. э.). Опубликованный в «Альмагесте» Птолемея звёздный каталог Гиппарха содержит положения 1022 звёзд в эклиптической системе небесных координат.
Наблюдения изменений небесных координат привели к величайшим открытиям в астрономии, которые имеют огромное значение для познания Вселенной. К ним относятся явления прецессии, нутации, аберрации, параллакса, собственных движений звёзд и другие. Небесные координаты позволяют решать задачу измерения времени, определять географические координаты различных мест земной поверхности. Широкое применение находят небесные координаты при составлении различных звёздных каталогов, при изучении истинных движений небесных тел — как естественных, так и искусственных — в небесной механике и астродинамике и при изучении пространственного распределения звёзд в проблемах звёздной астрономии.
Использование различных систем координат[править | править код]
Использование горизонтальной топоцентрической системы координат[править | править код]
Горизонтальная топоцентрическая система координат используется наблюдателем, находящимся в определённом месте на поверхности земного шара для определения положения какого-либо светила на небе.
Координаты небесных светил в данной системе координат могут быть получены с помощью угломерных инструментов и при наблюдениях в телескоп, смонтированный на азимутальной установке.
Большинство астрономических компьютерных программ способны выдавать положения светил в данной системе координат.
При наблюдениях следует учитывать поправку на рефракцию.
Использование первой экваториальной системы координат[править | править код]
Первая экваториальная система координат используется для определения точного времени и при наблюдениях в телескоп, смонтированный на экваториальной установке.
Использование второй экваториальной системы координат[править | править код]
Вторая экваториальная система координат является общепринятой в астрометрии.
В экваториальной гелиобарицентрической системе координат составляются современные звёздные карты и описываются положения светил в каталогах. При этом координаты светил приводятся к определённому положению небесного экватора и точки весеннего равноденствия, то есть к определённой эпохе (в астрономии применяются эпохи B1950 и J2000.0).
Экваториальная геоцентрическая система координат отличается от экваториальной гелиобарицентрической системы координат тем, что координаты звёзд скорректированы в ней из-за явления годичного параллакса, а положение небесного экватора и точки весеннего равноденствия приводятся к текущей дате.
Использование эклиптической системы координат[править | править код]
Эклиптическая геоцентрическая система координат используется в небесной механике для расчёта орбиты Луны, а также является основной или единственной в большинстве школ астрологии.
Эклиптическая гелиоцентрическая система координат используется для расчёта орбит планет и других тел Солнечной системы обращающихся вокруг Солнца.
Применение различных систем небесных координат[править | править код]
На практике, как правило, требуется пользоваться несколькими системами координат.
Например для расчёта положения Луны на небе необходимо сначала рассчитать координаты Луны в эклиптической геоцентрической системе координат, пересчитать координаты в экваториальную геоцентрическую систему координат, затем перейти к горизонтальной топоцентрической системе координат.
См. также[править | править код]
- Небесная сфера
- Сферическая система координат
Примечания[править | править код]
- ↑ Зигель Ф. Ю. Сокровища звёздного неба — путеводитель по созвездиям и Луне / Под ред. Г. С. Куликова. — 5-е изд. — М.: Наука, 1986. — С. 57—58. — 296 с. — 200 000 экз.
Литература[править | править код]
- Smart, William Marshall. Text-book on spherical astronomy. — Cambridge University Press, 1949.
- Lang, Kenneth R. Astrophysical Formulae. — Springer, 1978. — ISBN 3-540-09064-9.
- Taff, L. G. Computational spherical astronomy. — Wiley, 1980.
- Karttunen, H.; Kröger, P.; Oja, H.; Poutanen, M.; Donner, H. J. Fundamental Astronomy. — 2006. — ISBN 978-3-540-34143-7.
- Roth, G. D. Handbuch für Sternenfreunde. — Springer. — ISBN 3-540-19436-3.
Ссылки[править | править код]
- NOVAS, the U.S. Naval Observatory’s Vector Astrometry Software, an integrated package of subroutines and functions for computing various commonly needed quantities in positional astronomy (англ.)
- SOFA, the IAU’s Standards of Fundamental Astronomy, an accessible and authoritative set of algorithms and procedures that implement standard models used in fundamental astronomy (англ.)
)
