Наталья Игоревна Восковская
Эксперт по предмету «Математика»
Задать вопрос автору статьи
В аналитической геометрии часто требуется составить общее уравнение прямой по принадлежащей ей точке и вектору нормали к прямой.
Замечание 1
Нормаль – синоним для слова перпендикуляр.
Общее уравнение прямой на плоскости выглядит как $Ax + By + C = 0$. Подставляя в него различные значениях $A$, $B$ и $C$, в том числе нулевые, можно определить любые прямые.
Можно выразить уравнение прямой и другим способом:
$y = kx + b$.
Это уравнение прямой с угловым коэффициентом. В нем геометрический смысл коэффициента $k$ заключается в угле наклона прямой по отношению к оси абсцисс, а независимого члена $b$ – в расстоянии, на которое прямая отстоит от центра координатной плоскости, т.е. точки $O(0; 0)$.
Рисунок 1. Варианты расположения прямых на координатной плоскости. Автор24 — интернет-биржа студенческих работ
Нормальное уравнение прямой можно выразить и в тригонометрическом виде:
$x cdot cos{alpha} + y cdot sin{alpha} – p = 0$
где $alpha$ – угол между прямой и осью абсцисс, а $p$ – расстояние от начала координат до рассматриваемой прямой.
Возможны четыре варианта зависимости наклона прямой от величины углового коэффициента:
- когда угловой коэффициент положителен, направляющий вектор прямой идёт снизу вверх;
- когда угловой коэффициент отрицателен, направляющий вектор прямой идёт сверху вниз;
- когда угловой коэффициент равен нулю, описываемая им прямая параллельна оси абсцисс;
- для прямых, параллельных оси ординат, углового коэффициента не существует, поскольку тангенс 90 градусов является неопределенной (бесконечной) величиной.
«Нормальный вектор прямой» 👇
Чем больше абсолютное значение углового коэффициента, тем круче наклонен график прямой.
Зная угловой коэффициент, легко составить уравнение графика прямой, если дополнительно известна точка, принадлежащая искомой прямой:
$y – y_0 = k cdot (x – x_0)$
Таким образом, геометрически прямую на координатной всегда можно выразить с помощью угла и расстояния от начала координат. В этом и заключается смысл нормального вектора к прямой – самого компактного способа записи ее положения, если известны координаты хотя бы одной точки, принадлежащей этой прямой.
Определение 1
Вектором нормали к прямой, иначе говоря, нормальным вектором прямой, принято называть ненулевой вектор, перпендикулярный рассматриваемой прямой.
Для каждой прямой можно найти бесконечное множество нормальных векторов, равно как и направляющих векторов, т.е. таких, которые параллельны этой прямой. При этом все нормальные векторы к ней будут коллинеарными, хотя и не обязательно сонаправлены.
Обозначив нормальный вектор прямой как $vec{n}(n_1; n_2)$, а координаты точки как $x_0$ и $y_0$, можно представить общее уравнение прямой на плоскости по точке и вектору нормали к прямой как
$n_1 cdot (x – x_n) + n_2 cdot (y – y_0) = 0$
Таким образом, координаты вектора нормали к прямой пропорциональны числам $A$ и $B$, присутствующим в общем уравнении прямой на плоскости. Следовательно, если известно общее уравнение прямой на плоскости, то можно легко вывести и вектор нормали к прямой. Если прямая, задана уравнением в прямоугольной системе координат
$Ax + By + C = 0$,
то нормальный вектор описывается формулой:
$bar{n}(A; B)$.
При этом говорят, что координаты нормального вектора “снимаются” с уравнения прямой.
Нормальный к прямой вектор и ее направляющий вектор всегда ортогональны по отношению друг к другу, т.е. их скалярные произведения равны нулю, в чем легко убедиться, вспомнив формулу направляющего вектора $bar{p}(-B; A)$, а также общее уравнение прямой по направляющему вектору $bar{p}(p_1; p_2)$ и точке $M_0(x_0; y_0)$:
$frac{x – x_0}{p_1} = frac{y – y_0}{p_2}$
В том, что вектор нормали к прямой всегда ортогонален направляющему вектору к ней можно убедиться с помощью скалярного произведения:
$bar{p} cdot bar{n} = -B cdot A + A cdot B = 0 implies bar{p} perp bar{n}$
Всегда можно составить уравнение прямой, зная координаты принадлежащей ей точки и нормального вектора, поскольку направление прямой следует из его направления. Описав точку как $M(x_0; y_0)$, а вектор как $bar{n}(A; B)$, можно выразить уравнение прямой в следующем виде:
$A(x – x_0) + B(y – y_0) = 0$
Пример 1
Составить уравнение прямой по точке $M(-1; -3)$ и нормальному вектору $bar(3; -1)$. Вывести уравнение направляющего вектора.
Для решения задействуем формулу $A cdot (x – x_0) + B cdot (y – y_0) = 0$
Подставив значения, получаем:
$3 cdot (x – (-1)) – (-1) cdot (y – (-3)) = 0$
$3 cdot (x + 1) – (y + 3) = 0$
$3x + 3 – y – 3 = 0$
$3x – y = 0$
Проверить правильность общего уравнения прямой можно “сняв” из него координаты для нормального вектора:
$3x – y = 0 implies A = 3; B = -1 implies bar{n}(A; B) = bar{n}(3; -1),$
Что соответствует числам исходных данных.
Подставив реальные значения, проверим, удовлетворяет ли точка $M(-1; -3)$ уравнению $3x – y = 0$:
$3 cdot (-1) – (-3) = 0$
Равенство верно. Осталось лишь найти формулу направляющего вектора:
$bar{p}(-B; A) implies bar{p}(1; 3)$
Ответ: $3x – y = 0; bar{p}(1; 3).$
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
2.2.5. Нормальный вектор прямой
Или вектор нормали.
Что такое нормаль? Простыми словами, нормаль – это перпендикуляр. То есть, вектор нормали прямой перпендикулярен данной прямой. Очевидно, что у любой прямой их бесконечно много (так же, как и направляющих векторов), но нам хватит одного:
Если прямая задана общим уравнением ![]() в декартовой системе координат, то вектор
в декартовой системе координат, то вектор ![]() является вектором нормали данной прямой.
является вектором нормали данной прямой.
Обратите внимание, что это утверждение справедливо лишь для «школьной» системы координат; все предыдущие выкладки п. 2.2 работают и в общем аффинном случае.
Вектор нормали всегда ортогонален направляющему вектору прямой. Убедимся в ортогональности данных векторов с помощью скалярного произведения:
![]()
И тут всё ещё проще: если координаты направляющего вектора ![]() приходилось аккуратно «вытаскивать» из уравнения, то координаты вектора нормали
приходилось аккуратно «вытаскивать» из уравнения, то координаты вектора нормали ![]() достаточно просто «снять».
достаточно просто «снять».
Приведу примеры с теми же уравнениями, что и для направляющего вектора:

Можно ли составить уравнение прямой, зная одну точку и вектор нормали? Нутром чувствуется, можно. Ведь вектор нормали ортогонален направляющему вектору и образует с ним «жесткую конструкцию».
 2.2.6. Как составить уравнение прямой по точке и вектору нормали?
2.2.6. Как составить уравнение прямой по точке и вектору нормали?
 2.2.4. Как составить уравнение прямой по двум точкам?
2.2.4. Как составить уравнение прямой по двум точкам?
| Оглавление |
Автор: Aлeксaндр Eмeлин
Определение.
Любой ненулевой вектор, перпендикулярный
прямой называется её нормальным
вектором,
и обозначается
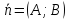 .
.
Теорема.
Алгебраическое уравнение 1-й степени
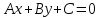 ,
,
где
коэффициенты
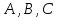 – произвольные действительные числа,
– произвольные действительные числа,
одновременно не равные нулю, являетсяуравнением
прямой на плоскости
 ,
,
а вектор
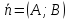 является её нормальным вектором.
является её нормальным вектором.
Верно
обратное:
на координатной плоскости
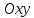 уравнение
уравнение
любой прямой с нормальным вектором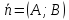 ,
,
может быть записано в виде алгебраического
уравнения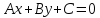 .
.
Определение.
Уравнение прямой вида
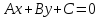 ,
,
где
коэффициенты
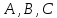 – произвольные действительные числа,
– произвольные действительные числа,
одновременно не равные нулю, называетсяобщим
уравнением прямой.
Известно,
что прямая определяется двумя точками.
Пусть
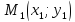
и
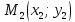
–
точки, лежащие на прямой
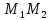 ,
,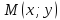
–
произвольная точка этой прямой. Тогда
векторы
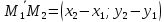 и
и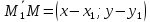 – коллинеарны, а их координаты
– коллинеарны, а их координаты
пропорциональны. Получаемуравнение
прямой, проходящей через две точки:
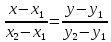 .
.
Определение.
Вектор,
параллельный прямой, называется
направляющим
вектором прямой.
Определение.
Пусть
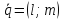 – направляющий вектор прямой. Тогда из
– направляющий вектор прямой. Тогда из
предыдущего уравнения получаемканоническое
уравнение прямой:
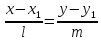 .
.
Определение.
В
тех же обозначениях, параметрическое
уравнение прямой
имеет вид:
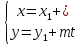 .
.

Определение.
Уравнение прямой вида
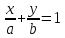 ,
,
где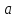 и
и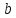 – произвольные, не равные нулю
– произвольные, не равные нулю
действительные числа, называетсяуравнением
прямой в отрезках.
Теорема.
Пусть
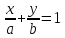 – уравнение прямой в отрезках. Тогда
– уравнение прямой в отрезках. Тогда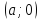 ,
,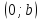 – координаты точек пересечения данной
– координаты точек пересечения данной
прямой с осями координат.
Определение.
Уравнение прямой вида
 ,
,
где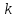 и
и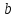 – произвольные действительные числа,
– произвольные действительные числа,
называетсяуравнением
прямой с угловым коэффициентом,
коэффициент
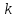 называетсяугловым
называетсяугловым
коэффициентом данной
прямой.
Теорема.
Пусть
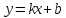 – уравнение прямой с угловым коэффициентом.
– уравнение прямой с угловым коэффициентом.
Тогда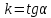 ,
,
где угол
α
равен углу наклона данной прямой к оси
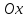 ,
,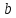 – ордината точки пересечения с осью
– ордината точки пересечения с осью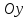 .
.
Если
известны угловые коэффициенты
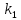 и
и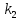 двух прямых, то один из углов
двух прямых, то один из углов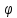 между этими прямыми определяется по
между этими прямыми определяется по
формуле:
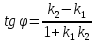 .
.
Признаком
параллельности двух прямых является
равенство их угловых коэффициентов:
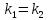 .
.
Признаком
перпендикулярности двух прямых является
соотношение:
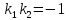 или
или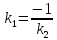 .
.
Теорема.
(Связь нормального вектора прямой с её
направляющим вектором и её угловым
коэффициентом.)
1)
Если
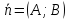 – нормальный вектор прямой, то
– нормальный вектор прямой, то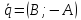 – её направляющий вектор, и, если
– её направляющий вектор, и, если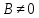 ,
,
то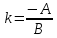 – её угловой коэффициент.
– её угловой коэффициент.
2)
Если
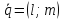 – направляющий вектор прямой, то
– направляющий вектор прямой, то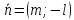 – её нормальный вектор, и, если
– её нормальный вектор, и, если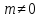 , то
, то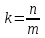 – её угловой коэффициент.
– её угловой коэффициент.
3)
Если
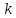 угловой коэффициент прямой, то
угловой коэффициент прямой, то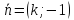 – её нормальный вектор,
– её нормальный вектор,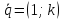
–
направляющий вектор.
Взаимное
расположение двух прямых на плоскости.
Две
прямые на плоскости могут пересекаться,
совпадать или быть параллельными.
Теорема.
Пусть прямые заданы общими уравнениями:
L1: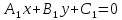 ,L2:
,L2: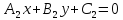 .
.
Тогда:
1)
если
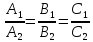 ,
,
то прямые совпадают, и система уравнений
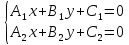
имеет
бесконечное множество решений;
2)
если
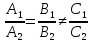 , то прямые параллельные, и система
, то прямые параллельные, и система
уравнений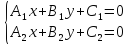 не имеет решений;
не имеет решений;
3)
если
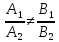 , то прямые пересекаются и координаты
, то прямые пересекаются и координаты
точки их пересечения являются единственным
решением системы уравнений
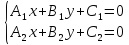 .
.
Определение.
Уравнение вида
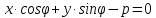 ,
,
где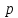 – расстояние от прямой до начала
– расстояние от прямой до начала
координат, называетсянормальным
уравнением прямой,
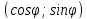 – координаты орта вектора
– координаты орта вектора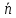 .
.
Чтобы
привести прямую к указанному виду,
разделим общее уравнение прямой на
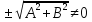 , причем со знаком «+» в случае, когда
, причем со знаком «+» в случае, когда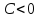 , и со знаком «-» в случае, когда
, и со знаком «-» в случае, когда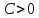 , получим:
, получим:
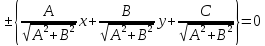 .
.
Теорема.
Орт нормального вектора
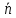 имеет координаты:
имеет координаты:
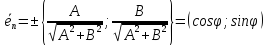 ,
,
где
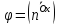 .
.
Теорема.
Расстояние от прямой до произвольной
точки
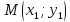
находится
по формуле:
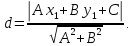
Чтобы
найти расстояние
между двумя параллельными прямыми,
нужно взять произвольную точку на одной
из прямых и найти расстояние от нее до
другой прямой.
Чтобы
найти множество
точек, равноудаленных от двух прямых
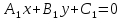 и
и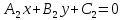 , составим уравнение:
, составим уравнение:
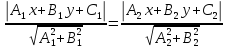 .
.
Раскрывая
модули в случае параллельных прямых,
получаем параллельную им прямую, лежащую
между данными прямыми, а в случае
пересекающихся прямых – биссектрисы
углов,
образованных пересечением прямых.
Определение.
Совокупность прямых, проходящих через
некоторую точку S,
называется пучком
прямых с центром S.
Теорема.
Если
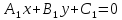 и
и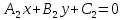 – уравнения двух прямых, пересекающихся
– уравнения двух прямых, пересекающихся
в точкеS,
то уравнение:
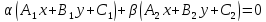 ,
,
где
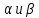 – какие угодно числа, не равные
– какие угодно числа, не равные
одновременно нулю, определяют прямую,
также проходящую через точкуS.
Более
того, в указанном уравнении числа всегда
возможно подобрать так, чтобы оно
определяло любую (заранее назначенную)
прямую, проходящую через точку S,
иначе говоря, любую прямую пучка с
центром S.
Поэтому уравнение вида называется
уравнением пучка с центром S.
Решение
типовых задач
Задача
№1:
Даны
уравнения двух сторон параллелограмма
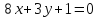 ,
,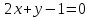 и уравнение одной из его диагоналей
и уравнение одной из его диагоналей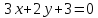 .
.
Определить координаты вершин этого
параллелограмма.
Решение:

Найдём
координаты т.
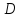 как точки пересечения прямых
как точки пересечения прямых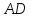 и
и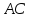 :
: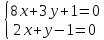 ;
;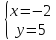 ;
;
т.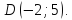 Выясним, какая из диагоналей задана.
Выясним, какая из диагоналей задана.
Подставим
координаты т.
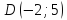 в уравнение диагонали
в уравнение диагонали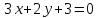 :
: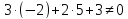 ;
;
т.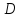 не принадлежит заданной диагонали,
не принадлежит заданной диагонали,
следовательно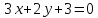 – уравнение диагонали
– уравнение диагонали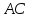 .
.
Найдём
координаты т.
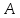 ,
,
как точки пересечения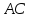 и
и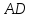 :
:
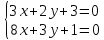 ;
;
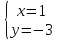 ;
;
т.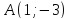 .
.
Найдём
координаты т.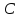 ,
,
как точки пересечения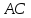 и
и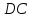 :
:
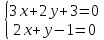 ;
;
 ;
;
т.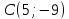 .
.
Найдём
координаты т.B:
в параллелограмме диагонали делят друг
друга пополам:
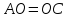 .
.
Найдём координаты т.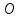 :
:
т.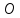 – середина
– середина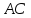 ,
,
следовательно, т.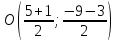 ;
;
т.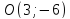 ,
,
но т.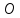 – середина
– середина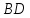 ,
,
следовательно,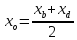 и
и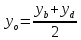 , поэтому
, поэтому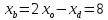 и
и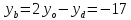 ,
,
т.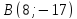 .
.
Ответ:
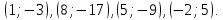
Задача
№2:
Дана
прямая
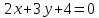 .
.
Составить уравнение прямой, проходящей
через точку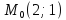 :
:
-
параллельно
данной прямой. -
перпендикулярно
к данной прямой.
Решение:
-
Искомая
прямая параллельна прямой
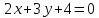 ,
,
поэтому её уравнение имеет вид: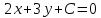 .
.
Найдём
т.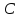 :
:
точка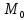 принадлежит этой прямой, поэтому её
принадлежит этой прямой, поэтому её
координаты удовлетворяют записанному
уравнению: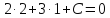 ,
,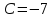 .
.
Итак, прямая принимает вид: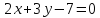 .
.
-
Т.к.
заданная и искомые прямые перпендикулярны,
то их угловые коэффициенты удовлетворяют
условию:
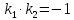 .
.
Найдём
угловой коэффициент прямой
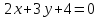 ;
;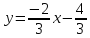 ;
;
итак,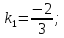 тогда
тогда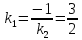 .
.
Запишем уравнение искомой прямой: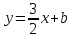 .
.
Точка
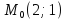 принадлежит этой прямой, поэтому
принадлежит этой прямой, поэтому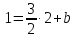 ;
;
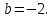
Уравнение
прямой принимает вид:
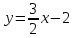
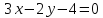 .
.
Ответ:
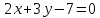 ;
;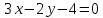 .
.
Задача
№3:
Определить,
при каких значениях a
и b
две прямые
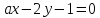 ,
,
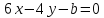 :
:
-
имеют
одну общую точку; -
параллельны;
-
совпадают.
Решение:
-
Прямые
имеют одну общую точку, когда они не
параллельны (их коэффициенты при x
и y
не пропорциональны):
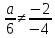 ;
;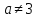
-
Прямые
параллельны, когда коэффициенты при x
и y
пропорциональны:
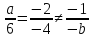 ;
;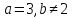 .
. -
Прямые
совпадают, когда все их коэффициенты
пропорциональны:
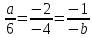 ;
;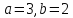 .
.
Задача
№4:
Найти
проекцию точки
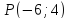 на прямую
на прямую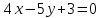 .
.
Решение:
Проведём
через т.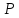 прямую
прямую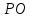 ,
,
перпендикулярную прямой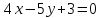 .
.
Точка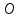 пересечения прямых и является искомой
пересечения прямых и является искомой
проекцией.
Прямая
 перпендикулярна заданной прямой, поэтому
перпендикулярна заданной прямой, поэтому
её направляющим вектором служит
нормальный вектор прямой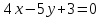 ,
,
т.е.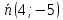 .
.
Запишем
уравнение прямой
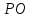 в каноническом виде:
в каноническом виде:
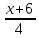
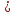
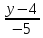 ;
;
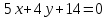 – уравнение
– уравнение .
.
Найдём
координаты т. :
:
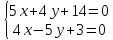 ;
;
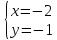 ;
;
т.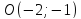
Ответ:
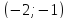
Задача
№5:
Найти
точку
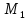 ,
,
симметричную точке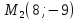 относительно прямой, проходящей через
относительно прямой, проходящей через
точки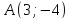 и
и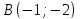 .
.
Решение:
Составим
уравнение
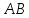 ,
,
как прямой проходящей через 2 точки:
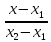
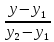 ;
;
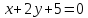 – уравнение
– уравнение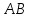 .
.
Найдём
уравнение прямой
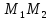 перпендикулярной
перпендикулярной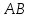 .
.
Нормальный
вектор
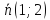 прямой
прямой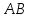 является направляющим вектором прямой
является направляющим вектором прямой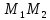 ,
,
поэтому используем каноническое
уравнение прямой: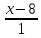
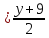 ;
;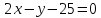 – уравнение прямой
– уравнение прямой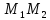 .
.
Найдём
координат т.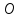 ,
,
как точки пересечения прямых и
и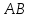 :
:
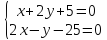 ;
;
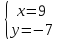 ;
;
т.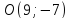 .
.
Так
как точка
 симметрична точке
симметрична точке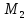 относительно
относительно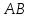 ,
,
следовательно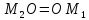 ,
,
то есть т.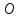 – середина отрезка
– середина отрезка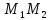 .
.
Найдём координаты точки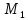 ,
,
зная начало и середину отрезка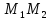 :
:
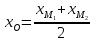 ,
,
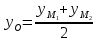
, тогда
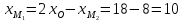 ,
,
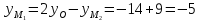 ,
,
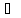 т.
т.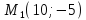 .
.
Ответ:
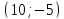 .
.
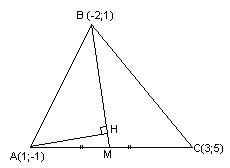
Задача
№6:
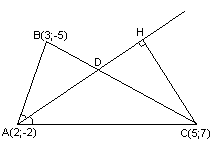
Даны
вершины треугольника
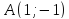 ,
,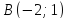 и
и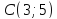 .
.
Составить уравнение перпендикуляра,
опущенного из вершины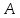 на медиану, проведенную из вершины
на медиану, проведенную из вершины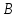 .
.
Решение:
Найдём
координаты т.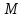 ,
,
как середины отрезка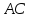 :
:
т.
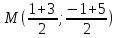 , т.
, т.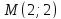 .
.
Запишем
уравнение медианы
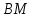 ,
,
как прямой, проходящей через две известные
точки:
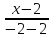
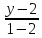 ;
;
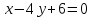 – уравнение
– уравнение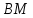 .
.
Нормальный
вектор для
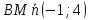 является направляющим для прямой
является направляющим для прямой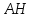 перпендикулярной
перпендикулярной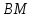 ,
,
тогда уравнение примет вид:
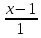
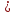
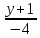 ;
;
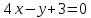 – уравнение
– уравнение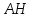 .
.
Ответ:
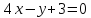 .
.
Задача
№7:
Даны
вершины треугольника
 ,
,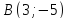 ,
,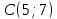 .
.
Составить уравнение перпендикуляра,
опущенного из вершины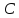 на биссектрису внутреннего угла при
на биссектрису внутреннего угла при
вершине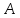 .
.
Решение:
Пусть
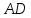 – биссектриса.
– биссектриса.
Найдём
координаты т.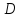 воспользовавшись свойством биссектрисы:
воспользовавшись свойством биссектрисы: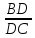
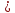
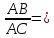
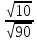
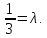
Тогда:
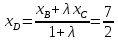 ;
;
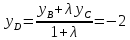 ;
;
т.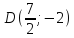 ;
;
Уравнение
биссектрисы
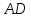 примет вид:
примет вид: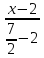
=
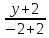
⇒
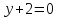 ,
,
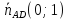 ,
,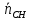 перпендикулярен
перпендикулярен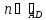 ⇒
⇒
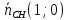 .
.
Точка
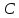 принадлежит искомому перпендикуляру,
принадлежит искомому перпендикуляру,
поэтому уравнение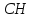 примет вид:
примет вид: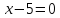 .
.
Ответ:
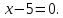
Задача
№8:
Две
стороны квадрата лежат на прямых
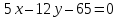 ,
,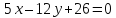 .
.
Вычислить его площадь.
Решение:
-
Выберем
на прямой
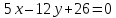 некоторую точку
некоторую точку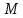 :
:
пусть
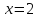 ,
,
тогда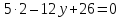 ⇒
⇒
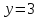 ,
,
т.е.
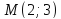 .
.
-
Найдём
расстояние от точки
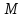 до прямой
до прямой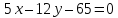 :
:
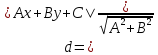 ⇒
⇒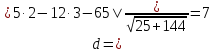 ,
,
где
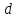 и есть длина стороны квадрата.
и есть длина стороны квадрата.
-
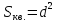 т.е.
т.е.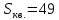 .
.
Ответ:
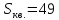 .
.
Задача
№9:
Даны
две противоположные вершины квадрата
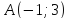 и
и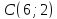 .
.
Составить уравнения его сторон.
Решение:
Зная
вершины
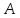 и
и составим уравнение диагонали
составим уравнение диагонали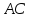 ,
,
как прямой проходящей через две точки: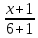
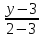 ⇒
⇒
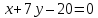
– уравнение прямой
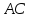 .
.
Т.к.
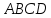 – квадрат, его диагонали являются
– квадрат, его диагонали являются
биссектрисами, поэтому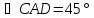 ;
;
найдём угловой коэффициент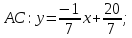
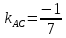 .
.
Зная
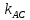 и
и ,
,
найдём угловой коэффициент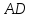 :
: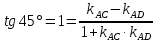 ;⇒
;⇒
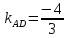 .
.
Уравнение
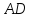 примет вид:
примет вид: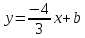 .
.
Найдём
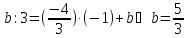 ;
;
Тогда уравнение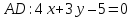 .
.
Т.к.
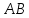 перпендикулярно
перпендикулярно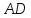 ⇒
⇒
угловой коэффициент
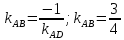 .
.
Уравнение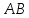 имеет вид:
имеет вид: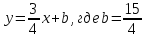 ,
,
тогда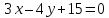 – уравнение
– уравнение .
.
Т.к.
 – квадрат, то
– квадрат, то ,
,
то уравнение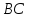 примет вид:
примет вид: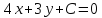 .
.
Зная,
что точка
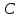 принадлежит прямой
принадлежит прямой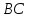 ,
,
найдём свободный член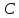 искомого уравнения, итак
искомого уравнения, итак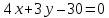 – уравнение стороны
– уравнение стороны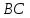 .
.
Аналогично
найдём уравнение стороны
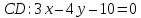 .
.
Ответ:
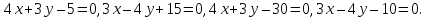
Задача
№10:
Вычислить
площадь треугольника, отсекаемого
прямой
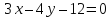 от координатного угла.
от координатного угла.
Решение:
Запишем
уравнение прямой
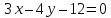 в отрезках:
в отрезках: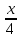 +
+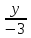
 1.
1.
Из
этого уравнения следует, что длины
отрезков
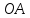 и
и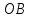 соответственно равны
соответственно равны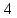 и
и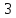 ,
,
поэтому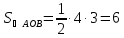 кв. ед.
кв. ед.
Ответ:
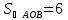 кв.ед.
кв.ед.
Задача
№11:
Составить
уравнения сторон треугольника, зная
одну из его вершин
 и уравнения двух его медиан
и уравнения двух его медиан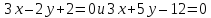 .
.
Решение:
Выясним,
что точка
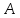 не принадлежит известным медианам
не принадлежит известным медианам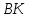 и
и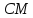 .
.
Найдём
координаты точки
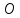 – пересечения медиан
– пересечения медиан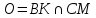 :
: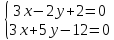 ⇒
⇒
т.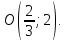
Продолжим
медиану
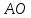 ,
,
и на её продолжении отложим отрезок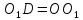 .
.
Соединим точку с вершинами
с вершинами и
и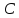 .
.
Полученный четырёхугольник – параллелограмм (его диагонали
– параллелограмм (его диагонали
пересекаясь в точке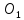 ,
,
делятся пополам).
Найдём
координаты точки
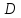 ,
,
как конца отрезка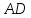 с известным началом
с известным началом и серединой
и серединой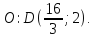
Найдём
уравнение прямой
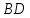 ,
,
зная, что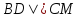 и точка
и точка лежит на этой прямой:
лежит на этой прямой: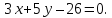
Найдём
координаты вершины
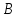 ,
,
как точки пересечения прямых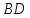 и
и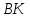 :
: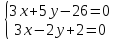 ⇒
⇒
т.
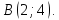
Точка
 – середина отрезка
– середина отрезка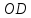 ,
,
поэтому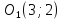 .
.
Найдём
координаты точки
 ,
,
как конца отрезка с известными началом
с известными началом и серединой
и серединой :
: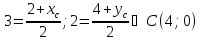 .
.
Зная
координаты всех вершин треугольника
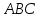 ,
,
найдём уравнения его сторон, как прямых
проходящих через две точки.
Ответ:
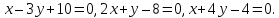
Задача
№12:
Составить
уравнения сторон треугольника, зная
одну из его вершин
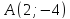 и уравнения биссектрис двух его углов:
и уравнения биссектрис двух его углов: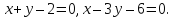
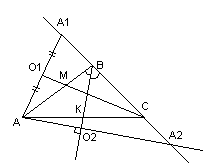
Решение:
Очевидно,
что точка
 не принадлежит заданным биссектрисам
не принадлежит заданным биссектрисам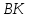 и
и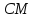 .
.
Найдём точку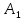 ,
,
симметричную точке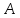 относительно биссектрисы
относительно биссектрисы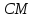 .
.
Можно доказать, что точка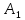 принадлежит прямой
принадлежит прямой .
.
Опустим из т. перпендикуляр на биссектрису
перпендикуляр на биссектрису до пересечения в точке
до пересечения в точке и отложим
и отложим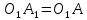 .
.
Т.к.
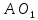 перпендикулярно
перпендикулярно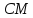 ,
,
то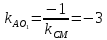 ;
;
точка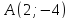 принадлежит прямой
принадлежит прямой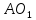 ,
,
поэтому её уравнение примет вид: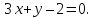
Координаты
точки
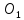 найдём как точки пересечения прямых
найдём как точки пересечения прямых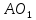 и
и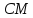 :
: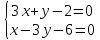 ⇒
⇒
т.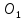 (
(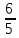 ;
;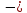
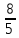 ).
).
Найдём
координаты точки
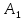 ,
,
как конца отрезка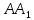 с известными началом
с известными началом и серединой
и серединой :
: (
(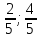 ).
).
Аналогично
найдём точку
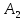 ,
,
симметричную т.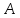 относительно биссектрисы
относительно биссектрисы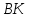 .
.
Точка принадлежит прямой
принадлежит прямой ,
, .
.
Тогда
уравнение стороны
 примет вид:
примет вид: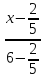
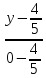 или
или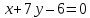 .
.
Найдём
координаты точек
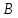 и
и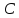 ,
,
как точек пересечения прямой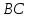 и заданных биссектрис:
и заданных биссектрис: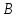 (
(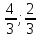 );
);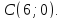
Зная
координаты вершин треугольника
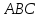 ,
,
найдём уравнения его сторон.
Ответ:
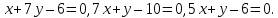
Задача
№13:
Составить
уравнения биссектрис углов, образованных
двумя пересекающимися прямыми:
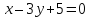 и
и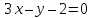 .
.
Решение:
Известно
свойство: биссектриса есть геометрическое
место точек, равноудалённых от сторон
угла.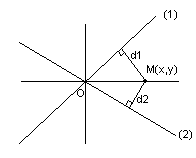
Пусть
 – произвольная точка искомой биссектрисы,
– произвольная точка искомой биссектрисы,
тогда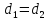 ;
;
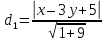 ;
;
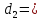
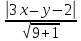 ;
;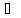
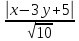
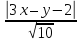 ;
;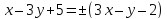 .
.
Тогда
уравнения биссектрис примут вид:
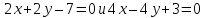 .
.
Ответ:
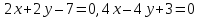 .
.
Задача
№14:
Составить
уравнение биссектрисы угла между прямыми
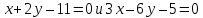 ,
,
в котором лежит точка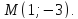
Решение:
Найдём
отклонение точки
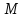 отзаданных
отзаданных
прямых, для этого приведём их уравнения
к нормальному виду: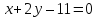 ;
;
нормирующий множитель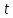
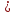 +
+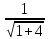
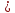
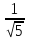 ;
;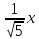 +
+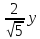
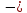
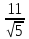
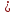 0.
0.
Найдём
отклонение
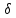 1
1
т.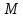 от прямой, для этого в левую часть
от прямой, для этого в левую часть
нормального уравнения подставим
координаты т. :
: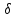 1
1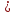
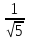 –
–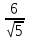 –
–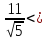 0.
0.
Аналогично
найдём отклонение
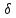 2
2
т. от второй прямой:
от второй прямой: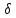 2
2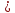 0.
0.
Отклонения имеют разные знаки, поэтому
при раскрытии модулей (см. решение
предыдущей задачи) справа ставим знак
«минус».
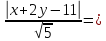
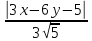 ⇒
⇒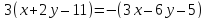
Уравнение
биссектрисы принимает вид:
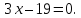
Ответ:
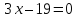 .
.
Задача
№15:
На
прямой
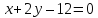 найти точки, равноудалённые от прямых
найти точки, равноудалённые от прямых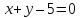 и
и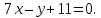
Решение:
Точки
равноудалённые от прямых
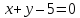 и
и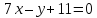 ,
,
лежат на биссектрисах углов, образованных
этими прямыми. Аналогично решению
предыдущих задач найдём их: .
.
Тогда
искомые точки являются точками пересечения
этих биссектрис и прямой
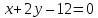 ,
,
поэтому найдём их, решая системы: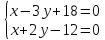 и
и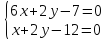 .
.
Ответ:
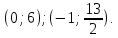
Задача
№16:
Составить
уравнения сторон треугольника, зная
одну из его вершин
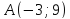 и уравнения медианы
и уравнения медианы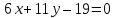 и высоты
и высоты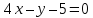 ,
,
проведённых из различных вершин.
Решение:
Убедимся,
что точка
 не принадлежит заданным медиане и
не принадлежит заданным медиане и
высоте.
Найдём
уравнение стороны
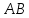 ,
,
зная, что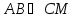 .
.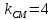 ⇒
⇒
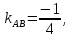
тогда уравнение примет вид:
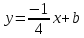 ,
,
зная координаты т.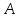 ,
,
принадлежащей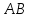 ,
,
найдём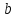 ,
,
тогда уравнение примет вид: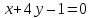 .
.
Найдём
координаты т.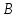 ,
,
как точки пересечения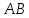 и
и
медианы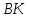 :
: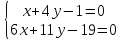 ⇒
⇒
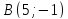 .
.
Пусть
точка
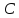 имеет координаты
имеет координаты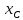 и
и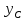 ,
,
найдём их. Точка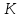 – середина
– середина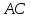 ,
,
поэтому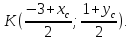
Точка
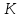 принадлежит медиане
принадлежит медиане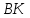 ,
,
точка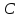 принадлежит высоте
принадлежит высоте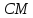 ,
,
поэтому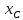 и
и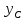 найдём, решая систему:
найдём, решая систему: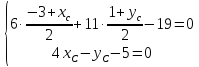
Откуда
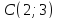 Зная координаты вершин треугольника,
Зная координаты вершин треугольника,
найдём уравнения всех его сторон.
Ответ:
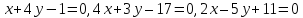 .
.
Задача
№17:
Через
точку
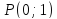 провести прямую так, чтобы её отрезок,
провести прямую так, чтобы её отрезок,
заключённый между прямыми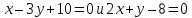 ,
,
делился бы в точке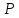 пополам.
пополам.
Решение:
Обозначим
через
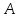 и
и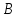 точки пересечения заданных прямых и
точки пересечения заданных прямых и
искомой прямой и пусть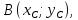 тогда
тогда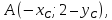 т.к.
т.к.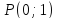 – середина отрезка
– середина отрезка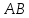 .
.
Координаты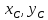 найдём, составив систему уравнений:
найдём, составив систему уравнений: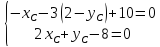 ⇒
⇒
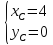 ⇒
⇒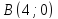 .
.
Составим
уравнение искомой прямой, которая
проходит через две точки, например,
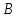 и
и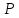 :
: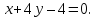
Ответ:
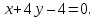
Задача
№18: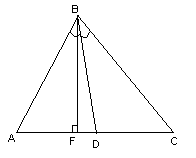
Составить
уравнения сторон треугольника
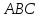 ,
,
зная одну из его вершин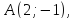 а также уравнение высоты
а также уравнение высоты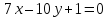 и биссектрисы
и биссектрисы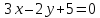 ,
,
проведённых из одной вершины. Решить
задачу, не вычисляя координат вершин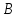 и
и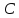 .
.
Решение:
Можно
проверить, что т.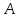 не принадлежит ни высоте,
не принадлежит ни высоте,
ни биссектрисе.
Найдём уравнение стороны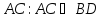 ,
,
поэтому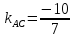 ;
;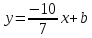 ,
,
зная координаты т.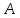 ,
,
найдём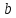 .
.
Итак,
уравнение
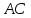 имеет вид:
имеет вид: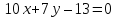 .
.
Рассмотрим
пучок с центром в т.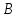 :
: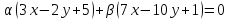 .
.
Пусть
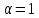 ,
,
тогда уравнение пучка примет вид:
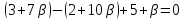 .
.
(1)
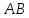 –прямая
–прямая
пучка, причём координаты т.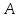 известны, поэтому найдём
известны, поэтому найдём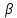 для прямой
для прямой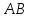 :
: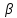
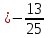 ,
,
поэтому уравнение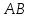 примет вид:
примет вид: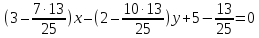 ,
,
т.е.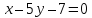 .
.
Найдём
угол между прямыми
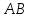 и
и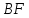 :tg
:tg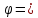
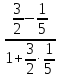
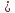 1⇒
1⇒
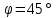 .
.
Тогда
угол
 равен 90°, т.е.
равен 90°, т.е.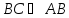 ;
;
–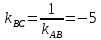 .
.
С другой стороны найдём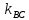 из уравнения (1):
из уравнения (1):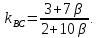
Итак,
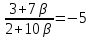 ⇒
⇒
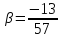 .
.
Найдём
уравнение стороны
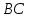 зная, что она принадлежит пучку. Подставим
зная, что она принадлежит пучку. Подставим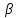 в уравнение (1) и получим уравнение
в уравнение (1) и получим уравнение
стороны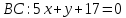 .
.
Ответ:
Образовательным
результатом после изучения данной темы
является сформированность компонент,
заявленных во введении, совокупности
компетенций (знать, уметь, владеть) на
двух уровнях: пороговый и продвинутый.
Пороговый уровень соответствует оценке
«удовлетворительно», продвинутый
уровень соответствует оценкам «хорошо»
или «отлично» в зависимости от результатов
защиты кейс-заданий.
Для
самостоятельной диагностики данных
компонент вам предлагаются следующие
задания.
Прямая имеет несколько видов задающих ее уравнений. Рассмотрим некоторые из них и разберем примеры.
Здесь будет калькулятор
Уравнение прямой с угловым коэффициентом
y=kx+by=kx+b,
где kk — угловой коэффициент, а bb — свободный коэффициент.
Уравнения данного вида составляются следующим образом по формуле:
y−y0=k(x−x0)y-y_0=k(x-x_0),
где (x0;y0)(x_0; y_0) — координаты любой точки, лежащей на данной прямой.
Составить уравнение прямой, если координаты точки, принадлежащей данной прямой, таковы: x0=1,y0=2x_0=1, y_0=2. Угловой коэффициент принять равным 11.
Решение
Подставляем значения в формулу:
y−y0=k(x−x0)y-y_0=k(x-x_0)
y−2=1⋅(x−1)y-2=1cdot(x-1)
Приводим подобные слагаемые:
y=x+1y=x+1
Ответ
y=x+1y=x+1
Общее уравнение прямой
Для приведения прямой к такому виду из предыдущего вида достаточно просто перенести все слагаемые в одну часть. Возьмем уравнение прямой из предыдущей задачи y=x+1y=x+1. Тогда общее уравнение этой прямой запишется в виде:
y−x−1=0y-x-1=0
Уравнение прямой по двум точкам
Если в задаче даны координаты двух точек и необходимо составить уравнение прямой, то это делается при помощи такой формулы:
x−x2x1−x2=y−y2y1−y2frac{x-x_2}{x_1-x_2}=frac{y-y_2}{y_1-y_2},
где (x1;y1),(x2;y2)(x_1; y_1), (x_2; y_2) — координаты двух точек, через которые проходит данная прямая.
Найти уравнение прямой, если координаты точек имеют значения: (2;3)(2;3) и (4;−1)(4;-1).
Решение
x1=2x_1=2
y1=3y_1=3
x2=4x_2=4
y2=−1y_2=-1
x−x2x1−x2=y−y2y1−y2frac{x-x_2}{x_1-x_2}=frac{y-y_2}{y_1-y_2}
x−42−4=y−(−1)3−(−1)frac{x-4}{2-4}=frac{y-(-1)}{3-(-1)}
x−4−2=y+14frac{x-4}{-2}=frac{y+1}{4}
x−4=−y−12x-4=frac{-y-1}{2}
y+1=2⋅(4−x)y+1=2cdot(4-x)
y=8−2x−1y=8-2x-1
y=−2x+7y=-2x+7
Ответ
y=−2x+7y=-2x+7
Уравнение прямой при помощи точки и вектора нормали
(x−x0)⋅n1+(y−y0)⋅n2=0(x-x_0)cdot n_1+(y-y_0)cdot n_2=0,
где (x0;y0)(x_0; y_0) — координаты точки, лежащей на данной прямой, а (n1;n2)(n_1; n_2) — координаты вектора нормали к этой прямой.
Составить уравнение прямой, если координаты нормального вектора — (1;−5)(1;-5), а точка, через которую проходит данная прямая имеет координаты (7;8)(7;8).
Решение
x0=7x_0=7
y0=8y_0=8
n1=1n_1=1
n2=−5n_2=-5
(x−x0)⋅n1+(y−y0)⋅n2=0(x-x_0)cdot n_1+(y-y_0)cdot n_2=0,
(x−7)⋅1+(y−8)⋅(−5)=0(x-7)cdot 1+(y-8)cdot (-5)=0,
x−7+40−5y=0x-7+40-5y=0
x−5y=−40+7x-5y=-40+7
x−5y=−33x-5y=-33
5y=x+335y=x+33
y=x5+335y=frac{x}{5}+frac{33}{5}
Проверка
Чтобы проверить правильность решения, достаточно подставить координаты точки в данное уравнение и, если оно будет верным, то задача решена верно.
8=75+3358=frac{7}{5}+frac{33}{5}
8=88=8 — верно, ответ правильный.
Ответ
y=x5+335y=frac{x}{5}+frac{33}{5}
Прямая в пространстве
Уравнение прямой, заданной в пространстве имеет такой вид:
x−x0ν1=y−y0ν2=z−z0ν3frac{x-x_0}{nu_1}=frac{y-y_0}{nu_2}=frac{z-z_0}{nu_3},
где (x0;y0;z0)(x_0;y_0;z_0) — координаты точки, через которую проходит прямая, а (ν1,ν2,ν3)(nu_1,nu_2,nu_3) — координаты напрявляющего вектора данной прямой.
Написать уравнение прямой по заданной точке (1;5;−23)(1;5;-23) и вектору направления (3;11;7)(3;11;7).
Решение
x0=1x_0=1
y0=5y_0=5
z0=−23z_0=-23
ν1=3nu_1=3
ν2=11nu_2=11
ν3=7nu_3=7
x−x0ν1=y−y0ν2=z−z0ν3frac{x-x_0}{nu_1}=frac{y-y_0}{nu_2}=frac{z-z_0}{nu_3}
x−13=y−511=z−(−23)7frac{x-1}{3}=frac{y-5}{11}=frac{z-(-23)}{7}
Проверка
Проверим, удовлетворяет ли это уравнение прямой точке (x0;y0;z0)(x_0;y_0;z_0). Для этого подставим в него координаты этой точки:
1−13=5−511=−23−(−23)7frac{1-1}{3}=frac{5-5}{11}=frac{-23-(-23)}{7} — верно, значит ответ правильный.
Такой вид уравнения прямой называется каноническим.
Ответ
x−13=y−511=z−(−23)7frac{x-1}{3}=frac{y-5}{11}=frac{z-(-23)}{7}
Тест по теме “Составление уравнения прямой”
Метод координат в пространстве
30 мая 2011
Для того, чтобы использовать метод координат, надо хорошо знать формулы. Их три:
-
Главная формула — косинус угла φ между векторами a = (x1; y1; z1) и b = (x2; y2; z2):
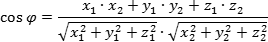
- Уравнение плоскости в трехмерном пространстве: Ax + By + Cz + D = 0, где A, B, C и D — действительные числа, причем, если плоскость проходит через начало координат, D = 0. А если не проходит, то D = 1.
- Вектор, перпендикулярный к плоскости Ax + By + Cz + D = 0, имеет координаты: n = (A; B; C).
На первый взгляд, выглядит угрожающе, но достаточно немного практики — и все будет работать великолепно.
Задача. Найти косинус угла между векторами a = (4; 3; 0) и b = (0; 12; 5).
Решение. Поскольку координаты векторов нам даны, подставляем их в первую формулу:
![]()
Задача. Составить уравнение плоскости, проходящей через точки M = (2; 0; 1), N = (0; 1; 1) и K = (2; 1; 0), если известно, что она не проходит через начало координат.
Решение. Общее уравнение плоскости: Ax + By + Cz + D = 0, но, поскольку искомая плоскость не проходит через начало координат — точку (0; 0; 0) — то положим D = 1. Поскольку эта плоскость проходит через точки M, N и K, то координаты этих точек должны обращать уравнение в верное числовое равенство.
Подставим вместо x, y и z координаты точки M = (2; 0; 1). Имеем:
A · 2 + B · 0 + C · 1 + 1 = 0 ⇒ 2A + C + 1 = 0;
Аналогично, для точек N = (0; 1; 1) и K = (2; 1; 0) получим уравнения:
A · 0 + B · 1 + C · 1 + 1 = 0 ⇒ B + C + 1 = 0;
A · 2 + B · 1 + C · 0 + 1 = 0 ⇒ 2A + B + 1 = 0;
Итак, у нас есть три уравнения и три неизвестных. Составим и решим систему уравнений:
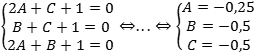
Получили, что уравнение плоскости имеет вид: − 0,25x − 0,5y − 0,5z + 1 = 0.
Задача. Плоскость задана уравнением 7x − 2y + 4z + 1 = 0. Найти координаты вектора, перпендикулярного данной плоскости.
Решение. Используя третью формулу, получаем n = (7; − 2; 4) — вот и все!
Вычисление координат векторов
А что, если в задаче нет векторов — есть только точки, лежащие на прямых, и требуется вычислить угол между этими прямыми? Все просто: зная координаты точек — начала и конца вектора — можно вычислить координаты самого вектора.
Чтобы найти координаты вектора, надо из координат его конца вычесть координаты начала.
Эта теорема одинаково работает и на плоскости, и в пространстве. Выражение «вычесть координаты» означает, что из координаты x одной точки вычитается координата x другой, затем то же самое надо сделать с координатами y и z. Вот несколько примеров:
Задача. В пространстве расположены три точки, заданные своими координатами: A = (1; 6; 3), B = (3; − 1; 7) и C = (− 4; 3; − 2). Найти координаты векторов AB, AC и BC.
Рассмотрим вектор AB: его начало находится в точке A, а конец — в точке B. Следовательно, чтобы найти его координаты, надо из координат точки B вычесть координаты точки A:
AB = (3 − 1; − 1 − 6; 7 − 3) = (2; − 7; 4).
Аналогично, начало вектора AC — все та же точка A, зато конец — точка C. Поэтому имеем:
AC = (− 4 − 1; 3 − 6; − 2 − 3) = (− 5; − 3; − 5).
Наконец, чтобы найти координаты вектора BC, надо из координат точки C вычесть координаты точки B:
BC = (− 4 − 3; 3 − (− 1); − 2 − 7) = (− 7; 4; − 9).
Ответ: AB = (2; − 7; 4); AC = (− 5; − 3; − 5); BC = (− 7; 4; − 9)
Обратите внимание на вычисление координат последнего вектора BC: очень многие ошибаются, когда работают с отрицательными числами. Это касается переменной y: у точки B координата y = − 1, а у точки C y = 3. Получаем именно 3 − (− 1) = 4, а не 3 − 1, как многие считают. Не допускайте таких глупых ошибок!
Вычисление направляющих векторов для прямых
Если вы внимательно прочитаете задачу C2, то с удивлением обнаружите, что никаких векторов там нет. Там только прямые да плоскости.
Для начала разберемся с прямыми. Здесь все просто: на любой прямой найдутся хотя бы две различные точки и, наоборот, любые две различные точки задают единственную прямую…
Кто-нибудь понял, что написано в предыдущем абзаце? Я и сам не понял, поэтому объясню проще: в задаче C2 прямые всегда задаются парой точек. Если ввести систему координат и рассмотреть вектор с началом и концом в этих точках, получим так называемый направляющий вектор для прямой:
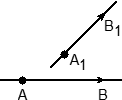
Зачем нужен этот вектор? Дело в том, что угол между двумя прямыми — это угол между их направляющими векторами. Таким образом, мы переходим от непонятных прямых к конкретным векторам, координаты которых легко считаются. Насколько легко? Взгляните на примеры:
Задача. В кубе ABCDA1B1C1D1 проведены прямые AC и BD1. Найдите координаты направляющих векторов этих прямых.
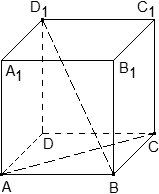
Поскольку длина ребер куба в условии не указана, положим AB = 1. Введем систему координат с началом в точке A и осями x, y, z, направленными вдоль прямых AB, AD и AA1 соответственно. Единичный отрезок равен AB = 1.
Теперь найдем координаты направляющего вектора для прямой AC. Нам потребуются две точки: A = (0; 0; 0) и C = (1; 1; 0). Отсюда получаем координаты вектора AC = (1 − 0; 1 − 0; 0 − 0) = (1; 1; 0) — это и есть направляющий вектор.
Теперь разберемся с прямой BD1. На ней также есть две точки: B = (1; 0; 0) и D1 = (0; 1; 1). Получаем направляющий вектор BD1 = (0 − 1; 1 − 0; 1 − 0) = (− 1; 1; 1).
Ответ: AC = (1; 1; 0); BD1 = (− 1; 1; 1)
Задача. В правильной треугольной призме ABCA1B1C1, все ребра которой равны 1, проведены прямые AB1 и AC1. Найдите координаты направляющих векторов этих прямых.
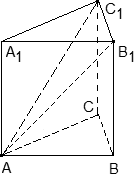
Введем систему координат: начало в точке A, ось x совпадает с AB, ось z совпадает с AA1, ось y образует с осью x плоскость OXY, которая совпадает с плоскостью ABC.
Для начала разберемся с прямой AB1. Тут все просто: у нас есть точки A = (0; 0; 0) и B1 = (1; 0; 1). Получаем направляющий вектор AB1 = (1 − 0; 0 − 0; 1 − 0) = (1; 0; 1).
Теперь найдем направляющий вектор для AC1. Все то же самое — единственное отличие в том, что у точки C1 иррациональные координаты. Итак, A = (0; 0; 0), поэтому имеем:
![]()
Ответ: AB1 = (1; 0; 1);
![]()
Небольшое, но очень важное замечание насчет последнего примера. Если начало вектора совпадает с началом координат, вычисления резко упрощаются: координаты вектора просто равны координатам конца. К сожалению, это верно лишь для векторов. Например, при работе с плоскостями присутствие на них начала координат только усложняет выкладки.
Вычисление нормальных векторов для плоскостей
Нормальные векторы — это не те векторы, у которых все в порядке, или которые чувствуют себя хорошо. По определению, нормальный вектор (нормаль) к плоскости — это вектор, перпендикулярный данной плоскости.
Другими словами, нормаль — это вектор, перпендикулярный любому вектору в данной плоскости. Наверняка вы встречали такое определение — правда, вместо векторов речь шла о прямых. Однако чуть выше было показано, что в задаче C2 можно оперировать любым удобным объектом — хоть прямой, хоть вектором.
Еще раз напомню, что всякая плоскость задается в пространстве уравнением Ax + By + Cz + D = 0, где A, B, C и D — некоторые коэффициенты. Не умаляя общности решения, можно полагать D = 1, если плоскость не проходит через начало координат, или D = 0, если все-таки проходит. В любом случае, координаты нормального вектора к этой плоскости равны n = (A; B; C).
Итак, плоскость тоже можно успешно заменить вектором — той самой нормалью. Всякая плоскость задается в пространстве тремя точками. Как найти уравнение плоскости (а следовательно — и нормали), мы уже обсуждали в самом начале статьи. Однако этот процесс у многих вызывает проблемы, поэтому приведу еще парочку примеров:
Задача. В кубе ABCDA1B1C1D1 проведено сечение A1BC1. Найти нормальный вектор для плоскости этого сечения, если начало координат находится в точке A, а оси x, y и z совпадают с ребрами AB, AD и AA1 соответственно.
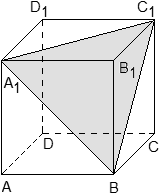
Поскольку плоскость не проходит через начало координат, ее уравнение выглядит так: Ax + By + Cz + 1 = 0, т.е. коэффициент D = 1. Поскольку эта плоскость проходит через точки A1, B и C1, то координаты этих точек обращают уравнение плоскости в верное числовое равенство.
Подставим вместо x, y и z координаты точки A1 = (0; 0; 1). Имеем:
A · 0 + B · 0 + C · 1 + 1 = 0 ⇒ C + 1 = 0 ⇒ C = − 1;
Аналогично, для точек B = (1; 0; 0) и C1 = (1; 1; 1) получим уравнения:
A · 1 + B · 0 + C · 0 + 1 = 0 ⇒ A + 1 = 0 ⇒ A = − 1;
A · 1 + B · 1 + C · 1 + 1 = 0 ⇒ A + B + C + 1 = 0;
Но коэффициенты A = − 1 и C = − 1 нам уже известны, поэтому остается найти коэффициент B:
B = − 1 − A − C = − 1 + 1 + 1 = 1.
Получаем уравнение плоскости: − A + B − C + 1 = 0, Следовательно, координаты нормального вектора равны n = (− 1; 1; − 1).
Задача. В кубе ABCDA1B1C1D1 проведено сечение AA1C1C. Найти нормальный вектор для плоскости этого сечения, если начало координат находится в точке A, а оси x, y и z совпадают с ребрами AB, AD и AA1 соответственно.
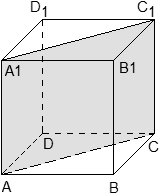
В данном случае плоскость проходит через начало координат, поэтому коэффициент D = 0, а уравнение плоскости выглядит так: Ax + By + Cz = 0. Поскольку плоскость проходит через точки A1 и C, координаты этих точек обращают уравнение плоскости в верное числовое равенство.
Подставим вместо x, y и z координаты точки A1 = (0; 0; 1). Имеем:
A · 0 + B · 0 + C · 1 = 0 ⇒ C = 0;
Аналогично, для точки C = (1; 1; 0) получим уравнение:
A · 1 + B · 1 + C · 0 = 0 ⇒ A + B = 0 ⇒ A = − B;
Положим B = 1. Тогда A = − B = − 1, и уравнение всей плоскости имеет вид: − A + B = 0, Следовательно, координаты нормального вектора равны n = (− 1; 1; 0).
Вообще говоря, в приведенных задачах надо составлять систему уравнений и решать ее. Получится три уравнения и три переменных, но во втором случае одна из них будет свободной, т.е. принимать произвольные значения. Именно поэтому мы вправе положить B = 1 — без ущерба для общности решения и правильности ответа.
Координаты середины отрезка
Очень часто в задаче C2 требуется работать с точками, которые делят отрезок пополам. Координаты таких точек легко считаются, если известны координаты концов отрезка.
Итак, пусть отрезок задан своими концами — точками A = (xa; ya; za) и B = (xb; yb; zb). Тогда координаты середины отрезка — обозначим ее точкой H — можно найти по формуле:
![]()
Другими словами, координаты середины отрезка — это среднее арифметическое координат его концов.
Задача. Единичный куб ABCDA1B1C1D1 помещен в систему координат так, что оси x, y и z направлены вдоль ребер AB, AD и AA1 соответственно, а начало координат совпадает с точкой A. Точка K — середина ребра A1B1. Найдите координаты этой точки.
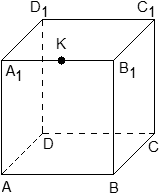
Поскольку точка K — середина отрезка A1B1, ее координаты равных среднему арифметическому координат концов. Запишем координаты концов: A1 = (0; 0; 1) и B1 = (1; 0; 1). Теперь найдем координаты точки K:
![]()
Задача. Единичный куб ABCDA1B1C1D1 помещен в систему координат так, что оси x, y и z направлены вдоль ребер AB, AD и AA1 соответственно, а начало координат совпадает с точкой A. Найдите координаты точки L, в которой пересекаются диагонали квадрата A1B1C1D1.
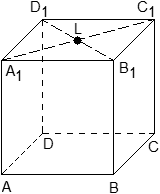
Из курса планиметрии известно, что точка пересечения диагоналей квадрата равноудалена от всех его вершин. В частности, A1L = C1L, т.е. точка L — это середина отрезка A1C1. Но A1 = (0; 0; 1), C1 = (1; 1; 1), поэтому имеем:
![]()
Ответ: L = (0,5; 0,5; 1)
Смотрите также:
- Введение системы координат

- Четырехугольная пирамида в задаче C2

- В 2012 году ЕГЭ по математике станет двухуровневым?

- Сводный тест по задачам B12 (1 вариант)

- Симметрия корней и оптимизация ответов в тригонометрии

- ЕГЭ 2022, задание 6. Касательная и уравнение с параметром


