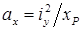Уравнение нулевой линии
Для
получения уравнения нулевой линии
достаточно приравнять напряжения (8.1)
нулю:
Математически
это уравнение прямой в отрезках:

где

Нулевую
линию можно построить с помощью отрезков,
отсекаемых этой прямой на координатных
осях, которые определяются поочередным
заданием нулевых значений каждой из
координат:
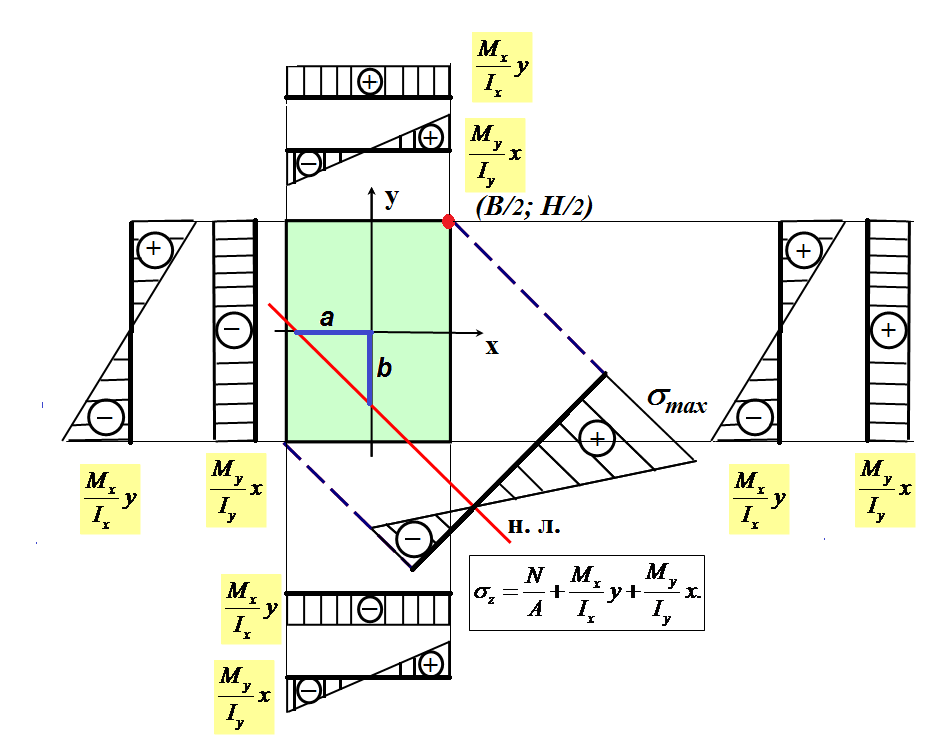
Рис. 8.5
На рис. 8.5 показаны
эпюры напряжений для случая положительных
изгибающих моментов. В этом случае
величины отрезков a,
b,
отсекаемых нейтральной линией (8.2) от
осей координат будут отрицательны.
Показаны законы изменения составляющих
нормальных напряжений от действия
положительных изгибающих моментов
вдоль сторон прямоугольного сечения
шириной В
и высотой Н.
Построена
епюра нормальных напряжений z .
Максимальное
напряжение max
будет
достигаться в правом верхнем углу
сечения где все три слагаемых в формуле
(8.1) будут положительны.
8.2 Расчет балки, подверженной косому или пространственному изгибу
Косым
называют
изгиб, при
котором плоскость действия изгибающего
момента ,
возникающего в сечении, не совпадает
ни с одной из главных плоскостей бруса
(при этом плоскость действия изгибающего
момента обязательно должна проходить
через центр тяжести сечения) (рис. 8.6).
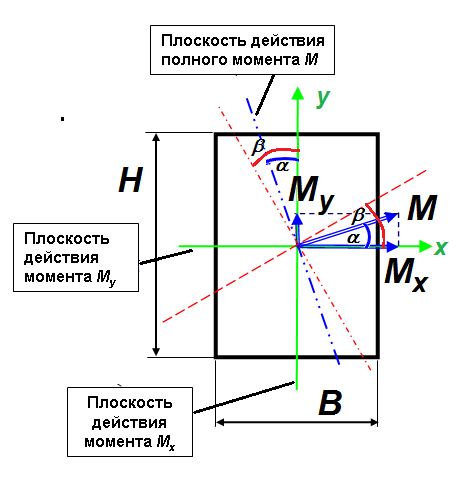
Рис. 8.6
При косом изгибе
изогнутая ось представляет собой плоскую
кривую, и плоскость, в которой она
расположена, не совпадает с плоскостью
действия нагрузки. При пространственном
изгибе
нагрузка приложена в разных плоскостях,
деформированная ось является
пространственной кривой.
Определение внутренних усилий при косом изгибе
Внутренние усилия
при косом изгибе определяются как и при
поперечном изгибе методом сечений. В
поперечных сечениях бруса действуют
следующие внутренние усилия: Mx,
My
– изгибающие моменты и Qx,
Qy
–поперечные (перерезывающие) силы.
Правило знаков
для внутренних усилий:
изгибающие моменты – положительны,
если вызывают растяжение в первом
квадранте координатной системы Oxyz;
поперечные силы – положительны, если
под их действием отсеченный элемент
поворачивается по
часовой
стрелке.
Если разложить
внешние силы по главным осям инерции
Ох
и Оу (рис.
8.6),
то получим две системы сил, каждая из
которых
вызывает прямой изгиб с изгибающими
моментами Мx
и My.
Следовательно,
сочетание двух прямых (плоских) изгибов
вызывает косой изгиб.
То есть мы имеем
частный случай уже рассмотренного в п.
8.1
напряженного состояния бруса, когда,
отсутствует продольная сила (N =0) при
одновременном действии изгибающих
моментов Mx и My.
И
нормальные напряжения в произвольной
точке сечения теперь определяется
выражением:
(8.4)
Изобразим изгибающие
моменты в виде векторов моментов пар
сил, как это делалось в теоретической
механике, совпадающими по направлению
с положительными направлениями осей:
Рис. 8.7
Полный изгибающий
момент есть векторная сумма этих
векторов, модуль которого равен:
Изгибающие моменты
и полный момент связаны известными
соотношениями:
Тогда
напряжения (8.4) в произвольной точке
сечения можно выразить через полный
изгибающий момент:
(8.5)
Здесь учтено,
что напряжения в первой четверти (x
> 0 и y
> 0) от изгибающего момента My
отрицательны, поскольку поворот плоскости
поперечного сечения от этого момента
происходит против часовой стрелки при
взгляде навстречу вектору момента и
вызывает сжатие волокон в этой четверти
О
положение нейтральной линии, задавая
напряжения (8.5) равными нулю:
или
Окончательно
получаем
(8.6)
Уравнение нейтральной
линии представляет собой уравнение
прямой, проходящей через начало координат.
Тангенс угла наклона (угловой коэффициент)
равен:
(8.7)
В
случае Ix
> Iy,
что обычно и бывает при проектировании
балки, несущей преимущественно
вертикальную нагрузку, угол наклона
нулевой линии b
больше угла наклона полного изгибающего
момента a.
Это означает, что полный
прогиб не совпадает с плоскостью действия
полного момента.
Отсюда и происходит название косого
изгиба.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Для внецентренно сжатой колонны из хрупкого материала построить эпюры напряжений по контуру сечения, дать оценку прочности. Сила F =100 кН приложена в точке 2. Построить ядро сечения. Допускаемые напряжения на растяжение [σр]=3 МПа, на сжатие [σс]=30 МПа.
- Определим координаты центра тяжести сечения. Сечение вычертим строго в масштабе. Разобьем фигуру на 1, 2, 3 – прямоугольники, 4, 5 – прямоугольные треугольники.
Ось у – ось симметрии, значит хС=0. Выбираем случайную ось х1 по низу сечения.
Координаты «у» фигур:
Проводим главные центральные оси через центр тяжести сечения.
2.Определяем необходимые геометрические характеристики для расчета. Моменты инерции сечений определяем по формулам перехода:
где а – расстояние от центра тяжести каждой фигуры до оси х.
Аналогично ,
где b – расстояние от центра тяжести каждой фигуры до оси у.
Определим квадраты радиусов инерции.
Общая площадь сечения А=1920см2.
- Определим положение нулевой линии (линии, напряжения в которой равны 0) и построим эпюры напряжений по сторонам заданного сечения.
Т.2 – точка приложения силы.
Определим её координаты.
хF=-36 см, уF=20-17,3=2,7 см.
Координаты нулевой линии:
Проводим нулевую линию, отсекая на главных осях х и у найденные координаты.
Напряжения в точках сечения будем определять по формуле:
где F – сжимающая сила,
А – площадь сечения,
хF, уF – координаты точки приложения силы,
х, у – координаты точки, в которой определяется напряжение.
Определим координаты точек по контуру сечения и напряжения в них.
Чтобы дать заключение о прочности, сравним максимальные сжимающие и растягивающие напряжения с допускаемыми напряжениями.
σmax p= 1,48 МПа < [σр]=3 МПа;
|σmax с|=2,24 МПа < [σс]=30 МПа.
Прочность обеспечена.
- Построение ядра сечения.
Для построения ядра сечения следует вычертить сечение в масштабе и провести нулевую линию по её координатам.
Проведем сечения по граням фигуры (I-I, II-II … VI-VI).
Пусть сечение I-I является нулевой линией, тогда координаты этой нулевой линии будут:
х0=∞ (параллельна оси х), у0=22,7 см.
Определяем координаты ядра сечения по формулам:
Тогда для сечения I-I:
Пусть сечение II-II является нулевой линией. Как видно из рисунка, сечение II-II наклонно, его координаты можно определить различными способами: из подобия треугольников, с помощью тригонометрических функций, при помощи измерений в масштабе.
Для второго сечения измерим отрезки, которые сечение II отсекает на осях х и у.
Пусть сечение III-III – нулевая линия
Строим ядро сечения по определенным координатам.
Как видно из рисунка, нулевая линия и ядро сечения соприкасаются в т. 5, ядро построено верно (нулевая линия не должна проходить сквозь ядро сечения, может соприкасаться в точке или грани).
Нулевая линия при внецентренном сжатии
Преобразуем формулу моментов при внецентренном сжатии 
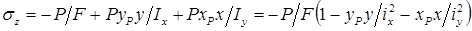
Обозначим координаты некоторой точки нулевой линии при внецентренном сжатии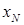
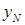
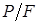
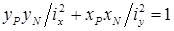
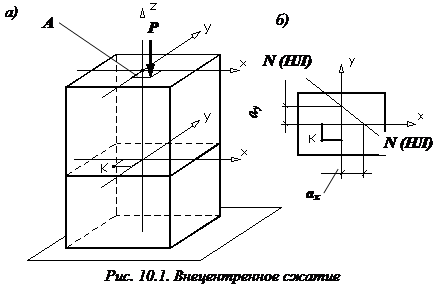
Нулевая линия при внецентренном сжатии и точка приложения нагрузки всегда расположены по разные стороны от центра тяжести поперечного сечения (см. рис. 10.1, б).
Отрезки, отсекаемые нулевой линией от осей координат, обозначенные 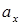
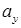
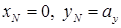
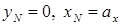
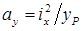
Многие элементы строительных конструкций (колонны, стойки, опоры) находятся под воздействием сжимающих сил, приложенных не в центре тяжести сечения. На рис. 12.9 показана колонна, на которую опирается балка перекрытия. Как видно, сила действует по отношению к оси колонны с эксцентриситетом е,
и таким образом, в произвольном сечении а-а
колонны наряду с продольной силой N
= -Р
возникает изгибающий момент, величина которого равна Ре.
Внецентренное растяжение (сжатие) стержня представляет такой вид деформирования, при котором равнодействующие внешних сил действуют вдоль прямой, параллельной оси стержня. В дальнейшем будем рассматривать главным образом задачи внецентренного сжатия. При внецентренном растяжении во всех приводимых расчетных формулах следует изменить знак перед силой Р
на противоположный.
Пусть стержень произвольного поперечного сечения (рис. 12.10) нагружен на торце внецентренно приложенной сжимающей силой Р,
направленной параллельно оси Ох.
Примем положительные
направления главных осей инерции сечения Оу
и Oz
таким образом, чтобы точка приложения силы Р
находилась в первой четверти осей координат. Обозначим координаты точки приложения силы Р
через у р
и z P –
Внутренние усилия в произвольном сечении стержня равны
Знаки минус у изгибающих моментов обусловлены тем, что в первой четверти осей координат эти моменты вызывают сжатие. Величины внутренних усилий в данном примере не изменяются по длине стержня, и таким образом, распределение напряжений в сечениях, достаточно удаленных от места приложения нагрузки, будет одинаковым.
Подставляя (12.11) в (12.1), получим формулу для нормальных напряжений при внецентренном сжатии:
Эту формулу можно преобразовать к виду
где i , i-
главные радиусы инерции сечения. При этом
Положив в (12.12) о = 0, получим уравнение нулевой линии:
Здесь у 0 и z 0 –
координаты точек нулевой линии (рис. 12.11). Уравнение (12.14) является уравнением прямой, не проходящей через центр тяжести сечения. Чтобы провести нулевую линию, найдем точки ее пересечения с осями координат. Полагая в (12.14) последовательно у 0 = 0 и z 0
= 0, соответственно найдем
где a z
и а у –
отрезки, отсекаемые нулевой линией на осях координат (рис. 12.11).
Установим особенности положения нулевой линии при вне- центренном сжатии.
- 1. Из формул (12.15) следует, что а у
и a z
имеют знаки, противоположные знакам соответственно у р
и z P –
Таким образом, нулевая линия проходит через те четверти осей координат, которые не содержат точку приложения силы (рис. 12.12). - 2. С приближением точки приложения силы Р
по прямой к центру тяжести сечения координаты этой точки у р
и z P
уменьшаются. Из (12.15) следует, что при этом абсолютные значения длин отрезков а у
и a z
увеличиваются, то есть нулевая линия удаляется от центра тяжести, оставаясь параллельной самой себе (рис. 12.13). В пределе при Z P = y P =
0 (сила приложена в центре тяжести) нулевая линия удаляется в бесконечность. В этом случае в сечении напряжения будут постоянными и равными о = -P/F.
- 3. Если точка приложения силы Р
находится на одной из главных осей, нулевая линия параллельна другой оси. Действительно, положив в (12.15), например, у р
= 0, получим, что а у
= то есть нулевая линия не пересекает ось Оу
(рис. 12.14). - 4. Если точка приложения силы перемещается по прямой, не проходящей через центр тяжести, то нулевая линия поворачивается вокруг некоторой точки. Докажем это свойство. Точкам приложения сил Р х
и Р 2 ,
расположенным на осях координат, соответствуют нулевые линии 1 – 1 и 2-2, параллельные осям (рис. 12.15), которые пересекаются в точке D.
Так как эта точка принадлежит двум нулевым линиям, то напряжения в этой точке от одновременно приложенных сил Р х
и Р 2
будут равны нулю. Поскольку любую силу Р 3 ,
точка приложения которой расположена на прямой Р { Р 2 ,
можно
разложить на две параллельные составляющие, приложенные в точках Pj и Р 2 ,
то отсюда следует, что напряжения в точке D
от действия силы Р 3
также равны нулю. Таким образом, нулевая линия 3-3, соответствующая силе Р 3 ,
проходит через точку D.
Другими словами, множеству точек Р,
расположенных на прямой Р { Р 2 ,
соответствует пучок прямых, проходящих, через точку D.
Справедливо и обратное утверждение: при вращении нулевой линии вокруг некоторой точки точка приложения силы перемещается по прямой, не проходящей через центр тяжести.
Если нулевая линия пересекает сечение, то она делит его на зоны сжатия и растяжения. Так же как и при косом изгибе, из гипотезы плоских сечений следует, что напряжения достигают наибольших значений в точках, наиболее удаленных от нулевой линии. Характер эпюры напряжений в этом случае показан на рис. 12.16, а.
Если нулевая линия расположена вне сечения, то во всех точках сечения напряжения будут одного знака (рис. 12.16, б).
Пример 12.3.
Построим эпюру нормальных напряжений в произвольном сечении внецентренно сжатой колонны прямоугольного сечения с размерами b
х h
(рис. 12.17). Квадраты радиусов инерции сечения согласно (12.22) равны
Отрезки, отсекаемые нулевой линией на осях координат, определяются по формулам (12.15):
Подставляя последовательно в (12.12) координаты наиболее удаленных от нулевой линии точек С и В
(рис. 12.18)
найдем
Эпюра о показана на рис. 12.18. Наибольшие сжимающие напряжения по абсолютной величине в четыре раза превосходят значения напряжений, которые были бы в случае центрального приложения силы. Кроме того, в сечении появились значительные растягивающие напряжения. Заметим, что из (12.12) следует, что в центре тяжести (у = z
= 0) напряжения равны о = -P/F.
Пример 12.4.
Полоса с вырезом нагружена растягивающей силой Р
(рис. 12.19, а).
Сравним напряжения в сечении ЛВ,
достаточно удаленном от торца и места выреза, с напряжениями в сечении CD
в месте выреза.
В сечении АВ
(рис. 12.19, б)
сила Р
вызывает центральное растяжение и напряжения равны а = P/F = P/bh.
В сечении CD
(рис. 12.19, в)
линия действия силы Р
не проходит через центр тяжести сечения, и поэтому возникает внецентренное растяжение. Изменив знак в формуле (12.12) на противоположный и приняв у р
= 0, получим для этого сечения
Принимая
Нулевая линия в сечении CD
параллельна оси Оу
и пересекает ось Oz
на расстоянии а =
-i 2 y /z P
– Ь/
12. В наиболее удаленных от нулевой линии точках сечения C(z – -Ь/
4) и D(z – Ь/
4) напряжения согласно (12.16) равны
Эпюры нормальных напряжений для сечений ЛВ
и CD
показаны на рис. 12.19, б, в.
Таким образом, несмотря на то что сечение CD
имеет площадь в два раза меньшую, чем сечение АВ,
за счет внецентренного приложения силы растягивающие напряжения в ослабленном сечении возрастают не в два, а в восемь раз. Кроме того, в этом сечении появляются значительные по величине сжимающие напряжения.
Следует заметить, что в приведенном расчете не учитываются дополнительные местные напряжения, возникающие вблизи точки С из-за наличия выточки. Эти напряжения зависят от радиуса выточки (с уменьшением радиуса они увеличиваются) и могут значительно превысить по величине найденное значение а с
= 8P/bh.
При этом характер эпюры напряжений вблизи точки С будет существенно отличаться от линейного. Определение местных напряжений (концентрация напряжений) рассматривается в главе 18.
Многие строительные материалы (бетон, кирпичная кладка и др.) плохо сопротивляются растяжению. Их прочность на растяжение во много раз меньше, чем на сжатие. Поэтому в элементах конструкций из таких материалов нежелательно появление растягивающих напряжений. Чтобы это условие выполнялось, необходимо, чтобы нулевая линия находилась вне сечения. В противном случае нулевая линия пересечет сечение и в нем появятся растягивающие напряжения. Если нулевая линия является касательной к контуру сечения, то соответствующее положение точки приложения силы является предельным. В соответствии со свойством 2 нулевой линии, если точка приложения силы будет приближаться к центру тяжести сечения, нулевая линия будет удаляться от него. Геометрическое место предельных точек, соответствующих различным касательным к контуру сечения, является границей ядра сечения.
Ядром сечения называется выпуклая область вокруг центра тяжести, обладающая следующим свойством: если точка приложения силы находится внутри или на границе этой области, то во всех точках сечения напряжения имеют один знак. Ядро сечения является выпуклой фигурой, поскольку нулевые линии должны касаться огибающей контура сечения и не пересекать его.
Через точку А
(рис. 12.20) можно провести бесчисленное множество касательных (нулевых линий); при этом только касательная АС
является касательной к огибающей, и ей должна соответствовать определенная точка контура ядра сечения. В то же время, например, нельзя провести касательную к участку АВ
контура сечения, поскольку она пересекает сечение.
Построим ядро сечения для прямоугольника (рис. 12.21). Для касательной 1 – 1 а 7 – Ь/
2; а
= . Из (12.15) находим для точки 1, соответствующей этой касательной, z P = -i 2 y / а 7 =-Ь/6; у р –
0. Для касательной 2-2 а у – к/
2; а 7 =°°,
и координаты точки 2 будут равны у
р
– -h/6; z P –
0. Согласно свойству 4 нулевой линии точки приложения силы, соответствующие различным касательным к правой нижней угловой точке сечения, расположены на прямой 1-2. Положение точек 3 и 4 определяется из условий симметрии. Таким образом, ядро сечения для прямоугольника представляет собой ромб с диагоналями Ь
/3 и И/З
.
Чтобы построить ядро сечения для круга, достаточно провести одну касательную (рис. 12.22). При этом а = R; а
= °о.
“У У ^ ^
Учитывая, что для круга i у – J у /F – R /
4, из (12.15) получим
Таким образом, ядро сечения для круга представляет собой круг с радиусом R/4.
На рис. 12.23, а, 6
показаны ядра сечения для двутавра и швеллера. Наличие четырех угловых точек ядра сечения в каждом из этих примеров обусловлено тем, что огибающая контура и у двутавра и у швеллера является прямоугольником.
Расчет стержней при внецентренном сжатии-растяжении
Пример
1.
Чугунный короткий
стержень сжимается продольной силой F
= 600 кН, приложенной в точке В
.
Требуется:
1. Определить
положение нейтральной линии;
2. Вычислить
наибольшие растягивающие и наибольшие сжимающие напряжения.
Решение.
1. Изобразим
сечение в масштабе.
2. Определим
положение главных центральных осей. Сечение обладает осью симметрии, поэтому
ось
Y
можем
показать сразу.
3. Определим
положение центра тяжести фигуры (фи
гура состоит из
двух квадратов). Выберем произвольную вспомогательную систему координат.
х 1 С 1 Y
–
вспомогательная система координат;
определим
координаты точек С
1
и С
2 в системе х 1 С 1 Y
.
А
1
, А
2 – площадь первого и
второго квадрата соответственно.
А = А 1
–
А 2
– площадь всей фигуры.
А
1
=
b
2 = 2500 см 2
С
(х
с
= 0; у
с = -5,89) –
положение центра тяжести во вспомогательной системе координат х 1 С 1 Y
.
Ось X
проводим перпендикулярно оси Y
через точку С
.
Так как
сечение симметричное, то XС
Y
– главная центральная система координат.
4. Определим
главные центральные моменты инерции и квадраты главных радиусов сечения.
где а
1
=
5,89см – расстояние между осями Х
и х
1 ;
а
2
= 5,89 + 17,68 = 23,57 – расстояние
между осями Х
и х
2 .
5. Определим
координаты точки В
(точки приложения силы) в главной центральной системе координат х с Су с.
6. Определим
положение нейтральной линии.
,
где х
N
, у
N
– координаты точек нейтральной линии.
В данной
задаче
Нейтральная
линия проходит через точку (х
N
=0;у
N
=11,36) параллельно
оси х
с.
7. В данной
задаче на стержень действует сжимающая сила, поэтому нормальные напряжения в
любой точке поперечного сечения будем определять по формуле
гдех, у
– это координаты точки, в которой считают напряжения.
8. Наибольшие
сжимающие напряжения достигаются в точке В
.
Эта точка,наиболее удаленная от
нейтральной линии в области сжатия.
Наибольшее
растягивающие напряжения достигаются в точках К
и
L
y
K
= у
L
= 23,57 см.
Ответ:
,
Пример 2.
Построить ядро
сечения.
Решение.
1. Определяем
тип контура ядра сечения.
2.
Определяемчисло вершин многоугольника,
получившегося внутри контура (то есть число предельных касательных к сечению
стержня). 6 предельных касательных – 6 вершин.
3. Определяем
положение главных центральных осей. Сечение обладает горизонтальной осью
симметрии, поэтому ось «Х
» можем
показать сразу. ХО
Y
0 – вспомогательная система координат (ось «Y
0 »проводим произвольно).
Сечение
состоит из двух простых фигур (прямоугольника и квадрата). Определим координаты
центров тяжести С
1
и С
2 в произвольной
системе координат ХО
Y
0 .
Центр тяжести
прямоугольника.
Центр тяжести
квадрата.
Площадь
прямоугольника.
Площадь квадрата.
(так как С
1
и С
2 лежат на оси).
Центр тяжести
всего сечения в системе координат ХО
Y
0 имеет координаты С
(0,015; 0). (Покажем на
чертеже).
Ось
Y
проводим перпендикулярно оси Y
0 через центр тяжести С
.
Так как
сечение симметричное, то ось симметрии и ось ей перпендикулярная, проходящая
через центр тяжести образуют главную центральную систему координат.
X, Y
– главные центральные оси сечения.
4. Определяем
геометрические характеристики сечения относительно главных центральных осей.
Вычисляем
главные центральные моменты инерции J
x
и J
y
.
Главные центральные
моменты инерции прямоугольника.
Главные центральные
моменты инерции квадрата.
(здесь использовали формулы для определения моментов инерции
относительно параллельных осей.
Осевые моменты инерции плоского сечения
относительно произвольных осей х
1
и у
1 ,
параллельных центральным осям х
и у
, определяют по формулам
;
где а,
b
– расстояния между
осями х
и х
1 , у
и у
1 , А
– площадь поперечного сечения. принимается, что х, у
– центральные оси, то есть оси,
проходящие через центр тяжести С
плоского сечения).
Вычислим
квадраты главных радиусов инерции
5. Определяем
вершины ядра сечения.
Пусть известно
положение нейтральной линии. Требуется определить координаты точки приложения
силы.
1. Рассмотрим
положение нейтральной линии 1 – 1.
Используем
свойство нейтральной линии. Так как нейтральная линия 1–1 проходит параллельно
оси Y
, то точка приложения силы Я
1
находится на оси X
, то есть у
F
=0.
х
N
–
абсцисса точки нейтральной линии 1 – 1 (расстояние отточки С
до нейтральной линии 1 – 1).
2. Рассмотрим
положение нейтральной линии 2 – 2.
Возьмем две
точки нейтральной линии 2 – 2 (лучше выбирать точки, где легко можно подсчитать
координаты)
В
(-0,615; 0,3)и D
(-0,015; 0,6)
Подставим
координаты точек В
и D
в
уравнение нейтральной линии.
(1)
(2)
Решим систему
уравнений (1) – (2)
Из первого
уравнения
(3)
Подставим (3)
в (2)
3. Рассмотрим
положение нейтральной линии 3 – 3.
Используем
свойство нейтральной линии. Так как нейтральная линия 3 – 3 проходит
параллельно оси X
, то точка
приложения силы Я
3
находится на оси Y
, то есть х
F
=0.
у
N
– ордината точки нейтральной
линии 3 – 3 (расстояние от точки С
до нейтральной линии 3 – 3).
4. Рассмотрим
положение нейтральной линии 4 – 4.
Используем
свойство нейтральной линии. Так как нейтральная линия 4 – 4 проходит
параллельно оси Y
, то точка
приложения силы Я
4
находится на оси X
, то есть у
F
= 0.
Пример
3
.
Жесткий
стержень загружен двумя силами – растягивающей
и
сжимающей (рис. 1). Стержень выполнен из хрупкого материала с
характеристиками и . Сечение стержня симметрично и имеет форму и размеры,
соответствующие рис. 2.
Требуется:
1) найти допускаемую нагрузку на стержень из
условия прочности, если отношение сжимающей и растягивающей сил
2) построить ядро сечения.
Рис.1Рис.2
Решение.
Положение
главных центральных осей инерции и моменты инерции относительно этих осей
заданного сечения найдены ранее (см. раздел «Геометрические характеристики
плоских сечений»). Найдем внутренние усилия в произвольном сечении стержня:
Для
определения положения опасных точек построим нейтральную линию. Уравнение
нейтральной линии 
Отсюда найдем
отрезки, отсекаемые нейтральной линией на осях и . Если , то
и, если , то
Нейтральная
линия показана на рис. 3.
Рис.3
Проведем
касательные к контуру сечения, параллельные нейтральной линии. Опасными
являются точки 1 и 1¢
(см. рис. 3), наиболее отдаленные от нейтральной линии. Для хрупкого
материала более опасной является точка с максимальными растягивающими
напряжениями, т.е. точка 1. Найдем напряжение в этой точке, подставляя в
формулу 
Условие
прочности в точке 1 И
ли
Отсюда можно найти допускаемое значение нагрузки (не забывайте
правильно подставлять единицы измерения.
Множитель
перед F
p
в данном примере имеет
размерность см -2).
В заключение
необходимо убедиться в том, что и в точке 1¢
, которая в данном
примере дальше удалена от нейтральной оси, чем точка 1, и в которой действуют
сжимающие напряжения, условие прочности тоже выполняется, т.е.
Теперь
построим ядро сечения. Поместим полюсы во внешних угловых точках сечения.
Учитывая симметрию сечения, достаточно расположить полюсы в трех точках: 1, 2 и
3 (см. рис. 3). Подставляя в формулы ; координаты полюсов, найдем отрезки,
отсекаемые нейтральными линиями на осях и . Если полюс находится в точке 1, то его координаты и
Нейтральная
линия 1–1, соответствующая полюсу в точке 1 показана на рис. 3. Аналогично
строим нейтральные линии 2–2 и 3–3, соответствующие полюсам 2 и 3. При
построении нейтральной линии следите за тем, чтобы она проходила в квадранте,
противоположном тому, в котором находится полюс. Область, заштрихованная на
рис. 3, является ядром сечения. Для контроля на рис. 3 показан эллипс
инерции. Ядро сечения должно находиться внутри эллипса инерции, нигде не
пересекая его.
Пример 4.
Стержень
несимметричного сечения сжимается силой, приложенной в точке А
(рис. 1). Поперечное сечение имеет форму и размеры,
показанные на рис. 2. Материал стержня – хрупкий.
Требуется:
1) найти
допускаемую нагрузку, удовлетворяющую условию прочности;
2) построить
ядро сечения.
Решение.
Прежде всего,
надо определить моменты и радиусы инерции поперечного сечения относительно
главных центральных осей. Эта часть решения задачи приведена в разделе
«Геометрические характеристики плоских сечений». На рис. 1 показаны
главные центральные оси инерции сечения , , положение которых найдено ранее. В системе центральных осей
Y
,
Z
(рис.2) координаты точки
приложения силы А
, . Вычислим координаты точки А
в системе главных центральных осей по формулам
.
Рис.1Рис.2
Для
определения положения опасных точек построим нейтральную линию, используя
формулы ; . Радиусы инерции , найдены ранее.
Отложим эти
отрезки вдоль главных осей и проведем через полученные точки нейтральную линию (см. рис. 3).
Рис.3
Опасными
точками, т.е. точками, наиболее удаленными от нейтральной оси, будут точки 1 и
3 (см. рис.3). В точке 1 действует наибольшее растягивающее напряжение. Запишем
условие прочности в этой точке, используя формулу :
Подставим в
условие прочности координаты опасной точки 1 в главных осях, вычислив их по
формулам
или измерив на
рисунке, выполненном в масштабе, Тогда из условия
прочности в точке 1 можно найти допускаемое значение нагрузки:

Для найденного
значения допускаемой нагрузки необходимо убедиться, что условие прочности
выполняется и в точке 3, которая дальше удалена от нейтральной линии и в
которой д
ействует сжимающее напряжение. Для
определения напряжения в точке 3 подставим в формулу координаты этой
точки

Это напряжение
не должно превосходить . Если условие прочности в точке с максимальными сжимающими
напряжениями выполняться не будет, надо найти значение допускаемой нагрузки
заново из условия прочности в этой точке.
В заключение
построим ядро сечения. Поместим полюсы во внешние угловые точки сечения, т.е. в
точки 1, 2, 3, 4, 5 (см. рис. 3). Точка 4, находящаяся на контуре
квадранта круга, получена следующим образом. Отсекая внутреннюю угловую точку , проводим линию, касательную к контуру сечения (пунктир на
рис. 3). Точка 4 является точкой касания этой линией квадранта круга.
Последовательно находим положение нейтральных линий, соответствующих полюсам в
указанных точках, находя отрезки, отсекаемые нейтральными линиями на осях , , по формулам ; .Например,
если полюс находится в точке 1, то, подставляя в ; координаты точки 1 (), найдем
Поскольку существенно больше , то это значит, что нейтральная линия 1–1 практически
параллельна оси . Отрезок откладываем в масштабе
вдоль оси и проводим прямую 1–1,
параллельную оси (см. рис. 3). Аналогично строим нейтральные линии,
соответствующие полюсам, расположенным в других точках. Ядро сечения
(заштрихованная область) показано на рис. 3. Отметим, что контур ядра
сечения между нейтральными линиями 4–4 и 5–5 очерчен по кривой, т.к. переход
полюса из точки 4 в точку 5 происходит не по прямой линии. На рис. 3
показан также эллипс инерции сечения, построенный ранее.
Пример 5.
На брус
заданного поперечного сечения в точке D
верхнего
торца действует продольная сжимающая сила Р
=300 кН (см. рис.). Требуется
найти положение нулевой линии, определить наибольшие (растягивающие и
сжимающие) напряжения и построить ядро сечения.
Решение:
1. Нахождение положения главных
центральных осей инерции и определение площади поперечного сечения
Так как
поперечное сечение бруса (рис.1) имеет две оси симметрии, а они всегда проходят
через центр тяжести сечения и являются главными, то главные центральные оси
сечения х
с и у
с будут совпадать с этими
осями симметрии.
Центр тяжести
сечения С
в
этом случае определять не надо, так как он совпадает с геометрическим центром
сечения.
Площадь
поперечного сечения бруса равна:
2. Определение главных центральных
моментов инерции и главных радиусов инерции
Моменты
инерции определяем по формулам:
Вычисляем
квадраты главных радиусов инерции:
3. Определение положения нулевой линии
Отрезки,
отсекаемые нулевой линией на главных центральных осях инерции, определяем по
формулам:
где х р
=2,3 см и у р
=2 см –
координаты точки приложения силы Р
(точка Р рис.11). Отложив отрезки и соответственно на осях
х с
и у с
и проводя через их концы прямую,
получим нулевую линию сечения, на которой нормальные напряжения равны нулю ().
На рис.1 эта линия обозначена n
-n
.
4. Определение наибольших сжимающих и
растягивающих напряжений и построение эпюры напряжений
Точка
D
,
координаты которой х
D
=5,25 см и у
D
=5 см, наиболее удалена от нулевой линии в сжатой зоне
сечения, поэтому наибольшие сжимающие напряжения возникают в ней и определяются
по формуле
Наибольшие
растягивающие напряжения возникают в точке К
, имеющей
координаты х к
= ‑5,25 см, у к
= ‑5
см.
По полученным
значениям и строим эпюру
нормальных напряжений (см. рис.11).
5.
Построение ядра сечения
Для построения
ядра сечения, учитывая, что сечение симметричное, рассмотрим два положения
касательной к контуру сечения I
-I
и II
-II
(см. рис.1).
Отрезки, отсекаемые
касательной I
-I
на осях координат,
равны:
Координаты
граничной точки 1 ядра сечения определяются по формулам:
Касательная II
-II
отсекает
отрезки =5,25 см, =¥
.
Координаты
граничной точки 2
:
Координаты
граничных точек второй половины ядра сечения можно не определять, так как
сечение бруса симметричное. Учитывая это для касательных III
-III
и IV
-IV
, координаты граничных
точек 3
и 4
будут:
= 0; = 15,2×
10 -3
м;
=23,0×
10 -3 м = 0.
Соединив
последовательно точки 1, 2, 3 и 4прямыми
получим ядро сечения (рис.1).
Пример 6.
В сечении,
указанном на рисунке и принадлежащем внецентренно
сжатой колонне, определить наиболее опасные точки и напряжения в них. Сжимающая
сила F
= 200 кН = 20 т приложена в точке A
.
Решение.
Так как оси X
и Y
являются осями симметрии, то они главные
центральные оси.
Наиболее
опасными точками будут точки, в которых возникают максимальные
нормальные
напряжения, а это точки, наиболееудаленные от нулевой линии.
Следовательно,нам необходимо сначала
определить положение нулевой линии. Записываем уравнение нулевой линии.
В нашем случае
координаты точки приложения силы следующие (см. рис.):
= – 90 мм = – 0,09 м;
= – 60 мм = – 0,06 м.
Квадраты
радиусов инерции и определяются так:
здесь и –
осевые моменты инерции относительно главных центральных осей X и Y.
Определение
осевых моментов инерции. Для нашего сечения будем иметь:
М 4
;
М 4
.
Площадь всего
сечения будет равна:
М 2
,
и тогда
квадраты радиусов инерции:
м 2
;
м 2
.
По формулам
определим отрезки, которые нулевая линия отсекает на осях X
и Y
:
м
;
м.
Отложим эти
отрезки на координатных осях, получим точки, в которых нулевая линия пересекает
координатные оси. Через эти точки проводим прямую
(см.
рис.). Видим, что наиболее удаленные точки –
это точка B
в зоне отрицательных
напряжений и точка D
в
зоне положительных напряжений.
Определим
напряжения в этих точках:
;
На основании
чертежа (см. рис.) получим:
= – 0,12 м; = – 0,03 м.
= –5,39×
10 4
кН/м 2
= – 53,9 МПа.
;
0,12 м; = 0,03 м.
1,86×
10 4 кН/м 2
= 18,6 МПа.
Пример 7.
Чугунныйкороткий
стержень, поперечное сечение которого изображено на рисунке, сжимается
продольной силой F
, приложенной в
точке А
.
Требуется:
1) вычислить наибольшее растягивающее и
наибольшее сжимающее напряжения в поперечном сечении, выразив величины этих
напряжений через F
и размеры сечения;
а
= 40 мм, b
= 60 мм;
2) найти допускаемую нагрузку F
при заданных размерах сечения и допускаемых
напряжениях для чугуна на сжатие = 100 МПа и на растяжение = 30 МПа.
Решение.
Выше указывалось, что геометрические
характеристикиврасчетныхформулах берутсяотносительно
главных центральных осей, поэтому определим центр тяжести сечения. Ось
X является осью симметрии, и
следовательно, она проходит через центр тяжести, поэтому намдостаточно найти его местоположение на этой
оси.Разобьемсечениена два составных(1 и 2)ивыберемвспомогательные оси .Запишемкоординатыцентровтяжести С
1
и С
2 в этих осях.
Будем иметь С
1
(0,0); С
2 (0,04;
0), тогда:
м
;
Итак, в осяхxy
1 центр тяжести всего сечения имеет координаты С
(0,0133; 0). Проводим через центр
тяжести сечения ось
Y, перпендикулярную
оси
X. Оси
X и Y и будут главными центральными осями сечения.
Определим положение нулевой линии.
Координаты
точки приложения силы (точки А
) будут
следующие: =(0,02–0,0133)+0,04 =0,0467 м; = 0,06 м;
м 4
,
м 4
,
где = 0,0133 м;
м 2
.
м 2 ,
м 2 ;
и получим
отрезки, отсекаемые нейтральной осью на главных осях инерции X и Y
соответственно:
Откладываем на оси X
, а на оси Y
и проводим через полученные
точки нулевую линию (см. рис.). Видим, что наиболее удаленные точки сечения от
нулевой линии –
это точка А
в сжатой зоне и точка В
в
растянутой зоне. Координаты этих точек следующие: А
(0,0467; 0,06); В
(– 0,0333; –0,12). Определим напряжения в этих точках, выразив их
через F
.
Напряжение в
точке А
не
должно превышать допускаемое напряжение на сжатие , а напряжение в точке В
не должно превышать допускаемое напряжение на растяжение , т.е. должны выполняться условия:
, ,
или
(а),
(б).
Из (а):
из (б):
Чтобы одновременно удовлетворить условие
прочности и в растянутой, и в сжатой зонах колонны, мы должны взять в качестве
допускаемой нагрузки меньшую
из двух полученных, т.е. = 103 кН.
Пример 8.
Чугунный короткий
стержень прямоугольного поперечного
сечения, изображенный на рисунке, сжимается продольной силой F
, приложенной в точке
А
.
Требуется:
1) вычислить
наибольшее растягивающее и наибольшее сжимающее напряжения в поперечном
сечении, выразив величины этих напряжений через F
и размеры
сечения;
2) найти
допускаемую нагрузку F
при
заданных размерах сечения и допускаемых напряжениях для чугуна на сжатие и на растяжение
.
Решение.
Определим
положение нулевой линии. Для этого воспользуемся формулами
Координаты
точки приложения силы (точки А) будут следующими:
Квадраты
радиусов инерции определим по формулам:
Определяем
отрезки, которые нулевая линия отсекает на осях х
и у
.
Откладываем на
оси х
– х
0
,
а на оси у
– у
0 и проводим через полученные точки нулевую линию n
– n
(см. рис.).
Видим, что наиболее удаленные точки сечения – это точка А
в сжатой области и точка В в
растянутой области.
Координаты этих точек следующие: А (0,04; 0,06), В (–0,04; –0,06). Определим
величину напряжения в этих точках, выразив их через силу F
:
Напряжение в
точке А
не должно превышать допускаемое напряжение на
сжатие , а напряжение в точке В не должно превышать допускаемое
напряжение на растяжение , т.е. должно выполняться условие
Из первого
выражения величина F
Принимается
нагрузка наименьшая из двух найденных, т.е. = 567кн.
Пример 9.
Короткий
чугунный стержень с поперечным сечением, изображенным на
рис. а
, сжимается продольной силой P
, приложенной в точке A
. Определить наибольшее
растягивающее и наибольшее сжимающее напряжения в поперечном сечении стержня,
выразив их через силу P
и размеры сечения см, см. Найти допускаемую
нагрузку при заданных допускаемых
напряжениях для материала на сжатие кН/см 2
и на растяжение кН/см 2 .
Решение.
Действующая на
стержень сила P
помимо сжатия осуществляет изгиб
стержня относительно главных центральных осей x
и y
. Изгибающие моменты соответственно равны:
где см
и см – координаты точки
приложения силы P
(координаты точки A
).
Нормальные
напряжения в некоторой точке с координатами x
и y
любого
поперечного
сечения стержня определяются по формуле

где F
– площадь, а и – радиусы инерции
поперечного сечения.
1. Определяем
геометрические характеристики поперечного сечения стержня.
Площадь
поперечного сечения стержня равна:
Главные
центральные моменты инерции определяем следующим образом.
Вычисляя
момент инерции всего
сечения
относительно оси x
, разобьем всю фигуру на один
прямоугольник с шириной и высотой и два прямоугольника с
шириной и высотой , чтобы ось x
была
для всех этих трех фигур центральной. Тогда
.
Для вычисления
момента инерциивсего сечения
относительно оси y
разобьем всю фигуру несколько
иначе: один прямоугольник с шириной и высотой и два прямоугольника с
шириной и высотой , чтобы теперь уже ось y
была
для всех этих трех фигур центральной. Получим
.
Квадраты
радиусов инерции равны:
;
.
2. Определяем
положение нулевой линии.
Отрезки и , отсекаемые нулевой линией от осей координат, равны:

; 
Показываем
нулевую линию N
–
N
на
рис. б
. Нулевая линия делит поперечное
сечение на две области, одна из которых испытывает растяжение, а другая –
сжатие. На рисунке 1, б
растянутая
область поперечного сечения
стержня нами заштрихована
.
3. Вычисляем
наибольшее растягивающее
напряжение.
Оно возникает
в точках 6
и 7
, то есть в точках, наиболее удаленных от нулевой линии. Значение
этого напряжения, вычисленное, например, для точки 6
равно:
4. Вычисляем
наибольшее сжимающее
напряжение.
Оно возникает
в точках 2
и 3
, также наиболее удаленных от нулевой линии. Значение этого
напряжения, вычисленное, например, для точки 2
, равно:
5. Определяем
допускаемую нагрузку из условия прочности на растяжение:
кН/см 2
; кН.
6. Определяем допускаемую нагрузку из условия
прочности на сжатие:
кН/см 2
; кН.
из двух найденных в п. 6 и 7
значений:
Пример 10.
Короткая
колонна, поперечное сечение которой изображено на рис.1, сжимается продольной
силой F
=
200 кН,
приложенной
в точке К
. Размеры сечения
а=
40
см,
b
=
16 см.
Расчетное сопротивление материала на
растяжение R t
= 3 МПа, на сжатиеR
с
=
30 МПа.
Требуется
:
1. Найти
положение нулевой линии.
2. Вычислить
наибольшие сжимающие и растягивающие напряжения и построить эпюру напряжений.
Дать заключение о прочности колонны.
3. Определить
расчетную несущую способность (расчетную нагрузку) F
max
при заданных размерах сечения.
4. Построить
ядро сечения.
Рис.1
Решение.
1. Определение координат центра тяжести
сечения
.
Поперечное
сечение колонны имеет ось симметрии Х с
, следовательно
центр
тяжести лежит на этой оси и для отыскания координаты х с
относительно
вспомогательной оси Y o
(см. рис.1)
сложное сечение разбиваем на три прямоугольника
2. Геометрические характеристики сечения.
Для вычисления
главных центральных моментов инерции воспользуемся зависимостью между моментами
инерции при параллельном переносе осей.
Определяем
квадраты радиусов инерции
Координаты
точки приложения силы F
3.
Положение нулевой линии
По найденным отрезкам, отсекаемым на осях координат проводим
нулевую
линию (см. рис. 2).
4. Определение наибольших сжимающих и
растягивающих напряжений
. Эпюра .
Наиболее
удаленные от нулевой линии точки: В
(-60;
16) и
D
(60; -32).
Напряжения
в этих опасных точках с координатами х
dan
, у
dan
не должны превосходить соответствующего расчетного
сопротивления

Растягивающее
напряжение
Сжимающее
напряжение
Прочность
колонны обеспечена.
По результатам расчета напряжений и на рис. 2 построена
эпюра .
5. Вычисление расчетной несущей способности
колонны
F max
.
Поскольку при
заданном значении сжимающей силы прочность материала колонны существенно
недоиспользована, найдем максимальное значение внешней нагрузки, приравнивая
наибольшие напряжения s
t
и s
c
расчётным сопротивлениям.
Окончательно
выбираем меньше значение F max
=
425,8 кН,
обеспечивающее прочность как растянутой, так и сжатой зон сечения.
Рис.2
6. Построение ядра сечения
.
Чтобы получить
очертание ядра сечения, необходимо рассмотреть все возможные положения
касательных к контуру сечения и, предполагая, что эти касательные являются
нулевыми линиями, вычислить координаты граничных точек ядра относительно
главных центральных осей сечения. Соединяя затем эти точки, получим очертание
ядра сечения.
Касательная
1-1: y o
= 32 см,
.
Касательная
2-2: , 
Касательная
3-3: , .
Касательная
4-4: ; ;
;
;
;
.
Касательная
5-5: ; .
Касательная
6-6: ; ;
Пример 11.
В точке
P
колонны прямоугольного сечения приложена сжимающая сила P
(см. рис.). Определить максимальное
и минимальное нормальные напряжения.
Решение.
Нормальное
напряжение при внецентренном
сжатии определяем по формуле:
В нашей задаче
Момент инерции
, площадь ,
Следовательно
На нейтральной
линии . Поэтому ее уравнение
Наиболее
удаленными точками от нейтральной оси являются точки A
и B
:
в точке A
и
в точке B
и
Если материал
сопротивляется растяжению и сжатию различно, то следует составить два уравнения
прочности:
Пример 12
.
Найти допускаемую
нагрузку для бруса, показанного на рисунке, если расчетные сопротивления
материала бруса на растяжение и сжатие равны R adm
,
t
= 20 МПа; R adm
,с
= 100 МПа.
Решение.
Запишем условие прочности для наиболее напряженных точек любого сечения бруса,
так как все сечения равноопасны:
Перепишем эти
условия, учитывая, что
и , тогда
и
Отсюда определяем
значения допустимых нагрузок.
Сила Р приложена в точке с координатами – х р, у р.
В этом случае говорят, что нагрузка по отношению к продольной оси z приложена с эксцентриситетом е (рис.8.2).
Напряжения в произвольной точке поперечного сечения определяются по формуле (8.3):

(+) перед выражением (8.3) соответствует внецентренному растяжению,
(–) – сжатию.
х, y
– координаты точки, в которой определяются нормальные напряжения.
Условие прочности при внецентренном приложении нагрузки записывается для опасных точек А
и В
, наиболее удаленных от нейтральной линии.

Здесь – квадраты радиусов инерции.
R
– расчетное сопротивление материала растяжения или сжатия.
8.2.2. Уравнение нейтральной линии
На нейтральной линии нормальные напряжения равны нулю.
Приравняв нулю выражение (8.3) получим уравнения нейтральной линии

x N , y N
– координаты точек, лежащих на нейтральной линии.
Решая полученное уравнение (8.5) в отрезках по осям координат, можно определить положение нейтральной линии.

8.2.3. Ядро сечения

– область, расположенная вокруг центра тяжести сечения, приложенная внутри которой нагрузка, вызывает по всему поперечному сечению напряжения одного знака.
Для построения ядра сечения задаются положениями нейтральной линии, совпадающей со сторонами сечения N i
(х N
и у N
) и в соответствии с формулой (8.5) определяют две координаты точки приложения силы соответствующей этой линии
Проведя по всему контуру сечения нейтральные линии, получим n
точек. На основании теоремы о вращении нейтральной линии, соединив последовательно полученные точки, получим ядро сечения (рис. 8.3). Для прямоугольного поперечного сечения ядром сечения является ромб.
Устойчивость сжатых стержней
Общие положения
Явление потери устойчивости сжатого стержня наблюдается в том случае, когда при известной форме и размерах поперечного сечения его длина превышает определенное значение.
При потере устойчивости элемента происходит нарушение первоначальной прямолинейной формы равновесия.
Различают устойчивое (а
), безразличное (b
) и не устойчивое (с
) состояние равновесия (рис. 9.1).
 |
Продольный изгиб опасен тем, что происходит большое нарастание прогибов при малом росте сжимающей нагрузки.
Потеря устойчивости гибких стержней наступает при сравнительно небольших сжимающих напряжениях, которые с точки зрения прочности материала являются не опасными.
Для определения внутренних усилий, в поперечных сечениях бруса при внецентренном растяжении (сжатии) заменим заданную систему сил на статически эквивалентную систему других сил. На основании принципа Сен-Венана такая замена не вызовет изменений в условиях нагружения и деформации частей бруса, достаточно удаленных от места приложения сил.
Сначала перенесем точку приложения силы на ось и приложим в этой точке силу, равную силе, но противоположно направленную (рис.3.2). Чтобы оставить силу на оси, к ее действию необходимо добавить действие пары сил, отмеченных двумя чертами, или момент. Далее перенесем силу в центр тяжести сечения и в этой точке приложим силу, равную силе, но противоположно направленную (рис.3.2). Чтобы оставить силу в центре тяжести, к ее действию необходимо добавить еще одну пару сил, отмеченных крестиками, или момент.
Таким образом, действие силы, приложенной к сечению внецентренно, эквивалентно совместному действию центрально приложенной силы и двух внешних сосредоточенных моментов и.
Пользуясь методом сечений, нетрудно установить, что во всех поперечных сечениях внецентренно растянутого (сжатого) бруса действуют следующие внутренние силовые факторы: продольная сила и два изгибающих момента и (рис.3.3).
Напряжения в поперечных сечениях бруса определим, используя принцип независимости действия сил. От всех внутренних силовых факторов в поперечных сечениях возникают нормальные напряжения. Знаки напряжений устанавливают по характеру деформаций: плюс – растяжение, минус – сжатие. Расставим знаки напряжений от каждого из внутренних силовых факторов в точках, пересечения осей и с контуром поперечного сечения (рис.3.3). От продольной силы во всех точках сечения одинаковы и положительны; от момента в точке напряжения – плюс, в точке – минус, в точках и, т.к. ось является в этом случае нейтральной линией; от момента в точке напряжения – плюс, в точке – минус, в точках и, т.к. ось в этом случае является нейтральной линией.
Полное напряжение в точке с координатами и, будет равно:
Самой нагруженной точкой в сечении произвольной формы является точка, наиболее удаленная от нейтральной линии. В связи с этим, большое значение приобретают вопросы, связанные с определением положения нейтральной линии.
Определение положения нейтральной линии
Положение нейтральной линии можно определить с помощью формулы (3.1), приравняв нормальные напряжения нулю
здесь и – координаты точки, лежащей на нейтральной линии.
Последнее выражение можно преобразовать, используя формулы для радиусов инерции: и. Тогда
Из уравнения (3.2) видно, что нейтральная линия при внецентренном растяжении (сжатии) – это прямая, не проходящая через начало координат (центр тяжести поперечного сечения).
Проведем эту прямую через две точки, лежащие на координатных осях (рис. 3.4). Пусть точка 1 лежит на оси, тогда ее координатами будет и, а точка 2 – на оси, тогда ее координатами будет и (на основании уравнения (3.2)).
Если координаты точки приложения силы (полюса) положительны, то координаты точек 1 и 2 отрицательны, и наоборот. Таким образом, полюс и нейтральная линия располагаются по разные стороны от начала координат.
Определения положения нейтральной линии позволяет выявить опасные точки сечения, т.е. точки, в которых нормальные напряжения принимают наибольшие значения. Для этого следует построить касательные к контуру сечения, параллельные нейтральной линии. Точки касания и будут являться опасными (рис. 3.4).
Условия прочности для опасных точек составляют в зависимости от свойств того материала, из которого изготовлен брус. Так как хрупкий материал обладает различными свойствами в условиях растяжения и сжатия – плохо сопротивляется растяжению и хорошо сжатию, условия прочности составляют для двух точек: где действуют максимальные растягивающие (т.) и максимальные сжимающие (т.) напряжения (рис. 3.4)
Для пластичного материала, который одинаково сопротивляется и растяжению и сжатию, составляют одно условие прочности для точки поперечного сечения, где имеют место максимальные по абсолютной величине нормальные напряжения. В нашем случае такой точкой является точка, в которой действуют напряжения одного знака
Понятие о ядре сечения
При построении нейтральной линии (рис. 3.4) определялись координаты точек 1 и 2, через которые она и проводилась
Координаты точек, лежащих на нейтральной линии, зависят от положения точки приложения силы (полюса) с координатами. Если координаты полюса уменьшаются, т.е. полюс приближается к центру тяжести сечения, то увеличиваются, т.е. нейтральная линия может выйти за пределы сечения или касаться контура сечения. В этом случае в сечении будут иметь место напряжения одного знака.
Область приложения продольных сил, которые в этом случае вызывают в поперечном сечении напряжения одного знака, называется ядром сечения
.
Вопрос определения ядра сечения является наиболее актуальным для элементов конструкций из хрупкого материала, работающих на внецентренное сжатие, с целью получения в поперечном сечении только сжимающих напряжений, т.к. хрупкий материал плохо сопротивляется деформации растяжения. Для этого необходимо задаться рядом положений нейтральной линии, проводя ее через граничные точки контура, и вычислить координаты соответствующих точек приложения силы, по формулам, вытекающим из (3.5).
Геометрическое место рассчитанных таким образом точек и определит контур ядра сечения. На рис. 3.6 показаны примеры ядра сечения для распространенных форм.
Рассмотрим пример расчетов на внецентренное растяжение-сжатие.
Пример 3.1.
Стальная полоса шириной =10 см и толщиной =1 см, центрально растянутая силами =70 кН, имеет прорезь шириной =3 см (рис. 3.6). Определить наибольшие нормальные напряжения в сечении, не учитывая концентрации напряжений. Какой ширины могла бы быть прорезь при той же величине растягивающего усилия, если бы она была расположена посередине ширины полосы?
Решение.
При несимметричной прорези центр тяжести ослабленного сечения смещается от линии действия силы вправо и возникает внецентренное растяжение. Для определения положения центра тяжести () ослабленное сечение представим как большой прямоугольник размерами (фигура I) из которого удален малый прямоугольник с размерами (фигура II). За исходную ось примем ось.
В этом случае в поперечном сечении возникает два внутренних силовых фактора: продольная сила и изгибающий момент.
С целью определения опасной точки расставим знаки напряжений по боковым сторонам поперечного сечения (рис. 3.6). От продольной силы во всех точках сечения имеют место положительные (растягивающие) напряжения. От изгибающего момента слева от оси имеют место растягивающие напряжения (знак плюс), справа – сжимающие (знак минус).
Таким образом, максимальные нормальные напряжения возникают в т.
где – площадь ослабленного сечения, равная =7 см 2 ;
Момент инерции ослабленного сечения относительно главной центральной оси
Расстояние от нейтральной линии () до наиболее удаленной точки (т.)
В результате максимальные нормальные напряжения будут равны
При симметричной прорези шириной возникает только растяжение
Рассмотрим прямой стержень, нагруженный на торце силами, направленными параллельно оси Ох.
Равнодействующая этих сил F
приложена в точке С.
В локальной правосторонней системе координат yOz
, совпадающей с главными центральными осями сечения, координаты точки С
равны а
и b
(рис. 5.18).
Заменим приложенную нагрузку статически эквивалентной ей системой сил и моментов. Для этого перенесем равнодействующую силу F
в центр тяжести сечения О
и догрузим стержень двумя изгибающими моментами, равными произведению силы Т^на ее плечи относительно осей координат: M ff = Fa
и M z = Fb.
Отметим, что по правилу правосторонней системы координат для точки С, лежащей в первой четверти, изгибающие моменты формально получат сле-
Рис. 5.18.
Прямой стержень, нагруженный на торце силами, направленными параллельно оси
Ох
дующие знаки: М у = Fa
и М 7 = -Fb.
При этом в элементарной площадке, лежащей в первой четверти, оба момента вызывают растягивающее напряжение.
Используя принцип независимости действия сил, определим напряжения в текущей точке сечения с координатами у
и z
от каждого силового фактора отдельно. Общее напряжение получим суммированием всех трех составляющих напряжений:
Определим положение нейтральной оси. Для этого в соответствии с формулой (5.69) приравняем к нулю значение нормального напряжения в текущей точке:
В результате простых преобразований получим уравнение нейтральной линии
где i y
и i z – главные радиусы инерции
, определяемые по формулам (3.14).
Таким образом, в случае внецентренного растяжения-сжатия нейтральная линия не проходит через центр тяжести сечения (рис. 5.19), на что указывает наличие в уравнении (5.70) отличающегося от нуля свободного члена.
Максимальные напряжения возникают в точках сечения А
и В,
наиболее удаленных от нейтральной линии. Установим соотношение между координатами точки приложения силы и положением нейтральной линии. Для этого определим точки пересечения этой линией координатных осей:
Рис. 5.19.
Полученные формулы показывают, что координата точки приложения силы а
и координата точки пересечения нейтральной линией оси координат Oz
(точка г 0) имеют противоположные знаки. То же самое можно сказать о величинах b
и у 0 .
Таким образом, точка приложения равнодействующей силы и нейтральная линия находятся по разные стороны относительно начала координат.
Согласно полученным формулам при приближении точки приложения силы к центру тяжести сечения нейтральная линия отдаляется от центральной зоны. В предельном случае (а = b =
0) приходим к случаю центрального растяжения-сжатия.
Представляет интерес определение зоны приложения силы, при котором напряжения в сечении будут иметь одинаковый знак. В частности, для материалов, плохо сопротивляющихся растяжению, сжимающую силу рационально прилагать именно в этой зоне, чтобы в сечении действовали только сжимающие напряжения. Такая зона вокруг центра тяжести сечения называется ядром сечения.
Если сила приложена в ядре сечения, то нейтральная линия не пересекает сечение. В случае приложения силы по границе ядра сечения нейтральная линия касается контура сечения. Для определения ядра сечения можно использовать формулу (5.71).
Если нейтральную линию представить как касательную к контуру сечения и рассмотреть все возможные положения касательной и соответствующие этим положениям точки приложения силы, то точки приложения силы очертят ядро сечения.
Рис. 5.20.
а –
эллипс; 6
– прямоугольник
Определение положения нулевой линии (нейтральной оси) при внецентренном растяжении (сжатии)
Линия, соединяющая все точки сечения колонны, в которой напряжения равны нулю, называется нулевой линии (нейтральной оси).
Пусть произвольная точка расположена на нулевой линии. Обозначим ее координаты 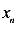
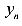
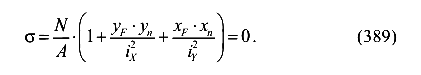
Так как 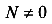
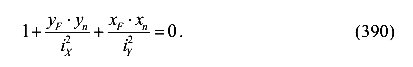
Перенесем 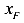
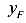

Так как 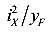
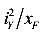
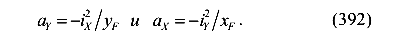
Тогда уравнение можно записать в следующем виде

Полученное уравнение — это уравнение прямой линии в отрезках. Здесь
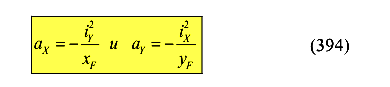
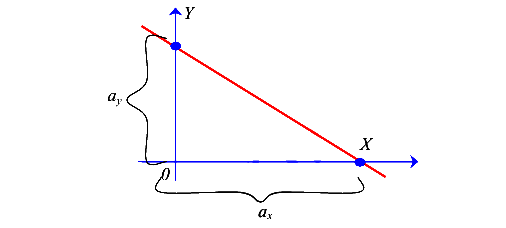
это отрезки, отсекаемые нулевой линией на главных центральных осях инерции (рис. 120).
Эта теория взята со страницы подробного решения задач по предмету «Сопротивление материалов»:
Решение задач по сопротивлению материалов
Дополнительные страницы которые вам будут полезны: