1. Типовые задачи с решениями
Задача 1.1.
Найти координаты образа
и прообраза
точки
при повороте вокруг начала координат
на угол
.
Решение.
Найдем аналитическое выражение поворота,
данного в задаче:
Чтобы найти
координаты образа
точки
,
надо подставить в эти формулы вместо
и
данные координаты точки
,
т.е.
.
Тогда
;
,
т.е.
.
Чтобы найти
координаты прообраза
точки
,
т.е. координаты точки, для которой
теперь является образом, надо положить
и найти
и
:
Умножив второе
уравнение системы на
и сложив с первым, найдем
:
Подставляя найденное
значение
в одно из уравнений системы, найдем
:
Таким образом,
.
Ответ:
,
.
Задача 1.2.
Найти уравнение образа
и прообраза
прямой
при осевой симметрии с осью
.
Решение.
Аналитическое выражение осевой симметрии
имеет вид:
Чтобы найти
уравнение образа
прямой
,
нужно выразить из этой системы
и
и подставить их в уравнение прямой
:
.
Опуская штрихи, получаем:
.
Чтобы найти
уравнение прообраза
прямой
,
запишем уравнение прямой
(образа прямой
)
в виде
и подставим в него
и
из аналитического выражения
:
.
Получили для прямых
и
одно и то же уравнение. Это не случайно,
т.к. при осевой симметрии (так же как и
при центральной) образ и прообраз любой
фигуры всегда совпадают.
Ответ:
,
.
Задача 1.3.
Даны прямые
и
.
Найти такие точки
и
,
что
и
,
где
.
Решение.
,
т.е.
.
Тогда учитывая, что
,
получаем:
(рис. 18).
С
ледовательно,
чтобы найти координаты точки
,
надо сначала найти уравнение образа
прямой
при параллельном переносе на вектор
,
а затем решить систему уравнений прямых
и
.
Найдем аналитическое
выражение параллельного переноса на
вектор
:
Найдем уравнение
образа
:
,
т.е.
.
Решаем систему
Сложив почленно
уравнения системы, получим:
.
Итак,
.
Так как
,
то
,
т.е.
−
прообраз точки
.
Найдем координаты прообраза
точки
:
откуда
,
т.е.
.
Ответ:
,
.
2. Задачи для решения на практическом занятии
2.1.
Вывести аналитическое выражение
центральной симметрии с центром
.
2.2. Найти
координаты образа
и прообраза
точки
в центральной симметрии с центром
.
2.3.
Найти уравнение образа
и прообраза
прямой
при повороте на угол
вокруг начала координат.
2.4.
В ортонормированном репере дано
аналитическое выражение преобразований
и
:
Доказать, что
и
− движения. Определить их род. Найти их
инвариантные точки.
2.5.
Даны прямые
и
.
Найти координаты таких точек
и
,
что
,
и
.
2.6.
Найти уравнение оси симметрии точек
и
.
3. Задачи для самостоятельного решения
3.1.
Найти координаты образа
и прообраза
точки
при параллельном переносе на вектор
.
3.2.
Найти уравнение образа
и прообраза
прямой
при
центральной симметрии с центром
.
3.3.
Даны прямые
и
.
Найти координаты таких точек
и
,
что
,
и
.
3.4.
Найти инвариантные точки преобразования,
заданного формулами:
а)
б)
3.5.
Найти аналитическое выражение композиции
осевых симметрий
и определить вид этого движения.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
§ 3. Аналитическое
задание движения.
Задачи.
-
Записать формулы движения, имеющего
единственную инвариантную точку и
переводящего
,
а окружность
в окружность
.
.
Решение. Во-первых, определим вид
движения. Смотрим в таблицу §1 и видим,
что единственную инвариантную точку
имеет поворот. Во-вторых, нарисуем
картинку и решим задачу “на картинке”,
как мы делали это в §1, 2. Мы знаем, что
при движении центр окружности переходит
в центр ее образа, то есть
при этом повороте перейдет в точку
.
Итак, поворот задан двумя парами
соответствующих точек:
и
.
Такую задачу мы уже решали в §1. Центр
поворота О есть пересечение серединных
перпендикуляров к отрезкам
и
.
Напишем уравнения этих прямых. Пусть
–
середина отрезка
.
Тогда
.
Серединный перпендикуляр
задается точкой
и перпендикулярным вектором
.
Тогда
.
Аналогично найдем второй серединный
перпендикуляр
.
Имеем
– середина отрезка
и
.
Тогда серединный перпендикуляр
задается точкой
и перпендикулярным вектором
.
Тогда
.
Найдем координаты точки
:
,
то есть
.
Найдем угол поворота
.
Используем формулы для нахождения
синуса и косинуса ориентированного
угла. Тогда
.
Нам достаточно данных, чтобы составить
формулы поворота. Посмотрим в таблицу
§1 и подставим в общие формулы поворота
наши данные:
.
-
Найти
уравнение образа прямой
при движении, не имеющем инвариантных
точек, при котором прямая
и
.
.
Решение. Разделим задачу на три части:
во-первых, определим вид движения,
во-вторых, запишем его формулы, в-третьих,
по формулам найдем образ заданной
прямой.
Для определения вида движения берем
только вторую часть задачи (временно
забудем про первую прямую). Нарисуем
картинку. Мы видим, что
,
и
.
Движениями, не имеющими инвариантных
точек, являются параллельный перенос
и скользящая симметрия. Скользящая
симметрия переводит прямую
в параллельную ей прямую
только когда прямая параллельна оси
или перпендикулярна ей. Если бы скользящая
симметрия переводила
,
то
.
Что противоречит условию задачи.
Следовательно, это параллельный перенос.
Найдем координаты вектора этого
параллельного переноса.
Рассмотрим точку
и найдем образ этой точки при параллельном
переносе. Удобно записывать следующим
образом:
,
то есть
.
Ищем координаты точек
и
,
затем вектора
.
;
.
Тогда
.
Запишем уравнения параллельного
переноса:
.
Приступим к третьей части задачи. Чтобы
найти образ прямой
,
выразим из формул параллельного переноса
и
и подставим в уравнение прямой
.
Удобная запись:
.
Итак,
.
-
Найти
прообраз прямой
при
движении, имеющем инвариантную прямую
и инвариантную точку
.
при
.
Решение. Во-первых, определим вид
движения. Нарисуем картинку. Мы видим,
что точка
не принадлежит данной прямой. Инвариантные
точки имеют поворот (центральная
симметрия) и осевая симметрия. Инвариантные
прямые имеют центральная симметрия и
осевая симметрия. Но у центральной
симметрии все инвариантные прямые
проходят через инвариантную точку.
Следовательно, это – осевая симметрия
.
Найдем уравнение оси
.
Все инвариантные точки лежат на оси
,
следовательно,
.
Инвариантные прямые осевой симметрии,
отличные от ее оси, перпендикулярны ей,
то есть
.
Пишем уравнение прямой, проходящей
через данную точку перпендикулярно
данной прямой. Тогда
.
Смотрим в таблицу §1 и записываем формулы
осевой симметрии с осью
.
.
Найдем прообраз прямой
при этой осевой симметрии. Данная прямая
является образом для своего прообраза,
значит, ее переменные должны быть
обозначены буквами со штрихами:
.
Чтобы найти ее прообраз, нужно подставить
и
из формул осевой симметрии в уравнение
прямой
.
Получим уравнение прямой
– прообраза прямой
.
-
Написать
формулы движения, имеющего единственную
инвариантную прямую
,
при котором
.
.
Решение. Единственную инвариантную
прямую имеет только скользящая симметрия.
Эта прямая является ее осью, то есть ось
скользящей симметрии
.
Нам осталось найти только вектор
параллельного переноса. Нарисуем
картинку. Пусть
.
Тогда искомый вектор
.
Определив координаты точки
,
мы найдем координаты вектора
.
Рассмотрим одно из возможных решений
этой вспомогательной задачи. Оно не
самое короткое, но самое универсальное.
Идея этого решения у нас уже записана:
!
Здесь написано, что мы должны сначала
записать формулы осевой симметрии, а
затем найти образ точки
,
пользуясь этими формулами. Реализуем
эту идею. Подставим в общие формулы
осевой симметрии наши данные.
.
Чтобы найти координаты образа точки
,
нужно подставить ее координаты в формулы
вместо
и
.
Получим
.
Тогда
.
У нас достаточно данных, чтобы записать
ответ задачи. Смотрим в таблицу и
записываем формулы скользящей симметрии:
.
-
На
прямых
и
найти точки, которые являются соседними
вершинами квадрата с центром в точке
О(0,1).
Идея решение. Забудем сначала про
уравнения и решим задачу “в картинках”
как мы делали это в §1,2. Нам даны две не
параллельные прямые и точка, не
принадлежащая этим прямым. Пусть задача
решена и построен квадрат
,
где
и
– центр квадрата. Рассмотрим поворот
вокруг точки О на угол
.
Тогда
и по условию
,
следовательно,
.
Из этой записи мы видим, как построить
вершину
квадрата: надо построить образ прямой
при повороте вокруг точки
на угол
и пересечь его с прямой
.
Тогда вершину
легко найти как прообраз точки
при рассматриваемом повороте. Точки
найдем, зная, что
– середина отрезков
и
.
Осталось только провести занудные
вычисления. Проведите их самостоятельно!
Задачи
к проверочной работе.
-
Найти уравнение образа прямой
при движении с единственной инвариантной
точкой, при котором точки
,
а
. -
На
плоскости дан квадрат
.
Составить формулы движений 1 рода, не
имеющих инвариантных прямых, при которых
квадрат переходит в себя, если
,
. -
Записать
уравнения скользящей симметрии, при
которой синусоида
инвариантна. -
Написать
формулы движения, имеющего одну
единственную инвариантную точку,
инвариантные прямые, и переводящего
окружность
в окружность
.
-
Написать
формулы движения, имеющего инвариантную
прямую и инвариантную окружность,
заданные уравнениями
и
,
соответственно. Найти уравнение
прообраза прямой
при этом движении. -
Написать
формулы движения, единственная
инвариантная прямая которого параллельна
прямой
и
. -
Найти
уравнение прообраза прямой
при движении 1 рода, при котором прямая
инвариантна, а прямая
переходит в прямую
.
-
Найти
образ точки
при движении, не имеющем инвариантных
точек и переводящем
,
а
. -
Найти
координаты прообраза точки
при движении первого рода, для которого
точка
инвариантна,
прямая
переходит в прямую
. -
Написать
формулы движения 1 рода, при котором
прямая
,
и точка
инвариантна. -
Найти
координаты вершин А и В равнобедренного
прямоугольного треугольника АВС с
прямым углом С, если С(1,0), точка А лежит
на прямой
,
а точка В принадлежит окружности
. -
Найти
координаты вершин квадрата
,
если уравнение прямой, содержащей его
диагональ АС
,
а вершины В и
принадлежат соответственно оси ординат
и окружности
.
,
.
,
.
.
,
.
,
.
инвариантна,
.
,
,
.
,
.
13*. Составить формулы движений второго
рода, если известно, что образы точек
А(0,1), В(1,0), С(1,1) принадлежат соответственно
прямым
.
14*. Дан треугольник АВС. Определить вид
движения
и элементы его задающие.
15*. Дан треугольник АВС. Во внешнюю
сторону построены правильные треугольники.
Доказать, что их центры образуют
правильный треугольник.
§4. Определение
вида движения.
Рассмотрим
три типа задач на определение вида
движения:
1.
Движение задано парой ортонормированных
реперов.
Пусть даны два
ортонормированных репера
и
(проще говоря, нарисованы два прямоугольных
равнобедренных треугольника
и
,
у которых углы
– прямые). Чтобы определить вид движения
нужно:
1) Определим, сохраняет или
меняет движение ориентацию плоскости.
Для этого нарисуем стрелки от вектора
к вектору
и от вектора
к вектору
.
Если стрелки обе направлены по часовой
стрелке (или обе – против часовой
стрелки), то движение не меняет ориентации
плоскости, то есть является движением
первого рода. Если одна стрелка направлена
по часовой, а другая – против часовой
стрелки, то движение меняет ориентацию
плоскости, то есть является движением
второго рода.
2) Если движение первого
рода, то это либо параллельный перенос,
либо поворот. Параллельный перенос
характеризуется тем, что векторы
равны между собой – это вектор
параллельного переноса. Поворот
характеризуется тем, что серединные
перпендикуляры к отрезкам, соединяющим
соответствующие точки движения,
пересекаются в одной точке, то есть если
провести через середины отрезков
перпендикуляры, то они пересекутся в
одной точке – центре поворота. Рисуем
картинку и смотрим, что получается.
Найдите на картинке угол поворота.
3)
Если движение второго рода, то это либо
осевая симметрия, либо скользящая
симметрия. Рассмотрим середины отрезков
.
В обоих случаях они будут лежать на
одной прямой
.
Если прямая
перпендикулярна отрезкам
,
то это осевая симметрия, а если – нет,
то скользящая симметрия. Сообразите,
как найти вектор переноса для этой
скользящей симметрии.
2.
Движение задано формулами.
Напомним, что
формулы
,
где матрица
– ортогональна, задают движение.
Напомним,
что матрица С называется ортогональной,
если
1)
;
2)
;
3)
.
Чтобы определить вид движения, нужно
-
Определить род движения (вычислить
определитель
). -
Найти
количество инвариантных точек (в формулы
движения подставить
и решить систему уравнений
.
Количество ее решений
равно количеству инвариантных точек
движения). -
Посмотреть
в таблицу §1.
).
.
3.
Определение вида движения с помощью
разложения в композицию осевых симметрий.
Напомним,
что
,
где
,
,
где
,
Например,
надо определить вид движения
(рисуем
картинку). Постараемся разложим каждое
из этих движений в композицию двух
осевых симметрий так, чтобы первая
осевая симметрия от поворота была такая
же, как вторая осевая симметрия от
параллельного переноса, то есть
.
Тогда эти прямые должны удовлетворять
требованиям
,
,
,
.
Из этих требований видим, что прямая
должна проходить через точку О
перпендикулярно вектору
.
Две остальные прямые достраиваются по
прямой
однозначно (рисуем их на картинке). Итак,
,
где
,
(так как
),
то есть
=
является поворотом вокруг точки
на угол
(нарисуйте картинку).
Задачи.
-
Выяснить, определяют ли формулы
,
записанные в ПДСК, движение? Найти образ
и прообраз точки
при этом движении; образ и прообраз
прямой
при этом же движении.
,
Решение. Проверим, является ли матрица
ортогональной. Действительно,
,
,
.
Матрица ортогональна, следовательно,
формулы задают движение. Найдем образ
точки
.
Запишем
.
Из этой записи хорошо видно, что координаты
точки
нужно подставить вместо
и
в формулы движения. Тогда вычислив
значения
,
получим координаты точки
.
Считаем
,
.
Найдем прообраз точки
.
Запишем
,
где точка
– прообраз точки
.
Теперь точка М сама является образом и
ее координаты нужно подставлять в
формулы движения вместо
.
Получим систему, решив которую найдем
координаты точки
.
.
Найдем образ прямой
.
Первый способ. Взять две точки на прямой
,
найти их образы и через них провести
прямую. Это будет
.
Второй способ. Запишем
.
Нужно из формул движения выразить
и подставить в уравнение прямой
.
Получим уравнение с переменными
.
Это и будет уравнение прямой
.
Запишем его на место, которое мы оставили.
Проведите вычисление тем способом,
который вам понравился больше.
Найдем прообраз прямой
.
Первый способ решения такой же как для
нахождения образа. Второй способ. Запишем
.
Теперь прямая
сама является образом, следовательно,
ее переменные надо обозначать
.
Переобозначим
.
Теперь видно, чтобы найти ее прообраз,
нужно подставить выражения для
из формул в уравнение прямой
.
Ответ запишем на свободное место.
.
Раскрывая скобки и приводя подобные,
получим уравнение прообраза прямой
.
-
Определить
вид движения и элементы его определяющие
а)
;
б)
;
в)
;
г)
;
д)
;
е)
;
ж)
.
Записать уравнения инвариантных прямых.
;
;
;
;
;
;
.Решение.
а) Определим род движения
1
род
Найдем
инвариантные точки. Точка является
инвариантной тогда и только тогда, когда
,
то есть
.
Подставим в формулы движения:
.
Движение 1 рода и имеет одну инвариантную
точку – это поворот вокруг точки
на угол
такой, что
.
Инвариантных прямых нет.
б)
Определим род движения
II
род
Найдем
инвариантные точки. Точка является
инвариантной тогда и только тогда, когда
,
то есть
.
Подставим в формулы движения:
.
Система противоречива, следовательно,
инвариантных точек нет. Это скользящая
симметрия. Найдем элементы ее определяющие
(см. таблицу). Рассмотрим точку
.
Найдем ее образ по формулам
.
Найдем координаты середины отрезка
:
.
Эта точка принадлежит оси скользящей
симметрии, также как и точка
(мы подставили координаты точки
в формулы движения). Вектор
параллельного переноса, входящего в
скользящую симметрию, есть вектор
.
Ось скользящей симметрии:
.
Единственная инвариантная прямая –
ось скользящей симметрии
.
в)
Определим род движения
II
род
Найдем
инвариантные точки. Точка является
инвариантной тогда и только тогда, когда
,
то есть
.
Подставим в формулы движения:
.
Система имеет бесконечно много решений,
то есть движение имеет прямую
инвариантных точек. Это осевая симметрия
с осью
.
Инвариантными прямыми являются ось
осевой симметрии
и все прямые перпендикулярные оси:
,
С – произвольная константа.
г)
Определим род движения:
род. Найдем инвариантные точки:
. Система противоречива, следовательно,
инвариантных точек нет. Это параллельный
перенос на вектор
(свободные члены в формулах движения).
Инвариантные прямые: все прямые,
параллельные вектору
.
Их уравнения:
,
где С – произвольная константа.
д)
Определим род движения:
род. Найдем инвариантные точки:
.
Система противоречива, следовательно,
инвариантных точек нет. Это скользящая
симметрия. Найдем ее определяющие
элементы. Рассмотрим точку
.
Найдем ее образ по формулам
.
Найдем координаты середины отрезка
:
.
Эта точка принадлежит оси скользящей
симметрии, также как и точка
(мы подставили координаты точки
в формулы движения). Вектор
параллельного переноса, входящего в
скользящую симметрию, есть вектор
.
Ось скользящей симметрии:
.
Единственная инвариантная прямая –
ось скользящей симметрии
.
е)
Определим род движения:
род. Найдем инвариантные точки:
.
Система имеет бесконечно много решений,
то есть движение имеет бесконечно много
инвариантных точек, лежащих на прямой
.
Это осевая симметрия с осью
.
Инвариантными прямыми являются ось
осевой симметрии
и все прямые перпендикулярные оси:
,
С – произвольная константа.
ж)
Определим род движения:
род. Найдем инвариантные точки:
.
Движение имеет единственную инвариантную
точку, следовательно, это поворот вокруг
этой точки
на угол
,
для которого
,
то есть
.
Это центральная симметрия. Инвариантными
прямыми являются все прямые, проходящие
через точку
,
то есть прямые
для любых
.
Задачи
к проверочной работе.
1.
Доказать, что формулы, записанные в
ПДСК, задают движение, определить его
вид и задающие элементы, записать
уравнения инвариантных прямых, найти
образ и прообраз прямой
при этом движении, образ и прообраз
окружности
.
1)
;
2)
;
3)
;
4)
;
5)
;
6)
;
7)
;
8)
;
9)
;
10)
;
11)
.
2.
Нарисована пара ортонормированных
реперов. Определить вид движения и
элементы, его задающие.
3.
Определить вид движения
;
;
;
;
;
.
§ 5. Преобразование подобия.
Гомотетия.
Определение.
Пусть на плоскости фиксирована точка
и дано число
.
Гомотетией называется такое преобразование
плоскости
,
что
.
Точка
называется центром гомотетии, а число
называется коэффициентом гомотетии.
Свойства
гомотетии.
1.
– единственная инвариантная точка
гомотетии.
2.
Гомотетия
является подобием первого рода с
коэффициентом
.
3.
;
.
Формулы
гомотетии:
Задачи.
-
Построить
образ и прообраз точки, прямой, окружности
при гомотетии, заданной центром
и парой соответствующих точек
.
Решение. Изобразим на картинке точку
и пару соответствующих точек
.
Посмотрим на определение гомотетии и
убедимся, что все три точки лежат на
одной прямой.
Возьмем точку В на плоскости и построим
ее образ. Во-первых, точка
должна лежать на одной прямой с точками
и В. Проводим прямую
.
Во-вторых, прямые
и
должны быть параллельны по свойству
гомотетии, следовательно,
принадлежит прямой, проходящей через
точку
параллельно прямой
.
Обозначим эту прямую
.
Тогда
.
Возьмем точку
на
плоскости и построим ее прообраз.
Рассуждения полностью аналогичны
проведенным выше. Во-первых, точка
(прообраз точки
)
лежит на одной прямой с точками
и
.
Во-вторых, прямые
и
должны быть параллельны по свойству
гомотетии, следовательно,
принадлежит прямой, проходящей через
точку
параллельно прямой
.
Обозначим эту прямую
.
Тогда
.
Чтобы построить образ (прообраз) данной
прямой при гомотетии, достаточно
построить образ (прообраз) одной ее
точки и через эту точку провести прямую
параллельную денной. Подумайте, почему
это так?
Чтобы построить образ (прообраз) данной
окружности, достаточно построить образ
(прообраз) ее центра
и какой-нибудь точки
этой
окружности. Получим точку
.
Проведем окружность с центром в точке
радиуса
.
Это будет образ данной окружности.
-
На
плоскости даны две прямые
и точка О, им не принадлежащая. Построить
образ и прообраз произвольной прямой
при гомотетии с центром в точке О и
переводящей
.
.
Решение. Проведем через точку О
какую-нибудь прямую
.
Обозначим
и
.
Убедимся, что такое обозначение не
случайно и точка
действительно является образом точки
.
Как обычно запишем
(действительно, прямая
инвариантна, так как проходит через
центр гомотетии). Теперь гомотетия у
нас задана центром и парой соответствующих
точек. Такие задачи мы уже умеем решать
(см. задачу 1).
-
Составить
формулы гомотетии, зная две инвариантные
прямые
и
и коэффициент гомотетии
.
Найти образ окружности
при
этой гомотетии.
при
Решение. Общие формулы для гомотетии у
нас есть. Если мы подставим в них
координаты центра и коэффициент
гомотетии, то получим ответ. Коэффициент
у нас дан:
.
Ищем координаты центра гомотетии. По
свойству гомотетии все ее инвариантные
прямые пересекаются в ее центре,
следовательно, определив координаты
точки пересечения прямых
и
мы найдем координаты центра
гомотетии.
.
Получаем
.
Найдем теперь образ
окружности
.
Вычислим координаты образа точки
– центра окружности
–
при данной гомотетии (подставим координаты
точки
в формулы гомотетии). Получим
.
Так как гомотетия является подобием с
коэффициентом
,
то окружность
будет
иметь радиус в 2 раза больше, чем исходная
окружность. Итак, окружность
имеет центр в точке
и радиус 4. Запишем ее уравнение:
.
-
Подобие
задано парой реперов. Представить его
в виде композиции гомотетии с тем же
коэффициентом и любым центром и движения.
Определить вид движения.
Решение. Пусть даны ортонормированный
репер
и репер
.
Так как они задают подобие, должны
выполняться условия:
и
(почему?) Определим коэффициент подобия.
Он равен
.
Возьмем произвольную точку плоскости
– это будет центр гомотетии. Построим
образ репера
при гомотетии с центром
и коэффициентом
(для построения воспользуемся теоремой
Фалеса). В результате получим репер
.
Тогда пара реперов
и
задаст движение. Нам нужно определить
вид этого движения. Во-первых, определим
род движения по ориентации реперов
(одинаковая ориентация – первый род,
противоположная – второй род).
Движение 1 рода:
а)
параллельный
перенос на вектор
;
б) иначе, поворот. Определим центр и угол
поворота. Пусть прямая
– серединный перпендикуляр к отрезку
,
прямая
– серединный перпендикуляр к отрезку
.
Тогда точка
– центр поворота. Угол поворота
.
Движение
2 рода:
а) если
прямая
,
проходящая через середины отрезков
перпендикулярна им, то данное движение
– осевая симметрия с осью
.
б) иначе
это скользящая симметрия с осью
,
проходящей через середины отрезков
.
Чтобы найти вектор параллельного
переноса этой скользящей симметрии,
отразим точку
от оси
.
Получим точку
.
Тогда вектор
будет искомым вектором.
-
Представить
преобразование подобия
в виде композиции гомотетии с отрицательным
коэффициентом и движения. Определить
вид движения.
Решение. Вспомним общий вид формул
подобия:
,
где
.
Тогда
– коэффициент подобия.
Мы видим, что формулы из задачи
удовлетворяют этим условиям, следовательно,
задают подобие с коэффициентом
.
Пусть данное подобие
представлено в виде
,
где
– гомотетия,
– движение. Запишем их формулы. Начнем
с гомотетии, общие формулы которой у
нас есть.
.
Теперь найдем формулы движения
.
Для этого умножим обе части равенства
справа на
.
Получим
.
Из этой записи мы видим, чтобы найти
формулы движения
,
нужно записать формулы гомотетии
, затем найти композицию
и
.
.
Чтобы найти композицию гомотетии и
подобия, введем другие обозначения для
переменных. Заметим, что гомотетия и
подобие действуют на точку в следующей
последовательности:
.
Точка
является образом для точки
при гомотетии и исходной точкой для
подобия
.
Тогда
и
.
Движение
,
следовательно, в формулах нам надо
“избавиться” от переменных
.
Подставим их из уравнений гомотетии в
уравнения подобия:
.
Нам осталось только определить вид
движения по его формулам (см. §3). Это
движение 1 рода, имеющее единственную
инвариантную точку
.
Это поворот вокруг точки
на угол
такой, что
.
Задачи
к проверочной работе.
-
Построить
образ и прообраз точки, прямой, окружности
при гомотетии, заданной центром
и коэффициентом
(
). -
Составить
формулы гомотетии, заданной двумя
парами соответствующих точек
. -
Построить
образ данной прямой при гомотетии,
заданной двумя парами прямых
(
)
и коэффициентом
.
-
Построить
образ данной прямой при гомотетии,
заданной двумя парами прямых
()
и коэффициентом
. -
Составить
формулы гомотетии с коэффициентом
,
при которой прямая
переходит в прямую
,
а прямая
– в прямую
. -
Найти
образ окружности
при гомотетии с центром в точке
и переводящей прямую
в прямую
. -
Написать
формулы гомотетии, при которой прямые
и
инвариантны, а образом прямой
является
прямая
. -
Написать
формулы гомотетии с положительным
коэффициентом, при которой окружность
переходит в окружность
. -
Построить
образ и прообраз данной прямой при
гомотетии, переводящей данные прямые
и данные точки
. -
Построить
прообраз данной окружности при гомотетии,
переводящей данные точки
. -
Найти
уравнение прообраза прямой
при гомотетии с центром в точке
,
которая переводит прямую
в прямую
. -
Построить
прообраз данной прямой при гомотетии,
заданной парой соответствующих точек
и инвариантной прямой
. -
Даны
два параллельных отрезка
.
Построить образ данной окружности при
гомотетии, переводящей один из данных
отрезков в другой. Сколько решений
имеет задача? -
Представить
подобие в виде композиции гомотетии с
тем же коэффициентом и движения.
Определить вид движения, если
1)
;
2)
;
3)
. -
Представить
подобия предыдущей задачи в виде
композиции движения и гомотетии с
отрицательным коэффициентом и
произвольным центром. -
Представить
подобие
в виде композиции гомотетии с центром
в точке
и отрицательным коэффициентом и
движения. Определить вид движения. -
Подобие
задано парой реперов (нарисуйте
картинку!). Разложить его в композицию
гомотетии с положительным (отрицательным)
коэффициентом и движения. Определить
вид движения.
).
.
)
,
,
.
является
.
.
.
,
.
.
;
;
.
18*.
Составить формулы подобия первого рода,
переводящего отрезок с концами в точках
в отрезок с концами
.
Сколько решений имеет задача?
19*.
Доказать, что квадрат подобия второго
рода есть гомотетия.
20*.
Доказать, что любые две равносторонние
гиперболы подобны.
21*.
Доказать, что две любые параболы подобны.
Чему равен коэффициент подобия?
22*.
Подобие задано парой реперов (нарисуйте
картинку!). Разложить его в композицию
гомотетии с положительным (отрицательным)
коэффициентом и движения с общей
инвариантной точкой. Определить вид
движения.
§ 6. Аффинные преобразования.
Определение.
Преобразование плоскости называется
аффинным, если оно любые три точки,
лежащие на одной прямой переводит в три
точки также лежащие на одной прямой и
при этом сохраняет простое отношение
трех точек.
Определение.
Нетождественное аффинное преобразование
называется перспективно-аффинным
(или родством), если оно имеет по
крайней мере две инвариантные точки А
и В.
При
этом вся прямая (АВ) состоит из инвариантных
точек. Она называется осью родства.
Свойства
родства.
-
Прямые,
соединяющие соответствующие точки
родства параллельны или совпадают. -
Если
прямая пересекает ось родства в некоторой
точке, то ее образ также пересекает ось
родства в этой же точке. Если прямая не
пересекает ось родства, то ее образ
также не пересекает ось родства.
Примеры
перспективно-аффинных преобразований.
|
Сдвиг
|
Косое сжатие
|
Косое
сжатие называется сжатием, если
.
Задачи.
-
Сдвиг
(косое сжатие) задано осью и парой
соответствующих точек. Построить образ
и прообраз данной точки при этом
преобразовании.
Решение. Рисуем картинку для сдвига.
Нам даны ось
и пара соответствующих точек
.
Так как мы рассматриваем сдвиг,
.
Возьмем произвольную точку В плоскости
и построим ее образ
.
Воспользуемся свойствами родства.
Во-первых,
по 1 свойству, то есть
принадлежит прямой
,
проходящей через точку В параллельно
прямой
.
Во-вторых, если
,
то
по 2 свойству, то есть
.
Тогда
.
Прообраз произвольной точки
плоскости строится аналогично. Возьмем
произвольную точку
плоскости и построим ее прообраз
.
Воспользуемся свойствами родства.
Во-первых,
по 1 свойству, то есть
принадлежит прямой
,
проходящей через точку
параллельно прямой
.
Во-вторых, если
,
то
по 2 свойству, то есть
.
Тогда
.
В случае косого сжатия рассуждения
точно такие же.
-
Сдвиг
(косое сжатие) задано осью и парой
соответствующих точек. Построить образ
и прообраз данного квадрата при этом
преобразовании. Рассмотреть различное
расположение квадрата относительно
оси родства.
Решение. Достаточно построить образы
вершин квадрата и соединить их отрезками
(в результате этих действий мы получим
параллелограмм). Подумайте, как построить
образ квадрата проще.
-
Построить
образ точки при косом сжатии, заданном
инвариантной точкой С , парой
соответствующих параллельных
(пересекающихся) прямых
и направлением сжатия – прямой
.
Решение. Рисуем картинку. Мы знаем, что
все инвариантные точки лежат на оси
родства
,
то есть
.
Непараллельные соответствующие прямые
пересекаются на оси родства, то есть
.
У нас появилась ось родства
.
Нам осталось получить две соответствующие
точки
,
которые лежат на прямых
и
соответственно. Мы знаем, что все прямые,
соединяющие соответствующие точки
родства параллельны между собой. Это и
есть направление сжатия. Оно задается
прямой
,
то есть
.
Кроме того,
.
Следовательно,
.
Теперь косое сжатие задано осью и парой
соответствующих точек. Дальше решение
такое же как в задаче 1.
-
Родство
задано двумя парами пересекающихся
соответствующих прямых
и
.
Построить образ (прообраз) данной точки
при данном родстве.
.
Решение. Если мы построим ось родства
и пару соответствующих точек, то сможем
решить задачу по аналогии с задачей 1.
Мы знаем, что соответствующие прямые
пересекаются на оси родства, следовательно,
ось родства
.
Найдем образ точки
.
Тогда родство задано осью
и парой соответствующих точек
.
Задачи
к проверочной работе.
-
Построить
образ (прообраз) данной трапеции при
косом сжатии, заданном осью и парой
соответствующих точек. -
Построить
образ данной прямой при сдвиге, заданном
осью и парой пересекающихся соответствующих
прямых. -
Сдвиг
задан парой соответствующих прямых
и инвариантной прямой
.
Построить образ данного треугольника
(квадрата, параллелограмма) при данном
сдвиге. Сколько решений имеет задача? -
Построить
образ (прообраз) данной трапеции при
сдвиге, заданном парой соответствующих
точек
и инвариантной точкой В.
5.
Доказать, что любое аффинное преобразование
можно представить в виде композиции
родства и подобия.
6*.
Показать, что перспективно-аффинное
преобразование, вообще говоря, не
сохраняет величину угла. Но при этом
верно следующее утверждение: при всяком
перспективно-аффинном преобразовании
через каждую точку плоскости проходят
две взаимно перпендикулярные прямые,
образы которых при этом преобразовании
также взаимно перпендикулярны.
7*.
Доказать, что любое аффинное преобразование
можно представить в виде композиции
двух сжатий к взаимно перпендикулярным
прямым и движения.
Образ точки на векторе
Пусть 
— вектор пространства. Рассмотрим отображение пространства на себя, при котором образом любой точки M пространства является такая точка M ′ , что вектор 
′ равен вектору : ′ = (рис. 23).
Можно доказать, что точка M имеет при данном отображении единственный образ — точку М ′ , а для точки М ′ существует единственный прообраз — точка М .
Таким образом, получаем биективное отображение пространства на себя, т. е. преобразование пространства, которое называют параллельным переносом на вектор 
.
Определение. Параллельным переносом на вектор называется такое преобразование пространства, при котором любая точка М отображается на такую точку M ′ , что выполняется векторное равенство: 
′ = .
Иногда параллельный перенос называют коротко переносом. При этом вектор называют вектором переноса. Если при переносе на вектор точка М отображается на точку M ′ , то пишут: М ′ = ( М ) или ( M ) = M ′ .
Из определения следует, что параллельный перенос задаётся либо вектором, либо парой соответствующих точек ( М, М ′ ) .
Если при переносе на вектор точка М отображается на точку M ′ , то ′ = (рис. 24). Тогда 
= – . Значит, точка М ′ отображается на точку M переносом на вектор – , т. е. преобразование, обратное переносу на вектор 
, есть перенос на вектор – .
Перенос на нулевой вектор 
является тождественным преобразованием: ( М ) = М для любой точки М пространства.
5.2. Параллельный перенос в координатах
Пусть в прямоугольной системе координат Охyz задан вектор 
( a ; b ; с ) . Найдём зависимость между координатами точки М ( x ; y ; z ) и её образа M ′ ( х ′ ; y ′ ; z ′ ) при переносе на вектор .
Так как M ′ = ( М ) , то ′ = (рис. 25). Вектор ′ имеет координаты: ′ ( x ′ – x ; y ′ – y ; z ′ – z ). Тогда векторное равенство ′ = равносильно системе трёх равенств x ′ – х = a, y ′ – у = b, z ′ – z = с, откуда
(1)
Соотношения (1) называются формулами параллельного переноса пространства на вектор 
( a ; b ; c ) .
Докажем, что параллельный перенос пространства есть движение . Пусть: A ( x 1 ; y 1 ; z 1 ) и C ( x 2 ; y 2 ; z 2 ) — данные точки; A ′ ( 
; 
; 
), C ′ ( 
; 
; 
) — их образы при переносе на вектор ( a ; b ; с ). На основании (1) имеем
= x 1 + a, 
= y 1 + b, 
= z 1 + c,
= x 2 + a, 
= y 2 + b, 
= z 2 + c . (2)
Расстояние между точками А и C равно
.
Найдём расстояние между точками А ′ и C ′ .
Учитывая (2), получаем
| A ′ C ′ | = 
=
= 
= | AC| .
Таким образом, при параллельном переносе расстояние между точками сохраняется. Значит, параллельный перенос есть движение.
5.3. Свойства параллельного переноса
Можно доказать, что параллельный перенос отображает :
— прямую на параллельную ей прямую либо на себя;
— луч на сонаправленный с ним луч;
— вектор 
на равный ему вектор 
(на себя);
— плоскость на параллельную ей плоскость либо на себя.
Докажем, например, что параллельный перенос отображает плоскость на параллельную ей плоскость или на себя.
Действительно, параллельный перенос — движение, поэтому он отображает плоскость α на некоторую плоскость α′ . Докажем, что α′ || α или α′ совпадает с α .
На плоскости α выберем две пересекающиеся прямые a и b ; a ∩ b = O.
Пусть ( a ) = a ′ , ( b ) = b ′ (рис. 26). Тогда a || a ′ , b || b ′ .
Так как любое преобразование отображает пересечение фигур на пересечение их образов и прямые a и b пересекаются в точке O, то пересекаются и прямые a ′ и b ′ в такой точке O ′ , что O ′ = ( О ). Тогда либо плоскости α и α′ совпадают, либо по признаку параллельности плоскостей эти плоскости параллельны, что и требовалось доказать. ▼
Рассмотрим вопрос о неподвижных точках, неподвижных прямых и неподвижных плоскостях при параллельном переносе.
Неподвижных точек параллельный перенос на ненулевой вектор не имеет.
Неподвижной прямой при параллельном переносе на ненулевой вектор является любая прямая, параллельная вектору ; на каждой из этих прямых индуцируется параллельный перенос на вектор .
Неподвижной плоскостью при параллельном переносе на ненулевой вектор является любая плоскость, параллельная вектору ; на каждой из этих плоскостей индуцируется параллельный перенос на вектор .
Параллельный перенос, отображая любой вектор на себя, не меняет ориентацию пространства, следовательно, является движением первого рода.
Рассмотрим композицию двух переносов, заданных векторами и 
. Её обычно обозначают не ∘ , а + .
Пусть М — любая точка пространства. Перенос на вектор точку М отображает на такую точку М ′ , что ′ = (рис. 27). Последующий перенос на вектор точку М ′ отображает на такую точку M ″ , что ″ = . По правилу сложения векторов имеем ″ = ′ + ″ = + . Это означает, что ( + )( M ) = M ″ , т. e. перенoc на вектор ( + ) точку М отображает на точку М ″ .
Таким образом, композиция переносов на векторы и 
есть перенос на вектор + .
Так как + = + , то композиция переносов обладает свойством коммутативности: ( + )( M ) = ( + )( М ).
5 .4. Скользящая симметрия
Среди преобразований пространства важное место занимает «скользящая симметрия», представляющая собой композицию симметрии S α относительно плоскости α и параллельного переноса на вектор , который параллелен этой плоскости (рис. 28).
Отметим ряд характерных свойств скользящей симметрии:
— скользящая симметрия является движением (как композиция двух движений);
— скользящая симметрия не имеет неподвижных точек;
— любая прямая плоскости α , параллельная вектору переноса, является неподвижной прямой скользящей симметрии; на каждой из них индуцируется параллельный перенос;
— неподвижной плоскостью скользящей симметрии является не только плоскость симметрии α (на ней индуцируется параллельный перенос на вектор ) , а также любая плоскость, перпендикулярная плоскости α и параллельная вектору переноса (на каждой из таких плоскостей индуцируется скользящая симметрия, осью которой является прямая пересечения этой плоскости с плоскостью α , а вектором переноса — вектор );
— скользящая симметрия меняет ориентацию тетраэдра (значит, и ориентацию пространства), т. е. является движением второго рода;
— преобразованием, обратным скользящей симметрии, заданной плоскостью α и вектором , является скользящая симметрия, заданная той же плоскостью α и вектором – .
Попробуйте доказать самостоятельно, что композиция двух центральных симметрий есть параллельный перенос, причём Z B ∘ Z A = 2 
. Наоборот, любой параллельный перенос может быть разложен (неоднозначно) в композицию двух центральных симметрий.
Параллельный перенос
Параллельный перенос — это преобразование плоскости, при котором точки смещаются в одном и том же направлении на одно и то же расстояние.
Строгое определение параллельного переноса даётся либо через декартовы координаты, либо через вектор.
1) Введём на плоскости декартовы координаты x, y.
Параллельный перенос — это такое преобразование фигуры F, при котором её произвольная точка (x;y) переходит в точку (x+a; y+b), где a и b — некоторые числа, одинаковые для всех точек (x;y) фигуры F.
Формулы параллельного переноса
Если при параллельном переносе точка A(x;y) переходит в точку A1(x1;y1)
то параллельный перенос задаётся формулами:
Говорят также, что A1 является образом точки A при параллельном переносе на вектор (a; b). Точка A называется прообразом.
2) Параллельный перенос на данный вектор ā называется отображение плоскости на себя, при котором каждая точка A отображается в такую точку A1, то вектор AA1 равен вектору ā:
Свойства параллельного переноса
1) Параллельный перенос есть движение (то есть параллельный перенос сохраняет расстояние).
2) При параллельном переносе точки смещаются по параллельным (или совпадающим) прямым на одно и то же расстояние.
3) При параллельном переносе каждая прямая переходит в параллельную ей прямую (или в себя).
4) Каковы бы ни были точки A и A1, существует единственный параллельный перенос, при котором точка A переходит в точку A1.
В алгебре параллельный перенос широко используется для построения графиков функций.
Геометрия для новичков. Часть 1: координаты и векторы – теория
Внимание! Этот документ ещё не опубликован.
О чем данная статья
В данной статье дается теоретическое описание векторов, координат векторов и операций над ними.
На кого рассчитана статья
Прежде чем читать эту статью, нужно знать:
- что такое прямоугольная система координат и координаты точки на плоскости
- что такое теорема Пифагора
Введение
Зачем нужны координаты точек в играх
В любой игре положение игрового объекта задается координатами какой-либо точки, привязанной к этому объекту, т.е. эта точка перемещается вместе с объектом. Например, мы можем задать координаты объектов в «Супер Марио» следующим образом:
На этом рисунке крупные черные точки – это точки, привязанные к игровым объектам. Координаты этих точек мы и будем считать координатами игровых объектов.
Итак, на этом рисунке:
- координаты Марио равны (-0.5, -2)
- координаты улитки равны (3, -2)
- координаты кубика равны (4, 1)
Пример координат вектора
Я намеренно не написал конкретные значения для координат точек – пусть они будут произвольными.
Зададим себе вопрос «Как нужно изменить начальные координаты Марио, что получить конечные?» Чтобы ответить на этот вопрос, нам нужно найти пару чисел (x, y), таких, чтобы:
Ax + x = Bx
Ay + y = By
Решая эти 2 уравнения, получаем:
x = Bx – Ax
y = By – Ay
Пара (x, y) в нашей задаче является координатами вектора перемещения Марио. Но это – лишь конкретный пример координат вектора. Что такое вектор и что такое его координаты в общем случае? Сейчас узнаем.
Векторы
Что такое направленный отрезок
Стрелка показывает, что А – начало отрезка, а B – конец.
Что такое вектор
Что у этих отрезков общего? Хм, пожалуй 2 вещи:
- Направление
- Длина
Так вот, вектор – это как раз и есть совокупность направления и длины.
Направленный отрезок – не вектор, который мы изучаем в геометрии. Направленный отрезок задает, или как еще говорят, представляет вектор. Но это – не вектор.
В нашем примере направленный отрезок 
представляет вектор 
. Разницу в черточках наверху заметили? Еще часто вектор обозначают 1 буквой, например: 
Примечание: о тонкостях приведенного мной определения – в конце статьи.
Равенство векторов
Если задуматься, все направленные отрезки одинаковой длины, которые лежат на параллельных прямых и указывают в одну сторону, имеют одинаковое направление и длину. Следовательно, все эти направленные отрезки представляют один и тот же вектор. Из этого следует определение равенства 2 векторов:
Два вектора и 
, представленные направленными отрезками и 
называются равными, если:
Из данного определения следует, что при параллельном переносе произвольный направленный отрезок продолжает представлять тот же вектор, что он представлял до переноса. Это свойство активно используется для операций над векторами.
Длина вектора
Коллинеарные векторы
На рисунке любая пара из векторов , , 
является коллинеарными векторами
Если отрезки, представляющие коллинеарные векторы, имеют одинаковое направления, то векторы называют сонаправленными:
Пишут: 
Если отрезки, представляющие коллинеарные векторы, имеют противоположное направления, то векторы, представленные данными отрезками, называют противоположно направленными:
Пишут: 
Нулевой вектор
Единичные векторы
=1
Обратный вектор
Арифметические операции над векторами
- Вектор можно умножать на число. Вектор
, умноженный на число, записывается как k*. Вектор будет сонаправлен (противоположно направлен) с вектором , если k – положительное (отрицательное) число. Вектор k* будет иметь длину |k|*||:
|k*| = |k|*||
k* , если k>0
k* , если k 0, такое, что:
|k * |=1
Т.е. в результате нормализации мы получаем единичный вектор, сонаправленный с исходным вектором
Важно: нулевой вектор НЕЛЬЗЯ нормализовать, так как для любого числа k:
|k*
| = |k|*|| = k * 0 = 0
Итак, как же найти это число k?
Распишем |k * | по определению:
|k * | = |k| * || = k * || = 1
Здесь мы убрали с k знак модуля, так как по определению k > 0.
Итак:
k * || = 1
Из этого следует, что:
k = 1 / ||
Т.е. чтобы нормализовать произвольный ненулевой вектор, нам нужно разделить вектор на его длину.
Координаты вектора
Вроде бы из примера, приведенного в начале статьи, все понятно: координаты вектора – разность координат конца и начала направленного отрезка, представляющего вектор.
Но это не так. Действительно, значения координат вектора численно равны этой разности. Но определение координат вектора в корне отличается от определения координат точки.
Разложение вектора по 2 неколлинеарным векторам
В геометрии доказывается следующий факт.
Ecли мы возьмем 2 неколлинеарных вектора и ,
то для каждого вектора можно подобрать 2 числа k и s, для которых выполняется равенство:
= k* + s*
Теперь возьмем в качестве таких неколлинеарных векторов и следующие векторы:
- вектор – направление – вдоль оси Ox, длина равна 1
- вектор – направление – вдоль оси Oy, длина равна 1
Векторы 
и 
называют координатными векторами.
Определение координат вектора
= x* + y*
то пара чисел (x, y) будет называться координатами вектора .
Часто пишут:
= (x, y)
Эта запись означает, что вектор имеет координаты x и y.
Арифметические операции над координатами векторов
– = (-ax, -ay)
Координаты вектора, умноженного на число, равны координатам исходного вектора, умноженными на это число:
k* = (k*ax, k*ay)
Пусть у нас есть 2 произвольных вектора =(ax, ay) и =(bx, by). Тогда:
- кoординаты суммы 2 векторов равны сумме x- и y-координат векторов: + = (ax + bx, ay + by)
- как следствие из предыдущих свойств, координаты разности 2 векторов равны разности координат этих векторов: – = (ax – bx, ay – by)
Т.е. арифметика для координат векторов – такая же, как и для обычных чисел, только все считается покоординатно.
Радиус-вектор
Можно доказать, что численные значения координат точки совпадают со значения координат ее радиус-вектора. Здесь примем это как факт: 
=(Ax, Ay)
где (Ax, Ay) – координаты точки A
Связь между координатами вектора и координатами концов отрезка
если – направленный отрезок, представляющий вектор , то значения координат вектора (x, y) вычисляются по формуле:
(x, y) = (Bx – Ax, By – Ay)
где (Ax, Ay), (Bx, By) – координаты точек А и B соответственно.
Докажем это.
Мы можем записать простое равенство для произвольного вектора :
= 
–
Заметим, что и – радиус векторы.
Из равенства значений координат точки и радиус-вектора и предыдущей формулы следует, что:
(x, y) = (Bx – Ax, By – Ay)
Нахождение длины вектора по его координатам
Пусть у нас есть вектор , представленный отрезком . Координаты вектора равны (x, y).
Чтобы найти длину вектора через его координаты, воспользуемся теоремой Пифагора и равенством:
= 
+ 
По теореме Пифагора:
AC = || = |x|,
СB = || = |y|
то в итоге получаем равенство:
Заключение
Применению векторов в реальных задачах игровой разработки будет посвящена следующая моя статья. В ней практически не будет математики и будет много программирования.
Здесь же я описал то, что будет необходимо для понимания практических приемов использования векторов.
Если не иметь представления, как связаны координаты точек и координаты векторов, очень сложно понять, как работают алгоритмы определения расстояний от точки до геометрической фигуры, алгоритмы обнаружения столкновений и т.д.
Так что не жалейте, если вы (о ужас!) кое-что запомнили из «всей этой математики». Все это вам пригодится очень скоро, обещаю.
Литература
Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б., Позняк Э.Г., Юдина И.И. «Геометрия», 7-9 классы»
Главы: «Векторы», «Метод координат».
PS: корректность определения вектора в статье
Вся хитрость в том, что существует несколько определений вектора даже в рамках геометрии.
Направленный отрезок – тоже вектор, так называемый фиксированный вектор. Но нужно учитывать один важный факт – 2 фиксированных вектора равны тогда и только тогда, когда их концы и начала совпадают. А это не то определение равенства 2 векторов, что дает учебник геометрии.
Определение вектора, данное в этой статье – определение так называемого свободного вектора.
Каждый свободный вектор – это множество фиксированных векторов, которые имеют равную длину и одинаковое направление.
Именно это определение учебник геометрии и пытается дать в неявном виде, когда вводит понятие равенства векторов. Но здесь возникает нестыковка – учебник объясняет, как работать со свободными векторами, изначально дав определение фиксированного вектора.
Надеюсь, вышесказанное объясняет, почему я привел в данной статье “свое” определение вектора.
[spoiler title=”источники:”]
http://gamedev.ru/code/articles/geometry_for_beginners_1
[/spoiler]
Написано специально для студентов Бизнес‑информатики, которые только начинают осваивать OpenCV и всякий там Computer Vision, которым тяжело с математикой
Здесь с геометрической точки зрения объясняются основы формирование изображения.
В частности, рассматривается математика, стоящая за тем, как точка в 3D‑изображении проецируется на плоскость изображения.
Статья по своей природе не математическая и предназначена исключительно для новичков. Тем не менее, что такое перемножение матриц знать надо.
Проблема
Для понимания задачи, предположим, что у нас есть камера, установленная в комнате.
Зная, что в комнате есть точка mathbf{P} в трехмерном пространстве (3D‑точка, Декартова система координатએ), мы хотим найти координаты пикселя (u, v) этой 3D‑точки на снимке, сделанном камерой.
В этом контексте есть три системы координат. Давайте с ними разберёмся.
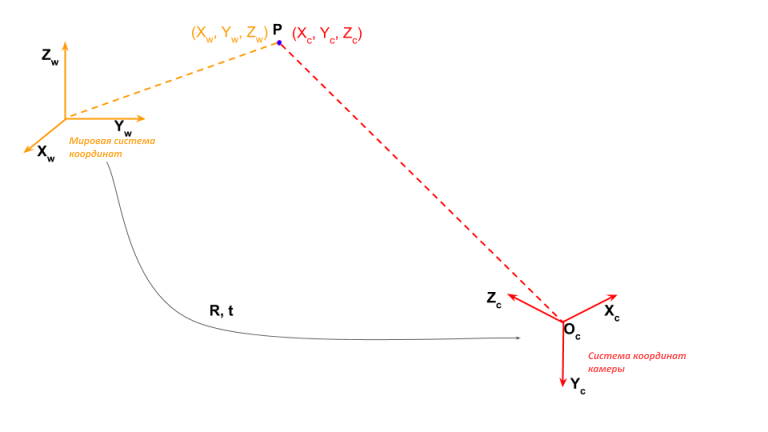
1. Мировая система координат
Чтобы определить расположение точек в помещении, нам нужно сначала определить систему координат этого помещения. Это требует знания двух вещей:
- начало координат: можно произвольно назвать любой угол комнаты началом (0, 0, 0).
- направление осей X, Y, Z: оси X и Y можно направить в плоскости пола вдоль двух стенок, а ось Z вдоль вертикального угла стены.
Принимая во внимание всё это, можно найти три координаты любой точки в комнате, измерив расстояние от неё до начала координат по осям X, Y и Z.
Эта система координат, связанная с комнатой, называется мировой системой координат. На рисунке 1 она показан осями оранжевого цвета. Мы будем использовать жирный шрифт (например, X_w), чтобы показать ось, и обычный шрифт, чтобы показать координату точки (например, X_w).
Давайте рассмотрим точку Р в этой комнате. В мировой системе координат координаты Р задаются по осям (X_w, Y_w, Z_w). Вы можете найти X_w, Y_w, и Z_w координаты этой точки, просто измеряя расстояние от этой точки до начала координат по трем осям.
2. Система Координат Камеры
А теперь давайте поставим камеру в комнате.
Снимать будем этой камерой и поэтому нас интересует связанная с ней трехмерная система координат.
Если бы мы поместили камеру в начало координат комнаты и выровняли ее таким образом, чтобы ее оси X, Y и Z совпадали с осями X_w, Y_w и Z_w комнаты, то эти две системы координат были бы одинаковыми.
Однако, это вряд ли возможно на практике. Мы хотели бы поставить камеру в любом месте и она должна видеть любое месте. Поэтому нам нужно найти связь между координатами 3D‑комнаты (т.е. мира) и координатами 3D‑камеры.
Допустим, наша камера стоит где‑то произвольно (t_X, t_Y, t_Z) в комнате. На техническом жаргоне мы можем перевести координаты камеры по (t_X, t_Y, t_Z) по отношению к мировым координатам.
Камера может также смотреть куда угодно. Другими словами, можно сказать, что камера вращается относительно мировой системы координат.
Вращение в 3D определяется тремя параметрами — тангаж, рыскание и крен. Образно это представляется движением руки от локтя: вверх‑вниз — тангаж, слева‑направо — рыскание, вращение кулака — крен.
Однако часто для математической манипуляции удобно задавать вращение в виде матрицы 3 × 3. Теперь вы можете подумать, что матрица 3 × 3 имеет 9 элементов и, следовательно, 9 параметров, но у вращения только 3 параметра. И это правильно, именно поэтому любая произвольная матрица 3 × 3 не является матрицей вращения. Не вдаваясь в детали, давайте пока просто узнаем, что матрица вращения имеет только три степени свободы, хотя она имеет 9 элементов.
Вернемся к нашей первоначальной проблеме. Мировая координата и координаты камеры связаны матрицей вращения mathbf{R} и вектором перемещения 3 элементов mathbf{t}
Что это значит?
Это значит, что точка mathbf{P}, имеющая координаты (X_w, Y_w, Z_w) в мировой системе координат, в системе координат камеры будет иметь другие значения (X_c, Y_c, Z_c). Система координат камеры на рисунке изображена красным цветом.
Эти координаты связаны следующим уравнением.
begin{bmatrix}X_c\Y_c\Z_cend{bmatrix}= mathbf{R} begin{bmatrix}X_w\Y_w\Z_wend{bmatrix} + mathbf{t}
Обратите внимание, что представление вращения в виде матрицы позволило нам выполнять вращение простым умножением матрицы вместо утомительной манипуляции символами, требуемой в других представлениях, таких как тангаж, рыскание, крен. Я надеюсь, что это поможет вам понять, почему мы описываем вращение, используя матрицы.
Иногда приведенное выше выражение пишется в более компактной форме. Вектор перевода 3 × 1 добавляется в виде столбца в конец матрицы вращения 3 × 3, чтобы получить матрицу 3 × 4, называемую внешней матрицей .
begin{bmatrix} X_c\ Y_c\ Z_c end{bmatrix}= begin{bmatrix} mathbf{R} / mathbf{t} end{bmatrix} begin{bmatrix} X_w\ Y_w Z_w \ 1 end{bmatrix}
где, внешняя матрица mathbf{P} задается с помощью
mathbf{P} = begin{bmatrix} mathbf{R} / mathbf{t} end{bmatrix}
Однородные координаты: в проективной геометрии мы часто работаем с забавным представлением координат, где к координатам добавляется дополнительное измерение. Трехмерная точка (X, Y, Z) в декартовых координатах может быть записана как (X, Y, Z, 1) в однородных координатах. В более общем случае точка в однородной координате (X, Y, Z, W) совпадает с точкой (X / W, Y/ W, Z / W) в декартовых координатах. Однородные координаты позволяют нам представлять бесконечные величины, используя конечные числа. Например, точку на бесконечности можно представить в виде (1, 1, 1, 0) в однородных координатах. Вы можете заметить, что мы использовали однородные координаты в уравнении 2 для представления мировых координат.
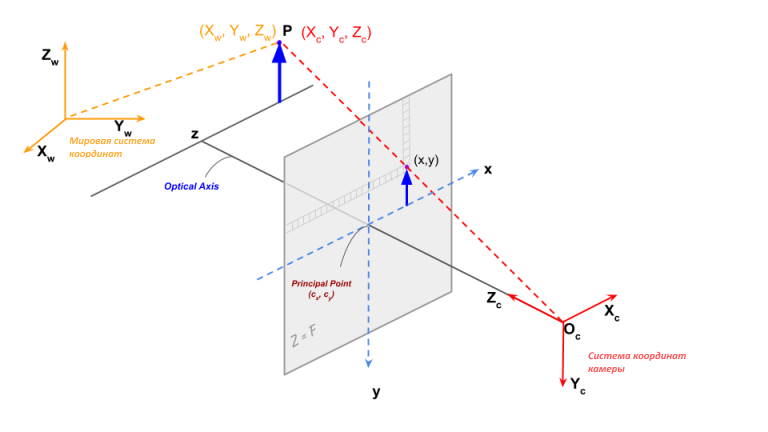
3. Система координат изображения
После того, как мы получим точку в трехмерной системе координат камеры, применяя вращение и перевод к точкам мировых координат, мы находимся в положении, когда можем спроецировать точку на плоскости изображения для вычисления местоположение точки на изображении.
На изображении выше мы смотрим на точку mathbf{P} с координатами (X_c, Y_c, Z_c) в системе координат камеры. Напомним только, что если бы мы не знали координаты этой точки в системе координат камеры, мы могли бы преобразовать ее координаты в мировой системе координат, используя внешнюю матрицу, чтобы получить координаты в системе координат камеры, используя уравнение 2.
Рисунок 2, показывает проекцию камеры в случае простой камеры с контактным отверстием.
Оптический центрએ (ось наблюдения) представлен с помощью O_c. В действительности на плоскости формируется перевернутое изображение. Для математического удобства мы просто делаем все вычисления, как будто плоскость изображения находится перед оптическим центром, потому что изображение, считанное с матрицы, может быть тривиально повернуто на 180 градусов, чтобы компенсировать инверсию. На практике даже этого не требуется. Всё еще проще: реальная светочувствительная матрица камеры просто читается начиная самого нижнего ряда в обратном порядке (справа налево), а затем снизу вверх для каждого ряда. Такой метод автоматически формируется правильное изображение и по вертикали и по горизонтали. Так что на практике нет необходимости переворачивать изображение.
Плоскость изображения размещается на расстоянии mathbf{phi} (фокусное расстояниеએ) от оптического центра.
Используя геометрию средней школы (подобные треугольники), мы можем показать проектное изображение (x, y) 3D‑точки (X_c, Y_c, Z_c), заданной.
x = f frac{X_c}{Z_c} \ y = f frac{Y_c}{Z_c}
Приведенные выше два уравнения можно переписать в матричной форме следующим образом:
begin{bmatrix}x’\y’\z’end{bmatrix} = begin{bmatrix}f&0&0\0&f&0\0&0&1end{bmatrix} begin{bmatrix}X_c\Y_c\Z_cend{bmatrix}
Матрица mathbf{К}, показанная ниже, называется внутренней матрицей и содержит внутренние параметры камеры.
mathbf{K} = begin{bmatrix}f&0&0\0&f&0\0&0&1end{bmatrix}
Приведенная выше простая матрица показывает только фокусное расстояние.
Однако, пиксели в светочувствительной матрице камеры могут быть не квадратными, и поэтому мы можем иметь два разных фокусных f_x и f_y расстояния.
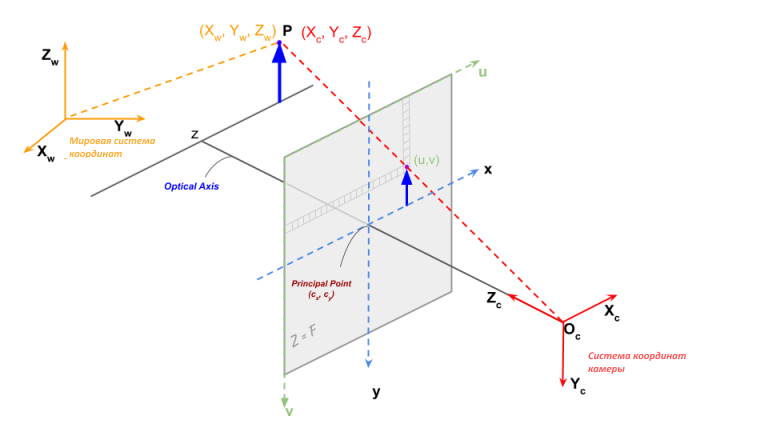
Оптический центр (c_x, c_y) камеры может не совпадать с центром системы координат изображения.
Кроме того, может наблюдаться небольшой перекос mathbf{gamma} между осями mathbf{x} и mathbf{y} датчика камеры.
Учитывая это все, матрицу камеры нужно переписать так:
mathbf{K} = begin{bmatrix}f_x&gamma&c_x\0&f_y&c_y\0&0&1end{bmatrix}
В приведенном выше уравнении координаты mathbf{x} и mathbf{y} пикселей находятся относительно центра изображения. Однако при работе с изображениями источник находится в верхнем левом углу изображения.
Давайте представим координаты изображения по (u, v).
begin{bmatrix}u’\v’\w’end{bmatrix} = begin{bmatrix}f_x&gamma&c_x\0&f_y&c_y\0&0&1end{bmatrix} begin{bmatrix}X_c\Y_c\Z_cend{bmatrix}
где,
u = frac{u’}{w’} \ v = frac{v’}{w’}
Итого
Проецирование трехмерной точки в мировой системе координат на пиксельные координаты камеры выполняется в три этапа.
- Трехмерная точка преобразуется из мировых координат в координаты камеры с помощью внешней матрицы, которая состоит из вращения и перемещения между двумя системами координат.
- Новая трехмерная точка в системе координат камеры проецируется на плоскость изображения с помощью встроенной матрицы, которая состоит из внутренних параметров камеры, таких как фокусное расстояние, оптический центр и т. д.
В следующем посте этой серии мы узнаем о калибровке камеры и о том, как выполнять ее с помощью функции OpenCV.
Оригинал (англ.): Geometry of Image Formation
