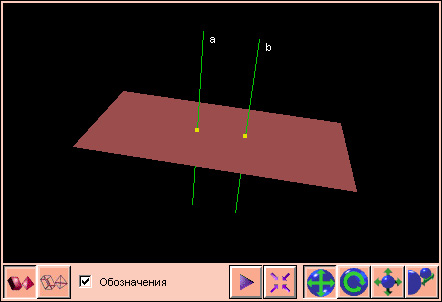
Как найти координаты основания перпендикуляра к прямой - Сайт, где вы сможете решить свои вопросы

Как найти основание перпендикуляра опущенного из точки на прямую

Перпендикуляр, опущенный из точки на прямую

(не проходящую через ), представляется уравнениями

или в векторной форме уравнениями

Взятое отдельно, уравнение (2) представляет плоскость (рис. 175), проведенную через перпендикулярно (§ 155), а уравнение (3) — плоскость проведенную через точку и прямую

Замечание. Если прямая проходит через точку то уравнение (3) обращается в тождество (через точку, взятую на прямой можно провести бесчисленное множество перпендикуляров , § 120). Пример. Найти уравнение перпендикуляра, опущенного из точки (1; 0; 1) на прямую

Найти также основание перпендикуляра. Решение. Уравнения (1а) можно записать в симметричном виде (§ 151) так:

Искомый перпендикуляр представляется уравнениями

или после упрощений

Координаты основания К перпендикуляра найдем, решив систему трех уравнений (16), (2в). Уравнение должно удовлетворяться само собой. Получаем .

Замечание. Система трех уравнений (1б), (3в) имеет бесчисленное множество решений (так как плоскость проходит через прямую а не пересекает ее).

Проекция точки на прямую

Пусть необходимо спроектировать точку на прямую Ах+Ву+С=0. проекцией точки на прямую является основание перпендикуляра, опущенного из точки на прямую. Нормалью к данной прямой является вектор . Составим уравнение проецирующей прямой. Она проходит через точку и параллельна вектору . Подставив координаты точки и вектора в каноническое уравнение прямой , получим: . Теперь необходимо найти координаты точки пересечения данной прямой и проектирующей, для чего объединим их в систему: решение этой системы есть координаты точки, являющейся проекцией точки на прямую

Пример: Даны вершины треугольника : ; ; . Найти:

1) уравнение высоты, опущенной из вершины ;

2) точку пересечения высоты и стороны ;

3) точку пересечения медиан треугольника .

Решение: 1) Составим уравнение высоты , проходящей через точку перпендикулярно вектору :

2) Составим уравнение стороны :

Найдем точку пересечения высоты и стороны .Обозначим эту точку N, она является проекцией точки А на сторону ВС. Для нахождения точки N, решим следующую систему уравнений:

Перпендикуляр к прямой

Что такое перпендикуляр к прямой? Как построить перпендикуляр к прямой? Сколько перпендикуляров можно провести из точки к прямой? Что такое наклонная? Что называется проекцией наклонной? Об этом — ниже.

Перпендикуляр, опущенный из точки A на прямую a — это отрезок, лежащий на прямой, перпендикулярной прямой a, один конец которого — точка A, второй — точка пересечения этих двух прямых.

Как построить перпендикуляр к прямой?

На рисунке 1 изображены прямая a и точка A, не лежащая на прямой a.

Чтобы построить перпендикуляр, воспользуемся угольником.

Угольник располагаем так,

чтобы одна сторона прямого угла проходила вдоль прямой a,

а вторая — через точку A.

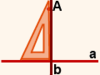
Если провести через точку A вдоль стороны угольника прямую,

то получим прямую b, перпендикулярную данной прямой a.

Нам нужно построить перпендикуляр, то есть отрезок — часть этой прямой.

Соединим точку A с точкой на пересечении прямых a и b

(назовем вторую точку B).

Отрезок AB — перпендикуляр, проведенный из точки A к прямой a.

Точка B называется основанием перпендикуляра.

Расстояние от точки до прямой измеряется длиной перпендикуляра.

Расстояние от точки A до прямой a (рисунок 4) равно длине отрезка AB.

Из данной точки к данной прямой можно провести только один перпендикуляр.

Любой другой отрезок, который соединяет точку A с точкой на прямой a, называется наклонной.

Наклонной, проведенной из точки A к прямой a, называется отличный от перпендикуляра отрезок, соединяющий точку A с некоторой точкой на прямой a.

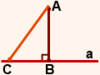
На рисунке 5 AC — наклонная, проведенная из точки A к прямой a.

Точка C называется основанием наклонной AC.

Отрезок, который соединяет основание перпендикуляра с основанием данной наклонной, называется проекцией этой наклонной на прямую.

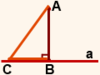
На рисунке 6 BC — проекция наклонной AC на прямую a.

Перпендикуляр часто встречается при решении задач, связанных с треугольниками. В частности, определение высоты треугольника опирается на перпендикуляр.

Источник

Макеты страниц

Перпендикуляр, опущенный из точки на прямую

(не проходящую через ), представляется уравнениями

или в векторной форме уравнениями

Найти также основание перпендикуляра. Решение. Уравнения (1а) можно записать в симметричном виде (§ 151) так:

Искомый перпендикуляр представляется уравнениями

Рис. 175

или после упрощений

Источник

LFK

Мыслитель

(6194)

11 лет назад

y = kx+в – уравнение перпендикуляра, проходящего через (3;5), поэтому : 5=3к+в, к=(5-в) /3 . Данное в условии уравнение перепишем в виде: у= 3/7х -12/7 . Так как графики перпендикулярны, то (5-в) /3=-7/3, значит в=12, имеем у=-7/3х+12 – искомое уравнение

LFKМыслитель (6194)

11 лет назад

Теперь ищем общую точку этих графиков – это и есть основание перпендикуляра, для этого решим уравнение: 3/7х-12/7 = -7/3х +12, х= 144/29, у= 12/29. Получили: ( 144/29; 12/29)

Z!ckУченик (249)

6 лет назад

“Так как графики перпендикулярны, то (5-в) /3=-7/3…”. Как было вычислено -7/3?

LFK
Мыслитель
(6194)
к2=-1/к1, а по условию к1=3/7

Источник

Перпендикулярные прямые

Две прямые на плоскости называются
перпендикулярными, если при пересечении
образуют 4 прямых угла.

В
аналитическом выражении прямые, заданные
линейными функциями
и
будут
перпендикулярны, если выполнено
условие
.
Эти же прямые будут перпендикулярны,
если
.
(Здесь
—
углы наклона прямой к горизонтали)

Для
обозначения перпендикулярности имеется
общепринятый символ:
,
предложенный в 1634
году французским
математиком Пьером
Эригоном.

[Править]Построение перпендикуляра

Построение
перпендикуляра

Шаг
1: (красный)
С помощью циркуля проведём полуокружность
с центром в точке P, получив точки А’ и
В’.

Шаг
2: (зелёный)
Не меняя радиуса, построим две
полуокружности с центром в точках A’ и
В’ соответственно, проходящими через
точку Р. Кроме точки Р есть ещё одна
точка пересечения этих полуокружностей,
назовём её Q.

Шаг
3: (синий)
Соединяем точки Р и Q. PQ и есть перпендикуляр
к прямой АВ.

[Править]Координаты точки основания перпендикуляра к прямой

A(xa,ya)
и B(xb,yb) — прямая, O(xo,yo) — основание
перпендикуляра, опущенного из точки
P(xp,yp).

xo
= (xa*(yb-ya)^2 + xp*(xb-xa)^2 + (xb-xa) * (yb-ya) * (yp-ya)) /
((yb-ya)^2+(xb-xa)^2);

yo
= (yb-ya)*(xo-xa)/(xb-xa)+ya.

Признак
перпендикулярности прямой и плоскости

ПРИЗНАК
ПЕРПЕНДИКУЛЯРНОСТИ ПРЯМОЙ И
ПЛОСКОСТИ.

Если
прямая, пересекающая плоскость,
перпендикулярна двум прямым в этой
плоскости, проходящим через точку
пересечения данной прямой и плоскости,
то она перпендикулярна плоскости.

Доказательство:

Пусть а прямая,
перпендикулярная прямым b и c в
плоскости
.
Тогда прямая а проходит
через точку А пересечения
прямых b и c.
Докажем, что прямая а перпендикулярна
плоскости
.

Проведем
произвольную прямую х через
точку А в
плоскости
и
покажем, что она перпендикулярна
прямой а.
Проведем в плоскости
произвольную
прямую, не проходящую через точку А и
пересекающую прямые b, c и х.
Пусть точками пересечения
будут В, С и Х.

Отложим
на прямой а от
точки А в
разные стороны равные отрезки АА₁ иАА₂.
Треугольник А₁СА₂ равнобедренный,
так как отрезок АС является
высотой по условию теоремы и медианой
по построению (АА₁=АА₂).
по той же причине треугольник А₁ВА₂ тоже
равнобедренный. Следовательно,
треугольники А₁ВС и А₂ВС равны
по трем сторонам.

Из равенства
треугольников А₁ВС и А₂ВС следует
равенство углов А₁ВХи А₂ВХ и,
следовательно равенство
треугольников А₁ВХ и А₂ВХ по
двум сторонам и углу между ними.

35)теорема
о трёх перпендикулярах

О
ТРЕХ ПЕРПЕНДИКУЛЯРАХ.

Если
прямая, проведенная на плоскости
черезоснование
наклонной,
перпендикулярна еепроекции,
то она перпендикулярна наклонной.

И
обратно:
Если прямая на плоскости перпендикулярна
наклонной, то она перпендикулярна
и проекции
наклонной.

Доказательство: Пусть АВ –
перпендикуляр плоскости
, АС –
наклонная и с –
прямая в плоскости
,
проходящая через основание С.

Проведем
прямую СA₁,
параллельную прямой АВ.
Она перпендикулярна плоскости
.
Проведем через прямые АВ и СA₁ плоскость
.
Прямая сперпендикулярна
прямой СA₁.
Если она перпендикулярна прямой СВ,
то она перпендикулярна плоскости
,
а значит, и прямой АС.

АНАЛОГИЧНО.
Если прямая с перпендикулярна
наклонной АС то
она, будучи перпендикулярна и
прямой СA₁ перпендикулярна
плоскости
,
а значит, и проекции наклонной СВ.
Теорема доказана.

36)
признак перпендикулярности плоскостей

ПРИЗНАК
ПЕРПЕНДИКУЛЯРНОСТИ ПЛОСКОСТЕЙ.

Если
плоскость проходит через прямую
перпендикулярную другой плоскости,
то эти плоскости перпендикулярны.

Доказательство: Пусть
–
плоскость , b –
перпендикулярная ей прямая,
–
плоскость проходящая через прямую b,
и с –
прямая по которой пересекаются
плоскости
и
.
Докажем, что плоскости
и
перпендикулярны.

Проведем
в плоскости
через
точку пересечения прямой b с
плоскостью
прямую а,
перпендикулярную прямой с.
Проведем через прямые а и bплоскость
.
Она перпендикулярна прямой с,
так как прямые а и bперпендикулярны,
то плоскости
и
перпендикулярны.
Теорема доказана.

37)
связь между параллельностью и
перпендикулярностью плоскостью

Определение 3.3.

Прямая
называется перпендикулярной плоскости,
если она перпендикулярна любой прямой
из этой плоскости.

Т
еорема 3.1. Признак
перпендикулярности прямой и плоскости.

Если
прямая перпендикулярна каждой из двух
пересекающихся прямых плоскости, то
она перпендикулярна этой плоскости.

Доказательство

Сформулируем
некоторые теоремы, устанавливающие
связь между параллельностью и
перпендикулярностью в пространстве.

Т
еорема 3.2.

Плоскость,
перпендикулярная одной из двух
параллельных прямых, перпендикулярна
и другой.

Чертеж
3.2.2.

Т
еорема 3.3.

Две
прямые, перпендикулярные одной плоскости,
параллельны между собой.

Т
еорема 3.4.

Если
прямая перпендикулярна одной из двух
параллельных плоскостей, то она
перпендикулярна и другой.

Т
еорема 3.5.

Две
плоскости, перпендикулярные одной
прямой, параллельны между собой.

Чертеж
3.2.3.

Докажите
эти теоремы самостоятельно, используя
такое свойство: если векторы

коллинеарные
и
то

О
пределение 3.4.

Перпендикуляром,
проведенным из данной точки на данную
плоскость, называется отрезок прямой,
перпендикулярной данной плоскости,
который соединяет данную точку с точкой
плоскости.

38)
двугранный угол

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Перпендикуля́рность (от лат. perpendicularis — букв. отвесный)^[1] — бинарное отношение между различными объектами (векторами, прямыми, подпространствами и т. д.).

Для обозначения перпендикулярности имеется общепринятый символ:
⊥, предложенный в 1634 году французским математиком Пьером Эригоном.
Например, перпендикулярность прямых и записывают как .

На плоскости[править | править код]

Перпендикулярные прямые на плоскости[править | править код]

Две прямые на плоскости называются перпендикулярными, если при пересечении они образуют 4 прямых угла.

Про прямую перпендикулярную к прямой ell проведённую через точку вне прямой ell , говорят, что есть перпендикуляр опущенный из на ell .
Если же точка лежит на прямой ell , то говорят, что есть перпендикуляр к восстановленный из к ell (устаревший термин восставленный^[2]).

В координатах[править | править код]

В аналитическом выражении прямые, заданные линейными функциями

будут перпендикулярны, если выполнено следующее условие на их угловые коэффициенты

Построение перпендикуляра[править | править код]

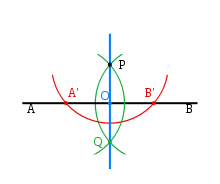
Построение перпендикуляра

Шаг 1: С помощью циркуля проведём полуокружность с центром в точке P, получив точки А и В.

Шаг 2: Не меняя радиуса, построим две полуокружности с центром в точках A и В соответственно, проходящими через точку P. Кроме точки P есть ещё одна точка пересечения этих полуокружностей, назовём её Q.

Шаг 3: Соединяем точки P и Q. PQ и есть перпендикуляр к прямой AB.

Координаты точки основания перпендикуляра к прямой[править | править код]

Пусть прямая задаётся точками и . На прямую опускается перпендикуляр из точки .
Тогда основание перпендикуляра можно найти следующим образом.

Если (вертикаль), то и .
Если (горизонталь), то и .

Во всех остальных случаях:

$x_o = frac{x_acdot(y_b-y_a)^2 +x_pcdot(x_b-x_a)^2 + (x_b-x_a)cdot(y_b-y_a)cdot(y_p-y_a)}{(y_b-y_a)^2+(x_b-x_a)^2}$

;

$y_o = frac{(x_b-x_a)cdot(x_p-x_o)}{(y_b-y_a)}+y_p$

В трёхмерном пространстве[править | править код]

Перпендикулярные прямые[править | править код]

Две прямые в пространстве перпендикулярны друг другу, если они соответственно параллельны некоторым двум другим взаимно перпендикулярным прямым, лежащим в одной плоскости. Две прямые, лежащие в одной плоскости, называются перпендикулярными (или взаимно перпендикулярными), если они образуют четыре прямых угла.

Перпендикулярность прямой к плоскости[править | править код]

Определение: Прямая называется перпендикулярной к плоскости, если она перпендикулярна всем прямым, лежащим в этой плоскости.

Признак: Если прямая перпендикулярна двум пересекающимся прямым плоскости, то она перпендикулярна этой плоскости.

Плоскость, перпендикулярная одной из двух параллельных прямых, перпендикулярна и другой. Через любую точку пространства проходит прямая, перпендикулярная к данной плоскости, и притом только одна.

Перпендикулярные плоскости[править | править код]

Две плоскости называются перпендикулярными, если двугранный угол между ними равен 90°.

Если плоскость проходит через прямую, перпендикулярную другой плоскости, то эти плоскости перпендикулярны.
Если из точки, принадлежащей одной из двух перпендикулярных плоскостей, провести перпендикуляр к другой плоскости, то этот перпендикуляр полностью лежит в первой плоскости.
Если в одной из двух перпендикулярных плоскостей провести перпендикуляр к их линии пересечения, то этот перпендикуляр будет перпендикулярен второй плоскости.
Плоскость, перпендикулярная двум пересекающимся плоскостям, перпендикулярна их линии пересечения^[3].

В многомерных пространствах[править | править код]

Перпендикулярность плоскостей в 4-мерном пространстве[править | править код]

Перпендикулярность плоскостей в четырёхмерном пространстве имеет два смысла: плоскости могут быть перпендикулярны в 3-мерном смысле, если они пересекаются по прямой (а следовательно, лежат в одной гиперплоскости), и двугранный угол между ними равен 90°.

Плоскости могут быть также перпендикулярны в 4-мерном смысле, если они пересекаются в точке (а следовательно, не лежат в одной гиперплоскости), и любые 2 прямые, проведённые в этих плоскостях через точку их пересечения (каждая прямая в своей плоскости), перпендикулярны.

В 4-мерном пространстве через данную точку можно провести ровно 2 взаимно перпендикулярные плоскости в 4-мерном смысле (поэтому 4-мерное евклидово пространство можно представить как декартово произведение двух плоскостей). Если же объединить оба вида перпендикулярности, то через данную точку можно провести 6 взаимно перпендикулярных плоскостей (перпендикулярных в любом из двух вышеупомянутых значений).

Существование шести взаимно перпендикулярных плоскостей можно пояснить таким примером. Пусть дана система декартовых координат x y z t. Для каждой пары координатных прямых существует плоскость, включающая эти две прямые. Количество таких пар равно : xy, xz, xt, yz, yt, zt, и им соответствуют 6 плоскостей. Те из этих плоскостей, которые включают одноимённую ось, перпендикулярны в 3-мерном смысле и пересекаются по прямой (например, xy и xz, yz и zt), а те, которые не включают одноимённых осей, перпендикулярны в 4-мерном смысле и пересекаются в точке (например, xy и zt, yz и xt).

Перпендикулярность прямой и гиперплоскости[править | править код]

Пусть задано n-мерное евклидово пространство $mathbb {R} ^{n}$ (n>2) и ассоциированное с ним векторное пространство W^n , а прямая l с направляющим векторным пространством L^1 и гиперплоскость $Pi_{k}$ с направляющим векторным пространством $L^{k}$ (где , ) принадлежат пространству $mathbb {R} ^{n}$ .

Прямая l называется перпендикулярной гиперплоскости $Pi_{k}$ , если подпространство $L_{1}$ ортогонально подпространству $L^{k}$ , то есть

Вариации и обобщения[править | править код]

См. также[править | править код]

Нормаль
Параллельность
Ортогональность
Высота
Теорема о трёх перпендикулярах

Примечания[править | править код]

↑ Словарь иностранных слов. — М.: «Русский язык», 1989. — 624 с. ISBN 5-200-00408-8
↑ А. П. Киселёв. Элементарная геометрия / под редакцией Н. А. Глаголева. — 1938.
↑ Александров А.Д., Вернер А. Л., Рыжик В.И. Стереометрия. Геометрия в пространстве. — Висагинас: Alfa, 1998. — С. 46. — 576 с. — (Библиотека школьника). — ISBN 9986582539.

Источник

Как найти основание перпендикуляра опущенного из точки на прямую

Проекция точки на прямую

Перпендикуляр к прямой

Перпендикулярные прямые

[Править]Построение перпендикуляра

[Править]Координаты точки основания перпендикуляра к прямой

На плоскости[править | править код]

Перпендикулярные прямые на плоскости[править | править код]

В координатах[править | править код]

Построение перпендикуляра[править | править код]

Координаты точки основания перпендикуляра к прямой[править | править код]

В трёхмерном пространстве[править | править код]

Перпендикулярные прямые[править | править код]

Перпендикулярность прямой к плоскости[править | править код]

Перпендикулярные плоскости[править | править код]

В многомерных пространствах[править | править код]

Перпендикулярность плоскостей в 4-мерном пространстве[править | править код]

Перпендикулярность прямой и гиперплоскости[править | править код]

Вариации и обобщения[править | править код]

См. также[править | править код]

Примечания[править | править код]

Вам также может понравиться

Как найти человека в осинниках

Как легко найти слизней в майнкрафте

Как найти мне новую девушку

Добавить комментарий Отменить ответ