В предыдущем уроке мы подробно разобрали,
как построить параболу.
В этом уроке мы разберем, как решать типовые задачи на квадратичную функцию.
Как найти нули квадратичной функции
Запомните!
![]()
Чтобы найти координаты точек нулей функции, нужно
в исходную функцию подставить вместо «y» число
ноль.
Рассмотрим задачу.
Найти нули квадратичной
функции «y = x2 − 3».
Подставим в исходную функцию вместо «y» ноль и решим полученное
квадратное уравнение.
0 = x2 − 3
x2 − 3 = 0
x1;2 =
| 0 ± √02 − 4 · 1 · (−3) |
| 2 · 1 |
x1;2 =
x1;2 =
x1;2 =
x1;2 = ±√3
Ответ: нули функции «y = x2 − 3» :
x1 = √3;
x2 = −√3 .
Как найти при каких значениях
«x» квадратичная функция принимает заданное
числовое значение
Запомните!
![]()
Чтобы найти при каких значениях «x» квадратичная функция принимает заданное числовое значение,
нужно:
- вместо «y» подставить в функцию заданное числовое значение;
- решить полученное квадратное уравнение относительно «x».
Рассмотрим задачу.
При каких значениях «x» функция
«y = x2 − x − 3» принимает значение
«−3».
Подставим в исходную функцию
«y = x2 − x − 3» вместо «y = −3» и
найдем «x».
y = x2 − x − 3
−3 = x2 − x − 3
x2 − x − 3 = −3
x2 − x − 3 + 3 = 0
x2 − x = 0
x1;2 =
| 1 ± √12 − 4 · 1 · 0 |
| 2 · 1 |
x1;2 =
x1;2 =
| x1 = | x2 = |
| x1 = | x2 = |
| x1 = 1 | x2 = 0 |
Ответ: при «x = 0» и
«x = 1» функция «y = x2 − x − 3»
принимает значение «y = −3».
Как найти координаты точек пересечения параболы и прямой
Запомните!
![]()
Чтобы найти точки пересечения параболы с прямой нужно:
- приравнять правые части функций (те части функций, в которых содержатся «x»);
- решить полученное уравнение относительно «x»;
- подставить полученные числовые значения «x»
в любую из функций и найти координаты точек по оси «Оy».
Рассмотрим задачу.
Найти координаты точек пересечения параболы «y = x2»
и прямой «y = 3 − 2x».
Приравняем правые части функций и решим
полученное уравнение относительно «x».
x2 = 3 − 2x
x2 − 3 + 2x = 0
x2 + 2x − 3 = 0
x1;2 =
| −2 ± √22 − 4 · 1 · (−3) |
| 2 · 1 |
x1;2 =
x1;2 =
x1;2 =
| x1 = | x2 = |
| x1 = | x2 = |
| x1 = 1 | x2 = −3 |
Теперь подставим в любую из заданных функций (например, в
«y = 3 − 2x») полученные
числовые значения «x», чтобы найти координаты
«y» точек пересечения.
1) x = −3
y = 3 − 2x
y(−3) = 3 − 2 · (−3) = 3 − (−6) = 3 + 6 = 9
(·) A (−3; 9) — первая точка пересечения.
2) x = 1
y = 3 − 2x
y(1) = 3 − 2 · 1 = 3 − 2 = 1
(·) B (1; 1) — вторая точка пересечения.
Запишем полученные точки пересечения с их координатами в ответ.
Ответ: точки пересечения параболы
«y = x2»
и прямой «y = 3 − 2x»:
(·) A (−3; 9) и
(·) B (1; 1).
Как определить, принадлежит ли точка графику функции параболы
Запомните!
![]()
Чтобы проверить принадлежность точки параболе нет необходимости строить график функции.
Достаточно подставить координаты точки в формулу функции (координату по оси
«Ox» вместо
«x», а координату по оси
«Oy» вместо «y») и выполнить арифметические расчеты.
- Если получится верное равенство, значит, точка принадлежит графику функции.
- Если получится неверное равенство, значит, точка
не принадлежит графику функции.
Рассмотрим задачу:
Не строя графика функции «y = x2», определить, какие точки принадлежат ему:
(·) А(2; 6),
(·) B(−1; 1).
Подставим в функцию
«y = x2»
координаты точки (·) А(2; 6).
y = x2
6 = 22
6 = 4
(неверно)
Значит, точка (·) А(2; 6)
не принадлежит графику функции
«y = x2».
Подставим в функцию
«y = x2»
координаты точки (·) B(−1; 1).
y = x2
1 = (−)12
1 = 1
(верно)
Значит, точка (·) B(−1; 1)
принадлежит графику функции
«y = x2».
Как найти точки пересечения параболы с осями координат
Рассмотрим задачу
Найти координаты точек пересечения параболы
«y = x2 −3x + 2» с осями координат.
Сначала определим точки пересечения функции с осью «Ox».
На графике функции эти точки выглядят так:
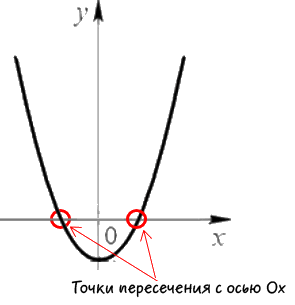
Как видно на рисунке выше, координата «y» точек пересечения с осью «Ox»
равна нулю, поэтому подставим «y = 0» в
исходную функцию «y = x2 −3x + 2»
и найдем их координаты по оси «Ox».
0 = x2 −3x + 2
x2 −3x + 2 = 0
x1;2 =
| 3 ± √32 − 4 · 1 · 2 |
| 2 · 1 |
x1;2 =
x1;2 =
x1;2 =
| x1 = | x2 = |
| x1 = | x2 = |
| x1 = 2 | x2 = 1 |
Запишем координаты точек пересечения графика с осью «Ox»:
(·) A (2; 0) и
(·) B (1; 0).
Теперь найдем координаты точки пересечения с осью «Oy».
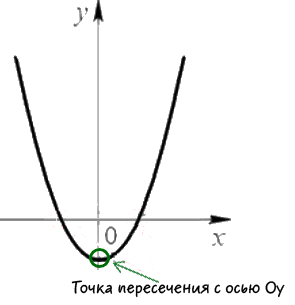
Как видно на рисунке выше, координата «x»
точки пересечения с осью «Oy» равна нулю.
Подставим «x = 0»
в исходную функцию
«y = x2 −3x + 2»
и найдем координату точки по оси
«Oy».
y(0) = 02 − 3 · 0 + 2 = 2
Выпишем координаты полученной точки: (·) C (0; 2)
Запишем в ответ все координаты точек пересечения параболы с осями.
Ответ: точки пересечения с осью «Ox»:
(·) A (2; 0) и
(·) B (1; 0).
С осью «Oy»: (·)C (0; 2).
Как определить при каких значениях x функция принимает
положительные или
отрицательные значения
Напоминаем, что когда в задании говорится «функция принимает
значения» — речь идет о
значениях«y».
Другими словами, необходимо ответить на вопрос: при каких значениях
«x», координата
«y» положительна или отрицательна.
Запомните!
![]()
Чтобы по графику функции определить, где функция принимает положительные или отрицательные значения нужно:
- провести прямые через точки в местах, где график пересекает ось «Ox»;
- определить положительные или отрицательные значения принимает функция на промежутках между проведенными прямыми;
- записать ответ для каждого промежутка относительно «x».
Рассмотрим задачу.
С помощью графика квадратичной функции, изображенного на рисунке, ответить:
При каких значениях «x» функция принимает 1) положительные значения; 2) отрицательные значения.
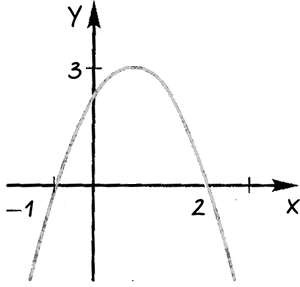
Проведем через точки, где график функции пересекает ось «Ox» прямые.
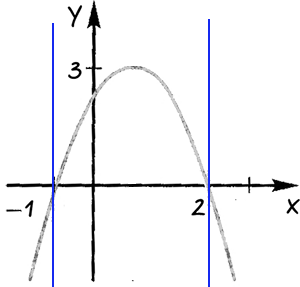
Определим области, где функция принимает отрицательные или положительные значения.
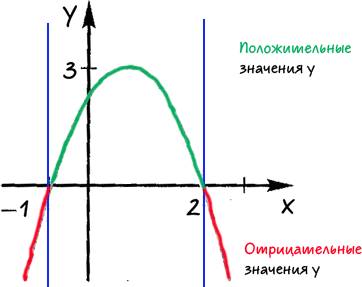
Подпишем над каждой полученной областью, какие значения принимает
«x» в каждой из выделенных областей.
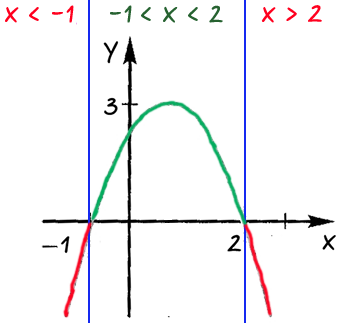
Ответ: при «x < −1» и
«x > 2» функция принимает отрицательные значения;
при «−1 < x < 2» функция принимает
положительные значения.
Ваши комментарии
Важно!

Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
Квадратичная функция и ее график
В этой статье мы поговорим о том, что такое квадратичная функция, научимся строить ее график и определять вид графика в зависимости от знака дискриминанта и знака старшего коэффициента.
Итак.
Функция вида , где 0″ title=”a<>0″/> называется квадратичной функцией.
В уравнении квадратичной функции:
a – старший коэффициент
b – второй коэффициент
с – свободный член.
Графиком квадратичной функции является квадратичная парабола, которая для функции имеет вид:
Обратите внимание на точки, обозначенные зелеными кружками – это, так называемые “базовые точки”. Чтобы найти координаты этих точек для функции , составим таблицу:
Внимание! Если в уравнении квадратичной функции старший коэффициент , то график квадратичной функции имеет ровно такую же форму, как график функции при любых значениях остальных коэффициентов.
График функции имеет вид:
Для нахождения координат базовых точек составим таблицу:
Обратите внимание, что график функции симметричен графику функции относительно оси ОХ.
Итак, мы заметили:
Если старший коэффициент a>0 , то ветви параболы напрaвлены вверх .
Если старший коэффициент a , то ветви параболы напрaвлены вниз .
Второй параметр для построения графика функции – значения х, в которых функция равна нулю, или нули функции. На графике нули функции – это точки пересечения графика функции с осью ОХ.
Поскольку ордината (у) любой точки, лежащей на оси ОХ равна нулю, чтобы найти координаты точек пересечения графика функции с осью ОХ, нужно решить уравнение .
В случае квадратичной функции нужно решить квадратное уравнение .
В процессе решения квадратного уравнения мы находим дискриминант: , который определяет число корней квадратного уравнения.
И здесь возможны три случая:
1. Если ,то уравнение не имеет решений, и, следовательно, квадратичная парабола не имеет точек пересечения с осью ОХ. Если 0″ title=”a>0″/>,то график функции выглядит как-то так:
2. Если ,то уравнение имеет одно решение, и, следовательно, квадратичная парабола имеет одну точку пересечения с осью ОХ. Если 0″ title=”a>0″/>,то график функции выглядит примерно так:
3 . Если 0″ title=”D>0″/>,то уравнение имеет два решения, и, следовательно, квадратичная парабола имеет две точки пересечения с осью ОХ:
,
Если 0″ title=”a>0″/>,то график функции выглядит примерно так:
Следовательно, зная направление ветвей параболы и знак дискриминанта, мы уже можем в общих чертах определить, как выглядит график нашей функции.
Следующий важный параметр графика квадратичной функции – координаты вершины параболы:
Прямая, проходящая через вершину параболы параллельно оси OY является осью симметрии параболы.
И еще один параметр, полезный при построении графика функции – точка пересечения параболы с осью OY.
Поскольку абсцисса любой точки, лежащей на оси OY равна нулю, чтобы найти точку пересечения параболы с осью OY, нужно в уравнение параболы вместо х подставить ноль: .
То есть точка пересечения параболы с осью OY имеет координаты (0;c).
Итак, основные параметры графика квадратичной функции показаны на рисунке:
Рассмотрим несколько способов построения квадратичной параболы. В зависимости от того, каким образом задана квадратичная функция, можно выбрать наиболее удобный.
1. Функция задана формулой .
Рассмотрим общий алгоритм построения графика квадратичной параболы на примере построения графика функции
1. Направление ветвей параболы.
Так как 0″ title=”a=2>0″/>,ветви параболы направлены вверх.
2. Найдем дискриминант квадратного трехчлена
0″ title=”D=b^2-4ac=9-4*2*(-5)=49>0″/>
Дискриминант квадратного трехчлена больше нуля, поэтому парабола имеет две точки пересечения с осью ОХ.
Для того, чтобы найти их координаты, решим уравнение:
,
3. Координаты вершины параболы:
4. Точка пересечения параболы с осью OY: (0;-5),и ей симметричная относительно оси симметрии параболы.
Нанесем эти точки на координатную плоскость, и соединим их плавной кривой:
Этот способ можно несколько упростить.
1. Найдем координаты вершины параболы.
2. Найдем координаты точек, стоящих справа и слева от вершины.
Воспользуемся результатами построения графика функции
Кррдинаты вершины параболы
Ближайшие к вершине точки, расположенные слева от вершины имеют абсциссы соответственно -1;-2;-3
Ближайшие к вершине точки, расположенные справа имеют абсциссы соответственно 0;1;2
Подставим значения х в уравнение функции, найдем ординаты этих точек и занесем их в таблицу:
Нанесем эти точки на координатную плоскость и соединим плавной линией:
2 . Уравнение квадратичной функции имеет вид – в этом уравнении – координаты вершины параболы
или в уравнении квадратичной функции , и второй коэффициент – четное число.
Построим для примера график функции .
Вспомним линейные преобразования графиков функций. Чтобы построить график функции , нужно
- сначала построить график функции ,
- затем одинаты всех точек графика умножить на 2,
- затем сдвинуть его вдоль оси ОХ на 1 единицу вправо,
- а затем вдоль оси OY на 4 единицы вверх:
Теперь рассмотрим построение графика функции . В уравнении этой функции , и второй коэффициент – четное число.
Выделим в уравнении функции полный квадрат:
Следовательно, координаты вершины параболы: . Старший коэффициент равен 1, поэтому построим по шаблону параболу с вершиной в точке (-2;1):
3 . Уравнение квадратичной функции имеет вид y=(x+a)(x+b)
Построим для примера график функции y=(x-2)(x+1)
1. Вид уравнения функции позволяет легко найти нули функции – точки пересечения графика функции с осью ОХ:
(х-2)(х+1)=0, отсюда
2. Координаты вершины параболы:
3. Точка пересечения с осью OY: с=ab=(-2)(1)=-2 и ей симметричная.
Нанесем эти точки на координатную плоскость и построим график:
График квадратичной функции.
Перед вами график квадратичной функции вида .
Кликните по чертежу.
Подвигайте движки.
Исследуйте зависимость
– ширины графика функции от значения коэффициента ,
– сдвига графика функции вдоль оси от значения ,
– сдвига графика функции вдоль оси от значения
– направления ветвей параболы от знака коэффициента
– координат вершины параболы от значений и :
И.В. Фельдман, репетитор по математике.
Вычислите координаты точек пересечения графиков уравнений x в квадрате минус yв квадрате = 13 и x + y = – 5?
Алгебра | 5 – 9 классы
Вычислите координаты точек пересечения графиков уравнений x в квадрате минус yв квадрате = 13 и x + y = – 5.
Посчитай х сама).
Найдите координаты точек пересечения графиков функций y = x (в квадрате) и y = 2x – 3 ?
Найдите координаты точек пересечения графиков функций y = x (в квадрате) и y = 2x – 3 .
Выполните графическую иллюстрацию.
Найдите координаты точек пересечения графиков функции игрек равен минус икс в квадрате и игрик равен два икс минус 3?
Найдите координаты точек пересечения графиков функции игрек равен минус икс в квадрате и игрик равен два икс минус 3.
Вычислите координаты точек пересечения графиков уравнений : х ^ 2 – y ^ 2 = 13 и х + у = – 5?
Вычислите координаты точек пересечения графиков уравнений : х ^ 2 – y ^ 2 = 13 и х + у = – 5.
Найдите координаты точек пересечения графиков функций y = – x в квадрате и y = 2x – 3?
Найдите координаты точек пересечения графиков функций y = – x в квадрате и y = 2x – 3.
Найдите координаты точек пересечения с осями координат графика функции : а) у = 7х + 1, 4 ; б) у = 2х(в квадрате) + 9х – 5?
Найдите координаты точек пересечения с осями координат графика функции : а) у = 7х + 1, 4 ; б) у = 2х(в квадрате) + 9х – 5.
Координаты точек пересечения графиков функций 1) у = минус одна третья х в квадрате + 3 и у = х в квадрате + 3х?
Координаты точек пересечения графиков функций 1) у = минус одна третья х в квадрате + 3 и у = х в квадрате + 3х.
Найти координаты точек пересечения графиков функций : y = xв квадрате ; y = x P?
Найти координаты точек пересечения графиков функций : y = xв квадрате ; y = x P.
S построением пожалуйста.
Постройте график функций у = минус 2 / x и у = – – 2х?
Постройте график функций у = минус 2 / x и у = – – 2х.
Укажите координаты точек пересечения этих графиков.
Срочно?
Найти координаты точек пересечения графиков функций у = 4 – 2х у = 4 – х в квадрате.
Найдите координаты точек пересечения графиков функций y = x ^ 2 (x в квадрате) и y = 7x – 12?
Найдите координаты точек пересечения графиков функций y = x ^ 2 (x в квадрате) и y = 7x – 12.
На этой странице сайта, в категории Алгебра размещен ответ на вопрос Вычислите координаты точек пересечения графиков уравнений x в квадрате минус yв квадрате = 13 и x + y = – 5?. По уровню сложности вопрос рассчитан на учащихся 5 – 9 классов. Чтобы получить дополнительную информацию по интересующей теме, воспользуйтесь автоматическим поиском в этой же категории, чтобы ознакомиться с ответами на похожие вопросы. В верхней части страницы расположена кнопка, с помощью которой можно сформулировать новый вопрос, который наиболее полно отвечает критериям поиска. Удобный интерфейс позволяет обсудить интересующую тему с посетителями в комментариях.
2) 9y – y ^ 2 + 45 – 5y = – y ^ 2 + 4y + 45 4) 2b – b ^ 2 + 6 – 3b = – b ^ 2 – b + 6 6) d ^ 2 + 3d + 11d + 33 = d ^ 2 + 14d + 33.
Ответ 4 – ый задачи “сравнить числа”.
X + 3 / 3 + х + 4 / 4 – 3, 5 = x – 3 / 6 x + x – x = – 3 / 6 – 3 / 3 – 4 / 4 – 3, 5 1х = – 1 х = – 1 : 1 х = – 1 Ответ : – 1.
1. 10а руб. – стоят 10 мячей 5b руб. – стоят 5 ракеток 10а + 5b – стоимость всей покупки. 2. 2n руб. – стояли 2 тетради 100% – 3% = 97% ; 2n * 97% = 2n * 0, 97 = 1, 94n руб. – стали стоить 2 тетради 3m руб. – стояли 3 ручки 100% – 2% = 98% ; 3m..
3у = 24 – 2х у = (24 – 2х) : 3 2х = 24 – 3у х = (24 – 3у) : 2.
Пусть скорость катера в стоячей воде равна х, тогда по течению х + 1, против течения х – 1. Катер проплыл по течению (х + 1) * 3, а против течения(х – 1) * 5 (х + 1) * 3 = (х – 1) * 5 3х + 3 = 5х – 5 2х = 8 х = 4 скорость катера в стоячей воде 4 км ..
1) x17 × x23 = x40 2) (x8)3 = x24 3) (x2)5 = x10 4) x24 × x5 × x10 = x39 5) x = x40 / x39 = 104.
Действия в скобке 1 выполняется в скобках справа – 0, 04 дробь в неправильную – 11 / 6 = 0, 11 Ответ – 2, 75.
А 4 49 121 0, 25 3600 2 0, 4 5 99 √а 2 7 11 0, 5 60 √2 √0, 4 √5 √99 = √9 * 11 = 3√11.
Пересечение с осями онлайн
Наш онлайн калькулятор, построенный на основе системы Wolfram Alpha, предназначен для решения задачи нахождения точек пересечения графика функции с осями координат.
Найти точки пересечения функции с осями координат:
При проведении исследования функции, возникает задача нахождения точек пересечения этой функции с осями координат. Рассмотрим на конкретном примере алгоритм решения такой задачи. Для простоты будем работать с функцией одной переменной:
График данной функции представлен на рисунке:
Как следует из рисунка, наша функция пересекает ось в двух точках, а ось – в одной.
Сначала найдём точки пересечения функции с осью . Сразу отметим, что в этих точках координата . Поэтому для их поиска, нам нужно решить уравнение:
Таким образом, мы нашли две точки пересечения нашей функции с осью абсцисс: и . Стоит отметить, что задача поиска пересечений функции с осью эквивалентна задаче нахождения нулей функции.
Теперь найдём точку пересечения с осью ординат. В этой точке координата . Поэтому для их поиска, просто подставляем значение в нашу функцию:
Таким образом, мы нашли точку пересечения нашей функции с осью ординат .
Другие полезные разделы:
Оставить свой комментарий:
Мы в социальных сетях:
Группа ВКонтакте | Бот в Телеграмме
[spoiler title=”источники:”]
http://algebra.my-dict.ru/q/387912_vycislite-koordinaty-tocek-peresecenia-grafikov-uravnenij/
http://mathforyou.net/online/calculus/intercepts/
[/spoiler]
Расположение графика квадратного трёхчлена относительно осей координат
В §28 данного справочника мы показали, что квадратный трёхчлен можно представить в виде:
$$ ax^2+bx+c = a(x+ frac{b}{2a})^2-frac{D}{4a}, D = b^2-4ac $$
Мы получаем:
- ось симметрии $x = -frac{b}{2a}$
- вершину параболы на оси симметрии $(–frac{b}{2a}; -frac{D}{4a})$
- точку пересечения (0;c) с осью OY
Любая парабола $y = ax^2+bx+c, a ≠ 0$ пересекается с осью OY в единственной точке (0;c).
Количество точек пересечения параболы $y = ax^2+bx+c$ с осью OX зависит от знака дискриминанта.
Если $D gt 0$, парабола имеет две точки пересечения с $x_1,2 = frac{-b pm sqrt{D}}{2a}$ на оси OX.
Если D = 0, парабола имеет одну точку пересечения $x_0 = -frac{b}{2a}$, которая лежит на оси OX и является вершиной параболы.
Если $D lt 0$ у параболы нет ни одной точки пересечения с осью OX.
Точки пересечения параболы с осью OX
|
$a gt 0$ |
$a lt 0$ |
|
|
$D gt 0$ |
 |
 |
|
$x_(1,2) = frac{-b pm sqrt{D}}{2a}$ |
||
|
D = 0 |
 |
 |
|
$x_0 = -frac{b}{2a}$ |
||
|
$ D lt 0 $ |
 |
 |
|
${ varnothing }$-нет пересечений |
Точки пересечения двух парабол
На практике часто возникает задача «перехвата» одного тела другим, т.е. поиска точек пересечения двух траекторий; а тела в поле тяготения Земли нередко движутся по параболе.

Поэтому исследовать возможные точки пересечения двух парабол – важная прикладная задача. Пусть уравнения парабол:
$$ y = a_1 x^2+b_1 x+c_1, quad y = a_2 x^2+b_2 x+c_2 $$
В точках пересечения выполняется равенство:
$$ a_1 x^2+b_1 x+c_1 = a_2 x^2+b_2 x+c_2 $$
$$ (a_1-a_2 ) x^2+(b_1-b_2 )x+(c_1-c_2 ) = 0 $$
Если ввести обозначения $A = a_1-a_2, B = b_1-b_2, C = c_1-c_2$, получаем уравнение:
$$ Ax^2+Bx+C = 0 $$
Количество решений этого уравнения в зависимости от нулевых и ненулевых значений параметров равно 11 и описывается схемой общего алгоритма решений квадратного уравнения (см.§25 данного справочника).
A = B = C = 0
$ a_1 = a_2, b_1 = b_2, $
$ c_1 = c_2 $
Две параболы совпадают
Бесконечное множество общих точек, $x in Bbb R$

$A = B = 0, C neq 0$
$ a_1 = a_2, b_1 = b_2, $
$ c_1 neq c_2 $
Параболы имеют вид
$y = ax^2+bx+c_1$
$ y = ax^2+bx+c_2 $
У них общая ось симметрии
$ x = -frac{b}{2a}$, одна парабола находится над другой.
Ветки сходятся только на бесконечности.
Точек пересечения нет

$A = 0, B neq 0, C = 0$
$ a_1 = a_2, b_1 neq b_2 $
$ c_1 = c_2 $
Параболы имеют вид
$y = ax^2+b_1 x+c$
$ y = ax^2+b_2 x+c $
Обе проходят через точку (0;c).
Это – единственная точка пересечения.
Одна точка пересечения
(0;c)

$A = 0, B neq 0, C neq 0$
$ a_1 = a_2, b_1 neq b_2 $
$ c_1 neq c_2 $
Параболы имеют вид
$y = ax^2+b_1 x+c_1$
$ y = ax^2+b_2 x+c_2 $
Абсцисса точки пересечения
$ x = – frac{C}{B} = -frac{c_1-c_2}{b_1-b_2}$
Одна точка пересечения (касание)

$A neq 0, B = 0, C = 0$
$ a_1 neq a_2, b_1 = b_2 $
$ c_1 = c_2 $
Параболы имеют вид
$ y = a_1 x^2+bx+c$
$ y = a_2 x^2+bx+c $
Пересекаются при x=0 (точка касания)
Одна точка пересечения (касание) (0;c)

$A neq 0, B = 0, C neq 0$
$ a_1 neq a_2, b_1 = b_2 $
$ c_1 neq c_2 $
Параболы имеют вид
$ y = a_1 x^2+bx+c_1$
$ y = a_2 x^2+bx+c_2 $
Не пересекаются, если
$- frac{c_1-c_2}{a_1-a_2} lt 0 $
Две точки пересечения

Если
$- frac{c_1-c_2}{a_1-a_2} gt 0 $
Пересекаются в двух точках
$$ x_{1,2} = pm sqrt{-frac{c_1-c_2}{a_1-a_2}} $$
Две точки пересечения

$A neq 0, B neq 0, C = 0$
$ a_1 neq a_2, b_1 neq b_2 $
$ c_1 = c_2 $
Параболы имеют вид
$$ y = a_1 x^2+b_1 x+c $$
$$ y = a_2 x^2+b_2 x+c $$
Две точки пересечения
$ x_1 = 0 $
$$x_2 = -frac{b_1-b_2}{a_1-a_2}$$
Две точки пересечения,
одна из которых (0;c)

$A neq 0, B neq 0, C neq 0$
$ a_1 neq a_2, b_1 neq b_2 $
$ c_1 neq c_2 $
Все параметры парабол разные
Ищем дискриминант:
$$ D = B^2-4AC $$
Если $D gt 0$
Две точки пересечения
$$ x_1,2 = frac{-B pm sqrt{D}}{2A} $$
Две точки пересечения

Если D = 0
Одна точка пересечения (касание)
$$ x_0 = -frac{B}{2A} $$
Одна точка пересечения
(касание)

Если $D lt 0$
Точек пересечения нет
Точек пересечения нет

Внимание!
Если две параболы не совпадают, то они могут иметь 1) две точки пересечения; 2) одну точку пересечения; 3) ни одной точки пересечения.
Иметь ровно 3, 4, 5 и т.д. точек пересечения две параболы не могут!
Примеры
Пример 1. Найдите точки пересечения параболы с осями координат:
$а) y = 3x^2+2x-1$

Пересечение с осью OY: ${left{ begin{array}{c} x = 0 \ y = -1end{array} right.}$
Пересечение с осью OX:
$$ 3x^2+2x-1 = 0 Rightarrow (3x-1)(x+1) = 0 Rightarrow $$
$ Rightarrow left[ begin{array}{cc} {left{ begin{array}{c} x = frac{1}{3} \ y = 0 end{array} right.} \ {left{ begin{array}{c} x = -1 \ y = 0 end{array} right.} end{array} right.$ – две точки пересечения
$б) y = -4x^2-3x+1$

Пересечение с осью OY: ${left{ begin{array}{c} x = 0 \ y = 1end{array} right.}$
Пересечение с осью OX:
$$ -4x^2-3x+1 = 0 Rightarrow 4x^2+3x-1 = 0 $$
$$ (4x-1)(x+1) = 0 Rightarrow$$
$ Rightarrow left[ begin{array}{cc} {left{ begin{array}{c} x = frac{1}{4} \ y = 0 end{array} right.} \ {left{ begin{array}{c} x = -1 \ y = 0 end{array} right.} end{array} right.$ – две точки пересечения
$в) y = 5x^2-2x+1$

Пересечение с осью OY: ${left{ begin{array}{c} x = 0 \ y = 1end{array} right.}$
Пересечение с осью OX:
$$ 5x^2-2x+1 = 0 $$
$$ D = 2^2-4 cdot 5 cdot 1 = 4-20 = -16 lt 0 $$
Парабола не пересекает ось OX
$ г) y = -x^2+4x-4 $

Пересечение с осью OY: ${left{ begin{array}{c} x = 0 \ y = -4end{array} right.}$
Пересечение с осью OX:
$$ -x^2+4x-4 = 0 Rightarrow x^2-4x+4 = 0 Rightarrow $$
$$ Rightarrow (x-2)^2 = 0 Rightarrow {left{ begin{array}{c} x = 2 \ y = 0 end{array} right.}$$ – одна точка пересечения
Пример 2*. Даны две параболы
$$ y = 2x^2+5x+1 и y = x^2+3x+k $$
Найдите такое значение параметра k, чтобы параболы
1) имели две точки пересечения; 2) имели одну точку пересечения; 3) не пересекались.
По условию
$$ a_1 = 2, b_1 = 5, c_1 = 1, a_2 = 1, b_2 = 3, c_2 = k $$
$$ a_1 neq a_2, b_1 neq b_2 $$
A = 2-1 = 1, B = 5-3 = 2, C = 1-k
Нам необходимо рассмотреть 4 последних случая из представленных выше, в таблице §29.
1) Параболы имеют две точки пересечения в двух случаях:
1 случай: $c_2 = c_1$, k = 1

$$x_1 = 0, x_2 = -frac{B}{A} = -2$$
$${left{ begin{array}{c} y = 2x^2+5x+1 \ y = x^2+3x+1 end{array} right.} Rightarrow left[ begin{array}{cc} {left{ begin{array}{c} x_1 = 0 \ y_1 = 1end{array} right.} \ {left{ begin{array}{c} x_2 = -2 \ y_2 = -1 end{array} right.} end{array} right.$$
2 случай: $c_2 ≠ c_1, D gt 0$
$$ D = B^2-4AC = 2^2-4 cdot 1 cdot (1-k) = 4k gt 0 Rightarrow k gt 0 $$

Например, k = 4
$$ D = 4k = 16 = 4^2 $$
$$ x_1,2 = frac{-B pm sqrt{D}}{2A} = frac{-2 pm 4}{2} = left[ begin{array}{cc} x_1 = -3\ x_2 = 1 end{array} right. $$
Оба случая можем объединить требованием $k gt 0$.
2) Параболы имеют одну точку пересечения, если:
$$ D = 4k = 0 Rightarrow k = 0 $$

$${left{ begin{array}{c} y = 2x^2+5x+1 \ y = x^2+3x end{array} right.} $$
$$ x_0 = frac{-B}{2A} = -1 $$
3) Параболы не имеют общих точек, если:
$$ D = 4k lt 0 Rightarrow k lt 0 $$

Например, k = -1
Ответ: 1) $k gt 0$; 2) k = 0; 3) $k lt 0$
Пример 3. Две параболы с общей вершиной
Найдите соотношение параметров двух парабол, при котором они будут пересекаться в одной точке – вершине парабол.
Пусть уравнения парабол:
$$ y = a_1 x^2+b_1 x+c_1, y = a_2 x^2+b_2 x+c_2 $$
Координаты вершин:
$$ left( -frac{b_1}{2a_1}, – frac{D_1}{4a_1} right), left(- frac{b_2}{2a_2},- frac{D_2}{4a_2} right) $$
По условию:
$$ {left{ begin{array}{c} -frac{b_1}{2a_1} = -frac{b_2}{2a_2} \ -frac{D_1}{4a_1} = -frac{D_2}{4a_2} end{array} right.} Rightarrow {left{ begin{array}{c} frac{b_1}{a_1} = frac{b_2}{2a_2} \ frac{D_1}{a_1} = frac{D_2}{a_2} end{array} right.} $$
Получаем две пропорции, которым параметры уравнений должны удовлетворять одновременно.
Пример 4. Используя результаты примера 3, найдите две параболы, у которых такая же вершина, как у $y = frac{x^2}{2}-3x+1$.
Координаты вершины:
$$ x_0 = – frac{b}{2a} = – frac{-3}{2 cdot frac{1}{2}} = 3, D = b^2-4ac = 3^2-4 cdot frac{1}{2} cdot 1 = 7 $$
$$ y_0 = – frac{D}{4a} = – frac{7}{4 cdot frac{1}{2}} = -3,5 $$
Уравнение искомой параболы: $y = ax^2+bx+c$
Пропорции для параметров (см. пример 3):
$$ {left{ begin{array}{c} frac{b}{a} = frac{-3}{1/2} = -6 \ frac{D}{a} = frac{7}{1/2} = 14 end{array} right.} Rightarrow {left{ begin{array}{c} b = -6a \ D = 14a end{array} right.} $$
Пусть для искомых двух парабол a=1 и a=-0,2 (можно взять любые другие значения). Получаем:
$$ {left{ begin{array}{c} a = 1 \ b = -6a = -6 \ D = 14a = 14 end{array} right.} Rightarrow {left{ begin{array}{c} a = 1 \ b = -6 \ b^2-4ac = 14 end{array} right.} Rightarrow {left{ begin{array}{c} a = 1 \ b = -6 \ 36-4c = 14 end{array} right.} Rightarrow {left{ begin{array}{c} a = 1 \ b = -6 \ c = frac{36-14}{4} = 5,5 end{array} right.}$$
$$ y = x^2-6x+5,5 $$
$$ {left{ begin{array}{c} a = -0,2 \ b = -6a = 1,2 \ D = 14a = -2,8 end{array} right.} Rightarrow {left{ begin{array}{c} a = -0,2 \ b = 1,2 \ 1,2^2-4 cdot (-0,2)c = -2,8 end{array} right.} Rightarrow {left{ begin{array}{c} a = -0,2 \ b = 1,2 \ c = – frac{1,44+2,8}{0,8} = -5,3 end{array} right.} $$
$$ y = -0,2x^2+1,2x-5,3 $$
Параболы
$$ y = frac{x^2}{2}-3x+1, y = x^2-6x+5,5, y = -0,2x^2+1,2x-5,3 $$
имеют общую вершину (3;-3,5)

Пример 5. Комета движется по параболической траектории, которая в выбранной системе координат описывается уравнением $y = frac{x^2}{3}-2x+5$.
Космический аппарат запускается из начала координат и также движется по параболической траектории. Рассчитайте уравнение этой траектории так, чтобы её вершина совпала с вершиной траектории кометы.
Координаты вершины траектории кометы:
$$ x_0 = -frac{b}{2a} = -frac{-2}{2 cdot frac{1}{3}} = 3, D = b^2-4ac = 2^2-4 cdot frac{1}{3} cdot 5 = – frac{8}{3} $$
$$ y_0 = – frac{D}{4a} = – frac{-8/3}{4 cdot 1/3} = 2 $$
Уравнение траектории космического аппарата: $y = ax^2+bx+c$.
Аппарат запускается из начала координат, т.е. его траектория пересекается с осью OY в точке (0;0). Значит, в уравнении параболы c = 0.
Пропорции для параметров (см. пример 3) с учетом c = 0:
$$ {left{ begin{array}{c} frac{b}{a} = frac{-2}{1/3} = -6 \ frac{D}{a} = frac{-frac{8}{3}}{frac{1}{3}} = -8 end{array} right.} Rightarrow {left{ begin{array}{c} b = -6a \ D = b^2-4a underbrace{c}_{text{= 0 }} = b^2 = -8a end{array} right.} Rightarrow {left{ begin{array}{c} b = -6a \ b^2 = -8a end{array} right.} Rightarrow $$
$$ {left{ begin{array}{c} b = frac{-8a}{-6a} = frac{4}{3} \ a = -frac{b}{6} = -frac{2}{9} end{array} right.} $$
Уравнение траектории космического аппарата с «перехватом» кометы в вершине:
$$ y = -frac{2}{9} x^2+ frac{4}{3} x $$

Уважаемые студенты!
Заказать решение задач по 200+ предметам можно здесь всего за 10 минут.
Координаты точки пересечения графиков функций
Как найти?
- Чтобы найти координаты точки пересечения графиков функций нужно приравнять обе функции друг к другу, перенести в левую часть все члена, содержащие $ x $, а в правую остальные и найти корни, полученного уравнения.
- Второй способ заключается в том, что нужно составить систему уравнений и решить её путём подстановки одной функции в другую
- Третий способ подразумевает графическое построение функций и визуальное определение точки пересечения.
Случай двух линейных функций
Рассмотрим две линейные функции $ f(x) = k_1 x+m_1 $ и $ g(x) = k_2 x + m_2 $. Эти функции называются прямыми. Построить их достаточно легко, нужно взять любые два значения $ x_1 $ и $ x_2 $ и найти $ f(x_1) $ и $ (x_2) $. Затем повторить тоже самое и с функцией $ g(x) $. Далее визуально найти координату точки пересечения графиков функций.
Следует знать, что линейные функции имеют только одну точку пересечения и только тогда, когда $ k_1 neq k_2 $. Иначе, в случае $ k_1=k_2 $ функции параллельны друг другу, так как $ k $ – это коэффициент угла наклона. Если $ k_1 neq k_2 $, но $ m_1=m_2 $, тогда точкой пересечения будет $ M(0;m) $. Это правило желательно запомнить для ускоренного решения задач.
| Пример 1 |
| Пусть даны $ f(x) = 2x-5 $ и $ g(x)=x+3 $. Найти координаты точки пересечения графиков функций. |
| Решение |
|
Как это сделать? Так как представлены две линейные функции, то первым делом смотрим на коэффициент угла наклона обеих функций $ k_1 = 2 $ и $ k_2 = 1 $. Замечаем, что $ k_1 neq k_2 $, поэтому существует одна точка пересечения. Найдём её с помощью уравнения $ f(x)=g(x) $: $$ 2x-5 = x+3 $$ Переносим слагаемые с $ x $ в левую часть, а остальные в правую: $$ 2x – x = 3+5 $$ $$ x = 8 $$ Получили $ x=8 $ абциссу точки пересечения графиков, а теперь найдём ординату. Для этого подставим $ x = 8 $ в любое из уравнений хоть в $ f(x) $, либо в $ g(x) $: $$ f(8) = 2cdot 8 – 5 = 16 – 5 = 11 $$ Итак, $ M (8;11) $ – является точкой пересечения графиков двух линейных функций. Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$ M (8;11) $$ |
| Пример 2 |
| Дано $ f(x)=2x-1 $ и $ g(x) = 2x-4 $. Найти точки пересечения графиков функций. |
| Решение |
| Как найти? Опять же обращаем внимание на то, что угловые коэффициенты равны $ k_1 = k_2 = 2 $. Это означает, что линейные функции параллельны между собой, поэтому у них нет точек пересечения! |
| Ответы |
| Графики функций параллельны, нет точек пересечения. |
Случай двух нелинейных функций
| Пример 3 |
| Найти координаты точки пересечения графиков функций: $ f(x)=x^2-2x+1 $ и $ g(x)=x^2+1 $ |
| Решение |
|
Как быть с двумя нелинейными функциями? Алгоритм простой: приравниваем уравнения друг к другу и находим корни: $$ x^2-2x+1=x^2+1 $$ Разносим по разным сторонам уравнения члены с $ x $ и без него: $$ x^2-2x-x^2=1-1 $$ $$ -2x=0 $$ $$ x=0 $$ Найдена абцисса искомой точки, но её недостаточно. Ещё нехватает ординаты $ y $. Подставляем $ x = 0 $ в любое из двух уравнений условия задачи. Например: $$ f(0)=0^2-2cdot 0 + 1 = 1 $$ $ M (0;1) $ – точка пересечения графиков функций |
| Ответ |
| $$ M (0;1) $$ |
Точки пересечения графиков функций
В алгебре и начале анализа можно встретить множество задач на поиск точек пересечения графиков функций с помощью их построения или другими методами. Благодаря определенному алгоритму действий, найти ответ достаточно просто. В большинстве случаев решение заключается в определении корней различного вида уравнений.
График функции (y = f(x)) является множеством точек ((x; y)), координаты которых связаны соотношением (y = f(x).)
Равенство (y = f(x)) называют уравнением данного графика. Таким образом, график функции представляет собой множество точек (x; y), где x — является аргументом, а y — определяется как значение функции, соответствующее данному аргументу.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
В том случае, когда графики пересекаются в какой-то точке, можно сделать вывод о существовании общего решения системы уравнений. Определить координаты точки можно с помощью графического или аналитического метода. В первом случае требуется построить график уравнения с переменной. Аналитический метод поиска координат точек, в которых графики функций пересекаются, подразумевает решение уравнения, а найденные корни и являются искомыми точками.
Как найти координаты, примеры решения
Существует несколько способов решения подобных задач:
- Поиск точек пересечения графиков функций заключается в приравнивании обеих функций друг к другу. При этом все члены с х переносят в левую сторону, а оставшиеся – в правую. Затем остается найти корни уравнения, которое получилось после преобразований.
- Второй метод состоит в записи системы уравнения для ее последующего решения с помощью подстановки одной функции в другую.
- Третий способ подразумевает построение графиков функций, чтобы определить точки их пересечения визуально.
В качестве примера можно рассмотреть две линейные функции:
(f(x) = k_1 x+m_1)
(g(x) = k_2 x + m_2)
Данные функции являются прямыми. Их можно графически изобразить, если принять какие-либо два значения (x_1) и (x_2) и найти (f(x_1)) и ((x_2)). Далее действия необходимо повторить с функцией (g(x)). Затем достаточно легко определить визуально координаты точки пересечения рассматриваемых функций.
Важно отметить, что для линейных функций характерна лишь одна точка пересечения только в том случае, когда (k_1 neq k_2). В противном случае (k_1=k_2), а функции будут параллельными друг другу, в связи с тем, что k является коэффициентом угла наклона. При( k_1 neq k_2) и (m_1=m_2) точка пересечения будет соответствовать (M(0;m)). Данная закономерность упрощает решение многих подобных задач.
Задача № 1
Имеются функции: (f(x) = 2x-5)
(g(x)=x+3)
Требуется определить координаты точки, в которой пересекаются графики рассматриваемых функций.
Решение
В первую очередь стоит отметить, что функции являются линейными. Важно обратить внимание на коэффициент угла наклона рассматриваемых функций:
(k_1 = 2)
(k_2 = 1)
Заметим, что:
(k_1 neq k_2)
По этой причине имеется лишь одна точка пересечения графиков функций. Определить ее можно путем решения уравнения:
(f(x)=g(x))
(2x-5 = x+3)
Необходимо перенести члены с x в левую часть, а остальные – в правую:
(2x – x = 3+5)
(x = 8)
В результате удалось найти x=8, что соответствует абсциссе точки пересечения графиков. Требуется определить ординату y с помощью подстановки x = 8 в любое из уравнений – в (f(x)), либо в (g(x)):
(f(8) = 2cdot 8 – 5 = 16 – 5 = 11)
Таким образом, M (8;11) – представляет собой точку, в которой пересекаются графики пары линейных функций.
Ответ: M (8;11)
Задача № 2
Записаны две функции: (f(x)=2x-1)
(g(x) = 2x-4.)
Необходимо определить точки, в которых графики рассматриваемых функций пересекаются.
Решение
Угловые коэффициенты:
(k_1 = k_2 = 2)
Таким образом, линейные функции параллельны между собой, что объясняет отсутствие точек пересечения их графиков.
Ответ: графики функций параллельны, точки пересечения отсутствуют.
Задача № 3
Требуется определить координаты точки, в которой пересекаются графики следующих функций: (f(x)=x^2-2x+1)
(g(x)=x^2+1)
Решение
В данном случае функции являются нелинейными. Поэтому алгоритм решения задачи будет несколько отличаться от предыдущих примеров. В первую очередь следует приравнять уравнения:
(x^2-2x+1=x^2+1)
Далее необходимо разнести в разные стороны уравнения члены с x и без него:
(x^2-2x-x^2=1-1)
(-2x=0)
(x=0)
Таким образом, будет определена абсцисса искомой точки. Затем необходимо найти ординату у. Для этого нужно подставить (x = 0) в какое-либо из двух начальных уравнений. К примеру:
(f(0)=0^2-2cdot 0 + 1 = 1)
M (0;1) является точкой, в которой пересекаются графики функций.
Ответ: M (0;1)
Приравнивание функций друг к другу и нахождение корней
Выяснить, имеют ли точки пересечения графики функций, можно путем сравнения соответствующих тождеств и решения уравнения. Однако при этом допускается получение различных равенств с неизвестными. Тогда целесообразно воспользоваться специальными методиками.
Когда уравнение относится к первой степени или является линейным, решение получить достаточно просто. Метод заключается в переносе переменных величин в одну часть уравнения, а известных – в другую. Алгоритм действий:
- раскрытие скобок, приведение подобных коэффициентов;
- перенос членов с неизвестными в одну сторону, а с известными – в другую;
- математические преобразования;
- определение корня.
Квадратные уравнения решают с помощью одного из способов:
- разложение на множители;
- выделение полного квадрата;
- поиск дискриминанта;
- теорема Виета.
В первом случае представляется возможным понизить степень при неизвестной величине. Второй метод заключается в выделении квадрата по одной из формул сокращенного умножения. Каждая из этих методик реализуема при наличии знаний соответствующих тождеств, в том числе правил разложения на множители.
Третий способ состоит в поиске корней через дискриминант (Д), который является дополнительным параметром, позволяющим сразу решить задачу. Дискриминант определяется с помощью формулы:
((-S)^2-4PU)
В том случае, когда Д>0, переменная может иметь пару значений, которые превращают равенство в справедливое тождество. Если Д=0, то корень является единственным. Когда Д<0, искомое тождество с неизвестными не имеет решений.
Квадратные уравнения решают таким образом:
- выполнение необходимых алгебраических преобразований, в том числе раскрытие скобок и приведение подобных слагаемых;
- выбор наиболее оптимального способа решения и его реализация;
- проверка корней с помощью их подстановки в начальное выражение.
Примечание
Распространенной ошибкой является пренебрежение проверкой результатов решения. Некорректные действия могут привести к образованию ложных корней.
Существует несколько методик решения тождеств кубического и биквадратного типов:
- понижение степени, то есть разложение на множители;
- замена переменной.
Первый вариант решения подразумевает выполнение преобразований для последующего применения одной из формул сокращенного умножения. Такой способ применяют нечасто. Второй способ состоит в том, что при решении необходимо ввести переменную с более низкой степенью, которая упрощает выражение. Порядок действий при этом следующий:
- выполнение математических преобразований;
- выражение переменной через другую;
- решение квадратного или линейного уравнения;
- подстановка промежуточных корней, которые получилось найти на третьем шаге, во второй;
- вычисление искомых корней;
- проверка;
- исключение ложных решений;
- запись ответа.
Путем составления системы уравнений
Данный метод определения точек пересечения графиков функций предполагает запись системы уравнения. К примеру:
Решение системы уравнений представляет собой пару чисел (х, у), являющуюся одновременно решением для первого и второго уравнения системы. Решить систему уравнений – значит, отыскать все ее решения, либо установить их отсутствие.
Порядок действий при решении системы уравнений можно рассмотреть на примере:
Решение будет иметь следующий вид:
Данные уравнения являются линейными, поэтому график каждого из них представляет собой прямую. График первого уравнения проходит через точки (0; 1) и (-1; 0). График второго уравнения проходит через точки (0; -1) и (-1; 0). Прямые пересекаются в точке (-1; 0), это и является решением системы уравнений.
Решение системы представляет сбой единственную пару чисел:
Если подставить данные числа в любое из уравнений, то получится справедливое равенство. Таким образом, имеется единственное решение линейной системы. Можно записать отчет: (-1;0).
В процессе решения линейной системы можно столкнуться с разными ситуациями:
- система обладает единственным решением, прямые пересекаются;
- решения системы отсутствуют. прямые параллельны;
- система обладает бесчисленным множеством решений, прямые совпадают.
При рассмотрении частного случая системы p(x; y) и q(x; y) являются линейными выражениями от x и y.
В задачах нередко требуется решить нелинейную систему уравнений. К примеру, необходимо решить следующую систему:
Решение имеет следующий вид:
График первого уравнения будет иметь вид прямой, а второго – являться окружностью. Можно построить первый график по точкам:
Центр окружности в точке О(0; 0), радиус равен 1.
Графики пересекаются в точке А(0; 1) и в точке В(-1; 0).
Ответ: (0; 1); (-1; 0).
Можно решить систему графическим способом:
В первую очередь необходимо построить график первого уравнения, который будет представлять собой окружность с центром в точке О (0; 0) и радиусом 2. График второго уравнения является параболой, которая смещена относительно начала координат на 2 вверх, то есть ее вершина – точка (0; 2).
Графики обладают одной общей точкой А(0; 2). Данная точка является решением системы. Если подставить два числа в уравнение, можно проверить корректность ответа и записать его. Ответ: (0; 2).
В качестве еще одного примера можно решить следующую систему:
Первым шагом является построение графика первого уравнения, который будет представлять собой окружность с центром в точке О (0; 0) и радиусом 1.
Далее необходимо построить график функции:
График будет являться ломанной:
Далее следует сместить ее на 1 вниз по оси oy. В результате получится график функции:
При помещении обоих графиков в одну систему координат получится следующая ситуация:
Таким образом, получились три точки пересечения: А(1; 0), т. В(-1; 0), т. С(0; -1)
Нахождение через графическое построений функций
Любой определенный график задают с помощью соответствующей функции. Найти точки, в которых пересекаются графики, можно путем решения уравнения, имеющего вид:
(f1(x)=f2(x))
Решение данного уравнения будет являться искомой точкой.
Построить график можно с помощью бумаги и ручки. В процессе необходимо обратить внимание на то, что количество точек пересечения пары графиков определяется видом функции. Линейные функции обладают лишь одной точкой пересечения, линейная и квадратная – двумя, квадратные – двумя, либо четырьмя.
В общем случае двух линейных функций можно предположить, что:
(y1=k1x+b1)
(y2=k2x+b2)
Для поиска точки пересечения графиков необходимо решить уравнение:
(y1=y2 или k1x+b1=k2x+b2)
После преобразований получится, что:
(k1x-k2x=b2-b1.)
Далее нужно выразить x:
(x=(b2-b1)/(k1-k2).)
При известной координате точки по оси абсцисс следует определить координату по оси ординат. Таким образом, можно найти координаты точки пересечения графиков:
(((b2-b1)/(k1-k2); k1(b2-b1)/(k1-k2)+b2))
График функции y = f (х) представляет собой множество точек плоскости, координаты (х, у) которых соответствуют выражению y = f(x). График функции наглядно иллюстрирует поведение и свойства функции. Для построения графика определяют несколько значений довода х и для них рассчитывают соответствующие значения функции y=f(x). Для больше точного и наглядного построения графика следует обнаружить его точки пересечения с осями координат.
С целью определить точку пересечения графика функции с осью y, нужно определить значение функции при х=0, то есть обнаружить f(0). В качестве примера можно рассмотреть график линейной функции, изображенной на рисунке:
В данном случае при х=0 ((y=a*0+b)) функция равна b. Таким образом, график пересекает ось ординат (ось Y) в точке (0,b). Когда пересекается ось абсцисс (ось Х) функция равна 0, то есть (y=f(x)=0). Для того чтобы определить х, следует решить уравнение (f(x)=0). В случае линейной функции получаем уравнение (ax+b=0), откуда и находим (x=-b/a). В результате можно сделать вывод, что ось Х пересекается в точке ((-b/a,0).)
При наличии квадратичной зависимости y от х, уравнение (f(x)=0) обладает двумя корнями. Таким образом, ось абсцисс пересекается два раза. В случае периодической зависимости y от х, например, (y=sin(x)), график функции обладает бесконечным количеством точек пересечения с осью Х. Проверить корректность расчета координат точек, в которых пересекаются графики функций, можно с помощью подстановки найденных значений х в выражение f(x). Значение выражения при любом из вычисленных х должно быть равно 0.
