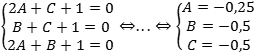Как найти координаты плоскости в кубе

Метод координат в пространстве

30 мая 2011

Для того, чтобы использовать метод координат, надо хорошо знать формулы. Их три:

1. Главная формула — косинус угла φ между векторами a = (x₁; y₁; z₁) и b = (x₂; y₂; z₂):

   

2. Уравнение плоскости в трехмерном пространстве: Ax + By + Cz + D = 0, где A, B, C и D — действительные числа, причем, если плоскость проходит через начало координат, D = 0. А если не проходит, то D = 1.
3. Вектор, перпендикулярный к плоскости Ax + By + Cz + D = 0, имеет координаты: n = (A; B; C).

На первый взгляд, выглядит угрожающе, но достаточно немного практики — и все будет работать великолепно.

Задача. Найти косинус угла между векторами a = (4; 3; 0) и b = (0; 12; 5).

Решение. Поскольку координаты векторов нам даны, подставляем их в первую формулу:

Задача. Составить уравнение плоскости, проходящей через точки M = (2; 0; 1), N = (0; 1; 1) и K = (2; 1; 0), если известно, что она не проходит через начало координат.

Решение. Общее уравнение плоскости: Ax + By + Cz + D = 0, но, поскольку искомая плоскость не проходит через начало координат — точку (0; 0; 0) — то положим D = 1. Поскольку эта плоскость проходит через точки M, N и K, то координаты этих точек должны обращать уравнение в верное числовое равенство.

Подставим вместо x, y и z координаты точки M = (2; 0; 1). Имеем:
A · 2 + B · 0 + C · 1 + 1 = 0 ⇒ 2A + C + 1 = 0;

Аналогично, для точек N = (0; 1; 1) и K = (2; 1; 0) получим уравнения:
A · 0 + B · 1 + C · 1 + 1 = 0 ⇒ B + C + 1 = 0;
A · 2 + B · 1 + C · 0 + 1 = 0 ⇒ 2A + B + 1 = 0;

Итак, у нас есть три уравнения и три неизвестных. Составим и решим систему уравнений:

Получили, что уравнение плоскости имеет вид: − 0,25x − 0,5y − 0,5z + 1 = 0.

Задача. Плоскость задана уравнением 7x − 2y + 4z + 1 = 0. Найти координаты вектора, перпендикулярного данной плоскости.

Решение. Используя третью формулу, получаем n = (7; − 2; 4) — вот и все!

Вычисление координат векторов

А что, если в задаче нет векторов — есть только точки, лежащие на прямых, и требуется вычислить угол между этими прямыми? Все просто: зная координаты точек — начала и конца вектора — можно вычислить координаты самого вектора.

Чтобы найти координаты вектора, надо из координат его конца вычесть координаты начала.

Эта теорема одинаково работает и на плоскости, и в пространстве. Выражение «вычесть координаты» означает, что из координаты x одной точки вычитается координата x другой, затем то же самое надо сделать с координатами y и z. Вот несколько примеров:

Задача. В пространстве расположены три точки, заданные своими координатами: A = (1; 6; 3), B = (3; − 1; 7) и C = (− 4; 3; − 2). Найти координаты векторов AB, AC и BC.

Рассмотрим вектор AB: его начало находится в точке A, а конец — в точке B. Следовательно, чтобы найти его координаты, надо из координат точки B вычесть координаты точки A:
AB = (3 − 1; − 1 − 6; 7 − 3) = (2; − 7; 4).

Аналогично, начало вектора AC — все та же точка A, зато конец — точка C. Поэтому имеем:
AC = (− 4 − 1; 3 − 6; − 2 − 3) = (− 5; − 3; − 5).

Наконец, чтобы найти координаты вектора BC, надо из координат точки C вычесть координаты точки B:
BC = (− 4 − 3; 3 − (− 1); − 2 − 7) = (− 7; 4; − 9).

Ответ: AB = (2; − 7; 4); AC = (− 5; − 3; − 5); BC = (− 7; 4; − 9)

Обратите внимание на вычисление координат последнего вектора BC: очень многие ошибаются, когда работают с отрицательными числами. Это касается переменной y: у точки B координата y = − 1, а у точки C y = 3. Получаем именно 3 − (− 1) = 4, а не 3 − 1, как многие считают. Не допускайте таких глупых ошибок!

Вычисление направляющих векторов для прямых

Если вы внимательно прочитаете задачу C2, то с удивлением обнаружите, что никаких векторов там нет. Там только прямые да плоскости.

Для начала разберемся с прямыми. Здесь все просто: на любой прямой найдутся хотя бы две различные точки и, наоборот, любые две различные точки задают единственную прямую…

Кто-нибудь понял, что написано в предыдущем абзаце? Я и сам не понял, поэтому объясню проще: в задаче C2 прямые всегда задаются парой точек. Если ввести систему координат и рассмотреть вектор с началом и концом в этих точках, получим так называемый направляющий вектор для прямой:

Зачем нужен этот вектор? Дело в том, что угол между двумя прямыми — это угол между их направляющими векторами. Таким образом, мы переходим от непонятных прямых к конкретным векторам, координаты которых легко считаются. Насколько легко? Взгляните на примеры:

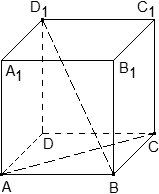
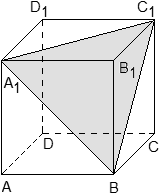
Задача. В кубе ABCDA₁B₁C₁D₁ проведены прямые AC и BD₁. Найдите координаты направляющих векторов этих прямых.

Поскольку длина ребер куба в условии не указана, положим AB = 1. Введем систему координат с началом в точке A и осями x, y, z, направленными вдоль прямых AB, AD и AA₁ соответственно. Единичный отрезок равен AB = 1.

Теперь найдем координаты направляющего вектора для прямой AC. Нам потребуются две точки: A = (0; 0; 0) и C = (1; 1; 0). Отсюда получаем координаты вектора AC = (1 − 0; 1 − 0; 0 − 0) = (1; 1; 0) — это и есть направляющий вектор.

Теперь разберемся с прямой BD₁. На ней также есть две точки: B = (1; 0; 0) и D₁ = (0; 1; 1). Получаем направляющий вектор BD₁ = (0 − 1; 1 − 0; 1 − 0) = (− 1; 1; 1).

Ответ: AC = (1; 1; 0); BD₁ = (− 1; 1; 1)

Задача. В правильной треугольной призме ABCA₁B₁C₁, все ребра которой равны 1, проведены прямые AB₁ и AC₁. Найдите координаты направляющих векторов этих прямых.

Введем систему координат: начало в точке A, ось x совпадает с AB, ось z совпадает с AA₁, ось y образует с осью x плоскость OXY, которая совпадает с плоскостью ABC.

Для начала разберемся с прямой AB₁. Тут все просто: у нас есть точки A = (0; 0; 0) и B₁ = (1; 0; 1). Получаем направляющий вектор AB₁ = (1 − 0; 0 − 0; 1 − 0) = (1; 0; 1).

Теперь найдем направляющий вектор для AC₁. Все то же самое — единственное отличие в том, что у точки C₁ иррациональные координаты. Итак, A = (0; 0; 0), поэтому имеем:

Ответ: AB₁ = (1; 0; 1);

Небольшое, но очень важное замечание насчет последнего примера. Если начало вектора совпадает с началом координат, вычисления резко упрощаются: координаты вектора просто равны координатам конца. К сожалению, это верно лишь для векторов. Например, при работе с плоскостями присутствие на них начала координат только усложняет выкладки.

Вычисление нормальных векторов для плоскостей

Нормальные векторы — это не те векторы, у которых все в порядке, или которые чувствуют себя хорошо. По определению, нормальный вектор (нормаль) к плоскости — это вектор, перпендикулярный данной плоскости.

Другими словами, нормаль — это вектор, перпендикулярный любому вектору в данной плоскости. Наверняка вы встречали такое определение — правда, вместо векторов речь шла о прямых. Однако чуть выше было показано, что в задаче C2 можно оперировать любым удобным объектом — хоть прямой, хоть вектором.

Еще раз напомню, что всякая плоскость задается в пространстве уравнением Ax + By + Cz + D = 0, где A, B, C и D — некоторые коэффициенты. Не умаляя общности решения, можно полагать D = 1, если плоскость не проходит через начало координат, или D = 0, если все-таки проходит. В любом случае, координаты нормального вектора к этой плоскости равны n = (A; B; C).

Итак, плоскость тоже можно успешно заменить вектором — той самой нормалью. Всякая плоскость задается в пространстве тремя точками. Как найти уравнение плоскости (а следовательно — и нормали), мы уже обсуждали в самом начале статьи. Однако этот процесс у многих вызывает проблемы, поэтому приведу еще парочку примеров:

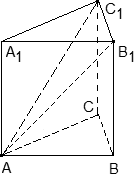
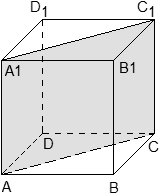
Задача. В кубе ABCDA₁B₁C₁D₁ проведено сечение A₁BC₁. Найти нормальный вектор для плоскости этого сечения, если начало координат находится в точке A, а оси x, y и z совпадают с ребрами AB, AD и AA₁ соответственно.

Поскольку плоскость не проходит через начало координат, ее уравнение выглядит так: Ax + By + Cz + 1 = 0, т.е. коэффициент D = 1. Поскольку эта плоскость проходит через точки A₁, B и C₁, то координаты этих точек обращают уравнение плоскости в верное числовое равенство.

Подставим вместо x, y и z координаты точки A₁ = (0; 0; 1). Имеем:
A · 0 + B · 0 + C · 1 + 1 = 0 ⇒ C + 1 = 0 ⇒ C = − 1;

Аналогично, для точек B = (1; 0; 0) и C₁ = (1; 1; 1) получим уравнения:
A · 1 + B · 0 + C · 0 + 1 = 0 ⇒ A + 1 = 0 ⇒ A = − 1;
A · 1 + B · 1 + C · 1 + 1 = 0 ⇒ A + B + C + 1 = 0;

Но коэффициенты A = − 1 и C = − 1 нам уже известны, поэтому остается найти коэффициент B:
B = − 1 − A − C = − 1 + 1 + 1 = 1.

Получаем уравнение плоскости: − A + B − C + 1 = 0, Следовательно, координаты нормального вектора равны n = (− 1; 1; − 1).

Задача. В кубе ABCDA₁B₁C₁D₁ проведено сечение AA₁C₁C. Найти нормальный вектор для плоскости этого сечения, если начало координат находится в точке A, а оси x, y и z совпадают с ребрами AB, AD и AA₁ соответственно.

В данном случае плоскость проходит через начало координат, поэтому коэффициент D = 0, а уравнение плоскости выглядит так: Ax + By + Cz = 0. Поскольку плоскость проходит через точки A₁ и C, координаты этих точек обращают уравнение плоскости в верное числовое равенство.

Подставим вместо x, y и z координаты точки A₁ = (0; 0; 1). Имеем:
A · 0 + B · 0 + C · 1 = 0 ⇒ C = 0;

Аналогично, для точки C = (1; 1; 0) получим уравнение:
A · 1 + B · 1 + C · 0 = 0 ⇒ A + B = 0 ⇒ A = − B;

Положим B = 1. Тогда A = − B = − 1, и уравнение всей плоскости имеет вид: − A + B = 0, Следовательно, координаты нормального вектора равны n = (− 1; 1; 0).

Вообще говоря, в приведенных задачах надо составлять систему уравнений и решать ее. Получится три уравнения и три переменных, но во втором случае одна из них будет свободной, т.е. принимать произвольные значения. Именно поэтому мы вправе положить B = 1 — без ущерба для общности решения и правильности ответа.

Координаты середины отрезка

Очень часто в задаче C2 требуется работать с точками, которые делят отрезок пополам. Координаты таких точек легко считаются, если известны координаты концов отрезка.

Итак, пусть отрезок задан своими концами — точками A = (x_a; y_a; z_a) и B = (x_b; y_b; z_b). Тогда координаты середины отрезка — обозначим ее точкой H — можно найти по формуле:

Другими словами, координаты середины отрезка — это среднее арифметическое координат его концов.

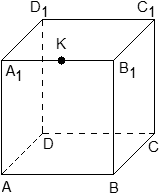
Задача. Единичный куб ABCDA₁B₁C₁D₁ помещен в систему координат так, что оси x, y и z направлены вдоль ребер AB, AD и AA₁ соответственно, а начало координат совпадает с точкой A. Точка K — середина ребра A₁B₁. Найдите координаты этой точки.

Поскольку точка K — середина отрезка A₁B₁, ее координаты равных среднему арифметическому координат концов. Запишем координаты концов: A₁ = (0; 0; 1) и B₁ = (1; 0; 1). Теперь найдем координаты точки K:

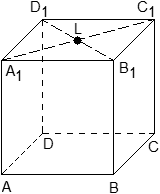
Задача. Единичный куб ABCDA₁B₁C₁D₁ помещен в систему координат так, что оси x, y и z направлены вдоль ребер AB, AD и AA₁ соответственно, а начало координат совпадает с точкой A. Найдите координаты точки L, в которой пересекаются диагонали квадрата A₁B₁C₁D₁.

Из курса планиметрии известно, что точка пересечения диагоналей квадрата равноудалена от всех его вершин. В частности, A₁L = C₁L, т.е. точка L — это середина отрезка A₁C₁. Но A₁ = (0; 0; 1), C₁ = (1; 1; 1), поэтому имеем:

Ответ: L = (0,5; 0,5; 1)

Смотрите также:

1. Введение системы координат
2. Четырехугольная пирамида в задаче C2
3. В 2012 году ЕГЭ по математике станет двухуровневым?
4. Сводный тест по задачам B12 (1 вариант)
5. Симметрия корней и оптимизация ответов в тригонометрии
6. ЕГЭ 2022, задание 6. Касательная и уравнение с параметром

Координаты вектора

Вектор – отрезок, имеющий длину и указывающий направление.

На самом деле, понимать, что такое вектор для решения задач методом координат необязательно. Можно просто использовать это понятие, как необходимый инструмент для решения задач по стереометрии. Любое ребро или отрезок на нашей фигуре мы будем называть вектором.

Для того, чтобы определить координаты вектора, нужно из координат конечной точки вычесть координаты начальной точки. Пусть у нас есть две точки (Рис. 4) :
$$ т.А(x_A,y_A,z_A); $$
$$ т.B(x_B,y_B,z_B); $$
Тогда координаты вектора (vec{AB}) можно определить по формуле:
$$ vec{AB}={x_B-x_A,y_B-y_A,z_B-z_A}. $$

Скрещивающиеся прямые

И так, мы научились находить координаты точек, и при помощи них определять координаты векторов. Теперь познакомимся с формулой нахождения косинуса угла между скрещивающимися прямыми (векторами). Пусть даны два вектора:
$$ a={x_a,y_a,z_a};$$
$$ b={x_b,y_b,z_b}; $$
тогда угол (alpha) между ними находится по формуле:
$$ cos{alpha}=frac{x_a*x_b+y_a*y_b+z_a*z_b}{sqrt{{x_a}^2+{y_a}^2+{z_a}^2}*sqrt{{x_b}^2+{y_b}^2+{z_b}^2}}. $$

Уравнение плоскости

В задачах №14 (С2) ЕГЭ по профильной математике часто требуется найти угол между прямой и плоскостью и расстояние между скрещивающимися прямыми. Но для этого вы должны уметь выводить уравнение плоскости. В общем виде уравнение плоскости задается формулой:
$$ A*x+B*y+C*z+D=0,$$
где (A,B,C,D) – какие-то числа.

Если найти (A,B,C,D), то мы мы найдем уравнений плоскости. Плоскость однозначно задается тремя точками в пространстве, значит нужно найти координаты трех точек, лежащий в данной плоскости, а потом подставить их в общее уравнение плоскости.

Например, пусть даны три точки:

$$ K(x_K,y_K,z_K);,L(x_L,y_L,z_L);,P(x_P,y_P,z_P). $$

Подставим координаты точек в общее уравнение плоскости:

$$begin{cases} A*x_K+B*y_K+C*z_K+D=0,\ A*x_L+B*y_L+C*z_L+D=0, \ A*x_P+B*y_P+C*z_P+D=0.end{cases}$$

Получилась система из трех уравнений, но неизвестных 4: (A,B,C,D). Если наша плоскость не проходит через начало координат, то мы можем (D) приравнять (1), если же проходит, то (D=0). Объяснение этому простое: вы можете поделить каждое ваше уравнения на (D), от этого уравнение не изменится, но вместо (D) будет стоять (1), а остальные коэффициенты будут в (D) раз меньше.

Теперь у нас есть три уравнения и три неизвестные – можем решить систему:

Пример 3

Найти уравнение плоскости, проходящей через точки
$$ K(1;2;3);,P(0;1;0);,L(1;1;1). $$
Подставим координаты точек в уравнение плоскости (D=1):
$$begin{cases} A*1+B*2+C*3+1=0,\ A*0+B*1+C*0+1=0, \ A*1+B*1+C*1+1=0.end{cases}$$
$$begin{cases} A+2*B+3*C+1=0,\ B+1=0, \ A+B+C+1=0.end{cases}$$
$$begin{cases} A-2+3*C+1=0,\ B=-1, \ A=-C.end{cases}$$
$$begin{cases} A=-0.5,\ B=-1, \ C=0.5.end{cases}$$
Получаем искомое уравнение плоскости:
$$ -0.5x-y+0.5z+1=0.$$

Расстояние от точки до плоскости

Зная координаты некоторой точки (M(x_M;y_M;z_M)), легко найти расстояние до плоскости (Ax+By+Cz+D=0:)
$$ rho=frac{|A*x_M+B*y_M+C*z_M+D|}{sqrt{A^2+B^2+C^2}}. $$

Пример 4

Найдите расстояние от т. (H (1;2;0)) до плоскости, заданной уравнением
$$ 2*x+3*y-sqrt{2}*z+4=0.$$

Из уравнения плоскости сразу находим коэффициенты:
$$ A=2,,B=3,,C=-sqrt{2},,D=4.$$
Подставим их в формулу для нахождения расстояния от точки до плоскости.
$$ rho=frac{|2*1+3*2-sqrt{2}*0+4|}{sqrt{2^2+3^2+{-sqrt{2}}^2}}. $$
$$ rho=frac{12}{sqrt{16}}=3.$$

Расстояние между скрещивающимися прямыми

Расстояние между скрещивающимися прямыми – это расстояние от любой точки одной из прямых до параллельной ей плоскости, проходящей через вторую прямую.

Таким образом, если требуется найти расстояние между скрещивающимися прямыми, то нужно через одну из них провести плоскость параллельно второй прямой. Затем найти уравнение этой плоскости и по формуле расстояния от точки до плоскости найти расстояние между скрещивающимися прямыми. Точку на прямой можно выбрать произвольно (у которой легче всего найти координаты).

Пример 5

Рассмотрим задачу из досрочного ЕГЭ по математике 2018 года.

Дана правильная треугольная призма (ABCFDE), ребра которой равны 2. Точка (G) – середина ребра (CE).

• Докажите, что прямые (AD) и (BG) перпендикулярны.
• Найдите расстояние между прямыми (AD) и (BG).

Решение:

Решим задачу полностью методом координат.

Нарисуем рисунок и выберем декартову систему координат. (Рис 5).

Уравнение плоскости, которая проходит через три заданные точки, не лежащие на одной прямой.

В этой статье мы разберемся с задачей нахождения уравнения плоскости в прямоугольной системе координат в трехмерном пространстве, когда известны координаты трех различных точек этой плоскости, не лежащих на одной прямой. Сначала покажем принцип нахождения уравнения плоскости, после чего перейдем к решению примеров и задач, в которых требуется составить уравнение плоскости, проходящей через три заданные точки.

Навигация по странице.

Нахождение уравнения плоскости, проходящей через три заданные точки.

Прежде чем приступать к составлению уравнения плоскости, проходящей через три заданные точки пространства, вспомним одну аксиому: через три несовпадающие и не лежащие на одной прямой точки трехмерного пространства проходит единственная плоскость. Таким образом, задав три различных и не лежащих на одной прямой точки, мы в трехмерном пространстве однозначно определим плоскость, проходящую через эти точки.

Пусть в трехмерном пространстве зафиксирована прямоугольная система координат Oxyz , в ней заданы три несовпадающие точки , которые не лежат на одной прямой. Поставим перед собой следующую задачу: написать уравнение плоскости, проходящей через эти три точки.

Покажем два способа ее решения.

Первый способ составления уравнения плоскости, проходящей через три заданные точки .

Известно, что общее уравнение плоскости вида задает в прямоугольной системе координат Oxyz плоскость , которая проходит через точку , а нормальный вектор плоскости имеет координаты . Следовательно, мы можем составить общее уравнение плоскости, если знаем координаты точки, через которую она проходит, и координаты нормального вектора этой плоскости. От этого знания и будем отталкиваться при нахождении уравнения плоскости, проходящей через три заданные точки .

Итак, из условия задачи нам известны координаты точки (даже координаты трех точек), через которую проходит плоскость, уравнение которой нам требуется составить. Осталось отыскать координаты нормального вектора этой плоскости.

Так как нормальный вектор плоскости и любой ненулевой вектор этой плоскости перпендикулярны, то вектор перпендикулярен как вектору , так и вектору . Следовательно, в качестве вектора можно принять векторное произведение векторов и . Так как и (при необходимости обращайтесь к статье вычисление координат вектора по координатам точек), то . После вычисления записанного определителя, станут видны координаты нормального вектора , и можно записывать требуемое уравнение плоскости, проходящей через три заданные точки.

Второй способ нахождения уравнения плоскости, проходящей через три заданные точки .

Очевидно, что множество точек определяет в прямоугольной системе координат Oxyz в трехмерном пространстве плоскость, проходящую через три различные и не лежащие на одной прямой точки , тогда и только тогда, когда три вектора и компланарны.

Следовательно, должно выполняться условие компланарности трех векторов и , то есть, смешанное произведение векторов должно быть равно нулю: . Это равенство в координатной форме имеет вид . Оно, после вычисления определителя, представляет собой общее уравнение плоскости, проходящей через три заданные точки .

Далее, от полученного общего уравнения плоскости, проходящей через три заданные точки, Вы при необходимости можете перейти к уравнению плоскости в отрезках или к нормальному уравнению плоскости.

Осталось рассмотреть решения примеров, в которых находится уравнение плоскости, проходящей через три несовпадающие и не лежащие на одной прямой точки.

Примеры составления уравнения плоскости, проходящей через три заданные точки.

В предыдущем пункте статьи мы рассмотрели два способа нахождения уравнения плоскости, проходящей через три различные и не лежащие на одной прямой точки. Давайте рассмотрим их применение при решении задачи.

Уравнение плоскости, проходящей через три точки

Если плоскость проходит через три точки М₁(x₁;y₁;z₁), M₂(x₂;y₂;z₂) и M₃₍x₃;y₃;z₃), не лежащие на одной прямой, то проходящая через них плоскость представляется уравнением:

Точка М(х; у; z) лежит в одной плоскости с точками M₁, M₂ и M₃ только в том случае, когда векторы:

Точки M₁(2;3;1), M₂(1;2;2) и M₃(1;5;4) не лежат на одной прямой, так как

Плоскость с точками M₁, M₂ и M₃ представляется уравнением

Уравнение плоскости через 3 точки

Вы будете перенаправлены на Автор24

Для начала стоит напомнить, как выглядит общее уравнение плоскости:

$Ax cdot + By + Cz + D = 0left(1right)$,

при этом: $$ — координаты нормального вектора данной плоскости, а $D$ — свободный член.

В общем уравнении коэффициенты $A, B, C$ не могут быть одновременно равны нулю, если же один из коэффициентов нулевой — уравнение называется неполным. При $D=0$ плоскость проходит через центр осей координат.

Также в дальнейшем нам пригодится уравнение плоскости, заданной точкой, лежащей в данной плоскости и нормальным вектором:

здесь $(x_0; y_0; z_0)$ — координаты точки плоскости.

Теперь непосредственно к делу.

Уравнение плоскости через три точки можно выразить несколькими способами: с помощью смешанного произведения векторов и выразив сначала нормальный вектор плоскости и используя одну точку.

Уравнение плоскости, проходящей через 3 точки, через смешанное произведение векторов

Рассмотрим три точки $M_1, M_2, M_3$, не находящиеся на одной прямой. Соответственно аксиоме стереометрии о том, что три точки задают плоскость, и притом только одну, все эти точки лежат в одной плоскости $α$.

Рисунок 1. Плоскость через 3 точки. Автор24 — интернет-биржа студенческих работ

Рассмотрим точку $M$, лежащую в плоскости $α$. Если описать плоскость $α$ как множество точек $M$, вектора $vec$, $vec$ и $vec$ должны быть компланарны между собой. А как известно, вектора компланарны между собой если их смешанное произведение равно нулю.

Соответственно, для того чтобы вычислить это смешанное произведение, необходимо вычислить определитель третьего порядка, каждая строка которого является координатами вышеперечисленных векторов.

Готовые работы на аналогичную тему

Пусть координаты точек $M, M_1, M_2, M_3$ — $(x; y; z), (x_1;y_1; z_1), (x_2;y_2; z_2), (x_3;y_3;z_3)$ соответственно. Тогда координаты каждого из вышеперечисленных векторов составят:

Составим определитель, описывающий смешанное произведение векторов:

$begin <|ccc|>x-x_1 && y-y_1 && z-z_1 \ x_2-x_1 && y_2-y_1 && z_2-z_1 \ x_3-x_1 && y_3-y_1 &&z_3-z_1 \ end=0$ — уравнение плоскости через 3 точки.

При вычислении этого определителя получается общее уравнение плоскости, проходящей через три точки. Это можно увидеть, раскрыв определитель по первой строке:

$begin <|cc|>y_2-y_1 && z_2-z_1 \ y_3-y_1 &&z_3-z_1 \ end cdot ( x-x_1) + begin <|cc|>x_2-x_1 && z_2-z_1 \ x_3-x_1 &&z_3-z_1 \ end cdot (y-y_1) + begin <|cc|>x_2-x_1 && y_2-y_1 \ x_3-x_1 && y_3-y_1 \ end cdot (z-z_1) = 0left(3right)$.

Коэффициенты из уравнения $(3)$ также совпадают с координатами векторного произведения $vec×vec$ и, так как два этих вектора неколлинеарны и параллельны рассматриваемой плоскости $α$, данное векторное произведение представляет собой нормальный вектор к плоскости, для которой составляется уравнение.

Уравнение плоскости, заданной 3 точками, через нормальный вектор и точку

Другим альтернативным методом задания плоскости является использование нормального вектора плоскости и точки, принадлежащей данной плоскости.

Для того чтобы воспользоваться данным методом, найдём векторное произведение векторов $vec$ и $vec$:

$[vec × vec]= begin <|ccc|>vec &&vec &&vec \ x_2-x_1 &&y_2-y_1 &&z_2-z_1 \ x_3-x_1 &&y_3-y_1 &&z_3-z_1 \ end=0$.

Данное произведение является нормальным вектором плоскости, для которой составляется уравнение. Полученные координаты нормального вектора можно использовать непосредственно для составления уравнения плоскости.

Зная точку, принадлежащую этой плоскости, можно подставить координаты нормального вектора и координаты точки в уравнение $(2)$ и получить уравнение плоскости:

В этом уравнении $n_x; n_y; n_z$ — координаты нормального вектора, определённого из векторного произведения векторов $vec$ и $vec$, а $(x_3; y_3; z_3)$ — некая точка, принадлежащая данной плоскости.

По сути, два вышеприведённых метода представляют одно и то же, так как в обоих необходимо найти координаты нормального вектора и затем, используя их и координаты третьей неиспользованной точки, получить уравнение самой плоскости.

К данной задаче можно также свести задачу с нахождением уравнения плоскости по уравнениям лежащих в ней параллельных и пересекающихся прямых.

Cоставить уравнение плоскости, проходящей через 3 точки $M_1,M_2, M_3$ c координатами $(1;2;3), (1;2;4)$ и $(4;2;-1)$ соответственно.

Воспользуемся вторым способом и найдём координаты вектора через векторное произведение. Для этого сначала выразим координаты векторов:

Найдём их векторное произведение:

Подставим координаты нормального вектора в уравнение $(2)$:

$0cdot(x-4)+(-3) cdot (y-2)+0 cdot(z+1)=0$.

$-3y+6=0$ — искомое уравнение плоскости.

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 14 03 2021

[spoiler title=”источники:”]

Уравнение плоскости, проходящей через три точки

http://spravochnick.ru/matematika/uravnenie_ploskosti_cherez_3_tochki/

[/spoiler]

Координатный метод в
стереометрии

1) Координаты
вектора определяются через координаты начала и конца вектора

Координаты начала
вектора ,
координаты конца вектора .

Координаты вектора

2) Угол между
векторами   и

определяется с
помощью формулы скалярного произведения: 

Угол между
прямыми,
содержащими векторы                
      

3) Положение
плоскости в пространстве характеризуется вектором-нормалью  к
плоскости.

Если известны три
точки плоскости  ,
то по ним можно определить координаты нормали 

Для этого
необходимо решить систему уравнений, где вместо одной из переменных (обычно D)
берут любое число, не равное 0.

Уравнение
плоскости
задается уравнением  

4) Расстояние
от точки до плоскости

Расстояние от
точки с координатами  до плоскости
с нормалью 

определяется по
формуле  

5) Угол между
плоскостями равен углу между нормалями  к плоскостям:

Угол между
плоскостями по определению меньше 90 градусов, это обеспечивается положительным
значением косинуса в формуле.

6) Угол между прямой
и плоскостью       определяется с помощью вектора , лежащего
на прямой и нормалью  к
плоскости:

7) Площадь
ортогональной проекции     многоугольника ,
где —
площадь проекции многоугольника,  —
площадь многоугольника,

— косинус
угла между плоскостью многоугольника и плоскостью проекции.

Площадь
многоугольника     находится по площади его проекции
 

8) Уравнение
прямой в пространстве

Если прямая
параллельна вектору  и
проходит через точку ,

то уравнение
прямой задается формулой  

Метод координат в пространстве: формулы и комментарии
репетитора

Метод координат — весьма эффективный и универсальный
способ нахождения любых углов или расстояний между стереометрическими объектами
в пространстве. Если Ваш репетитор по
математике имеет высокую квалификацию, то он должен это знать. В противном
случае я бы советовал для «С» части сменить репетитора. Моя подготовка к ЕГЭ
по математике С1-С6 обычно включает разбор основных алгоритмов и формул,
описанных ниже.

Угол
между прямыми а и b

Углом между прямыми в пространстве называется угол между
любыми параллельными им пересекающимися прямыми. Этот угол равен углу между
направляющими векторами данных прямых (или дополняет его до 180 град).

Какой алгоритм использует репетитор по математике для
поиска угла?

1) Выбираем любые вектора и , имеющие направления прямых а и b (параллельные им).
2) Определяем координаты векторов и
по соответствующим координатам их начал и
концов (от координат конца вектора нужно отнять координаты начала).
3) Подставляем найденный координаты в формулу:
.
Для нахождения самого угла, нужно найти арккосинус полученного результата.

Нормаль
к плоскости

Нормалью к плоскости называется любой
вектор, перпендикулярный к этой плоскости.
Как найти нормаль? Для поиска координат нормали достаточно
узнать координаты любых трех точек M, N и K, лежащих в данной плоскости. По
этим координатам находим координаты векторов и и требуем выполнения условий и . Приравнивая скалярные
произведение векторов к нулю, составляем систему уравнений с тремя переменными,
из которой можно найти координаты нормали.

Замечание: Совсем не обязательно решать систему полностью, ибо достаточно
подобрать хотя бы одну нормаль. Для этого можно подставить вместо какой-нибудь
из ее неизвестных координат любое число (например единицу) и решить систему
двух уравнений с оставшимися двумя неизвестными. Если она решений не имеет, то
это значит, что в семействе нормалей нет той, у которой по выбранной переменной
стоит единица. Тогда подставьте единицу вместо другой переменной (другой
координаты) и решите новую систему. Если опять промахнетесь, то Ваша нормаль
будет иметь единицу по последней координате, а сама она окажется параллельной
какой-нибудь координатной плоскости (в таком случае ее легко найти и без
системы).

Угол
между прямой и плоскостью

Допустим, что нам заданы прямая и плоскость координатами направляющего
вектора и нормали
Угол между прямой и плоскость вычисляется
по следующей формуле:

Угол
между плоскостями

Пусть и  — две любые нормали к данным
плоскостям. Тогда косинус угла между плоскостями равен модулю косинуса угла между
нормалями:

Уравнение
плоскости в пространстве

Точки, удовлетворяющие равенству образуют плоскость с нормалью . Коэффициент отвечает за величину
отклонения (параллельного сдвига) между двумя плоскостями с одной и той же
заданной нормалью . Для того, чтобы
написать уравнение плоскости нужно сначала найти ее нормаль (как это описано
выше), а затем подставить координаты любой точки плоскости вместе с
координатами найденной нормали в уравнение и найти коэффициент .

Расстояние
от точки до плоскости

Для вычисления расстояния от точки до плоскости , заданной
уравнением можно
использовать следующую формулу:

В знаменателе стоит длина нормали, а числителе — значение выражения из
левой части уравнения плоскости в точке

Комментарий
репетитора по математике:

Методом координат можно находить не только углы и расстояния в
пространстве, но и
1) площади многоугольников (треугольника, параллелограмма), расположенных в
заданной плоскости.
2) объемы простейших многогранников (параллелепипедов и пирамид).

Для понимания таких формул нужно изучить понятия векторного и
смешанного произведения векторов, а также определителя матрицы. В скором
времени я сделаю для вычисления объемов соответствующую справочную страничку.

Средства аналитической геометрии репетитор по математике
практически не использует в работе со средним и тем более слабым учеником. И
очень жаль, что загруженность среднестатистического сильного школьника не
позволяет репетитору провести более-менее серьезную работу на уровне
определений из высшей математики и с соответствующей практикой решения задач.
Поэтому я часто ограничиваюсь простым сообщением формул и демонстрацией одного
– двух примеров их использования. В школьной программе не предусмотрено время
для изучения векторных приемов вообще, однако на ЕГЭ Вы имеете право решать
задачу С2 любым из известных науке способов. Отсюда мораль: учите координаты. Расширенная
подготовка к ЕГЭ по математике с изучением приемов аналитической
геометрии даст Вам мощное и универсальное средство для решения огромного класса
задач типа С2. Пользуйтесь этой страничкой на здоровье!

Республиканская
научно-практическая конференция школьников

«От школьного
проекта к формированию интеллектуальной элиты РТ»

Секция:
Математика. Информатика. Физика.

Тема:
«Координатный метод решения задач на ЕГЭ 2012»

ученица 11 класса

МБОУ «Чувашско-Дрожжановская СОШ»

Научный руководитель:

учитель математики

Буинск 2012

Содержание

1.Введение

2.Цели и задачи

3.Система координат

4.История открытия системы
координат

5.Системы координат на плоскости

6.Системы координат в пространстве

7.Введение системы координат в
заданиях С2

8.Применение метода координат при
решении геометрических задач в заданиях С2 из ЕГЭ 2012 года.

9.Недостатки системы координат

10.Вывод

11.Список использованной литературы

Введение

В геометрии применяются различные
методы решения задач – это синтетический (чисто геометрический) метод, метод
преобразований, а также векторно-координатный метод, метод ключевых задач.
Методы делятся на методы алгебры и геометрии. Геометрические методы: метод
треугольников, метод площадей, метод вспомогательных фигур, координатный метод,
векторный метод и др. Они занимают различное положение в школе. Основным
методом считается синтетический, а из других наиболее высокое положение
занимает векторно-координатный метод потому, что он тесно связан с геометрией.
Изящество синтетического метода достигается с помощью интуиции, догадок,
дополнительных построений. Векторно-координатный метод этого не требует:
решение задач во многом алгоритмизировано, что в большинстве случаев упрощает
поиск и само решение задачи. Координатный метод решения задач на сегодняшний
день самый мощный и при правильном подходе позволяет решить фактически все виды
математический, физических, астрономических, и
технических задач. Кроме того, координатный метод в рамках школьной программы
используется достаточно ограниченно и неполно. В своей работе я решила
исследовать: как решаются стереометрические задачи, если на них взглянуть
по-иному, то есть если рассмотреть задачу в трехмерной системе координат.

Цели и задачи

Рассказать об истории появления
этого метода решения задач.

Раскрыть содержание метода,
рассказать основные формулы и теоремы.

Показать применение метода на
несложных, элементарных задачах.

Решить сложные стереометрические
задачи с использованием векторно-координатного метода, сравнить и показать его
преимущества.

Система координат

Система координат —
комплекс определений, реализующий метод координат, то есть способ определять
положение точки или тела с помощью чисел или других символов. Совокупность
чисел, определяющих положение конкретной точки, называется координатами
 этой точки.

История открытия
системы координат

Рене Декарт является одним из
создателей аналитической геометрии (которую он разрабатывал одновременно с
Пьером Ферма), позволявшей алгебраизировать эту науку с помощью метода координат.
Предложенная им система координат получила его имя.

Системы координат
на плоскости

Декартова система
координат на плоскости

Декартова система координат хорошо
известна. И всё же сформулируем подробнее, каким образом она задаётся на
плоскости, и какие величины в результате однозначно определяют положение точки
на плоскости. Задать декартову систему координат на плоскости означает
зафиксировать, во-первых, точку начала координат, а во-вторых, две
перпендикулярные направленные оси (так называемые, оси координат). Причём, эти
оси занумерованы. И, конечно, понадобится единичный отрезок, чтобы численно
обозначать расстояние между двумя точками.

Стандартным образом декартова
система координат обозначается Oxy, оси нумеруются таким образом, что поворот
от первой оси ко второй осуществляется против часовой стрелки. Координаты точки
– (x, y).

Полярная система
координат на плоскости

Для того, чтобы задать полярную
систему координат на плоскости, надо зафиксировать, во-первых, точку начала
координат, а во-вторых, луч, выходящий из этой точки. Необходимо также
определить единичный отрезок и положительное направление отсчета угла между
лучом и отрезком, соединяющим начало координат с какой-либо точкой плоскости.

Положение точки на плоскости
задаётся двумя числами. Первое – расстояние от точки до начала координат, а
второе – угол между зафиксированным лучом и отрезком, соединяющим точку и
начало координат.

Обычно направление отсчета угла
выбирают против часовой стрелки. Стандартное обозначение координат точки в
полярной системе – (ρ,φ). Очевидно, ρ0.

Системы координат
в пространстве

Декартова система
координат в пространстве

Декартовы координаты в пространстве
задаются с помощью точки начала координат и трёх взаимно-перпендикулярных
направленных прямых. Прямые занумерованы, задан единичный отрезок. Положение
любой точки в пространстве однозначно определено тремя числами: первое число –
величина проекции точки на первую ось, второе – величина проекции на вторую
ось, третье – на третью.

Цилиндрическая
система координат в пространстве

Цилиндрическая система координат в
пространстве – “родственница” полярной системы координат на плоскости. Чтобы
получить цилиндрическую систему надо на плоскости ввести полярную систему
координат и добавить вертикальную координатную ось. То есть, координаты точки –
три числа: первые два – полярные координаты проекции нашей точки на плоскость,
третье – величина проекции точки на вертикальную ось.

Сферическая
система координат в пространстве

Сферическая система координат
вводится следующим образом: фиксируем плоскость, на ней — точку О начала
координат, а из точки О выпускаем луч, перпендикулярный плоскости, и луч,
лежащий в плоскости. Положение точки М задаётся тремя числами: первое –
расстояние от начала координат О до точки М; второе – угол между проекцией
отрезка ОМ на плоскость и лежащим в плоскости лучом; третье – угол между
перпендикулярным плоскости лучом и отрезком ОМ.

Введение системы
координат в заданиях С2

Метод координат — это довольно
лёгкий способ, но в настоящих задачах C2 никаких координат
и векторов нет. Поэтому их придется вводить: указать начало отсчета,
единичный отрезок и направление осей x, y и z.

Самое замечательное свойство этого
метода заключается в том, что не имеет никакого значения, как именно
вводить систему координат. Если все вычисления будут правильными,
то и ответ будет правильным.

Тем не менее, решив некоторые
задачи я пришла к выводу, как лучше ввести систему координат для самых часто
встречающихся в задаче C2 многогранников. С указанием конкретных
точек. Во всех случаях упор делается на минимизацию объема
вычислений.

Координаты куба

Это самый простой многогранник, все
двугранные углы которого равны 90°.

Система координат также вводится
очень просто:

1.  Начало координат —
в точке A;

2.  Чаще всего ребро куба
не указано, поэтому принимаем его за единичный отрезок;

3.  Ось x направляем
по ребру AB, y — по ребру AD, а ось z —
по ребру AA1.

Обратите внимание: ось z
направляется вверх! После двумерной системы координат это несколько непривычно,
но на самом деле очень логично.

Итак, теперь у каждой вершины
куба есть координаты. Соберем их в таблицу — отдельно
для нижней плоскости куба:

Точка	A	B	C	D
Координаты	(0; 0; 0)	(1; 0; 0)	(1; 1; 0)	(0; 1; 0)

И для верхней:

Точка	A1	B1	C1	D1
Координаты	(0; 0; 1)	(1; 0; 1)	(1; 1; 1)	(0; 1; 1)

Несложно заметить, что точки
верхней плоскости отличаются соответствующих точек нижней только
координатой z. Например, B = (1; 0; 0),
B1 = (1; 0; 1).

Координаты
трехгранной призмы

При правильном подходе
достаточно знать координаты только нижнего основания — верхнее будет
считаться автоматически.

В задачах C2 встречаются
исключительно правильные трехгранные призмы (прямые призмы, в основании
которых лежит правильный треугольник). Для них система координат вводится почти
так же, как и для куба.

Вводим систему координат:

1.  Начало координат —
в точке A;

2.  Сторону призмы принимаем
за единичный отрезок, если иное не указано в условии задачи;

3.  Ось x направляем
по ребру AB, z — по ребру AA1, а ось y
расположим так, чтобы плоскость OXY совпадала с плоскостью
основания ABC.

Получаем следующие координаты
точек:

Как видим, точки верхнего основания
призмы снова отличаются от соответствующих точек нижнего лишь
координатой z. Основная проблема — это точки C и C1.
У них есть иррациональные координаты, и для того чтобы довольно просто
решить задание С2 эти иррациональные координаты надо просто запомнить. Ну,
или понять, откуда они возникают.

Координаты
шестигранной призмы

Шестигранная призма — это
«клонированная» трехгранная. Можно понять, как это происходит, если взглянуть
на нижнее основание — обозначим его ABCDEF. Проведем
дополнительные построения: отрезки AD, BE и CF. Получилось шесть
треугольников, каждый из которых (например, треугольник ABO) является
основанием для трехгранной призмы.

Теперь введем собственно систему
координат. Начало координат — точку O — поместим в центр
симметрии шестиугольника ABCDEF. Ось x пойдет вдоль FC,
а ось y — через середины отрезков AB и DE. Получим
такую картинку:

Нужно обратить внимание на то, что
начало координат не совпадает с вершиной многогранника. На самом
деле, при решении настоящих задач выясняется, что это очень удобно, поскольку
позволяет значительно уменьшить объем вычислений.

Осталось добавить ось z.
По традиции, проводим ее перпендикулярно плоскости OXY
и направляем вертикально вверх. Получим итоговую картинку:

Запишем теперь координаты точек.
Предположим, что все ребра нашей правильной шестигранной призмы равны 1.
Итак, координаты нижнего основания:

Координаты верхнего основания
сдвинуты на единицу по оси z:

Координаты
четырехугольной пирамиды

Пирамида — это вообще очень
сложно, поэтому я разобрала только самый простой случай — правильную
четырехугольную пирамиду, все ребра которой равны единице.

Итак, правильная четырехугольная
пирамида. Обозначим ее SABCD, где S — вершина. Введем
систему координат: начало в точке A, единичный отрезок
AB = 1, ось x направим вдоль AB, ось y —
вдоль AD, а ось z — вверх, перпендикулярно
плоскости OXY. Для дальнейших вычислений нам потребуется высота SH —
вот и построим ее. Получим следующую картинку:

Теперь найдем координаты точек. Для
начала рассмотрим плоскость OXY. Здесь все просто: в основании лежит
квадрат, его координаты известны. Проблемы возникают с точкой S.
Поскольку SH — высота к плоскости OXY, точки S и H отличаются
лишь координатой z. Собственно, длина отрезка SH — это
и есть координата z для точки S, поскольку
H = (0,5; 0,5; 0).

Заметим, что треугольники ABC
и ASC равны по трем сторонам (AS = CS =
AB = CB = 1, а сторона AC — общая).
Следовательно, SH = BH. Но BH — половина диагонали квадрата ABCD,
т. е. BH = AB · sin 45°. Получаем координаты всех
точек:

Применение метода
координат при решении геометрических задач в заданиях С2 из ЕГЭ 2012 года.

Проанализировав различные
геометрические задачи, в том числе задания из ЕГЭ я сделала вывод, что при
решении геометрических задач координатным методом постоянно приходится
опираться на несколько совсем простых стандартных задач: определение расстояния
между точками, отыскание середины отрезка и др. Я смогла сделать вывод об
основах метода координат, которые необходимы для решения многих задач уровня С2
части 2 Егэ 2012 по математике. В таких задачах обычно требуется найти угол
между прямыми, или между плоскостями, или между прямой о плоскостью, а также
расстояние между аналогичными объектами. Для этого удобно использовать векторы
и метод координат

Для того, чтобы использовать метод
координат, надо хорошо знать формулы. Их три:

1.  Главная формула —
косинус угла φ между векторами a = (x1; y1; z1)
и b = (x2; y2; z2):

2.  Уравнение плоскости
в трехмерном пространстве:
Ax + By + Cz + D = 0, где A, B, C
и D — действительные числа, причем, если плоскость проходит через
начало координат, D = 0. А если не проходит,
то D = 1.

3.  Вектор, перпендикулярный
к плоскости Ax + By + Cz + D = 0,
имеет координаты: n = (A; B; C).

На первый взгляд, выглядит
угрожающе, но достаточно немного практики — и все будет работать
великолепно.

·  Задача. Найти
косинус угла между векторами a = (4; 3; 0)
и b = (0; 12; 5).

Решение.
Поскольку координаты векторов нам даны, подставляем их в первую формулу:

Ответ: 36/65

·  Задача.
Составить уравнение плоскости, проходящей через точки
M = (2; 0; 1), N = (0; 1; 1)
и K = (2; 1; 0), если известно, что она
не проходит через начало координат.

Решение. Общее
уравнение плоскости:
Ax + By + Cz + D = 0, но, поскольку
искомая плоскость не проходит через начало координат — точку
(0; 0; 0) — то положим D = 1. Поскольку эта
плоскость проходит через точки M, N и K, то координаты этих
точек должны обращать уравнение в верное числовое равенство.

Подставим вместо x, y и z
координаты точки M = (2; 0; 1). Имеем:
A · 2 + B · 0 + C · 1 +
1 = 0 ⇒ 2A + C + 1 = 0;
Аналогично, для точек N = (0; 1; 1)
и K = (2; 1; 0) получим уравнения:
A · 0 + B · 1 + C · 1 +
1 = 0 ⇒ B + C + 1 = 0;
A · 2 + B · 1 + C · 0 +
1 = 0 ⇒ 2A + B + 1 = 0; Итак,
у нас есть три уравнения и три неизвестных. Составим и решим
систему уравнений:

Получили, что уравнение плоскости
имеет вид:
− 0,25A − 0,5B − 0,5C + 1 = 0.

Ответ: − 0,25A − 0,5B − 0,5C + 1 = 0

·  Задача.
Плоскость задана уравнением
7x − 2y + 4z + 1 = 0. Найти координаты
вектора, перпендикулярного данной плоскости.

Решение.
Используя третью формулу, получаем n = (7; − 2; 4) — вот и
все!

Ответ: n =
(7; − 2; 4)

Вычисление
координат векторов

Зная координаты точек — начала
и конца вектора — можно вычислить координаты самого вектора.

Теорема. Чтобы
найти координаты вектора, надо из координат его конца вычесть координаты
начала.

Эта теорема одинаково работает
и на плоскости, и в пространстве. Выражение «вычесть
координаты» означает, что из координаты x одной точки вычитается
координата x другой, затем то же самое надо сделать
с координатами y и z. Вот несколько примеров:

·  Задача.
В пространстве расположены три точки, заданные своими координатами:
A = (1; 6; 3), B = (3; − 1; 7)
и C = (− 4; 3; − 2). Найти координаты
векторов AB, AC и BC.

Решение.
Рассмотрим вектор AB: его начало находится в точке A,
а конец — в точке B. Следовательно, чтобы найти его
координаты, надо из координат точки B вычесть координаты
точки A:
AB = (3 − 1; − 1 − 6;
7 − 3) = (2; − 7; 4).

Аналогично, начало вектора
AC — все та же точка A, зато конец — точка C. Поэтому
имеем:
AC = (− 4 − 1;
3 − 6; − 2 − 3) =
(− 5; − 3; − 5).

Наконец, чтобы найти координаты
вектора BC, надо из координат точки C вычесть координаты
точки B:
BC = (− 4 − 3;
3 − (− 1); − 2 − 7) = (− 7;
4; − 9).

Ответ:
AB = (2; − 7; 4); AC =
(− 5; − 3; − 5); BC = (− 7;
4; − 9)

Вычисление
направляющих векторов для прямых

Если вы внимательно прочитать
задачу C2, то с можно удивлением обнаружить, что никаких векторов
там нет. Там только прямые и плоскости.

Для начала разберемся
с прямыми. В задаче C2 прямые всегда задаются парой точек. Если
ввести систему координат и рассмотреть вектор с началом и концом
в этих точках, получим так
называемый направляющий вектор для прямой:

Зачем нужен этот вектор? Дело
в том, что угол между двумя прямыми — это угол между
их направляющими векторами. Таким образом, мы переходим от непонятных
прямых к конкретным векторам, координаты которых легко считаются. Задача.
В кубе ABCDA1B1C1D1 проведены прямые AC и BD1. Найдите
координаты направляющих векторов этих прямых.

Решение.
Поскольку длина ребер куба в условии не указана, положим
AB = 1. Введем систему координат с началом в точке A
и осями x, y, z, направленными вдоль прямых AB,
AD и AA1 соответственно. Единичный отрезок
равен AB = 1.

Теперь найдем координаты
направляющего вектора для прямой AC. Нам потребуются две точки:
A = (0; 0; 0) и C = (1; 1; 0).
Отсюда получаем координаты вектора AC = (1 − 0;
1 − 0; 0 − 0) = (1; 1; 0) — это
и есть направляющий вектор.

Теперь разберемся
с прямой BD1. На ней также есть две точки:
B = (1; 0; 0) и D1 = (0; 1; 1).
Получаем направляющий вектор BD1 = (0 − 1;
1 − 0; 1 − 0) = (− 1; 1; 1).

Ответ:
AC = (1; 1; 0);
BD1 = (− 1; 1; 1)

·  Задача.
В правильной треугольной призме ABCA1B1C1, все ребра которой
равны 1, проведены прямые AB1 и AC1. Найдите координаты
направляющих векторов этих прямых.

Решение. Введем
систему координат: начало в точке A, ось x совпадает с AB,
ось z совпадает с AA1, ось y образует с осью x
плоскость OXY, которая совпадает с плоскостью ABC.

Для начала разберемся
с прямой AB1. Тут все просто: у нас есть точки
A = (0; 0; 0) и B1 = (1; 0; 1).
Получаем направляющий вектор AB1 = (1 − 0;
0 − 0; 1 − 0) = (1; 0; 1).

Теперь найдем направляющий вектор
для AC1. Все то же самое — единственное отличие в том, что
у точки C1 иррациональные координаты. Итак,
A = (0; 0; 0), поэтому имеем:

Ответ:

AB1 = (1; 0; 1);

Вычисление
нормальных векторов для плоскостей

Нормаль — это вектор,
перпендикулярный любому вектору в данной плоскости. Всякая плоскость
задается в пространстве уравнением
Ax + By + Cz + D = 0,
где A, B, C и D — некоторые коэффициенты.
Не умаляя общности решения, можно полагать D = 1, если плоскость
не проходит через начало координат, или D = 0, если
все-таки проходит. В любом случае, координаты нормального вектора
к этой плоскости равны n = (A; B; C).

Итак, плоскость тоже можно успешно
заменить вектором — той самой нормалью. Всякая плоскость задается
в пространстве тремя точками. Задача.
В кубе ABCDA1B1C1D1 проведено сечение A1BC1. Найти
нормальный вектор для плоскости этого сечения, если начало координат
находится в точке A, а оси x, y и z совпадают
с ребрами AB, AD и AA1 соответственно.

Решение.
Поскольку плоскость не проходит через начало координат, ее уравнение
выглядит так: Ax + By + Cz + 1 = 0, т.
е. коэффициент D = 1. Поскольку эта плоскость проходит через
точки A1, B и C1, то координаты этих точек обращают
уравнение плоскости в верное числовое равенство.

Подставим вместо
x, y и z координаты
точки A1 = (0; 0; 1). Имеем:
A · 0 + B · 0 + C · 1 + 1 = 0 ⇒
C + 1 = 0 ⇒ C = − 1;

Аналогично, для точек B = (1; 0; 0)
и C1 = (1; 1; 1) получим уравнения:
A · 1 + B · 0 + C · 0 + 1 = 0 ⇒
A + 1 = 0 ⇒ A = − 1;
A · 1 + B · 1 + C · 1 + 1 = 0 ⇒
A + B + C + 1 = 0;

Но коэффициенты
A = − 1 и C = − 1 нам уже известны, поэтому
остается найти коэффициент B:
B = − 1 − A − B = − 1 + 1 + 1 = 1.

Получаем уравнение
плоскости: − A + B − C + 1 = 0,
Следовательно, координаты нормального вектора равны n = (− 1;
1; − 1).

Ответ:
n = (− 1; 1; − 1)

·  Задача.
В кубе ABCDA1B1C1D1 проведено сечение AA1C1C. Найти
нормальный вектор для плоскости этого сечения, если начало координат находится
в точке A, а оси x, y и z совпадают
с ребрами AB, AD и AA1 соответственно.

Решение.
В данном случае плоскость проходит через начало координат, поэтому
коэффициент D = 0, а уравнение плоскости выглядит так:
Ax + By + Cz = 0. Поскольку плоскость проходит
через точки A1 и C, координаты этих точек обращают уравнение
плоскости в верное числовое равенство.

Подставим
вместо x, y и z координаты
точки A1 = (0; 0; 1). Имеем:
A · 0 + B · 0 + C · 1 = 0 ⇒
C = 0;

Аналогично, для
точки C = (1; 1; 0) получим уравнение:
A · 1 + B · 1 + C · 0 = 0 ⇒
A + B = 0 ⇒ A = − B;

Положим B = 1. Тогда
A = − B = − 1, и уравнение всей плоскости
имеет вид: − A + B = 0, Следовательно, координаты
нормального вектора равны n = (− 1; 1; 0).

Ответ:
n = (− 1; 1; 0)

Координаты
середины отрезка

Очень часто в задаче C2
требуется работать с точками, которые делят отрезок пополам. Координаты
таких точек легко считаются, если известны координаты концов отрезка.

Итак, пусть отрезок задан своими
концами — точками A = (xa; ya; za)
и B = (xb; yb; zb). Тогда координаты середины
отрезка — обозначим ее точкой H — можно найти
по формуле:

Другими словами, координаты
середины отрезка — это среднее арифметическое координат его концов.

·  Задача.
Единичный куб ABCDA1B1C1D1 помещен в систему координат так, что
оси x, y и z направлены вдоль
ребер AB, AD и AA1 соответственно, а начало
координат совпадает с точкой A. Точка K — середина
ребра A1B1. Найдите координаты этой точки.

Решение.
Поскольку точка K — середина отрезка A1B1, ее координаты
равных среднему арифметическому координат концов. Запишем координаты концов:
A1 = (0; 0; 1) и B1 = (1; 0; 1).
Теперь найдем координаты точки K:

Ответ:
K = (0,5; 0; 1)

·  Задача. Единичный
куб ABCDA1B1C1D1 помещен в систему координат так, что
оси x, y и z направлены вдоль
ребер AB, AD и AA1 соответственно, а начало
координат совпадает с точкой A. Найдите координаты точки L,
в которой пересекаются диагонали квадрата A1B1C1D1.

Решение.
Из курса планиметрии известно, что точка пересечения диагоналей квадрата
равноудалена от всех его вершин. В частности, A1L = C1L, т.
е. точка L — это середина отрезка A1C1.
Но A1 = (0; 0; 1), C1 = (1; 1; 1),
поэтому имеем:

Ответ:
L = (0,5; 0,5; 1)

Недостатки метода
координат

Метод координат — это,
конечно, хороший инструмент, однако у него есть недостаток. Даже два:

1.  Иногда приходится много
считать. И чем сложнее многогранник — тем больше объем
вычислений. Это становится особенно заметно, когда в дело вступают
иррациональные координаты и плоскости;

2.  К сожалению,
в школе этой теме уделяется недостаточно внимания. Проходят что-то
в 10 классе — и благополучно забывают. Из-за этого
возникают проблемы с оформлением готового решения.

Однако нет ничего невозможного.
Если освоить метод координат, научиться вычислять углы между всевозможными
комбинациями прямых и плоскостей, то научиться оформлять свои
выкладки — дело пяти минут. А может быть и двух — если эти
выкладки немного оптимизировать.

Вывод

Проанализировав задания С2 и их
решения, можно сделать вывод что метод координат является наиболее удобным для
решения. Но у этого метода есть некоторые недостатки: приходится делать
громоздкие вычисления и могут возникнуть проблемы с оформлением. Не смотря на
это, метод координат показался мне намного удобнее других методов. Так же
результатом моего анализа заданий стало то, что я смогла сделать вывод о том,
какие алгоритмы нужно чаще всего использовать при решении задач

Список
использованной литературы

1. Габович И., Горнштейн П.
Вооружившись методом координат// Квант. – 1978. – №11. – с. 42 – 47.

2. Гельфанд Е. Г., Нириллов
координат. – М.: Наука, 1973.

3. Готман З. А., Решение
геометрических задач аналитическим методом. – М.: Просвещение, 1979.

4. Ефимов курс аналитической
геометрии: Учебн. пособие. — М.: ФИЗМАТЛИТ, 2005.4. , Яглом . Векторы. – М.:
Просвещение, 1964. – 303с.

5. , Корнева стереометрических
задач: Методические рекомендации. – Бийск: РИО БПГУ им. , 2005. – 60с.

6. Геометрия 10-11 кл.: учебник для
естественно-научного профиля. Под ред. – М.: Просвещение, 2003.

7. Глаголев, геометрия:
стереометрия для 10-11 кл. ср. шк. в 2ч. – М.: Просвещение, 1954. – ч. 2.

8. , , Мордкович по элементарной
математике:

Метод координат в пространстве

30 мая 2011

Для того, чтобы использовать метод координат, надо хорошо
знать формулы. Их три:

1.      Главная формула — косинус угла φ между векторами a = (x₁; y₁;
z₁) и b = (x₂; y₂; z₂):

1. Уравнение
   плоскости в трехмерном пространстве: Ax + By + Cz + D = 0, где A, B, C и D
   — действительные числа, причем, если плоскость проходит через начало
   координат, D = 0. А если не проходит, то D = 1.
2. Вектор,
   перпендикулярный к плоскости Ax + By + Cz + D = 0, имеет координаты: n =
   (A; B; C).

На первый взгляд, выглядит угрожающе, но достаточно немного
практики — и все будет работать великолепно.

Задача. Найти косинус угла между векторами a = (4; 3; 0) и b =
(0; 12; 5).

Решение. Поскольку координаты векторов нам даны, подставляем
их в первую формулу:

Задача. Составить уравнение плоскости, проходящей через точки
M = (2; 0; 1), N = (0; 1; 1) и K = (2; 1; 0), если известно, что она не
проходит через начало координат.

Решение. Общее уравнение плоскости: Ax + By + Cz + D = 0, но,
поскольку искомая плоскость не проходит через начало координат — точку (0; 0;
0) — то положим D = 1. Поскольку эта плоскость проходит через точки M, N и K,
то координаты этих точек должны обращать уравнение в верное числовое равенство.

Подставим вместо x, y и z координаты точки M = (2; 0; 1).
Имеем:
A · 2 + B · 0 + C · 1 + 1 = 0 ⇒
2A + C + 1 = 0;

Аналогично, для точек N = (0; 1; 1) и K = (2; 1; 0) получим
уравнения:
A · 0 + B · 1 + C · 1 + 1 = 0 ⇒ B + C + 1 = 0;
A · 2 + B · 1 + C · 0 + 1 = 0 ⇒ 2A + B + 1 = 0;

Итак, у нас есть три уравнения и три неизвестных. Составим и
решим систему уравнений:

Получили, что уравнение плоскости имеет вид: − 0,25x − 0,5y −
0,5z + 1 = 0.

Задача. Плоскость задана уравнением 7x − 2y + 4z + 1 = 0.
Найти координаты вектора, перпендикулярного данной плоскости.

Решение. Используя третью формулу, получаем n = (7; − 2; 4) —
вот и все!

Вычисление координат векторов

А что, если в задаче нет векторов — есть только точки, лежащие
на прямых, и требуется вычислить угол между этими прямыми? Все просто: зная
координаты точек — начала и конца вектора — можно вычислить координаты самого
вектора.

Чтобы найти координаты вектора, надо из координат его конца
вычесть координаты начала.

Эта теорема одинаково работает и на плоскости, и в
пространстве. Выражение «вычесть координаты» означает, что из координаты x
одной точки вычитается координата x другой, затем то же самое надо сделать с
координатами y и z. Вот несколько примеров:

Задача. В пространстве расположены три точки, заданные своими
координатами: A = (1; 6; 3), B = (3; − 1; 7) и C = (− 4; 3; − 2). Найти
координаты векторов AB, AC и BC.

Рассмотрим вектор AB: его начало находится в точке A, а конец
— в точке B. Следовательно, чтобы найти его координаты, надо из координат точки
B вычесть координаты точки A:
AB = (3 − 1; − 1 − 6; 7 − 3) = (2; − 7; 4).

Аналогично, начало вектора AC — все та же точка A, зато конец
— точка C. Поэтому имеем:
AC = (− 4 − 1; 3 − 6; − 2 − 3) = (− 5; − 3; − 5).

Наконец, чтобы найти координаты вектора BC, надо из координат
точки C вычесть координаты точки B:
BC = (− 4 − 3; 3 − (− 1); − 2 − 7) = (− 7; 4; − 9).

Ответ: AB = (2; − 7; 4); AC = (− 5; − 3; − 5); BC = (− 7; 4; −
9)

Обратите внимание на вычисление координат последнего вектора
BC: очень многие ошибаются, когда работают с отрицательными числами. Это
касается переменной y: у точки B координата y = − 1, а у точки C y = 3.
Получаем именно 3 − (− 1) = 4, а не 3 − 1, как многие считают. Не допускайте
таких глупых ошибок!

Вычисление направляющих векторов для прямых

Если вы внимательно прочитаете задачу C2, то с удивлением
обнаружите, что никаких векторов там нет. Там только прямые да плоскости.

Для начала разберемся с прямыми. Здесь все просто: на любой прямой
найдутся хотя бы две различные точки и, наоборот, любые две различные точки
задают единственную прямую…

Кто-нибудь понял, что написано в предыдущем абзаце? Я и сам не
понял, поэтому объясню проще: в задаче C2 прямые всегда задаются парой точек.
Если ввести систему координат и рассмотреть вектор с началом и концом в этих
точках, получим так называемый направляющий вектор для прямой:

Зачем нужен этот вектор? Дело в том, что угол между двумя прямыми — это угол между их
направляющими векторами. Таким образом, мы переходим от непонятных прямых к
конкретным векторам, координаты которых легко считаются. Насколько легко?
Взгляните на примеры:

Задача. В кубе ABCDA₁B₁C₁D₁
проведены прямые AC и BD₁. Найдите координаты направляющих векторов
этих прямых.

Поскольку длина ребер куба в условии не указана, положим AB =
1. Введем систему координат с началом в точке A и осями x, y, z, направленными
вдоль прямых AB, AD и AA₁ соответственно. Единичный отрезок равен AB
= 1.

Теперь найдем координаты направляющего вектора для прямой AC.
Нам потребуются две точки: A = (0; 0; 0) и C = (1; 1; 0). Отсюда получаем
координаты вектора AC = (1 − 0; 1 − 0; 0 − 0) = (1; 1; 0) — это и есть
направляющий вектор.

Теперь разберемся с прямой BD₁. На ней также есть
две точки: B = (1; 0; 0) и D₁ = (0; 1; 1). Получаем направляющий
вектор BD₁ = (0 − 1; 1 − 0; 1 − 0) = (− 1; 1; 1).

Ответ: AC = (1; 1; 0); BD₁ = (− 1; 1; 1)

Задача. В правильной треугольной призме ABCA₁B₁C₁,
все ребра которой равны 1, проведены прямые AB₁ и AC₁.
Найдите координаты направляющих векторов этих прямых.

Введем систему координат: начало в точке A, ось x совпадает с
AB, ось z совпадает с AA₁, ось y образует с осью x плоскость OXY,
которая совпадает с плоскостью ABC.

Для начала разберемся с прямой AB₁. Тут все просто:
у нас есть точки A = (0; 0; 0) и B₁ = (1; 0; 1). Получаем
направляющий вектор AB₁ = (1 − 0; 0 − 0; 1 − 0) = (1; 0; 1).

Теперь найдем направляющий вектор для AC₁. Все то
же самое — единственное отличие в том, что у точки C₁ иррациональные
координаты. Итак, A = (0; 0; 0), поэтому имеем:

Ответ: AB₁ = (1; 0; 1);

Небольшое, но очень важное замечание насчет последнего
примера. Если начало вектора совпадает с началом координат, вычисления резко
упрощаются: координаты вектора просто равны координатам конца. К сожалению, это
верно лишь для векторов. Например, при работе с плоскостями присутствие на них
начала координат только усложняет выкладки.

Вычисление нормальных векторов для плоскостей

Нормальные векторы — это не те векторы, у которых все в
порядке, или которые чувствуют себя хорошо. По определению, нормальный вектор
(нормаль) к плоскости — это вектор, перпендикулярный данной плоскости.

Другими словами, нормаль — это вектор, перпендикулярный любому вектору в данной плоскости.
Наверняка вы встречали такое определение — правда, вместо векторов речь шла о
прямых. Однако чуть выше было показано, что в задаче C2 можно оперировать любым
удобным объектом — хоть прямой, хоть вектором.

Еще раз напомню, что всякая плоскость задается в пространстве
уравнением Ax + By + Cz + D = 0, где A, B, C и D — некоторые коэффициенты. Не
умаляя общности решения, можно полагать D = 1, если плоскость не проходит через
начало координат, или D = 0, если все-таки проходит. В любом случае, координаты
нормального вектора к этой плоскости равны n = (A; B; C).

Итак, плоскость тоже можно успешно заменить вектором — той
самой нормалью. Всякая плоскость задается в пространстве тремя точками. Как
найти уравнение плоскости (а следовательно — и нормали), мы уже обсуждали в
самом начале статьи. Однако этот процесс у многих вызывает проблемы, поэтому
приведу еще парочку примеров:

Задача. В кубе ABCDA₁B₁C₁D₁
проведено сечение A₁BC₁. Найти нормальный вектор для
плоскости этого сечения, если начало координат находится в точке A, а оси x, y
и z совпадают с ребрами AB, AD и AA₁ соответственно.

Поскольку плоскость не проходит через начало координат, ее
уравнение выглядит так: Ax + By + Cz + 1 = 0, т.е. коэффициент D = 1. Поскольку
эта плоскость проходит через точки A₁, B и C₁, то
координаты этих точек обращают уравнение плоскости в верное числовое равенство.

Подставим вместо x, y и z координаты точки A₁ = (0;
0; 1). Имеем:
A · 0 + B · 0 + C · 1 + 1 = 0 ⇒
C + 1 = 0 ⇒ C = − 1;

Аналогично, для точек B = (1; 0; 0) и C₁ = (1; 1;
1) получим уравнения:
A · 1 + B · 0 + C · 0 + 1 = 0 ⇒ A + 1 = 0 ⇒ A = − 1;
A · 1 + B · 1 + C · 1 + 1 = 0 ⇒ A + B + C + 1 = 0;

Но коэффициенты A = − 1 и C = − 1 нам уже известны, поэтому
остается найти коэффициент B:
B = − 1 − A − C = − 1 + 1 + 1 = 1.

Получаем уравнение плоскости: − A + B − C + 1 = 0,
Следовательно, координаты нормального вектора равны n = (− 1; 1; − 1).

Задача. В кубе ABCDA₁B₁C₁D₁
проведено сечение AA₁C₁C. Найти нормальный вектор для
плоскости этого сечения, если начало координат находится в точке A, а оси x, y
и z совпадают с ребрами AB, AD и AA₁ соответственно.

В данном случае плоскость проходит через начало координат,
поэтому коэффициент D = 0, а уравнение плоскости выглядит так: Ax + By + Cz =
0. Поскольку плоскость проходит через точки A₁ и C, координаты этих
точек обращают уравнение плоскости в верное числовое равенство.

Подставим вместо x, y и z координаты точки A₁ = (0;
0; 1). Имеем:
A · 0 + B · 0 + C · 1 = 0 ⇒ C = 0;

Аналогично, для точки C = (1; 1; 0) получим уравнение:
A · 1 + B · 1 + C · 0 = 0 ⇒ A + B = 0 ⇒ A = − B;

Положим B = 1. Тогда A = − B = − 1, и уравнение всей плоскости
имеет вид: − A + B = 0, Следовательно, координаты нормального вектора равны n =
(− 1; 1; 0).

Вообще говоря, в приведенных задачах надо составлять систему
уравнений и решать ее. Получится три уравнения и три переменных, но во втором
случае одна из них будет свободной, т.е. принимать произвольные значения.
Именно поэтому мы вправе положить B = 1 — без ущерба для общности решения и
правильности ответа.

Координаты середины отрезка

Очень часто в задаче C2 требуется работать с точками, которые
делят отрезок пополам. Координаты таких точек легко считаются, если известны
координаты концов отрезка.

Итак, пусть отрезок задан своими концами — точками A = (x_a;
y_a; z_a) и B = (x_b; y_b; z_b).
Тогда координаты середины отрезка — обозначим ее точкой H — можно найти по
формуле:

Другими словами, координаты середины отрезка — это среднее
арифметическое координат его концов.

Задача. Единичный куб ABCDA₁B₁C₁D₁
помещен в систему координат так, что оси x, y и z направлены вдоль ребер AB, AD
и AA₁ соответственно, а начало координат совпадает с точкой A. Точка
K — середина ребра A₁B₁. Найдите координаты этой точки.

Поскольку точка K — середина отрезка A₁B₁,
ее координаты равных среднему арифметическому координат концов. Запишем
координаты концов: A₁ = (0; 0; 1) и B₁ = (1; 0; 1).
Теперь найдем координаты точки K:

Задача. Единичный куб ABCDA₁B₁C₁D₁
помещен в систему координат так, что оси x, y и z направлены вдоль ребер AB, AD
и AA₁ соответственно, а начало координат совпадает с точкой A.
Найдите координаты точки L, в которой пересекаются диагонали квадрата A₁B₁C₁D₁.

Из курса планиметрии известно, что точка пересечения
диагоналей квадрата равноудалена от всех его вершин. В частности, A₁L
= C₁L, т.е. точка L — это середина отрезка A₁C₁.
Но A₁ = (0; 0; 1), C₁ = (1; 1; 1), поэтому имеем:

Ответ: L = (0,5; 0,5; 1)

Смотрите также:

1. Введение системы
   координат
2. Четырехугольная
   пирамида в задаче C2
3. Схема
   Бернулли. Примеры решения задач
4. Теорема Виета
   
5. Пробный ЕГЭ по
   математике 2015: 3 вариант
6. Проценты
   в задачах на наибольшее-наименьшее значение используем пропорции

Геометрия, 11 класс

Урок № 3. Координатный метод решения задач

Перечень вопросов, рассматриваемых в теме:

• специфика и преимущества решения задач в пространстве координатным методом;
• типы задач, решаемые координатным методом;
• этап решения задачи координатным методом;
• решение несложных задач методом координат.

Глоссарий по теме

Уравнение вида задает в пространстве плоскость α.

При этом вектор – это вектор, перпендикулярный плоскости α. Его называют вектор нормали, или нормальный вектор, или нормаль. Очевидно, что нормалью является любой вектор, коллинеарный вектору .

Вектор и любой коллинеарный ему вектор называются направляющим векторами прямой и прямой соответственно.

Основная литература:

Шарыгин И.Ф. Геометрия. 10–11 кл. : учеб. для общеобразоват. Учреждений – М.: Дрофа, 2009. – 235, : ил., ISBN 978–5–358–05346–5, сс. 163-170.

Потоскуев Е.В., Звавич Л. И. Геометрия. 11кл.: учеб. Для классов с углубл. И профильным изучением математики общеобразоват. Учреждений – М.: Дрофа, 2004. – 368 с.: ил., ISBN 5–7107–8310–2, сс. 353-260.

Открытые электронные ресурсы:

Решу ЕГЭ образовательный портал для подготовки к экзаменам https://ege.sdamgia.ru/

Теоретический материал для самостоятельного изучения

Работа по теме урока. Объяснение новой темы

Мы рассмотрели несложную задачу на применение метода координат в пространстве.

Векторы , угол между которыми мы искали, называются направляющими векторами прямой и прямой соответственно.

Рассмотрим этот метод более подробно.

Суть метода координат на плоскости и в пространстве заключается в следующем.

1. Ввести систему координат удобным образом (исходя их свойств заданной фигуры)
2. Записать условие задачи в координатах, определив во введенной системе координат координаты точек и/или векторов
3. Используя алгебраические преобразования, решить задачу
4. Интерпретировать полученный результат в соответствии с условием данной задачи

В рассмотренном нами примере, поскольку был дан куб, мы могли ввести систему координат с центром в любой его вершине.

В координатах удобно решать задачи, связанные с поиском расстояний и углов. Но для того чтобы его использовать, нужно знать некоторые формулы:

1. Угол между прямыми
2. Угол между прямой и плоскостью
3. Угол между плоскостями
4. Расстояние от точки до плоскости
5. Расстояние от точки до прямой в пространстве
6. Расстояние между скрещивающимися прямыми

Расстояние между параллельными плоскостями определяется как расстояние от точки, лежащей в одной плоскости, до другой плоскости.

Мы рассмотрим только первые четыре формулы.

Введем их.

Угол между прямыми

Если прямая задана двумя точками A и B, то известен направляющий вектор этой прямой с координатами {}. Пусть вторая прямая имеет направляющий вектор . Тогда угол между векторами вычисляется по формуле:

.

Дальше ищется арккосинус от найденного числа. Заметим, что если косинус получился отрицательным, то это значит, что угол между векторами тупой. Поэтому мы берем модуль получившегося числа.

Фактически мы уже рассмотрели пример вычисления угла между прямыми в пространстве.

Угол между прямой и плоскостью

Сначала рассмотрим уравнение плоскости, проходящей через три точки.

.

Вам известно, что в пространстве плоскость задается уравнением, аналогичным тому, которое на плоскости задает прямую.

Если линейное уравнение вида на плоскости задает прямую l, то уравнение вида задает в пространстве плоскость α. При этом вектор – это вектор, перпендикулярный плоскости α. Его называют вектор нормали, или нормальный вектор, или нормаль.

Вам известно, что три точки в пространстве определяют единственную плоскость. Поэтому, если заданы три точки, то мы можем найти уравнение плоскости

Мы можем подставить координаты заданных точек в уравнение плоскости и решить систему из трех уравнений с тремя переменными:

В этой системе четыре неизвестных, однако, мы можем избавиться от одной, если разделим все уравнения на D:

.

Для изучения данного способа в 11 классе на базовом уровне введение понятий матрица, определитель матрицы не желателен, данные понятия не входят в базовый курс изучения геометрии.

Иногда эта система оказывается несложной. Но иногда бывает трудно ее решить, и тогда можно использовать следующую формулу:

Обозначение |M| означает определитель матрицы М.

В нашем случае матрица представляет собой таблицу 3х3 элемента. И определитель |M| вычисляется следующим образом:

.

Таким образом, уравнение плоскости будет записано так:

Пример 1:

Написать уравнение плоскости, проходящей через точки K(1; -2; 3), L (0; 1; 1), M (1; 0; 1).

Составим систему.

.

Решая ее, получим значения А, В и С: . То есть уравнение плоскости имеет вид:

.

Ответ: .

Теперь запишем формулу угла между прямой и плоскостью.

Пусть дано уравнение плоскости: и известен – направляющий вектор прямой.

Тогда – синус угла между прямой и плоскостью.

Пример 2:

Найдем угол между прямой и плоскостью. В качестве плоскости возьмем ту, уравнение которой мы только что написали:

Прямая проходит через точки Т(2; -1; 4) и Р(3; 2; 2).

Направляющий вектор прямой: .

Найдем синус угла между прямой и плоскостью:

.

Угол между прямой и плоскостью .

Ответ: .

Угол между плоскостями

Пусть:

уравнение первой плоскости:

уравнение второй плоскости:

Тогда – косинус угла между этими плоскостями.

Пример 3:

Найдем угол между плоскостями:

и .

Найдем косинус угла между плоскостями:

.

Угол между плоскостями:

Ответ:

Расстояние от точки до плоскости

Пусть координаты точки: , уравнение плоскости: .

Тогда Расстояние от точки до плоскости вычисляется по формуле: .

Пример 4.

Найдем расстояние от точки М(4; 3; 4) до плоскости .

.

Теперь рассмотрим решение задачи координатным методом с использованием рассмотренных формул.

Пример 5.

АВС…D1 – куб с ребром 4. Найти расстояние от точки А до плоскости ЕКС (Е – середина D1C1, K – середина C1B1)

Введем систему координат с началом в вершине А так, как показано на рисунке:

Интересующие нас точки будут иметь координаты:

A(0; 0; 0), C(4; 4; 0), E(4; 2; 4), K(2; 4; 4).

Напишем уравнение плоскости ЕКС:

.

Решая ее, получим значения А, В, С и D: .

Уравнение плоскости имеет вид:

Теперь найдем расстояние от точки А до плоскости ЕКС: .

Ответ: .

Рассмотрим задачу (№14 из варианта ЕГЭ).

В кубе ABC…D₁ все рёбра равны 4. На его ребре BB₁ отмечена точка K так, что KB = 3. Через точки K и C₁ построена плоскость α, параллельная прямой BD₁.

а) Докажите, что A₁P : PB₁ = 2 : 1, где P — точка пересечения плоскости α с ребром A₁B₁.

б) Найдите угол наклона плоскости α к плоскости грани BB₁C₁C.

Решение:

Переформулируем первый пункт этой задачи таким образом:

Проведем плоскость через точки Р, K и C₁ и докажем, что она параллельна прямой BD₁.

Введем систему координат так, как показано на рисунке:

Найдем координаты точек :

Р(; 0; 4), К(4; 0; 3),(4; 4; 4).

Напишем уравнение плоскости :

;

Решая ее, получим значения А, В, С и D: .

– уравнение плоскости

Теперь докажем, что плоскость параллельна прямой BD₁.

Найдем угол между прямой BD₁ и плоскостью .

Точки В и D₁ имеют координаты: В (4; 0; 0), D₁ (0; 4; 4).

Направляющий вектор прямой BD₁ – это вектор .

Он имеет координаты .

Теперь найдем синус угла между вектором и плоскостью .

.

В этом случае нам не нужно считать знаменатель дроби. Так как числитель получился равен 0, то дробь равна 0, то есть синус угла между плоскостью и прямой равен 0, значит, плоскости параллельны или совпадают. Но, так как точка В, например, в плоскости, очевидно, не лежит, то плоскости параллельны.

Это значит, что плоскость, параллельная прямой BD₁ и проходящая через точки действительно пересекает ребро A₁B₁в точке Р так, что A₁P : PB₁ = 2 : 1. Что и требовалось доказать.

Теперь рассмотри второй пункт задачи. Уравнение плоскости у нас есть. Плоскость BB₁C₁ параллельна координатной плоскости YOZ и проходит через точку

В(4; 0; 0). Поэтому она имеет уравнение .

То есть ее коэффициенты .

Найдем угол между плоскостями, используя формулу

Ответ: .