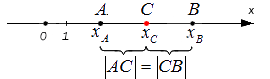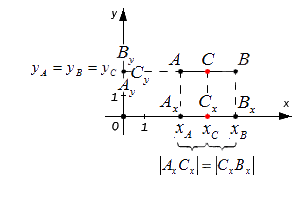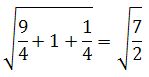Как найти координаты середины вектора треугольника

Примечание: дробные числа записывайте
через точку, а не запятую.

Округлять до -го знака после запятой.

Нахождение координат середины отрезка: примеры, решения

В статье ниже будут освещены вопросы нахождения координат середины отрезка при наличии в качестве исходных данных координат его крайних точек. Но, прежде чем приступить к изучению вопроса, введем ряд определений.

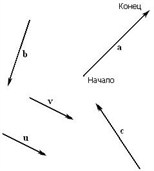
Отрезок – прямая линия, соединяющая две произвольные точки, называемые концами отрезка. В качестве примера пусть это будут точки A и B и соответственно отрезок A B .

Если отрезок A B продолжить в обе стороны от точек A и B , мы получим прямую A B . Тогда отрезок A B – часть полученной прямой, ограниченный точками A и B . Отрезок A B объединяет точки A и B , являющиеся его концами, а также множество точек, лежащих между. Если, к примеру, взять любую произвольную точку K , лежащую между точками A и B , можно сказать, что точка K лежит на отрезке A B .

Длина отрезка – расстояние между концами отрезка при заданном масштабе (отрезке единичной длины). Длину отрезка A B обозначим следующим образом: A B .

Середина отрезка – точка, лежащая на отрезке и равноудаленная от его концов. Если середину отрезка A B обозначить точкой C , то верным будет равенство: A C = C B

И далее мы рассмотрим, как же определять координаты середины отрезка (точки C ) при заданных координатах концов отрезка ( A и B ), расположенных на координатной прямой или в прямоугольной системе координат.

Середина отрезка на координатной прямой

Исходные данные: координатная прямая O x и несовпадающие точки на ней: A и B . Этим точкам соответствуют действительные числа x A и x B . Точка C – середина отрезка A B : необходимо определить координату x C .

Поскольку точка C является серединой отрезка А В , верным будет являться равенство: | А С | = | С В | . Расстояние между точками определяется модулем разницы их координат, т.е.

| А С | = | С В | ⇔ x C – x A = x B – x C

Тогда возможно два равенства: x C – x A = x B – x C и x C – x A = – ( x B – x C )

Из первого равенства выведем формулу для координаты точки C : x C = x A + x B 2 (полусумма координат концов отрезка).

Из второго равенста получим: x A = x B , что невозможно, т.к. в исходных данных – несовпадающие точки. Таким образом, формула для определения координат середины отрезка A B с концами A ( x A ) и B ( x B ):

Полученная формула будет основой для определения координат середины отрезка на плоскости или в пространстве.

Середина отрезка на плоскости

Исходные данные: прямоугольная система координат на плоскости О x y , две произвольные несовпадающие точки с заданными координатами A x A , y A и B x B , y B . Точка C – середина отрезка A B . Необходимо определить координаты x C и y C для точки C .

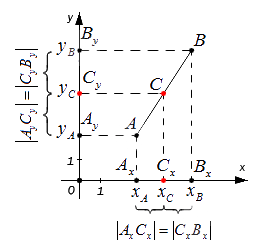
Возьмем для анализа случай, когда точки A и B не совпадают и не лежат на одной координатной прямой или прямой, перпендикулярной одной из осей. A x , A y ; B x , B y и C x , C y – проекции точек A , B и C на оси координат (прямые О х и О y ).

Согласно построению прямые A A x , B B x , C C x параллельны; прямые также параллельны между собой. Совокупно с этим по теореме Фалеса из равенства А С = С В следуют равенства: А x С x = С x В x и А y С y = С y В y , и они в свою очередь свидетельствуют о том, что точка С x – середина отрезка А x В x , а С y – середина отрезка А y В y . И тогда, опираясь на полученную ранее формулу, получим:

x C = x A + x B 2 и y C = y A + y B 2

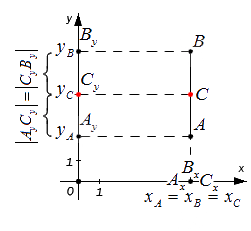
Этими же формулами можно воспользоваться в случае, когда точки A и B лежат на одной координатной прямой или прямой, перпендикулярной одной из осей. Проводить детальный анализ этого случая не будем, рассмотрим его лишь графически:

Резюмируя все выше сказанное, координаты середины отрезка A B на плоскости с координатами концов A ( x A , y A ) и B ( x B , y B ) определяются как:

( x A + x B 2 , y A + y B 2 )

Середина отрезка в пространстве

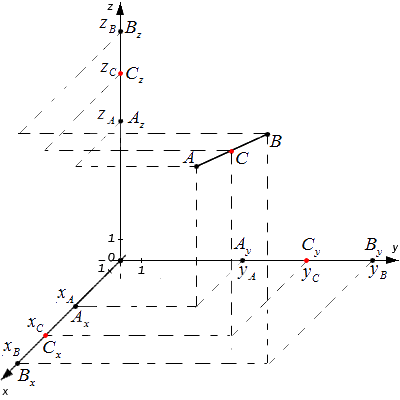
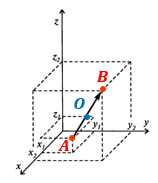
Исходные данные: система координат О x y z и две произвольные точки с заданными координатами A ( x A , y A , z A ) и B ( x B , y B , z B ) . Необходимо определить координаты точки C , являющейся серединой отрезка A B .

A x , A y , A z ; B x , B y , B z и C x , C y , C z – проекции всех заданных точек на оси системы координат.

Согласно теореме Фалеса верны равенства: A x C x = C x B x , A y C y = C y B y , A z C z = C z B z

Следовательно, точки C x , C y , C z являются серединами отрезков A x B x , A y B y , A z B z соответственно. Тогда, для определения координат середины отрезка в пространстве верны формулы:

x C = x A + x B 2 , y c = y A + y B 2 , z c = z A + Z B 2

Полученные формулы применимы также в случаях, когда точки A и B лежат на одной из координатных прямых; на прямой, перпендикулярной одной из осей; в одной координатной плоскости или плоскости, перпендикулярной одной из координатных плоскостей.

Определение координат середины отрезка через координаты радиус-векторов его концов

Формулу для нахождения координат середины отрезка также можно вывести согласно алгебраическому толкованию векторов.

Исходные данные: прямоугольная декартова система координат O x y , точки с заданными координатами A ( x A , y A ) и B ( x B , x B ) . Точка C – середина отрезка A B .

Согласно геометрическому определению действий над векторами верным будет равенство: O C → = 1 2 · O A → + O B → . Точка C в данном случае – точка пересечения диагоналей параллелограмма, построенного на основе векторов O A → и O B → , т.е. точка середины диагоналей.Координаты радиус-вектора точки равны координатам точки, тогда верны равенства: O A → = ( x A , y A ) , O B → = ( x B , y B ) . Выполним некоторые операции над векторами в координатах и получим:

O C → = 1 2 · O A → + O B → = x A + x B 2 , y A + y B 2

Следовательно, точка C имеет координаты:

x A + x B 2 , y A + y B 2

По аналогии определяется формула для нахождения координат середины отрезка в пространстве:

C ( x A + x B 2 , y A + y B 2 , z A + z B 2 )

Примеры решения задач на нахождение координат середины отрезка

Среди задач, предполагающих использование полученных выше формул, встречаются, как и те, в которых напрямую стоит вопрос рассчитать координаты середины отрезка, так и такие, что предполагают приведение заданных условий к этому вопросу: зачастую используется термин «медиана», ставится целью нахождение координат одного из концов отрезка, а также распространены задачи на симметрию, решение которых в общем также не должно вызывать затруднений после изучения настоящей темы. Рассмотрим характерные примеры.

Исходные данные: на плоскости – точки с заданными координатами А ( – 7 , 3 ) и В ( 2 , 4 ) . Необходимо найти координаты середины отрезка А В .

Решение

Обозначим середину отрезка A B точкой C . Координаты ее буду определяться как полусумма координат концов отрезка, т.е. точек A и B .

x C = x A + x B 2 = – 7 + 2 2 = – 5 2 y C = y A + y B 2 = 3 + 4 2 = 7 2

Ответ: координаты середины отрезка А В – 5 2 , 7 2 .

Исходные данные: известны координаты треугольника А В С : А ( – 1 , 0 ) , В ( 3 , 2 ) , С ( 9 , – 8 ) . Необходимо найти длину медианы А М .

Решение

1. По условию задачи A M – медиана, а значит M является точкой середины отрезка B C . В первую очередь найдем координаты середины отрезка B C , т.е. точки M :

x M = x B + x C 2 = 3 + 9 2 = 6 y M = y B + y C 2 = 2 + ( – 8 ) 2 = – 3

1. Поскольку теперь нам известны координаты обоих концов медианы (точки A и М ), можем воспользоваться формулой для определения расстояния между точками и посчитать длину медианы А М :

A M = ( 6 – ( – 1 ) ) 2 + ( – 3 – 0 ) 2 = 58

Ответ: 58

Исходные данные: в прямоугольной системе координат трехмерного пространства задан параллелепипед A B C D A 1 B 1 C 1 D 1 . Заданы координаты точки C 1 ( 1 , 1 , 0 ) , а также определена точка M , являющаяся серединой диагонали B D 1 и имеющая координаты M ( 4 , 2 , – 4 ) . Необходимо рассчитать координаты точки А .

Решение

Диагонали параллелепипеда имеют пересечение в одной точке, которая при этом является серединой всех диагоналей. Исходя из этого утверждения, можно иметь в виду, что известная по условиям задачи точка М является серединой отрезка А С 1 . Опираясь на формулу для нахождения координат середины отрезка в пространстве, найдем координаты точки А : x M = x A + x C 1 2 ⇒ x A = 2 · x M – x C 1 = 2 · 4 – 1 + 7 y M = y A + y C 1 2 ⇒ y A = 2 · y M – y C 1 = 2 · 2 – 1 = 3 z M = z A + z C 1 2 ⇒ z A = 2 · z M – z C 1 = 2 · ( – 4 ) – 0 = – 8

Ответ: координаты точки А ( 7 , 3 , – 8 ) .

[spoiler title=”источники:”]

http://mathhelpplanet.com/static.php?p=onlain-reshit-treugolnik

http://zaochnik.com/spravochnik/matematika/vektory/nahozhdenie-serediny-otrezka/

[/spoiler]

Уважаемые студенты!
Заказать решение задач по 200+ предметам можно здесь всего за 10 минут.

Середина вектора

Формула

Чтобы найти середину вектора по координатам нужно вычислить сумму координат начала и конца вектора и разделить на два.

Например, пусть на плоскости заданы точки $ A(x_1;y_1) $ и $ B(x_2;y_2) $ вектора $ overline{AB} $. Тогда его середина находится по формуле: $$ O (x;y) = O bigg(frac{x_1+x_2}{2};frac{y_2+y_2}{2}bigg) $$

Если вектор задан в пространстве трёмя координатами $ A (x_1;y_1;z_1),B (x_2;y_2;z_2) $, то середину можно найти по аналогичной формуле: $$ O (x;y,z) = O bigg(frac{x_1+x_2}{2};frac{y_1+y_2}{2}; frac{z_1+z_2}{2} bigg) $$

Откуда выведена формула? Если вектор спроецировать на координатную ось $ Ox $, то можно будет применить формулу для нахождения середины отрезка к самому вектору. По сути вектор это направленный отрезок, который имеет начало и конец.

Примеры решений

Пример

Пусть вектор $ overline{AB} $ задан в пространстве трёмя точками $ A(1,3,5) $ и $ B(3,7,1) $. Найти середину вектора.

Решение

Итак, как найти середину вектора? По правилу мы должны сложить соответствующие координаты точек начала и конца вектора и разделить пополам: $$ O = bigg (frac{1+3}{2};frac{3+7}{2};frac{5+1}{2} bigg) = (2;5;3) $$ Точка $ O (2;5;3) $ – является серединой вектора $ overline{AB} $ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!

Ответ

$$ O (2;5;3) $$

ОСИ КООРДИНАТ:

Для понимания темы «вектор», надо сначала разобраться с понятием «декартовы координаты».

• ось x — ось абсцисс;
• ось y — ось ординат,
• точка О — начало координат.

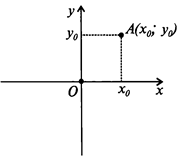
Любой точке плоскости сопоставляются два числа:

• абсцисса x₀,
• ордината y_0.

Эти числа называются декартовыми координатами данной точки.

ВЕКТОР:

Вектор — направленный отрезок прямой. То есть это отрезок, для которого указано, какая из его точек является началом, а какая — концом.

Пусть имеются две точки:

• A с координатами $(x_1;,y_1)$
• B с координатами $(x_2;,y_2)$.

Тогда мы имеем вектор $,overline {!AB,}$, который обозначим за $overline a.$

На примере вектора рассмотрим основные понятия, связанные с векторами.

Во-первых, для каждого вектора можно найти его координаты и модуль.

КООРДИНАТЫ ВЕКТОРА И МОДУЛЬ ВЕКТОРА:

Координаты вектора — разности координат конца и начала вектора. На примере вектора $overline a$ его координатами будут: $(a_x;,a_y).$ Свойства координат вектора:

• Координаты вектора не изменяются при параллельном переносе.
• У равных векторов соответствующие координаты равны.

Нахождение координат вектора:

Координаты вектора $overline a;(a_x;,a_y)colon$

$begin{aligned}&a_x=x_2-x_1\&a_y=y_2-y_1end{aligned}$

То есть, координаты вектора $overline acolon (x_2-x_1;,y_2-y_1;,z_2-z_1).$

Модуль вектора — длина вектора (обозначается ). Находится как квадратный корень из суммы квадратов координат вектора.

$|overline a|=sqrt{(a_x)^2+(a_y)^2vphantom{bigl(}}=sqrt{(x_2-x_1)^2+(y_2-y_1)^2vphantom{bigl(}}$

Если рассмотреть пространственный вектор, то в эти формулы добавляется третья координата — z.

Координаты вектора $overline a;(a_x;,a_y;,a_z)$:

$begin{aligned}&a_x = x_2-x_1 \ &a_y = y_2-y_1 \ &a_z = z_2 – z_1end{aligned}$

То есть, координаты вектора $overline acolon (x_2-x_1;,y_2-y_1;,z_2-z_1).$

Модуль вектора $overline acolon$

$|overline a|=sqrt{(a_x)^2+(a_y)^2+(a_z)^2vphantom{bigl(}}=sqrt{(x_2-x_1)^2+(y_2-y_1)^2+(z_2-z_1)^2vphantom{bigl(}}$

СЕРЕДИНА ВЕКТОРА:

Чтобы найти середину вектора по координатам нужно:

1. Вычислить сумму координат начала и конца вектора.

2. Разделить на два.

НА ПЛОСКОСТИ	В ПРОСТРАНСТВЕ
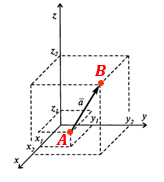
O — середина вектора $,overline {!AB,}$
$begin{aligned}&A,(x_1;,y_1), B,(x_2;,y_2) \[3pt] &O(x;y)=left(frac{x_1+x_2}{2};,frac{y_1+y_2}{2}right)end{aligned}$	$begin{aligned}&A,(x_1;,y_1;,z_1), B,(x_2;, y_2;, z_2) \[3pt] &O(x;y;z)=left(frac{x_1+x_2}{2};,frac{y_1+y_2}{2};,frac{z_1+z_2}{2}right)end{aligned}$

ВИДЫ ВЕКТОРОВ:

Единичный вектор — вектор, длина которого равна 1.

Нулевой вектор — отдельные точки плоскости. У такого вектора конец и начало совпадают, а его длина (его модуль) равен нулю.

Коллинеарные и компланарные векторы

Коллинеарные векторы — векторы, которые параллельны одной прямой или которые лежат на одной прямой. Два коллинеарных вектора $|overline a| и |b|$ называются сонаправленными только тогда, когда их направления соответствуют друг другу: $|overline a|{small uparrowuparrow}|overline b|$

Компланарные векторы — векторы, которые параллельны одной плоскости или которые лежат на общей плоскости. В любое мгновение существует плоскость одновременно параллельная двум любым векторам, поэтому два произвольных вектора являются компланарными.

АЛГЕБРАИЧЕСКИЕ ДЕЙСТВИЯ НАД ВЕКТОРАМИ:

	НА ПЛОСКОСТИ	В ПРОСТРАНСТВЕ
Координаты вектора $overline {c,}$	Сложение векторов: $overline {c,}=overline a + overline b$
$x$	$c_x = a_x + b_x$	$c_x = a_x + b_x$
$y$	$c_y = a_y + b_y$	$c_y = a_y + b_y$
$z$	—	$c_z = a_z + b_z$
Координаты вектора $overline {c,}$	Вычитание векторов: $overline {c,}=overline a – overline b$
$x$	$c_x = a_x – b_x$	$c_x = a_x – b_x$
$y$	$c_y = a_y – b_y$	$c_y = a_y – b_y$
$z$	—	$c_z = a_z – b_z$
Координаты вектора $overline {b}$	Умножение вектора на число: $overline b = lambdaoverline a$
$x$	$overline b_x = lambda a_x$	$overline b_x = lambda a_x$
$y$	$overline b_y = lambda a_y$	$overline b_y = lambda a_y$
$z$	—	$overline b_z = lambda a_z$
Значение числа $s$	Скалярное умножение векторов: $s = overline acdotoverline b$
$s=a_x!cdot b_x + a_y!cdot b_y$	$s=a_x!cdot b_x + a_y!cdot b_y + a_z!cdot b_z$

ГЕОМЕТРИЧЕСКОЕ СЛОЖЕНИЕ И ГЕОМЕТРИЧЕСКАЯ РАЗНОСТЬ ВЕКТОРОВ:

СЛОЖЕНИЕ

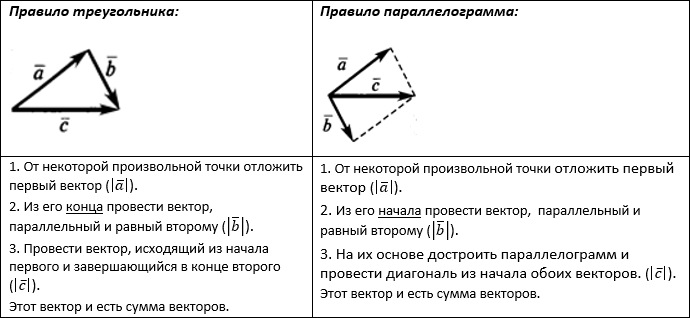
Сумма двух векторов находится с помощью правила треугольника или правила параллелограмма: $overline {c,} = overline a + overline b$.

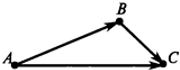
${mathbf {Теоремаcolon}}\ Для любых трёх точек A,,B,,C справедливо соотношениеcolon overline{!AB,}+,overline{!BC,}=,overline{!AC,}!.$

${mathbf {РАЗНОСТЬ}}\Разность двух векторов overline a и overline b;— это вектор overline {c,}, который в сумме с вектором overline b даёт вектор overline a \ overline b + overline{c,} = overline aquadRightarrowquadoverline{c,} = overline a – overline b$

$Вектор overline {c,} можно найти также, складывая с вектором overline a вектор bigl(-overline bbigr), противоположный вектору overline bcolon \ overline {c,} = overline a + bigl(-overline bbigr)$

Вспомним для начала основные понятия и формулы.

Пусть даны две точки: А(x1; x2) и B(y1; y2). Рассмотрим отрезок AB.

Длина отрезка АВ – это расстояние между точками A и B, его величина вычисляется по следующей формуле:

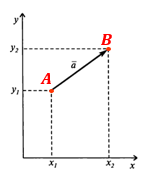
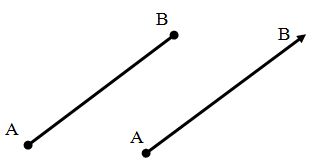
Рассмотрим теперь вектор AB. Напомню, что вектор – это направленный отрезок, то есть для него указано, какая из двух точек A и B является началом, а какая – концом. На рисунке ниже слева изображен отрезок AB, а справа – вектор AB с началом в точке A и концом в точке B.

Координаты вектора AB вычисляются следующим образом: из соответствующих координат конца вектора вычитаются соответствующие координаты начала вектора. Например, для нашего вектора AB это будет выглядеть так: AB(x2 – x1; y2 – y1).

Замечу, что модулем вектора AB называется длина отрезка AB.

Вспомним как найти координаты середины отрезка AB. Для этого есть простая формула:

x = (x1 + x2)/2, y = (y1 + y2)/2.

До этого момента мы рассматривали координаты на плоскости, а что, если речь пойдет о пространстве? Тут, оказывается, тоже все просто.

Пусть даны две точки A(x1; x2; x3) и B(y1; y2; y3).

Формула для вычисления длины отрезка AB, расположенного в пространстве будет выглядеть так:

А координаты середины отрезка AB найдем по формуле

x = (x1 + x2)/2, y = (y1 + y2)/2, z = (z1 + z2)/2.

И еще одна полезная формула: если вектор задан своими координатами, например,  MN(x1; x2; x3), то его модуль вычисляется по формуле:

Чтобы сложить два или более векторов, нужно сложить их соответствующие координаты, например,

(x1; x2; x3) + (y1; y2; y3) = (x1 + y1; x2 + y2; x3 + y3).

Чтобы умножить вектор на число, нужно умножить каждую его координату на это число, например,

5 · (x1; x2; x3) = (5 · x1; 5 · x2; 5 · x3).

Скалярным произведением двух векторов а и b называется число

a · b = |a”b| · сos (a, b),

Чтобы вычислить скалярное произведение векторов, заданных координатами, например, MN(x1; x2; x3) и PK(y1; y2; y3), можно воспользоваться следующей формулой:

MN · PK = x1 · y1 + x2 · y2 + x3 · y3.

Два вектора называются коллинеарными, если они лежат на параллельных прямых или на одной прямой.

На практике коллинеарность векторов (x1; x2) и (y1; y2) проще всего проверить, используя следующее свойство: коллинеарные векторы имеют пропорциональные координаты, то есть существует число p, такое, что (x1; x2) = p · (y1; y2).

Существуют также такие понятия, как сонаправленные векторы и противоположно направленные векторы. Сонаправленные векторы – это коллинеарные векторы, которые направлены в одну сторону, соответственно, противоположно направленные векторы – это коллинеарные векторы, которые направлены в разные стороны.

Теперь давайте рассмотрим несколько задач на эту тему.

Задача 1.

Доказать, что треугольник с вершинами A(6; -4; 2), B(3; 2; 3) и C(3; -5; -1) прямоугольный.

Решение.

Вполне очевидно, что для доказательства этой задачи достаточно показать, что один из углов треугольника ABC равен 90 градусов. Вспомним формулу для вычисления скалярного произведения через модули соответствующих векторов и косинус угла между ними, преобразуем ее и воспользуемся для нахождения угла.

сos (a, b) = a · b/|a”b|.

Для начала нам понадобятся координаты всех векторов, задающих стороны треугольника, их модули и всевозможные скалярные произведения. Вычисляем их.

Координаты векторов:

AB(3 – 6; 2 – (-4); 3 – 2) = AB(-3; 6; 1);

BC(3 – 3; -5 – 2; -1 – 3) = BC(0; -7; -4);

CA(6 – 3; -4 – (-5); 2 – (-1)) = CA(3; 1; 3).

Модули:

|AB| =

|BC| =

|CA| =

Скалярные произведения:

AB · BC = (-3) · 0 + 6 · (-7) + 1 · (-4) = 0 – 42 – 4 = -46;

BC · CA = 0 · 3 + (-7) · 1 + (-4) · 3 = 0 – 7 – 12 = -19;

AB · CA = (-3) · 3 + 6 · 1 + 1 · 3 = -9 + 6 + 3 = 0.

Теперь легко заметить, что угол между векторами AB и CA равен 90 градусов, так как

сos (AB, CA) = AB · CA / |AB”CA| = 0.

А, значит, угол А треугольника ABC равен 90 градусов, то есть треугольник ABC – прямоугольный, что и требовалось доказать.

Задача 2.

Даны точки А(0; 1; 2), B(1; 2; 4), C(-1; -1; 3) и D(1; 0; 0). Точки M и N – середины отрезков AC и BD. Найдите вектор MN и его модуль.

Решение.

Для начала найдем координаты точек M и N.

M((0 – 1)/2; (1 – 1)/2; (2 + 3)/2) = M(-1/2; 0; 5/2);

N((1 + 1)/2; (2 + 0)/2; (4 + 0)/2) = N(1; 1; 2).

Теперь найдем координаты вектора MN:

MN(1 – (-1/2); 1 – 0; 2 – 5/2) = MN(3/2; 1; -1/2).

Осталось найти модуль вектора MN.

|MN| =

Задача 3.

При каких значениях x векторы (x³ – 1)a и 2xa сонаправлены, где a – вектор, не равный нулевому вектору?

Решение.

Для того чтобы данные векторы были сонаправлены, необходимо, чтобы коэффициенты (x³ – 1) и 2x имели одинаковый знак, а значит, чтобы выполнялось следующее неравенство: (x³ – 1) · 2x > 0. Решим его методом интервалов и найдем соответствующие x.

Получим x € (-∞; 0) U (1; +∞).

Если бы в задаче требовалось узнать, при каких x данные векторы будут противоположно направлены, мы бы потребовали, чтобы у коэффициентов (x³ – 1) и 2x были различные знаки.

Задача 4.

Даны координаты вершин четырехугольника: A(2; -2), B(-3; 1), C(7; 7) и D(7; 1). Доказать, что ABCD – трапеция.

Решение.

Так как трапеция – это четырехугольник, у которого одна пара противолежащих сторон параллельна, то для доказательства нам достаточно показать, что векторы BC и AD – коллинеарны, то есть лежат на параллельных прямых. Найдем для начала их координаты.

BC(7 – (-3); 7 – 1) = BC(10; 6);

AD(7 – 2; 1 – (-2)) = AD(5; 3).

Заметим, что координаты векторов пропорциональны: (10; 6) = 2 · (5; 3). Это и указывает на то, что данные векторы коллинеарны, а, значит, ABCD – трапеция.

Остались вопросы? Не знаете, как выполнять действия над векторами?
Чтобы получить помощь репетитора – зарегистрируйтесь.
Первый урок – бесплатно!

© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.

Как найти середину вектора

Вектор – это величина, характеризуемая своим численным значением и направлением. Другими словами, вектор – это направленный отрезок. Положение вектора AB в пространстве задается координатами точки начала вектора A и точки конца вектора B. Рассмотрим, как определить координаты середины вектора.

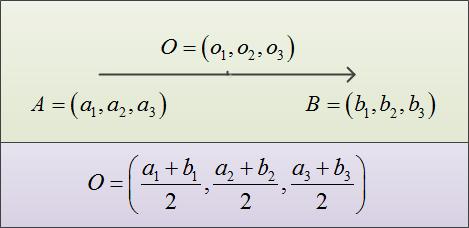
Инструкция

Для начала определимся с обозначениями начала и конца вектора. Если вектор записан как AB, то точка A является началом вектора, а точка B – концом. И наоборот, для вектора BA точка B является началом вектора, а точка A – концом. Пусть нам задан вектор AB с координатами начала вектора A = (a1, a2, a3) и конца вектора B = (b1, b2, b3). Тогда координаты вектора AB будут следующими: AB = (b1 – a1, b2 – a2, b3 – a3), т.е. из координаты конца вектора необходимо вычесть соответствующую координату начала вектора. Длина вектора AB (или его модуль) вычисляется как корень квадратный из суммы квадратов его координат: |AB| = √((b1 – a1)^2 + (b2 – a2)^2 + (b3 – a3)^2).

Найдем координаты точки, являющейся серединой вектора. Обозначим ее буквой O = (o1, o2, o3). Находятся координаты середины вектора так же, как координаты середины обычного отрезка, по следующим формулам: o1 = (a1 + b1)/2, o2 = (a2 + b2)/2 , o3 = (a3 + b3)/2. Найдем координаты вектора AO: AO = (o1 – a1, o2 – a2, o3 – a3) = ((b1 – a1)/2, (b2 – a2)/2, (b3 – a3)/2).

Рассмотрим пример. Пусть дан вектор AB с координатами начала вектора A = (1, 3, 5) и конца вектора B = (3, 5, 7). Тогда координаты вектора AB можно записать как AB = (3 – 1, 5 – 3, 7 – 5) = (2, 2, 2). Найдем модуль вектора AB: |AB| = √(4 + 4 + 4) = 2 * √3. Значение длины заданного вектора поможет нам для дальнейшей проверки правильности координат середины вектора. Далее найдем координаты точки O: O = ((1 + 3)/2, (3 + 5)/2, (5 + 7)/2) = (2, 4, 6). Тогда координаты вектора AO рассчитываем как AO = (2 – 1, 4 – 3, 6 – 5) = (1, 1, 1).

Выполним проверку. Длина вектора AO = √(1 + 1 + 1) = √3. Вспомним, что длина исходного вектора равна 2 * √3, т.е. половина вектора действительно равна половине длины исходного вектора. Теперь рассчитаем координаты вектора OB: OB = (3 – 2, 5 – 4, 7 – 6) = (1, 1, 1). Найдем сумму векторов AO и OB: AO + OB = (1 + 1, 1 + 1, 1 + 1) = (2, 2, 2) = AB. Следовательно, координаты середины вектора были найдены верно.

Полезный совет

Выполнив вычисления координат середины вектора, обязательно выполните хотя бы самую простую проверку – посчитайте длину вектора и сравните ее с длиной данного вектора.

Источники:

• как найти первую координату

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?