Как найти координаты снаряда

Как рассчитать движение снаряда

Когда объект запускается, он следует параболическому пути и движению, известному как движение снаряда. В этом посте мы рассмотрим параметры и способы их расчета. движение снаряда в подробном анализе.

Когда объект запускается и движется по симметричной параболической траектории, движение называется движением снаряда, а параболический путь объекта называется его траекторией. В этом случае объект перемещается одновременно по вертикали и горизонтали. В результате движение снаряда становится двумерным. При движении снаряда вам нужно только приложить силу в начале траектории; после этого на объект действует только сила тяжести.

Теперь давайте посмотрим, как рассчитать движение снаряда:

Предположим, вы стреляете пушечным ядром. Он начинает двигаться вверх и вперед, пока не достигнет максимальной высоты. С этого момента он будет продолжать двигаться вперед, но в нисходящем направлении. Он отслеживает этот изогнутый маршрут, известный как траектория, имеющая форму параболы. Любой объект, движущийся таким образом, называется движущимся снарядом. Поскольку траектория движения снаряда всегда параболическая, она представляется как:

у = ах + bx 2

Прежде чем достичь Земли, пушечное ядро ​​во время своего путешествия пойдет по параболическому маршруту. скорость по оси X остается постоянной на протяжении всего движения, тогда как скорость по оси Y изменяется в зависимости от его положения. Только ускорение свободного падения 9.8 м / с 2 , управляет этим типом движения. Ускорение, направленное вниз, остается постоянным во время полета ядер.

Кинематические уравнения движения снаряда:

Формула начальной скорости:

Предположим, что начальная скорость равна u, а угол полета снаряда равен. У начальной скорости есть две составляющие: горизонтальная и вертикальная.

Горизонтальная составляющая начальной скорости u_x и предоставлено:

u_x = ты ᐧ потому что𝛳

Вертикальная составляющая начальной скорости равна uy и определяется выражением:

Время полета снаряда:

Время полета снаряда – это промежуток времени между запускаемым объектом и достижением земли. Величина стартовой скорости и угол полета снаряда определяют время полета, которое обозначается T.

Формула ускорения:

В горизонтальном направлении ускорение отсутствует, поскольку горизонтальная составляющая ускорения остается постоянной на протяжении всего движения. Единственное ускорение в вертикальном направлении происходит за счет силы тяжести.

Отрицательный знак означает ускорение вниз.

Формула скорости в момент времени t:

На протяжении всего движения горизонтальная составляющая скорости остается постоянной. Однако, поскольку вертикальное ускорение постоянно, вертикальная составляющая скорости изменяется линейно.

В результате скорость может быть рассчитана в любой момент времени t по следующей формуле:

v_y = u ᐧ sin𝛳 – g ᐧ t

Используя теорему Пифагора, можно найти величину скорости.

Формула смещения в момент времени t:

В момент времени t смещение может быть определено как:

y = (u ᐧ sin𝛳) ᐧ t – ½ (gt 2 )

Формула параболической траектории:

Мы можем использовать уравнения смещения в направлениях x и y, чтобы вывести уравнение для параболической формы движения снаряда:

Формула дальности снаряда:

Общее горизонтальное расстояние, пройденное объектом за время полета, определяется как его дальность. Если объект запускается с земли (начальная высота = 0), формула выглядит следующим образом:

Согласно приведенному выше уравнению, максимальная дальность полета по горизонтали может быть получена при угле полета снаряда 𝛳 = 45 °. Rm представляет собой максимальный диапазон.

Формула максимальной высоты:

Когда вертикальная составляющая скорости равна нулю, v_y = 0, максимальная высота может быть достигнута. Поскольку время полета – это полное время снаряда, для достижения максимальной высоты потребуется половина этого времени. Таким образом, время для достижения максимальной высоты составляет:

Таким образом, из уравнения перемещения максимальная высота может быть определена как:

Формула движения снаряда по горизонтали:

Горизонтальный снаряд Движение – это тип движения снаряда, при котором объект запускается горизонтально с возвышенной плоскости, а не с земли.

Угол запуска указывать не нужно, поскольку он параллелен земле (т. Е. Угол равен 0 °). В результате у нас есть только одна начальная составляющая скорости: Vx = V, тогда как Vy = 0.

В этом случае уравнения движения следующие:

Скорость горизонтального движения снаряда:

Горизонтальная скорость: v_x = V

И вертикальная скорость: v_x = -g ᐧ т

Расстояние, пройденное объектом при горизонтальном движении снаряда:

В этом случае горизонтальное расстояние рассчитывается следующим образом:

А расстояние по вертикали можно определить как:

y = – (g ᐧ t 2 ) / 2

Ускорение при горизонтальном движении снаряда:

Горизонтальное ускорение а_x = 0, поскольку горизонтальная скорость постоянна.

Вертикальное ускорение а_y = -г

Уравнение траектории горизонтального движения снаряда:

Уравнение траектории в этом случае может быть задано следующим образом:

Время полета при горизонтальном движении снаряда:

Время полета в этом случае может быть определено как:

Дальность полета снаряда при горизонтальном движении снаряда:

Дальность полета снаряда при горизонтальном движении снаряда составляет:

Поскольку мы запускаем объект с максимальной высоты, нам не нужно рассчитывать максимальную высоту в этом сценарии.

Давайте посмотрим на некоторые проблемы движения снаряда.

Проблема 1: Каким будет θmax, при котором расстояние от частицы до метателя всегда увеличивается до конца пути снова у земли?

Решение: Горизонтальное расстояние, пройденное объектом, называется его горизонтальным диапазоном и определяется по формуле:

Максимальная дальность полета может быть достигнута при угле выстрела 45 °.

Таким образом, для максимального угла Rm θmax = 45 °.

Задача 2: Если мяч брошен вертикально вверх со скоростью u, расстояние, пройденное за последние t секунд его всплытия, будет:

Решение: Поскольку мяч брошен вертикально, угол полета снаряда 𝛳 = 90 °.

Где Tm – время, необходимое объекту для достижения максимальной высоты.

Предположим, что h представляет собой расстояние, пройденное объектом за последние t секунд его подъема. Затем скорость в этот момент рассчитывается следующим образом:

Таким образом, расстояние, пройденное за последнюю t секунду, составляет:

3 задачи: Частица проецируется под углом 60 ° над горизонтом со скоростью 10 м / с. Через некоторое время скорость составит угол 30 ° от горизонтали. Скорость частицы в этот момент составляет?

Решение: Горизонтальная составляющая скорости определяется как:

v_x = ты ᐧ потому что𝛳

Здесь в первом случае угол проекции составляет 60 °, а начальная скорость u = 10 м / с. Таким образом,

Теперь вертикальная составляющая скорости v_y изменяется во время движения, но v_x остается постоянным. Таким образом,

Где 𝛳2 = 30 °, а v – скорость, когда объект составляет угол 𝛳 = 30 ° с горизонтом.

Последние выпуски в области передовой науки и исследований

Уравнение траектории снаряда имеет вид

2017-10-05
Зенитное орудие может сообщить снаряду начальную скорость $v_<0>$ в любом направлении. Требуется найти зону поражения, т. е. границу, отделяющую цели, до которых снаряд из данного орудия может долететь, от недостижимых целей. Сопротивлением воздуха пренебречь.

Свободным полётом снаряда называется фаза его движения после выстрела до попадания в твёрдое препятствие (цель, грунт) или до дистанционного подрыва. В этом процессе на снаряд действуют только сила тяжести и силы, возникающие при движении тела в газообразной среде (атмосфере Земли). В общем случае в атмосфере Земли также могут существовать упорядоченные движения масс воздуха (ветер), которые оказывают определённое влияние на полёт снаряда.

Путь, описываемый центром тяжести снаряда в пространстве после вылета его из канала ствола, называется траекторией.

Принято считать за траекторию полёта снаряда кривую, которую при движении описывает его центр масс. Эта кривая также имеет название баллистической. В самом общем случае она не является ни прямой, ни параболической, ни даже плоской.

Основные элементами траектории (рис.1) являются:

1. Точка вылетаО — центр дульного среза орудия.

2. Горизонт орудия ОС— горизонтальная плоскость, проходящая через точку вылета.

3. Точка падения С — точка пересечения траектории с горизонтом орудия.

4. Точка встречи Ав — точка встречи снаряда с преградой.

5. Линия выстрела ОА — направление оси канала ствола наведенного орудия.

6. Линия бросания ОБ — направление оси канала ствола в момент вылета снаряда; из-за вибрации ствола в момент вылета снаряда, линия бросания не совпадает с линией выстрела.

7. Линия цели ОЦ — прямая, проходящая через точку вылета и цель,

8. Угол прицеливания α(альфа) — угол между линией цели ОЦ и линией выстрела ОА.

9. Угол места цели ε(эпсилон) — угол между горизонтом орудия ОС и линией цели ОЦ, угол места цели считается положительным, когда цель выше горизонта орудия, и отрицательным, когда цель ниже горизонта орудия.

10. Угол возвышения φ(фи) — угол между горизонтом орудия ОС и линией выстрела ОА.

11. Угол вылета γ(гамма) — угол между линией выстрела ОА и линией бросания ОБ.

12. Угол бросания θ₀ (тета) — угол между горизонтом орудия ОС и линией бросания ОБ.

13. Угол падения θ_с (тета) — угол между горизонтом орудия ОС и касательной к траектории в точке падения.

14. Угол встречи μ(мю) — угол между касательной к траектории в точке встречи и плоскостью, касательной к поверхности цели (преграды) в той же точке; угол встречи может быть от 0 до 90°.

15. Вершина траектории S — точка траектории, превышение которой над горизонтом орудия ОС является наибольшим.

16. Высота траектории — вертикальное расстояние от горизонта орудия ОС до вершины траектории S.

17. Восходящая ветвьОS — отрезок траектории от точки вылета до вершины траектории.

18. Нисходящая ветвь SС — отрезок траектории от ее вершины до точки падения.

19. Дальность до цели ОЦ — расстояние по прямой от орудия до цели.

С увеличением угла возвышения увеличивается и дальность падения снаряда, однако увеличение дальности имеет предел. В безвоздушном пространстве наибольшая дальность получилась бы при угле возвышения 45°. При дальнейшем увеличении угла возвышения снаряд полетел бы выше, но дальность падения уменьшилась бы. То же происходит и при стрельбе в действительных условиях, но траектория снаряда имеет другую форму.

Мерой крутизны траектории является величина угла возвышения φ (фи). Траекторию с углом возвышения не более 20° принято называть отлогой, а траекторию с углом возвышения более 20°— крутой.

Стрельбу, при которой траектория получается отлогой, называют настильной. Стрельбу, при которой траектория получается крутой, называют навесной.

Навесную стрельбу при углах возвышения более 45° называют мортирной.

Траектория снаряда в воздухе значительно отличается от траектории в безвоздушном пространстве (рис.2).

В безвоздушном пространстве траектория снаряда симметрична относительно вершины траектории, а в действительных условиях траектория несимметрична, нисходящая ветвь траектории короче и круче восходящей; угол падения больше угла возвышения; вершина траектории находится ближе к точке падения.

Восходящие Ветви

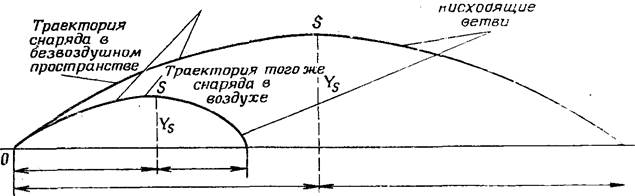Рис. 2. Траектория снаряда в безвоздушном пространстве и в воздухе

Под действием силы сопротивления воздуха снаряд за каждую секунду проходит меньшее расстояние по направлению оси канала ствола, а понижается на ту же величину, что и в безвоздушном пространстве. В результате этого траектория в воздухе будет ниже и короче, чем в безвоздушном пространстве.

Угол бросания, отвечающий наибольшей дальности, при стрельбе в воздухе зависит от начальной скорости, массы и формы снаряда, а также от способа стабилизации снаряда на полете и может находиться в пределах от 28 до 55°.

При стрельбе из танков, БМП, противотанковых орудий и гранатометов и стрелкового оружия используются обычно настильные траектории. Чем меньше высота траектории и чем меньше угол падения, тем траектория более настильна.

Траектория в воздухе имеет следующие свойства:

§ траектория несимметрична, ее нисходящая ветвь короче и круче восходящей.

§ вершина траектории находится ближе к точке падения.

§ угол падения больше угла бросания.

У снаряда, движущегося в воздухе, окончательная скорость меньше начальной.

[spoiler title=”источники:”]

http://earthz.ru/solves/Zadacha-po-fizike-4147

http://helpiks.org/4-1510.html

[/spoiler]

Изобретение относится к мишенным средствам для определения координат положения в пространстве и во времени пуль и снарядов в различных средах с возможностью восстановления их траектории при стрельбе в тире или на полигоне. Способ включает регистрацию моментов времени прохождения фронта звуковой волны через акустические датчики, установленные по крайней мере на одной мишени в количестве, выбранном по числу неизвестных в регрессионной или математической модели мишени, одним из которых является начало отсчета времени, соответствующее моменту пролета пули или снаряда через плоскость мишени, вычисление характеристик движения по регрессионной или математической модели мишени с помощью вычислителя. Каждую мишень выполняют в виде пулепробиваемой пластины из материала, расчетная скорость звука в котором в условиях местоположения мишени больше расчетной скорости звука в среде размещения мишени, при этом в заданное число неизвестных в регрессионной или математической модели мишени включают фактическую скорость звука в материале мишени. Техническим результатом является получение данных о пространственно-временном положении (траектории) пули или снаряда при движении в любой среде, упрощение способа и повышение точности определения координат. 2 ил.

Изобретение относится к мишенным средствам для определения координат положения в пространстве и во времени пуль и снарядов в различных средах с возможностью восстановления их траектории при стрельбе в тире или на полигоне.

Известен способ определения координат точки попадания пуль, реализованный в электронно-акустической мишени (Захаров В.А. “Электронно-акустическая мишень”, М.: Радио, 1979, №5, с.13-15), содержащей толстую пуленепробиваемую металлическую пластину с расположенными на ее торцах акустическими датчиками, с помощью которых фиксируют моменты времени прихода звуковой волны от места удара пули по плите до мест расположения пьезокерамических акустических датчиков.

Недостатками способа, использующего в работе указанную электронно-акустическую мишень, является то, что данный способ не позволяет проводить регистрацию пространственно-временного положения движущегося снаряда или пули в среде, отличной от воздушной; не позволяет получать траекторию снаряда или пули; имеет свойство изменять точность измерений, так как при многочисленных выстрелах изменяются свойства пластины; для измерений используются достаточно дорогие пьезокерамические датчики; малые размеры поля регистрации и громоздкость мишени.

Известен “Способ определения внешнебаллистических характеристик полета пуль и снарядов”, патент RU 2231738, МПК F41J 5/06, G01S 5/18, опубликован 27.06.2004, выбранный в качестве прототипа, включающий фиксацию моментов времени прохождения фронта звуковой волны через акустические датчики, установленные на мишени в количестве не менее шести, и вычисление характеристик по регрессионной или математической модели с помощью вычислителя. Число датчиков выбирают по минимальному числу неизвестных, которыми являются начало отсчета времени, соответствующее моменту пролета пули или снаряда через плоскость мишени, скорость пули или снаряда, углы наклона их траектории и величина и направление силы ветра, при этом для определения положения датчиков осуществляют идентификацию модели, для чего предварительно на мишень устанавливают контрольную рамку и производят серию выстрелов в заданные точки, причем после каждого выстрела измеряют время срабатывания датчиков и координаты пробоин в контрольной рамке, а затем по методу наименьших квадратов определяют координаты датчиков.

Основным недостатком способа, который не позволяет получить необходимый результат, является низкая точность из-за влияния параметров атмосферы, таких как влажность, температура, плотность и т.д., которые влияют на скорость звука в атмосфере (в среде размещения мишени); движение воздуха (ветер) не обязательно равномерно и однонаправлено, особенно у поверхности земли и у препятствий. Для снарядов с притупленной головной частью при движении со скоростью, большей скорости звука в среде, наблюдается отход головной ударной волны от снаряда, т.е. положение снаряда относительно фронта ударной волны имеет смещение; реальный профиль головной ударной волны не конический, т.е. конус Маха можно рассматривать лишь как упрощенную модель распространения возмущений в окружающей среде от источника малых возмущений; при движении снаряда на дозвуковой скорости способ не работает, так как звуковое возмущение уходит вперед от снаряда.

Изобретение направлено на решение задачи, заключающейся в разработке способа, обеспечивающего контактную регистрацию пространственно-временного положения пуль и снарядов, движущихся практически в любой преграде.

Технический результат – получение данных о пространственно-временном положении (траектории) пули или снаряда при движении в любой среде, упрощение способа и повышение точности определения координат.

Указанный технический результат достигается тем, что в заявляемом способе определения координат положения в пространстве и во времени пуль и снарядов, включающем регистрацию моментов времени прохождения фронта звуковой волны через акустические датчики, установленные по крайней мере на одной мишени в количестве, выбранном по числу неизвестных в регрессионной или математической модели мишени, одним из которых является начало отсчета времени, соответствующее моменту пролета пули или снаряда через плоскость мишени, вычисление характеристик движения по регрессионной или математической модели мишени с помощью вычислителя, в отличие от прототипа каждую мишень выполняют в виде пулепробиваемой пластины из материала, расчетная скорость звука в котором в условиях местоположения мишени больше расчетной скорости звука в среде размещения мишени, при этом в заданное число неизвестных в регрессионной или математической модели мишени включают фактическую скорость звука в материале мишени.

Выполнение каждой мишени в виде пулепробиваемой пластины из материала, расчетная скорость звука в котором в условиях местоположения мишени больше расчетной скорости звука в среде размещения мишени, позволяет минимизировать влияние среды размещения на передачу информации (в нашем случае, передача информации осуществляется за счет распространения звуковых колебаний в пластине от удара о нее снарядом). Снижение количества неизвестных в регрессионной или математической модели (в отличие от прототипа не надо учитывать скорость полета пули или снаряда, углы наклона их траектории и величины и направления силы ветра), возможность непосредственного определения координат по пробоине в пластине от пули или снаряда, возможность размещения пластины в любой среде – все это приводит к повышению точности и надежности измерений.

Включение в заданное число неизвестных в регрессионной или математической модели мишени фактической скорости звука в материале мишени также повышает точность определения координат практически в любой среде размещения мишени.

Изобретение поясняется фигурами. На фигуре 1 схематично изображен пример устройства, реализующего заявленный способ. На фигуре 2 показана схема размещения датчиков на мишени.

Устройство для реализации способа состоит из пулепробиваемой мишени в виде квадратной алюминиевой пластины 1, акустических (тензометрических) датчиков 2 (Д1, Д2, Д3 и Д4), количество которых выбрано по числу неизвестных в математической модели мишени, вычислителя (компьютера, на фигуре не показан). Датчики 2 расположены на поверхности мишени 1 в ее углах на одинаковом расстоянии от краев мишени. В данном случае мишень 1 располагают в среде типа песчаный грунт, при этом соблюдают условие, что скорость звука в мишени 1 (расчетная скорость звука в алюминии с_зм≈5000÷6000 м/с) в условиях месторасположения мишени (т.е. с учетом температуры окружающей среды, давления и т.п.) больше скорости звука в среде размещения мишени (расчетная скорость звука в песке с_зср≈300 м/с). Таким образом, звуковое возмущение от удара снаряда о мишень будет распространяться по мишени с большей скоростью, чем в среде ее размещения, это позволяет не учитывать параметры среды размещения, которые могут приводить к изменению скорости звука в среде размещения (разноплотность, массовая скорость, локальные температурные перепады и т.д.), то есть минимизируется влияние среды размещения на передачу информации, что в свою очередь приводит к повышению точности определения координат.

Материал мишени 1 выбирают инертным к среде размещения, имеющим небольшую прочность (должен быть пробиваемым и обеспечивающим несущую способность конструкции мишени); плотность материала мишени (в общем случае должна быть как можно более близкой к плотности среды размещения) примерно в 2 раза больше плотности среды размещения. Скорость звука в материале мишени 1 практически не изменяется при ее размещении в песчаном грунте на глубине нескольких метров. Толщину мишени 1 выбирают минимальной, исходя из размеров мишени, которая зависит от отклонений траектории снаряда 3, а также из условия обеспечения несущей способности конструкции мишени (в данном примере выполнения толщина мишени примерно 1 мм при длине стороны мишени 1 м).

Заявляемый способ осуществляют следующим образом (см. фигуры 1, 2). Расстояние S между двумя соседними по периметру мишени датчиками 2 определяют заранее (в данном случае расстояния между датчиками равны). Мишень 1 устанавливают в среде размещения, в данном примере в песке. Снаряд 3 пробивает поверхность алюминиевой пластины 1. От точки удара по алюминиевой пластине распространяется акустическая волна со скоростью звука с_зм. Датчиками 2 (Д1, Д2, Д3 и Д4) фиксируют моменты прихода акустической волны (t₁, t₂, t₃, t₄), то есть количество датчиков меньше, чем в прототипе, следовательно повышается надежность измерений.

Осуществляя непосредственную привязку между точкой попадания и датчиком Д1 (примем, что датчик Д1 находится ближе всех к точке соударения), через геометрические соотношения, например через расстояние r₁ между точкой попадания и датчиком Д1, расстояние между датчиками S, угол α (например, угол α между линией, соединяющей точку соударения с датчиком Д1 и линией, соединяющей датчики Д1, Д2, см. фиг.2) выражают неизвестные, составляют систему уравнений, являющуюся математической моделью мишени 1.

С помощью вычислителя решают систему

где c_зфм – фактическая скорость звука в алюминиевой пластине 1;

t₀ – момент удара снаряда 3 об алюминиевую пластину 1;

t₁, t₂, t₃ и t₄ – моменты прихода акустической волны на регистрирующие датчики 2 (Д1, Д2, Д3 и Д4);

r₁ – расстояние от точки соударения до 1-го датчика 2 (Д1), соответственно, r₂, r₃ и r₄ – до 2-го (Д2), 3-го (Д3) и 4-го (Д4);

S – расстояние между соседними по периметру мишени датчиками 2;

α – угол между линией, соединяющей точку соударения с датчиком Д1 и линией, соединяющей датчики Д1, Д2.

Система четырех уравнений содержит четыре неизвестные (t₀, c_зфм, r₁ и α), на мишени установлено четыре датчика, находятся значения всех четырех неизвестных (t₀, c_зфм, r₁ и α). Аналогично по теореме косинусов выводятся уравнения для различного количества датчиков 2 и для их любого местоположения.

Соответственно, по найденным значениям r₁, α и известному расстоянию S между датчиками 2 определяют расстояния от точки соударения до датчиков 2 (r₂, r₃ и r₄), а по координатной привязке мишени в пространстве и координаты точки соударения в пространстве.

Модель мишени может быть регрессионной.

Включение в заданное число неизвестных в регрессионной или математической модели мишени фактической скорости звука в материале мишени также повышает точность определения координат практически в любой среде размещения мишени.

По нескольким мишеням, установленным на пути движения пули или снаряда, определяют траекторию движения пули или снаряда в преграде.

Таким образом, при осуществлении заявляемого способа получаем данные (координаты и момент времени попадания снаряда в мишень) о пространственно-временном положении (в том числе траекторию) пули или снаряда, движущихся в любой среде, в том числе отличной от воздушной, повышается точность и надежность измерений.

Способ определения координат положения в пространстве и во времени пуль и снарядов, включающий регистрацию моментов времени прохождения фронта звуковой волны через акустические датчики, установленные по крайней мере на одной мишени в количестве, выбранном по числу неизвестных в регрессионной или математической модели мишени, одним из которых является начало отсчета времени, соответствующее моменту пролета пули или снаряда через плоскость мишени, вычисление характеристик движения по регрессионной или математической модели мишени с помощью вычислителя, отличающийся тем, что каждую мишень выполняют в виде пулепробиваемой пластины из материала, расчетная скорость звука в котором в условиях местоположения мишени больше расчетной скорости звука в среде размещения мишени, при этом в заданное число неизвестных в регрессионной или математической модели мишени включают фактическую скорость звука в материале мишени.

Моделирование динамических систем: задача внешней баллистики

Введение

Надеюсь что мы с вами набрались достаточно опыта, чтобы смоделировать что-нибудь более серьезное, чем полет камня. Предлагаю такую задачу

Пушка, стреляющая сферическими ядрами сообщает им начальную скорость 400 м/с. Определить траекторию полета снаряда при стрельбе под углом в 35 градусов к горизонту. Поле силы тяжести считать однородным, кривизной Земли пренебречь.

Надо сказать, это пример некорректно поставленной задачи. Во-первых, не сказано учитываем мы, или не учитываем сопротивление воздуха. А если учитываем, то в задаче явно не хватает параметров. К сожалению такого рода постановка задач весьма распространенное явление. Поэтому мы решим задачу для обоих случаев, а нужные параметры введем в неё сами. Заодно научимся чему-то новому. Поехали!

1. Расчетная схема

В прошлые разы я сознательно не рисовал никаких схем, чтобы потренировать ваше воображение. Несложно представить себе камень, падающий вертикально вниз. Сейчас задачка посложнее, и без чертежа нам не обойтись.

Подобные чертежи называют расчетной схемой — условным графическим изображением процесса или объекта, выполненным с учетом введенных в задачу допущений.

Обратите внимание, что на схеме нарисовано произвольное положение снаряда, то, в которое он попадет по истечении некоторого времени от начала движения. В задачах динамики так удобнее представить себе взаимное расположение векторов сил и правильно разложить их на осевые проекции. Единственное, что мы показали в начальном положении — вектор начальной скорости. Это пригодится при задании начальных условий.

2. Формализация задачи (без учета сопротивления среды)

Все готово к составлению системы дифференциальных уравнений движения

Мы не учитываем сопротивления воздуха, и у нас всего одна сила: на ось x она проецируется в ноль, на ось y — в истинную величину с минусом. Ведь мы приняли допущение, что поле силы тяжести однородно а Земля плоская. Значит сила тяжести всегда постоянна и направлена вертикально вниз. Как видно, от массы тут ничего не зависит, масса сокращается в обоих уравнениях

Получилась система двух уравнений второго порядка. Нам нужно привести её к форме Коши. Помните что это? Если помните, попробуйте сделать это сами, не заглядывая под спойлер

3. Скрипты Octave, или как заново не делать одну и ту же работу

В прошлый раз мы вводили команды в прямо в консоли Octave. Хорошо задачка у нас была маленькая. А если большая? А если хочется поменять параметры? А если хочется вернуться к отложенной работе? А если… Короче говоря, хорошо иметь возможность сохранять свои программы на Octave. И таки тут нет ничего невозможного.

Внизу экрана, под командным окном есть вкладки: Command Window, Editor и Documentation. Вкладка Editor — то что нам нужно. Это редактор скриптов на m-языке. Откроем эту вкладку и введем в неё такой текст

%-------------------------------------------------------------------------------
%
%   Баллистическая задача без учета сопротивления среды
%   система ОДУ движения
%
%-------------------------------------------------------------------------------
function dYdt = f(Y, t)

  g = 9.81; % Ускорение свободного падения

  dYdt(1) = Y(3); % dx/dt = vx
  dYdt(2) = Y(4); % dy/dt = vy
  dYdt(3) = 0;    % dvx/dt = 0
  dYdt(4) = -g;   % dvy/dt = -g
  
endfunction

Это ничто иное, как правая часть системы дифференциальных уравнений движения снаряда, в нашей задаче, оформленная в виде функции на m-языке. Смысл тот же самый что и прошлый раз. Только теперь уравнений у нас аж четыре. Ну и ускорение свободного падения берем уже нормальной, взрослой величины. Сохраним этот файл на диске под именем f.m

Внимание! Каждая функция на m-языке требует сохранения в собственный файл, имя которого совпадает с именем функции. В нашем случае функция имеет имя f, значит и файл имеет имя f.

Что за строки, начинающиеся с “%”? А это, братья-апачи, комментарии! Текст, предваренный этим символом в Octave игнорируется интерпретатором. Комментариями не только можно, но и нужно снабжать свои программы, чтобы хотя бы самому в них ориентироваться, не говоря уже о других людях, желающих воспользоваться вашей программой.

Итак, мы задали октаве систему уравнений. Создадим новый файл, назовем его, например, ballistics.m и сохраним там же, где и сохранили предыдущий файл. Начнем решать задачу!

%-------------------------------------------------------------------------------
% Параметры стрельбы
%-------------------------------------------------------------------------------

% начальная скорость снаряда
v0 = 400; 
% угол наклона ствола пушки к горизонту
alpha = 35 * pi / 180; 

%-------------------------------------------------------------------------------
% Начальные условия
%-------------------------------------------------------------------------------
x0 = 0;
y0 = 0;
vx0 = v0 * cos(alpha);
vy0 = v0 * sin(alpha);

Y0 = [x0; y0; vx0; vy0];

%-------------------------------------------------------------------------------
% Параметры временного интервала
%-------------------------------------------------------------------------------

% начальный момент времени
t0 = 0;
% конечный момент времени
tend = 10.0;
% шаг выдачи решения
deltaT = 0.1;

% Массив интересующих нас моментов времени
t = [t0:deltaT:tend];

% Интрегрируем систему уравнений движения
Y = lsode("f", Y0, t);

% Рисуем траекторию полета снаряда
plot(Y(:,1), Y(:,2));

Смысл большинства операций понятен из комментариев. Отдельно поясню начальные условия. У нас четыре фазовых координаты: две декартовы координаты снаряда, две проекции его скорости на оси координат

Для каждой из фазовых координат нужно задать их начальное значение. Логично задать начальное положение в начале координат. Что качается двух других переменных, то это, внимание, начальные величины проекций вектора скорости на оси x и y. Затем я и нарисовал вектор начальной скорости, чтобы легко было найти его проекции на оси

Теперь всё готово. Жмем на кнопку с шестерней и желтым треугольником, чтобы запустить скрипт. В ответ система выдаст окошко

попросит нас добавить путь, по которому лежит скрипт в пути поиска скриптов. Это нужно сделать один раз после загрузки скрипта в редактор или создании нового скрипта. Жмем кнопку «Add…» и получаем результат

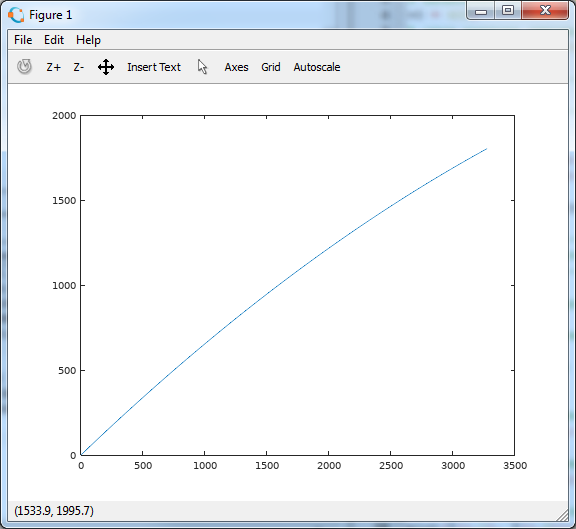
Выглядит многообещающе. Время 10 секунд мало, чтобы наряд приземлился. Меняем значение tend и запускаем скрипт снова, пока не получим похожую картинку

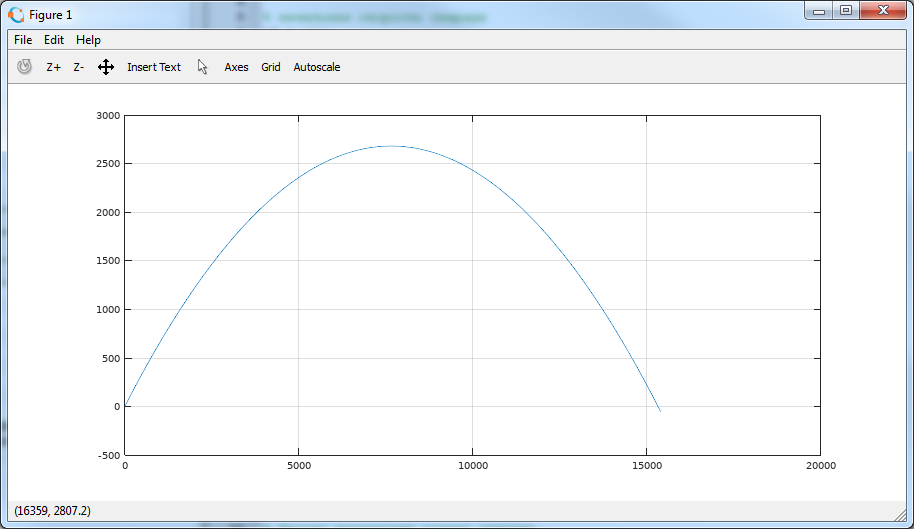
соответствующую tend = 47 секунд. Симуляция закончилась, снаряд пролетел ниже оси x, но это нормально, ведь мы никак не моделируем его встречу с поверхностью.

4. Формализация задачи (с учетом сопротивления среды)

Шар в качестве формы снаряда мы выбрали не случайно. Как его не верти, со всех сторон у него одинаковое сечение — круг (кстати, то той же причина КК «Восток» имел шарообразную форму спускаемого аппарата). А значит, как ни направляй поток воздуха, при обтекании сила сопротивления движению будет одинакова и равна

где c_f = 0.47 — коэффициент лобового сопротивления формы; S — площадь поперечного сечения;

= 1.29 кг/м³ — плотность воздуха; v — скорость набегающего потока, в нашем случае скорость снаряда.

Вектор силы сопротивления всегда будет направлен против вектора скорости. Поэтому перерисуем расчетную схему

Как учесть тот факт, что для любого момента времени вектор

направлен против скорости? Очень просто. Мы знаем, что вектор скорости направлен по касательной к траектории. Введем вектор

с длинной равной 1 и направленные туда же, куда направлена скорость. Тогда вектор

можно выразить через вектор

и модуль силы сопротивления

А как найти вектор

? Очень просто, его проекции на оси координат будут равны

Модуль вектора скорости легко выражается через его проекции

Тогда проекции вектора силы сопротивления воздуха на оси координат легко посчитать

И это меняет уравнения движения

Это что же выходит, массу теперь не сократить? Да, теперь динамика полета снаряда будет зависеть от массы. Но на массу никто не запрещает делить, делим на неё оба уравнения

где

коэффициент, определяющий вклад силы сопротивления в ускорение снаряда. Его можно сильно упростить, если вспомнить, что снаряд — шар

Первая формула — масса шара, и тут

— плотность материала, из которого сделано ядро, а r — радиус ядра. Вторая формула — площадь поперечного сечения шара. Подставим эти формулы в выражение для коэффициента и упростим

где d — диаметр ядра, калибр нашей пушки. Из этой формулы уже видно, что чем больше будет калибр и плотнее материал снаряда, тем меньше будет влияние силы сопротивления воздуха.

Зададимся значениями параметров снаряда. Добавим в конец файла ballistics.m следующие строки

%-------------------------------------------------------------------------------
% Параметры снаряда
%-------------------------------------------------------------------------------

% плотность материала снаряда
global gamma = 7800; 
% коэффициент сопростивления формы (для шара)
global c_f = 0.47;
% калибр
global d = 0.1;

Пускай ядро будет чугунным калибра 100 мм. Что за слово такое, global перед каждой из переменных. Таким образом мы говорим системе, что созданные переменные будут доступны для всех скриптов и определенных в них функций, то есть будут глобальными.

Остается записать для Octave построенную нами модель в виде функции, пусть это будет функция f_air. Естественно, для неё нужно создать отдельный файл f_air.m. Попробуйте провернуть это самостоятельно. Дам подсказку: начале тела этой функции следует определить ещё раз наши глобальные параметры снаряда, но уже без значений. Это необходимо, чтобы функция видела глобальные переменные

global c_f;
global gamma;
global d; 

Если будут совсем трудно, загляните под спойлер.

function dYdt = f_air(Y, t)
  
  global c_f;
  global gamma;
  global d; 
 
  % Ускорение свободного падения
  g = 9.81;
  
  % Плотность воздуха
  rho = 1.29;
  
  % Коэффициент сопротивления снаряда
  k = 3 * c_f * rho / 4 / gamma / d;
 
  % Модуль скорости снаряда
  v = sqrt(Y(3) * Y(3) + Y(4) * Y(4));  
  
  % Система уравнений движения
  dYdt(1) = Y(3);
  dYdt(2) = Y(4);
  dYdt(3) = - k * v * Y(3);
  dYdt(4) = - k * v* Y(4) - g;
 
endfunction

Теперь решаем систему уравнений движения, в файле ballistics.m даем команды

Y_air = lsode("f_air", Y0, t);
plot(Y_air(:,1), Y_air(:,2));

то есть интегрируем новые уравнения движения с теми же начальными условиями и на том же временном интервале, что и для задачи без учета сопротивления воздуха, а так же рисуем график траектории

Ого, максимальная высота полета уменьшилась весьма существенно. И 47 секунд теперь слишком большой диапазон, снаряд падает на землю намного раньше. Поиграем со временем

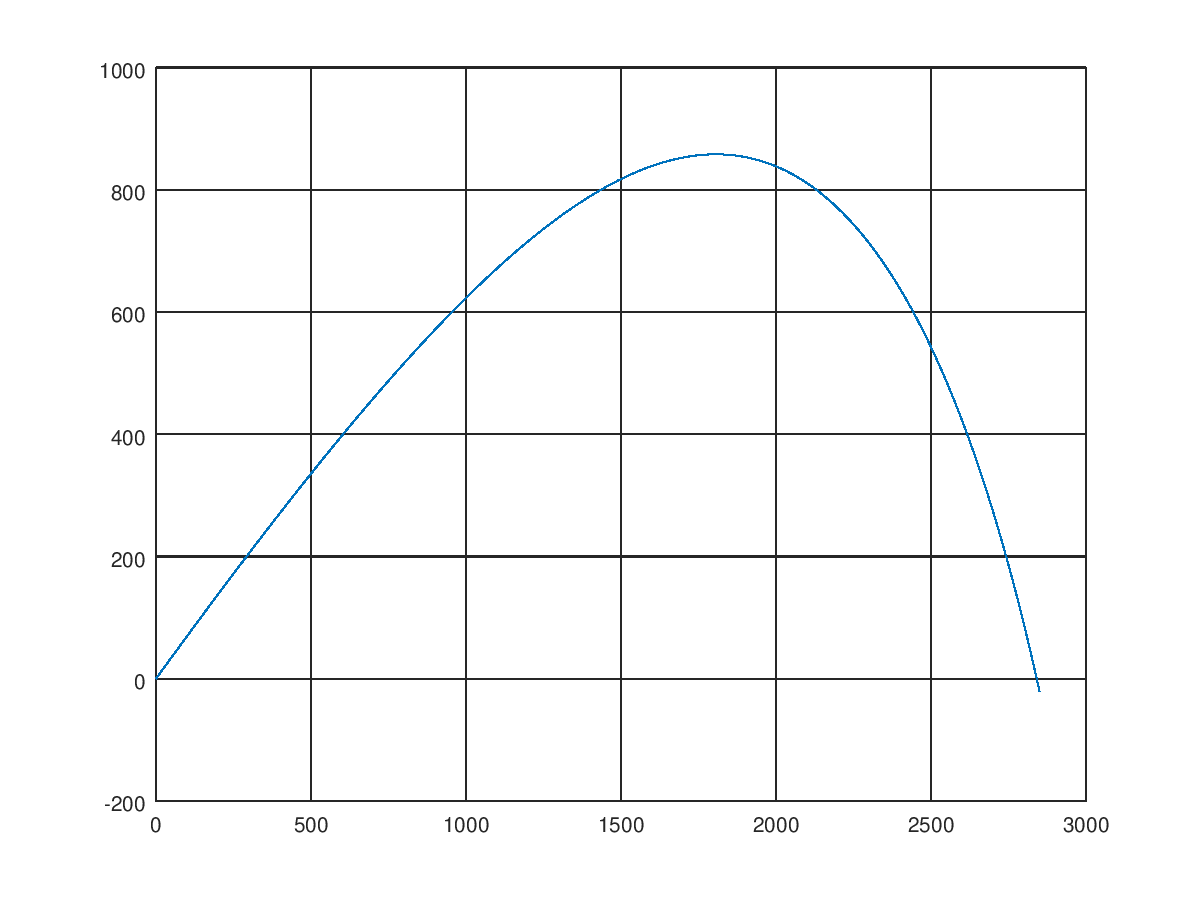
При tend = 26 секунды видим, что и дальность полета весьма значительно. Видно, что аэродинамическое сопротивление очень существенно влияет на характеристики нашего орудия и в реальности пренебрегать им нельзя. Меняется и форма траектории: она более полога на восходящем участке, и круто идет вниз на нисходящем, мало напоминая идеальную параболу.

5. Сравнение траекторий снаряда

Мы уже видим, что результаты моделирования полета ядра различаются между собой. Но всё познается в наглядном сравнении. Построим две траектории одновременно. Можно? Да проще простого

% Строим обе траектории
plot(Y_air(:,1), Y_air(:,2), Y(:,1), Y(:,2));

Сначала мы указали абсциссу и ординату для одной траектории, потом для другой. Что получилось?

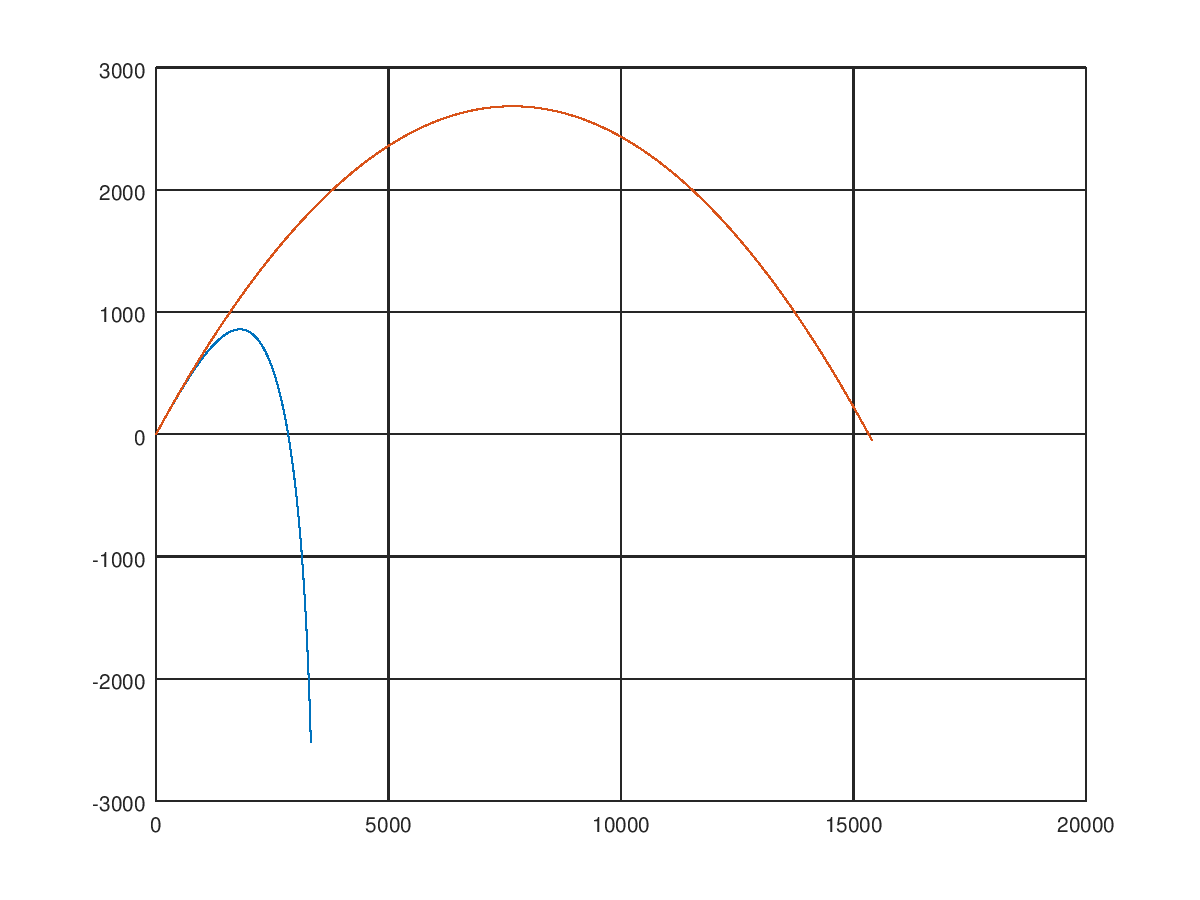
Эмм, это какой-то бред. Правильно, время полета снаряда в разных решениях разное. Столкновение ядра с поверхностью мы не моделируем. Из этой ситуации можно выкрутится, задав пределы изменения координат по осям командной axis(), вот так

% Задаем пределы отображения графиков по осям координат
xmin = 0;
xmax = 16000;
ymin = 0;
ymax = 3000;

axis([xmin xmax ymin ymax], "manual");

Теперь графики будут выглядеть так

Уже лучше. По крайней мере траектории можно сравнить между собой. А если нам хочется, чтобы по всем осям графика был одинаковый масштаб? Гугление дало такую команду

set(gca,'dataaspectratio',[1 1 1]);

определяющий одинаковый масштаб осей графика по всем осям координат

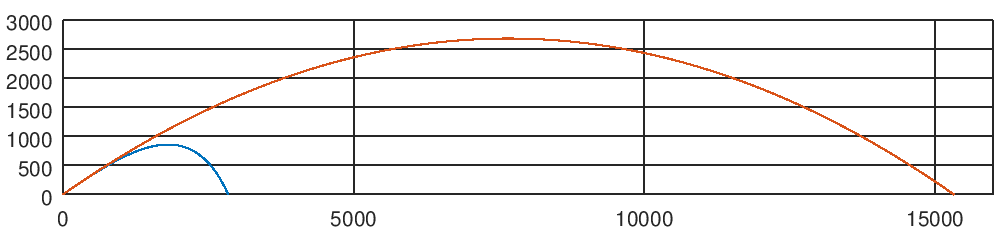
Под спойлером полный текст файла ballistics.m

%-------------------------------------------------------------------------------
% Параметры стрельбы
%-------------------------------------------------------------------------------

% начальная скорость снаряда
v0 = 400; 
% угол наклона ствола пушки к горизонту
alpha = 35 * pi / 180; 

%-------------------------------------------------------------------------------
% Начальные условия
%-------------------------------------------------------------------------------
x0 = 0;
y0 = 0;
vx0 = v0 * cos(alpha);
vy0 = v0 * sin(alpha);

Y0 = [x0; y0; vx0; vy0];

%-------------------------------------------------------------------------------
% Параметры временного интервала
%-------------------------------------------------------------------------------

% начальный момент времени
t0 = 0;
% конечный момент времени
tend = 47.0;
% шаг выдачи решения
deltaT = 0.1;

% Массив интересующих нас моментов времени
t = [t0:deltaT:tend];

% Интрегрируем систему уравнений движения
Y = lsode("f", Y0, t);

%-------------------------------------------------------------------------------
% Параметры снаряда
%-------------------------------------------------------------------------------

% плотность материала снаряда
global gamma = 7800; 
% коэффициент сопростивления формы (для шара)
global c_f = 0.47;
% калибр
global d = 0.1;

% Интегрируем систему уравнений движения 
Y_air = lsode("f_air", Y0, t);

% Строим обе траектории
plot(Y_air(:,1), Y_air(:,2), Y(:,1), Y(:,2));

% Задаем пределы отображения графиков по осям координт
xmin = 0;
xmax = 16000;
ymin = 0;
ymax = 3000;

axis([xmin xmax ymin ymax]);

% Задаем масштаб по осям
set(gca,'dataaspectratio',[1 1 1]);

Заключение

В рассмотренном нами примере мы столкнулись с фундаментальным свойством законов природы — они нелинейны. Если учитывать сопротивление воздуха, то правые в части дифференциальных уравнений фазовые координаты входят нелинейно. Аналитического решения, то есть выраженного в элементарных функциях задача не имеет. Наличие аналитического решения для реальных задач техники скорее исключение. И без моделирования при их решении уже никак не обойтись.

Но само по себе решение уравнений движения на практике имеет мало смысла. Что нам дало это решение? Да, мы увидели влияние силы сопротивления воздуха на полет пушечного ядра. Но мы, например, не ответили на многие вопросы, например, какова точная дальность стрельбы нашей пушки? Какова максимальная высота подъема снаряда? Под каким углом надо стрелять, чтобы достичь максимальной дальности?

Математические модели создают для того, чтобы решать с помощью них практические задачи техники. Вот об этом мы и поговорим в следующий раз.

P.S.: Проекты примеров теперь будут доступны на Github