Как найти координаты собственного вектора

Нахождение собственных чисел и собственных векторов

Данный калькулятор поможет найти собственные числа и векторы, используя характеристическое уравнение.

Больше:

Выводить десятичную дробь

,

• Оставляйте лишние ячейки пустыми для ввода неквадратных матриц.

• Элементы матриц – десятичные (конечные и периодические) дроби: 1/3, 3,14, -1,3(56) или 1,2e-4; либо арифметические выражения: 2/3+3*(10-4), (1+x)/y^2, 2^0,5 (=2), 2^(1/3), 2^n, sin(phi), cos(3,142rad), a_1 или (root of x^5-x-1 near 1,2).

  • decimal (finite and periodic) fractions:

    1/3, 3,14, -1,3(56) или 1,2e-4

  • 2/3+3*(10-4), (1+x)/y^2, 2^0,5 (=2), 2^(1/3), 2^n, sin(phi), cos(3,142rad), a_1 или (root of x^5-x-1 near 1,2)

  • matrix literals:

    {{1,3},{4,5}}

  • operators:

    +, -, *, /, , !, ^, ^{*}, ,, ;, ≠, =, ⩾, ⩽, > и <

  • functions:

    sqrt, cbrt, exp, log, abs, conjugate, min, max, gcd, rank, adjugate, inverse, determinant, transpose, pseudoinverse, cos, sin, tan, cot, cosh, sinh, tanh, coth, arccos, arcsin, arctan, arccot, arcosh, arsinh, artanh и arcoth

  • units:

    rad, deg

  • special symbols:

    • pi, e, i — mathematical constants
    • k, n — integers
    • I or E — identity matrix
    • X, Y — matrix symbols
• Используйте ↵ Ввод, Пробел, ←↑↓→, ⌫ и Delete для перемещения по ячейкам, Ctrl⌘ Cmd+C/Ctrl⌘ Cmd+V – для копирования матриц.
• Перетаскивайте матрицы из результата (drag-and-drop), или даже из текстового редактора.
• За теорией о матрицах и операциях над ними обращайтесь к страничке на Википедии.

Примеры

• Найти собственные векторы ({{-26,-33,-25},{31,42,23},{-11,-15,-4}})

Собственные числа и собственные векторы линейного оператора

Определение . Ненулевой вектор x называется собственным вектором оператора A , если оператор A переводит x в коллинеарный ему вектор, то есть A· x = λ· x . Число λ называется собственным значением или собственным числом оператора A, соответствующим собственному вектору x .
Отметим некоторые свойства собственных чисел и собственных векторов.
1. Любая линейная комбинация собственных векторов x ₁, x ₂, . x _m оператора A , отвечающих одному и тому же собственному числу λ, является собственным вектором с тем же собственным числом.
2. Собственные векторы x ₁, x ₂, . x _m оператора A с попарно различными собственными числами λ₁, λ₂, …, λ_m линейно независимы.
3. Если собственные числа λ₁=λ₂= λ_m= λ, то собственному числу λ соответствует не более m линейно независимых собственных векторов.

Итак, если имеется n линейно независимых собственных векторов x ₁, x ₂, . x _n, соответствующих различным собственным числам λ₁, λ₂, …, λ_n, то они линейно независимы, следовательно, их можно принять за базис пространства R_n. Найдем вид матрицы линейного оператора A в базисе из его собственных векторов, для чего подействуем оператором A на базисные векторы: 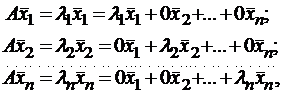тогда .
Таким образом, матрица линейного оператора A в базисе из его собственных векторов имеет диагональный вид, причем по диагонали стоят собственные числа оператора A.
Существует ли другой базис, в котором матрица имеет диагональный вид? Ответ на поставленный вопрос дает следующая теорема.

Теорема. Матрица линейного оператора A в базисе < ε _i> (i = 1..n) имеет диагональный вид тогда и только тогда, когда все векторы базиса – собственные векторы оператора A.

Правило отыскания собственных чисел и собственных векторов

Система (1) имеет ненулевое решение, если ее определитель D равен нулю

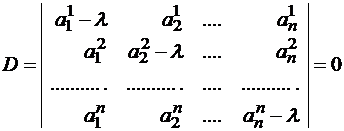
Пример №1 . Линейный оператор A действует в R₃ по закону A· x =(x₁-3x₂+4x₃, 4x₁-7x₂+8x₃, 6x₁-7x₂+7x₃), где x₁, x₂, . x_n – координаты вектора x в базисе e ₁=(1,0,0), e ₂=(0,1,0), e ₃=(0,0,1). Найти собственные числа и собственные векторы этого оператора.
Решение. Строим матрицу этого оператора:
A· e ₁=(1,4,6)
A· e ₂=(-3,-7,-7)
A· e ₃=(4,8,7)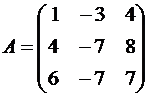
.
Составляем систему для определения координат собственных векторов:
(1-λ)x₁-3x₂+4x₃=0
x₁-(7+λ)x₂+8x₃=0
x₁-7x₂+(7-λ)x₃=0
Составляем характеристическое уравнение и решаем его:

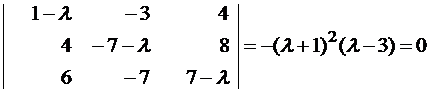
Пример №2 . Дана матрица .
1. Доказать, что вектор x =(1,8,-1) является собственным вектором матрицы A. Найти собственное число, соответствующее этому собственному вектору.
2. Найти базис, в котором матрица A имеет диагональный вид.

Решение находим с помощью калькулятора.
1. Если A· x =λ· x , то x – собственный вектор

Определение . Симметрической матрицей называется квадратная матрица, в которой элементы, симметричные относительно главной диагонали, равны, то есть в которой a_i k =a_k i .

Замечания .

1. Все собственные числа симметрической матрицы вещественны.
2. Собственные векторы симметрической матрицы, соответствующие попарно различным собственным числам, ортогональны.

В качестве одного из многочисленных приложений изученного аппарата, рассмотрим задачу об определении вида кривой второго порядка.

5.1.3. Собственные числа и собственные векторы матрицы

Вектор Х называется Собственным вектором матрицы А, если найдется такое число L, что выполняется равенство: АХ = LХ, то есть результатом применения к Х линейного оператора, задаваемого матрицей А, является умножение этого вектора на число L. Само число L называется Собственным числом матрицы А.

Подставив в формулы (3) X’J = LXj, получим систему уравнений для определения координат собственного вектора:

.

Эта линейная однородная система будет иметь нетривиальное решение только в случае, если ее главный определитель равен 0 (правило Крамера). Записав это условие в виде:

Получим уравнение для определения собственных чисел L, называемое Характеристическим уравнением. Кратко его можно представить так:

Поскольку в его левой части стоит определитель матрицы А-LЕ. Многочлен относительно L | A – LE| называется Характеристическим многочленом матрицы А.

Свойства характеристического многочлена:

1) Характеристический многочлен линейного преобразования не зависит от выбора базиса.

(см. (11.4)), но Следовательно, . Таким образом, не зависит от выбора базиса. Значит, и |A–LE| не изменяется при переходе к новому базису.

2) Если матрица А линейного оператора является Симметрической (т. е. АIj=Aji), то все корни характеристического уравнения (11.6) – действительные числа.

Свойства собственных чисел и собственных векторов:

1) Если выбрать базис из собственных векторов Х1, х2, х3, соответствующих собственным значениям λ1, λ2, λ3 матрицы А, то в этом базисе линейное преобразование А имеет матрицу диагонального вида:

Доказательство этого свойства следует из определения собственных векторов.

2) Если собственные значения оператора А различны, то соответствующие им собственные векторы линейно независимы.

3) Если характеристический многочлен матрицы А имеет три различных корня, то в некотором базисе матрица А имеет диагональный вид.

Найдем собственные числа и собственные векторы матрицы

Составим характеристическое уравнение:

Найдем координаты собственных векторов, соответствующих каждому найденному значению L. Из (5) следует, что если Х(1)=<X1,X2,X3> – собственный вектор, соответствующий L1=-2, то

Совместная, но неопределенная система. Ее решение можно записать в виде Х(1)=(A,0,-A), где А – любое число. В частности, если потребовать, чтобы |X(1)|=1,

Подставив в систему (5) L2=3, получим систему для определения координат второго собственного вектора – X(2)=(Y1,Y2,Y3):

Спектральная кластеризация

Дата публикации Feb 21, 2019

Введение

В этом посте мы рассмотрим тонкости спектральной кластеризации для графиков и других данных. Кластеризация является одной из главных задач в машинном обучении без учителя. Цель состоит в том, чтобы назначить немаркированные данные группам, где, возможно, аналогичные точки данных будут назначены в одну группу.

Спектральная кластеризация – это метод с корнями в теории графов, где этот подход используется для идентификации сообществ узлов в графе на основе соединяющих их ребер. Этот метод является гибким и позволяет кластеризовать не графовые данные.

Спектральная кластеризация использует информацию из собственных значений (спектра) специальных матриц, построенных из графика или набора данных. Мы узнаем, как построить эти матрицы, интерпретировать их спектр и использовать собственные векторы для назначения наших данных кластерам.

Собственные векторы и собственные значения

Критическим для этой дискуссии является концепция собственных значений и собственные векторы. Для матрицы A, если существует вектор x, который не является всеми 0 и скалярным λ, таким, что Ax = λx, то x называется собственным вектором A с соответствующим собственным значением λ.

Мы можем думать о матрице A как о функции, которая отображает векторы на новые векторы. Большинство векторов окажутся где-то совершенно разными, когда к ним будет применен A, но собственные векторы меняются только по величине. Если вы проведете линию через начало координат и собственный вектор, то после отображения собственный вектор все равно попадет на линию. Величина, по которой вектор масштабируется вдоль линии, зависит от λ.

Мы можем легко найти собственные значения и собственные векторы матрицы, используя numpy в Python:

Собственные векторы являются важной частью линейной алгебры, потому что они помогают описать динамику систем, представленных матрицами. Существует множество приложений, в которых используются собственные векторы, и мы будем использовать их непосредственно здесь для выполнения спектральной кластеризации.

диаграммы

Графики являются естественным способом представления многих типов данных. Граф – это набор узлов с соответствующим набором ребер, которые соединяют узлы. Края могут быть направленными или ненаправленными и даже иметь веса, связанные с ними.

Сеть роутеров в интернете легко представить в виде графика. Маршрутизаторы – это узлы, а ребра – это соединения между парами маршрутизаторов. Некоторые маршрутизаторы могут разрешать трафик только в одном направлении, поэтому границы могут быть направлены в направлении направления трафика. Веса на краях могут представлять полосу пропускания, доступную вдоль этого края. При такой настройке мы могли бы затем запросить график, чтобы найти эффективные пути для передачи данных от одного маршрутизатора к другому по сети.

Давайте использовать следующий неориентированный граф в качестве рабочего примера:

Этот граф имеет 10 узлов и 12 ребер. Он также имеет два соединенных компонента <0,1,2,8,9>и <3,4,5,6,7>. Связанный компонент – это максимальный подграф узлов, у всех из которых есть пути к остальным узлам подграфа.

Связанные компоненты кажутся важными, если наша задача – назначить эти узлы сообществам или кластерам. Простая идея – сделать каждый связанный компонент отдельным кластером. Это кажется разумным для нашего примера графа, но возможно, что весь граф может быть связан, или что связанные компоненты очень велики. Могут также быть меньшие структуры в связанном компоненте, которые являются хорошими кандидатами для сообществ. Вскоре мы увидим важность идеи связанного компонента для спектральной кластеризации.

Матрица смежности

Мы можем представить наш примерный граф в виде матрицы смежности, где индексы строк и столбцов представляют узлы, а записи представляют отсутствие или наличие ребра между узлами. Матрица смежности для нашего примера графа выглядит следующим образом:

В матрице мы видим, что строка 0, столбец 1 имеет значение 1. Это означает, что существует ребро, соединяющее узел 0 с узлом 1. Если ребра были взвешены, веса ребер были бы в этой матрице вместо только 1 и 0. Так как наш график не направлен, записи для строки i, col j будут равны записи в строке j, col i. Последнее, что следует отметить, это то, что диагональ этой матрицы равна 0, поскольку ни один из наших узлов не имеет ребер.

Степень Матрица

Степень узла – это количество ребер, соединенных с ним. В ориентированном графе мы могли бы говорить о степени и степени, но в этом примере у нас просто есть степень, так как ребра идут в обе стороны. Глядя на наш график, мы видим, что узел 0 имеет степень 4, поскольку он имеет 4 ребра. Мы также можем получить степень, взяв сумму строки узла в матрице смежности.

Матрица степеней – это диагональная матрица, где значение на входе (i, i) является степенью узла i Давайте найдем матрицу степеней для нашего примера:

Сначала мы взяли сумму по оси 1 (строки) нашей матрицы смежности, а затем поместили эти значения в диагональную матрицу. Из матрицы степеней мы легко видим, что узлы 0 и 5 имеют 4 ребра, в то время как остальные узлы имеют только 2.

График лапласианский

Теперь мы собираемся вычислить граф Лапласа. Лапласиан – это просто еще одно матричное представление графа. У него есть несколько прекрасных свойств, которыми мы воспользуемся для спектральной кластеризации. Чтобы вычислить нормальный лапласиан (есть несколько вариантов), мы просто вычитаем матрицу смежности из нашей матрицы степеней:

Диагональ лапласиана – это степень наших узлов, а вне диагонали – вес отрицательного края. Это представление, которое мы ищем для выполнения спектральной кластеризации.

Собственные значения графа лапласиана

Как уже упоминалось, лапласиан обладает некоторыми прекрасными свойствами. Чтобы понять это, давайте рассмотрим собственные значения, связанные с лапласианом, когда я добавлю ребра в наш граф:

Мы видим, что когда граф полностью отключен, все десять наших собственных значений равны 0. Когда мы добавляем ребра, некоторые из наших собственных значений увеличиваются. Фактически, число собственных значений 0 соответствует числу связанных компонент в нашем графе!

Посмотрите внимательно, как добавлен этот последний край, соединяя два компонента в один. Когда это происходит, все собственные значения, кроме одного, были отменены:

Первое собственное значение равно 0, потому что у нас есть только один связный компонент (весь граф связен). Соответствующий собственный вектор всегда будет иметь постоянные значения (в этом примере все значения близки к 0,32).

Первое ненулевое собственное значение называется спектральной щелью. Спектральная щель дает нам некоторое представление о плотности графика. Если бы этот граф был плотно связан (все пары из 10 узлов имели ребро), то спектральный разрыв был бы 10.

Второе собственное значение называется значением Фидлера, а соответствующий вектор является вектором Фидлера. Значение Фидлера приблизительно соответствует минимальному срезу графа, необходимому для разделения графа на два связанных компонента. Напомним, что если бы в нашем графе уже было два связанных компонента, то значение Фидлера было бы равно 0. Каждое значение в векторе Фидлера дает нам информацию о том, какой стороне разреза принадлежит этот узел. Давайте раскрасим узлы в зависимости от того, положительна ли их запись в векторе Филдера:

Этот простой трюк разделил наш график на две группы! Почему это работает? Помните, что нулевые собственные значения представляют связанные компоненты. Собственные значения около нуля говорят нам, что существует почти разделение двух компонентов. Здесь у нас есть одно преимущество: если бы его не было, у нас было бы два отдельных компонента. Таким образом, второе собственное значение мало.

Подводя итог, что мы знаем до сих пор: первое собственное значение 0, потому что у нас есть один связанный компонент. Второе собственное значение около 0, потому что мы на расстоянии одного края от двух соединенных компонентов. Мы также видели, что вектор, связанный с этим значением, говорит нам, как разделить узлы на эти приблизительно связанные компоненты.

Возможно, вы заметили, что следующие два собственных значения также довольно малы. Это говорит нам о том, что мы «близки» к четырем отдельным подключенным компонентам. В общем, мы часто ищем первый большой разрыв между собственными значениями, чтобы найти число кластеров, выраженных в наших данных. Видите разрыв между собственными значениями четыре и пять?

Наличие четырех собственных значений перед разрывом указывает на то, что, вероятно, существует четыре кластера. Векторы, связанные с первыми тремя положительными собственными значениями, должны дать нам информацию о том, какие три разреза необходимо сделать на графике, чтобы назначить каждый узел одному из четырех приближенных компонентов. Давайте построим матрицу из этих трех векторов и выполним кластеризацию K-средних для определения назначений:

График был сегментирован на четыре квадранта, причем узлы 0 и 5 произвольно назначены одному из их связанных квадрантов. Это действительно круто, и это спектральная кластеризация!

Подводя итог, мы сначала взяли наш граф и построили матрицу смежности. Затем мы создали лапласиан графа, вычтя матрицу смежности из матрицы степеней. Собственные значения лапласиана указывали на наличие четырех кластеров. Векторы, связанные с этими собственными значениями, содержат информацию о том, как сегментировать узлы. Наконец, мы выполнили K-средства для этих векторов, чтобы получить метки для узлов. Далее мы увидим, как это сделать для произвольных данных.

Спектральная кластеризация произвольных данных

Посмотрите на данные ниже. Точки нарисованы из двух концентрических кругов с добавлением шума Нам бы хотелось, чтобы алгоритм позволял группировать эти точки в два круга, которые их генерировали.

Эти данные не в форме графика. Итак, во-первых, давайте просто попробуем алгоритм обрезки печенья, такой как K-Means. K-Means найдет два центроида и пометит точки, в зависимости от того, к какому центроиду они ближе всего. Вот результаты:

Очевидно, K-Means не собирался работать. Он действует на евклидовом расстоянии и предполагает, что скопления примерно сферические. Эти данные (и часто данные реального мира) нарушают эти предположения. Давайте попробуем решить эту проблему с помощью спектральной кластеризации.

График ближайших соседей

Есть несколько способов обработать наши данные как график. Самый простой способ – построить граф k-ближайших соседей. Граф k-ближайших соседей обрабатывает каждую точку данных как узел в графе. Затем ребро рисуется от каждого узла до его k ближайших соседей в исходном пространстве. Как правило, алгоритм не слишком чувствителен к выбору k. Меньшие числа, такие как 5 или 10, обычно работают довольно хорошо.

Посмотрите на изображение данных еще раз и представьте, что каждая точка связана со своими 5 ближайшими соседями. Любая точка во внешнем кольце должна быть в состоянии следовать по пути вдоль кольца, но во внутреннем круге не будет никаких путей. Довольно легко увидеть, что этот график будет иметь два связанных компонента: внешнее кольцо и внутренний круг.

Поскольку мы разделяем эти данные только на два компонента, мы должны использовать наш векторный метод Фидлера ранее. Вот код, который я использовал для спектральной кластеризации этих данных:

И вот результаты:

Другие подходы

Граф ближайших соседей – хороший подход, но он основан на том факте, что «близкие» точки должны принадлежать одному кластеру. В зависимости от ваших данных, это может быть не так. Более общий подход заключается в построении аффинной матрицы. Матрица сходства похожа на матрицу смежности, за исключением того, что значение для пары точек показывает, насколько эти точки похожи друг на друга. Если пары точек сильно различаются, то сродство должно быть 0. Если точки идентичны, то сродство может быть 1. Таким образом, сродство действует как вес для ребер нашего графа.

Как решить, что означает совпадение двух точек данных, является одним из наиболее важных вопросов в машинном обучении. Часто знание предметной области – лучший способ построить меру подобия. Если у вас есть доступ к экспертам по доменам, задайте им этот вопрос.

Есть также целые поля, посвященные изучению того, как строить метрики подобия непосредственно из данных. Например, если у вас есть некоторые помеченные данные, вы можете обучить классификатор, чтобы предсказать, похожи ли два входа или нет, основываясь на том, имеют ли они одинаковую метку. Затем этот классификатор можно использовать для присвоения сходства парам немаркированных точек.

Вывод

Мы рассмотрели теорию и применение спектральной кластеризации для графов и произвольных данных. Спектральная кластеризация – это гибкий подход для поиска кластеров, когда ваши данные не соответствуют требованиям других распространенных алгоритмов.

Сначала мы сформировали график между нашими точками данных. Края графика отражают сходство точек. Собственные значения графа лапласиана могут затем использоваться для поиска наилучшего числа кластеров, а собственные векторы могут использоваться для поиска фактических меток кластеров.

Я надеюсь, что вам понравился этот пост, и вы нашли спектральную кластеризацию полезной в вашей работе или исследовании.

[spoiler title=”источники:”]

http://matica.org.ua/metodichki-i-knigi-po-matematike/lineinaia-algebra-i-analiticheskaia-geometriia/5-1-3-sobstvennye-chisla-i-sobstvennye-vektory-matritcy

http://www.machinelearningmastery.ru/spectral-clustering-aba2640c0d5b/

[/spoiler]

Собственные числа и собственные векторы матрицы.

Определение 9.3. Вектор х
называется собственным вектором
матрицы А, если найдется такое число
λ, что выполняется равенство: Ах
= λх, то есть результатом
применения к х линейного
преобразования, задаваемого матрицей
А, является умножение этого вектора
на число λ. Само число λ называется
собственным числом матрицы А.

Подставив в формулы (9.3) x`_j
= λx_j,
получим систему уравнений для определения
координат собственного вектора:

.

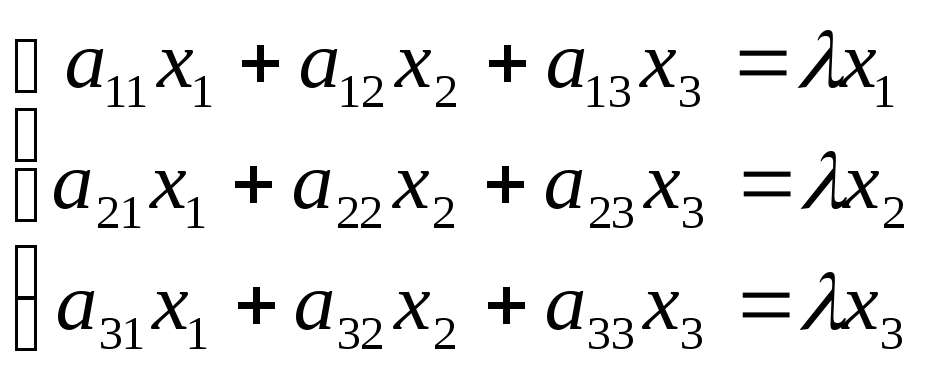Отсюда

.
(9.5)

Эта линейная однородная система будет
иметь нетривиальное решение только в
случае, если ее главный определитель
равен 0 (правило Крамера). Записав это
условие в виде:

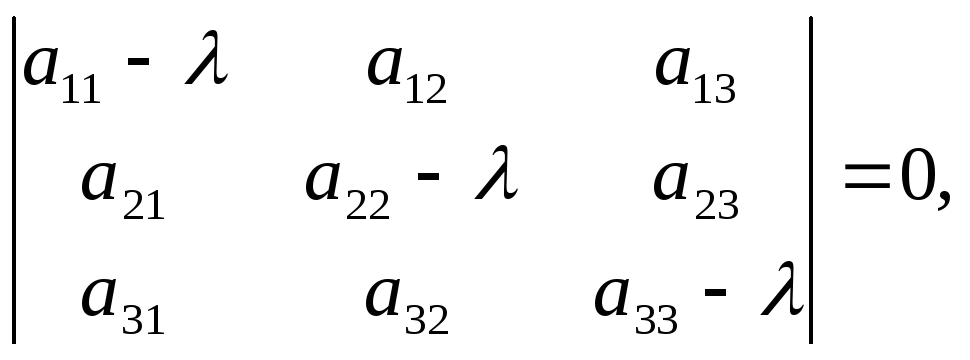
получим уравнение для определения
собственных чисел λ, называемое
характеристическим уравнением.
Кратко его можно представить так:

| A
– λE
| = 0,
(9.6)

поскольку в его левой части стоит
определитель матрицы А-λЕ. Многочлен
относительно λ | A
– λE| называется
характеристическим многочленом
матрицы А.

Свойства характеристического
многочлена:

1. Характеристический многочлен линейного
   преобразования не зависит от выбора
   базиса.
   Доказательство.
   (см.
   (9.4)), но
   следовательно,
   .
   Таким образом,
   
   не зависит от выбора базиса. Значит, и
   |A-λE|
   не изменяется при переходе к новому
   базису.

2. Если матрица А линейного преобразования
   является симметрической (т.е.
   а_ij=a_ji),
   то все корни характеристического
   уравнения (9.6) – действительные числа.

Свойства собственных чисел и
собственных векторов:

1. Если выбрать базис из собственных
   векторов х₁,
   х₂, х₃,
   соответствующих собственным значениям
   λ₁, λ₂, λ₃
   матрицы А, то в этом базисе линейное
   преобразование А имеет матрицу
   диагонального вида:

(9.7)
Доказательство
этого свойства следует из определения
собственных векторов.

1. Если собственные значения преобразования
   А различны, то соответствующие им
   собственные векторы линейно независимы.

2. Если характеристический многочлен
   матрицы А имеет три различных корня,
   то в некотором базисе матрица А
   имеет диагональный вид.

Пример.

Найдем собственные числа и собственные
векторы матрицы

Составим характеристическое уравнение:

(1- λ)(5 –
λ)(1 – λ) + 6 – 9(5 – λ) – (1 – λ) –
(1 – λ) = 0, λ³ – 7λ² + 36 = 0, λ₁
= -2, λ₂ = 3, λ₃ = 6.

Найдем координаты собственных векторов,
соответствующих каждому найденному
значению λ. Из (9.5) следует, что если
х₍₁₎={x₁,x₂,x₃}
– собственный вектор, соответствующий
λ₁=-2, то

– совместная, но неопределенная система.
Ее решение можно записать в виде
х₍₁₎={a,0,-a},
где а – любое число. В частности, если
потребовать, чтобы |x₍₁₎|=1,
х₍₁₎=

Подставив в систему (9.5) λ₂=3,
получим систему для определения координат
второго собственного вектора –
x₍₂₎={y₁,y₂,y₃}:

,
откуда х₍₂₎={b,-b,b}
или, при условии |x₍₂₎|=1,
x₍₂₎=

Для λ₃ = 6 найдем собственный
вектор x₍₃₎={z₁,
z₂, z₃}:

,
x₍₃₎={c,2c,c}
или в нормированном варианте

х₍₃₎ =
Можно
заметить, что х₍₁₎х₍₂₎
= ab – ab
= 0, x₍₁₎x₍₃₎
= ac – ac
= 0, x₍₂₎x₍₃₎
= bc – 2bc
+ bc = 0. Таким
образом, собственные векторы этой
матрицы попарно ортогональны.

Лекция 10.

Квадратичные формы и их связь с
симметричными матрицами. Свойства
собственных векторов и собственных
чисел симметричной матрицы. Приведение
квадратичной формы к каноническому
виду.

Определение 10.1. Квадратичной
формой действительных переменных
х₁, х₂,…,х_n
называется многочлен второй степени
относительно этих переменных, не
содержащий свободного члена и членов
первой степени.

Примеры квадратичных форм:

(n = 2),

(n = 3). (10.1)

Напомним данное в прошлой лекции
определение симметрической матрицы:

Определение 10.2. Квадратная матрица
называется симметрической, если
,
то есть если равны элементы матрицы,
симметричные относительно главной
диагонали.

Свойства собственных чисел и
собственных векторов симметрической
матрицы:

1. Все собственные числа симметрической
   матрицы действительные.

Доказательство (для n
= 2).

Пусть матрица А имеет вид:
.
Составим характеристическое уравнение:

(10.2) Найдем дискриминант:

следовательно, уравнение имеет только
действительные корни.

1. Собственные векторы симметрической
   матрицы ортогональны.

Доказательство (для n
= 2).

Координаты собственных векторов

и

должны удовлетворять уравнениям:

Следовательно, их можно задать так:

.
Скалярное произведение этих векторов
имеет вид:

По теореме Виета из уравнения (10.2)
получим, что

Подставим эти соотношения в предыдущее
равенство:

Значит,
.

Замечание. В примере, рассмотренном в
лекции 9, были найдены собственные
векторы симметрической матрицы и
обращено внимание на то, что они оказались
попарно ортогональными.

Определение 10.3. Матрицей квадратичной
формы (10.1) называется симметрическая
матрица
.
(10.3)

Таким образом, все собственные числа
матрицы квадратичной формы действительны,
а все собственные векторы ортогональны.
Если все собственные числа различны,
то из трех нормированных собственных
векторов матрицы (10.3) можно построить
базис в трехмерном пространстве. В этом
базисе квадратичная форма будет иметь
особый вид, не содержащий произведений
переменных.

Соседние файлы в папке лекции, 1 сем.

• #
• #

Со́бственный ве́ктор — понятие в линейной алгебре, определяемое для произвольного линейного оператора как ненулевой вектор, применение к которому оператора даёт коллинеарный вектор — тот же вектор, умноженный на некоторое скалярное значение (которое может быть равно 0). Скаляр, на который умножается собственный вектор под действием оператора, называется собственным числом (или собственным значением) линейного оператора, соответствующим данному собственному вектору. Одним из представлений линейного оператора является квадратная матрица, поэтому собственные векторы и собственные значения часто определяются в контексте использования таких матриц^[1][2].

Понятия собственного вектора и собственного числа^[3] являются одними из ключевых в линейной алгебре, на их основе строится множество конструкций. Это связано с тем, что многие соотношения, связанные с линейными операторами, существенно упрощаются в системе координат, построенной на базисе из собственных векторов оператора. Множество собственных значений линейного оператора (спектр оператора) характеризует важные свойства оператора без привязки к какой-либо конкретной системе координат. По этим причинам собственные векторы имеют важное прикладное значение. Так, например, собственные векторы часто встречаются в механике, квантовой теории и так далее. В частности, оператор проекции спина на произвольную ось имеет два собственных значения и соответствующие им собственные векторы.

Понятие линейного векторного пространства не ограничивается «чисто геометрическими» векторами и обобщается на разнообразные множества объектов, таких как пространства функций (в которых действуют линейные дифференциальные и интегральные операторы). Для такого рода пространств и операторов говорят о собственных функциях операторов.

Множество всех собственных векторов линейного оператора, соответствующих данному собственному числу, дополненное нулевым вектором, называется собственным подпространством^[4] этого оператора.

Поиск оптимальных алгоритмов вычисления собственных значений для заданного линейного оператора является одной из важных задач вычислительной математики.

Определения[править | править код]

Собственным вектором линейного преобразования , где  — линейное пространство над полем , называется такой ненулевой вектор , что для некоторого имеет место .

Собственным значением (собственным числом) линейного преобразования называется такое число , для которого существует собственный вектор, то есть уравнение имеет ненулевое решение .

Упрощённо говоря, собственный вектор — любой ненулевой вектор , который отображается в коллинеарный ему вектор оператором , а соответствующий скаляр называется собственным значением оператора.

Собственным подпространством (или характеристическим подпространством) линейного преобразования для данного собственного числа (или отвечающим этому числу) называется множество всех собственных векторов , соответствующих данному собственному числу, дополненное нулевым вектором. Обозначим собственное подпространство, отвечающее собственному числу , через , а единичный оператор — через . По определению, собственное подпространство является ядром оператора то есть множеством векторов, отображаемых этим оператором в нулевой вектор:

.

Корневым вектором линейного преобразования для данного собственного значения называется такой ненулевой вектор , что для некоторого натурального числа имеет место:

.

Если является наименьшим из таких натуральных чисел (то есть ), то называется высотой корневого вектора .

Корневым подпространством линейного преобразования для данного собственного числа называется множество всех корневых векторов , соответствующих данному собственному числу, если это множество дополнить нулевым вектором. Обозначим корневое подпространство, отвечающее собственному числу λ, через . По определению:

.

История[править | править код]

Собственные значения обычно вводятся в контексте линейной алгебры, однако исторически они возникли при исследовании квадратичных форм и дифференциальных уравнений.

В XVIII веке Эйлер, изучая вращательное движение абсолютно твёрдого тела, обнаружил значимость главных осей, а Лагранж показал, что главные оси соответствуют собственным векторам матрицы инерции. В начале XIX века Коши использовал труды Эйлера и Лагранжа для классификации поверхностей второго порядка и обобщил результаты на высшие порядки. Коши также ввёл термин «характеристический корень» (фр. racine caractéristique) для собственного значения. Этот термин сохранился в контексте характеристического многочлена матрицы^[5][6].

В начале XX века Гильберт занимался исследованием собственных значений интегральных операторов, рассматривая последние как матрицы бесконечного размера^[7]. В 1904 году для обозначения собственных значений и собственных векторов Гильберт начал использовать термины eigenvalues и eigenvectors, основанные на немецком слове eigen (собственный)^[8]. Впоследствии эти термины перешли и в английский язык, заменив используемые ранее «proper value» и «proper vector»^[9].

Свойства[править | править код]

Общий случай[править | править код]

Подпространство называется инвариантным подпространством линейного преобразования (-инвариантным подпространством), если:

.

Собственные подпространства , корневые подпространства и подпространства линейного оператора являются -инвариантными.

Собственные векторы являются корневыми (высоты 1): ;

Корневые векторы могут не быть собственными: например, для преобразования двумерного пространства, заданного матрицей:

, и все векторы являются корневыми, соответствующими собственному числу , но имеет единственный собственный вектор (с точностью до умножения на число).

Для разных собственных значений корневые (и, следовательно, собственные) подпространства имеют тривиальное (нулевое) пересечение:

если .

Метод поиска собственных значений для самосопряжённых операторов и поиска сингулярных чисел для нормального оператора даёт теорема Куранта — Фишера.

Конечномерные линейные пространства[править | править код]

Выбрав базис в -мерном линейном пространстве , можно сопоставить линейному преобразованию квадратную матрицу и определить для неё характеристический многочлен матрицы:

.

Характеристический многочлен не зависит от базиса в . Его коэффициенты являются инвариантами оператора . В частности, , не зависят от выбора базиса.

Собственные значения, и только они, являются корнями характеристического многочлена матрицы. Количество различных собственных значений не может превышать размер матрицы. Если выбрать в качестве базисных векторов собственные векторы оператора, то матрица в таком базисе станет диагональной, причём на диагонали будут стоять собственные значения оператора. Отметим, однако, что далеко не любая матрица допускает базис из собственных векторов (общая структура описывается нормальной жордановой формой). Для положительно определённой симметричной матрицы процедура нахождения собственных значений и собственных векторов является не чем иным, как поиском направлений и длин полуосей соответствующего эллипса.

Если числовое поле алгебраически замкнуто (например, является полем комплексных чисел), то характеристический многочлен разлагается в произведение линейных множителей:

,

где  — собственные значения; некоторые из могут быть равны. Кратность собственного значения  — это число множителей, равных в разложении характеристического многочлена на линейные множители (называется также алгебраическая кратность собственного значения).

Размерность корневого пространства равна кратности собственного значения.

Векторное пространство разлагается в прямую сумму корневых подпространств (по теореме о жордановой форме):

где суммирование производится по всем  — собственным числам .

Геометрическая кратность собственного значения  — это размерность соответствующего собственного подпространства ; геометрическая кратность собственного значения не превосходит его кратности, поскольку

Нормальные операторы и их подклассы[править | править код]

Все корневые векторы нормального оператора являются собственными. Собственные векторы нормального оператора , соответствующие различным собственным значениям, ортогональны, то есть если , и , то (для произвольного оператора это неверно).

Все собственные значения самосопряжённого оператора являются вещественными, антиэрмитового оператора — мнимыми, а все собственные значения унитарного оператора лежат на единичной окружности .

В конечномерном случае сумма размерностей собственных подпространств нормального оператора , соответствующих всем собственным значениям, равна размерности матрицы, а векторное пространство разлагается в ортогональную сумму собственных подпространств:

,

где суммирование производится по всем  — собственным числам , а взаимно ортогональны для различных . Это свойство для нормального оператора над в конечномерном случае является характеристическим: оператор нормален тогда и только тогда, когда его матрица имеет диагональный вид в каком-нибудь ортонормированном базисе.

Положительные матрицы[править | править код]

Квадратная вещественная матрица называется положительной, если все её элементы положительны: .

Теорема Перрона (частный случай теоремы Перрона — Фробениуса): Положительная квадратная матрица имеет положительное собственное значение , которое имеет алгебраическую кратность 1 и строго превосходит абсолютную величину любого другого собственного значения этой матрицы. Собственному значению соответствует собственный вектор , все координаты которого строго положительны. Вектор  — единственный собственный вектор (с точностью до умножения на число), имеющий неотрицательные координаты.

Собственный вектор может быть вычислен посредством прямых итераций: выбирается произвольный начальный вектор с положительными координатами, последующий элемент задаётся рекуррентной формулой:

,

получается последовательность , сходящаяся к нормированному собственному вектору .

Другая область применения метода прямых итераций — поиск собственных векторов положительно определённых симметричных операторов.

Неравенства для собственных значений[править | править код]

Неравенство Шура: для собственных значений  матрицы :

,

причём равенство достигается тогда и только тогда, когда  — нормальная матрица^[10].

Для собственных значений матрицы , где матрицы  — эрмитовы, имеет место:

и ^[11].

Для эрмитовых матриц  и их собственные значения, упорядоченные в порядке возрастания: дают: при и при ^[11].

Примечания[править | править код]

Литература[править | править код]

• Гантмахер Ф. Р.. Теория матриц. — М.: Наука, 1966. — 576 с. — ISBN ISBN 5-9221-0524-8.
• Уилкинсон Д. Х. Алгебраическая проблема собственных значений. — М.: Наука, 1970. — 564 с. — ISBN 978-5-458-25464-9.
• Гельфанд И. М.. Лекции по линейной алгебре. — М.: Добросвет, КДУ, 2009. — 320 с. — 1000 экз. — ISBN 978-5-98227-625-4.
• Фаддеев Д. К.. Лекции по алгебре. — М.: ЁЁ Медиа, 2012. — 416 с. — ISBN 978-5-458-25543-1.
• Шафаревич И. Р., Ремизов А. О. Линейная алгебра и геометрия. — М.: Физматлит, 2009. — 512 с. — ISBN 978-5-9221-1139-3.
• Прасолов В. В. Задачи и теоремы линейной алгебры. — М.: Наука, 1996. — 304 с. — ISBN 5-02-014727-3.
• Икрамов Х. Д. Несимметричная проблема собственных значений. — М.: Наука, 1991. — 240 с. — ISBN 5-02-014462-2.
• Herstein, I. N. (1964), Topics In Algebra, Waltham: Blaisdell Publishing Company, ISBN 978-1114541016
• Horn, Roger A. & Johnson, Charles F. (1985), Matrix analysis, Cambridge University Press, ISBN 0-521-30586-1
• Nering, Evar D. (1970), Linear Algebra and Matrix Theory (2nd ed.), New York: Wiley
• Kline, Morris (1972), Mathematical thought from ancient to modern times, Oxford University Press, ISBN 0-19-501496-0