Сложение векторов
Формула
Чтобы складывать вектора нужно найти суммы соответствующих координат данных векторов. Например, пусть есть векторы на плоскости $ overline{a} = (x_1;y_1) $ и $ overline{b}=(x_2;y_2) $, тогда их сумму можно найти по формуле: $$ overline{a}+overline{b} = (x_1+x_2;y_1+y_2)$$
Если векторы заданы в пространстве тремя координатами $ overline{a} = (x_1;y_1;z_1) $ и $ overline{b}=(x_2;y_2;z_2) $, то выполнить сложение нужно по другой формуле:
$$ overline{a}+overline{b} = (x_1+x_2;y_1+y_2; z_1+z_2) $$
При сложении первая координата первого вектора складывается с первой координатой второго вектора, вторая координата первого вектора складывается со второй координатой второго вектора и так далее в зависимости от размерности векторов. Стоит отметить, что складывать векторы можно только одинаковой размерности.
Примеры решений
| Пример |
| Даны два вектора $ overline{a} = (1,3) $ и $ overline{b} = (2,4) $. Нужно сложить два вектора. |
| Решение |
|
Итак, как складывать вектора по координатам? К первой прибавляем первую, вторую ко второй: $$ overline{a}+overline{b} = (1+2;3+4) = (3;7) $$ В этой задаче векторы заданы в двумерном пространстве и имеют только две координаты. Если бы координат было бы три, то применять нужно вторую формулу для трехмерной задачи. Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$ overline{a}+overline{b} = (3;7) $$ |
Операции над векторами в прямоугольной системе координат
Если задана плоскость O x y с векторами a → = a x , a y и b → = ( b x , b y ) , то мы можем разложить их по координатным векторам i → и j → . Тогда это будет иметь вид a → = a x · i → + a y · j → и b → = b x · i → + b y · j → . Чтобы найти сумму a → и b → и произведение a → на λ , рассмотрим:
a → + b → = a x · i → + a y · j → + b x · i → + b y · j → = ( a x + b x ) · i → + ( a y + b y ) · j →
λ · a → = λ · ( a x · i → + a y · j → ) = ( λ · a x ) · i → + ( λ · a y ) · j →
Это равенство справедливо по свойству операций над векторами.
Разложение векторов – это a → + b → и λ · a → , представленное в частях неравенства по i → и j → координатам. Координаты векторов a → + b → и λ · a → равны соответственно ( a x + b x , a y + b y ) и ( λ · a x , λ · a y ) .
Таким же образом a → = ( a x , a y , a z ) и b → = ( b x , b y , b z ) записываются как a → + b → = a x · i → + a y · j → + a z · k → + b x · i → + b y · j → + b z · k → = ( a x + b x ) · i ⇀ + ( a y + b y ) · j → + ( a z + b z ) · k → λ · a → = λ · ( a x · i → + a y · j → + a z · k → ) = ( λ · a x ) · i → + ( λ · a y ) · j → + ( λ · a z ) · k →
а значит a → + b → = ( a x + b x , a y + b y , a z + b z ) , λ · a → = ( λ · a x , λ · a y , λ · a z )
Отсюда делаем вывод, что координаты векторов a → и b → равны сумме соответствующих координат векторов a → и b → , координаты произведения вектора a → на λ приравниваются к соответствующим координатам вектора a → , умноженным на число в заданной системе координат.
При необходимости нахождения координат суммы нескольких векторов, необходимо сложить координаты каждого вектора соответственно. Рассмотрим примеры.
Нужно выполнить сложение a → = ( 2 , 3 – 1 3 ) и b → = ( – 1 , – 1 3 ) . Чему равны координаты произведения вектора a → на 3 .
Решение
Из определения имеем, что сумма векторов равна сумме их координат соответственно, тогда a → + b → = ( 2 + ( – 1 ) , 3 – 1 3 + ( – 1 3 ) ) = ( 1 , – 1 3 ) .
Числовое значение умножается на каждую координату: 3 · a → = ( 3 · 2 , 3 · 3 – 1 3 ) = 2 3 , 3 – 3 3 .
Ответ: a → + b → = ( 1 , – 1 3 ) , 3 · a → = ( 2 3 , 3 – 3 3 )
Заданы векторы a → = ( 0 , 1 , – 2 ) , b → = ( – 1 , – 1 , 3 ) , c → = ( 4 , – 3 , 2 ) .
Каковы координаты вектора 2 · a → + 3 · ( b → – c → ) = 2 · a → + 3 · b → + ( – 3 ) · c → .
Решение
Применяя свойства векторов, получим: 2 · a → + 3 · ( b → – c → ) = 2 · a → + 3 · b → + ( – 3 ) · c → .
Подставляем значения координат и получаем: 2 · a → + 3 · b → + ( – 3 ) · c → = 2 · ( 0 , 1 , – 2 ) + 3 · ( – 1 , – 1 , 3 ) + ( – 3 ) · ( 4 , – 3 , 2 ) =
= ( 2 · 0 , 2 · 1 , 2 · ( – 2 ) ) + ( 3 · ( – 1 ) , 3 · ( – 1 ) , 3 · 3 ) + ( ( – 3 ) · 4 , ( – 3 ) · ( – 3 ) · 2 ) =
= ( 0 , 2 , – 4 ) + ( – 3 , – 3 , 9 ) + ( – 12 , 9 – 6 ) =
= ( 0 + ( – 3 ) + ( – 12 ) , 2 + ( – 3 ) + 9 , – 4 + 9 + ( – 6 ) ) = ( – 15 , 8 , – 1 )
Можно решить другим способом.
Обратим внимание на разложение a → , b → и c → :
a → = 0 · i → + 1 · j → + ( – 2 ) · k → = j → – 2 · k →
b → = ( – 1 ) · i → + ( – 1 ) · j → + 3 · k → = – i → – j → + 3 · k →
c → = 4 · i → + ( – 3 ) · j → + 2 · k → = 4 · i → – 3 · j → + 2 · k →
Исходя из свойств векторов, видим, что: 2 · a → + 3 · ( b → – c → ) = 2 · ( j → – 2 · k → ) + 3 · ( – i → – j → + 3 · k → – ( 4 · i → – 3 · j → + 2 · k → ) ) = = 2 · j → – 4 · k → + 3 · ( – 5 · i → + 2 · j → + 1 · k → ) = – 15 · i → + 8 · j → – k →
Значит, координаты вектора 2 · a → + 3 · ( b → – c → ) равны ( – 15 , 8 , – 1 ) .
Ответ: 2 · a → + 2 · ( b → – c → ) = ( – 15 , 8 , – 1 )
Координаты вектора. Направляющие косинусы
Для решения задач с векторами необходимо определить вектор на плоскости или в пространстве, то есть дать информацию о его направлении и длине.
Координаты вектора
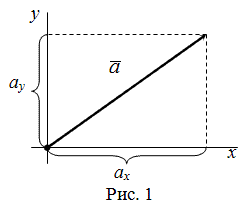
Пусть задана прямоугольная декартова система координат (ПДСК) $x O y$ и произвольный вектор $overline$, начало которого совпадает с началом системы координат (рис. 1).
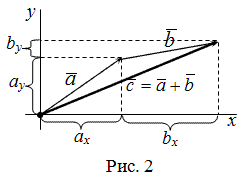
Сумма двух векторов, заданных координатами
Чтобы найти сумму двух векторов, заданных своими координатами, надо сложить их соответствующие координаты.

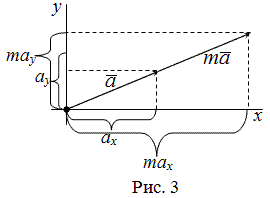
Умножение вектора на число
Чтобы умножить вектор на число, надо каждую координату этого вектора умножить на заданное число.
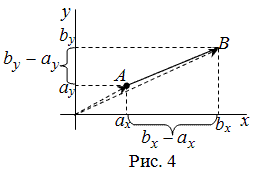
Рассмотрим далее случай, когда начало вектора не совпадает с началом системы координат. Предположим, что в ПДСК заданы две точки $Aleft(a_ ; a_right)$ и $Bleft(b_ ; b_right)$. Тогда координаты вектора $overline=left(x_ <1>; y_<1>right)$ находятся по формулам (рис. 4):
Чтобы найти координаты вектора, заданного координатами начала и конца, надо от координат конца отнять соответствующие координаты начала.
Задание. Найти координаты вектора $overline$, если $A(-4 ; 2), B(1 ;-3)$
Решение. $overline=(1-(-4) ;-3-2)=(5 ;-5)$
Направляющие косинусы
Направляющими косинусами вектора называются косинусы углов, образованных вектором с положительными направлениями осей координат.
Направление вектора однозначно задается направляющими косинусами. Для единичного вектора направляющие косинусы равны его координатам.
Здесь $alpha$, $beta$ и $gamma$ – углы, которые составляет вектор с положительными направлениями осей $O x$, $O y$ и $O z$ соответственно.
Основное свойство направляющих косинусов
Сумма квадратов направляющих косинусов равна единице.
Сложение и вычитание векторов
Формулы сложения и вычитания векторов
Формулы сложения и вычитания векторов для плоских задач
В случае плоской задачи сумму и разность векторов a = < ax ; ay > и b = < bx ; by > можно найти, воспользовавшись следующими формулами:
Формулы сложения и вычитания векторов для пространчтвенных задач
В случае пространственной задачи сумму и разность векторов a = < ax ; ay ; az > и b = < bx ; by ; bz > можно найти, воспользовавшись следующими формулами:
Формулы сложения и вычитания n -мерных векторов
В случае n -мерного пространства сумму и разность векторов a = < a 1 ; a 2 ; . ; an > и b = < b 1 ; b 2 ; . ; bn > можно найти, воспользовавшись следующими формулами:
Примеры задач на сложение и вычитание векторов
Примеры плоских задач на сложение и вычитание векторов
Примеры пространственных задач на сложение и вычитание векторов
Примеры задач на сложение и вычитание векторов с размерностью большей 3
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
[spoiler title=”источники:”]
http://www.webmath.ru/poleznoe/formules_4_5.php
http://ru.onlinemschool.com/math/library/vector/add_subtract/
[/spoiler]
Если задана плоскость Oxy с векторами a→=ax, ay и b→=(bx, by), то мы можем разложить их по координатным векторам i→ и j→. Тогда это будет иметь вид a→=ax·i→+ay·j→ и b→=bx·i→+by·j→. Чтобы найти сумму a→ и b→ и произведение a→ на λ, рассмотрим:
a→+b→=ax·i→+ay·j→+bx·i→+by·j→=(ax+bx)·i→+(ay+by)·j→
λ·a→=λ·(ax·i→+ay·j→)=(λ·ax)·i→+(λ·ay)·j→
Это равенство справедливо по свойству операций над векторами.
Разложение векторов – это a→+b→ и λ·a→, представленное в частях неравенства по i→ и j→ координатам. Координаты векторов a→+b→ и λ·a→ равны соответственно (ax+bx, ay+by) и (λ·ax, λ·ay).
Таким же образом a→=(ax, ay, az) и b→=(bx, by, bz) записываются как a→+b→=ax·i→+ay·j→+az·k→+bx·i→+by·j→+bz·k→=(ax+bx)·i⇀+(ay+by)·j→+(az+bz)·k→λ·a→=λ·(ax·i→+ay·j→+az·k→)=(λ·ax)·i→+(λ·ay)·j→+(λ·az)·k→
а значит a→+b→=(ax+bx, ay+by, az+bz), λ·a→=(λ·ax, λ·ay, λ·az)
Отсюда делаем вывод, что координаты векторов a→ и b→ равны сумме соответствующих координат векторов a→и b→, координаты произведения вектора a→ на λ приравниваются к соответствующим координатам вектора a→, умноженным на число в заданной системе координат.
При необходимости нахождения координат суммы нескольких векторов, необходимо сложить координаты каждого вектора соответственно. Рассмотрим примеры.
Нужно выполнить сложение a→=(2, 3-13) и b→=(-1,-13). Чему равны координаты произведения вектора a→ на 3.
Решение
Из определения имеем, что сумма векторов равна сумме их координат соответственно, тогда a→+b→=(2+(-1),3-13+(-13))=(1, -13).
Числовое значение умножается на каждую координату: 3·a→=(3·2, 3·3-13)=23,3-33.
Ответ: a→+b→=(1, -13), 3·a→=(23, 3-33)
Заданы векторы a→=(0, 1, -2), b→=(-1, -1, 3), c→=(4, -3, 2) .
Каковы координаты вектора 2·a→+3·(b→-c→)=2·a→+3·b→+(-3)·c→.
Решение
Применяя свойства векторов, получим: 2·a→+3·(b→-c→)=2·a→+3·b→+(-3)·c→.
Подставляем значения координат и получаем: 2·a→+3·b→+(-3)·c→=2·(0,1,-2)+3·(-1,-1, 3)+(-3)·(4,-3, 2)=
=(2·0, 2·1, 2·(-2))+(3·(-1), 3·(-1), 3·3)+((-3)·4,(-3)·(-3)·2)=
=(0, 2, -4)+(-3, -3, 9) + (-12, 9 -6)=
=(0+(-3)+(-12), 2+(-3)+9, -4+9+(-6))=(-15, 8, -1)
Можно решить другим способом.
Обратим внимание на разложение a→, b→ и c→ :
a→=0·i→+1·j→+(-2)·k→=j→-2·k→
b→=(-1)·i→+(-1)·j→+3 ·k→=-i→-j→+3·k→
c→=4·i→+(-3)·j→+2·k→=4·i→-3·j→+2·k→
Исходя из свойств векторов, видим, что: 2·a→+3·(b→-c→)=2·(j→-2·k→)+3·(-i→-j→+3·k→-(4·i→-3·j→+2·k→))==2·j→-4·k→+3·(-5·i→+2·j→+1·k→)=-15·i→+8·j→-k→
Значит, координаты вектора 2·a→+3·(b→-c→) равны (-15, 8, -1).
Ответ: 2·a→+2·(b→-c→)=(-15, 8, -1)
![]()
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
- Главная
- Справочники
- Справочник по геометрии 7-9 класс
- Метод координат
- Координаты вектора
Прямоугольная система координат (декаротова система координат) — прямолинейная система координат с взаимно перпендикулярными осями на плоскости или в пространстве. Для задания прямоугольной системы координат нужно провести две взаимно перпендикулярные прямые, на каждой из них выбрать направление (оно обозначается стрелкой) и выбрать единицу измерения отрезков.
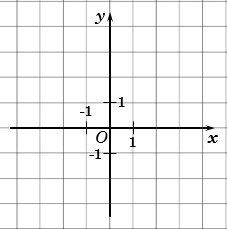
На рисунке выше оси 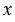 и
и 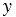 перпендикулярны. При выбранной единице измерения отрезков длина каждого отрезка выражается положительным числом. В дальнейшем под длиной отрезка мы будем понимать это число. Так, единичный вектор – это вектор, длина которого равна 1.
перпендикулярны. При выбранной единице измерения отрезков длина каждого отрезка выражается положительным числом. В дальнейшем под длиной отрезка мы будем понимать это число. Так, единичный вектор – это вектор, длина которого равна 1.
Отложим от начала координат О единичные векторы 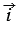 и
и 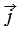 так, чтобы их направления совпадали с направлениями осей
так, чтобы их направления совпадали с направлениями осей 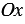 и
и 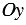 соответственно.
соответственно.
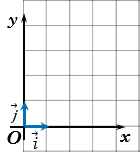
Векторы 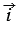 и
и 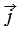 называют координатными векторами.
называют координатными векторами.
Координатные векторы не коллинеарны, поэтому любой вектор 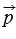 можно разложить по координатным векторам, т.е. представить в виде
можно разложить по координатным векторам, т.е. представить в виде 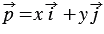 , причем коэффициенты разложения
, причем коэффициенты разложения 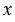 и
и 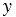 определяются единственным образом. Коэффициенты разложения вектора
определяются единственным образом. Коэффициенты разложения вектора 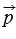 по координатным векторам называются координатами вектора
по координатным векторам называются координатами вектора 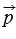 в данной системе координат.
в данной системе координат.
Координаты вектора записывают в фигурных скобках после обозначения вектора: 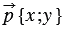 .
.
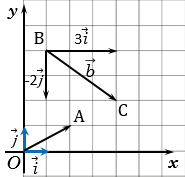
На рисунке выше 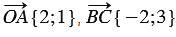 .
.
Нулевой вектор можно представить в виде 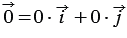 , следовательно, его координаты равны нулю:
, следовательно, его координаты равны нулю: 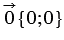 .
.
Если векторы 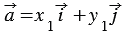 и
и 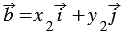 равны, то
равны, то 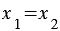 и
и 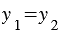 . Значит, координаты равных векторов соответственно равны.
. Значит, координаты равных векторов соответственно равны.
Правила, позволяющие по координатам векторов находить координаты их суммы, разности и произведения вектора на число:
10. Каждая координата суммы двух и более векторов равна сумме соответствующих координат этих векторов.
Доказательство
Дано: 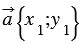 ,
, 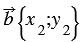 ,
, 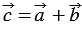 .
.
Доказать: 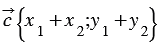 .
.
Доказательство:
По условию 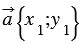 и
и 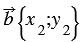 , тогда
, тогда 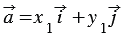 и
и 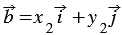 .
.
Сложим последние два равенства и применим свойства сложения векторов и умножения вектора на число, получим: 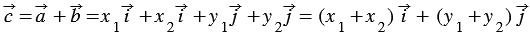 , следовательно, координаты вектора
, следовательно, координаты вектора 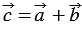 равны
равны  , т.е.
, т.е. 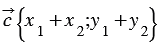 . Что и требовалось доказать.
. Что и требовалось доказать.
20. Каждая координата разности двух векторов равна разности соответствующих координат этих векторов.
Доказательство
Дано: 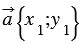 ,
, 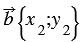 ,
, 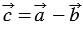 .
.
Доказать: 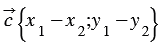 .
.
Доказательство:
По условию 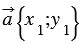 и
и 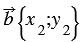 , тогда
, тогда 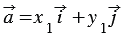 (1) и
(1) и 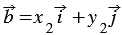 . (2)
. (2)
Вычтем из равенства (1) равенство (2) и применим свойства сложения векторов и умножения вектора на число, получим: 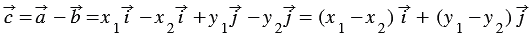 , следовательно, координаты вектора
, следовательно, координаты вектора 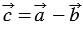 равны
равны 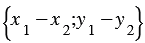 , т.е.
, т.е. 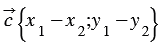 . Что и требовалось доказать.
. Что и требовалось доказать.
30. Каждая координата произведения вектора на число равна произведению соответствующей координаты вектора на это число.
Доказательство
Дано: 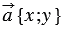 ,
, 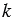 – число,
– число, 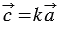 .
.
Доказать: 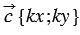 .
.
Доказательство:
По условию 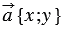 , значит,
, значит, 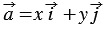 .
.
Умножим последнее равенство на число 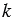 и используя свойства умножения вектора на число, получим:
и используя свойства умножения вектора на число, получим: 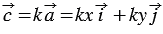 , следовательно, координаты вектора
, следовательно, координаты вектора 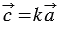 равны
равны 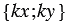 , т.е.
, т.е. 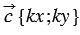 . Что и требовалось доказать.
. Что и требовалось доказать.
Данные правила позволяют определить координаты любого вектора, представленного в виде алгебраической суммы данных векторов с известными координатами.
Пример
Найти координаты вектора 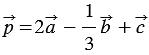 , если известно, что
, если известно, что 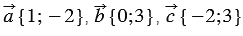 .
.
Решение:
По правилу 30 вектор 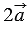 будет иметь координаты
будет иметь координаты 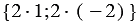 , т.е.
, т.е. 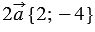 , вектор
, вектор 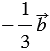 координаты
координаты 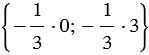 , т.е.
, т.е. 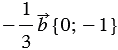 .
.
Так как 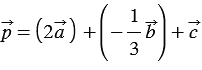 , то координаты вектора
, то координаты вектора 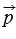 можно найти по правилу 10:
можно найти по правилу 10: 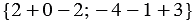 , т.е.
, т.е. 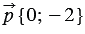 .
.
Ответ: 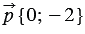 .
.
Советуем посмотреть:
Разложение вектора по двум неколлинеарным векторам
Связь между координатами вектора его начала и конца
Простейшие задачи в координатах
Уравнение линии на плоскости
Уравнение окружности
Уравнение прямой
Взаимное расположение двух окружностей
Метод координат
Правило встречается в следующих упражнениях:
7 класс
Задание 922,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 927,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 935,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 949,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 953,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 957,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 958,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 959,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 8,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 18,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник