Даны точки
![]() Требуется найти координаты точкиK(x,y),
Требуется найти координаты точкиK(x,y),
 делящей
делящей
отрезокMN
в отношении
![]() Рассмотрим векторы
Рассмотрим векторы![]() Эти векторы коллинеарны
Эти векторы коллинеарны![]() Из векторной алгебры известно, что если
Из векторной алгебры известно, что если
векторы коллинеарны, то соответствующие
координаты пропорциональны. Имеем:
![]()
![]() (по условию).
(по условию).
Из этих уравнений
легко найти x
и y
![]()
![]() (2.1.1)
(2.1.1)
Если
![]() то точкаK
то точкаK
является серединой отрезка MN.
Формулы (2.1) примут вид:
![]() (2.1.2)
(2.1.2)
Это формулы
координат середины отрезка.
Пример 1.
Найти
координаты
точки K,
делящей отрезок MN,
где M(-1,4)
и N(2,1),
в отношении 2 : 1.
Решение.
По условию
![]() Подставим координаты точкиM
Подставим координаты точкиM
и N
в формулы (2.1.1). Имеем:
![]()
Точка K
имеет координаты: x=1,
y=2.
Ответ: K(1,2).
Пример 2.
Отрезок АВ разделен на три равные части.
Определить координаты точек деления,
если А(3,-2), В(6,4).
Решение.
Обозначим точки деления С и D.
Точка D
делит отрезок АВ в отно-
шении АD:DB
= 2. Координаты точки D
найдем по формулам (2.1.1).
![]()
Итак, D(5,2).
Координаты точки
С можно найти аналогично, взяв
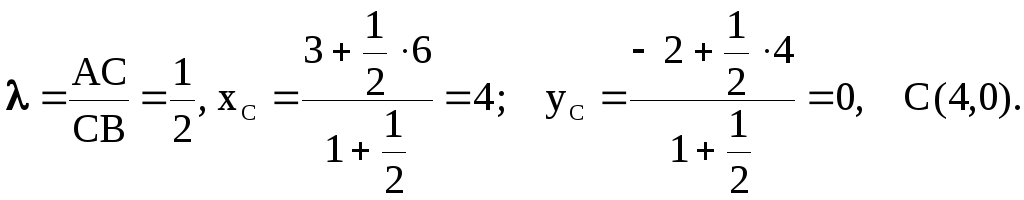
Существует другой
способ нахождения координат точки С.
Точка С является серединой отрезка АD.
По формулам (2.1.2) имеем
![]()
Ответ:
D(5,2)
; C(4,0).
Пример 3.
Найти точку пересечения медиан
треугольника АВС, где А(-1,3) ;
B(3,-2);
C(5,3).
Р ешение:
ешение:
Пусть точка О – точка пересечения медиан
AM
и BN
треугольника ABC.
Точка М является серединой отрезка ВС.
По формулам (2.1.2) получим координаты
точки М:
![]()
![]() Из школьного курса
Из школьного курса
планиметрии известно, что точка О делит
медиану АМ в отношении АО:ОМ = 2:1.
![]() По формулам (2.1.1) получим
По формулам (2.1.1) получим
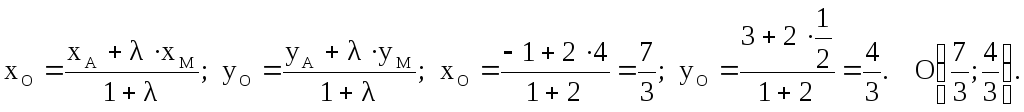
Ответ:
Точка пересечения медиан ![]()
Замечание: Точка
пересечения медиан треугольника является
его центром тяжести.
3. Прямая на плоскости.
3.1. Простейшей из
линий является прямая. Всякую прямую,
не параллельную оси ординат, можно
представить уравнением вида
![]() ,
,
(3.1.1)
где к есть тангенс
угла
![]() образованного прямой с положительным
образованного прямой с положительным
направлением оси абсцисс (ox).

![]()
Величину к называют
угловым
коэффициентом.
Величину b
– начальной
ординатой.
Если прямая
параллельна оси ox,
то
![]() Уравнение прямой примет вид:y
Уравнение прямой примет вид:y
= b
(3.1.2)

Если прямая
параллельна оси oy,
то
![]() не существует. В этом случае уравнение
не существует. В этом случае уравнение
прямой будет иметь вид:x
= a
(3.1.3),
где а – абсцисса точки, через которую
проходит данная прямая ( точки пересечения
прямой с осью ox).

Пример 1.
Какую прямую представляет уравнение
![]()
Р ешение. Данное
ешение. Данное
уравнение задает прямую, у которой
![]() Так как
Так как![]() Поэтому данное уравнение представляет
Поэтому данное уравнение представляет
прямую, проходящую через начало координат
(b
= 0) и образующую с осью ox
угол
![]()
Пример 2.
Написать
уравнение прямой, параллельной оси ox
и имеющей на-
 чальную
чальную
ординату b
=
![]() .
.
Решение: По
формуле (3.1.2) имеем y
=![]() где
где![]()
Итак, искомая
прямая задается уравнением
![]()
Ответ:
![]()
Пример 3.
Написать уравнение прямой, параллельной
оси oy
и проходящей
через точку
M(3,1).
 Решение:
Решение:
По формуле (3.1.3) уравнение прямой имеет
вид x
= a
, где а – абсцисса точки М. а = 3. Уравнение
прямой x
= 3.
Ответ:
x
= 3.
3.2. Уравнение
прямой по точке и угловому коэффициенту.
Пусть прямая
проходит через точку
![]() и имеет угловой коэффициент к. Уравнение
и имеет угловой коэффициент к. Уравнение
такой прямой можно записать в виде
(3.1.1)![]() гдеb
гдеb
– неизв естная
естная
величина. Так как прямая проходит через
точку![]() ,
,
то координаты точки удовлетворяют
уравнению (3.1.1). Имеем![]() Отсюда
Отсюда![]()
Подставим значение
“b”
в уравнение (3.1.1), получим
![]() –
–![]() или
или
![]() (3.2.1)
(3.2.1)
Полученное уравнение
называется уравнением прямой по точке
и угловому коэффициенту.
Пример 1.
Составить уравнение прямой, проходящей
через точку
![]()
и образующей с
положительным направлением оси ox
угол
![]()
Решение:
Так как
![]() то
то![]() Применив формулу (3.2.1), получимy-(-2)=-1(x-1)
Применив формулу (3.2.1), получимy-(-2)=-1(x-1)
![]() y+2
y+2
= -x+1
![]() y=-x-1.
y=-x-1.
Ответ:
y=-x-1.![]()
Пример 2.
Составить
уравнение прямой, проходящей через
точку А(-3,4) и имеющей угловой коэффициент
к = 2.
Решение:
Применяем
формулу (3.2.1) y
– 4 = 2 (x+3)
![]() y
y
– 4 = 2x
+ 6
![]()
y
= 2x
+
10.
Ответ:
y
= 2x
+ 10.
Пример 3.
Составить
уравнение прямой, проходящей через
точку М(-1, 2) параллельно оси ox.
Решение:
Если прямая параллельна оси ox,
то угол между прямой и положительным
направлением оси ox
равен нулю. Следовательно,
![]() По формуле (3.2.1) получимy
По формуле (3.2.1) получимy
– 2 = 0 (x
+ 1)
![]()
y
– 2 = 0
![]()
Ответ:
y
= 2.
3 .3.Уравнение
.3.Уравнение
прямой по точке и нормальному вектору.
Пусть прямая
проходит через точку
![]() Поднормальным
Поднормальным
вектором
понимают вектор, который перпендикулярен
данной прямой. Обозначим его
![]() Возьмем на прямой произвольную точкуM(x,y)
Возьмем на прямой произвольную точкуM(x,y)
и рассмотрим вектор
![]() Используя векторную алгебру, найдем
Используя векторную алгебру, найдем
координаты вектора![]() Вектор
Вектор![]() перпендикулярен вектору
перпендикулярен вектору![]() .Из векторной
.Из векторной
алгебры известно, что скалярное
произведение этих векторов равно нулю.
Следовательно,
![]() (3.3.1)
(3.3.1)
Полученное уравнение
называется уравнением
прямой по точке и нормальному вектору.
Преобразуем полученное уравнение:
Ax + By –
A![]() – B
– B![]() =
=
0.Пусть
C = -A![]() -B
-B![]() ,тогда
,тогда
получим:
Ax
+ By + C = 0 (3.3.2)
Уравнение (3.3.2)
называется общим
уравнением прямой.
Напомним, что коэффициенты А и В в
уравнении определяют координаты
нормального вектора
![]()
Рассмотрим общее
уравнение прямой подробнее.
1). Если А = 0, то
![]() уравнение примет вид
уравнение примет вид
By
+ C
= 0 ; y
= –![]() Прямая параллельна осиox.
Прямая параллельна осиox.
(3.1.2)
2). Если В = 0, то
![]() уравнение примет вид:
уравнение примет вид:
Ax
+ C
= 0, x
= –![]()
Прямая параллельна оси oy.
(3.1.3.)
3). Если С = 0, то
уравнение примет вид: Ax
+ By
= 0. y
= –
![]()
Прямая проходит через начало координат
и имеет угловой коэффициент k
= –
![]() См. пример 1 пункт 3.1.
См. пример 1 пункт 3.1.
Из общего
уравнения прямой, если
![]() можно найти угловой коэффициент к. Для
можно найти угловой коэффициент к. Для
этого выразимy
из этого уравнения : Ax
+ By
+ C
= 0.
By = – Ax –
C ; y = –![]() –
–![]() Отсюда,
Отсюда,
k
= –
![]() (3.3.3)
(3.3.3)
Пример 1.
Прямая задана уравнением 3x
– 4y
+5 = 0. Найти координаты нормального
вектора.
Решение:
Координатами
нормального вектора
![]() являются коэффициенты приx
являются коэффициенты приx
и y
данного уравнения прямой. Имеем А = 3;
В = – 4.
Ответ:
![]()
Пример 2.
Составить уравнение прямой, проходящей
через точку М(2,-1) и имеющей нормальный
вектор
![]()
Решение:
Применяем
формулу (3.3.1). Имеем 0(x
– 2) + 2(y
+ 1) = 0
![]()
2y
+ 2 = 0
![]()
y
+ 1 = 0.
Ответ:
y
+ 1 = 0.
Пример 3.
Составить уравнение прямой, проходящей
через точку М(0; 1) перпендикулярно вектору
![]() где А(-1; 2), В(1; -1).
где А(-1; 2), В(1; -1).
Решение:
Найдем координаты вектора
![]()
![]() –
–
(-1); -1-2);
![]() (2;
(2;
-3).
Вектор ![]() является нормальным
является нормальным
векторомискомой
прямой. По формуле (3.3.1) имеем 2(x
– 0) -3(y
-1) = 0
![]()
2x
– 3y
+ 3 = 0.
Ответ:
2x
– 3y
+ 3 = 0.
3.4. Уравнение
прямой по точке и направляющему вектору.
Пусть прямая
проходит через точку
![]() Направляющим вектором
Направляющим вектором![]() данной прямой называется вектор,
данной прямой называется вектор,
параллельный этой прямой. Пусть дан
вектор![]() Возьмем на прямой произвольную точкуM(x,y)
Возьмем на прямой произвольную точкуM(x,y)
и рассмотрим вектор
![]()
![]() Векторы
Векторы
![]() и
и![]() коллинеарны,следовательно, их
коллинеарны,следовательно, их
соответствующие координаты пропорциональны.
![]() (3.4.1)
(3.4.1)
Полученное уравнение
является уравнением прямой по
точке и направляющему вектору.
Пример 1.
Прямая задана
уравнением:
![]() Написать координаты
Написать координаты
направляющего вектора; найти координаты
точки, лежащей на прямой; составить
общее уравнение прямой.
Решение:
Направляющий
вектор
![]() = (−1; 2). Точку
= (−1; 2). Точку![]() мы получим, приравняв нулю числители
мы получим, приравняв нулю числители
данного уравнения:x
+ 2 = 0
![]()
x
=−2; y
– 3 = 0
![]()
![]()
y
= 3.
Итак,
![]() (−2; 3).
(−2; 3).
Общее уравнение
прямой получим по свойству пропорций:
(x+2)∙2
= (y−3)∙(−
1)
![]()
2x
+ 4 = −y
+ 3
![]()
2x
+ y
+ 1 = 0.
Ответ:
![]() (−1;
(−1;
2),
![]() (−2;
(−2;
3), 2x
+ y
+ 1 = 0.
Пример 2.
Составить
уравнение прямой по точке М(2,-5) и
направляющему вектору
![]() (-2,4).
(-2,4).
Решение:
Применяем
формулу
(3.4.1). Имеем:
![]()
4(x-2)
= -2(y+5)
4x
– 8 = – 2y
– 10
![]()
4x
+ 2y
+ 2 = 0
![]()
2x
+ y
+ 1 =0.
Ответ: 2x
+ y
+ 1 = 0.
Пример 3.
Через точку
С(- 2, 1) провести прямую, параллельную
вектору
![]() где А(2,-1), В(3,4).
где А(2,-1), В(3,4).
Решение:
Вектор ![]() можно взять за
можно взять за
направляющий вектор данной прямой. ![]() (3-2; 4-(-1)) = (1;
(3-2; 4-(-1)) = (1;
5). Применяем
формулу (3.4.1). Имеем:
![]()
5(x
+ 2) = y
– 1
![]()
5x
+ 10 = y
– 1
![]()
5x
– y
+ 11 = 0.
Ответ:
5x
– y
+11 = 0.
3.5. Уравнение
прямой, проходящей через две заданные
точки.
Известно, что
через две данные точки можно провести
единственную прямую. П усть
усть
прямая проходит через точки![]() За направляющий вектор
За направляющий вектор![]() данной прямой можно взять вектор
данной прямой можно взять вектор![]() .
.
![]()
Составим уравнение
прямой по точке ![]() и направляющему
и направляющему
вектору
![]()
По формуле (3.4.1)
имеем:
![]() (3.5.1)
(3.5.1)
Если
![]() то прямая параллельна осиoy.
то прямая параллельна осиoy.
Ее уравнение имеет вид:
![]() (3.5.2)
(3.5.2)
Если
![]() то прямая параллельна осиox.
то прямая параллельна осиox.
Ее уравнение :
y
=
![]()
(3.5.3)
Пример 1.
Составить уравнение прямой АВ, если
А(2,-1); В(1,3).
Решение:
Применяем
формулу (3.5.1):
![]() 4(x
4(x
– 2) = -(y
+ 1)
![]() 4x
4x
+ y
– 7 = 0.
Ответ:
4x
+ y
– 7 = 0.
Пример 2.
Составить уравнение прямой, проходящей
через точки М(4,-2) и N(4,5).
Решение:
Так как
![]()
то по формуле (3.5.2) уравнение прямой
имеет вид:
x = 4.
Прямая
параллельна оси oy.
Пример 3. Дан
треугольник АВС, у которого А(1,2), В(4,3),
С(1,3). Составить уравнения его сторон.
Решение: 1)
Найдем уравнение стороны АВ. ПО формуле
(3.5.1) имеем:
![]() x
x
– 1 = 3(y
– 2)
![]() x
x
– 3y
+ 5 = 0.
2) Сторона ВС
находится по формуле (3.5.3), так как
![]() y
y
= 3.
3) Уравнение стороны
АС выпишем по формуле (3.5.2), так как
![]() x
x
= 1.
Ответ:
AB:
x
– 3y
+ 5 = 0; BC:
y
= 3; AC:
x
= 1.
Пример 4.
Даны вершины треугольника АВС А(- 1, 3),
В(3,-2), С(5,3). Составить уравнение медианы,
проведенной из вершины В.
 Решение: Пусть
Решение: Пусть
ВМ – медиана, тогда точка М является
серединой отрезка АС. По формулам (2.1.2)
имеем:
![]()
![]() M(2,3).
M(2,3).
Уравнение медианы
ВМ получим по формуле (3.5.1):
![]()
![]() 5(x-
5(x-
3) = -(y
+2)
![]()
5x
+ y
– 13 = 0.
Ответ:
BM:
5x
+ y
– 13 = 0.
3.6. Уравнение
прямой в отрезках.
Если прямая отсекает
на осях отрезки а и b,
не равные нулю, то ее уравнение можно
записать в виде:
![]() .
.
(3.6.1)
Такое уравнение
называется уравнением
в отрезках.
Рассмотрим это уравнение. Пусть x
= 0, тогда
![]()
Пусть y
= 0, тогда
![]()
Прямая проходит
через точки А(а,0) и B(0,b).
 Пример.
Пример.
Записать
уравнение прямой в отрезках. Построить
эту прямую.
3x
– 2y + 12 = 0.
Решение:
3x
– 2y
= – 12. Разделим обе части этого уравнения
на – 12. П олучим:
олучим:
![]() a = – 4, b = 6.
a = – 4, b = 6.
Построим полученную
прямую. Для этого отложим на оси ox
a
= – 4, на оси oy
b
= 6 и соединим полученные точки.
3.7. Расстояние
от точки до прямой.
Пусть прямая
задана уравнением Ax
+ By
+ C
= 0. Найдем расстояние от точки
![]() до этой прямой. Подрасстоянием
до этой прямой. Подрасстоянием
от точки до прямой понимают длину о трезка
трезка![]() где М – основание перпендикуляра,
где М – основание перпендикуляра,
опущенного из точки![]() на данную прямую. Расстояние
на данную прямую. Расстояние![]()
![]() находим по формуле:
находим по формуле:
![]() (3.7.1)
(3.7.1)
Пример. Найти
расстояние от точки
![]() до прямой 3x
до прямой 3x
+ 4y
– 22 =0.
Решение: По
формуле (3.7.1) получим:
![]()
Ответ:
d
= 4.
Соседние файлы в предмете Математика
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
03.03.20154.96 Кб8Содержание OneNote.onetoc2
- #
Вычисление координат некоторой точки С, которая делит заданный отрезок АВ в определенном отношении, может быть выполнено по формулам:
хС = (хА + λхВ) / (1 + λ), уС = (уА + λуВ) / (1 + λ),
где (хА; уА) и (хВ; уВ) – координаты концов заданного отрезка АВ; число λ = АС/СВ – отношение, в котором отрезок АВ делится точкой С, имеющей координаты (хС; уС).
Если отрезок АВ делится точкой С пополам, то число λ = 1 и формулы для хС и уС примут вид:
хС = (хА + хВ)/2, уС = (уА + уВ)/2.
Нужно иметь ввиду, что в задачах λ – это отношение длин отрезков, а поэтому числа, входящие в данное отношение не есть длины самих отрезков в заданной единице измерения. Например, АС = 12 см, СВ = 16 см: λ = АС/СВ = 12 см / 16 см = 3/4.
1. Поиск координат середины некоторого отрезка, по заданным координатам его концов
Пример 1.
Точки А(-2; 3) и В(6; -9) – концы отрезка АВ. Найти точку С, являющиеся серединой отрезка АВ.
Решение.
В условии задачи задано, что хА = -2; хВ = 6; уА = 3 и уВ = -9. Требуется найти С(хС ; уС).
Применяя формулы хС = (хА + хВ)/2, уС = (уА + уВ)/2, получим:
хС = (-2 + 6)/2 = 2, уС = (3 + (-9))/2 = -3.
Таким образом, точка С, являющаяся серединой отрезка АВ, имеет координаты (-2; 3) (рис. 1).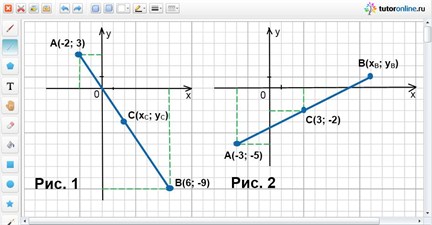
2. Вычисление координат конца некоторого отрезка, зная координаты его середины и другого конца
Пример 2.
Одним концом отрезка АВ является точка А, с координатами (-3; -5), а его серединой точка С(3; -2). Вычислите координаты второго конца отрезка – точки В.
Решение.
По условию задачи становится ясно, что хА = -3; уА = -5; хС = 3 и уС = -2.
Подставив эти значения в формулы хС = (хА + хВ)/2, уС = (уА + уВ)/2, получим:
3 = (-3 + хВ)/2 и
-2 = (-5 + уВ)/2.
Решив первое уравнение относительно хВ и второе относительно уВ, найдем: хВ = 9 и уВ = 1, получается, что нужная точка В будет задаваться координатами (9; 1) (рис. 2).
3. Вычисление координат вершин некоторого треугольника по заданным координатам середин его сторон
Пример 3.
Серединами сторон треугольника АВС являются точки D(1; 3), E(-1; -2) и F(4; -1). Найти координаты вершин А, В и С данного треугольника.
Решение.
Пусть точка D и есть середина стороны АВ, точка Е – середина ВС и точка F – середина сторона АС (рис. 3). Необходимо найти точки А, В и С.
Обозначаем вершины треугольника через А(хА; уА), В(хВ; уВ) и С(хС; уС) и зная координаты точек D, Е и F, по формулам хС = (хА + хВ)/2, уС = (уА + уВ)/2 получим:
{1 = (хА + хВ)/2, 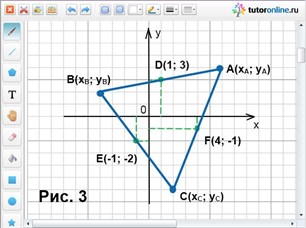
{-1 = (хВ + хС)/2,
{4 = (хА + хС)/2,
и
{3 = (уА + уВ)/2,
{-2 = (уВ + уС)/2,
{-1 = (уА + уС)/2.
Приведем уравнения к целому виду:
{хА + хВ = 2,
{хВ + хС = -2,
{хА + хС = 8,
и
{уА + уВ = 6,
{уВ + уС = -4,
{уА + уС = -2.
Решив системы, получим:
хА = 6; хВ = -4; хС = 2.
уА = 4; уВ = 2; уС = -6.
Точки А(6; 4), В(-4; 2) и С(2; -6) и есть необходимые вершины треугольника.
4. Вычисление координат точек, которые делят отрезок в определенном отношении, по заданным координатам концов этого отрезка
Пример 4.
Отрезок АВ поделен точкой С в отношении 3 : 5 (считая от точки А к точке В). Концы отрезка АВ – точки А(2; 3) и В(10; 11). Найти точку С.
Решение.
В условии задачи сказано, что хА = 2; хВ = 10; уА = 3; уВ = 11; λ = АС/СВ = 3/5. Найти С(хС; уС) (рис. 4).
по формулам хС = (хА + λхВ) / (1 + λ), уС = (уА + λуВ) / (1 + λ) получим:
хС = (2 + 3/5 · 10) / (1 + 3/5) = 5 и уС = (3 + 3/5 · 11) / (1 + 3/5) = 6. Таким образом, имеем С(5; 6).
Выполним проверку: АС = 3√2, СВ = 5√2, λ = АС/СВ = 3√2/5√2 = 3/5.
Замечание. В условии задачи указано, что деление отрезка производится в заданном отношении от точки А к точке В. Если бы это не уточнялось, то задача имела бы два решения. Второе решение: деление отрезка от точки В к точке А.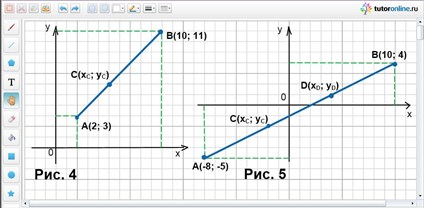
Пример 5.
Некоторый отрезок АВ разделен в отношении 2 : 3 : 5 (считая от точки А к точке В), его концы – есть точки с координатами А(-11; 1) и В(9; 11). Найти точки деления данного отрезка.
Решение.
Обозначим точки деления отрезка от А к В через С и D. В условии задачи дано, что
хА = -11; хВ = 9; уА = 1; уВ = 11. Найти С(хС; уС) и D(хD; уD), если АС : СD : DB = 2 : 3 : 5.
Точка С делит отрезок АВ в отношении λ = АС/СВ = 2/(3 + 5) = 2/8 = 1/4.
По формулам хС = (хА + λхВ) / (1 + λ), уС = (уА + λуВ) / (1 + λ) получим:
хС = (-11 + ¼ · 9) / (1 + 1/4) = -7 и уС = (1 + ¼ · 11) / (1 + 1/4) = 3.
Таким образом, С(-7; 3).
Точка D – есть середина отрезка АВ. Применив формулы хD = (хА + хВ)/2, уD = (уА + уВ)/2, найдем:
хD = (-11 + 9)/2 = -1, уD = (1 + 11)/2 = 6. Значит, D имеет координаты (-1; 6).
5. Вычисление координат точек, которые делят отрезок, если заданы координаты концов этого отрезка и число частей, на которые этот отрезок разделен
Пример 6.
Концы отрезка – точки А(-8; -5) и В(10; 4). Найти точки С и D, которые делят этот отрезок на три равные части.
Решение.
Из условия задачи известно, что хА = -8; хВ = 10; уА = -5; уВ = 4 и n = 3. Найдем С(хС; уС) и D(хD; уD) (рис. 5).
Найдем точку С. Она делит отрезок АВ в отношении λ = 1/2. Деление производим от точки А к точке В. По формулам хС = (хА + λхВ) / (1 + λ), уС = (уА + λуВ) / (1 + λ) имеем:
хС = (-8 + ½ · 10) / (1 + 1/2) = -2 и уС = (-5 + ½ · 4) / (1 + 1/2) = -2. Таким образом, С(-2; -2).
Деление отрезка СВ выполняется в отношении 1 : 1, поэтому используем формулы
хD = (хА + хВ)/2, уD = (уА + уВ)/2:
хD = (-2 + 10)/2 = 4, уD = (-2 + 4)/2 = 1. Таким образом, D(4; 1).
Точки деления С(-2; -2) и D(4; 1).
Замечание: Точку D можно найти, производя деление отрезок АВ в отношении 2 : 1. В таком случае надо будет снова применить формулы хD = (хА + λхВ) / (1 + λ), уD = (уА + λуВ) / (1 + λ).
Пример 7.
Точки А(5; -6) и В(-5; 9) – концами отрезка. Найти точки, которые поделят данный отрезок на пять равных частей.
Решение.
Пусть последовательные точки деления от А к В будут С(хС; уС), D(хD; уD), Е(хE; уE) и F(хF; уF). В условия задачи сказано, что хА = 5; хВ = -5; уА = -6; уВ = 9 и n = 5.
Найдем по формулам хС = (хА + λхВ) / (1 + λ), уС = (уА + λуВ) / (1 + λ) точку С. Она делит отрезок АВ в отношении λ = 1/4:
хС = (5 + 1/4 · (-5)) / (1 + 1/4) = 3 и уС = (-6 + 1/4 · 9) / (1 + 1/4) = -3, получаем, что точка С имеет координаты (3; -3).
Деление отрезка АВ точкой D производится в отношении 2 : 3 (т.е. λ = 2/3), поэтому:
xD = (5 + 2/3 · (-5)) / (1 + 2/3) = 1 и уD = (-6 + 2/3 · 9) / (1 + 2/3) = 0, значит D(1; 0).
Найдем точку Е. Она делит отрезок АВ в отношении λ = 2/3:
XЕ = (5 + 3/2 · (-5)) / (1 + 3/2) = -1 и уЕ = (-6 + 3/2 · 9) / (1 + 3/2) = 3. Таким образом, Е(-1; 3).
Точка F делит отрезок АВ в отношении λ = 4/1, поэтому:
XF = (5 + 4 · (-5)) / (1 + 4) = -3 и уF = (-6 + 4 · 9) / (1 + 4) = 6, F(-3; 6).
Точки деления С(-2; -2); D(4; 1); Е(-1; 3) и F(-3; 6).
Остались вопросы? Не знаете, как решить задачу на деление отрезка?
Чтобы получить помощь репетитора – зарегистрируйтесь.
Первый урок – бесплатно!
Зарегистрироваться
© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.
Найдём координаты точки делящей отрезок в данном отношении.
 Дано:
Дано:
A (x1;y1), B(x2;y2),
C∈AB, AC:CB=m:n.
Доказать:
![]()
![]()
Доказательство:
1) При x2>x1; y2>y1.
Проведём через точки A, B и C прямые, параллельные осям Ox и Oy.
Рассмотрим образованные этими прямыми прямоугольные треугольники ACF и CBK.
∠ACF=∠CBK (как соответственные при CF∥BK и секущей AB).
Следовательно, треугольники ACF и CBK подобны (по острому углу).
Следовательно,
![]()
AF=x-x1; CK=x2-x; CF=y-y1; BK=y2-y.
![]()
Отсюда
![]()
![]()
![]()
![]()
Аналогично,
![]()
 2) При x2=x1; y2>y1
2) При x2=x1; y2>y1
Абсциссы точек A, B и C одинаковы: x2=x1=x. Формула
![]()
также выполняется:
![]()
Формула
![]()
вытекает непосредственно из условия AC:CB=m:n, так что
![]()
3) При других вариантах взаимного расположения x2 и x1, y2 и y1 доказательство аналогично.
Что и требовалось доказать.
При m=n получаем формулы координат середины отрезка.
Деление отрезка в заданном отношении (векторный и координатный способы).
Литература: Сборник задач по математике. Часть 1. Под ред А. В. Ефимова, Б. П. Демидовича.
Зная координаты точек $M_1(x_1, y_1, z_1)$ и $M_2(x_2, y_2, z_2)$ и отношение $lambda,$ в котором точка $M$ делит направленный отрезок $overline{M_1M_2},$ найдем координаты точки $M.$
Пусть $O -$ начало координат. Обозначим $overline{OM_1}=r_1,$ $overline{OM_2}=r_2,$ $overline{OM}=r.$ Так как, $$overline{M_1M}=r-r_1, overline{MM_2}=r_2-r,$$ то $r-r_1=lambda(r_2-r),$ откуда (так как $lambdaneq -1$) $$r=frac{r_1+lambda r_2}{1+lambda}.$$ Полученная форма и дает решение задачи в векторной форме. Переходя в этой формуле к координатам, получим $$x=frac{x_1+lambda x_2}{1+lambda}, y=frac{y_1+lambda y_2}{1+lambda}, z=frac{z_1+lambda z_2}{1+lambda}.$$
Примеры.
2.57. Отрезок с концами в точках $A(3, -2)$ и $B(6, 4)$ разделен на три равные части. Найти координаты точек деления.
Решение.
Пусть $C(x_C, y_C)$ и $D(x_D, y_D) -$ точки, которые делят отрезок $AB$ на три равные части. Тогда $$lambda_1=frac{AC}{CB}=frac{1}{2};$$ $$x_C=frac{x_A+lambda_1x_B}{1+lambda_1}=frac{3+frac{1}{2}cdot 6}{1+frac{1}{2}}=4;$$
$$y_C=frac{y_A+lambda_1y_B}{1+lambda_1}=frac{-2+frac{1}{2}cdot 4}{1+frac{1}{2}}=0.$$
Далее находим координаты точки $D:$
$$lambda_2=frac{AD}{DB}=frac{2}{1}=2;$$ $$x_D=frac{x_A+lambda_2x_B}{1+lambda_2}=frac{3+2cdot 6}{1+2}=5;$$
$$y_D=frac{y_A+lambda_2y_B}{1+lambda_2}=frac{-2+2cdot 4}{1+2}=2.$$
Ответ: $(4, 0)$ и $(5, 2).$
2.58.Определить координаты концов отрезка, который точками $C(2, 0, 2)$ и $D(5, -2, 0)$ разделен на три равные части.
Решение.
Пусть $A(x_A, y_A, z_A)$ и $B(x_B, y_B, z_B) -$ концы заданного отрезка.
Выпишем формулы для нахождения координат точки $C$ и подставим известные координаты:
$$lambda_1=frac{AC}{CB}=frac{1}{2};$$ $$x_C=frac{x_A+lambda_1x_B}{1+lambda_1}Rightarrow 2=frac{x_A+frac{1}{2}cdot x_B}{1+frac{1}{2}}=2frac{x_A+frac{1}{2}cdot x_B}{3}Rightarrow $$ $$Rightarrow 3=x_A+frac{1}{2}cdot x_B;$$
$$y_C=frac{y_A+lambda_1y_B}{1+lambda_1}Rightarrow 0=frac{y_A+frac{1}{2}cdot y_B}{1+frac{1}{2}}Rightarrow 0=y_A+frac{1}{2}cdot y_B;$$
$$z_C=frac{z_A+lambda_1z_B}{1+lambda_1}Rightarrow 2=frac{z_A+frac{1}{2}cdot z_B}{1+frac{1}{2}}=2frac{z_A+frac{1}{2}cdot z_B}{3}Rightarrow$$ $$Rightarrow 3=z_A+frac{1}{2}cdot z_B.$$
Аналогичные равенства запишем для точки $D:$
$$lambda_2=frac{AD}{DB}=frac{2}{1}=2;$$ $$x_D=frac{x_A+lambda_2x_B}{1+lambda_2}Rightarrow 5=frac{x_A+2cdot x_B}{1+2}=frac{x_A+2cdot x_B}{3}Rightarrow $$ $$Rightarrow 15=x_A+2cdot x_B;$$
$$y_D=frac{y_A+lambda_2y_B}{1+lambda_2}Rightarrow -2=frac{y_A+2cdot y_B}{1+2}Rightarrow -6=y_A+2cdot y_B;$$
$$z_D=frac{z_A+lambda_2z_B}{1+lambda_2}Rightarrow 0=frac{z_A+2cdot z_B}{1+2}Rightarrow 0=z_A+2cdot z_B.$$
Далее запишем полученные уравнения относительно $x_A, x_B;$ $y_A, y_B$ и $z_A, z_B$ попарно в виде систем и решим их:
$$left{begin{array}{lcl}x_A+frac{1}{2}x_B=3\x_A+2x_B=15end{array}right.Rightarrowleft{begin{array}{lcl}x_A=3-0,5x_B\3-0,5x_B+2x_B=15end{array}right.Rightarrow$$ $$Rightarrowleft{begin{array}{lcl}x_A=3-0,5cdot8=-1\x_B=frac{12}{1,5}=8end{array}right.$$
$$left{begin{array}{lcl}y_A+frac{1}{2}y_B=0\y_A+2y_B=-6end{array}right.Rightarrowleft{begin{array}{lcl}y_B=-2y_A\y_A-4y_A=-6end{array}right.Rightarrow$$ $$Rightarrowleft{begin{array}{lcl}y_B=-4\y_A=2end{array}right.$$
$$left{begin{array}{lcl}z_A+frac{1}{2}z_B=3\z_A+2z_B=0end{array}right.Rightarrowleft{begin{array}{lcl}-2z_B+0,5z_B=3\z_A=-2z_Bend{array}right.Rightarrow$$ $$Rightarrowleft{begin{array}{lcl}z_B=-2\z_A=4end{array}right.$$
Таким образом, получили координаты концов отрезка $A(-1, 2, 4)$ и $B(8, -4, -2).$
Ответ: $A(-1, 2, 4),$ $B(8, -4, -2).$
Деление отрезка в данном отношении в пространстве определяется следующими уравнениями
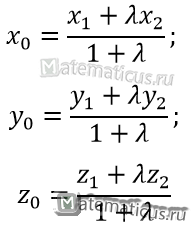
Данные уравнения получаются следующим образом
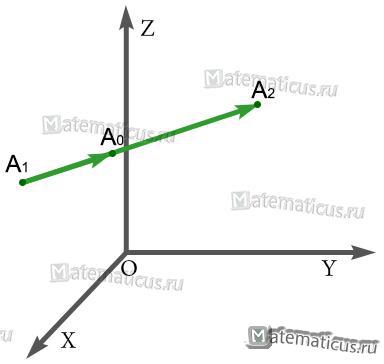
Пусть даны две точки A1(x1, y1,z1) и A2(x2, y2,z2).
Требуется найти координаты точки A0(x0, y0,z0), делящей отрезок в отношении λ, т.е.
$frac{{overrightarrow {{A_1}{A_0}} }}{{overrightarrow {{A_0}{A_2}} }} = lambda $ или $overrightarrow {{A_1}{A_0}} = lambda overrightarrow {{A_0}{A_2}} $
$overrightarrow {{A_1}{A_0}} = left( {{x_0} — {x_1},{y_0} — {y_1},{z_0} — {z_1}} right)$
$overrightarrow {{A_0}{A_2}} = left( {{x_2} — {x_0},{y_2} — {y_0},{z_2} — {z_0}} right)$
${x_0} — {x_1} = lambda left( {{x_2} — {x_0}} right)$
${z_0} — {z_1} = lambda left( {{z_2} — {z_0}} right)$
${z_0} — {z_1} = lambda left( {{z_2} — {z_0}} right)$
Отсюда получаем исходные уравнения, т.е.
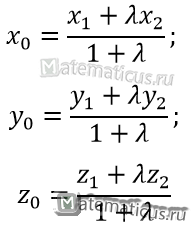
Деление отрезка в данном отношении на плоскости см. здесь
Рассмотрим ещё один из способов деления отрезка в данном отношении в пространстве.
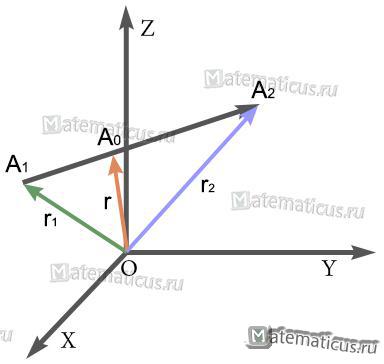
Пусть радиус-вектор r точки A0, делящий отрезок А1А2 в отношении А1А0:А0А2=m1:m2 определяется формулой:
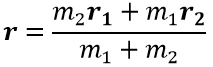
где r1 и r2 — радиус-вектор точек А1 и А2
Координаты точки A0 находятся по формулам
${x_0} = frac{{{m_2}{x_1} + {m_1}{x_2}}}{{{m_1} + {m_2}}},$
${y_0} = frac{{{m_2}{y_1} + {m_1}{y_2}}}{{{m_1} + {m_2}}},$
${z_0} = frac{{{m_2}{z_1} + {m_1}{z_2}}}{{{m_1} + {m_2}}}$
Координаты середины отрезка в пространстве
В частности координаты середины отрезка А1А2 в пространстве определяются уравнениями:
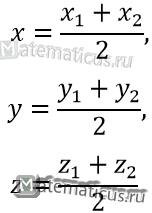
Пример
Найти координаты точки А, делящей отрезок А1А2 в отношении А1А:АА2=2:3, если A1{3; 4; -2} и A2{-6; -1; 3}
Находим
$x = frac{{{m_2}{x_1} + {m_1}{x_2}}}{{{m_1} + {m_2}}} = frac{{3cdot3 + 2cdotleft( { — 6} right)}}{{2 + 3}} = — frac{3}{5}$
$y = frac{{{m_2}{y_1} + {m_1}{y_2}}}{{{m_1} + {m_2}}} = frac{{3cdot4 + 2cdotleft( { — 1} right)}}{{2 + 3}} = — 2$
$z = frac{{{m_2}{z_1} + {m_1}{z_2}}}{{{m_1} + {m_2}}} = frac{{3cdotleft( { — 2} right) + 2cdot3}}{{2 + 3}} = 0$