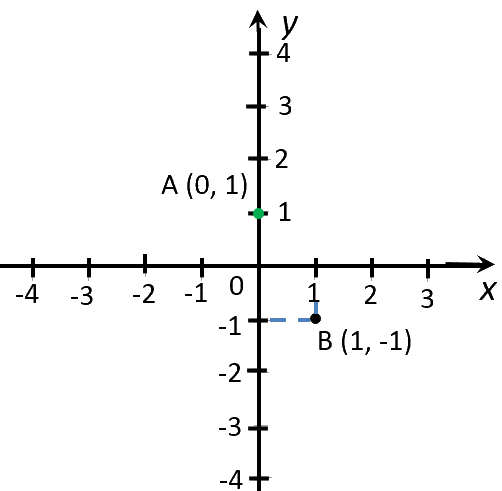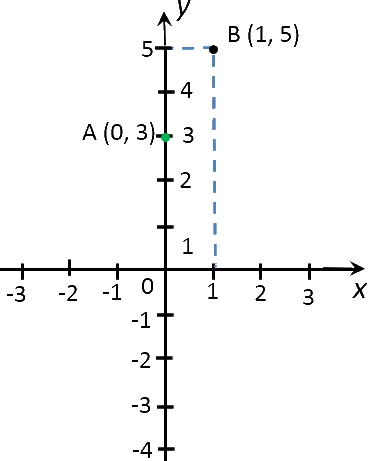Как найти координаты точек графика линейной функции

Прежде чем перейти к изучению функции «y = kx»
внимательно изучите урок
«Что такое функция в математике»
и
«Как решать задачи на функцию».

Другими словами, можно сказать, что «y = kx + b» — это семейство всевозможных функций, где вместо
«k» и «b» стоят числа.

Примеры функций типа «y = kx + b».

• y = 5x + 3
• y = −x + 1
• y = x − 2
• y = 0,5x

Давайте определим для каждой функций выше, чему равны числовые коэффициенты
«k» и
«b».

Функция	Коэффициент «k»	Коэффициент «b»
y = 5x + 3	k = 5	b = 3
y = −x + 1	k = −1	b = 1
y = 2 3 x − 2	k = 2 3	b = −2
y = 0,5x	k = 0,5	b = 0

Обратите особое внимание на функцию «y = 0,5x»
в таблице. Часто совершают ошибку при поиске в ней числового коэффициента «b».

Рассматривая
функцию «y = 0,5x», неверно утверждать, что числового коэффициента
«b» в функции нет.

Числовый коэффициент «b» присутствет в функции типа «y = kx + b» всегда.
В функции «y = 0,5x»
числовый коэффициент «b» равен нулю.

Как построить график линейной функции
«y = kx + b»

Так как графиком функции «y = kx + b»
является прямая линия, функцию называют линейной функцией.

Из геометрии вспомним аксиому (утверждение, которое не требует доказательств),
что через любые две точки можно провести прямую и притом только одну.

Исходя из аксиомы выше следует, что
чтобы построить график функции вида
«у = kx + b» нам достаточно будет найти всего
две точки.

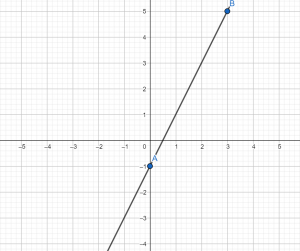
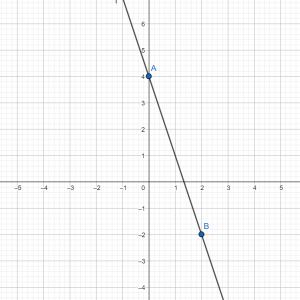
Для примера построим график функции «y = −2x + 1».

Найдем значение функции «y» для двух произвольных значений «x».
Подставим, например, вместо «x» числа «0» и «1».

x	Расчет «y = −2x + 1»
0	y(0) = −2 · 0 + 1 = 1
1	y(1) = −2 · 1 + 1 = −2 + 1 = −1

Полученные значения «x» и «y» — это координаты точек графика функции.

Запишем полученные координаты точек «y = −2x + 1» в таблицу.

Точка	Координата по оси «Оx» (абсцисса)	Координата по оси «Оy» (ордината)
(·)A	0	1
(·)B	1	−1

Отметим полученные точки на системе координат.

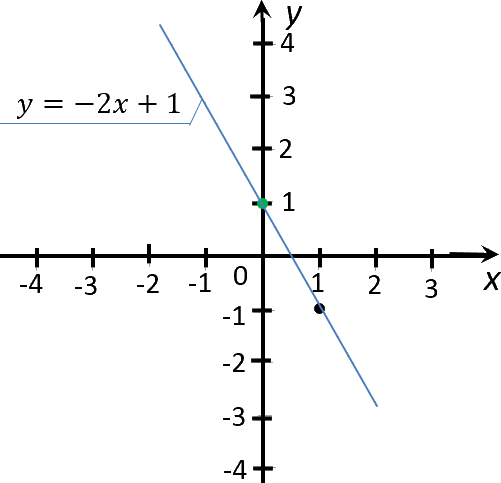
Теперь проведем прямую через отмеченные точки. Эта прямая будет
являться графиком функции «y = −2x + 1».

Как решать задачи на
линейную функцию «y = kx + b»

Рассмотрим задачу.

---

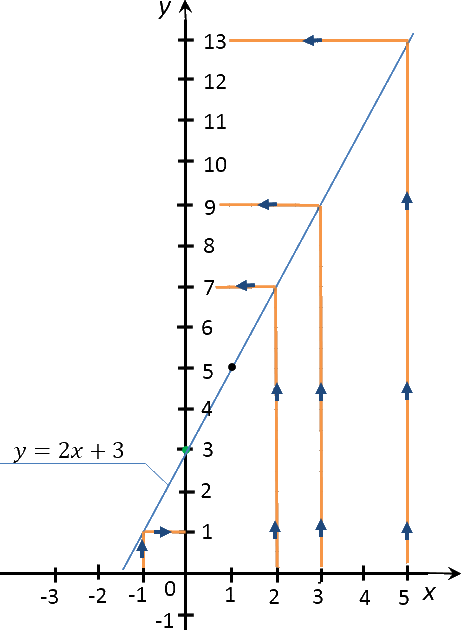
Построить график функции «y = 2x + 3». Найти по графику:

1. значение «y» соответствующее значению «x» равному −1; 2; 3; 5;
2. значение «x», если значение «y» равно
   1; 4; 0; −1.

---

Вначале построим график функции «y = 2x + 3».

Используем правила, по которым мы строили график функции выше.
Для построения графика функции «y = 2x + 3» достаточно найти всего две точки.

Выберем два произвольных числовых значения для «x». Для удобства расчетов выберем числа
«0» и «1».

Выполним расчеты и запишем их результаты в таблицу.

Точка	Координата по оси «Оx»	Координата по оси «Оy»
(·)A	0	y(0) = 2 · 0 + 3 = 3
(·)B	1	y(1) = 2 ·1 + 3 = 5

Отметим полученные точки на прямоугольной системе координат.

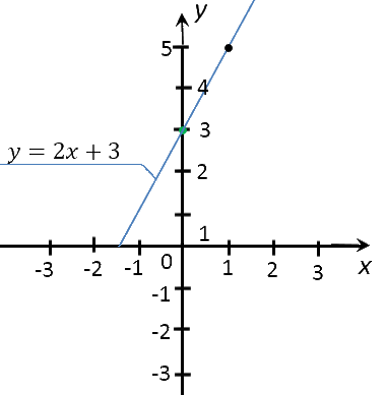
Соединим полученные точки прямой. Проведенная прямая будет являться графиком функции
«y = 2x + 3».

---

Теперь работаем с построенным графиком функции «y = 2x + 3».

Требуется найти значение «y»,
соответствующее значению «x»,
которое равно −1; 2; 3; 5.

---

Тему
«Как получить координаты точки функции» с графика функции
мы уже подробно рассматривали в уроке
«Как решать задачи на функцию».

В этому уроке для решения задачи выше вспомним только основные моменты.

По правилам выше найдем на построенном ранее графике функции «y = 2x + 3»
необходимые значения функции «y» для
«x» равным −1; 2; 3; 5.

Запишем полученные результаты в таблицу.

Заданное значение «x»	Полученное с графика значение «y»
−1	1
2	7
3	9
5	13

---

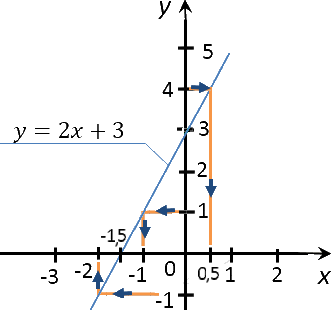
Переходим ко второму заданию задачи. Требуется найти значение «x»,
если значение «y» равно 1; 4; 0; −1.

Выполним те же действия, что и при решении предыдущего задания.
Разница будет лишь в том, что изначально мы будем проводить перпендикуляры от оси
«Oy».

Запишем полученные результаты в таблицу.

Заданное значение «y»	Полученное с графика значение «x»
−1	−2
0	−1,5
1	−1
4	0,5

---

Как проверить, проходит ли график через точку

Рассмотрим другое задание.

Не выполняя построения графика функции
«y = 2x −
», выяснить, проходит ли график
через точки с координатами (0;
− ) и (1; −2).

---

Подставим в функцию
«y = 2x −
»

координаты точки (0;
− ).

− = 2 · 0
−

   − =
−

(верно)

Это означает, что график функции «y = 2x −
» проходит через точку с координатами (0;
− ).

---

Проверим точку с координатами (1; −2).
Также подставим координаты
в функцию «y = 2x −
».

−2 = 2 · 1 −

−2 = 2 −

−2 = 1 −

        −2 = 1 (неверно)

Это означает, что график функции «y = 2x −
» не проходит через точку с координатами (1; −2).

---

Как найти точки пересечения графика с осями

Рассмотрим задачу.

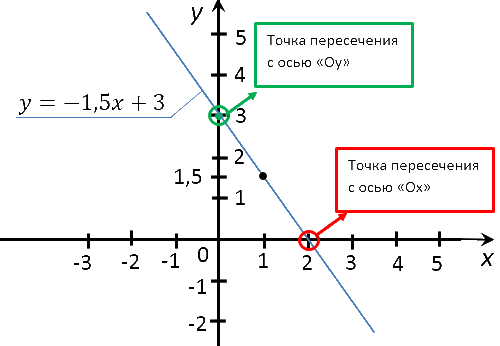
Найти координаты точек пересечения графика функции «y = −1,5x + 3» с осями координат.

Для начала построим график функции «y = −1,5x + 3» и на графике отметим точки пересечения
с осями.

Для построения графика функции найдем координаты двух точек
функции
«y = −1,5x + 3».

Выберем два произвольных числовых значения для «x» и рассчитаем значение
«y» по формуле
функции. Например, для x = 0 и
x = 1.

Точка	Координата по оси «Оx»	Координата по оси «Оy»
(·)A	0	y(0) = −1,5 · 0 + 3 = 3
(·)B	1	y(1) = −1,5 · 1 + 3 = 1,5

Отметим полученные точки на системе координат и проведем через них прямую.
Тем самым мы построим график функции «y = −1,5x + 3».

Теперь найдем координаты точек пересечения графика функции с осями по формуле функции.

Подставим вместо «x» в формулу функции «y = −1,5x + 3» число ноль.

y(0) = −1,5 · 0 + 3 = 3

(0; 3) — координаты точки пересечения графика функции «y = −1,5x + 3»
c осью «Oy».

Подставим вместо «y» в формулу функции «y = −1,5x + 3» число ноль.

0 = −1,5x + 3        
1,5x = 3        | :(1,5)
x = 3 : 1,5           
x = 2                   

(2; 0) — координаты точки пересечения графика функции «y = −1,5x + 3»
c осью «Ox».

Чтобы было проще запомнить, какую координату точки нужно приравнивать к нулю, запомните
«правило противоположности».

---

Ваши комментарии

Оставить комментарий:

---

b) Во втором случае функция та же, только значения (x=-6) и (x=3) не рассматриваются, так как они не принадлежат интервалу ((-6;3)). 

Поэтому точки ((-6); (-1)) и ((3); (2)) на рисунке отмечены светлыми кружочками.

По графику линейной функции, можно определить наибольшее и наименьшее значения линейной функции на заданном отрезке.

В случае

В этой статье мы рассмотрим линейную функцию, график линейной функции и его свойства. И, как обычно, решим несколько задач на эту тему.

Линейной функцией называется функция вида

В уравнении функции число , которое мы умножаем на называется коэффициентом наклона.

Например, в уравнении функции ;

в уравнении функции    ;

в уравнении функции   ;

в уравнении функции   .

Графиком линейной функции является прямая линия.

1. Чтобы построить график функции, нам нужны координаты двух точек, принадлежащих графику функции. Чтобы их найти, нужно взять два значения х, подставить их в уравнение функции, и по ним вычислить соответствующие значения y.

Например, чтобы построить график функции , удобно взять   и , тогда ординаты эти точек будут равны  и .

Получим точки А(0;2) и В(3;3). Соединим их и получим график  функции :

2. В уравнении функции  коэффициент  отвечает за наклон графика функции:

Коэффициент  отвечает за сдвиг графика вдоль оси :

На рисунке ниже изображены графики функций ; ; 

Заметим, что во всех этих функциях коэффициент больше нуля, и все графики функций наклонены вправо. Причем, чем больше значение , тем круче идет прямая.

Во всех функциях – и мы видим, что все графики пересекают ось OY в точке (0;3)

Теперь рассмотрим графики функций ; ; 

На этот раз  во всех  функциях коэффициент меньше нуля, и все графики функций наклонены влево.

Заметим, что чем больше |k|, тем круче идет прямая. Коэффициент b тот же, b=3, и графики также как в предыдущем случае пересекают ось OY в точке (0;3)

Рассмотрим графики функций  ; ;

Теперь  во всех уравнениях функций коэффициенты равны. И мы получили три параллельные прямые.

Но коэффициенты b различны, и эти графики пересекают ось OY  в различных точках:

График функции (b=3) пересекает ось OY  в точке (0;3)

График функции (b=0) пересекает ось OY  в точке (0;0) –  начале координат.

График функции (b=-2) пересекает ось OY  в точке (0;-2)

Итак, если мы знаем знаки коэффициентов k и b, то можем сразу представить, как выглядит график функции .

Если  k<0 и b>0, то график функции  имеет вид:

Если  k>0 и b>0, то график функции  имеет вид:

Если  k>0 и b<0, то график функции  имеет вид:

Если  k<0 и b<0, то график функции  имеет вид:

Если  k=0 , то  функция превращается в функцию    и ее график имеет вид:

Ординаты всех точек графика функции  равны 

Если b=0, то график функции  проходит через начало координат:

 Это график прямой пропорциональности.

3. Отдельно отмечу график уравнения . График этого уравнения представляет собой прямую линию, параллельую оси  все точки которой имеют абсциссу .

Например, график уравнения  выглядит так:

Внимание! Уравнение  не является функцией, так  как различным значениям функции соответствует одно и то же значение аргумента, что не соответствует определению функции.

4. Условие параллельности двух прямых:

График функции  параллелен графику функции , если 

5. Условие перпендикулярности двух прямых:

График функции  перпендикулярен графику функции , если  или 

6. Точки пересечения графика функции  с осями координат.

С осью ОY. Абсцисса любой точки, принадлежащей оси ОY равна нулю. Поэтому, чтобы найти точку пересечения с осью ОY нужно в уравнение функции вместо х подставить ноль. Получим y=b. То есть точка пересечения с осью OY имеет координаты (0;b).

С осью ОХ: Ордината любой точки, принадлежащей оси ОХ равна нулю. Поэтому, чтобы найти точку пересечения с осью ОХ нужно в уравнение функции вместо y подставить ноль. Получим 0=kx+b. Отсюда . То есть точка пересечения с осью OX имеет координаты (;0):

Рассмотрим решение задач.

1. Постройте график функции , если известно, что он проходит через точку А(-3;2) и параллелен прямой y=-4x.

В уравнении функции   два неизвестных параметра: k и b. Поэтому в тексте задачи должны быть два условия, характеризующих график функции.

а) Из того, что график функции  параллелен прямой y=-4x, следует, что k=-4. То есть уравнение функции имеет вид 

б) Нам осталось найти b. Известно, что график функции  проходит через точку А(-3;2). Если точка принадлежит графику функции, то при подстановке ее координат в уравнение функции, мы получим верное равенство:

  отсюда b=-10

Таким образом, нам надо построить график функции 

Точка А(-3;2) нам известна, возьмем точку B(0;-10)

Поставим эти точки в координатной плоскости и соединим их прямой:

2. Написать уравнение прямой, проходящей через точки A(1;1); B(2;4).

Если прямая проходит через точки с заданными координатами, следовательно, координаты точек удовлетворяют уравнению прямой  . То есть если мы координаты точек подставим в уравнение прямой, то получим верное равенство.

Подставим координаты каждой точки в уравнение   и получим систему линейных уравнений.

Вычтем из второго уравнения системы первое, и получим . Подставим значение k в первое уравнение системы, и получим b=-2.

Итак, уравнение прямой .

3. Постройте график уравнения

Чтобы найти,  при каких значениях неизвестного произведение нескольких множителей равно нулю, нужно каждый множитель приравнять к нулю и учесть ОДЗ каждого множителя. 

Это уравнение не имеет ограничений на ОДЗ. Разложим на множители вторую скобку и приравняем каждый множитель к нулю. Получим совокупность уравнений:

Построим графики всех  уравнений совокупности в одной коорднатной плоскости. Это и есть график уравнения  :

4. Постройте график функции , если он перпендикулярен прямой  и проходит через точку М(-1;2)

Мы не будем строить график, только найдем уравнение прямой.

а) Так как график функции , если он перпендикулярен прямой , следовательно , отсюда . То есть уравнение функции имеет вид 

б) Мы знаем, что  график функции  проходит через точку М(-1;2). Подставим ее координаты в уравнение функции. Получим:

, отсюда .

Следовательно, наша функция имеет вид: .

5. Постройте график функции 

Упростим выражение, стоящее в правой части уравнения функции.

Важно! Прежде чем упрощать выражение, найдем его ОДЗ.

Знаменатель дроби не может быть равен нулю, поэтому , .

Тогда наша функция принимает вид:

То есть нам надо построить график функции  и выколоть на нем две точки: с абсциссами x=1 и x=-1:

И.В. Фельдман, репетитор по математике.

Точки пересечения графиков функций

В алгебре и начале анализа можно встретить множество задач на поиск точек пересечения графиков функций с помощью их построения или другими методами. Благодаря определенному алгоритму действий, найти ответ достаточно просто. В большинстве случаев решение заключается в определении корней различного вида уравнений.

График функции (y = f(x)) является множеством точек ((x; y)), координаты которых связаны соотношением (y = f(x).)

Равенство (y = f(x)) называют уравнением данного графика. Таким образом, график функции представляет собой множество точек (x; y), где x — является аргументом, а y — определяется как значение функции, соответствующее данному аргументу.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

В том случае, когда графики пересекаются в какой-то точке, можно сделать вывод о существовании общего решения системы уравнений. Определить координаты точки можно с помощью графического или аналитического метода. В первом случае требуется построить график уравнения с переменной. Аналитический метод поиска координат точек, в которых графики функций пересекаются, подразумевает решение уравнения, а найденные корни и являются искомыми точками.

Как найти координаты, примеры решения

Существует несколько способов решения подобных задач:

1. Поиск точек пересечения графиков функций заключается в приравнивании обеих функций друг к другу. При этом все члены с х переносят в левую сторону, а оставшиеся – в правую. Затем остается найти корни уравнения, которое получилось после преобразований.
2. Второй метод состоит в записи системы уравнения для ее последующего решения с помощью подстановки одной функции в другую.
3. Третий способ подразумевает построение графиков функций, чтобы определить точки их пересечения визуально.

В качестве примера можно рассмотреть две линейные функции:

(f(x) = k_1 x+m_1)

(g(x) = k_2 x + m_2)

Данные функции являются прямыми. Их можно графически изобразить, если принять какие-либо два значения (x_1) и (x_2) и найти (f(x_1)) и ((x_2)). Далее действия необходимо повторить с функцией (g(x)). Затем достаточно легко определить визуально координаты точки пересечения рассматриваемых функций.

Важно отметить, что для линейных функций характерна лишь одна точка пересечения только в том случае, когда (k_1 neq k_2). В противном случае (k_1=k_2), а функции будут параллельными друг другу, в связи с тем, что k является коэффициентом угла наклона. При( k_1 neq k_2) и (m_1=m_2) точка пересечения будет соответствовать (M(0;m)). Данная закономерность упрощает решение многих подобных задач.

(g(x)=x+3)

Требуется определить координаты точки, в которой пересекаются графики рассматриваемых функций.

Решение

В первую очередь стоит отметить, что функции являются линейными. Важно обратить внимание на коэффициент угла наклона рассматриваемых функций:

(k_1 = 2)

(k_2 = 1)

Заметим, что:

(k_1 neq k_2)

По этой причине имеется лишь одна точка пересечения графиков функций. Определить ее можно путем решения уравнения:

(f(x)=g(x))

(2x-5 = x+3)

Необходимо перенести члены с x в левую часть, а остальные – в правую:

(2x – x = 3+5)

(x = 8)

В результате удалось найти x=8, что соответствует абсциссе точки пересечения графиков. Требуется определить ординату y с помощью подстановки x = 8 в любое из уравнений – в (f(x)), либо в (g(x)):

(f(8) = 2cdot 8 – 5 = 16 – 5 = 11)

Таким образом, M (8;11) – представляет собой точку, в которой пересекаются графики пары линейных функций.

Ответ: M (8;11)

(g(x) = 2x-4.)

Необходимо определить точки, в которых графики рассматриваемых функций пересекаются.

Решение

Угловые коэффициенты:

(k_1 = k_2 = 2)

Таким образом, линейные функции параллельны между собой, что объясняет отсутствие точек пересечения их графиков.

Ответ: графики функций параллельны, точки пересечения отсутствуют.

(g(x)=x^2+1)

Решение

В данном случае функции являются нелинейными. Поэтому алгоритм решения задачи будет несколько отличаться от предыдущих примеров. В первую очередь следует приравнять уравнения:

(x^2-2x+1=x^2+1)

Далее необходимо разнести в разные стороны уравнения члены с x и без него:

(x^2-2x-x^2=1-1)

(-2x=0)

(x=0)

Таким образом, будет определена абсцисса искомой точки. Затем необходимо найти ординату у. Для этого нужно подставить (x = 0) в какое-либо из двух начальных уравнений. К примеру:

(f(0)=0^2-2cdot 0 + 1 = 1)

M (0;1) является точкой, в которой пересекаются графики функций.

Ответ: M (0;1)

Приравнивание функций друг к другу и нахождение корней

Выяснить, имеют ли точки пересечения графики функций, можно путем сравнения соответствующих тождеств и решения уравнения. Однако при этом допускается получение различных равенств с неизвестными. Тогда целесообразно воспользоваться специальными методиками.

Когда уравнение относится к первой степени или является линейным, решение получить достаточно просто. Метод заключается в переносе переменных величин в одну часть уравнения, а известных – в другую. Алгоритм действий:

• раскрытие скобок, приведение подобных коэффициентов;
• перенос членов с неизвестными в одну сторону, а с известными – в другую;
• математические преобразования;
• определение корня.

Квадратные уравнения решают с помощью одного из способов:

• разложение на множители;
• выделение полного квадрата;
• поиск дискриминанта;
• теорема Виета.

В первом случае представляется возможным понизить степень при неизвестной величине. Второй метод заключается в выделении квадрата по одной из формул сокращенного умножения. Каждая из этих методик реализуема при наличии знаний соответствующих тождеств, в том числе правил разложения на множители.

Третий способ состоит в поиске корней через дискриминант (Д), который является дополнительным параметром, позволяющим сразу решить задачу. Дискриминант определяется с помощью формулы:

((-S)^2-4PU)

В том случае, когда Д>0, переменная может иметь пару значений, которые превращают равенство в справедливое тождество. Если Д=0, то корень является единственным. Когда Д<0, искомое тождество с неизвестными не имеет решений.

Квадратные уравнения решают таким образом:

• выполнение необходимых алгебраических преобразований, в том числе раскрытие скобок и приведение подобных слагаемых;
• выбор наиболее оптимального способа решения и его реализация;
• проверка корней с помощью их подстановки в начальное выражение.

Существует несколько методик решения тождеств кубического и биквадратного типов:

• понижение степени, то есть разложение на множители;
• замена переменной.

Первый вариант решения подразумевает выполнение преобразований для последующего применения одной из формул сокращенного умножения. Такой способ применяют нечасто. Второй способ состоит в том, что при решении необходимо ввести переменную с более низкой степенью, которая упрощает выражение. Порядок действий при этом следующий:

• выполнение математических преобразований;
• выражение переменной через другую;
• решение квадратного или линейного уравнения;
• подстановка промежуточных корней, которые получилось найти на третьем шаге, во второй;
• вычисление искомых корней;
• проверка;
• исключение ложных решений;
• запись ответа.

Путем составления системы уравнений

Данный метод определения точек пересечения графиков функций предполагает запись системы уравнения. К примеру:

Решение системы уравнений представляет собой пару чисел (х, у), являющуюся одновременно решением для первого и второго уравнения системы. Решить систему уравнений – значит, отыскать все ее решения, либо установить их отсутствие.

Порядок действий при решении системы уравнений можно рассмотреть на примере:

Решение будет иметь следующий вид:

Данные уравнения являются линейными, поэтому график каждого из них представляет собой прямую. График первого уравнения проходит через точки (0; 1) и (-1; 0). График второго уравнения проходит через точки (0; -1) и (-1; 0). Прямые пересекаются в точке (-1; 0), это и является решением системы уравнений.

Решение системы представляет сбой единственную пару чисел:

Если подставить данные числа в любое из уравнений, то получится справедливое равенство. Таким образом, имеется единственное решение линейной системы. Можно записать отчет: (-1;0).

В процессе решения линейной системы можно столкнуться с разными ситуациями:

• система обладает единственным решением, прямые пересекаются;
• решения системы отсутствуют. прямые параллельны;
• система обладает бесчисленным множеством решений, прямые совпадают.

При рассмотрении частного случая системы p(x; y) и q(x; y) являются линейными выражениями от x и y.

В задачах нередко требуется решить нелинейную систему уравнений. К примеру, необходимо решить следующую систему:

Решение имеет следующий вид:

График первого уравнения будет иметь вид прямой, а второго – являться окружностью. Можно построить первый график по точкам:

Центр окружности в точке О(0; 0), радиус равен 1.

Графики пересекаются в точке А(0; 1) и в точке В(-1; 0).

Ответ: (0; 1); (-1; 0).

Можно решить систему графическим способом:

В первую очередь необходимо построить график первого уравнения, который будет представлять собой окружность с центром в точке О (0; 0) и радиусом 2. График второго уравнения является параболой, которая смещена относительно начала координат на 2 вверх, то есть ее вершина – точка (0; 2).

Графики обладают одной общей точкой А(0; 2). Данная точка является решением системы. Если подставить два числа в уравнение, можно проверить корректность ответа и записать его. Ответ: (0; 2).

В качестве еще одного примера можно решить следующую систему:

Первым шагом является построение графика первого уравнения, который будет представлять собой окружность с центром в точке О (0; 0) и радиусом 1.

Далее необходимо построить график функции:

График будет являться ломанной:

Далее следует сместить ее на 1 вниз по оси oy. В результате получится график функции:

При помещении обоих графиков в одну систему координат получится следующая ситуация:

Таким образом, получились три точки пересечения: А(1; 0), т. В(-1; 0), т. С(0; -1)

Нахождение через графическое построений функций

Любой определенный график задают с помощью соответствующей функции. Найти точки, в которых пересекаются графики, можно путем решения уравнения, имеющего вид:

(f1(x)=f2(x))

Решение данного уравнения будет являться искомой точкой.

Построить график можно с помощью бумаги и ручки. В процессе необходимо обратить внимание на то, что количество точек пересечения пары графиков определяется видом функции. Линейные функции обладают лишь одной точкой пересечения, линейная и квадратная – двумя, квадратные – двумя, либо четырьмя.

В общем случае двух линейных функций можно предположить, что:

(y1=k1x+b1)

(y2=k2x+b2)

Для поиска точки пересечения графиков необходимо решить уравнение:

(y1=y2 или k1x+b1=k2x+b2)

После преобразований получится, что:

(k1x-k2x=b2-b1.)

Далее нужно выразить x:

(x=(b2-b1)/(k1-k2).)

При известной координате точки по оси абсцисс следует определить координату по оси ординат. Таким образом, можно найти координаты точки пересечения графиков:

(((b2-b1)/(k1-k2); k1(b2-b1)/(k1-k2)+b2))

График функции y = f (х) представляет собой множество точек плоскости, координаты (х, у) которых соответствуют выражению y = f(x). График функции наглядно иллюстрирует поведение и свойства функции. Для построения графика определяют несколько значений довода х и для них рассчитывают соответствующие значения функции y=f(x). Для больше точного и наглядного построения графика следует обнаружить его точки пересечения с осями координат.

С целью определить точку пересечения графика функции с осью y, нужно определить значение функции при х=0, то есть обнаружить f(0). В качестве примера можно рассмотреть график линейной функции, изображенной на рисунке:

В данном случае при х=0 ((y=a*0+b)) функция равна b. Таким образом, график пересекает ось ординат (ось Y) в точке (0,b). Когда пересекается ось абсцисс (ось Х) функция равна 0, то есть (y=f(x)=0). Для того чтобы определить х, следует решить уравнение (f(x)=0). В случае линейной функции получаем уравнение (ax+b=0), откуда и находим (x=-b/a). В результате можно сделать вывод, что ось Х пересекается в точке ((-b/a,0).)

При наличии квадратичной зависимости y от х, уравнение (f(x)=0) обладает двумя корнями. Таким образом, ось абсцисс пересекается два раза. В случае периодической зависимости y от х, например, (y=sin(x)), график функции обладает бесконечным количеством точек пересечения с осью Х. Проверить корректность расчета координат точек, в которых пересекаются графики функций, можно с помощью подстановки найденных значений х в выражение f(x). Значение выражения при любом из вычисленных х должно быть равно 0.

Определение

Функция, заданная формулой y=kx+b, где х – переменная, k и b – некоторые числа, называется линейной функцией. Переменную х называют независимой переменной, переменную у – зависимой переменной.

Графиком линейной функции является прямая. Для построения прямой достаточно взять два значения х, чтобы получить два значения у и, соответственно, две точки, через которые проходит единственная прямая.

Число k называется угловым коэффициентом прямой.

Свойства линейной функции

1. Область определения функции – множество всех действительных чисел. То есть в данную формулу мы можем подставлять любое значение х.
2. Областью значений также является множество всех действительных чисел.
3. Функция не имеет ни наибольших, ни наименьших значений.
4. При k – положительном, угол наклона к оси х острый, другими словами – график функции возрастает.
5. При k отрицательном угол наклона к оси х тупой, то есть график функции – убывает.
6. При k=0 прямая параллельна оси х.
7. Частный случай линейной функции: y=kx, где число b=0, эту функцию называют прямой пропорциональностью, график такой функции проходит через начало координат.

Рассмотрим на примерах расположение прямых в координатной плоскости в зависимости от значения чисел k и b.

Пример №1

Построить график функции у=2х – 1. Для того, чтобы удобнее было выполнять вычисления, построение и т.д. сделаем таблицу для значений х и у:

Для построения графика подбираем два значения х, одно из них желательно брать равное нулю, второе, например 3 (подбираем небольшие числа).

Теперь подставляем значения х в формулу и вычисляем соответствующие значения у:

у=2х – 1=2×0 – 1= –1;

у=2х – 1=2×3 – 1= 5.

Вписываем в таблицу значения у:

Теперь строим систему координат, отмечаем в ней точки с координатами      А(0; –1) и В(3;5), проводим через эти две точки прямую.

Итак, по формуле мы видим, что угловой коэффициент – положительный, значит, график – возрастает, что мы и видим на нашем графике.

Пример №2.

Построить график функции у= –3х+4. Итак, делаем таблицу на два значения, например, возьмем 0 и 2.

По формуле видим, что угловой коэффициент отрицательный, значит, прямая будет убывать. Строим убывающую прямую в системе координат через две точки А(0;4) и В(2; –2).

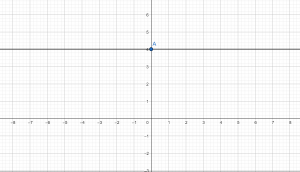
Пример №3

Построить график функции у=4. Видим, что в данном случае число х=0, значит, прямая будет проходить через точку с координатой (0;4) параллельно оси х. На графике это выглядит следующим образом:

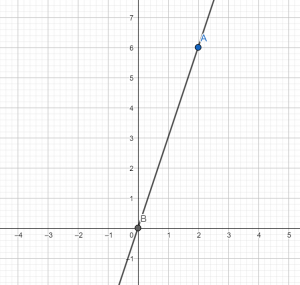
Построить график функции у=3х. Данная функция является частным случаем, когда прямая проходит через начало координат. Поэтому в данном случае можно взять устно одно значение х, например 2, тогда у получим равный 6. Таким образом, имеем две точки (2;6) и (0;0). Строим их в системе координат и проводим через них прямую, которая будет возрастать, так как угловой коэффициент равен 3, т.е. положительный.

Задание OM1106o

На рисунках изображены графики функций вида y=kx+b. Установите соответствие между графиками функций и знаками коэффициентов k и b.

ГРАФИКИ:

КОЭФФИЦИЕНТЫ:

1) k>0, b<0                   2) k>0, b>0                    3) k<0, b<0 

---

ассмотрим коэффициенты под №3. Если k<0, значит, график имеет тупой (>90⁰) угол с положит.направлением оси абсцисс (Ох). Если b<0, то это говорит, что график пересекает ось ординат (Оу) ниже нуля. Эти два условия реализованы на графике В. Итак, получаем для ответа пару: В–3.

У двух других пар коэффициентов (№№ 1 и 2) зафиксировано, что k>0. Это соответствует оставшимся графикам А и Б, т.к. они оба наклонены к положительно направлению оси Оx под острым углом (<90⁰). Следовательно, выбор соответствия должен быть выполнен по коэффициенту b.

В 1-й паре коэффициентов b<0. Это означает, что соответствующий им график должен пересекать ось Оу в точке ниже начала координат. Таковым является график Б, и мы получаем пару Б–1. В паре коэффициентов №2 b>0, что соответствует графику А, который пересекает ось Оу выше начала координат. Это подтверждает, что и оставшаяся пара А–2 тоже верна.

Ответ: 213

pазбирался: Даниил Романович | обсудить разбор

Задание OM1103o

Установите соответствие между функциями и их графиками.

Функции:

A) y = 3x

Б) y = -3x

В) y = (1/3)x

Графики:

---

Функция представляет собой линейную зависимость, а именно уравнение первого порядка вида:

y = kx + b

График данной функции зависит от k и b.

• если k < 0,  то функция убывает, то есть линия идет сверху вниз, как на третьем рисунке
• если k > 0, то функция возрастает, то есть линия идет снизу вверх, как на первых двух рисунках
• коэффициент b определяет сдвиг по оси y, если b < 0, то прямая пересекает ось y ниже 0 в точке y = b, если  b > 0, то выше ноля в точке y = b
• если k >1, то прямая идет круче, чем обычная y = x (как на втором и третьем графике), если k <1 , то положе, как на примере рисунка №1

Следовательно, графику y = 3x соответствует рисунок 2, так как прямая идет снизу вверх и она более крутая, чем кривая на рисунке 1, которому соответствует функция y = (1/3)x.

Графику 3 соответствует функция y = -3x так как k = -3 < 0, и график идет сверху вниз.

Ответ:

A) 2

Б) 3

В) 1

Ответ: 231

pазбирался: Даниил Романович | обсудить разбор

Даниил Романович | Просмотров: 6k