Как найти координаты точек отмеченных на прямой - Сайт, где вы сможете решить свои вопросы

Похоже, вы используете блокировщик рекламы. Наш сайт существует и развивается
только за счет дохода от рекламы.

Пожалуйста, добавьте нас в исключения блокировщика.

на главную

Как найти координаты точки

Поддержать сайт

Каждой точке координатной плоскости соответствуют две координаты.

Координаты точки на плоскости — это пара чисел, в которой на
первом месте стоит
абсцисса, а на
втором —
ордината точки.

Рассмотрим как в системе координат (на координатной плоскости):

находить координаты точки;
найти положение точки.

Чтобы найти координаты точки на плоскости, нужно опустить из этой точки
перпендикуляры на оси координат.

Точка пересечения с осью «x» называется абсциссой точки «А»,
а с осью y называется ординатой точки «А».

Обозначают координаты точки, как указано выше (·) A (2; 3).

Пример (·) A (2; 3) и (·) B (3; 2).

Запомните!

На первом месте записывают абсциссу (координату по оси «x»), а на втором —
ординату (координату по оси «y») точки.

Особые случаи расположения точек

Если точка лежит на оси «Oy»,
то её абсцисса равна 0. Например,
точка С (0, 2).
Если точка лежит на оси «Ox», то её ордината равна 0.
Например,
точка F (3, 0).
Начало координат — точка O имеет координаты, равные нулю O (0,0).
Точки любой прямой перпендикулярной оси абсцисс, имеют одинаковые абсциссы.
Точки любой прямой перпендикулярной оси ординат, имеют одинаковые ординаты.
Координаты любой точки, лежащей на оси абсцисс имеют вид (x, 0).
Координаты любой точки, лежащей на оси ординат имеют вид (0, y).

Как найти положение точки по её координатам

Найти точку в системе координат можно двумя способами.

Первый способ

Чтобы определить положение точки по её координатам,
например, точки D (−4 , 2), надо:

Отметить на оси «Ox», точку с координатой
«−4», и провести через неё прямую перпендикулярную оси «Ox».
Отметить на оси «Oy»,
точку с координатой 2, и провести через неё прямую перпендикулярную
оси «Oy».
Точка пересечения перпендикуляров (·) D — искомая точка.
У неё абсцисса равна «−4», а ордината равна 2.

Второй способ

Чтобы найти точку D (−4 , 2) надо:

Сместиться по оси «x» влево на
4 единицы, так как у нас
перед 4
стоит «−».
Подняться из этой точки параллельно оси y вверх на 2 единицы, так
как у нас перед 2 стоит «+».

Чтобы быстрее и удобнее было находить координаты точек или строить точки по координатам на
листе формата A4 в клеточку, можно скачать и использовать
готовую систему координат на нашем сайте.

Ваши комментарии

Важно!

Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи

«ВКонтакте».

Оставить комментарий:

Источник

Эта информация доступна зарегистрированным пользователям

В этом уроке мы познакомимся с положительными и отрицательными числами, поймем, к чему относится нуль.

Не забудем рассказать также про неположительные и неотрицательные числа, а после этого узнаем, что такое координатная прямая и из чего она состоит.

Начнем с сухих, но емких определений.

Определение: положительное число – это число со знаком «+» перед ним.

Обычно + не пишется, а просто подразумевается.

Числа 2, (mathbf{frac{1}{2}}), (mathbf{123frac{456}{789}}), 9871254 – перед ними не стоит никакой знак, соответственно, эти числа положительные.

Мы могли бы их записать и со знаком «+»:

+2, (mathbf{+frac{1}{2}}), (mathbf{+123frac{456}{789}}), +9871254

В таком случае нужно читать запись буквально: «плюс два», «плюс одна вторая» и так далее.

Такая запись добавляет громоздкости записи, и обычно все- таки «+» опускают.

Определение: отрицательное число – это число со знаком «-» перед ним.

Приведем примеры отрицательных чисел:

-3, (mathbf{-frac{1}{6}}), (mathbf{-32frac{4}{5}}), -784285332

Читать в данном случае также нужно дословно: «минус три», «минус одна шестая» и так далее.

Минус уже опустить нельзя, так как тогда получится, что число положительное.

Важные факты:

Все положительные числа строго больше нуля
Все отрицательные число строго меньше нуля
0 не относится ни к положительным, ни к отрицательным числам

Если нам надо сравнить два числа, одно из которых положительное, а другое отрицательное, то можно смело утверждать, что число, которое положительно, больше числа, которое отрицательно.

Если надо сравнить число с нулем, то достаточно понять, положительное оно или отрицательное. Если положительное, значит, больше нуля, если же отрицательное, то меньше нуля.

Более подробно про сравнение чисел мы поговорим в следующих уроках, а пока потренируемся отличать положительные и отрицательные числа.

Эта информация доступна зарегистрированным пользователям

Иногда необходимо обозначить множество чисел, больших или равных нулю, или же наоборот, меньших или равных нулю.

Удобно, что для этого есть специальные определения.

Определение: Неотрицательные числа – это все положительные числа и 0.

Соответственно, если мы хотим привести примеры неотрицательных чисел, то можем привести положительные числа или 0.

Примеры: 0, 1, 956, (mathbf{frac{4}{9}}), (mathbf{342frac{1}{9}}).

Определение: Неположительные числа – это все отрицательные числа и 0.

В данном случае примерами будут соответственно отрицательные числа или 0.

Примеры: 0, (mathbf{-1}), (mathbf{-922}), (mathbf{-frac{7}{8}}), (mathbf{-4frac{1}{4}}).

Если необходимо определить, является ли число неотрицательным или неположительным, то ответить надо следующим образом:

Отрицательное число является неположительным
Положительные число является неотрицательным
0 является одновременно и неположительным, и неотрицательным числом

Также отметим важные факты про сравнение неположительных и неотрицательных чисел с нулем:

Неположительные числа меньше или равны нулю.
Если а – неположительное, то (mathbf{aleq0})
Аналогично, неотрицательные числа больше или равны нулю.
Если a – неотрицательное, то (mathbf{ageq0})

Эта информация доступна зарегистрированным пользователям

Начнем с определения, а потом посмотрим на вариации и примеры координатных прямых в жизни.

Определение: координатная прямая – это прямая с указанной на ней точкой начала отсчета, направлением и единичным отрезком.

Эта информация доступна зарегистрированным пользователям

Если хотя бы одной из этих трех составляющих нет, то прямая уже не может быть координатной.

Выше мы показали самую простую вариацию координатной прямой.

Но обычно для удобства наносят штрихи по всей длине, чтобы не отмерять единичные отрезки.

Эта информация доступна зарегистрированным пользователям

Также мы можем подписывать числа не только под точкой начала отсчета и точкой, дающей понимание о длине единичного отрезка, но и под остальными точками тоже.

Эта информация доступна зарегистрированным пользователям

Если мы не хотим загромождать картинку, то можно отмечать точки с какой-то периодичностью.

Эта информация доступна зарегистрированным пользователям

Неизменным на всех этих картинках остается наличие трех пунктов из определения:

Точка начала отсчета
Направление
Единичный отрезок

В жизни координатные прямые, полностью удовлетворяющие нашему определению, могут встречаться довольно редко.

Например, на ртутном термометре подразумевается, что направление совпадает с направлением увеличения чисел на шкале.

На нем же мы видим, что числа стоят не у каждого штриха, а у каждого 5-го или каждого 10-го, так картинка становится более читаемой.

Эта информация доступна зарегистрированным пользователям

Еще один пример: обычная линейка или рулетка. Тут тоже направление подразумевается, поэтому нельзя однозначно сказать, что это координатная прямая.

На линейке, в отличие от градусника, не часто увидишь отрицательные числа. Действительно, -5 градусов интересуют нас больше, чем -5 сантиметров.

Введем еще одно определение: координата точки – это число, показывающее положение точки на координатной прямой.

Эта информация доступна зарегистрированным пользователям

На этом рисунке видно, что у точки начала координат (точка O) координата равна нулю, а у точки (А), дающей информацию о единичном отрезке,

координата- 1.

Чтобы найти координату точки мы должны отсчитать количество единичных отрезков между точкой и точкой начало отсчета. А дальше, если эта точка стоит после точки начала отсчета, то взять количество единичных отрезков. В противном случае, если точка находится перед точкой начала отсчета, то взять количество единичных отрезков со знаком «минус».

Например, чтобы найти координату точки C мы отсчитываем количество отрезков от начала координат; получаем, что их 2, запоминаем это.

Точка С находится справа от точки начала отсчета, или дальше по направлению, чем точка начала отсчета. Значит, берем непосредственно число 2 в качестве координаты.

Между точкой B и точкой начала отсчета 3 единичных отрезка, но если смотреть относительно точки начала отсчета, то она находится левее или раньше по направлению, значит, мы берем количество единичных отрезков со знаком «минус» и координатой точки B будет (mathbf{-3}).

Естественно, единичных отрезков между точкой и точкой начала отрезков может получиться нецелое число.

Этот случай иллюстрирует точка D – она находится на расстоянии полутора единичных отрезков от точки начала отсчета.

Точка D идет перед точкой начала отсчета, если смотреть по направлению, а значит, координата должна быть отрицательный.

Таким образом, координата точки D будет равна (mathbf{-1.5}).

Мы не случайно отходим от простых понятий «справа»/«слева», когда говорим о взаимном расположении точек.

Представьте, что направление идет в другую сторону.

Эта информация доступна зарегистрированным пользователям

В таком случае точки справа от точки начала отсчета будут иметь отрицательные координаты, а точки слева точки начал отсчета – положительные.

Ну и конечно же, прямая может быть вообще расположена вертикально, тогда говорить о направлениях «право»/«лево» вообще не приходится.

Эта информация доступна зарегистрированным пользователям

Сегодня Вы узнали про отрицательные числа. Интересно, а когда про отрицательные числа узнали впервые в истории?

Изначально люди оперировали в основном натуральными числами. Они удобны, когда надо посчитать количество голов скота, количество дней в каком- то процессе и так далее.

Мы уже обсуждали, что в какой- то момент пришлось работать с дробями, так как и они появляются в реальной жизни, когда мы говорим про половину килограмма крупы, треть часа на выполнение задания и так далее.

А отрицательных чисел в каком-то естественном эквиваленте не встретить, это все равно будет некоторая абстракция, поэтому древние люди относились к ним с недоверием.

Несмотря на это, китайские математики II века до нашей эры уже знали про них и умели применять к ним сложение и вычитание, но еще не научились их делить и умножать.

Различали же древние китайцы положительные и отрицательные числа не как мы, с помощью знаков, а с помощью цвета – положительным числам соответствовал красный цвет, а отрицательным- черный.

Так продолжалась до XII века, пока отрицательные числа не начали просто перечеркивать чертой слева направо.

Уже с VII века зафиксировано понимание того, что отрицательные числа нужны для оперирования долгами.

Условно, если у меня есть (mathbf{-5}) тысяч рублей, то это значит, что я кому- то 5 тысяч рублей должен.

Координатную прямую впервые ввел французский ученый Рене Декарт в 1637 году, что сильно поспособствовало популяризации отрицательных чисел.

Окончательно отрицательные числа закрепились только к началу XIX века.

Источник

Как найти точку на прямой

В современной математике точкой называются элементы весьма различной природы, из которых состоят различные пространства. Например, в n-мерном евклидовом пространстве точкой называется упорядоченная совокупность из n чисел.

Вам понадобится

Знания по математике.

Инструкция

Прямая – одно из основных понятий в математике. Аналитически прямая на плоскости задается уравнением первого порядка вида Ax+By=C. Принадлежность точки к заданной прямой легко определить, подставив координаты точки в уравнение прямой. Если уравнение обращается в верное равенство, значит точка принадлежит прямой. Например, рассмотрим точку с координатами A(4, 5) и прямую заданную уравнением 4х+3у=1. Подставим в уравнение прямой координаты точки А и получим следующее: 4*4+3*5 = 1 или 31 = 1. Получили равенство, которое является не верным, а значит, эта точка не принадлежит прямой.

Для поиска точки на прямой достаточно взять одну из координат, и подставить в уравнение, а затем выразить из полученного уравнение вторую. Таким образом найдется точка с заданной одной из координат. Так как прямая проходит через всю плоскость, то и точек, которые ей принадлежат бесконечно много, а значит, для любой одной координаты всегда найдется другая, такая что полученная точка будет принадлежать заданной прямой. Возьмем для примера прямую с уравнением 3x-2y=2. И возьмем координату равную x=0. Тогда подставим значение x в уравнение прямой и получим следующее: 3*0-2у=2 или у=-1. Таким образом мы нашли точку лежащую на прямой и ее координаты равны (0, -1). Аналогичным образом можно найти точку, принадлежащую прямой, когда известна координата y.

В трехмерном пространстве у точки 3 координаты, а прямая задается системой из двух линейных уравнений вида Ax+By+Cz=D. Аналогичным образом, как и в двумерном случае, если вы знаете хоть одну координату точки, решив систему, найдете две остальные и эта точка будет принадлежать исходной прямой.

Видео по теме

Обратите внимание

После того как найдены все координаты точки, необходимо проверить их правильность. Подставьте найденные координаты в уравнение прямой, и если получится верное равенство, все решено корректно.

Полезный совет

Способ поиска точки по известной координате справедлив для любой размерности пространства, разница лишь в том, сколько необходимо уравнений решить, для поиска остальных координат.

Источники:

найти точки прямой

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.

Источник

Прямая с выбранным
на ней началом отсчета, единичным
отрезком и направлением называется
координатной прямой. Число, показывающее
положение точки на прямой, называют
координатой этой точки

Расстояние d
между точками A(x₁)
и B(x₂)
на прямой:

Если
точка М(x) лежит на прямой, проходящей
через две данные точки

(
)
и

(
),
и дано отношение

,
в котором точка М делит отрезок

,
то координата точки М определяется по
формуле

,.

Если
точка М является серединой отрезка

,
то ее координата определяется по формуле

.

7. Координаты точки на плоскости, расстояние между двумя точками, деление отрезка в данном соотношении

Координаты точки
записываются в скобках рядом с названием
точки, причем всегда на первом месте в
прямоугольной системе координат
записывается абсцисса точки, а на втором
– ее ордината. Например, если x₁
– абсцисса точки A,
а y₁
– ее ордината, то это записывается так:
A(x₁,
y₁).

У точки, лежащей
на оси абсцисс, ордината равна нулю; у
точки, лежащей на оси ординат, абсцисса
равна нулю. Обе координаты начала
координат равны нулю.

Расстояние d
между точками A(x₁,
y₁)
и B(x₂,
y₂)
плоскости определяется по формуле:

Если
точка М(x; y) лежит на прямой, проходящей
через две данные точки

(
,

)
и

(
,

),
и дано отношение

,
в котором точка М делит отрезок

,
то координаты точки М определяются по
формулам

,

.

Если
точка М является серединой отрезка

,
то ее координаты определяются по формулам

,

.

8. График уравнения. Уравнение кривой. Примеры: график линейного уравнения, уравнение окружности

В
аналитической геометрии линия на
плоскости определяется как множество
точек, координаты которых удовлетворяют
уравнению F(x,y)=0. При этом на функцию F
должны быть наложены ограничения так,
чтобы, с одной стороны, это уравнение
имело бесконечное множество решений
и, с другой стороны, чтобы это множество
решений не заполняло “куска плоскости”.
Важный класс линий составляют те, для
которых функция F(x,y) есть многочлен от
двух переменных, в этом случае линия,
определяемая уравнением F(x,y)=0, называется
алгебраической. Алгебраические линии,
задаваемые уравнением первой степени,
cуть прямые. Уравнение второй степени,
имеющее бесконечное множество решений,
определяет эллипс, гиперболу, параболу
или линию, распадающуюся на две прямые.

График
функции —
множество точек, у которых абсциссы
являются допустимыми значениями
аргумента x,
а ординаты — соответствующими
значениями функции y.

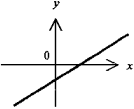
Прямая
линия – график
линейной функции y
= ax + b. Функция
y монотонно возрастает при a > 0 и убывает
при a < 0. При b = 0 прямая линия проходит
через начало координат т. 0 (y = ax – прямая
пропорциональность)

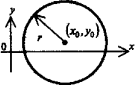
Круг
с центром в точке (x_o,
y_o)
радиуса r.
(x-x_o)²
+ (y-y_o)²
= r²

9. Уравнение прямой с заданным угловым коэффициентом, проходящей через заданную точку. Условие параллельности и перпендикулярности прямых.

Прямая
линия, пересекающая ось Oy
в точке

и
образующая угол

с
положительным направлением оси Ox:

Уравнение прямой с угловым коэффициентом
разрешено относительно текущей координаты
y.

Коэффициент
k
называется угловым
коэффициентом
прямой. В этом виде невозможно представить
прямую, параллельную оси Oy.

Если
прямые заданы уравнениями с угловым
коэффициентом, то необходимое и
достаточное условие их параллельности
состоит в равенстве их угловых
коэффициентов:

k₁
= k₂.

В случае, когда
прямые заданы уравнениями (4) с угловым
коэффициентом, необходимое и достаточное
условие их перпендикулярности заключается
в том, что их угловые коэффициенты
обратны по величине и противоположны
по знаку, т. е.