Точки перегиба графика функции
В задачах на исследование функции в одном из пунктов предлагается найти точки перегиба графика функции. Как это решить? Необходимо понимать, что такое точка перегиба по определению и её признаки.
Точка перегиба функции – это точка, в которой график функции изменяет свою выпуклость или вогнутость
Как найти?
- Найти вторую производную функции $ y”(x) $
- Найти точки $ x_0 $, в которых вторая производная равна нулю, имеет разрыв, или не существует
- Исследовать каждую найденную точку $ x_0 $ на перегиб, с помощью третьей производной $ y”'(x) $
Как проверить является ли найденная точка $ x_0 $ перегибом? Необходимо найти третью производную $ y”'(x)$. Если $ y”'(x_0) $ ≠ $ 0 $, то исследуемая точка – это точка перегиба.
Примеры решений
| Пример 1 |
| Найти точки перегиба графика функции: $ y = 2x^4-6x^2+1 $ |
| Решение |
|
Найдем первую производную, заданной функции: $$ y’ = (2x^4 – 6x^2 + 1)’ = 8x^3 – 12x $$ Теперь получим вторую производную: $$ y” = (y’)’ = (8x^3 – 12x)’ = 24x^2 – 12 $$ Приравниваем к нулю $ y” = 0 $ и решаем уравнение: $$ 24x^2 – 12 = 0 $$ $$ x^2 = frac{1}{2} $$ $$ x_1 = -frac{1}{sqrt{2}}, x_2 = frac{1}{sqrt{2}} $$ Найдем третью производную и вычислим её значения в точках $ x_1 $ и $ x_2 $: $$ y”'(x) = (y”(x))’ = 48x $$ $$ y”'(x_1) = y”'(-frac{1}{sqrt{2}}) = -frac{48}{sqrt{2}} $$ $$ y”'(x_2) = y”'(frac{1}{sqrt{2}}) = frac{48}{sqrt{2}} $$ Так как $ y”'(x_1) $ и $ y”'(x_2) $ не равны нулю, то точки $ x_1 $ и $ x_2 $ соответственно точки перегиба функции. Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
|
$$ x_1 = – frac{1}{sqrt{2}}, x_2 = frac{1}{sqrt{2}} $$ |
| Пример 2 |
| Узнать, является ли для графика функции $ y = cos x $ точка $ x_0 = frac{pi}{2} $ точкой перегиба |
| Решение |
|
Найдем производные до третьего порядка фунции, указанной в условии к задаче: $$ y'(x) = (cos x)’ = – sin x $$ $$ y”(x) = (-sin x)’ = -cos x $$ $$ y”'(x) = (-cos x)’ = sin x $$ Вычислим значения $ y”(x_0) text{ и } y”'(x_0) $: $$ y”(x_0) = y”(frac{pi}{2}) = – cos frac{pi}{2} = 0 $$ $$ y”'(x_0) = y”'(frac{pi}{2}) = sin frac{pi}{2} = 1 $$ Так как $ y”(frac{pi}{2}) = 0 $, а $ y”'(frac{pi}{2}) neq 0 $, то делаем вывод, что точка $ x_0 = frac{pi}{2} $ является точкой перегиба для функции $ y = cos x $ |
| Ответ |
| Точка $ x_0 = frac{pi}{2} $ точка перегиба |
Загрузить PDF
Загрузить PDF
В дифференциальном исчислении точка перегиба – эта точка кривой, в которой ее кривизна меняет знак (с плюса на минус или с минуса на плюс). Это понятие используется в машиностроении, экономике и статистике для определения существенных изменений в данных.
-

1
Определение вогнутой функции. Середина любой хорды (отрезок, соединяющий две точки) графика вогнутой функции лежит либо под графиком, либо на нем.
-

2
Определение выпуклой функции. Середина любой хорды (отрезок, соединяющий две точки) графика выпуклой функции лежит либо над графиком, либо на нем.
-

3
Определение корней функции. Корень функции – это такое значение переменной «х», при котором у = 0.
- При построении графика функции корни – это точки, в которых график пересекает ось Х.
Реклама
-

1
Найдите первую производную функции. Посмотрите правила дифференцирования в учебнике; вы должны научиться брать первые производные, и только потом переходить к более сложным вычислениям. Первые производные обозначаются как f ‘(х). Для выражений вида ax^p + bx^(p−1) + cx + d первая производная имеет вид: apx^(p−1) + b(p − 1)x^(p−2) + c.
- Например, найдите точки перегиба функции f(х) = х^3 +2х -1. Первая производная этой функции имеет вид:
f ′(x) = (x^3 + 2x − 1)′ = (x^3)′ + (2x)′ − (1)′ = 3x^2 + 2 + 0 = 3×2 + 2
- Например, найдите точки перегиба функции f(х) = х^3 +2х -1. Первая производная этой функции имеет вид:
-

2
Найдите вторую производную функции. Вторая производная – это производная от первой производной исходной функции. Вторая производная обозначается как f ′′(x).
- В приведенном выше примере вторая производная имеет вид:
f ′′(x) = (3×2 + 2)′ = 2 × 3 × x + 0 = 6x
- В приведенном выше примере вторая производная имеет вид:
-

3
Приравняйте вторую производную к нулю и решите полученное уравнение. Полученный результат будет предполагаемой точкой перегиба.
- В приведенном выше примере ваш расчет выглядит следующим образом:
f ′′(x) = 0
6x = 0
x=0
- В приведенном выше примере ваш расчет выглядит следующим образом:
-

4
Найдите третью производную функции. Чтобы убедиться, что полученный результат на самом деле является точкой перегиба, найдите третью производную, которая является производной от второй производной исходной функции. Третья производная обозначается как f ′′′(x).
- В приведенном выше примере третья производная имеет вид:
f ′′′(x) = (6x)′ = 6
Реклама
- В приведенном выше примере третья производная имеет вид:
-

1
Проверьте третью производную. Стандартное правило оценки предполагаемой точки перегиба: если третья производная не равна нулю (то есть f ′′′(x) ≠ 0), то предполагаемая точка перегиба является настоящей точкой перегиба. Проверьте третью производную; если она не равна нулю, то вы нашли настоящую точку перегиба.
- В приведенном выше примере третья производная равна 6, а не 0. Поэтому вы нашли настоящую точку перегиба.
-

2
Найдите координаты точки перегиба. Координаты точки перегиба обозначаются как (x,f(x)), где х – значение независимой переменной «х» в точке перегиба, f(х) – значение зависимой переменной «у» в точке перегиба.
- В приведенном выше примере при приравнивании второй производной к нулю вы нашли, что х = 0. Таким образом, чтобы определить координаты точки перегиба, найдите f(0). Ваш расчет выглядит следующим образом:
f(0) = 0^3 +2×0−1 = −1.
- В приведенном выше примере при приравнивании второй производной к нулю вы нашли, что х = 0. Таким образом, чтобы определить координаты точки перегиба, найдите f(0). Ваш расчет выглядит следующим образом:
-

3
Запишите координаты точки перегиба. Координаты точки перегиба – это найденные значения «х» и f(x).
- В приведенном выше примере точка перегиба – это точка с координатами (0, -1).
Реклама
Советы
- Первая производная от свободного члена (простого числа) всегда равна нулю.
Реклама
Об этой статье
Эту страницу просматривали 21 974 раза.
Была ли эта статья полезной?
Интервалы выпуклости и вогнутости графика функции
С помощью онлайн-калькулятора можно найти точки перегиба и промежутки выпуклости графика функции с оформлением решения в Word. Является ли функция двух переменных f(x1,x2) выпуклой решается с помощью матрицы Гессе.
- Решение онлайн
- Видеоинструкция
Направление выпуклости графика функции. Точки перегиба
Определение: Кривая y=f(x) называется выпуклой вниз в промежутке (a; b), если она лежит выше касательной в любой точке этого промежутка.
Определение: Кривая y=f(x) называется выпуклой вверх в промежутке (a; b), если она лежит ниже касательной в любой точке этого промежутка.
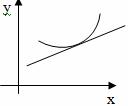
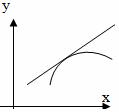
Определение: Промежутки, в которых график функции обращен выпуклостью вверх или вниз, называются промежутками выпуклости графика функции.
Выпуклость вниз или вверх кривой, являющейся графиком функции y=f(x), характеризуется знаком ее второй производной: если в некотором промежутке f’’(x) > 0, то кривая выпукла вниз на этом промежутке; если же f’’(x) < 0, то кривая выпукла вверх на этом промежутке.
Определение: Точка графика функции y=f(x), разделяющая промежутки выпуклости противоположных направлений этого графика, называется точкой перегиба.
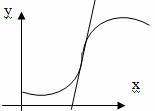
Точками перегиба могут служить только критические точки II рода, т.е. точки, принадлежащие области определения функции y = f(x), в которых вторая производная f’’(x) обращается в нуль или терпит разрыв.
Правило нахождения точек перегиба графика функции y = f(x)
- Найти вторую производную f’’(x).
- Найти критические точки II рода функции y=f(x), т.е. точки, в которой f’’(x) обращается в нуль или терпит разрыв.
- Исследовать знак второй производной f’’(x) в промежутка, на которые найденные критические точки делят область определения функции f(x). Если при этом критическая точка x0 разделяет промежутки выпуклости противоположных направлений, то x0 является абсциссой точки перегиба графика функции.
- Вычислить значения функции в точках перегиба.
Пример 1. Найти промежутки выпуклости и точки перегиба следующей кривой: f(x) = 6x2–x3.
Решение: Находим f ‘(x) = 12x – 3x2, f ‘’(x) = 12 – 6x.
Найдем критические точки по второй производной, решив уравнение 12-6x=0. x=2.

f(2) = 6*22 – 23 = 16
Ответ: Функция выпукла вверх при x∈(2; +∞); функция выпукла вниз при x∈(-∞; 2); точка перегиба (2;16).
Пример 2. Имеет ли точки перегиба функция: f(x)=x3-6x2+2x-1
Пример 3. Найти промежутки, на которых график функции является выпуклым и выгнутым: f(x)=x3-6x2+12x+4
Download Article
Learn how to take the derivative of a function to get its inflection points
Download Article
- Understanding Concavity and Inflection
- Finding the Derivatives of a Function
- Checking the Candidate Inflection Points
- Troubleshooting
- Using a Scientific Calculator
- Video
- Q&A
- Tips
|
|
|
|
|
|
|
You just learned about inflection points in calculus and now you’ve got a bunch of math problems asking you to find them. You’ve got a function and a graph, so where do you go from there? With our help and a bit of derivative magic, finding a function’s inflection points is actually pretty easy! In this article, we’ll provide you with all the steps you need to find and check points of inflection. As a bonus, we’ll show you how to use your scientific calculator to calculate points of inflection for you. If you’re ready to solve your math problems, read on!
Things You Should Know
- An inflection point is where a function changes concavity and where the second derivative of the function changes signs.
- Take the first and second derivative of the function using the power rule.
- Set the second derivative equal to 0 to find the candidate, or possible, inflection points.
- Plug in a value greater than and less than the candidate point to see if the second derivative changes signs at the point.
-

1
Learn the difference between concave up and concave down. To understand inflection points, you need to understand when a function is concave up or down on a graph. Many functions have both concave up and concave down intervals, with an inflection point existing where a function changes concavity. Luckily, concave up and down are easy to distinguish based on their names and what they look like.[1]
- A concave down function is shaped like a hill or an upside-down U. It’s a function where the slope is decreasing. When it’s graphed, no line segment that joins 2 points on its graph ever goes above the curve.
- A concave up function, on the other hand, is shaped like a U. It’s a function where the slope is increasing. No line segment that joins 2 points on its graph ever goes below the curve.
- In the graph above, the red curve is concave up, while the green curve is concave down.
-

2
Identify the roots of a function. A root of a function is the point where the function equals zero, or where the function intersects the x-axis. In the graph above, the roots of the green parabola are at
and
[2]
- A function can also have more than 1 root.
Advertisement
-

3
Find an inflection point where a function changes concavity. Remember how there’s a difference between concave up and concave down? An inflection point is a point on a function where its concavity changes, either from upwards to downwards or downwards to upwards. It is also the point where the second derivative of the function changes signs from positive to negative or negative to positive. For the point to be a point of inflection, it has to both switch concavity and change signs on the second derivative.[3]
- To find the inflection point on a graph, look for the point where the function switches concavity. On the graph above, it’s the middle point where the function changes from concave down to concave up.
Advertisement
-

1
Take the first derivative of the given function. You’ll need your function’s second derivative to find your inflection points. Before you get the second derivative, you have to find the first derivative of the function. First derivatives are denoted as
or
. To solve your function’s first derivative, use the power rule. Multiply x by its exponent and then reduce the exponent by 1.[4]
- For example, find the inflection point of the function below.
- The derivatives of basic functions are usually found in most calculus textbooks; you need to learn how to find basic derivatives before moving on to more complex functions.
-

2
-

3
Set f’’(x) equal to 0 to find the candidate inflection points. Solving f’’(x) = 0 only gives you the candidate inflection points. These are the x-values of the possible inflection points for the function. You still need to test the points on the second derivative to make sure it changes concavity, or switches its sign from positive to negative or negative to positive.[5]
- Set
equal to 0.
- Set
Advertisement
-

1
Plug a value higher and lower than the inflection point into f’’(x). To check if the second derivative changes signs, select 1 value that is greater than the candidate point and 1 value that is less than it. Then, plug each value into the second derivative. If the sign of the second derivative is different for both values, the candidate inflection point is an inflection point. If the sign doesn’t change, the candidate point is not an inflection point.[6]
-

2
Substitute the inflection point into the original function to get its y-value. While you now know the x-value of the inflection point, you don’t know where it is on the y-axis. Simply go back to the original function and plug in the inflection point to get its y-value.[7]
-

3
Evaluate the function to find the inflection point’s coordinates. The coordinate of the inflection point is denoted as
In our example, the coordinates of the inflection point are
[8]
Advertisement
-

1
Check the concavity of every candidate inflection point. Oftentimes, people assume there’s no inflection point when the candidate point is
. However, this isn’t true. Remember, 0 can be graphed, so if you get 0 as your candidate point, it might be an inflection point.[9]
-

2
Include candidate points where the derivative is undefined. When you find possible inflection points, you have to look for instances where the second derivative equals 0 and where the second derivative is undefined. If you only look for points where the second derivative is 0, you might miss inflection points where the function is undefined.[10]
-

3
Analyze the second derivative, not the first one. When you’re finding inflection points, you only consider the second derivative. If you set the first derivative equal to 0, your answer will give you extremum points instead.[11]
Advertisement
-

1
Head to your “Plots” function on your calculator. It’s easy to use a scientific calculator to find inflection points. On most scientific calculators, just press the “diamond” or the “second” button, then click F1. This takes you to your Y plots where you can enter up to 7 functions.[12]
- This is true on both the TI-84 and the TI-89, but it may not be the exact same on older models.
-

2
Enter the function into y1. Clear out any remaining functions you had in your y plots. Then, type in the function after the equal sign. Remember to keep any parentheses involved in the function so your answer is correct.[13]
- For example, the function might be
- For example, the function might be
-

3
Click “graph.” On most calculators, you press the “diamond” or “second” button then click F3. If you have to adjust your window on the calculator, hit “diamond” or “second” and press F2. Then, select “standard zoom.”[14]
- Don’t worry if your screen doesn’t show the whole graph just yet—you will adjust the zoom later.
-

4
Adjust the window until you see the whole graph. When you open up the graphing window, you might not see the entire curve of your graph. If that’s the case, click the “diamond” or “second” button, then open up F2 for zoom again. Simply increase or decrease your minimum and maximum axis to get the graph to fit inside the window.[15]
- It might take a little adjustment and back-and-forth to find your graph.
-

5
Click “Math,” then “Inflection.” Hit the “diamond” or “second” button, then select F5 to open up “Math.” In the dropdown menu, select the option that says “Inflection.”[16]
- This is—you guessed it—how to tell your calculator to calculate inflection points.
-

6
Place the cursor on the lower and upper bound of the inflection. Your calculator will give you a message saying “Lower?” Move the arrows on your calculator until the cursor is to the left of the inflection point. Then, your calculator will ask “Upper?” Move your cursor so it’s to the right of the inflection point. To get your inflection point, hit “Enter.”[17]
- This is how you get your calculator to guess where the inflection point is. Now you have your answer!
Advertisement
Add New Question
-
Question
What if the second derivative intersects with the x-axis, but does not dip below it?

This answer was written by one of our trained team of researchers who validated it for accuracy and comprehensiveness.

wikiHow Staff Editor
Staff Answer
The second derivative has to cross the x-axis for there to be an inflection point. If the second derivative only touches the x-axis but doesn’t cross it, there’s no inflection point.
-
Question
What if the second derivative is a constant? How do I find the inflection point?

Inflection points are where the second derivative changes sign. If it is constant, it never changes sign, so there exists no inflection point for the function.
-
Question
Can the first derivative become zero at an inflection point?

Orangejews
Community Answer
Yes, for example x^3. It changes concavity at x=0, and the first derivative is 0 there.
See more answers
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
Video
-
Alternatively, take the third derivative of a function to find the inflection points. If the third derivative does not equal 0, there is an inflection point. If the third derivative is positive, the inflection point is increasing; if it’s negative, the point is decreasing.[18]
However, taking such derivatives with more complicated expressions is often not desirable. -
All linear functions have no inflection points. This is because linear functions do not change slope (the entire graph has the same slope), so there is no point at which the slope changes.
-
When you’re testing the candidate points, you are only looking for a sign change. You are not actually evaluating the value.
Show More Tips
Thanks for submitting a tip for review!
Advertisement
References
About This Article
Article SummaryX
To find inflection points, start by differentiating your function to find the derivatives. Then, find the second derivative, or the derivative of the derivative, by differentiating again. To locate a possible inflection point, set the second derivative equal to zero, and solve the equation. Finally, find the inflection point by checking if the second derivative changes sign at the candidate point, and substitute back into the original function. For more tips on finding inflection points, like understanding concave up and down functions, read on!
Did this summary help you?
Thanks to all authors for creating a page that has been read 337,073 times.
Reader Success Stories
-

“Here is what helped me: If the sign of the second derivative changes as you pass through the candidate inflection…” more
Did this article help you?
Точки
перегиба и общее исследование функций.
Лекция 17.
Точки
перегиба.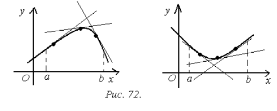
Основные
понятия.
График
дифференцируемой функции
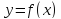
называется выпуклым
(вогнутом)
на интервале
 ,
,
если он расположен выше (ниже) ее любой
касательной на этом интервале (рис. 72).
Точка
графика непрерывной функции
 ,
,
в которой она меняет вогнутость на
выпуклость называется точкой
перегиба.

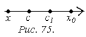
Так
на рис. 73 функция на интервале
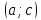
является выпуклой а на интервале
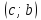
– вогнутой. Следовательно, точка
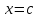
является точкой перегиба.
Достаточные
условия выпуклости и вогнутости функции
на интервале.
Выпуклость
и вогнутость функции на интервале можно
определить с помощью ее вторых производных.
Теорема
37.
Если
функция
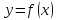
во всех точках из интервала
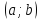
имеет отрицательную (положительную)
вторую производную

( ),
),
то график функции на этом интервале
является выпуклым (вогнутым).
Доказательство.
Пусть
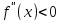 .
.
Возьмём на графике функции произвольную
точку М с координатами
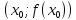
и проведём через неё касательную.
Покажем, что график функции расположен
ниже этой касательной. Для этого возьмём
произвольную точку

и сравним ординаты в этой точке графика

и касательной
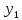 .
.
Уравнение касательной имеет вид
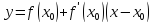 ,
,
поэтому
 .
.
Тогда
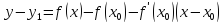 .
.
По теореме Лагранжа

=

Снова
применим теорему Лагранжа (для разности
производных):
 .
.
Исследуем
знак этого выражения в зависимости от
взаимного расположения точек
 .
.
Случай
1. Точка
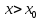
(рис. 74).
Тогда
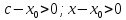
и
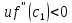 ,
,
следовательно

или
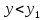 .
.
Случай
2.
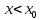
(рис. 75).
Тогда

и
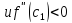 ,
,
следовательно

или опять
 .
.
В
любом случае
 ,
,
т.е. ордината касательной больше ординаты
графика для любой точки интервала
 .
.
По определению, график функции
является выпуклым. Аналогично можно
рассмотреть случай, когда

и показать, что график функции в этом
случае будет вогнутым.
Достаточное
условие существования точек перегиба.
Теорема
38.
Если
вторая производная

при переходе через точку

, в которой она не существует или равна
нулю, меняет знак, то точка

является точкой перегиба.
Доказательство.
Пусть
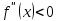
при
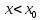
и
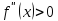
при
 .
.
Это означает, что слева график функции
является выпуклым, а справа – вогнутым,
следовательно, точка
 является
является
точкой перегиба по пределению.
Пример
62.
Найти промежутки выпуклости, вогнутости
функции

и
установить ее точки перегиба.
Решение.
Найдем последовательно первую и вторую
производные функции

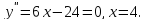

Определим
на числовой оси знаки второй производной.
Из рисунка видно, что вторая производная
отрицательна (там функция выпукла) на
интервале
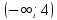
и положительна на интервале
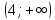 .
.
В точке

она меняет знак с (-) на (+), следовательно,
эта точка является точкой перегиба
(рис. 76). 
Асимптоты.
Асимптотой
кривой
называется прямая, расстояние до которой
от точки, лежащей на кривой, стремится
к нулю при неограниченном удалении этой
точки от начала координат.
Асимптоты
могут быть вертикальными, наклонными
и горизонтальными.
Вертикальные
асимптоты.
Прямая

является вертикальной асимптотой
графика функции
 ,
,
если

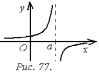
Обычно
такими точками являются точки разрыва
второго рода (рис. 77). Для отыскания
вертикальных асимптот нужно найти те
значения
 ,
,
вблизи которых функция неограниченно
возрастает по модулю. Так функция
обратной пропорциональности
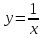
имеет вертикальную асимптоту
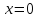 ,
,
т. е. ось
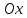
(рис. 78).
Наклонные
и горизонтальные асимптоты.
Уравнение
наклонной асимптоты имеет вид
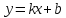 .
.
Пусть

– произвольная точка графика функции
 ,
,
по формуле расстояния от точки до прямой,
имеем

Так как
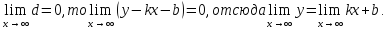
Разхделим
обе части равенства на
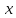 ,
,
получим

Применяя
к левой части правило Лопиталя, получим
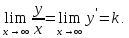
Коэффициент
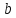
найдем из условия
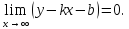
Отсюда

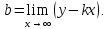
Если
хотя бы один из этих пределов (или оба)
не существуют, то функция
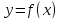
не имеет наклонных асимптот. Если
 ,
,
то прямая

в этом случае является горизонтальной
асимптотой. Так функция
имеет вертикальную асимптоту
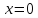
и наклонную
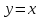
(рис. 79).
Пример
63.
Исследовать на асимптоты функцию

Решение.
Так как при

функция имееи разрыв 2 – го рода, то
график имеет вертикальную асимптоту
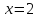 .
.
Наклонные асимптоты имеют вид
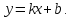
Найдем коэффициенты

и
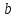

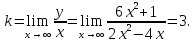
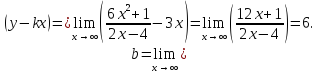
Таким
образом, график имеет наклонную асимптоту

(рис. 80).
Схема
исследования функций и построения их
графиков.
1)
Находят область определения функции
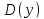 ;
;
2)
определяют (если возможно) точки
пересечения графика с осями координат;
3)
проверяют чётность или нечётность,
периодичность функции. Графики четной
и нечетной функции строят только для
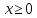 ,
,
затем четную функцию отображают
симметрично относительно оси
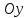 ,
,
нечетную – относительно точки
 .
.
Периодическую функцию строят на
интервале, равном периоду, затем
продолжают на всю числовую ось
 ;
;
4)
находят первую производную и исследуют
интервалы монотонности и находят точки
экстремума;
5)
находят вторую производную и исследуют
промежутки выпуклости и вогнутости,
устанавливают точки перегиба;
6)
исследуют функцию на наличие асимптот
(вертикальных, наклонных, горизонтальных).
На
основании всех этих свойств строят
эскиз графика
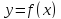 .
.
Пример
64.
Исследовать и построить график функции
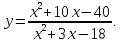
Решение.
1) Найдем область определения функции.
Так как знаменатель дроби равен нулю
при

и при
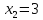 ,
,
то в этих точках функция не определена
и имеет разрыв второго рода, поэтому
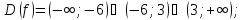
2)
При

переменная
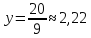 .
.
Таким образом, ось

пересекается в точке
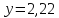 .
.
Если же
 ,
,
то

и
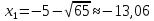 ,
,
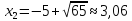 .
.
Эти точки иявляются точками пересечения
графика с осью
 ;
;
3)
Так как
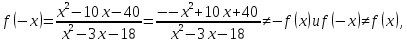
то
функция не является четной и не является
нечетной, т. е.
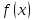
– функция общего вида. Заметим, что этот
вывод следует так же из того, что она
определена на не симметрическом
множестве. Из последнего факта следует
так же непериодичность функции;
4)
Найдем производную функции и исследуем
ее на монотонность и точки экстремума:
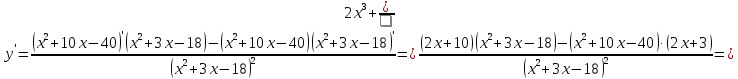
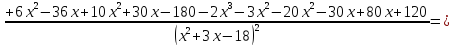

Отсюда
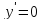
при

и
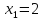 ,
,
 .
.
Нанесем на числовую ось критические
точки и определим знаки производной на
промежутках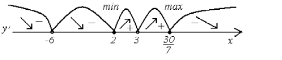
Из
рисунка видно, что функция

убывает на промежутках
 ,
,
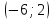 ,
,

и возрастает на промежутках
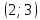 ,
,
 .
.
Точка

является точкой минимума а точка

– точкой максимума. Причем
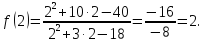
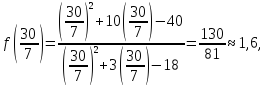
5)
Найдем вторую производную и исследуем
промежутки выпуклости, вогнутости
функции, определим точки перегиба:
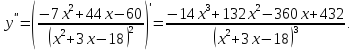
Отсюда

и
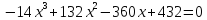
или

Проверяя
целые делители числа 216, убеждаемся,
что значение

является корнем уравнения. Разделив в
соответствии с теоремой Безу выражение
в правой части на
 ,
,
получим разложение на множители
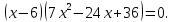
Уравнение

корней не имеет, так как дискриминант

Нанесем
на числовую ось точки, в которых вторая
производная равна нулю или не существует
и определим промежутки выпуклости и
вогнутости. 
Из
рисунка видно, что вторая производная
функции положительна на промежутках
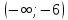
и
 ,
,
следовательно, на них график является
выпуклым. На промежутках
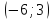
и

вторая производная отрицательна и
функция является выпуклой на них. В
точке
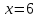
функция определена и

меняет знак с (+) на (-) и поэтому она
является точкой перегиба, причем
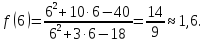
6)
Исследуем график на асимптоты.
Так как функция в точках
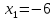
и

имеет разрыв второго рода, то прямые

и
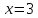
являются вертикальными асимптотами.
Для определения наклонных (и горизонтальных)
асимптот вида
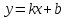 ,
,
определим коэффициенты
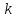
и
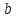 .
.
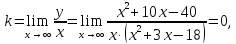

Таким
образом график функции имеет горизонтальную
асимптоту
 .
.
На
основании полученных данных, строим
график функции (рис. 81).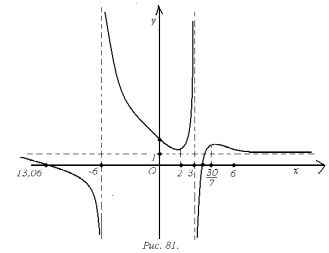
101


