Как найти координаты точек пересечения графика линейного

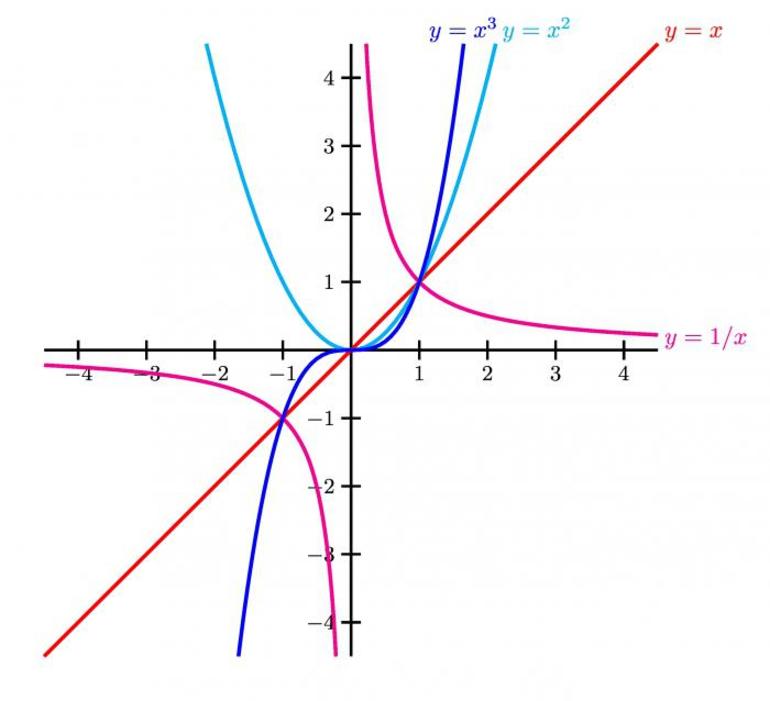
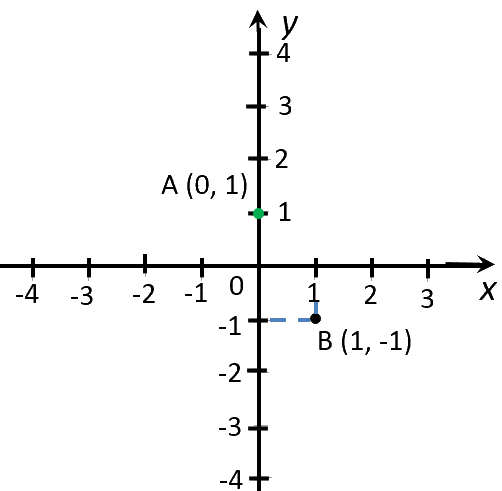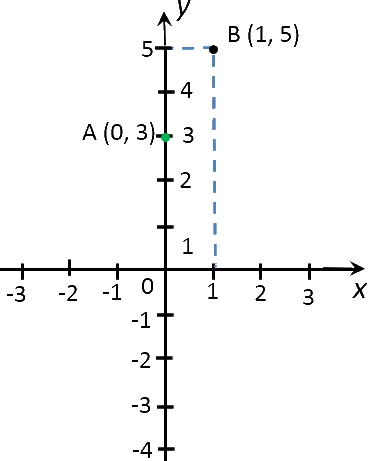Координаты точки пересечения графиков функций

Как найти?

1. Чтобы найти координаты точки пересечения графиков функций нужно приравнять обе функции друг к другу, перенести в левую часть все члена, содержащие $ x $, а в правую остальные и найти корни, полученного уравнения.
2. Второй способ заключается в том, что нужно составить систему уравнений и решить её путём подстановки одной функции в другую
3. Третий способ подразумевает графическое построение функций и визуальное определение точки пересечения.

Случай двух линейных функций

Рассмотрим две линейные функции $ f(x) = k_1 x+m_1 $ и $ g(x) = k_2 x + m_2 $. Эти функции называются прямыми. Построить их достаточно легко, нужно взять любые два значения $ x_1 $ и $ x_2 $ и найти $ f(x_1) $ и $ (x_2) $. Затем повторить тоже самое и с функцией $ g(x) $. Далее визуально найти координату точки пересечения графиков функций.

Следует знать, что линейные функции имеют только одну точку пересечения и только тогда, когда $ k_1 neq k_2 $. Иначе, в случае $ k_1=k_2 $ функции параллельны друг другу, так как $ k $ – это коэффициент угла наклона. Если $ k_1 neq k_2 $, но $ m_1=m_2 $, тогда точкой пересечения будет $ M(0;m) $. Это правило желательно запомнить для ускоренного решения задач.

Пример 1

Пусть даны $ f(x) = 2x-5 $ и $ g(x)=x+3 $. Найти координаты точки пересечения графиков функций.

Решение

Как это сделать? Так как представлены две линейные функции, то первым делом смотрим на коэффициент угла наклона обеих функций $ k_1 = 2 $ и $ k_2 = 1 $. Замечаем, что $ k_1 neq k_2 $, поэтому существует одна точка пересечения. Найдём её с помощью уравнения $ f(x)=g(x) $: $$ 2x-5 = x+3 $$ Переносим слагаемые с $ x $ в левую часть, а остальные в правую: $$ 2x – x = 3+5 $$ $$ x = 8 $$ Получили $ x=8 $ абциссу точки пересечения графиков, а теперь найдём ординату. Для этого подставим $ x = 8 $ в любое из уравнений хоть в $ f(x) $, либо в $ g(x) $: $$ f(8) = 2cdot 8 – 5 = 16 – 5 = 11 $$ Итак, $ M (8;11) $ – является точкой пересечения графиков двух линейных функций. Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!

Ответ

$$ M (8;11) $$

Пример 2

Дано $ f(x)=2x-1 $ и $ g(x) = 2x-4 $. Найти точки пересечения графиков функций.

Решение

Как найти? Опять же обращаем внимание на то, что угловые коэффициенты равны $ k_1 = k_2 = 2 $. Это означает, что линейные функции параллельны между собой, поэтому у них нет точек пересечения!

Ответы

Графики функций параллельны, нет точек пересечения.

 Случай двух нелинейных функций 

Пример 3

Найти координаты точки пересечения графиков функций: $ f(x)=x^2-2x+1 $ и $ g(x)=x^2+1 $

Решение

Как быть с двумя нелинейными функциями? Алгоритм простой: приравниваем уравнения друг к другу и находим корни: $$ x^2-2x+1=x^2+1 $$ Разносим по разным сторонам уравнения члены с $ x $ и без него: $$ x^2-2x-x^2=1-1 $$ $$ -2x=0 $$ $$ x=0 $$ Найдена абцисса искомой точки, но её недостаточно. Ещё нехватает ординаты $ y $. Подставляем $ x = 0 $ в любое из двух уравнений условия задачи. Например: $$ f(0)=0^2-2cdot 0 + 1 = 1 $$ $ M (0;1) $ – точка пересечения графиков функций

Ответ

$$ M (0;1) $$

Как найти точки пересечения графиков функций – алгоритмы и примеры правила и методики

Общие сведения

Функция — некоторое выражение, описывающее зависимость между двумя величинами. Следует отметить, что последних может быть несколько. Параметр, который не зависит от других элементов, называется аргументом, а зависимое тождество — значением функции.

Точка пересечения графиков означает, что у системы уравнений существует общее решение. Следует отметить, что для их нахождения можно воспользоваться графическим и аналитическим методом. Первый подразумевает построение графического представления выражения с переменной.

Чтобы найти пересечение графиков функций аналитическим способом, необходимо решить уравнение, корни которого являются искомыми точками. Для их нахождения специалисты рекомендуют получить базовые понятия о равенствах с переменными, а также о методах их решения.

Классификация уравнений

Уравнение — тождество, содержащее неизвестные величины (переменные), которые следует найти при помощи определенного алгоритма. Последний зависит от типа выражений. Тождества классифицируются на несколько типов:

Линейными являются уравнения, содержащие единичную степень, т. е. 2t=4. Квадратные — тождества, у которых переменная возведена в квадрат. Они имеют следующий вид: Pt^2+St+U=0, где Р и S – коэффициенты при неизвестных, а U – свободный член.

Кубическое — уравнение вида Ot^3+Pt^2+St+U=0, где O, Р и S – коэффициенты при переменных, а U – константа. Последний вид — равенства, в которых при переменной присутствует четвертая степень (Nt^4+Ot^3+Pt^2+St+U=0).

Равносильные тождества

При выполнении математических операций каждое выражение может быть заменено на эквивалентное, т. е. равносильное. Иными словами, равносильными называются уравнения, различные по составляющим их элементам, но имеющие одинаковые корни. Следует отметить, что ими являются также выражения, не имеющие решений. Математики выделяют три свойства: симметричность, транзитивность и разложение на множители.

Формулировка первого: когда I уравнение равносильно II, то значит, и II равносильно I. Суть транзитивности состоит в том, что если I равносильно II, а II – III, то значит I эквивалентно III. Второе свойство имеет такую формулировку: произведение двух элементов, содержащих переменные, равное нулевому значению, эквивалентно двум выражениям, которые можно приравнять к 0. Математическая запись утверждения имеет такой вид: R(t)*S(t)=0 .

Математические преобразования

Для решения уравнения необходимо выполнить некоторые математические преобразования. Они должны выполняться грамотно, поскольку любая ошибка приводит к образованию ложных корней. Допустимыми операциями являются следующие:

1. Правильное раскрытие скобок с учетом алгебраической операции и знаков.
2. Упрощение выражения (приведение подобных величин).
3. Перенос элементов в любые части равенства с противоположным знаком.
4. Возможность прибавлять или вычитать эквивалентные величины.
5. Деление и умножение на любые эквивалентные значения, не превращающие тождества в пустое множество.

Специалисты рекомендуют избегать операций, при которых сокращаются неизвестные величины. Следствием этого могут стать ложные корни. Кроме того, делитель не должен иметь значения, при которых его значение равно 0. Последнее условие следует всегда проверять, а при решении ни один корень уравнения не должен соответствовать значению переменной при нахождении окончательных корней.

Иными словами, в выражении (t+2)^2=0 для упрощения можно разделить обе части на (t+2) при условии, что t не равно -2, т. к. [(t+2)^2]/(t+2)=0/(t+2).

Однако при решении (t+2)=0 получается, что t=-2, а это недопустимо. Следовательно, вышеописанный метод не всегда подходит.

Разложение на множители

Для решения уравнений при выполнении математических преобразований могут потребоваться специальные формулы разложения на множители. Их еще называют тождествами сокращенного умножения. К ним относятся следующие:

1. Квадрат суммы и разности: (p+r)^2=p^2+2pr+r^2 и (p-r)^2=p^2-2pr+r^2 соответственно.
2. Разность квадратов: p^2-r^2=(p-r)(p+r).

В некоторых случаях можно воспользоваться сразу двумя соотношениями, т. е. выделить квадрат суммы, а затем из первого — разность квадратов. Выделение первого осуществляется группировкой посредством скобок в выражении, а затем введение положительного и отрицательного элементов, т. е. s^2+4s-5=s^2+4s+4-4-5=(s^2+4s+4)-4-5=(s+2)^2 -9. Для получения всех элементов формулы “p+r)^2=p^2+2pr+r^2” нужно прибавить, а затем отнять 4. При этом значение равенства не изменится, поскольку 4-4=0.

Следует отметить, что математические преобразования выражения (s+2)^2 -9 не заканчиваются, поскольку его можно представить в виде разности квадратов, т. е. (s+2-9)(s+2+9)=(s-7)(s+11). Кроме того, формулы сокращенного умножения рекомендуется применять при понижении степени.

Методики нахождения точек

Чтобы узнать, пересекаются ли графики функций, нужно приравнять соответствующие тождества, а затем решать уравнение. Однако при такой операции могут получиться различные равенства с неизвестными. В этом случае требуется обратить внимание на нижеописанные методики решения для каждого вида.

Первой и второй степени

Уравнение первой степени, или линейное, решается очень просто. Для этого необходимо перенести переменные величины в одну, а известные – в другую сторону. Методика решения имеет следующий вид:

1. Раскрыть скобки и привести подобные коэффициенты.
2. Выполнить перенос известных в одну, а неизвестных – в другую часть равенства.
3. Произвести необходимые математические преобразования.
4. Найти корень.

Сложнее решается квадратное уравнение. Существует несколько способов нахождения его корней:

1. Разложить на множители.
2. Выделить полный квадрат.
3. Найти дискриминант.
4. По теореме Виета.

Первый способ применяется довольно часто, поскольку с его помощью можно понижать степень при неизвестной величине. Второй подразумевает выделение квадрата по одной из формул сокращенного умножения. Чтобы воспользоваться одним из двух методов, необходимо знать соответствующие тождества (правила разложения на множители).

Однако не всегда можно быстро решить квадратное уравнение при помощи первых двух методов. Еще один вариант — нахождение корней через дискриминант (Д), т. е. дополнительный параметр, позволяющий сразу находить решения. Он находится по следующей формуле: Д=(-S)^2 -4PU.

Следует отметить, что при Д>0 переменная принимает два значения, которые превращают равенство в истину. Если Д=0, то корень только один. Когда Д 3 +St 2 +Ut+V=0 существует еще одна методика нахождения корней. Она имеет следующий вид:

1. Уравнение требуется разделить на P.
2. Осуществить замену: t=m-(S/(3P)). При этом получается тождество вида m^3 +km+l=0.
3. Найти значение коэффициентов по формулам: k=[2S 3 -9PSU+27(P 2 )V] / (27P 3 ) и l=[(3PU-S 2 )/(3P 2 )]. Подставить их во второй пункт и найти промежуточные корни, при помощи которых найти основные значения переменных.

Следует отметить, что важным пунктом методики является правильный выбор выражения замены, а затем верное выполнение математических преобразований.

Пример решения

Для закрепления знаний необходимо перейти к практическому решению заданий.Одной из простых задач является следующая: найдите координаты точки пересечения графиков линейных функций z=2t+7 и z=t-1. Решается задача по такому алгоритму:

1. Приравнять уравнения: 2t+7=t-1.
2. Перенести переменные влево, а константы – вправо: 2t-t=-1-7.
3. Привести подобные коэффициенты: t=-8.
4. Найти координаты второй составляющей: z=-8-1=-9.
5. Искомая точка пересечения: (-8;-9).

В четвертом пункте нужно подставить координату по оси абсцисс в любое из уравнений для получения второй составляющей, необходимой для точки. Следует отметить, что в этой задаче нет необходимости проводить математические преобразования. Однако существуют и более сложные задания, в которых необходимо решать квадратные уравнения, а также раскрывать скобки.

Таким образом, для определения точки пересечения графиков необходимо уметь находить корни уравнения, а также выполнять алгебраические преобразования.

ГДЗ учебник по алгебре 7 класс Мордкович. §8. Линейная функция и ее график. Номер №8.27.

Найдите координаты точки пересечения графиков линейных функций:
а ) y = x + 4 и y = 2 x;
б ) y = − 2 x + 3 и y = 2 x − 5 ;
в ) y = −x и y = 3 x − 4 ;
г ) y = 3 x + 2 и y = − 0,5 x − 5 .

Решение а

x + 4 = 2 x
x − 2 x = − 4
−x = − 4
x = 4

y = 2 x = 2 * 4 = 8
Ответ: точка пересечения имеет координаты ( 4 ; 8 ).

Решение б

− 2 x + 3 = 2 x − 5
− 2 x − 2 x = − 5 − 3
− 4 x = − 8
x = 2

y = 2 x − 5 = 2 * 2 − 5 = 4 − 5 = − 1
Ответ: точка пересечения имеет координаты ( 2 ;− 1 ).

Решение в

−x = 3 x − 4
−x − 3 x = − 4
− 4 x = − 4
x = 1

y = −x = − 1
Ответ: точка пересечения имеет координаты ( 1 ;− 1 ).

Решение г

3 x + 2 = − 0,5 x − 5
3 x + 0,5 x = − 2 − 5
3,5 x = − 7
x = − 2

y = 3 x + 2 = 3 * (− 2 ) + 2 = − 6 + 2 = − 4
Ответ: точка пересечения имеет координаты (− 2 ;− 4 ).

Как найти координаты точек пересечения графика функции: примеры решения

Вы будете перенаправлены на Автор24

В практике и в учебниках наиболее распространены нижеперечисленные способы нахождения точки пересечения различных графиков функций.

Первый способ

Первый и самый простой – это воспользоваться тем, что в этой точке координаты будут равны и приравнять графики, а из того что получится можно найти $x$. Затем найденный $x$ подставить в любое из двух уравнений и найти координату игрек.

Найдём точку пересечения двух прямых $y=5x + 3$ и $y=x-2$, приравняв функции:

Теперь подставим полученный нами икс в любой график, например, выберем тот, что попроще — $y=x-2$:

$y=-frac<1> <2>– 2 = – 2frac12$.

Точка пересечения будет $(-frac<1><2>;- 2frac12)$.

Второй способ

Второй способ заключается в том, что составляется система из имеющихся уравнений, путём преобразований одну из координат делают явной, то есть, выражают через другую. После это выражение в приведённой форме подставляется в другое.

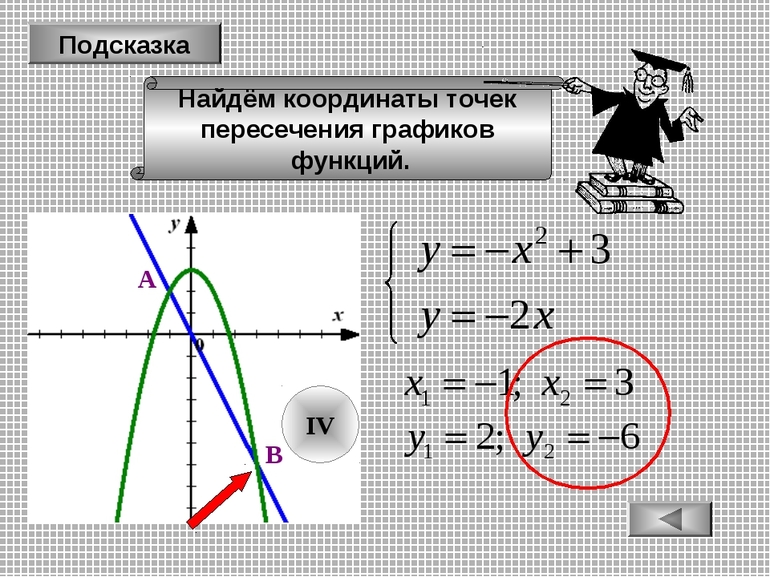
Узнайте, в каких точках пересекаются графики параболы $y=2x^2-2x-1$ и пересекающей её прямой $y=x+1$.

Решение:

Второе уравнение проще первого, поэтому подставим его вместо $y$:

Вычислим, чему равен x, для этого найдём корни, превращающие равенство в верное, и запишем полученные ответы:

Подставим наши результаты по оси абсцисс по очереди во второе уравнение системы:

$y_1= 2 + 1 = 3; y_2=1 – frac<1> <2>= frac<1><2>$.

Точки пересечения будут $(2;3)$ и $(-frac<1><2>; frac<1><2>)$.

Третий способ

Готовые работы на аналогичную тему

Перейдём к третьему способу — графическому, но имейте в виду, что результат, который он даёт, не является достаточно точным.

Для применения метода оба графика функций строятся в одном масштабе на одном чертеже, и затем выполняется визуальный поиск точки пересечения.

Данный способ хорош лишь в том случае, когда достаточно приблизительного результата, а также если нет каких-либо данных о закономерностях рассматриваемых зависимостей.

Найдите точку пересечения графиков на общем рисунке.

Рисунок 1. Точка пересечения двух функций. Автор24 — интернет-биржа студенческих работ

Решение:

Тут всё просто: ищем точки пересечения пунктиров, опущенных с графиков с осями абсцисс и ординат и записываем по порядку. Здесь точка пересечения равна $(2;3)$.

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 07 05 2021

[spoiler title=”источники:”]

http://reshalka.com/uchebniki/7-klass/algebra/mordkovich/328

http://spravochnick.ru/matematika/kak_nayti_koordinaty_tochek_peresecheniya_grafika_funkcii_primery_resheniya/

[/spoiler]

Прежде чем перейти к изучению функции «y = kx»
внимательно изучите урок
«Что такое функция в математике»
и
«Как решать задачи на функцию».

Другими словами, можно сказать, что «y = kx + b» — это семейство всевозможных функций, где вместо
«k» и «b» стоят числа.

Примеры функций типа «y = kx + b».

• y = 5x + 3
• y = −x + 1
• y = x − 2
• y = 0,5x

Давайте определим для каждой функций выше, чему равны числовые коэффициенты
«k» и
«b».

Функция	Коэффициент «k»	Коэффициент «b»
y = 5x + 3	k = 5	b = 3
y = −x + 1	k = −1	b = 1
y = 2 3 x − 2	k = 2 3	b = −2
y = 0,5x	k = 0,5	b = 0

Обратите особое внимание на функцию «y = 0,5x»
в таблице. Часто совершают ошибку при поиске в ней числового коэффициента «b».

Рассматривая
функцию «y = 0,5x», неверно утверждать, что числового коэффициента
«b» в функции нет.

Числовый коэффициент «b» присутствет в функции типа «y = kx + b» всегда.
В функции «y = 0,5x»
числовый коэффициент «b» равен нулю.

Как построить график линейной функции
«y = kx + b»

Так как графиком функции «y = kx + b»
является прямая линия, функцию называют линейной функцией.

Из геометрии вспомним аксиому (утверждение, которое не требует доказательств),
что через любые две точки можно провести прямую и притом только одну.

Исходя из аксиомы выше следует, что
чтобы построить график функции вида
«у = kx + b» нам достаточно будет найти всего
две точки.

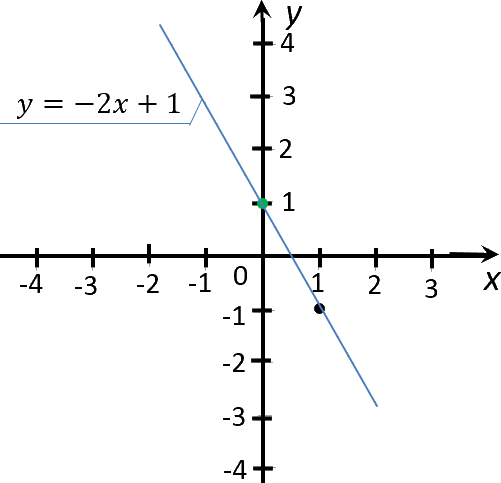
Для примера построим график функции «y = −2x + 1».

Найдем значение функции «y» для двух произвольных значений «x».
Подставим, например, вместо «x» числа «0» и «1».

x	Расчет «y = −2x + 1»
0	y(0) = −2 · 0 + 1 = 1
1	y(1) = −2 · 1 + 1 = −2 + 1 = −1

Полученные значения «x» и «y» — это координаты точек графика функции.

Запишем полученные координаты точек «y = −2x + 1» в таблицу.

Точка	Координата по оси «Оx» (абсцисса)	Координата по оси «Оy» (ордината)
(·)A	0	1
(·)B	1	−1

Отметим полученные точки на системе координат.

Теперь проведем прямую через отмеченные точки. Эта прямая будет
являться графиком функции «y = −2x + 1».

Как решать задачи на
линейную функцию «y = kx + b»

Рассмотрим задачу.

---

Построить график функции «y = 2x + 3». Найти по графику:

1. значение «y» соответствующее значению «x» равному −1; 2; 3; 5;
2. значение «x», если значение «y» равно
   1; 4; 0; −1.

---

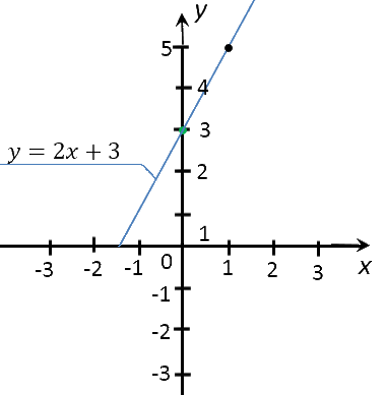
Вначале построим график функции «y = 2x + 3».

Используем правила, по которым мы строили график функции выше.
Для построения графика функции «y = 2x + 3» достаточно найти всего две точки.

Выберем два произвольных числовых значения для «x». Для удобства расчетов выберем числа
«0» и «1».

Выполним расчеты и запишем их результаты в таблицу.

Точка	Координата по оси «Оx»	Координата по оси «Оy»
(·)A	0	y(0) = 2 · 0 + 3 = 3
(·)B	1	y(1) = 2 ·1 + 3 = 5

Отметим полученные точки на прямоугольной системе координат.

Соединим полученные точки прямой. Проведенная прямая будет являться графиком функции
«y = 2x + 3».

---

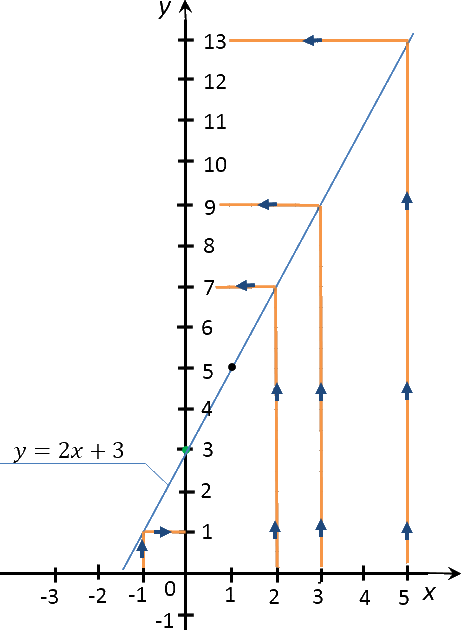
Теперь работаем с построенным графиком функции «y = 2x + 3».

Требуется найти значение «y»,
соответствующее значению «x»,
которое равно −1; 2; 3; 5.

---

Тему
«Как получить координаты точки функции» с графика функции
мы уже подробно рассматривали в уроке
«Как решать задачи на функцию».

В этому уроке для решения задачи выше вспомним только основные моменты.

По правилам выше найдем на построенном ранее графике функции «y = 2x + 3»
необходимые значения функции «y» для
«x» равным −1; 2; 3; 5.

Запишем полученные результаты в таблицу.

Заданное значение «x»	Полученное с графика значение «y»
−1	1
2	7
3	9
5	13

---

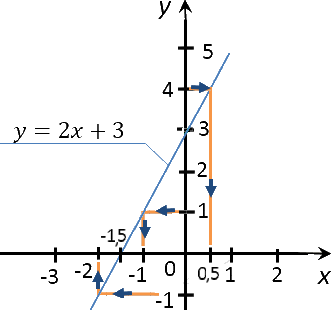
Переходим ко второму заданию задачи. Требуется найти значение «x»,
если значение «y» равно 1; 4; 0; −1.

Выполним те же действия, что и при решении предыдущего задания.
Разница будет лишь в том, что изначально мы будем проводить перпендикуляры от оси
«Oy».

Запишем полученные результаты в таблицу.

Заданное значение «y»	Полученное с графика значение «x»
−1	−2
0	−1,5
1	−1
4	0,5

---

Как проверить, проходит ли график через точку

Рассмотрим другое задание.

Не выполняя построения графика функции
«y = 2x −
», выяснить, проходит ли график
через точки с координатами (0;
− ) и (1; −2).

---

Подставим в функцию
«y = 2x −
»

координаты точки (0;
− ).

− = 2 · 0
−

   − =
−

(верно)

Это означает, что график функции «y = 2x −
» проходит через точку с координатами (0;
− ).

---

Проверим точку с координатами (1; −2).
Также подставим координаты
в функцию «y = 2x −
».

−2 = 2 · 1 −

−2 = 2 −

−2 = 1 −

        −2 = 1 (неверно)

Это означает, что график функции «y = 2x −
» не проходит через точку с координатами (1; −2).

---

Как найти точки пересечения графика с осями

Рассмотрим задачу.

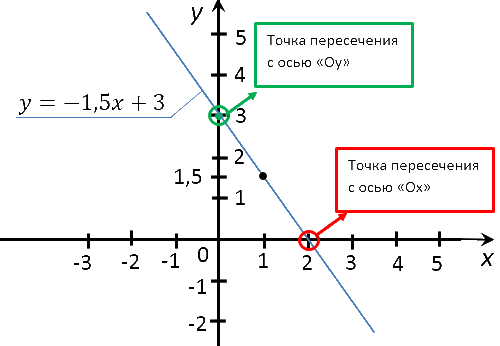
Найти координаты точек пересечения графика функции «y = −1,5x + 3» с осями координат.

Для начала построим график функции «y = −1,5x + 3» и на графике отметим точки пересечения
с осями.

Для построения графика функции найдем координаты двух точек
функции
«y = −1,5x + 3».

Выберем два произвольных числовых значения для «x» и рассчитаем значение
«y» по формуле
функции. Например, для x = 0 и
x = 1.

Точка	Координата по оси «Оx»	Координата по оси «Оy»
(·)A	0	y(0) = −1,5 · 0 + 3 = 3
(·)B	1	y(1) = −1,5 · 1 + 3 = 1,5

Отметим полученные точки на системе координат и проведем через них прямую.
Тем самым мы построим график функции «y = −1,5x + 3».

Теперь найдем координаты точек пересечения графика функции с осями по формуле функции.

Подставим вместо «x» в формулу функции «y = −1,5x + 3» число ноль.

y(0) = −1,5 · 0 + 3 = 3

(0; 3) — координаты точки пересечения графика функции «y = −1,5x + 3»
c осью «Oy».

Подставим вместо «y» в формулу функции «y = −1,5x + 3» число ноль.

0 = −1,5x + 3        
1,5x = 3        | :(1,5)
x = 3 : 1,5           
x = 2                   

(2; 0) — координаты точки пересечения графика функции «y = −1,5x + 3»
c осью «Ox».

Чтобы было проще запомнить, какую координату точки нужно приравнивать к нулю, запомните
«правило противоположности».

---

Ваши комментарии

Оставить комментарий:

---