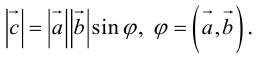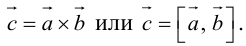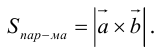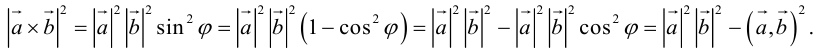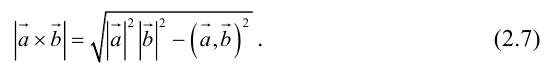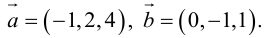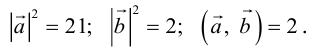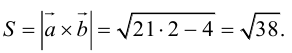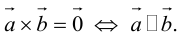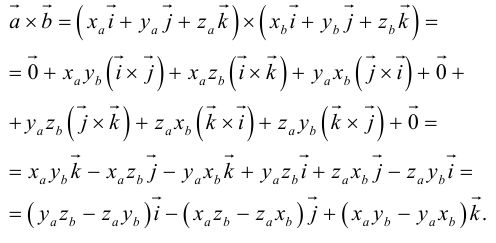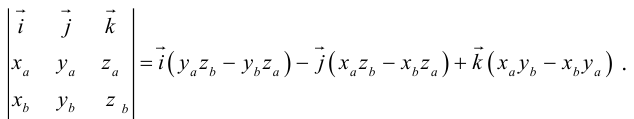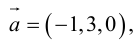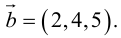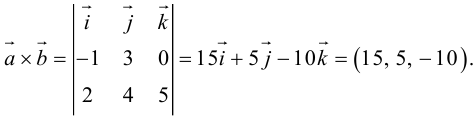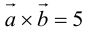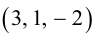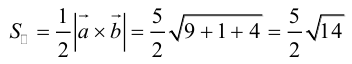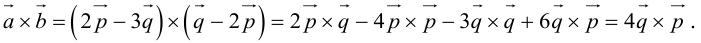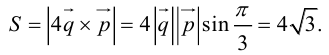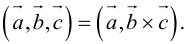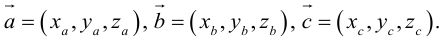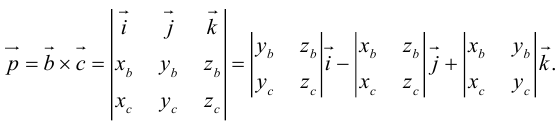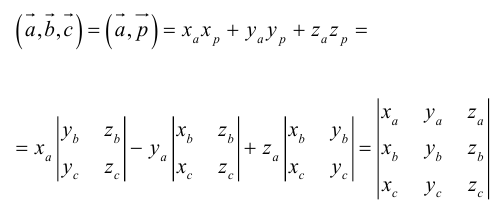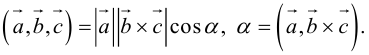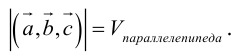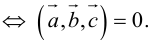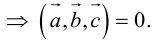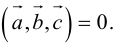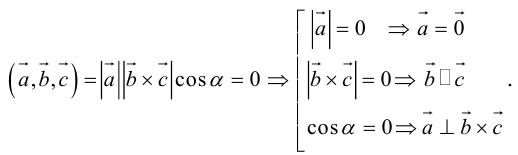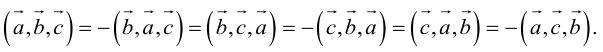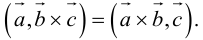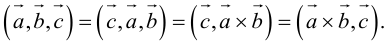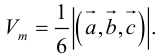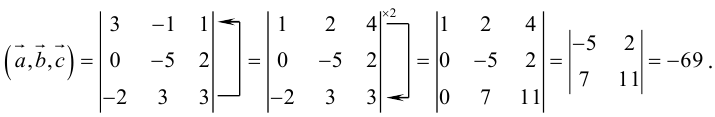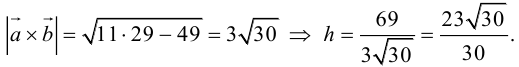Геометрия. Найти координаты пересечения векторов.
Nikitko Cent
Знаток
(483),
закрыт
10 лет назад
Как найти координаты пересечения векторов, зная координаты самих векторов? Вектора на плоскости.
Евгений Фёдоров
Гений
(57858)
10 лет назад
AB = B – A = (xB – xA; yB – yA)
CD = D – C = (xD – xC; yD – yC)
A + nAB = C + mCD
(1 – n)A + nB = (1 – m)C + mD
{ (1 – n)xA + nxB = (1 – m)xC + mxD
{ (1 – n)yA + nyB = (1 – m)yC + myD
Решаем и находим N = A + nAB
Тугеус Владимир
Искусственный Интеллект
(175030)
10 лет назад
Две координаты задают на плоскости бесконечно много векторов. Поэтому два вектора могут пересекаться в ЛЮБОЙ точке плоскости или вообще не иметь общих точек. А если они ещё и коллинеарны, то могут иметь много общих точек. Так что задача бессмысленна!
Точка пересечения 2 векторов
Координаты x,y я то нашел, спроецировав на плоскость вектора.
stl
А что такое пересечение векторов?
Есть обобщенная задача — поиск двух БЛИЖАЙШИХ ТОЧЕК у двух отрезков в пространстве. Я щас не дома и не могу показать код, да и в двух словах алгоритм не опишешь. Гугли.
stl
>Даны 2 вектора: x1,y1,z1; x2,y2,z2;
Как найти точку пересечения?
Элементарно: (0; 0; 0)
если честно , я не понял ваших ответов. Мне нужны не ближайшие точки, и причем тут 0,0,0 я тоже не понял.
2 вектора точно пересекаются в пространстве в какой-то точке. У векторов есть координаты начала и конца. Найти x,y точки пересечения легко — проецируем на экран, отбрасывая z, находим.
А как найти координату z, если она может потребоваться в дальнейшем?
stl
>2 вектора точно пересекаются в пространстве в какой-то точке. У векторов есть
>координаты начала и конца.
У настоящих брутальных векторов координаты начала находятся в точке
ты у каждого вектора указал лишь один набор координат. потому их от (0,0,0) и отсчитали 😉 вопрос надо правильней формулировать. тебя интересует пересение ОТРЕЗКОВ? ну так элементарно, пусть отрезки
(x1, y1, z1) — (x2, y2, z2) и (a1, b1, c1) — (a2, b2, c2)
тогда уравнение первого
x = x1*t + x2*(1 — t)
y = y1*t + y2*(1 — t)
z = z2*t + z2*(1 — t)
аналогично для второго
x = a1*s + a2*(1 — s)
y = b1*s + b2*(1 — s)
z = c2*s + c2*(1 — s)
приравниваем x,y,z, получаем
x1 t + x2 (1 — t) = a1 s + a2 (1 — s)
y1 t + y2 (1 — t) = b1 s + b2 (1 — s)
система из 2 уравнений с 2мя неизвестными, решаем, подставляем s и t во третьи уравнения, убеждаемся, что z-координаты совпали тоже (если нет, то и пересечения нет)
stl
>У векторов есть координаты начала и конца
А нету!
Вектор это упорядоченное конечное множество своих координат.
Вектор может представлять множество отрезков, которые будут по длине равны абсолютному значению вектора и паралельны.
И вот разница координат отрезков следовательно равна координатам вектора.
Если проще, вектор — это не отрезок. Вектор — это точка. А его направление — это направление отрезка из начала координат в эту точку.
Tweedle Dee
>ты у каждого вектора указал лишь один набор координат. потому их от (0,0,0) и отсчитали 😉
Он указал правильно а отсчитывают от нулей всегда.
>У настоящих брутальных векторов координаты начала находятся в точке
Координаты у труЪ-математиков задаются либо (0; 0; 0) либо <0, 0, 0> А вот — смахивает на неупорядоченное множество.
stl
Короче объясняю.
Такс. Если у тебя есть отрезок <(x1; y1; z1), (x2; y2; z2)> то вектор, который задаст множество отрезков, равных по модулю длине твоего отрезка и паралельных ему равен (x2 — x1; y2 — y1; z2 — z1). И любой отрезок, входящий в это множество будет равен <(c1 + x1; c2 + y1; c3 + z1), (c1 + x2; c2 + y2; c3 + z2)>,
Отрезок, совпадающий с радиус-вектором на графике будет равен <(0; 0; 0), <x, y, z>>.
Где c1, c2, c3 — произвольные константы из множества декартовой степени 1/n пространства, которому принадлежит вектор, где n — мерность пространства. Например пространство R^3 возводим в декартовую степень 1/3 получаем R — множество действительных чисел (частный случай для трёхмерного пространства).
x, y, z — координаты вектора, равные x2 — x1, y2 — y1 и z2 — z1 соответственно.
ПРАВКА: поумничал малость
ПРАВКА: афрографея
ПРАВКА: поумничал малость
Векторы в пространстве — не пересекаются! Их пересечение возможно только при строгом и абсолютно точном соотношении параметров (как минимум, “лежат в одной плоскости”). Однако, поскольку в реальном мире имеют место квантовые флуктуации, а малейшего отклонения параметра достаточно для разрушения необходимого равенства (в случае компутера эта особенность физического мира симулируется неабсолютной точностью вычислений), то вероятность пересечения изничтожающе стремится к нулю.
А поэтому мораль такова: не надо математически эстетствовать, ибо жизнь сурова. А надо взять и найти, как предлагали в посте 2, ближайшие точки A и B обоих векторов. Если расстояние AB меньше некоторого епсилон (скажем, 0.001), то можно условно считать, что вектора пересеклись, и точка пересечения — середина AB. Если же больше епсилона — значит, не пересеклись.
векторная-геометрия — Найти точку пересечения вектора и плоскости
Добрый день, возник такой вопрос: есть плоскость, в моем случае y = 0, положение точки 1: (x1, y1, z1), и положение точки 2 (x2, y2, z2). Как найти точку пересечения вектора, направленного от точки 1 к точке 2, и плоскости? Затем нужно посчитать расстояние до этой точки пересечения (но это уже не сложно).
задан 20 Май ’14 14:10
@сергей111: одно замечание по поводу терминологии. Обычно не говорят о пересечении вектора и плоскости. Задачу можно рассматривать в трёх вариантах, проводя либо прямую, либо луч, либо отрезок. В принципе, все они решаются однотипным способом.
@сергей111, Если вы получили исчерпывающий ответ, отметьте его как принятый.
2 ответа
Стандартный способ решения таких задач — использовать параметрическую запись прямой, заданной направляющим вектором и точкой: $$beginx=mt+x_0,\y=nt+y_0,\z=pt+z_0.end$$ Здесь $%(m,n,p)$% — координаты вектора от одной точки до другой, а $%(x_0,y_0,z_0)$% — координаты одной из точек. Подставляете эти значения в уравнение плоскости, откуда находите параметр $%t$%. По этому параметру находите $%(x,y,z)$%.
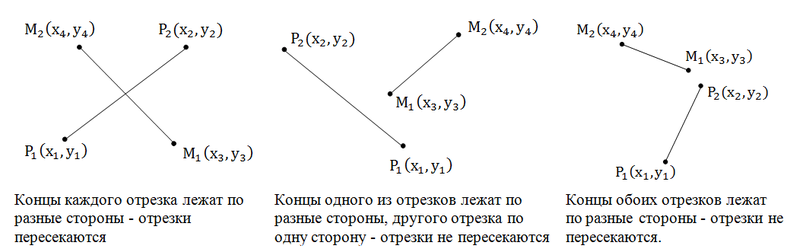
Определение точки пересечения двух отрезков
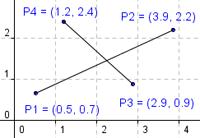
Пусть даны два отрезка. Первый задан точками P1(x1;y1) и P2(x2;y2). Второй задан точками P3(x3;y3) и P4(x4;y4).
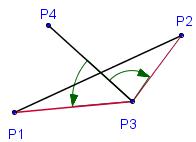
Взаимное расположение отрезков можно проверить с помощью векторных произведений:
Рассмотрим отрезок P3P4 и точки P1 и P2.
Точка P1 лежит слева от прямой P3P4, для нее векторное произведение v1 > 0, так как векторы положительно ориентированы.
Точка P2 расположена справа от прямой, для нее векторное произведение v2 < 0, так как векторы отрицательно ориентированы.
Для того чтобы точки P1 и P2 лежали по разные стороны от прямой P3P4, достаточно, чтобы выполнялось условие v1v2 < 0 (векторные произведения имели противоположные знаки).
Аналогичные рассуждения можно провести для отрезка P1P2 и точек P3 и P4.
Векторное произведение двух векторов вычисляется по формуле:
где:
ax, ay — координаты первого вектора,
bx, by — координаты второго вектора.
Уравнение прямой, проходящей через две различные точки, заданные своими координатами.
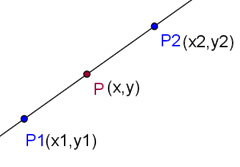
Пусть на прямой заданы две не совпадающие точки:P1 с координатами (x1;y1) и P2 с координатами (x2; y2). Соответственно вектор с началом в точке P1 и концом в точке P2 имеет координаты (x2-x1, y2-y1). Если P(x, y) – произвольная точка на прямой, то координаты вектора P1P равны (x — x1, y – y1).
Итак, прямую можно задать уравнением вида (1).
Как найти точку пересечения прямых?
Очевидное решение состоит в том, чтобы решить систему уравнений прямых:
Здесь D – определитель системы, а Dx,Dy — определители, получающиеся в результате замены столбца коэффициентов при соответствующем неизвестном столбцом свободных членов. Если D ≠ 0, то система (2) является определенной, то есть имеет единственное решение. Это решение можно найти по следующим формулам: x1=Dx/D, y1=Dy/D, которые называются формулами Крамера. Небольшое напоминание, как вычисляется определитель второго порядка. В определителе различают две диагонали: главную и побочную. Главная диагональ состоит из элементов, взятых по направлению от верхнего левого угла определителя в нижний правый угол. Побочная диагональ – из правого верхнего в нижний левый. Определитель второго порядка равен произведению элементов главной диагонали минус произведение элементов побочной диагонали.
Пусть даны два отрезка. Первый задан точками P1(x1;y1) и P2(x2;y2). Второй задан точками P3(x3;y3) и P4(x4;y4).
Взаимное расположение отрезков можно проверить с помощью векторных произведений:
Рассмотрим отрезок P3P4 и точки P1 и P2.
Точка P1 лежит слева от прямой P3P4, для нее векторное произведение v1 > 0, так как векторы положительно ориентированы.
Точка P2 расположена справа от прямой, для нее векторное произведение v2 < 0, так как векторы отрицательно ориентированы.
Для того чтобы точки P1 и P2 лежали по разные стороны от прямой P3P4, достаточно, чтобы выполнялось условие v1v2 < 0 (векторные произведения имели противоположные знаки).
Аналогичные рассуждения можно провести для отрезка P1P2 и точек P3 и P4.
Итак, если v1v2 < 0 и v3v4 < 0, то отрезки пересекаются.
Векторное произведение двух векторов вычисляется по формуле:
где:
ax, ay – координаты первого вектора,
bx, by – координаты второго вектора.
Уравнение прямой, проходящей через две различные точки, заданные своими координатами.
Пусть на прямой заданы две не совпадающие точки:P1 с координатами (x1;y1) и P2 с координатами (x2; y2). Соответственно вектор с началом в точке P1 и концом в точке P2 имеет координаты (x2-x1, y2-y1). Если P(x, y) – произвольная точка на прямой, то координаты вектора P1P равны (x – x1, y – y1).
С помощью векторного произведения условие коллинеарности векторов P1P и P1P2 можно записать так:
|P1P,P1P2|=0, т.е. (x-x1)(y2-y1)-(y-y1)(x2-x1)=0
или
(y2-y1)x + (x1-x2)y + x1(y1-y2) + y1(x2-x1) = 0
Последнее уравнение переписывается следующим образом:
ax + by + c = 0, (1)
где
a = (y2-y1),
b = (x1-x2),
c = x1(y1-y2) + y1(x2-x1)
Итак, прямую можно задать уравнением вида (1).
Как найти точку пересечения прямых?
Очевидное решение состоит в том, чтобы решить систему уравнений прямых:
ax1+by1=-c1
ax2+by2=-c2 (2)
Ввести обозначения:
Здесь D – определитель системы, а Dx,Dy – определители, получающиеся в результате замены столбца коэффициентов при соответствующем неизвестном столбцом свободных членов. Если D ≠ 0, то система (2) является определенной, то есть имеет единственное решение. Это решение можно найти по следующим формулам: x1=Dx/D, y1=Dy/D, которые называются формулами Крамера. Небольшое напоминание, как вычисляется определитель второго порядка. В определителе различают две диагонали: главную и побочную. Главная диагональ состоит из элементов, взятых по направлению от верхнего левого угла определителя в нижний правый угол. Побочная диагональ – из правого верхнего в нижний левый. Определитель второго порядка равен произведению элементов главной диагонали минус произведение элементов побочной диагонали.
Содержание:
Векторная алгебра
Векторная алгебра – это раздел векторного исчисления, изучающий линейные операции с векторами и их геометрические свойства; часть линейной алгебры, занимающаяся векторными пространствами; различные векторные алгебры XIX века (например, кватернионов, бикватернионов, сплит-кватернионов).
Векторы и линейные операции над ними
Займемся теперь таким важным как в самой математике, так и в ее многочисленных приложениях, понятием вектора.
Определение: Вектором, на плоскости или в пространстве называется отрезок прямой с заданным на нем направлением, т. е. одна из его граничных точек считается начальной, а вторая – конечной.
Обозначать векторы мы будем строчными латинскими буквами
Длина отрезка, изображающего вектор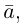
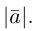
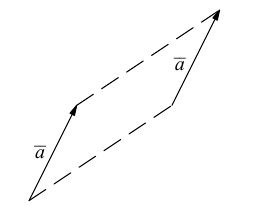
По определению, два вектора считаются равными, если один из них можно преобразовать в другой с помощью параллельного переноса.
Учитывая приведенное определение, всюду в дальнейшем мы без специальных оговорок будем перемещать вектор параллельным переносом в любую удобную для нас точку.
Два вектора 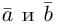
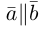
Аналогично, векторы а и b называются ортогональными (обозначение 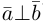
Три вектора называются компланарными, если после приведения их общему началу, они будут расположены в одной плоскости.
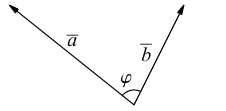
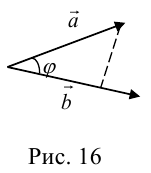
Углом между векторами 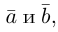
Два ненулевых вектора 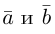
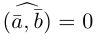
Введем теперь линейные операции над векторами.
а) Умножение числа на вектор.
Произведением действительного числа 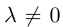
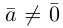
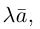
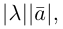
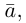
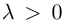
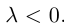
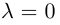
В частности, вектор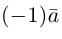
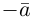
Если 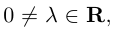
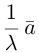
Из приведенного определения сразу же следует, что коллинеарные векторы 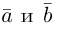
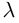
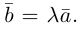
взять число 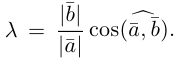
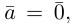
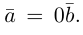
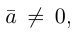
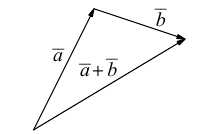
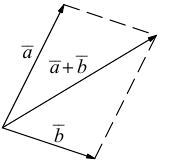
b) Сложение векторов.
Суммой двух векторов 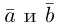
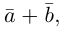
или по равносильному ему правилу параллелограмма
Вектор 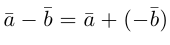
Свойства линейных операций над векторами аналогичны соответствующим свойствам действительных чисел.
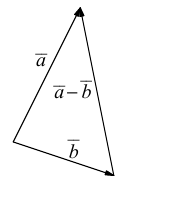
Проекцией вектора 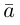
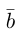
Геометрически очевидны следующие свойства проекции:
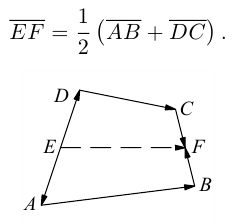
Пример №1
Пусть Е и F – середины сторон AD и ВС соответственно выпуклого четырехугольника ABCD. Доказать, что
Доказательство. Из четырехугольников EDCF и EABF по правил}’ сложения векторов получим:
Сложив данные равенства и учитывая, что 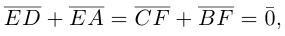
что и требовалось.
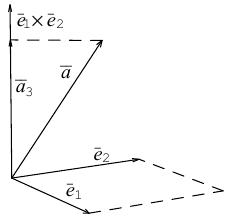
Базис и декартова система координат
Определение: Базисом на плоскости называется упорядоченная пара неколлинеарных векторов. Базисом в пространстве называется упорядоченная тройка некомпланарных векторов.
Обозначение: 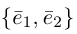
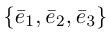
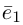
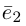
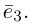
Теорема. Любой вектор единственным образом разлагается по базису, т. е. представляется в виде 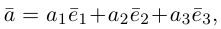
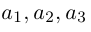
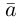
Приведем геометрическое доказательство этого утверждения.
Вектор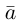
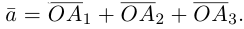
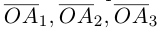
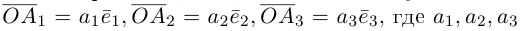
Если базис зафиксирован, то факт, что вектор а в этом базисе имеет координаты 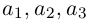
Из доказанной теоремы следует, что при выполнении линейных операций над векторами точно также преобразуются и их координаты, т. е. если 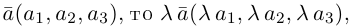
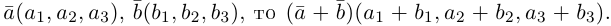
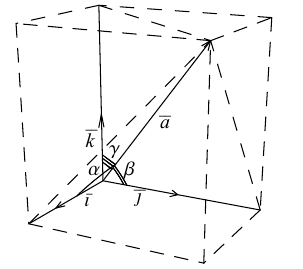
Рассмотрим теперь ортонормированный базис 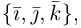
Как видно из чертежа, координаты вектора в ортонормированном базисе представляют собой проекции этого вектора на соответствующие орты. т. е.
Величины 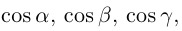
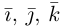
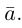
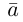
Очевидно также, что
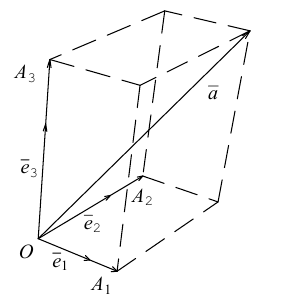
Свяжем теперь с ортонормированным базисом декартову (прямоугольную) систему координат. Для этого поместим начала ортов в некоторую точку О, ось Ох (абсцисс) направим вдоль орта 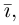
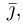
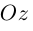
В выбранной системе координат координаты радиуса-вектора 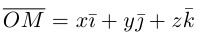
Если известны координаты начальной 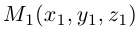
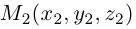
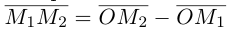
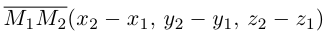
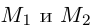
Найдем теперь координаты точки М, делящей отрезок с концами в точках 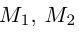
отношении 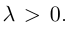
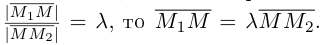
Следовательно, координаты искомой точки вычисляются по формулам:
Найдем, в частности, координаты середины отрезка. Здесь А = 1, поэтому
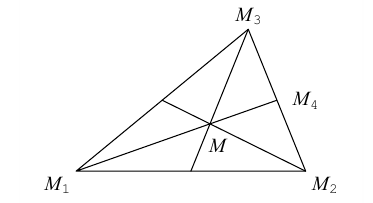
Пример №2
Треугольник задан координатами своих вершин 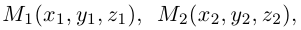
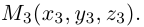
Пусть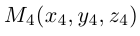
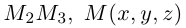
По известному свойству точки пересечения медиан 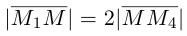
Подставив сюда найденные координаты точки 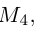
Таким образом, координаты точки пересечения медиан треугольника равны средним арифметическим соответствующих координат его вершин.
Замечание. Базисом n-мерного пространства 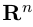
обладающая тем свойством, что любой вектор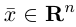
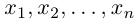
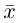
В качестве базиса в 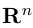
так как, очевидно, любой вектор 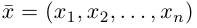
Скалярное произведение векторов
Определение: Скалярным произведением векторов 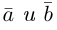
Из этого определения сразу же следует, что
и таким образом, если один из векторов имеет единичную длину, то их скалярное произведение равно проекции второго вектора на единичный.
Отметим основные свойства скалярного произведения.
Первые два и последнее свойства немедленно следуют из определения скалярного произведения, а третье и четвертое – из сформулированных в §1 свойств проекции.
Найдем теперь представление скалярного произведения в координатах. Пусть в орто-нормированном базисе 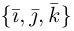
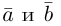
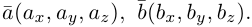
перемножим векторы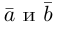
Таким образом, скалярное произведение в ортонормированном базисе равно сумме произведений соответствующих координат векторов.
Пример №3
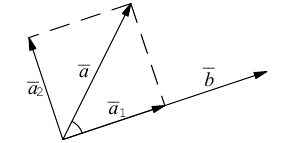
Разложить вектор 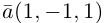
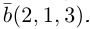
Решение.
Из чертежа следует, что 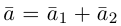
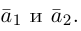
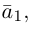
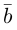
Тогда вторая ортогональная составляющая вектора 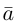
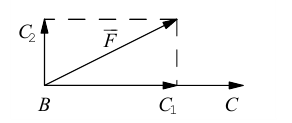
В заключение параграфа рассмотрим одно простое приложение скалярного произведения в механике. Пусть под действием постоянной силы 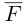
Найдем работу этой силы. Для этого разложим вектор силы 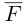
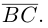
Составляющая 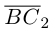
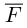
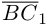
Окончательно, работа силы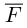
Замечание. Скалярным произведением векторов 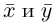
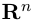
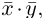
то
Несложной проверкой мы можем убедиться в том, что таким образом определенное скалярное произведение в 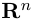
Длиной вектора 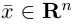
Векторы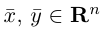
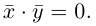
составляют ортонормированный базис пространства 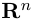
Любой вектор 
n-мерного пространства с координатами
Взяв еще одну точку 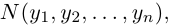
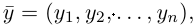
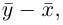
Таким образом переопределенное пространство 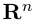
Совокупность точки О(0.0,…, 0) и ортонормированного базиса (1) называется декартовой системой координат евклидова пространства R”. Точка 0(0,0,… ,0) называется, естественно, началом координат.
Векторное произведение векторов
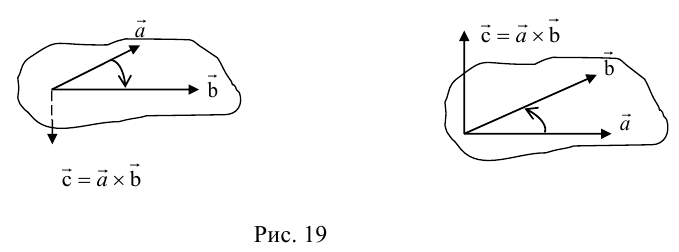
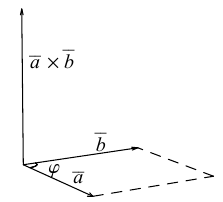
Определение: Векторным произведением некоялинеарных векторов 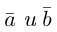

Из этого определения следует, что площадь параллелограмма, построенного на векторах 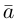
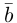

Сформулируем основные свойства векторного произведения.
Первые два свойства очевидным образом следуют из определения векторного произведения. Доказательство третьего ввиду его громоздкости мы приводить не будем.
Найдем формулу для вычисления векторного произведения в координатах. Пусть векторы 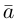
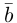
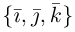
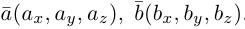
раскроем скобки в векторном произведении 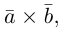
Полученный вектор мы можем записать в виде следующего символического определителя.
вычислять который удобно разложением по первой строке.
Пример №4
Найти составляющую вектора 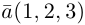
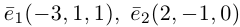
Решение.
Из чертежа видно, что искомая составляющая представляет собой вектор проекции данного вектора 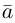

Переходим к вычислениям:
Тогда
Среди многочисленных приложений векторного произведения отметим его применение в механике при вычислении момента силы.
Итак, пусть сила 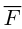
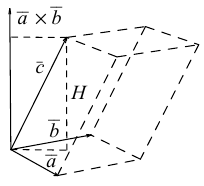
Смешанное произведение векторов
Определение: Смешанным произведением трех векторов 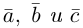
Выясним геометрический смысл смешанного произведения для тройки некомпланарных векторов.
По определению смешанного произведения
Поскольку 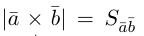
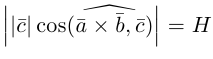
– объем параллелепипеда. Таким образом, абсолютная величина смешанного произведения трех векторов равна объему параллелепипеда, построенного на этих векторах.
Если векторы заданы своими координатами в ортонормированном базисе 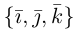
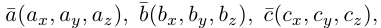
Следовательно (глава I. §2, пункт 3, свойство 7)), в координатах смешанное произведение вычисляется по формуле:
Докажем, пользуясь этой формулой, некоторые свойства смешанного произведения.
что следует из свойства 4) определителя (глава I. §2, пункт 3). Таким образом, в смешанном произведении можно менять местами знаки скалярного и векторного произведения, и поэтому для него используется более короткое обозначение 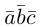
Эти свойства смешанного произведения также являются прямыми следствиями соответствующих свойств определителя.
Докажем еще одно, геометрическое свойство смешанного произведения.
Теорема. Три вектора 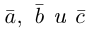
Доказательство. Докажем необходимость условия теоремы. Пусть векторы 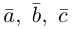
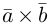
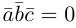
Следствие. Три вектора 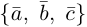
Заметим, кроме того, что, если 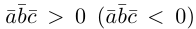
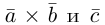
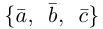
Пример №5
Доказать, что пять точек
расположены в одной плоскости.
Решение. Рассмотрим векторы 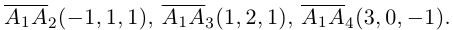
то по доказанной выше теореме эти векторы компланарны и, стало быть. точки 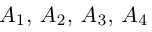
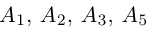
так как первая и третья строки в определителе пропорциональны. Плоскости 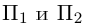
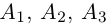
Векторы и линейные операции над ними
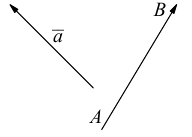
Определение: Вектором называется направленный отрезок (рис. 1).
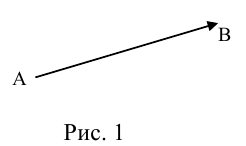
Рис. 1
Так как вектор определяется его началом и концом, то можно сформулировать эквивалентное данному определение.
Определение: Вектором называется упорядоченная пара точек.
Определение: Длина вектора 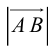
Определение: Два вектора называются равными, если они имеют равные длины и одинаково направлены. При этом одинаково направленными называются векторы, лежащие на параллельных прямых и имеющие одинаковые направления.
Из этого определения следует, что точка приложения вектора значения не имеет, то есть вектор не изменяется, если его перемещать параллельно самому себе, сохраняя длину. Такие векторы называются свободными.
Если начало и конец вектора совпадают, он называется нулевым:
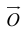
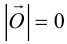
Определение: Векторы 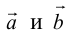
Так как направление нулевого вектора не определено, то он коллинеарен любому другому.
Определение: Векторы называются компланарными, если они параллельны одной плоскости.
Нулевой вектор компланарен любой системе компланарных векторов.
Линейные операции над векторами
Линейными называются операции сложения векторов и умножения на число.
Сложение
а) Правило параллелограмма (рис.2): начала 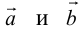
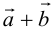
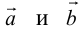
б) Правило треугольника (рис. 3): начало 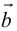
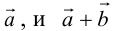
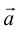
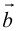
в) Правило сложения нескольких векторов (рис. 4).
Вектор 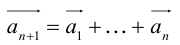
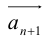
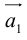
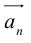
Умножение на число
Определение: Произведением вектора 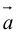
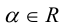
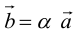
а) 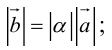
б) 
в)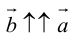
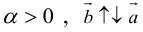
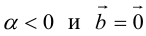
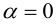
Произведение 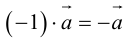
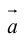
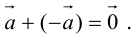
Определение: Разностью 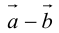
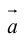
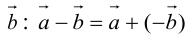
Начала 
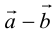
Свойства линейных операций
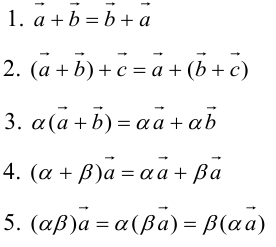
Определение: Результат конечного числа линейных операций над векторами называется их линейной комбинацией: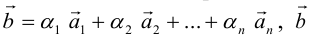
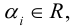
Пример №6
Пусть М – точка пересечения медиан треугольника АВС, а О – произвольная точка пространства. Представить 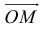
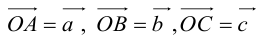
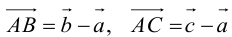
По правилу треугольника 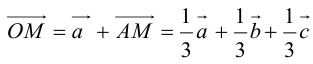
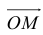
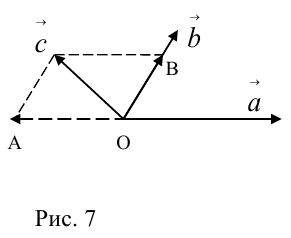
Теорема: Пусть 
где коэффициенты (2.1) определяются единственным образом.
Представление вектора 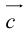
Доказательство:
- Пусть среди
есть два коллинеарных, например:
- Пусть среди
коллинеарных нет, тогда совместим начала всех трех векторов в одной точке. Построим параллелограмм, диагональ которого совпадает с
, а стороны параллельны прямым, на которых лежат
(рис. 7).
Тогда c 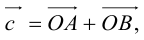
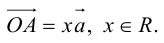
Докажем единственность разложения. Предположим, что 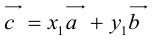
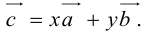
Если 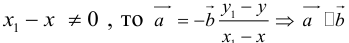
Теорема: Пусть 
причем единственным образом.
Представление вектора 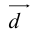
Доказать самостоятельно.
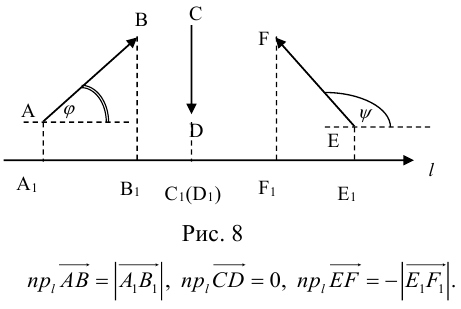
Проекция вектора на ось
Проекция вектора на ось — это скалярная величина (число), равная длине геометрической проекции вектора, если направление оси и геометрической проекции совпадают; или число, противоположное длине геометрической проекции вектора, если направления геометрической проекции и оси — противоположные.
Координаты вектора
Осью называется направленная прямая.
Определение: Ортом оси 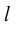
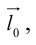
направление которого совпадает с направлением оси.
Определение: Ортогональной проекцией точки М на ось 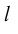
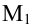
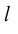
Определение: Ортогональной проекцией вектора 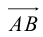
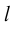
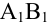
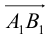
Определение: Углом между вектором и осью называется угол, на который нужно повернуть в положительном направлении ось до совпадения ее направления с направлением вектора (положительным считается поворот против часовой стрелки).
Очевидно, проекцию вектора на ось можно найти по формуле
Можно показать, что проекция линейной комбинации векторов равна та-
кой же линейной комбинации их проекций:
В частности, проекция суммы векторов равна сумме их проекций:
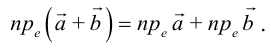
Рассмотрим прямоугольную декартову систему координат ХОY. Обозначим 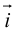
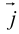

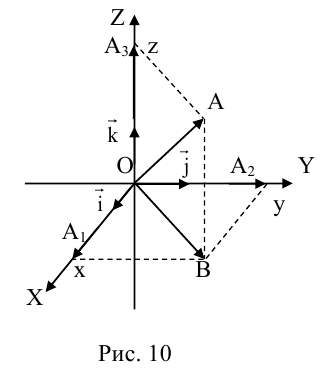
Аналогично в пространственной системе OXYZ 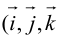
– разложение 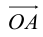
Таким образом, если задана прямоугольная декартова система координат (пдск), то со всяким пространственным вектором 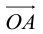
Определение: Координатами вектора 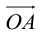
Таким образом, можно дать еще одно определение вектора.
Определение: Вектором называется упорядоченная тройка чисел (упорядоченная пара, если вектор плоский).
Пример №7
Если 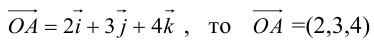
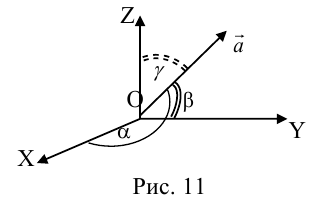
Так как, с одной стороны, вектор – объект, имеющий длину и направление, а с другой, – упорядоченная тройка чисел, то, зная длину и направление, можно определить его координаты и наоборот. Направление вектора в заданной системе координат характеризуется его направляющими косинусами (рис. 11):
Из этих формул очевидно следует основное свойство направляющих косинусов:
Если известны длина 
Пусть AB – произвольный вектор в системе OXYZ, OA,OB – радиус-векторы его начала и конца,
Тогда
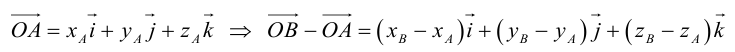
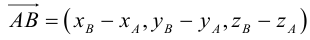
Определение: Базисом в пространстве называется любая упорядоченная тройка некомпланарных векторов (рис. 13).
Если 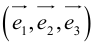
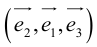
Определение: Базис называется прямоугольным декартовым, если базисные векторы взаимно перпендикулярны и длина каждого равна 1.
Такой базис принято обозначать
Из теоремы 2 следует, что всякий вектор 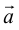
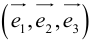
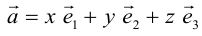
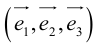
Определение: Базисом на плоскости называется любая упорядоченная пара неколлинеарных векторов.
Если 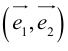
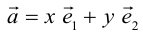
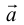
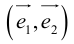
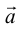
Определение: Базисом на прямой называется любой ненулевой вектор этой прямой.
Деление отрезка в данном отношении
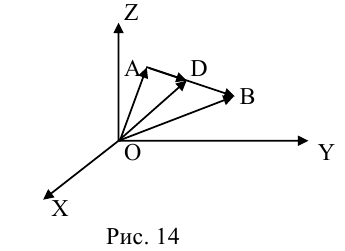
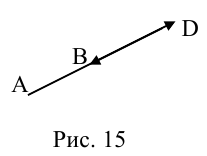
Рассмотрим задачу: дан отрезок AB . Найти точку D , которая делит AB в заданном отношении 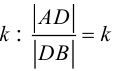
Введем прямоугольную декартову систему координат (пдск) OXYZ, тогда
Обозначим
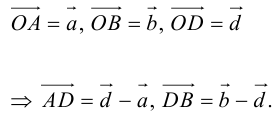
Так как 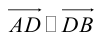
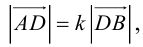
Переходя от этого векторного равенства к равенству соответствующих координат, получим:
ЗАМЕЧАНИЕ 1. Если D – середина отрезка AB , то k 1, поэтому
ЗАМЕЧАНИЕ 2. Если k < 0, 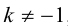
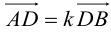
В этом случае
Скалярное произведение векторов
Определение: Скалярным произведением векторов 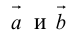
Скалярное произведение обозначается так: 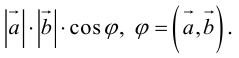
Так как 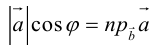
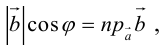
Свойства скалярного произведения
1.
2.
Доказательство:
3.
Доказательство:
а) 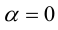
б)
в) 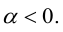
4.
Отсюда следует, что
Необходимым и достаточным условием перпендикулярности векторов является равенство нулю их скалярного произведения:
5.
Доказательство:
а) пусть
б) пусть
В первом и втором случаях один из сомножителей – нулевой вектор. Его направление не определено, поэтому можно считать, что 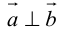
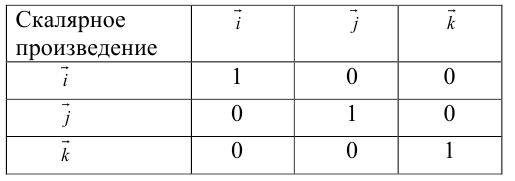
Используя свойства 4 и 5, составим таблицу вычисления скалярного произведения базисных векторов
Пусть в некоторой пдск 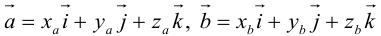
Таким образом,
Пример №8
Найти, при каком значении x векторы 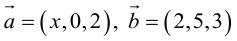
Два вектора перпендикулярны тогда и только тогда, когда их скалярное произведение равно нулю (свойство 5), поэтому найдем скалярное произведение по формуле (2.5):
Пример №9
Найти угол между биссектрисой AD и медианой 
Так как 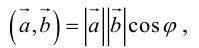
то
Найдем координаты векторов 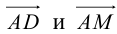
По теореме о биссектрисе внутреннего угла треугольника
Чтобы найти k , вычислим длины AC и AB :
Разделим отрезок CB в данном отношении по формулам (2.3):
отсюда
Заметим, что 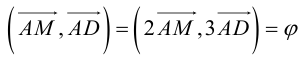
Пример №10
Найти
Воспользуемся свойствами 1–4 скалярного произведения:
Отсюда
ЗАМЕЧАНИЕ. Так как работа силы 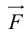
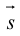
Определение векторного произведения векторов
Определение: Тройка некомпланарных векторов 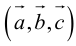
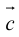
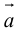
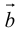
Определение: Векторным произведением вектора 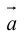
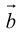
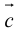
(
перпендикулярен плоскости векторов
и
).
- Направление
таково, что тройка
– правая.
Векторное произведение обозначается так:
ЗАМЕЧАНИЕ 1. Геометрический смысл векторного произведения: длина векторного произведения численно равна площади параллелограмма, построенного на этих векторах.
Это следует из того, что площадь параллелограмма равна произведению длин смежных сторон на синус угла между ними.
Заметим, что
Таким образом, длину вектора векторного произведения можно вычислить с помощью скалярного произведения по формуле
Пример №11
Найти площадь параллелограмма, построенного на векторах
По формуле (2.7):
ЗАМЕЧАНИЕ 2. Направление вектора 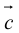
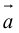
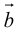
Свойства векторного произведения
1.
Доказательство:
а)пусть 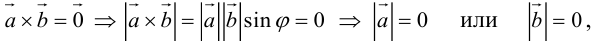
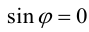
Его направление не определено, поэтому можно считать, что 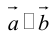
б)пусть
2. 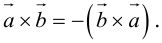
Доказательство: По определению направления векторов 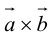
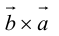
3.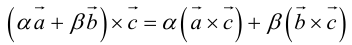
Векторное произведение также линейно и по второму сомножителю.
Используя определение и свойства 1 и 2, составим таблицу вычисления векторного произведения базисных векторов 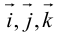
Пусть в некоторой пдск 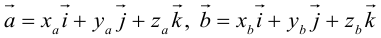
Заметим, что это выражение можно получить, вычислив символический определитель (сделать это можно по-разному, но лучше разложить по первой строке):
Таким образом,
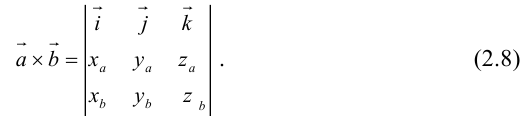
Пример №12
Вычислить векторное произведение векторов
По формуле (2.8):
Заметим, что площадь треугольника, построенного на векторах 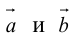
или
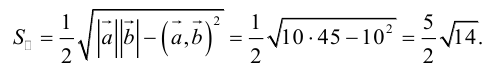
Пример №13
Вычислить площадь параллелограмма, построенного на векторах 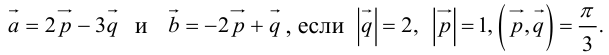
Так как 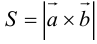
Отсюда
Определение смешанного произведения векторов
Определение: Смешанным произведением векторов 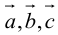
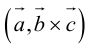
Смешанное произведение обозначается так:
Пусть в некоторой пдск
Обозначим
Тогда
по 7 свойству определителей.
Таким образом,
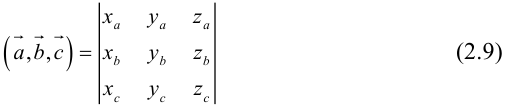
По определению скалярного произведения
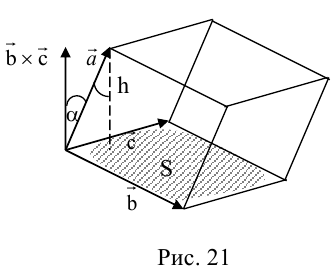
Совместим начала всех трех векторов в одной точке. Тогда (рис. 21)
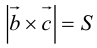
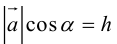
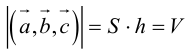
Геометрический смысл смешанного произведения: модуль смешанного произведения численно равен объему параллелепипеда, построенного на векторах-сомножителях, при этом 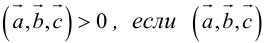
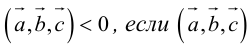
Свойства смешанного произведения
1. Необходимым и достаточным условием компланарности трех векторов является равенство нулю их смешанного произведения: 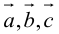
Доказательство: а) 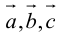
Если 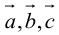
б)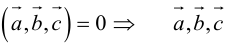
Во всех трех случаях 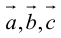
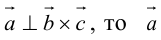
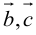
2. Круговая перестановка сомножителей в смешанном произведении не изменяет его величины. Перестановка соседних сомножителей изменяет его знак, не изменяя абсолютной величины:
Доказательство следует из формулы (2.9) и свойства 3 определителей, при этом круговая перестановка сомножителей соответствует двойной перемене строк в определителе, а потому оставляет его неизменным.
3. В смешанном произведении векторное и скалярное произведения можно менять местами:
Доказательство: из свойства 2 смешанного произведения и свойства 1 скалярного получим:
4. Смешанное произведение линейно по каждому из трех сомножителей.
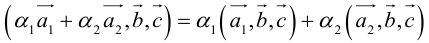
Доказательство следует из формулы (2.9) и свойств определителей.
Пример №14
Найти объем тетраэдра, построенного на векторах
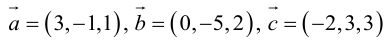
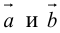
Объем тетраэдра в 6 раз меньше объема параллелепипеда, построенного на этих векторах, поэтому
Отсюда 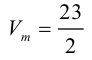

Чтобы найти высоту, воспользуемся формулой
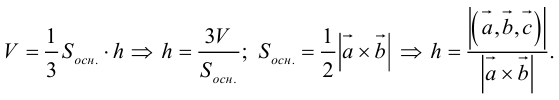
По формуле (2.7)
Лекции по предметам:
- Математика
- Алгебра
- Линейная алгебра
- Геометрия
- Аналитическая геометрия
- Высшая математика
- Дискретная математика
- Математический анализ
- Теория вероятностей
- Математическая статистика
- Математическая логика
Сайт переезжает. Большинство статей уже перенесено на новую версию.
Скоро добавим автоматические переходы, но пока обновленную версию этой статьи можно найти там.
Вычислительная геометрия
Напомним, что отрезок, для которого указано, какой из его концов считается началом, а какой — концом, называется вектором. Вектор на плоскости можно задать двумя числами — его координатами по горизонтали и вертикали.
Помимо очевидных сложения, вычитания и умножения на константу (скаляр — одно число), у векторов можно ввести и свои особенные операции, которые нам упростят жизнь.
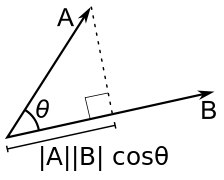
Скалярное произведение (англ. dot product) — произведение длин векторов на косинус угла между ними. Для него справедлива следующая формула:
[
a cdot b = x_a x_b + y_a y_b
]
Она доказывается муторно и чисто технически, так что мы это делать не будем.
Геометрически, она равна проекции вектора (b) на вектор (a), помноженный на длину (а):
У него есть полезные свойства:
- Скалярное произведение симметрично ((a cdot b = b cdot a)).
- Перпендикулярные вектора должны иметь нулевое скалярное произведение.
- Если угол острый, то скалярное произведение положительное.
- Если угол тупой, то скалярное произведение отрицательное.
Векторное произведение (англ. cross product) — произведение длин векторов на синус угла между ними, причём знак этого синуса зависит от порядка операндов. Оно тоже удобно выражается в координатах:
[
a times b = x_a y_b – y_a x_b
]
Геометрически, это ориентированный объем параллелограмма, натянутого на вектора (a) и (b):
Его свойства:
- Векторное произведение антисимметрично: (a times b = – (b times a)).
- Коллинеарные вектора должны иметь нулевое векторное произведение.
- Если (b) «слева» от (a), то векторное произведение положительное.
- Если (b) «справа» от (a), то векторное произведение отрицательное.
Вообще говоря, векторное произведение определяется не так. Оно определено как вектор такой же длины, но перпендикулярный обоим исходным векторам. Это имеет применение в трёхмерной геометрии и физике, но нам об этом думать не надо.
Всякие проверки
Благодаря этим свойствам, почти все проверки в геометрии можно описать через них, а не уравнениями.
Принадлежность точки треугольнику. Пусть у нас есть треугольник (ABC) (заданный против часовой стрелки) и точка (P). Тогда она должна лежать слева от всех трёх векторов (AB), (BC) и (CA). Это условие задаст пересечение трёх полуплоскостей, которое и будет нужным треугольником.
[
text{P лежит внутри ABC} iff begin{cases}
(B-A) times (P-A) geq 0 \
(C-B) times (P-B) geq 0 \
(A-C) times (P-C) geq 0 \
end{cases}
]
Площадь треугольника. Можно пользоваться готовыми формулами, а можно и свойством векторного произведения.
[
V = frac{1}{2} (B-A) times (C-A)
]
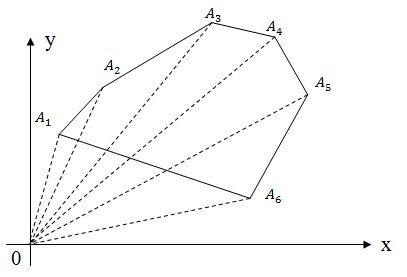
Площадь произвольного многоугольника. Если многоугольник задан последовательностью вершин в каком-то порядке, то можно считать так: для каждого ребра добавим его ориентированную площадь от начала координат. Какие-то слагаемые будут положительными (которые на последнем слое, а какие-то — отрицательными).
Забудьте о формуле Герона и всегда считайте площади через векторное произведение.
Кстати, из формулы для площади треугольника следует, что площадь любой фигуры будет либо целым числом, либо рациональным с двойкой в знаменателе. Часто в в задачах входные данные целочисленные, и, чтобы оставаться в целых числах, когда мы считаем какую-нибудь площадь, иногда имеет смысл умножить все входные числа на (2) (см. «точность»).
Проверка на выпуклость. Можно пройтись по сторонам многоугольника и проверять векторным произведением, что мы поворачиваем всегда в одну сторону, то есть для всех последовательных точек (a), (b), (c) проверить, что ((b-a)times(c-a) > 0).
Пересекаются ли отрезки.
Уравнение прямой
Прямую можно задать уравнением вида (Ax + By + C = 0). Полуплоскость можно задать таким же неравенством.
У прямой есть вектор нормали с координатами ((A, B)). Он перпендиуклярен прямой, а в случае с полуплоскостью (Ax + By + C geq 0) будет указывать в сторону самой полуплоскости.
Чтобы найти расстояние от точки ((x_0, y_0)) до прямой (Ax + By + C = 0), можно воспользоваться следующей формулой:
[
d = frac{|Ax_0+By_0+C|}{sqrt{A^2+B^2}}
]
Точка пересечения. По сути, найти точку пересечения двух прямых — это то же самое, что и найти точку, которая удовлетворяет обоим условиям их уравнений:
[
begin{cases}
A_1 x + B_1 y + C_1 = 0 \
A_2 x + B_2 y + C_2 = 0
end{cases}
implies
begin{cases}
-x = frac{B_1 y + C_1}{A_1} \
-x = frac{B_2 y + C_2}{A_2}
end{cases}
implies
frac{B_1 y + C_1}{A_1} = frac{B_2 y + C_2}{A_2}
implies
y = – frac{A_1 C_2 – A_2 C_1}{A_1 B_2 – A_2 B_1}
]
Аналогично, (x = frac{B_1 C_2 – B_2 C_1}{A_1 B_2 – A_2 B_1}) (обратите внимание на знаки).
Заметим, что знаменатель может оказаться нулем. Это означает, что векторное произведение векторов нормали нулевое, а значит прямые параллельны (в частности, это могут быть совпадающие прямые). Этот случай нужно обрабатывать отдельно.
Как это кодить в C++
Небольшой ликбез по объектно-ориентированному программированию в C++. Создадим класс, который будет отвечать за все операции с точками. В C++ есть два способа это сделать: через struct и через class. Их основное отличие в том, что по умолчанию в class все поля приватные — к ним нет прямого доступа снаружи. Это нужно для дополнительной защиты, чтобы в крупных промышленных проектах никто случайно ничего не поломал, но на олимпиадах это не очень актуально.
Точка (simeq) вектор. Будем считать точка и вектор это один и тот же объект, так как они оба — это просто пара чисел. Будем сопоставлять точке её радиус-вектор — вектор из начала координат, ведущий в эту точку. По принятой в математике и физике нотации, будем обозночать вектора как r. Вы можете обозвать их как point, pt, vec — как угодно.
struct r {
double x, y;
r() {}
r(int _x, int _y) { x = _x, y = _y; }
};Функция r внутри класса вызывается при инциализации объекта. Её называют конструктором, и её можно указывать разную для разных параметров. Здесь r()вернёт точку с неопределенными (какие оказались в памяти в тот момент) координатами, а r(x, y) вернет точку с координатами ((x, y)).
Операции над векторами
Давайте напишем функцию, которая принимает вектора и что-то с ними делает. Например, считает длину:
double len(r a) { return sqrt(a.x*a.x + a.y*a.y); }Операторы
В C++ можно перегружать почти все стандартные операторы, например, +, -, << и т. д.
Переопределим для будущих нужд + и -:
r operator+(r a, r b) { return r(a.x+b.x, a.y+b.y); }
r operator-(r a, r b) { return r(a.x-b.x, a.y-b.y); }Скалярное произведение:
int operator*(r a, r b) { return a.x*b.x + a.y*b.y; }Векторное произведение:
int operator^(r a, r b) { return a.x*b.y - b.x*a.y; }Ввод-вывод
Как вы думаете, как на самом деле работает cin >> x? Это тоже перегрузка оператора — >>. Делается это так:
istream& operator>>(istream &in, r &p) {
in >> p.x >> p.y;
return in;
}
ostream& operator<<(ostream &out, r &p) {
out << p.x << " " << p.y << endl;
return out;
}Почему алгебра это плохо
Мы могли не создавать никаких структур и работать с уравнениями, описывающими геометрические объекты. Такой подход будет популярен на олимпиадах по математике, а не по программированию. Когда математик говорит «пересечем две прямые», он представляет громоздкое уравнение, с которым он потом будет работать.
Программист же хочет абстрагироваться и просто написать intersect(a, b), в корректности которого он точно уверен. Программист хочет разбить задачу на много маленьких кусочков и делать по отдельности, а не возиться с формулами.
Приведем несколько примеров конструктивного подхода.
Векторное представление прямой
Прямую можно задать не через уравнение, а через два вектора (a) и (b):
[
Ax + By + C = 0 rightarrow r = at + b
]
Чтобы это сделать, достаточно выбрать две любые точки на прямой:
// даны A, B, C (A^2 + B^2 != 0)
r a, b;
if (eq(A, 0)) // значит, это горизонтальная прямая
a = r(0, -C/B), b = r(1, -C/B);
else
a = r(-C/A, 0), b = (1, -(C+B)/A, 1)Отражение от прямой
Пусть нам надо отразить точку ((x_0, y_0)) симметрично относительно заданной прямой (ax+by+c=0). Чисто в педагогических целях, начнём решать эту задачу как математики, чтобы никогда потом так не делать.
[
Pr_a b = frac{a cdot b}{|a|} frac{a}{|a|} = frac{|a| |b| cos alpha}{|a|} frac{a}{|a|} = |b| cos alpha frac{a}{|a|}
]
Геометрический смысл: длина на единичный вектор направления.
Мы не хотим раскрывать эти формулы покоординатно и предъявлять готовый ответ. Мы знаем, что он получится громоздким. Нам не жалко посчитать всё по частям — здесь нет смысла заниматься оптимизациями. Также мы хотим делать всё по частям, потому что так становится более наглядной логика алгоритма, и, как следствие, его проще дебажить.
// прямая r = at + b, точка c
r pr (r a, r b, r c) {
c -= b; // пусть c и a выходят из одной точки
return b + (a*b / len(a) / len(a)) * a;
}
r reflect (r a, r b, r c) {
return c + 2*(pr(a, b, c)-c);
}Типичные баги
Точность
Первое правило действительных чисел — не использовать действительные числа
Все переменные типа double хранятся в компьютере неточно (ну а как вы представите ⅓ в двоичной системе счисления?). Поэтому при работе с даблами нужно всегда учитывать эту погрешность. Например, чтобы сравнить два дабла, надо проверить, что они отличаются по модулю меньше, чем на очень маленькое число eps:
const double eps = 1e-8;
bool eq (double a, double b) { return abs(a-b) < eps }Чтобы так не делать, старайтесь по возможности использовать только инты и абсолютную точность. Иногда есть трюки, позволяющие так делать: например, если в задаче все входные точки целочисленные и нас просят посчитать какую-то площадь, то можно все координаты домножить на два, и тогда ответ тоже будет целым (см. векторное произведение), который только при выводе нужно будет поделить на четыре.
(0 neq -0)
Действительные числа так хранятся, что (0) и (-0) могут быть разными числами. Имейте это ввиду.
Область определения обратных функций
acos, asin и прочие обратные тригонометрические функций требуют, чтобы им на вход подавалось число от -1 до 1. Для безопасности, отмасштабируйте числа, перед тем как брать от них эти функции.

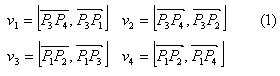
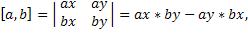
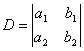
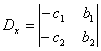
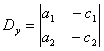
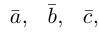
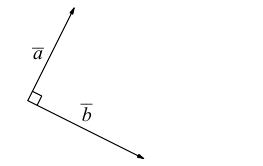
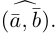
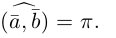
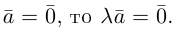
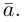
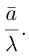
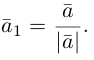
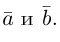
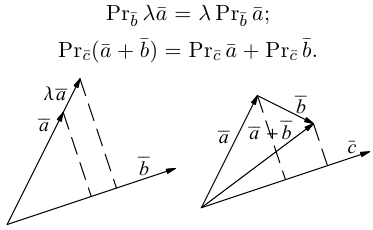
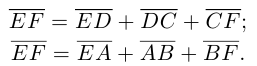
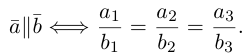
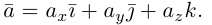
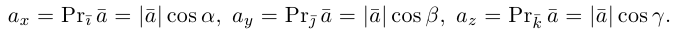
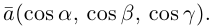
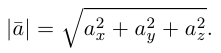
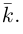

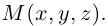
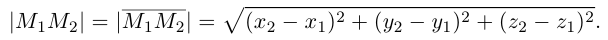
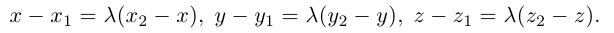
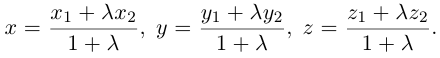
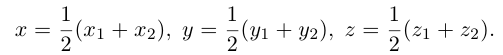
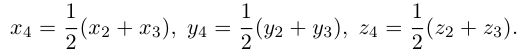
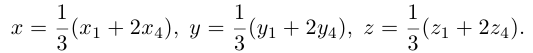
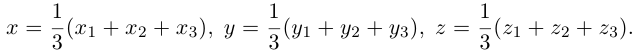


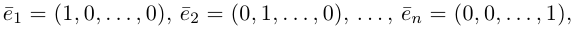
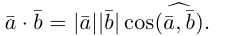
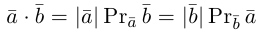
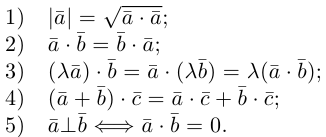
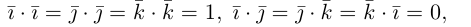
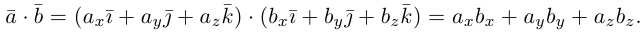
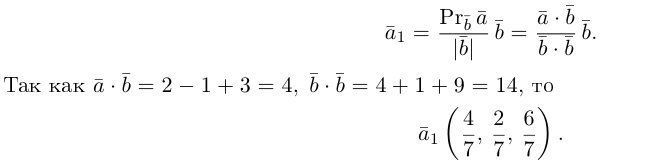
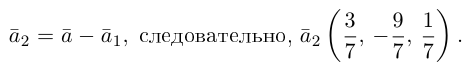
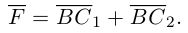
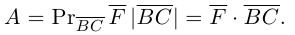
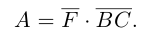
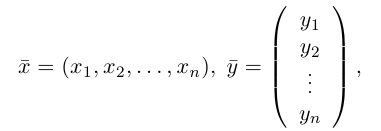
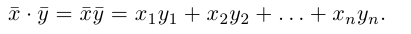
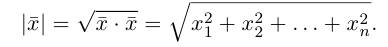
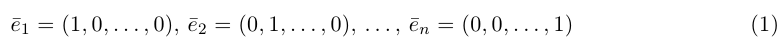
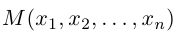

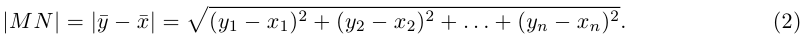
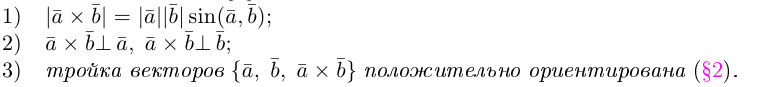
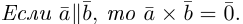
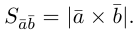
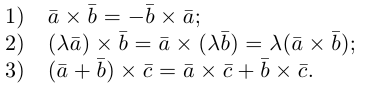
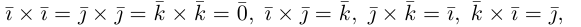
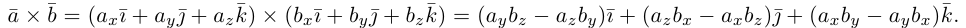
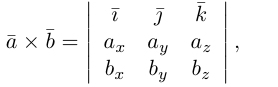
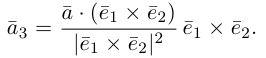
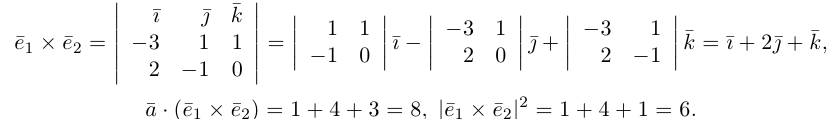
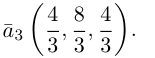
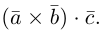
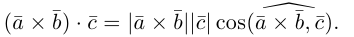
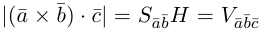
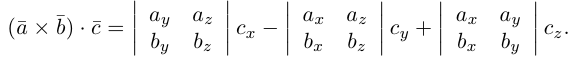
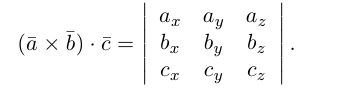
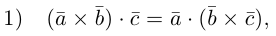
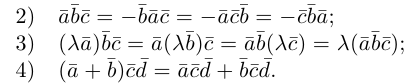
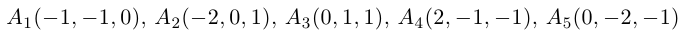
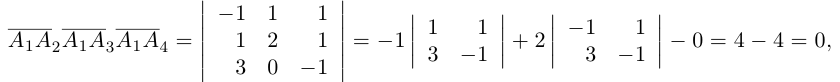
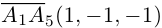
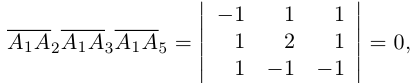
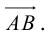
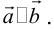
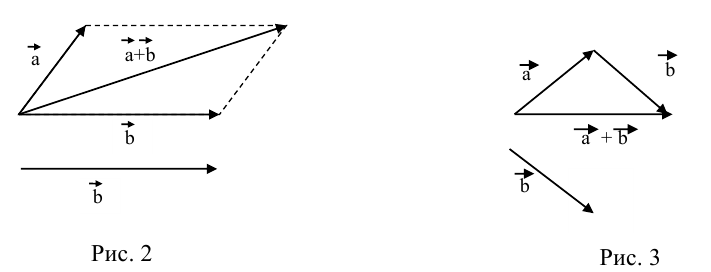
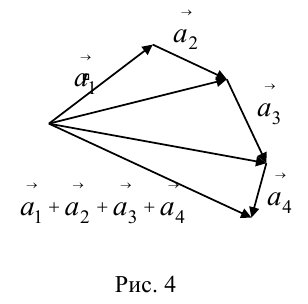

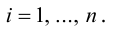
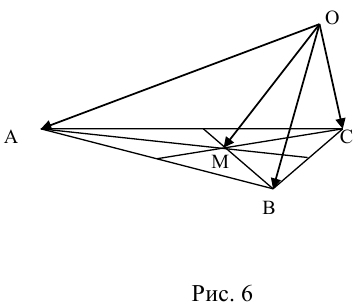
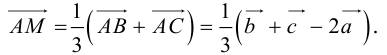
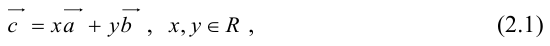
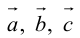 есть два коллинеарных, например:
есть два коллинеарных, например: 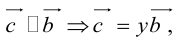
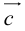 , а стороны параллельны прямым, на которых лежат
, а стороны параллельны прямым, на которых лежат 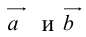 (рис. 7).
(рис. 7). 
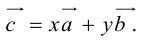
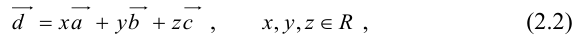
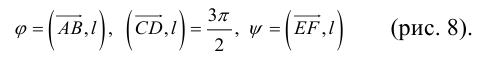
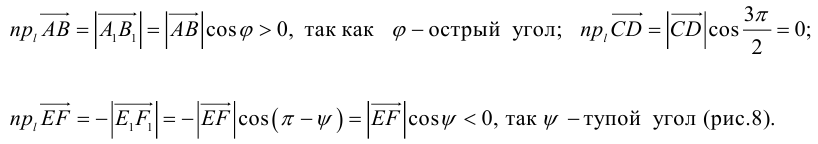
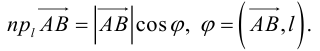
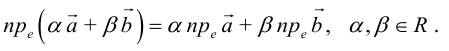
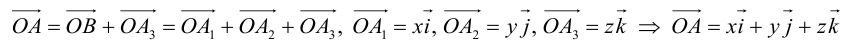
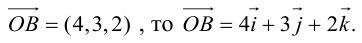
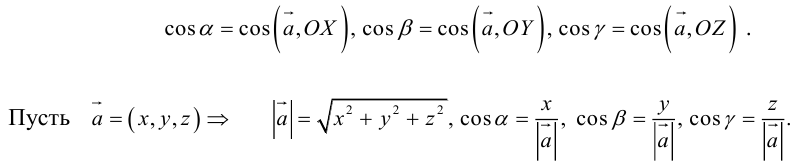
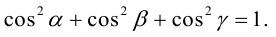
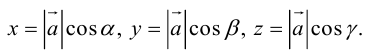
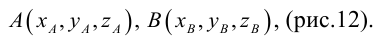
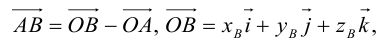
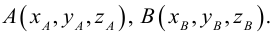

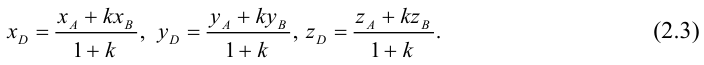
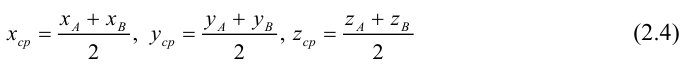
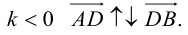
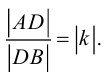
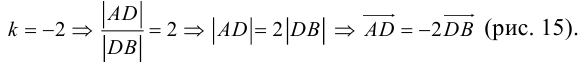
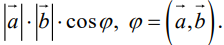
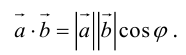
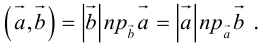
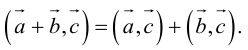
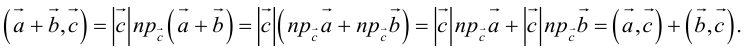
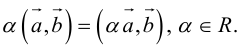
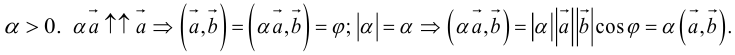
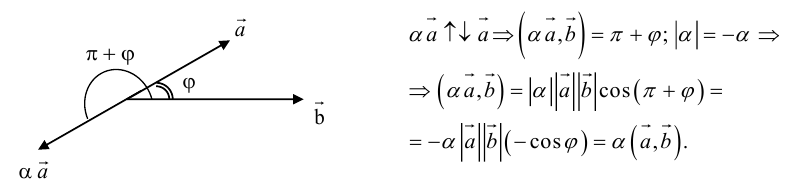
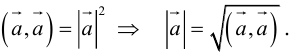
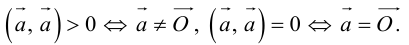
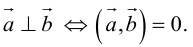
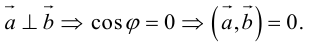
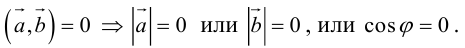
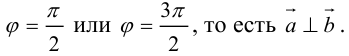
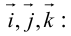
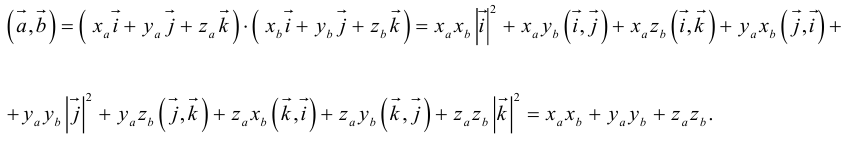

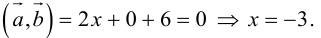
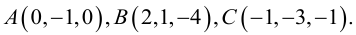

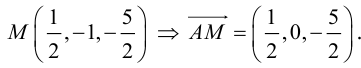
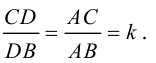
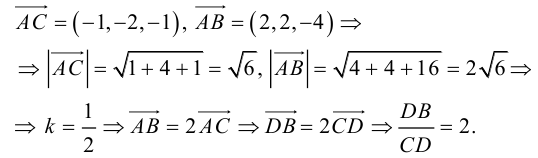
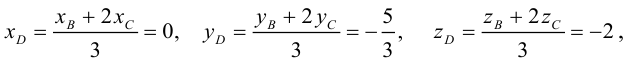
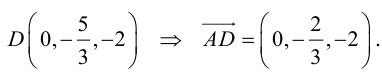
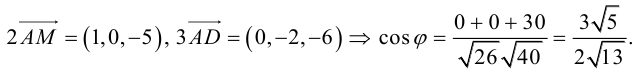
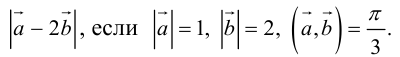
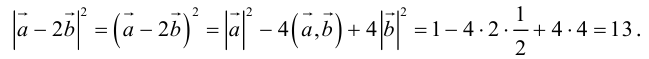
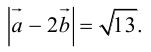
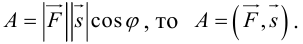
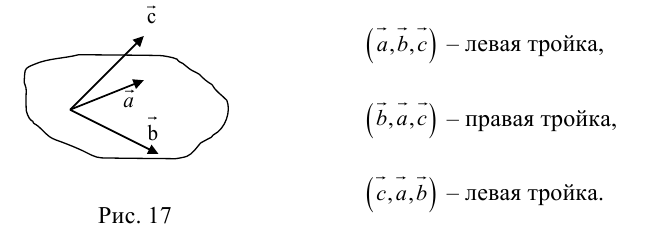
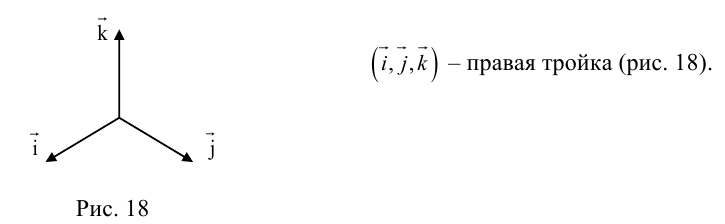
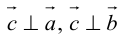 (
(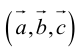 – правая.
– правая.