Вы уже знакомы с прямоугольной системой координат на
плоскости, другими словами прямоугольной координатной плоскостью. Такую
систему координат задают две взаимно перпендикулярные прямые, на каждой
из которых выбрано направление и величина единичного отрезка. Эти
прямые называют осями абсцисс и ординат.
Точку пересечения осей называют точкой начала координат.
Прямоугольную систему координат на плоскости
обозначают Оху.
Каждой точке плоскости сопоставляется только одна
пара чисел, которые называют её координатами. Для определения координат,
из точки нужно провести перпендикуляры к осям, тем самым мы и получим абсциссу
и ординату точки.
Определение:
Если же через точку пространства проведены
три попарно перпендикулярные прямые, а на каждой из них выбрано направление и
единичный отрезок, то говорят, что задана прямоугольная система координат
в пространстве.
Прямые с выбранными на них направлениями называют осями
координат, а точку их пересечения — началом координат.
Как и на плоскости её обычно обозначают буквой О.
Оси координат обозначают так: Ох, Оу, Оz.
И называют осью абсцисс, осью ординат и, новым
является название третьей оси, ось аппликат.
Прямоугольную систему координат в пространстве
обозначают Охуz.
Через каждые 2 оси координат проходят координатные
плоскости: Оху, Оуz и Охz.
Всего таких плоскостей 3.
Каждая ось делится точкой О на два луча. В
соответствии с этим, лучи, направление которых совпадает с направлением оси,
называют положительными полуосями, а оставшиеся лучи — отрицательными
полуосями.
Каждой точке пространства сопоставляется только одна
тройка чисел, которые называют её координатами. Их определяют
аналогично тому, как это делали на плоскости. Только через точку М проводят
плоскости перпендикулярные координатным осям.
Точки пересечения проведённых плоскостей с осями
координат назовём М1, М2 и М3.
Первая координата точки М, то есть её абсцисса,
равна длине отрезка ОМ1.
Вторая координата, которую называют ординатой, равна
длине отрезка ОМ2.
Ну, а третья координата, а точнее аппликата, равна
длине отрезка ОМ3.
Координаты точки записывают в скобках, при этом
первой записывают абсциссу, второй — ординату, а третьей — аппликату.
В данном случае точки М1, М2 и
М3 являются точками положительных полуосей, поэтому и координаты
точки М будут положительными числами.
Рассмотрим примеры различного расположения точек в
прямоугольной системе координат.
Задание:
определить координаты точек А, В, С, D,
Е и F.
После выполнения этого задания можно сделать вывод
о том, что если точка лежит в некоторой координатной плоскости или на
некоторой координатной оси, то её соответствующие координаты будут равны нулю.
Так если точка лежит в координатной плоскости
ОИксИгрек, то её аппликата равна нулю. Если точка лежит в координатной
плоскости ОИксЗэт, то её ордината равна нулю. И если точка лежит в координатной
плоскости ОИгрекЗэт, то её абсцисса равна нулю.
Ну, а в случаях, когда точка лежит на одной из осей,
только одна координата является ненулевой.
Задание:
По координатам точек 𝐴(3;−1;0), 𝐵(0;0;−7),
𝐶(2;0;0),
𝐷(−4;0;3),
𝐸(0;−1;0),
𝐹(1;2;3),
𝐺(0;5−7),
𝐻(−√5;√3;0)
определить, какие из них лежат на той или иной координатной оси или в той или
иной координатной плоскости.
Решение:
Задание:
найти координаты проекций точки 𝐴(2;−3;5)
на каждую из координатных плоскостей и на каждую из координатных осей.
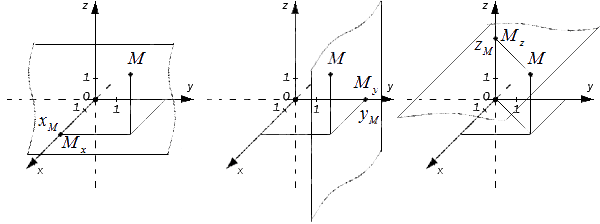
Далее найдём координаты проекций точки А на
координатные плоскости.
Проекцией точки А на координатную плоскость Оху
является основание перпендикуляра, проведённого из точки А к данной
координатной плоскости. При этом координаты полученной проекции будут такими же
как у точки А, только аппликата станет равной нулю.
Аналогично получим проекцию точки А на координатную
плоскость Оуz. Проведём
перпендикуляр из данной точки к данной координатной плоскости. Его основание и
является проекцией точки А на плоскость Оуz.
Координаты данной проекции равны координатам точки А, только абсцисса равна
нулю.
Ну, а проекция точки А на координатную плоскость Охz
будет иметь координаты 2, 0, 5.
Так мы с вами нашли координаты проекций точки А на
координатные оси и на координатные плоскости.
Задание:
𝐴𝐵𝐶𝐷𝐴1𝐵1𝐶1𝐷1−
куб; 𝐴(0;0;0),
𝐵(0;0;1),
𝐷(0;1;0),
𝐴1
(1;0;0). Найти координаты точек 𝐶,
𝐵1,
𝐶1
и 𝐷1.
Решение:
Изобразим прямоугольную систему координат. Отметим точки, являющиеся вершинами
куба, координаты которых известны.
Итоги:
На этом уроке вы познакомились с понятием
прямоугольной системы координат в пространстве. Узнали, что её задают три
взаимно перпендикулярные прямые, на которых выбраны направления и единичные
отрезки. Эти прямые называют координатными осями. Точку пересечения осей
называют точкой начала координат.
Ось Ох называют осью абсцисс, ось Оу называют осью
ординат, и новым для вас является название оси Оz
— ось аппликат. Помимо осей координат в прямоугольной системе координат
присутствуют и координатные плоскости: Оху, Оуz
и Охz.
Всю прямоугольную систему координат в пространстве
обозначают Охуz.
Любой точке пространства соответствует только одна
тройка чисел х, у и z, которые и
являются её координатами. Все координаты точки О начала координат равны нулю.
При введении системы координат на плоскости или в трехмерном пространстве появляется уникальная возможность описания геометрических фигур и их свойств при помощи уравнений и неравенств. Это имеет иное название – методы алгебры.
Данная статья поможет разобраться с заданием прямоугольной декартовой системой координат и с определением координат точек. Более наглядное и подробное изображение имеется на графических иллюстрациях.
Прямоугольная декартова система координат на плоскости
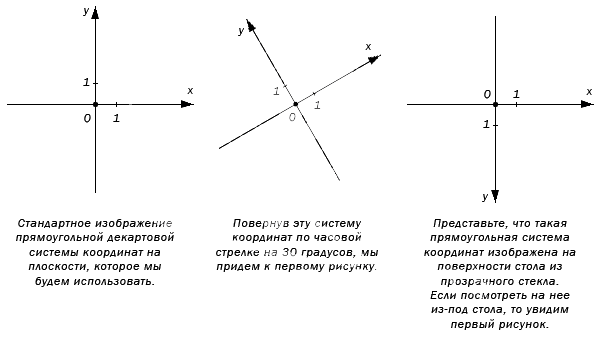
Чтобы ввести систему координат на плоскости, необходимо провести на плоскости две перпендикулярные прямые. Выбираем положительное направление, обозначая стрелочкой. Необходимо выбрать масштаб. Точку пересечения прямых назовем буквой O. Она считается началом отсчета. Это и называется прямоугольной системой координат на плоскости.
Прямые с началом O, имеющие направление и масштаб, называют координатной прямой или координатной осью.
Прямоугольная система координат обозначается Oxy. Координатными осями называют Ох и Оу, называемые соответственно ось абсцисс и ось ординат.
Изображение прямоугольной системы координат на плоскости.
Оси абсцисс и ординат имеют одинаковую единицу изменения и масштаб, что показано в виде штрихе в начале координатных осей. Стандартное направление Ох слева направо, а Oy – снизу вверх. Иногда используется альтернативный поворот под необходимым углом.
Прямоугольная система координат получила название декартовой в честь ее первооткрывателя Рене Декарта. Часто можно встретить название как прямоугольная декартовая система координат.
Прямоугольная система координат в трехмерном пространстве
Трехмерное евклидовое пространство имеет аналогичную систему, только оно состоит не из двух, а из трех Ох, Оу, Оz осей. Это три взаимно перпендикулярные прямые, где Оz имеет название ось аппликат.
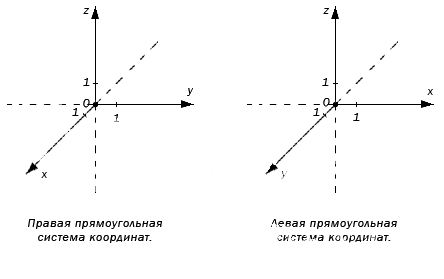
По направлению координатных осей делят на правую и левую прямоугольные системы координат трехмерного пространства.
Оси координат пересекаются в точке O, называемой началом. Каждая ось имеет положительное направление, которое указывается при помощи стрелок на осях. Если при повороте Ох против часовой стрелки на 90° ее положительное направление совпадает с положительным Оу, тогда это применимо для положительного направления Оz. Такую систему считают правой. Иначе говоря, если сравнить направление Х с большим пальцем руки, то указательный отвечает за Y, а средний за Z.
Аналогично образуется левая система координат. Обе системы совместить невозможно, так как соответствующие оси не совпадут.
Координаты точки в декартовой системе координат на плоскости
Для начала отложим точку М на координатной оси Ох. Любое действительное число xM равняется единственной точке М, расположенной на данной прямой. Если точка расположена на координатной прямой на расстоянии 2 от начала отсчета по положительному направлению, то она равна 2 , если -3, то соответственное расстояние 3. Ноль – это начало отсчета координатных прямых.
Иначе говоря, каждая точка М, расположенная на Ox, равна действительному числу xM . Этим действительным числом и является ноль, если точка M расположена в начале координат, то есть на пересечении Ox и Оу. Число длины отрезка всегда положительно, если точка удалена в положительном направлении и наоборот.
Имеющееся число xM называют координатой точки М на заданной координатной прямой.
Возьмем точку как проекцию точки Mx на Ох, а как проекцию точки My на Оу. Значит, через точку М можно провести перпендикулярные осям Оx и Оу прямые, где послучим соответственные точки пересечения Mx и My .
Тогда точка Mx на оси Ох имеет соответствующее число xM , а My на Оу – yM. На координатных осях это выглядит так:
Каждая точка M на заданной плоскости в прямоугольной декартовой системе координат имеет одну соответствующую пару чисел (xM, yM), называемую ее координатами. Абсцисса M – это xM , ордината M – это yM .
Обратное утверждение также считается верным: каждая упорядоченная пара (xM, yM) имеет соответствующую заданную в плоскости точку.
Координаты точки в прямоугольной системе координат в трехмерном пространстве
Определение точки М в трехмерном пространстве. Пусть имеются Mx, My, Mz, являющиеся проекциями точки М на соответствующие оси Ох, Оу, Оz. Тогда значения этих точек на осях Ох, Оу, Оz примут значения xM, yM, zM. Изобразим это на координатных прямых.
Чтобы получить проекции точки M, необходимо добавить перпендикулярные прямые Ох, Оу, Оz продолжить и изобразит в виде плоскостей, которые проходят через M. Таким образом, плоскости пересекутся в Mx, My, Mz
Каждая точка трехмерного пространства имеет свои данные (xM, yM, zM) , которые имеют название координаты точки M, , xM, yM, zM- это числа, называемые абсциссой, ординатой и аппликатой заданной точки M. Для данного суждения верно и обратное утверждение: каждая упорядоченная тройка действительных чисел (xM, yM, zM) в заданной прямоугольной системе координат имеет одну соответствующую точку M трехмерного пространства.
Марина Николаевна Ковальчук
Эксперт по предмету «Геометрия»
Задать вопрос автору статьи
Прямоугольная система координат
Чтобы определить понятие координат точек, нам необходимо ввести систему координат, в которой мы и будем определять ее координаты. Одна и та же точка в разных системах координат может иметь различные координаты. Здесь мы будем рассматривать прямоугольную систему координат в пространстве.
Возьмем в пространстве точку $O$ и введем для нее координаты $(0,0,0)$. Назовем ее началом системы координат. Проведем через нее три взаимно перпендикулярные оси $Ox$, $Oy$ и $Oz$, как на рисунке 1. Эти оси будут называться осями абсцисс, ординат и аппликат, соответственно. Осталось только ввести масштаб на осях (единичный отрезок) – прямоугольная система координат в пространстве готова (рис. 1)
Рисунок 1. Прямоугольная система координат в пространстве. Автор24 — интернет-биржа студенческих работ
Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽
Координаты точки
Теперь разберем, как определяют в такой системе координаты любой точки. Возьмем произвольную точку $M$ (рис. 2).
Рисунок 2. Произвольная точка. Автор24 — интернет-биржа студенческих работ
Построим на координатных осях прямоугольный параллелепипед, так, что точки $O$ и $M$ противоположные его вершины (рис. 3).
Рисунок 3. Построение прямоугольного параллелепипеда. Автор24 — интернет-биржа студенческих работ
«Координаты точки и координаты вектора. Как найти координаты вектора» 👇
Тогда точка $M$ будет иметь координаты $(X,Y,Z)$, где $X$ – значение на числовой оси $Ox$, $Y$ – значение на числовой оси $Oy$, а $Z$ – значение на числовой оси $Oz$.
Пример 1
Необходимо найти решение следующей задачи: написать координаты вершин параллелепипеда, изображенного на рисунке 4.
Рисунок 4. Параллелепипед. Автор24 — интернет-биржа студенческих работ
Решение.
Точка $O$ начало координат, следовательно, $O=(0,0,0)$.
Точки $Q$, $N$ и $R$ лежат на осях $Ox$, $Oz$ и $Oy$, соответственно, значит
$Q=(2,0,0)$, $N=(0,0,1.5)$, $R=(0,2.5,0)$
Точки $S$, $L$ и $M$ лежат в плоскостях $Oxz$, $Oxy$ и $Oyz$, соответственно, значит
$S=(2,0,1.5)$, $L=(2,2.5,0)$, $R=(0,2.5,1.5)$
Точка $P$ имеет координаты $P=(2,2.5,1.5)$
Координаты вектора по двум точкам и формула нахождения
Чтобы узнать, как найти вектор по координатам двух точек, необходимо рассмотреть введенную нами ранее систему координат. В ней от точки $O$ по направлению оси $Ox$ отложим единичный вектор $overline{i}$, по направлению оси $Oy$ – единичный вектор $overline{j}$, а единичный вектор $overline{k}$ нужно направлять по оси $Oz$.
Для того чтобы ввести понятие координат вектора, введем следующую теорему (здесь ее доказательство мы рассматривать не будем).
Теорема 1
Произвольный вектор в пространстве может быть разложен по трем любым векторам, которые не лежат в одной плоскости, причем коэффициенты в таком разложении будут единственным образом определены.
Математически это выглядит следующим образом:
$overline{δ}=moverline{α}+noverline{β}+loverline{γ}$
Так как векторы $overline{i}$, $overline{j}$ и $overline{k}$ построены на координатных осях прямоугольной системы координат, то они, очевидно, не будут принадлежать одной плоскости. Значит любой вектор $overline{δ}$ в этой системе координат, по теореме 1, может принимать следующий вид
$overline{δ}=moverline{i}+noverline{j}+loverline{k}$ (1)
где $n,m,l∈R$.
Определение 1
Три вектора $overline{i}$, $overline{j}$ и $overline{k}$ будут называться координатными векторами.
Определение 2
Коэффициенты перед векторами $overline{i}$, $overline{j}$ и $overline{k}$ в разложении (1) будут называться координатами этого вектора в заданной нами системе координат, то есть
$overline{δ}=(m,n,l)$
Линейные операции над векторами
Теорема 2
Теорема о сумме: Координаты суммы любого числа векторов определяются суммой их соответствующих координат.
Доказательство.
Будем доказывать эту теорему для 2-х векторов. Для 3-х и более векторов доказательство строится аналогичным образом. Пусть $overline{α}=(α_1,α_2,α_3)$, $overline{β}=(β_1,β_2 ,β_3)$.
Эти вектора можно записать следующим образом
$overline{α}=α_1overline{i}+ α_2overline{j}+α_3overline{k}$, $overline{β}=β_1overline{i}+ β_2overline{j}+β_3overline{k}$
$overline{α}+overline{β}=α_1overline{i}+α_2overline{j}+α_3overline{k}+β_1overline{i}+ β_2overline{j}+β_3overline{k}=(α_1+β_1 )overline{i}+(α_2+β_2 )overline{j}+(α_3+β_3)overline{k}$
Следовательно
$overline{α}+overline{β}=(α_1+β_1,α_2+β_2,α_3+β_3)$
Теорема доказана.
Замечание 1
Замечание: Аналогично, находится решение разности нескольких векторов.
Теорема 3
Теорема о произведении на число: Координаты произведения произвольного вектора на действительное число определяется произведением координат на это число.
Доказательство.
Возьмем $overline{α}=(α_1,α_2,α_3)$, тогда $overline{α}=α_1overline{i}+α_2overline{j}+α_3overline{k}$, а
$loverline{α}=l(α_1overline{i}+ α_2overline{j}+α_3overline{k})=lα_1overline{i}+ lα_2overline{j}+lα_3overline{k}$
Значит
$koverline{α}=(lα_1,lα_2,lα_3)$
Теорема доказана.
Пример 2
Пусть $overline{α}=(3,0,4)$, $overline{β}=(2,-1,1)$. Найти $overline{α}+overline{β}$, $overline{α}-overline{β}$ и $3overline{α}$.
Решение.
$overline{α}+overline{β}=(3+2,0+(-1),4+1)=(5,-1,5)$
$overline{α}-overline{β}=(3-2,0-(-1),4-1)=(1,1,3)$
$3overline{α}=(3cdot 3,3cdot 0,3cdot 4)=(9,0,12)$
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Прямоуго́льная (Декартова) систе́ма координа́т — прямолинейная система координат с взаимно перпендикулярными координатными осями на плоскости или в пространстве. Часто используемая система координат. Просто обобщается для пространств любой размерности.
Связанные термины: декартовой обычно называют прямоугольную систему координат с одинаковыми масштабами по осям (названной так по имени Рене Декарта), а общей декартовой системой координат называют аффинную систему координат (не обязательно прямоугольную).
История[править | править код]
Впервые прямоугольную систему координат ввёл Рене Декарт в своей работе «Геометрия» в 1637 году. Он применял координаты к исследованию многих геометрических вопросов. Поэтому прямоугольную систему координат называют также — Декартова система координат (хотя современный термин не во всех деталях соответствует тому, что использовал сам Декарт[1]). Координатный метод описания геометрических объектов положил начало аналитической геометрии. Вклад в развитие координатного метода внес также Пьер Ферма, однако его работы были впервые опубликованы уже после его смерти[2]. Декарт и Ферма применяли координатный метод только на плоскости. Французский священнослужитель Николай Орем использовал конструкции, подобные декартовым координатам, задолго до времён Декарта и Ферма[3].
Развитие системы декартовых координат далее сыграло важную роль в развитии диифференциального и интегрального исчисления Исааком Ньютоном и Лейбницем[4]. Двухкоординатное описание плоскости позднее было обобщено в понятие векторных пространств[5].
Координаты в трёхмерном пространстве впервые применил Леонард Эйлер в XVIII веке. Использование единичных векторов впервые применил, по-видимому, Гамильтон и Максвелл.
Прямоугольная система координат на плоскости[править | править код]
Прямоугольная система координат на плоскости образуется двумя взаимно перпендикулярными осями координат 


Положение точки 











При этом координате 








Ось 





Символически это записывают так:
,
или:
,
или указывают принадлежность координат конкретной точке с помощью индекса:
,
и т. д.
Прямоугольная система координат в пространстве[править | править код]
Прямоугольная система координат в пространстве (в этом параграфе имеется в виду трёхмерное пространство, о более многомерных пространствах — см. ниже) образуется тремя взаимно перпендикулярными осями координат 






Положение точки 
















- Координата
называется абсциссой точки
,
- координата
— ординатой точки
,
- координата
— аппликата (лат. applicata — прилегающая)[8] точки
.
Символически это записывают так:
,
или
,
или привязывают запись координат к конкретной точке с помощью индекса:
,
и т. п.
Каждая ось рассматривается как числовая прямая, то есть имеет положительное направление, а точкам, лежащим на отрицательном луче приписываются отрицательные значения координаты (расстояние берется со знаком минус). То есть, если бы, например, точка 






Все прямоугольные системы координат в трехмерном пространстве делятся на два класса — правые (также используются термины положительные, стандартные) и левые. Обычно по умолчанию стараются использовать правые координатные системы, а при их графическом изображении ещё и располагают их, если можно, в одном из нескольких обычных (традиционных) положений. (На рис. 2 изображена правая координатная система). Правую и левую системы координат невозможно поворотами[9] совместить так, чтобы совпали соответствующие оси (и их направления). Определить, к какому классу относится какая-либо конкретно взятая система координат, можно, используя правило правой руки, правило винта и т. п. (положительное направление осей выбирают так, чтобы при повороте оси 


Любая из восьми областей, на которые пространство делится тремя взаимно перпендикулярными координатными плоскостями, называется октантом.
Прямоугольная система координат в многомерном пространстве[править | править код]
Прямоугольная система координат может быть использована и в пространстве любой конечной размерности аналогично тому, как это делается для трехмерного пространства. Количество координатных осей при этом равно размерности пространства (в этом параграфе будем обозначать её 
Для обозначения координат обычно[10] применяют не разные буквы, а одну и ту же букву с числовым индексом. Чаще всего это:
Для обозначения произвольной 
а нередко обозначение 

В любой размерности пространства прямоугольные координатные системы делятся на два класса, правые и левые (или положительные и отрицательные). Для многомерных пространств какую-то одну из координатных систем произвольно (условно) называют правой, а остальные оказываются правыми или левыми в зависимости от того, той же они ориентации или нет[11].
Обобщение понятий двумерного квадранта и трёхмерного октанта для 
Прямоугольные координаты вектора[править | править код]
Для определения прямоугольных координат вектора (применимых для представления векторов любой размерности) можно исходить из того, что координаты вектора (направленного отрезка), начало которого находится в начале координат, совпадают с координатами его конца[12].
Для векторов (направленных отрезков), начало которых не совпадает с началом координат, прямоугольные координаты можно определить одним из двух способов:
- Вектор можно перенести так, чтобы его начало совпало с началом координат). Тогда его координаты определяются способом, описанным в начале параграфа: координаты вектора, перенесённого так, что его начало совпадает с началом координат, — это координаты его конца.
- Вместо этого можно просто вычесть из координат конца вектора (направленного отрезка) координаты его начала.
- Для прямоугольных координат понятие координаты вектора совпадает с понятием ортогональной проекции вектора на направление соответствующей координатной оси.
В прямоугольных координатах очень просто записываются все операции над векторами:
Сложение и умножение на скаляр:
,
или:
,
или:
,
а отсюда и вычитание и деление на скаляр:
,
или:
,
или:
(Это верно для любой размерности n и даже, наравне с прямоугольными, для косоугольных координат).
- Скалярное произведение:
,
или:
(Это справедливо только в прямоугольных координатах с единичным масштабом по всем осям).
- Через скалярное произведение можно вычислить длину вектора
- и угол между векторами:
.
Внешнее произведение:
,
для любой размерности пространства,
- Векторное произведение (только для трехмерного же пространства, на котором оно и определено):
,
,
.
Это позволяет свести все операции над векторами к достаточно простым операциям над числами.
Орты[править | править код]
Прямоугольная система координат[13] (любой размерности) также описывается[14] набором ортов (единичных векторов), сонаправленных с осями координат. Количество ортов равно размерности системы координат и все они перпендикулярны друг другу. Такие орты образуют ортонормированныйбазис, притом[15].
В трёхмерном случае такие орты обычно обозначаются:
,
и
,
или
,
и
.
Могут также применяться обозначения со стрелками (





При этом в случае правой системы координат действительны следующие формулы с векторными произведениями ортов:
Для размерностей пространства более 3, (или для общего случая, когда размерность может быть любой) обычно для ортов применяют вместо этого обозначения с числовыми индексами, достаточно часто[16] это:
где n — размерность пространства.
Вектор любой размерности раскладывается по базису (координаты служат коэффициентами разложения):
,
или:
а для ортонормированного базиса координаты ещё и очень легко найти через скалярные произведения с ортами:
См. также[править | править код]
- Аффинные координаты
- Проективные координаты
Примечания[править | править код]
- ↑ Декарт пользовался не двумя осями, а одной, на которой откладывались абсциссы; ординаты определялись как расстояние от точек плоскости до оси абсцисс; эти расстояния Декарт отсчитывал по любому заранее выбранному направлению, а не обязательно перпендикулярно.
Как абсциссы, так и ординаты у Декарта были всегда величинами положительными независимо от направления соответствующих отрезков. Различие направлений на осях знаками «+» и «‒» было введено лишь его учениками.
Источник: Выгодский М. Я. Раздел VI. Функции, графики (§ 6. Координаты) // Справочник по элементарной математике / сост. М. Я. Выгодский, под ред. Н. А. Шармай. — М.: АСТ; Астрель, 2015. — С. 461. — 509 с. — 1500 экз. — ISBN 978-5-17-084803-4, ББК 22.1я2, УДК 51(03). — ISBN 978-5-271-46916-9.
- ↑ Bix, Robert A.; D’Souza, Harry J. Analytic geometry. Encyclopædia Britannica. Дата обращения: 6 августа 2017. Архивировано 6 августа 2017 года.
- ↑ Kent, Alexander J. The Routledge Handbook of Mapping and Cartography : [англ.] / Alexander J. Kent, Peter Vujakovic. — Routledge, 2017-10-04. — ISBN 9781317568216. Архивная копия от 24 ноября 2021 на Wayback Machine
- ↑ A Tour of the Calculus, David Berlinski
- ↑ Axler, Sheldon. Linear Algebra Done Right – Springer. — 2015. — P. 1. — ISBN 978-3-319-11079-0. — doi:10.1007/978-3-319-11080-6.
- ↑ 1 2 Словарь иностранных слов. — М.: Рус. яз., 1989. — 624 с. ISBN 5-200-00408-8
- ↑ Иногда это просто принципиально невозможно, если по осям откладываются величины разной физической размерности; впрочем, с геометрической точки зрения это замечание не слишком существенно, так как можно тогда считать масштабы по осям равными условно (например масштабы так, чтобы единицы совпадали при изображая на геометрической плоскости).
- ↑ Словарь иностранных слов. — М.: «Русский язык», 1989. — 624 с. ISBN 5-200-00408-8
- ↑ Можно превратить правую координатную систему в левую и наоборот с помощью зеркального отражения.
- ↑ Но не обязательно: вопрос обозначений в конечном итоге определяется конкретным приложением.
- ↑ Это можно выяснить, исходя из того, можно ли какими-то вращениями (и переносами, если не совпадают начала координат) совместить данную координатную систему с той, ориентация которой правая по определению. Если да, то данная система считается правой, если нет, то левой. Ещё проще технически это выяснить через знак определителя матрицы преобразования от правого базиса к данному.
- ↑ Конец направленного отрезка — точка; прямоугольные координаты точки рассмотрены в статье выше.
- ↑ В этом параграфе будем подразумевать обычную декартову систему координат, то есть прямоугольную систему координат с одинаковым масштабом по всем осям; рассмотрение систем координат с разным масштабом по разным осям внесло бы здесь неоправданные формальные усложнения при довольно малом выигрыше содержательном отношении.
- ↑ Это описание очевидно полностью эквивалентно обычному заданию осей координат, надо только ещё задать начало координат (последнее нередко очевидно по умолчанию).
- ↑ При отказе от условия равномасштабности координатных осей — просто ортогональный базис.
- ↑ Впрочем, вместо буквы e нередко могут быть использованы и другие буквы. Как правило, это явно оговорено.
Ссылки[править | править код]
- В. И. Гервидс. Модель декартовой системы координат (flash). НИЯУ МИФИ (10 марта 2011). Дата обращения: 3 мая 2011.
Геометрия, 11 класс
Урок № 1. Координаты в пространстве. Система координат
Перечень вопросов, рассматриваемых в теме:
- Прямоугольная система координат в пространстве.
- Координаты вектора, радиус-вектор.
- Координаты середины отрезка, длина вектора, расстояние между точками.
Основная литература:
Гусева В.А., Куланин Е.Д. Геометрия. Профильный уровень. 10 класс – М.: Бином, 2010 – с. 130-148
Погорелов А.В. Геометрия. Учеб. для 7-11 кл. общеобразоват. Учреждение – 13-е изд-е. – М.: Просвещение, 2014. – с. 51-52
Атанасян Л.С., Бутузов В.Ф. и др. Геометрия. 7-9 кл. 20-е изд-е. – М.: Просвещение, 2010. – с. 259-270.
Открытые электронные ресурсы:
Решу ЕГЭ образовательный портал для подготовки к экзаменам https://ege.sdamgia.ru/
Теоретический материал для самостоятельного изучения

Прямоугольная система координат в пространстве задана, если выбрана точка – начало координат, через эту точку проведены три попарно перпендикулярные прямые, на каждой из них выбрано направление (оно обозначается стрелкой) и задана единица измерения отрезков (рис. 121). Прямые с выбранными на них направлениями называются осями координат, а их общая точка – началом координат.
Координаты вектора

единичный вектор оси абсцисс, через
– единичный вектор оси ординат и через
– единичный вектор оси аппликат (рис. 124). Векторы
,
,
– назовем координатными векторами. Очевидно, эти векторы не компланарны. Поэтому любой вектор a и можно разложить по координатным векторам, т. е. представить в виде
причем коэффициенты разложения х, у, z определяются единственным образом.
Коэффициенты х, у и z в разложении вектора по координатным векторам называются координатами вектора
в данной системе координат. Координаты вектора
будем записывать в фигурных скобках после обозначения вектора:
{х; у; z}.
Нулевой вектор можно представить в виде 
Так как нулевой вектор можно представить в виде то все координаты нулевого вектора равны нулю. Далее, координаты равных векторов соответственно равны, т. е. если векторы
{х1, y1, z1} и
{х2, y2, z2) равны, то х1 = x2, y1 = y2 и z1 = z2
Рассмотрим правила, которые позволяют по координатам данных векторов найти координаты их суммы и разности, а также координаты произведения данного вектора на данное число.
1)Каждая координата суммы двух или более векторов равна сумме соответствующих координат этих векторов. Другими словами, если {х1, у1, z1} и
{х2, у2, z2} — – данные векторы, то вектор
+
имеет координаты {х1+х2, у1 + у2, z1 + z2}.
2)Каждая координата разности двух векторов равна разности соответствующих координат этих векторов. Другими словами, если {х1, y1, z1} и b{х2 у2; z2} – данные векторы, то вектор
–
имеет координаты {х1 – х2, y1 – y2, z1 – z2}.
3)Каждая координата произведения вектора на число равна произведению соответствующей координаты вектора на это число. Другими словами, если {х; у; х} – данный вектор, α – данное число, то вектор α
имеет координаты {αх; αу; αz).
1)Признак коллинеарности векторов: Для того, чтобы два вектора были коллинеарны, необходимо и достаточно, чтобы один из них был произведением другого на некоторое число.
Следствие: ненулевой вектор коллинарен вектору
тогда и только тогда, когда существует такое число α, что
=α
.
Определение: Векторы называются компланарными, если при откладывании их от одной и той же точки они будут лежать в одной плоскости.
2)Признак компланарности трех векторов: если вектор можно разложить по векторам
и
, т. е. представить в виде
= x
+ y
, где x и y — – некоторые числа, то векторы
,
и
компланарны.
Определение: Вектор, конец которого совпадает с данной точкой, а начало – с началом координат, называется радиус-вектором данной точки.
Каждая координата вектора равна разности соответствующих координат его конца и начала.
Рис. 129
Каждая координата середины отрезка равна полусумме соответствующих координат его концов.
Длина вектора вычисляется по формуле:
Примеры и разбор решения заданий тренировочного модуля
Пример 1.
Выделите цветом верный ответ:
Дано: А (2; –1; 0), В (–3; 2; 1), С (1; 1; 4); CD = -2AB.
Найти: координаты точки D.
Варианты ответов:
(3; -1; 8)
(11, –5, 2)
(-6; 3; 11)
(8; 4; 2)
Решение:
Пусть D (х; у; z)
поэтому 
Правильные ответы:
(3; -1; 8)
(11, –5, 2)
(-6; 3; 11)
(8; 4; 2)
Пример 2.
Дано: координаты точек: А (3; –1; 2), В (x; ); координаты вектора
Рис. 127
AB{5; 8; 1}
Найти: x, у, z
Решение:
Решаем уравнения и получаем: х=8; у=; z=3, z=-1
Ответ: х=8; у=; z=3, z=-1
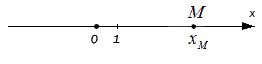
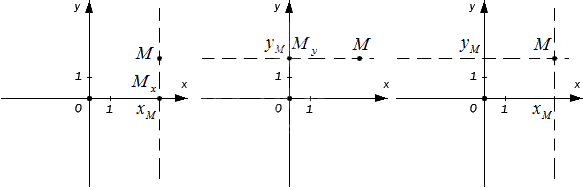
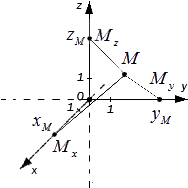




































![[mathbf{i},,mathbf{j}]=mathbf{k};](https://wikimedia.org/api/rest_v1/media/math/render/svg/a7a9e1f57b79d80f368252b33b3691aec04c19ff)
![[mathbf{j},,mathbf{k}]=mathbf{i};](https://wikimedia.org/api/rest_v1/media/math/render/svg/c0d64fcc16b5a953e286213cf5a4f955f9f5ebd4)
![[mathbf{k},,mathbf{i}]=mathbf{j}.](https://wikimedia.org/api/rest_v1/media/math/render/svg/3082939d9e2e341291d53f2ff7f49eac5a2eadeb)









