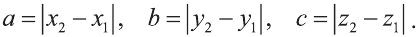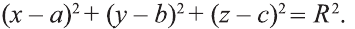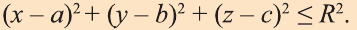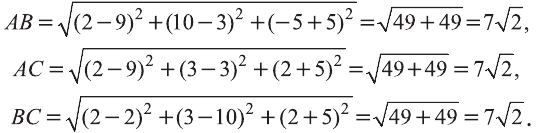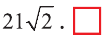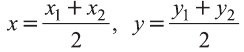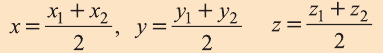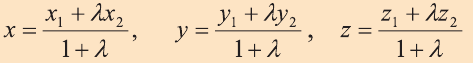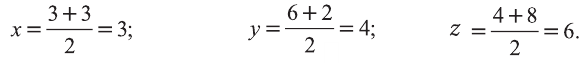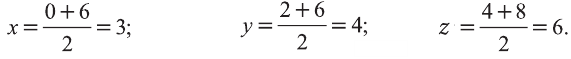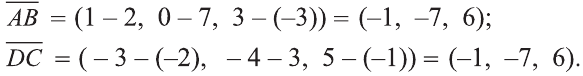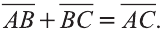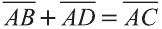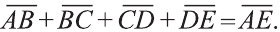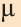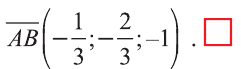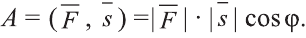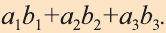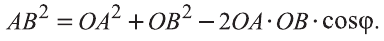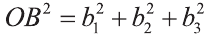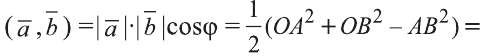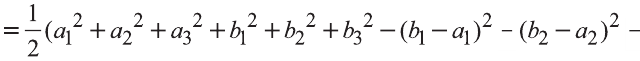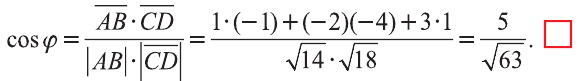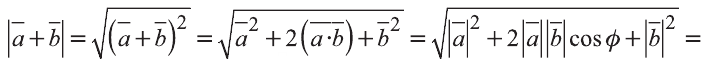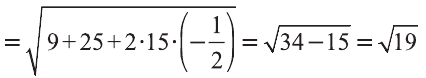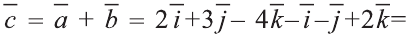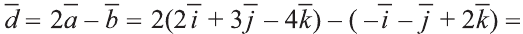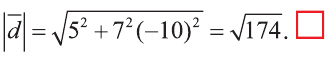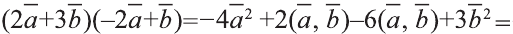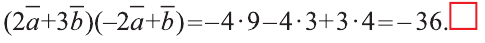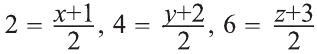Как найти координаты точек расположенных на расстоянии

Определение места по пеленгу

Если Вам необходимо найти географические координаты неизвестной точки, зная координаты двух точек и пеленг на неизвестную точку, тога этот калькулятор вам поможет. В качестве примера установлены простые числа, однако данная формула позволяет рассчитывать географические координаты в системе WGS 84 с максимальной точностью.

Введите координаты двух точек и азимуты

Как найти координаты точки по пеленгу

Углы пеленга или курса используется в области навигации самолетов, морских или транспортных средств или при работе с топографической съемкой для определения точного местоположения объекта на карте.

В качестве примера координат установлены небольшие числа, которые помогут понять как работает калькулятор, а так же на рисунке ниже обозначены заданные координаты на плоскости и углы пеленга.

Запомни! Ось Х на карте направлена на север, ось Y направлена на восток.

Пример. В качестве примера возьмем две случайные координаты, для этого воспользуемся Яндекс картами. 1-я координата X1=45.03373099391800, Y1=39.14066440251827 (аэропорт г. Краснодар). Вторая координата X2=45.11291532568151, Y2=42.10491305974482 (аэропорт г. Ставрополь). Если мы проведем вектор от аэр. Краснодар с курсом 22 градуса, и второй вектор из аэр.Ставрополь с курсом 324.5 градусов, то получим новую координату (точку пересечения двух векторов): X= 47.73696 , Y= 40.23282 (г. Шахты, Ростовской области) . Средняя дальность до новой точки составит 3.06947*100 или 306 километров.

Источник

Как получить координаты второй точки, зная координаты первой, и расстояние между ними?

точка 1 (x1,y1)
расстояние (x2,y2)

точка 2 = точка 1 + расстояние = (x1 + x2, y1 + y2)
просто складываешь всё

Есть точка А есть ее широта и долгота, я знаю что от точки А на определенном расстоянии (не большом макс 5 км), есть точка B, знаю расстояние между ними по x и y. Как мне получить координаты точки B?

знаю расстояние между ними по x и y

Алексей Аминодов-Борисов, Вот условия автора вопроса, по сути в Радиусе 5 км от точки А есть точка В но В КАКОМ МЕСТЕ этой окружности неизвестно:

Еще раз подробно:
— известна точка А есть ее широта и долгота
— я знаю что от точки А на определенном расстоянии (не большом макс 5 км), есть точка B
— знаю расстояние между ними по x и y. (диаметр окружности на которой лежит точка В)

Поэтому тут либо автор неправильно сформулировал либо вопрос в принципе некорректный.

Источник

Как найти координаты точки

Каждой точке координатной плоскости соответствуют две координаты.

Координаты точки на плоскости — это пара чисел, в которой на первом месте стоит абсцисса , а на втором — ордината точки.

Рассмотрим как в системе координат (на координатной плоскости):

• находить координаты точки;
• найти положение точки.

Чтобы найти координаты точки на плоскости, нужно опустить из этой точки перпендикуляры на оси координат.

Точка пересечения с осью « x » называется абсциссой точки « А », а с осью y называется ординатой точки « А ».

Обозначают координаты точки, как указано выше (·) A (2; 3) .

Пример (·) A (2; 3) и (·) B (3; 2) .

На первом месте записывают абсциссу (координату по оси « x »), а на втором — ординату (координату по оси « y ») точки.

Особые случаи расположения точек

1. Если точка лежит на оси « Oy », то её абсцисса равна 0 . Например,
   точка С (0, 2) .
2. Если точка лежит на оси « Ox », то её ордината равна 0 . Например,
   точка F (3, 0) .
3. Начало координат — точка O имеет координаты, равные нулю O (0,0) .

Как найти положение точки по её координатам

Найти точку в системе координат можно двумя способами.

Первый способ

Чтобы определить положение точки по её координатам,
например, точки D (−4 , 2) , надо:

1. Отметить на оси « Ox », точку с координатой « −4 », и провести через неё прямую перпендикулярную оси « Ox ».
2. Отметить на оси « Oy », точку с координатой 2 , и провести через неё прямую перпендикулярную оси « Oy ».
3. Точка пересечения перпендикуляров (·) D — искомая точка. У неё абсцисса равна « −4 », а ордината равна 2 .

Второй способ

Чтобы найти точку D (−4 , 2) надо:

1. Сместиться по оси « x » влево на 4 единицы, так как у нас
   перед 4 стоит « − ».
2. Подняться из этой точки параллельно оси y вверх на 2 единицы, так как у нас перед 2 стоит « + ».

Чтобы быстрее и удобнее было находить координаты точек или строить точки по координатам на листе формата A4 в клеточку, можно скачать и использовать готовую систему координат на нашем сайте.

Источник

Русские Блоги

Найти азимут и расстояние на основе широты и долготы двух точек и т. Д.

Небольшая вещь, которую я сделал недавно, использует вычисление широты и долготы. То, что я вижу на китайской веб-странице, это в основном группа «кирпичей», которые любят слова, как золото, или они похожи на пластыри. Было выложено много кода, и не было никакого объяснения, это сбивало с толку, и некоторые люди понимали это долгое время.В результате использованная им формула была либо ограничена в использовании (но без небольшого утверждения), либо она была просто неправильной. Так что теперь я подведу итог тому, что я узнал за несколько дней, чтобы позже люди стали меньше обходить.

Здесь рассматриваются четыре основных вопроса:

1. Учитывая широту и долготу двух точек, найдите расстояние между двумя точками;

2. Зная широту и долготу двух точек, найдите курс одной точки относительно другой;

3. Знать широту и долготу одной точки, расстояние и направление от другой точки, и найти широту и долготу другой точки;

Общее утверждение:

Поскольку эксцентриситет земли чрезвычайно низок, земля рассматривается здесь как сфера. Использование всех следующих формул в применимом диапазоне может гарантировать, что отклонение вычисленного результата от измерения в системе координат WGS84 не превышает 0,5%. Что касается Ду Ньянга, некоторые люди сказали, что необходимо преобразовать координаты WGS84 в Пекин 54 и Сиань 80, а затем рассчитать их. Моя точка зрения: пока это не геодезическая съемка, гражданское строительство, запуск ракеты или восстановление пилотируемого космического корабля, это просто Нет необходимости делать это, пожалуйста, воспользуйтесь этим словарным запасом, полным самого профессионального словаря, но даже формула расчета расстояния в системе координат WGS84 не может дать кирпичи и миномет «как далеко за горизонтом, просто переверни меня далеко». Название метода для удобства написания. Не обсуждайте его с другими как официальное название. Поскольку этот человек неглубокий и неуклюжий и плохо рассчитывает, ошибки неизбежны. Если они будут найдены, они будут исправлены вовремя. Пожалуйста, прости меня.

Для метода расчета расстояния и курса в системе координат WGS84, если вам нужен точный расчет, пожалуйста, нажмите ниже для просмотра

Больше информации, пожалуйстаGoogle Vincenty’s formula

Для системы координат WGS84, пожалуйста, нажмите на следующее:

Прежде чем рассчитать, мы сначала выполняем символ и единицуобещание：

Установите здесь, чтобы найти заголовок B относительно A, то есть A — текущая позиция, а B — целевая позиция

Aj: долгота в точке A

Aw: широта точки A

Bj: долгота в точке B

Bw: широта точки B

Северная широта положительная, южная широта отрицательная, восточная долгота положительная, западная долгота отрицательная

Широта и долгота используют десятичную систему, то есть.DDD.DDDDDD °, а не градусы или минуты.

Степени указаны без угла

A, B, C представляют три точки на сфере и угол между «дугой» на сфере, а положение C — северный полюс

a, b, c представляет угол между двумя точками «дуги» в трех точках A, B и C, соединенных с центром земли (фактически, удобнее интерпретировать дугу трех точек ABC к дуге)

L: сферическое расстояние между двумя точками AB, также называемое расстоянием большого круга, то есть длиной нижней дуги AB в дуге, создаваемой пересечением плоскости и сферы с тремя точками AOB

R: средний радиус земли

Подшипник: начальный истинный курс, также называемый стартовым курсом Великого круга Начните с истинного севера на 0 градусов и поверните на 360 градусов по часовой стрелке с востока на юг на запад.

(Примечание: я написал азимут Азимут в предыдущей статье, но поскольку слово склонно к недоразумению, на этот раз оно было изменено на Подшипник, то есть требуемый угол здесь не «географический относительный азимут», а «плавание» «Направление» также является «углом между касательной дуги L в точке A и истинным северным направлением». Например, давайте установим долготу и широту точки A: 40 ° с.ш., 10 ° E; долготу и широту точки B: 40 ° с.ш., 100 ° E. Очевидно, что точка B находится на 90 ° к востоку от точки A, но если кто-то идет в точку B с кратчайшим расстоянием от точки A, он должен идти в направлении 57.2676 ° в точке A, а затем постепенно менять курс (только измеренный Курс изменился, но он все еще находится в этой большой круговой плоскости.) Когда он, наконец, достиг точки B, направление ходьбы составило 122.7324 °. Здесь 57.2676 ° — это то, что я называю «первоначальным истинным курсом». Еще один противоположный этой концепции Заголовок называется заголовком строки заголовка. Для получения более подробной информации см. Google: прямая линия. В настоящее время расстояние линии заголовка и расчет заголовка линии заголовка в настоящее время не обсуждаются.)

(Примечание: я не обратил внимания на случай буквы C, потому что мне его не хватало, поэтому я напоминаю читателю обратить внимание на случай C в приведенной ниже формуле.

Для некоторых приемников GPS формат данных — NMEA-0183, а стиль сообщения широты и долготы — DDDMM.MMMM. Его необходимо преобразовать в десятичную систему. Формула:

Широта и долгота (градусы) = DDD + MM.MMMM / 60)

Во-первых, расчет расстояния

Метод 1, формула сферического косинуса

Сфера применения:Теоретически, этот метод подходит для расчета расстояния между любыми двумя точками на сфере, но поскольку в формуле есть термин cos, когда точность работы системы с плавающей запятой не высока, расстояние между двумя точками, которые находятся ближе, будет Есть большие ошибки (64-битные системы обычно не должны беспокоиться об этом).

Принимая во внимание:Aj，Aw，Bj，Bw，R

Искомое количество:

Шаг 1: Зная широту и долготу точки AB, используйте первую формулу, формулу сферического косинуса,

Здесь угол C равен углам A

B, который является двугранным углом между гранью AOC и гранью BOC, которая является Bj-Aj.

Здесь мы подставляем известные данные и формула записывается в виде:

После нахождения косинуса с, обратная функция косинуса может быть использована для нахождения угла с.

Найти расстояние после поворота угла в радианы

Обратите внимание, что здесь единица L такая же, как и единица R. Не забудьте преобразовать, если эти единицы разные. Кроме того, порядок последнего Bj-Aj здесь не имеет значения, поскольку значение симметрии оси Y функции cos одинаково.

Метод 2. Метод Хаверсайна

Сфера применения:Этот метод подходит для вычисления расстояния между любыми двумя точками на сфере. Со знанием математики в средней школе можно доказать, что этот метод является преобразованием функции сферического косинуса. Поскольку заменен термин cos, системы для вычисления на коротком расстоянии не существует Проблемы чрезмерной точности расчетов.

Принимая во внимание:Aj，Aw，Bj，Bw，R

Искомое количество:

Подставляя известные данные, формула записывается в виде

Здесь для удобства записи обратная функция синуса приведенной выше формулы рассчитывается в радианах.

Для получения этой формулы, пожалуйста, нажмите здесь:Haversine formula

Подробнее об этом методе, пожалуйстаGoogle Haversine

Метод 3. Метод декартовой системы координат

Сфера применения:Поскольку сферические координаты преобразуются в прямоугольные координаты и используется теорема Пифагора, их можно использовать только тогда, когда две точки находятся близко друг к другу: чем выше широта, тем уже диапазон использования.

Принимая во внимание:Aj，Aw，Bj，Bw，R

Искомое количество:

Основная идея упрощенного алгоритма состоит в том, чтобы преобразовать сферические координаты, выраженные в широте и долготе, в трехмерные прямоугольные координаты, а затем использовать знание геометрии твердого тела для ее решения.

Пусть: Xa, Ya, Za — координаты точки A в трехмерных прямоугольных координатах, а координаты точки B совпадают,

Ha — это высота в точке A, а Hb — это высота в точке b.

(Примечание: координаты здесь преобразуются в упрощенную форму формулы индукции. Формула для преобразования сферических координат в прямоугольные координаты можно посмотреть здесь:Сферические координаты в декартовых координатах）

ΔX=Xa-Xb ΔY=Ya-Yb ΔZ=Za-Zb

Зная разницу в направлениях трех координатных осей, а затем используя теорему Пифагора, можно получить расстояние между двумя точками, а именно:

Здесь мы объясняем, что высота H является необязательной, если она есть, обратите внимание на единство H и R. Высота, заданная обычными приемниками GPS, как правило, неточная, поэтому не рекомендуется. Кроме того, две величины в сообщении спецификации NMEA относятся к высоте. Обратите внимание на расчет.

(Примечание: L, рассчитанный здесь, на самом деле можно рассматривать как длину хорды, а длину дуги можно получить, комбинируя R с обратной тригонометрической функцией, но она выглядит немного «дополнительной». Лучше использовать два предыдущих метода, чтобы найти длину дуги.)

Расчет курса

Метод 1, формула сферического синуса

Сфера применения:Теоретически эту формулу можно использовать для расчета курса между любыми двумя точками на земле, но угол, полученный этим методом, находится в «постобработке»дефекты(Причина и решение проблемы будут объяснены позже), и поскольку используется косинусное значение формулы сферического синуса, оно также предъявляет высокие требования к точности операций системы с плавающей запятой, поэтомуЭтот метод не рекомендуется, Если он будет использоваться, этот метод может использоваться только на небольшом расстоянии: низкие широты рекомендуются ниже 300 км, средние широты рекомендуются ниже 100 км, а высокие широты рекомендуются ниже 40 км.

Принимая во внимание:Aj，Aw，Bj，Bw

Решение:

В «Способе 1» «Вычисления расстояния» получено значение косинуса угла c, и требуется его значение синуса. Используемая формула является модификацией самой основной функции преобразования синуса и косинуса в тригонометрической функции.

После нахождения синуса, мы будем использовать менее часто используемую формулу, формула сферического синуса

Подставьте известные данные и слегка деформируйте их. Формула записывается в виде:

Используя функцию arcsine, чтобы найти угол, приведенная выше формула записывается в виде

Здесь следует отметить, что наше первоначальное предположение состояло в том, чтобы найти заголовок точки B относительно точки A, так что здесь Bj-Aj. Не пишите обратное, иначе вы не получите правильный результат позже.

Считая здесь, он не является полным, и полученные результаты не всегда соответствуют нашему определению заголовка, поэтому мы должны обсудить четыре квадранта и две оси в соответствии с положением B относительно A, и выполнить различную обработку результатов расчета в зависимости от различных ситуаций. , Предполагая, что точка A зафиксирована в начале координат, тогда:

Точка B находится в первом квадранте, Bearing = A;

B находится во втором квадранте, Подшипник = 360 + A;

B находится в третьем и четвертом квадранте, а подшипник = 180-A.

Здесь упоминаются только результаты обсуждения квадранта, поскольку обсуждение по оси является более сложным и должно рассматриваться в сочетании с операционной средой программы. Основным фактором, который рассматривается, является точность расчета системы. Например, в формуле косинуса трехгранного угла, когда значение широты точки AB одинаково, термин, определяющий значение формулы, равен cos (Bj-Aj). Когда значение Bj-Aj относительно мало, например 0,0001 (это в Соответствующая длина в экваториальной области составляет около 11 м.) Значение времени рассчитывается с помощью общего калькулятора, поэтому последующие вычисления не могут быть завершены. Однако, если вычислить с помощью компьютера, это 0,999999999998476913 . Поэтому, исходя из вышеуказанных причин, необходимо «расширить диапазон оси» оси, и особое внимание следует уделить использованию однокристальных компьютеров и мобильных телефонов.

После серии расчетов был получен окончательный результат.

На данный момент вышеописанный метод — это метод, который я написал в начале, а окончательный результат обсуждался в зависимости от ситуации. Кажется, в этом нет ничего плохого. Фактически, это подквадрантное обсуждение делает этот метод более не совершенным, потому что результат в полярном Ошибочно обсуждать это в прямоугольных координатах. Ещё каштан отдай

(белые линии — линии долготы и широты, желтые линии — кратчайший путь AB)

Широта и долгота точки A: 40 ° с.ш., 80 ° в.д. Широта и долгота точки B: 37,55 ° с.ш., 120 ° в.д.

Согласно вышеописанному способу точка B должна находиться в четвертом квадранте, то есть курс должен составлять 98,53 °, но на самом деле, чтобы перейти от точки A к точке B, она должна сначала идти в направлении 81,4651 °. Поэтому можно сказать, что в приведенном выше обсуждении квадранта Это полная ошибка (хотя эта ошибка очень мало отклоняется от фактического значения на коротком расстоянии), и расширение диапазона оси усугубило эту ошибку. В настоящее время результат «синусоидальной дуги» «метода Хаверсайна» в «Вычислении расстояния» может быть слегка обработан для замены результата косинуса, полученного по формуле сферического косинуса, тем самым исключая расширение оси, но до сих пор я не нашел Вышеуказанные результаты воплощаются в разумный подход, который соответствует определению заголовка.

Метод 2: Метод плоской прямоугольной системы координат

Сфера применения:Моя основная идея этого метода состоит в том, чтобы преобразовать разницу долготы и широты в расстояние от земли, а затем использовать знание геометрии плоскости для ее решения, поэтому его можно использовать только для расчета на короткие расстояния. Рекомендуется, чтобы средняя широта была меньше 40 км. Поскольку вычисления проще, они относительно выгодны.

Принимая во внимание:Aj，Aw，Bj，Bw

Решение:

Точка B находится в первом квадранте и положительной полуоси оси Y, Bearing = A;

B находится во втором квадранте, Подшипник = 360 + A;

B находится в третьем и четвертом квадрантах и ​​отрицательной полуоси оси Y, а Bearing = 180 + A.

Для некоторых систем достаточно установить значение B на положительной и отрицательной полуосях по отдельности, и некоторые системы могут вернуть arctan (X / 0) = 90.

Метод 3, метод полярных координат

Сфера применения:Этот метод может быть использован для расчета курса между любыми двумя точками на земле, без каких-либо ограничений и дефектов. (По крайней мере, я еще не нашел)

Принимая во внимание:Aj，Aw，Bj，Bw

Решение:

Я изучил этот метод из других источников. Для доказательства этого метода, пожалуйста, нажмите здесь:Найти заголовок

Поскольку ввод естественных формул слишком утомителен для меня, как для ленивого человека, вот только идея его доказательства: его идея — поместить Землю в сферическую систему координат и соответствующим образом отрегулировать начальные точки трех параметров, чтобы уменьшить спину. Затем точки преобразуются из сферических координат в прямоугольные координаты, и затем двугранный угол, который является курсом, вычисляется в соответствии с теоремой о плоском нормальном векторе, а затем преобразуется в градусы, соответствующие определению курса.

Определите 3 временные переменные x, y, A перед вычислением

Подставим полученные значения x и y в следующую функцию

atan2 Эта функция является относительно редкой. Фактически это набор прямоугольных координат в метод полярных координат. Если эта функция доступна в библиотеке функций программы, вы можете сэкономить время, чтобы сделать ее более значимой Дело в том, что если вы не можете найти имя функции, нажмите здесь:функция atan2Напишите функцию, которая реализует эту функцию самостоятельно в соответствии с методами, перечисленными в ней.

После получения A наступает очень важный шаг, и функция MOD находит остаток.

Таким образом, вы получите результаты, которые соответствуют определению заголовка.

(Примечание: при вызове функции MOD обязательно посмотрите определение MOD на используемом языке. Здесь вам нужно определить его в соответствии со следующей формулой.

Если нет, вам нужно написать свое собственное утверждение для реализации вышеупомянутой функции MOD. Когда вы пишете свое собственное утверждение, вы должны увидеть определение функции INT на своем языке при использовании функции INT. Функция INT должна быть округлена вниз вместо округления или Округлить )

В-третьих, расчет долготы и широты второй точки

В последнее время я видел много людей в Интернете, спрашивающих о расчете второй долготы и широты, поэтому я также добавлю метод расчета здесь.

Один из самых глупых способов, который вы можете придумать, — это решить уравнения одновременно, используя формулы, использованные в предыдущих двух частях. Я думаю, что только специалисты из Du Niang знают этот метод (потому что этот метод стоит меньше всего плюнуть)。

Ближе к дому метод решения уравнения в порядке, но объем вычислений огромен и занимает много времени, что нереально для некоторых систем.

Метод 1, метод сферической тригонометрической функции

Сфера применения:Этот метод фактически является повторным применением «вычисления курса» и «формулы сферического синуса». До сих пор не было найдено никаких ограничений, потому что нет обсуждения квадрантов, поэтому не возникает ошибок низкого уровня, которые конфликтуют между двумя системами координат.

Принимая во внимание:Aj，Aw，L，R，Bearing

Решение:

Сначала найдите с,

(Обратите внимание, что единицы L и R должны быть объединены здесь)
После решения a подставьте известное количество в формулу:

После решения A мы решаем C,

Я должен был понять все здесь.

PS: Для понимания вышеупомянутых двух треугольных формул мы можем думать о точке A как о северном полюсе.

В-четвертых, наконец-то плевать

GFW раздражает, даже если вы поворачиваете %% наружу и %% к стене, вам все равно понадобится стена, когда вы вернетесь. Ваши студенты в Бейю помогают вашему мозгу.

Блог sina — это место, которое подходит только для политических обид и сплетен персикового цвета, и не подходит для рассылки научно-популярных учебников. Функция редактирования — просто подонок.

Из-за вышеупомянутых двух моментов я повторил эту статью 4 раза, прежде чем окончательно сохранил результаты.

Дата последнего изменения: 2014.4.28

(Du Niang знает источник ctrl + c партийной копии дяди. Все права защищены.)

Источник

Решение задач по математике у учащихся часто сопровождается многими трудностями. Помочь учащемуся справиться с этими трудности, а так же научить применять имеющиеся у него теоретические знания при решении конкретных задач по всем разделам курса предмета «Математика» – основное назначение нашего сайта.

Приступая к решению задач по теме «Расстояние между двумя точками на плоскости», учащиеся должны уметь строить точку на плоскости по ее координатам, а так же находить координаты заданной точки.

Вычисление расстояния между взятыми на плоскости двумя точками А(х_А; у_А) и В(х_В; у_В), выполняется по формуле d = √((х_А –  х_В)² + (у_А – у_В)²), где d – длина отрезка, который соединяет эти точки на плоскости.

Если один из концов отрезка совпадает с началом координат, а другой имеет координаты М(х_М; у_М), то формула для вычисления d примет вид ОМ = √(х_М² + у_М²).

1. Вычисление расстояния между двумя точками по данным координатам этих точек

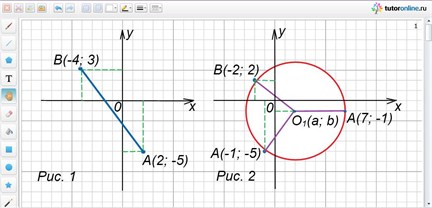
Пример 1.

Найти длину отрезка, который соединяет на координатной плоскости точки А(2; -5) и В(-4; 3) (рис. 1).

Решение.

В условии задачи дано: х_А = 2;  х_В = -4; у_А = -5 и у_В = 3. Найти d.

Применив формулу d = √((х_А – х_В)² + (у_А – у_В)²), получим:

d = АВ = √((2 – (-4))² + (-5 – 3)²) = 10.

2. Вычисление координат точки, которая равноудалена от трех заданных точек

Пример 2.

Найти координаты точки О₁, которая равноудалена от трех точек А(7; -1) и В(-2; 2) и С(-1; -5).

Решение.

Из формулировки условия задачи следует, что О₁А = О₁В = О₁С. Пусть искомая точка О₁ имеет координаты (а; b). По формуле d = √((х_А – х_В)² + (у_А – у_В)²) найдем:

О₁А = √((а – 7)² + (b + 1)²);

О₁В = √((а + 2)² + (b – 2)²);

О₁С = √((а + 1)² + (b + 5)²).

Составим систему из двух уравнений:

{√((а – 7)² + (b + 1)²) = √((а + 2)² + (b – 2)²),
{√((а – 7)² + (b + 1)²) = √((а + 1)² + (b + 5)²).

После возведения в квадрат левой и правой частей уравнений запишем:

{(а – 7)² + (b + 1)² = (а + 2)² + (b – 2)²,
{(а – 7)² + (b + 1)² = (а + 1)² + (b + 5)².

Упростив, запишем

{-3а + b + 7 = 0,
{-2а – b + 3 = 0.

Решив систему, получим: а = 2; b = -1.

Точка О₁(2; -1) равноудалена от трех заданных в условии точек, которые не лежат на одной прямой. Эта точка – есть центр окружности, проходящей через три заданные точки (рис. 2).

3. Вычисление абсциссы (ординаты) точки, которая лежит на оси абсцисс (ординат) и находится на заданном расстоянии от данной точки

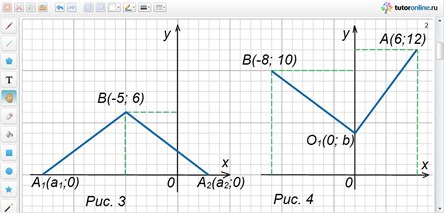
Пример 3.

Расстояние от точки В(-5; 6) до точки А, лежащей на оси Ох равно 10. Найти точку А.

Решение.

Из формулировки условия задачи следует, что ордината точки А равна нулю и  АВ = 10.

Обозначив абсциссу точки А через а, запишем А(а; 0).

По формуле d = √((х_А –  х_В)² + (у_А – у_В)²) находим:

АВ = √((а + 5)² + (0 – 6)²) = √((а + 5)² + 36).

Получаем уравнение √((а + 5)² + 36) = 10. Упростив его, имеем

а² + 10а – 39 = 0.

Корни этого уравнения а₁ = -13; а₂ = 3.

Получаем две точки А₁(-13; 0) и А₂(3; 0).

Проверка:

А₁В = √((-13 + 5)² + (0 – 6)²) = 10.

А₂В = √((3 + 5)² + (0 – 6)²) = 10.

Обе полученные точки подходят по условию задачи (рис. 3).

4. Вычисление абсциссы (ординаты) точки, которая лежит на оси абсцисс (ординат) и находится на  одинаковом расстоянии от двух заданных точек

Пример 4.

Найти на оси Оу точку, которая находится на одинаковом расстоянии от точек А(6; 12) и В(-8; 10).

Решение.

Пусть координаты нужной по условию задачи точки, лежащей на оси Оу, будут О₁(0; b) (у точки, лежащей на оси Оу, абсцисса равна нулю). Из условия следует, что О₁А = О₁В.

По формуле d = √((х_А – х_В)² + (у_А – у_В)²) находим:

О₁А = √((0 – 6)² + (b – 12)²) = √(36 + (b – 12)²);

О₁В = √((а + 8)² + (b – 10)²) = √(64 + (b – 10)²).

Имеем уравнение √(36 + (b – 12)²) = √(64 + (b – 10)²) или 36 + (b – 12)² = 64 + (b – 10)².

После упрощения получим: b – 4 = 0, b = 4.

Необходимая по условию задачи точка О₁(0; 4) (рис. 4).

5. Вычисление координат точки, которая находится на одинаковом расстоянии от осей координат и некоторой заданной точки

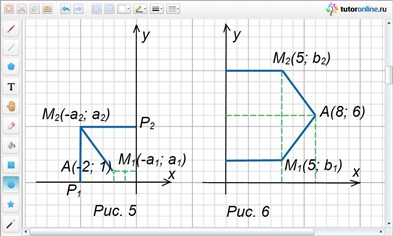
Пример 5.

Найти точку М, расположенную на координатной плоскости на одинаковом расстоянии от осей координат и от точки А(-2; 1).

Решение.

Необходимая точка М, как и точка А(-2; 1), располагается во втором координатном углу, так как она равноудалена от точек А, Р₁ и Р₂ (рис. 5). Расстояния точки М от осей координат одинаковые, следовательно, ее координатами будут (-a; a), где а > 0.

Из условия задачи следует, что МА = МР₁ = МР₂, МР₁ = а; МР₂ = |-a|,

т.е. |-a| = а.

По формуле d = √((х_А – х_В)² + (у_А – у_В)²) находим:

МА = √((-а + 2)² + (а – 1)²).

Составим уравнение:

√((-а + 2)² + (а – 1)²) = а.

После возведения в квадрат и упрощения имеем: а² – 6а + 5 = 0. Решим уравнение, найдем а₁ = 1; а₂ = 5.

Получаем две точки М₁(-1; 1) и М₂(-5; 5), удовлетворяющие условию задачи.

6. Вычисление координат точки, которая находится на одинаковом заданном расстоянии от оси абсцисс (ординат) и от данной точки

Пример 6.

Найти точку М такую, что расстояние ее от оси ординат и от точки А(8; 6) будет равно 5.

Решение.

Из условия задачи следует, что МА = 5 и абсцисса точки М равна 5. Пусть ордината точки М равна b, тогда М(5; b) (рис. 6).

По формуле d = √((х_А – х_В)² + (у_А – у_В)²) имеем:

МА = √((5 – 8)² + (b – 6)²).

Составим уравнение:

√((5 – 8)² + (b – 6)²) = 5. Упростив его, получим: b² – 12b + 20 = 0. Корни этого уравнения b₁ = 2; b₂ = 10. Следовательно, есть две точки, удовлетворяющие условию задачи: М₁(5; 2) и М₂(5; 10).

Известно, что многие учащиеся при самостоятельном решении задач нуждаются в постоянных консультациях по приемам и методам их решения. Зачастую, найти путь к решению задачи без помощи преподавателя учащемуся не под силу. Необходимые консультации по решению задач учащийся и может получить на нашем сайте.

 Остались вопросы? Не знаете, как найти расстояние между двумя точками на плоскости?
Чтобы получить помощь репетитора – зарегистрируйтесь.
Первый урок – бесплатно!

Зарегистрироваться

© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.

Veinar, я думаю, что существуют две точки, принадлежащие заданной прямой и находящиеся на заданном расстоянии от заданной плоскости. Не вдаваясь в подробности вычислений, могу предложить два способа решения задачи.

Первый способ заключается в том, что нужно найти плоскости, параллельные заданной и расположенные на заданном расстоянии от неё. Затем нужно найти точки пересечения заданной прямой с найденными плоскостями.

Второй способ заключается в том, что находится точка пересечения заданных прямой и плоскости. Затем находятся расстояния от точки [math](1,~0,~-1)[/math] до заданной плоскости и до найденной выше точки. Затем рассматриваются подобные треугольники, расположенные в плоскости, перпендикулярной заданной плоскости, и проходящей через заданную прямую.

Вроде бы так…

Содержание:

Система координат в пространстве

Декартова система координат в пространстве

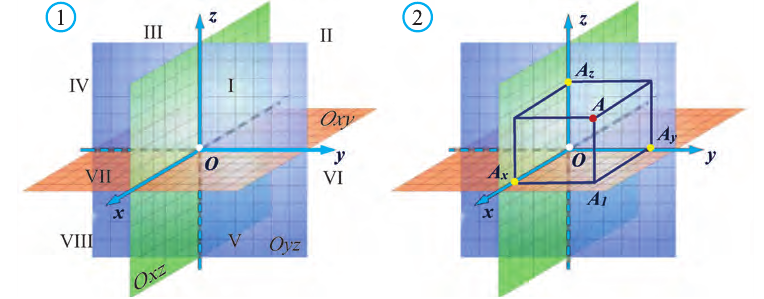
Вы познакомились с декартовой системой координат на плоскости в предыдущих классах. Систему координат в пространстве введём аналогично тому, как это было сделано на плоскости. Рассмотрим три взаимно перпендикулярных оси Ох, Оу и Оz, пересекающихся в точке О, являющейся началом координат. Через каждую пару этих прямых проведём плоскости Оху, 0xz и Оуz (рис. 1). Таким образом вводится система координат в пространстве, при этом

точку О – называют началом координат, прямые Ох, Оу и Оz — осями координат, Ох – ось абсцисс, Оу – ось ординат и Оz – ось аппликат, плоскости Оху, Оуz и Охz – координатными плоскостями.

Координатные плоскости делят пространство на 8 октант (получетвертей) (рис. 1).

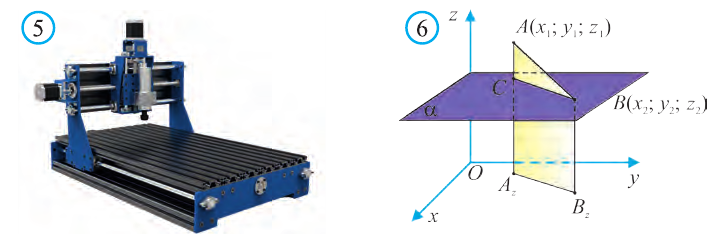
Пусть в пространстве задана произвольная точка А. Через эту точку проведём плоскости, перпендикулярные плоскостям Охz, Оуz и Охz (рис. 2). Одна из этих плоскостей пересечёт ось Ох в точке Ах.

Координату Ах на оси Ох называют координатой х или абсциссой точки А.

Аналогично определяют у – координату (ординату) и z- координату (аппликату) точки А.

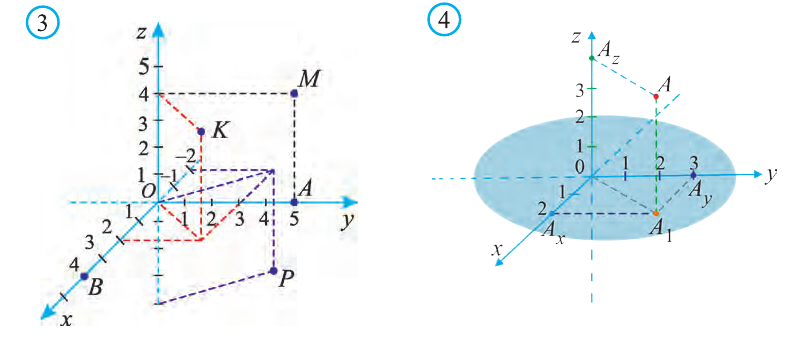
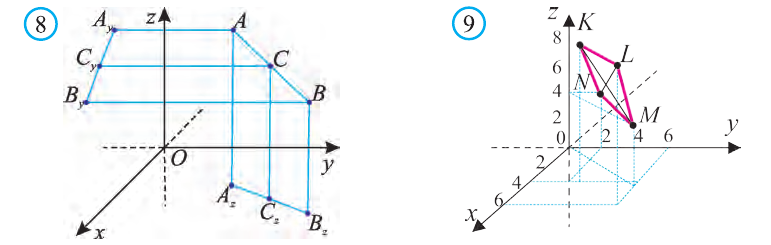
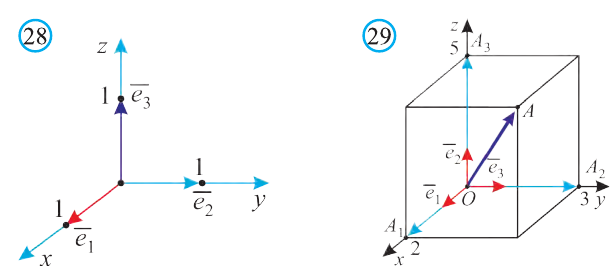
Координаты точки А записывают в виде А (х; у; z) или короче (х; у; z). Точки, изображённые на рисунке 3, имеют следующие координаты: А (0; 5; 0), B (4; 0; 0), М (0; 5; 4), К (2; 3; 4), Р (-2; 3; -4).

Пример:

Пусть в пространстве в декартовой системе координат

задана точка А (2; 3; 4). Где она расположена?

Решение:

От начала координат в положительном направлении осей Ох и Оу отложим отрезки ОА_х = 2 и ОА_у = 3 (рис. 4).

Через точку А_х проведём прямую, лежащую в плоскости Оху и параллельную оси Оу. А через точку Аy проведём прямую, лежащую в плоскости Оху и параллельную оси Ох. Точку пересечения этих прямых обозначим A₁ . Через точку A₁ проведём прямую, перпендикулярную плоскости Оху и на ней в положительном направлении Oz отложим отрезок АА₁ = 4. Тогда точка А (2; 3; 4) и будет искомой точкой.

Пользуясь системой координат, созданной для современных программируемых станков и автоматизированных роботов, составляются программы, на основе которых обрабатываются металлы (рис. 5).

Расстояние между двумя точками

Пусть заданы две точки А (х₁; у₁; z₁) и B (х₂; у₂; z₂).

1.Сначала рассмотрим случай, когда прямая АВ не параллельна оси Оz (рис. 6). Через точки А и В проведём прямые, параллельные оси Оz. И пусть они пересекают плоскость Оху в точках А_z и В_z .

Координаты х и у этих точек соответственно равны координатам х и у точек А, В, а координаты z равны 0.

Теперь через точку В проведём плоскость а, параллельную плоскости Оху. Она пересечёт прямую АА_z в некоторой точке С.

По теореме Пифагора: АВ² = АС² + СВ².

Однако

Поэтому

2.Пусть отрезок АВ параллелен оси Оz, тогда 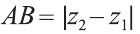и, так как

х₁= х₂ , у₁ = у₂ , мы опять приходим к вышеприведённой формуле.

Следовательно, расстояние между двумя точками А и В:

(1)

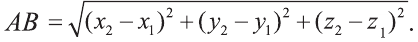
Примечание. Формула (1) выражает длину диагонали прямоугольного параллелепипеда, измерения которого равны

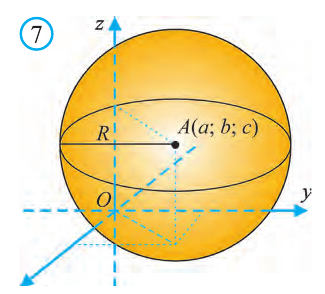
Уравнение сферы и шара

Известно, что множество всех точек М (х; у; z), расположенных на расстоянии R от данной точки А (а; Ь; с) образуют сферу (рис. 7). Тогда по формуле (1) координаты всех точек, расположенных на сфере радиуса R с центром в точке А (а; b; с), удовлетворяют равенству

Отсюда, ясно, что неравенство для точек шара радиуса R с центром в

точке А (а; b; с) имеет вид:

Пример:

Найдите периметр треугольника ABC с вершинами в

точках А (9; 3; -5), В (2; 10; -5), С (2; 3; 2).

Решение:

Р=АВ+АС+ВС периметр треугольника ABC. Воспользовавшись формулой 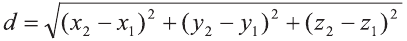расстояния между двумя точками, найдём длины сторон треугольника:

Следовательно, треугольник ABC равносторонний и его периметр .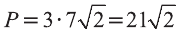

Ответ:

Координаты середины отрезка

Пусть А (x₁; y₁;z₁) и В (х₂; у₂; z₂) – произвольные точки, точка С (х; у; z) середина отрезка AB (рис. 8).

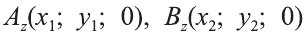
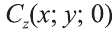
Через точки А, В и С проведём прямые, параллельные оси пересекающие плоскость Оху в точках и . Тогда по теореме Фалеса точка С_z – середина отрезка А_zВ_z.

Отсюда по формулам нахождения координат середины отрезка на плоскости

Чтобы найти координату z, нужно вместо плоскости Оху рассмотреть плоскость 0xz или Оуz.

Тогда и для z получим формулу, подобную вышеприведённой.

Аналогично, используя координаты концов A и B отрезка AB, по формулам

находят координаты точки Р(х1;у]; г,), делящей отрезок АВ в отношении X САР: РВ = X).

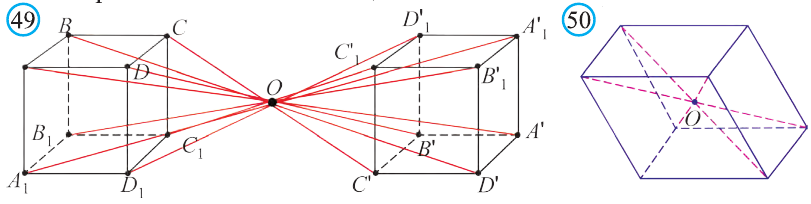
Задача 3. Докажите, что четырёхугольник МЛШЬ с вершинами М{3; 6; 4), N(0; 2; 4), К(3; 2; 8), 1(6; 6; 8) – параллелограмм (рис. 9).

Доказательство: Для решения задачи используем признак параллелограмма: Четырёхугольник, точка пересечения диагоналей которого делит их пополам, является параллелограммом.

Координаты середины отрезка МК:

Координаты середины отрезка NL:

Координаты середин отрезков МК и NL равны. Это говорит о том, что отрезки пeрeсeкаются и в точке пeрeсeчeния делятся пополам. Следовательно, четырёхугольник MNLK – параллелограмм.

В переписке с известным целителем и математиком Абу Али ибн Сино Абу Райхон Беруни задаёт следующий вопрос: «Почему Аристотель и другие (философы) называют шесть сторон?»

Рассматривая шестисторонний куб, Беруни говорит о фигурах «с другим количеством сторон» и добавляет, что «шарообразные фигуры не имеют сторон.» А Ибн Сино отвечает, что «во всех случаях нужно считать, что сторон шесть, так как у каждой фигуры, независимо от её формы, есть три измерения – длина, глубина и ширина».

Здесь Ибн Сино имеет ввиду три координаты, именуемые условно «шесть сторон».

В произведении «Канон Масъуда» Беруни приводит точное математическое определение шести сторон: «Сторон шесть, так как они ограничивают движение фигур по своим измерениям. Измерений три: длина, ширина и глубина. А их в два раза больше самих измерений.»

В предыдущих книгах автор определяет положение небесных тел с помощью двух координат относительно небесной сферы – эклиптического уравнения. Либо через те же координаты, но относительно небесного экватора или горизонта. Однако при определении взаимного расположения звёзд и небесных светил придётся учитывать и случаи затмений. Вот в таких случаях появляется необходимость в третьей сферической координате. Эта необходимость привела Беруни к отказу от теории небесных координат.

Векторы в пространстве и действия над ними

Векторы в пространстве

Понятие вектора в пространстве вводят также как на плоскости.

Вектором в пространстве называют направленный отрезок. Основные понятия, относящиеся к векторам в пространстве, аналогичны этим понятиям на плоскости: длина (модуль), направление вектора, равенство векторов.

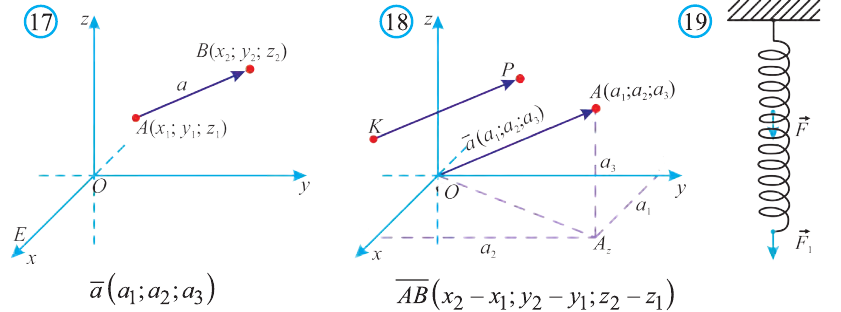
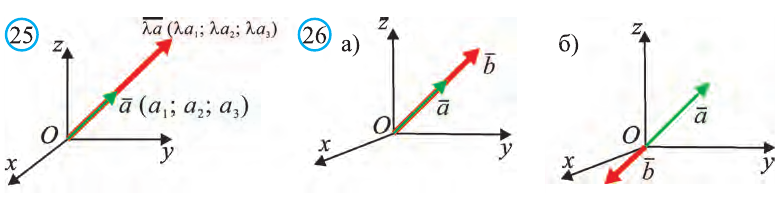
Координатами вектора с началом в точке А (х₁; у₁; z₁) и концом в точке В (х₁; у₁; z₁) называют числа 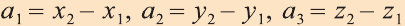, (рис. 17).

Приведем без доказательства свойства векторов, аналогичных свойствам на плоскости.

Также как на плоскости, соответствующие координаты равных векторов равны и, обратно, векторы с равными координатами равны.

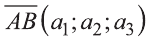
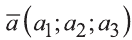
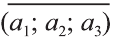
Hа основании этого вектор можно обозначить как или или кратко (рис. 18).

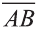
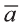
Вектор можно записать и без координат (или ). В этой записи

на первом месте начало вектора, а на втором – конец.

Вектор с координатами, равными нулю, называют нулевым вектором и обозначают 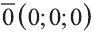или , направление этого вектора не определено.

Если начало вектора расположено в начале координат О, а числа а₁,

а₂ и а₃ – координаты точки А, то есть А (а₁; а₂; а₃), то эти же числа будут

координатами вектора 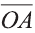: (а₁; а₂; а₃).

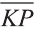
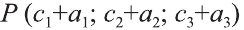
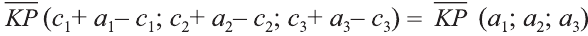
Однако вектор в пространстве с началом в точке К(с₁; с₂; с₃) и концом в точке будет иметь те же координаты: .

Отсюда следует, что вектор можно приложить к любой точке пространства. В геометрии мы рассматриваем такие свободные векторы. Но в физике, обычно вектор связан с некоторой точкой. Например, воздействие силы приложенная к пружине F на рисунке 19 зависит от точки её приложения.

Длинной вектора называют длину направленного отрезка

изображающего его (рис. 17). Длину вектора 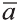записывают

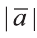
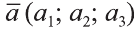
так. Длина вектора , заданного координатами,

вычисляется по формуле .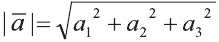

Пример:

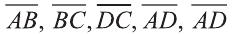
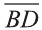
Даны точки А (2; 7;-3),В (1; 0; 3), С (-3;-4; 5) и D (-2; 3; -1). Какие из векторов и равны между собой?

Решение:

У равных векторов равны соответствующие координаты. Поэтому найдём координаты векторов:

Следовательно, .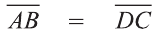

Докажите самостоятельно, что

Действия над векторами в пространстве

Действия над векторами. Сложение векторов, умножение на число и их скалярное произведение определяется также как на плоскости.

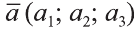
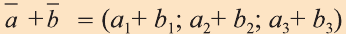
Суммой векторов и (b₁; b₂; b₃); называют вектор (рис. 20).

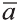
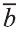
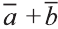
Пусть кран на рисунке 20.b движется вдоль вектора , а груз относительно крана вдоль вектора . В результате груз движется вдоль вектора . Поэтому из рисунка 20.с, на котором изображён сюжeт басни русского писателя И.А.Крылова, ясно, что герои басни не смогут сдвинуть телегу с места.

Свойства суммы векторов

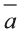
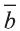
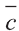
Для любых векторов , и имеют место следующие свойства:

a) – переместительный закон сложения векторов;

b) – распределительный закон сложения.

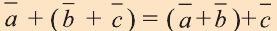
Правило треугольника сложения векторов

Для любых точек А, В и С (рис. 21):

Правило параллелограмма сложения векторов

Если АВСD – параллелограмм (рис. 22), то

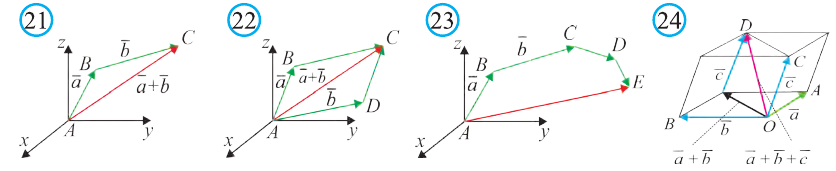
Правило многоугольника сложения векторов

Если точки А, В, С, D и Е – вершины многоугольника (рис. 23), то

Правило параллелепипеда сложения трёх векторов, не лежащих в одной плоскости. Если АВСDА₁В₁С₁D₁ параллелепипед (рис. 24), то

.

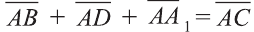
Вектор ​​​​​​= (a1; a₂; a₃) – называют умножением вектора

(a₁; a₂; a₃) на число (рис. 25). Свойства операции умножения вектора на число.

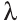
Для любых векторов и и чисел и

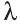
а);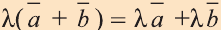

b);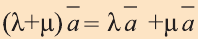

c)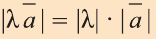 и направление вектора

совпадает с направлением вектора , если ,

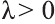
противоположно направлению вектора , если .

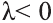
Коллинеарные и компланарные векторы

Пусть заданы ненулевые векторы и . Если векторы

и сонаправлены или противоположно направлены,

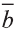
то их называют коллинеарными векторами (рис. 26).

Свойство 1. Если для векторов и имеет место равенство , то они коллинеарны и наоборот.

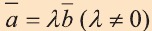
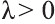
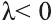
Если , то векторы и сонаправлены , если, то

противоположно направлены .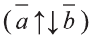

Свойство 2. Если векторы (a₁; a₂; a₃) и (b₁; b₂; b₃) коллинеарны,

то их соответствующие координаты пропорциональны:

и наоборот.

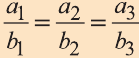
Пример:

Найдите вектор с началом в точке А (1; 1; 1) и концом в точке В, лежащей в плоскости Оху, коллинеарный вектору ( 1; 2; 3).

Решение:

Пусть точка В имеет координаты В (х; у; z). Так как точка В лежит в плоскости Оху, то z=0. Тогда (х – 1 ;у – 1; – 1).

По условию задачи векторы (х – 1 ;у – 1; – 1) и (1, 2, 3) коллинеарны. Следовательно, их координаты пропорциональны.

Тогда получаем следующие пропорции .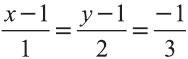

Откуда находим , .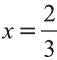

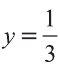
Итак,

Векторы, лежащие в одной плоскости или параллельных плоскостях, называют компланарными векторами (рис. 27).

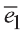
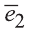
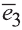
Векторы (1; 0; 0), (0; 1; 0) и (0; 0; 1) называют ортами (рис. 28).

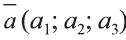
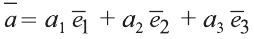
Любой вектор можно единственным образом разложить по ортам, то есть представить в виде (рис. 29).

Точно также, если заданы три нeкомпланарных вектора и , то любой вектор можно единственным образом представить в виде:

.

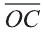
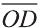
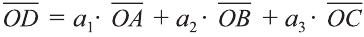
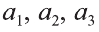
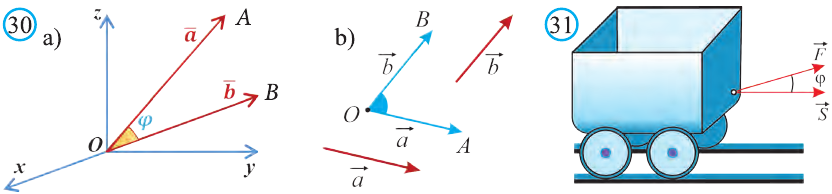
Здесь некоторые действительные числа. Тогда говорят, что вектор разложен по заданным векторам.

Скалярное произведение векторов

Углом между ненулевыми векторами и называют угол между направленными отрезками векторов = и =, исходящих из точки О (рис. 30).

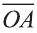
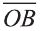
Угол между векторами и обозначают так .

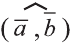
Скалярным произведением векторов и называют произведение длин этих векторов на косинус угла между ними.

Если один из векторов нулевой, то скалярное произведение этих векторов равно нулю.

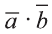
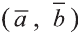
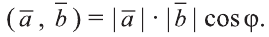
Скалярное произведение обозначают или . По определению (1)

Из определения следует, что если скалярное произведение векторов и равно нулю, то эти векторы перпендикулярны и наоборот.

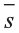
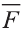
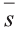
В физике работа A, выполненная при движении тела на расстоянии , под воздействием силы (рис. 31), равна скалярному произведению силы на расстояние:

Свойство. Если 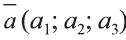и (b₁; b₂; b₃), то () =

Доказательство. Приложим векторы 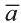и к началу

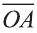
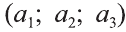
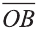
координат О (рис.32). Тогда = и = (b₁; b₂; b₃).

Если векторы неколлинеарны, то получаем треугольник АВО , для которого справедлива теорема косинусов.

Тогда .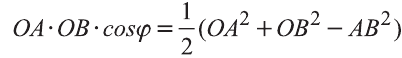

Однако, ,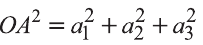

и .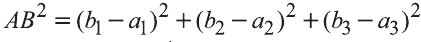

Следовательно,

.

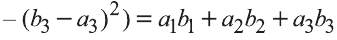
Самостоятельно докажите, что и в случае, когда данные векторы коллинеарны , также выполняется

это равенство.

Свойства скалярного произведения векторов

1. – переместительное свойство.

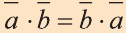
2. – распределительное свойство.

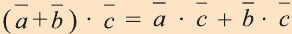
3. – сочетательное свойство.

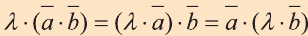
4.Если векторы а и b являются сонаправленными коллинеарными

векторами, то 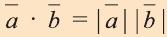, так как соs 0° = 1.

5.Если же векторы противоположно направлены, то 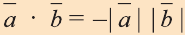, так как cos l80° = -1.

6. .

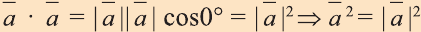
7. Если вектор перпендикулярен вектору , то . Следствия: а) Длина вектора ; (1) b) косинус угла между векторами

: ; (2)

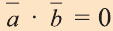
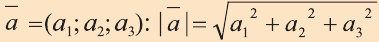
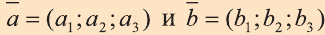
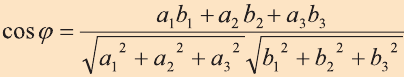
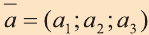
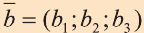
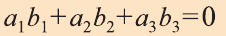
с) условие перпендикулярности векторов и

.

(3)

Пример:

– заданные точки. Найдите косинус угла между векторами .

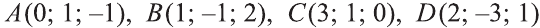
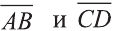
Решение:

Найдём длины векторов :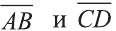

,

.

,

.

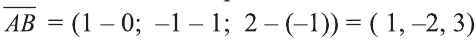
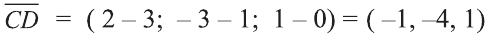
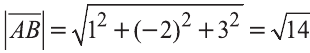
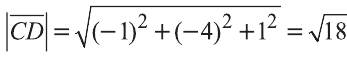
Следовательно,

Пример:

Найдите угол между векторами .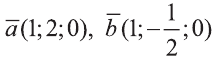

Решение:

Итак,

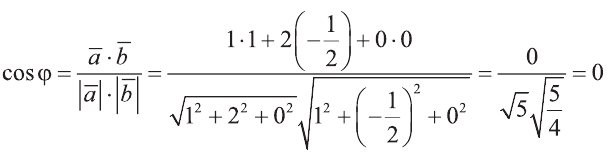
Пример:

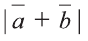
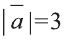
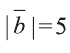
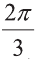
Найдите , если , и угол между векторамии равен .

Решение:

Пример:

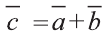
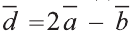
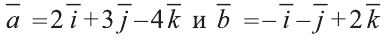
Найдите координаты и длины векторов 1); 2), если .

Решение:

Подставим в выражения искомых векторов разложения векторов и по координатам:

1)

. Следовательно,.

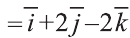
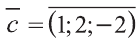
Тогда.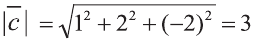

2)

.

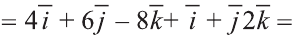
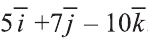
Следовательно, .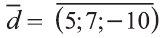

Тогда

• Заказать решение задач по высшей математике

Пример:

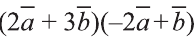
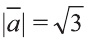
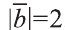
Найдите произведение, если угол между векторами и равен 30° и , .

Решение:

Сначала найдём поизведение векторов и :

.

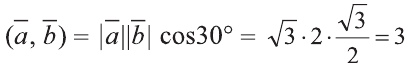
Затем перемножим заданные выражения как многочлены

и, пользуясь распределительным свойством умножения

вектора на число, получим:

.

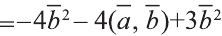
Учитывая, что ,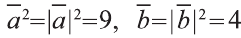

найдём искомое произведение

Преобразование и подобие в пространстве

Геометрические преобразования в пространстве

Если каждую точку заданной в пространстве фигуры F изменить одним и тем же способом, то получим фигуру F_1. Если при этом преобразовании различные точки первой фигуры переходят в различные точки второй, то говорят о преобразовании геометрической фигуры.

Если рассматривать все пространства как геометрическую фигуру, то также можно говорить о преобразовании геометрической фигуры.

Понятие геометрического преобразование в пространстве вводят также как на плоскости. Следовательно, свойства некоторых рассматриваeмых ниже видов преобразований и их доказательства также подобны соответствующим им на плоскости. Поэтому, мы не будем доказывать их и рекомендуем провести их самостоятельно.

Движение и параллельный перенос

Преобразование фигур, при котором сохраняются расстояния между точками, называют движением. Можно привести следующие свойства движения. При движении прямая переходит в прямую, луч – в луч, отрезок – в равный ему отрезок, угол – в равный ему угол, треугольник – в равный ему треугольник, плоскость – в плоскость, тетраэдр – в равный ему тетраэдр.

В пространстве фигуры, которые можно перевести одну в другую при некотором движении называют равными фигурами.

Простейшим примером движения является параллельный перенос.

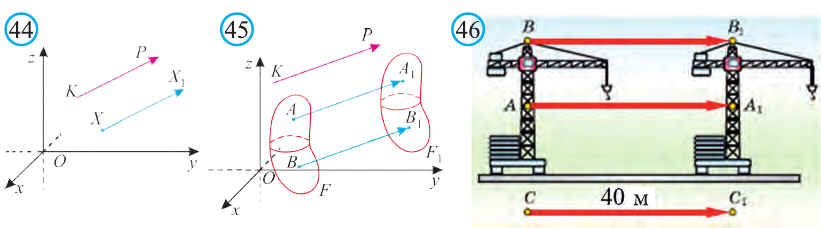
Пусть в пространстве даны вектор и произвольная точка Х

(рис. 44). Говорят, что точка Х перешла в точку X₁ параллельным

переносом на вектор , если выполняется условие . Если каждую точку фигуры F сдвинуть на вектор при помощи параллельного переноса (рис. 45), то получим фигуру F₁. Тогда говорят, что фигура F получена параллельным переносом фигуры F₁ . При параллельном переносе каждая точка фигуры F сдвигается в одном и том же направлении на одно и то же расстояние.

Каждая точка подъёмного крана, изображённого на рисунке 46, параллельно перенесена на 40 м относительно начального положения.

Ясно, что параллельный перенос является движением. Поэтому прямая переходит в прямую, луч – в луч, плоскость – в плоскость,

и т. д.

Пусть точка 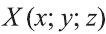фигуры F перешла в точку

фигуры F₁ при помощи параллельного переноса

на вектор .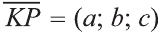

Тогда по определению получим:

или

.

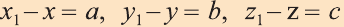
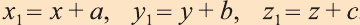
Эти равенства называют формулами параллельного переноса.

Пример:

В какую точку перейдёт точка Р (-2; 4; 6) при параллельном переносе на вектор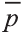 = (3; 2; 5)?

Решение:

По вышеприведённым формулам параллельного переноса: .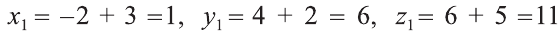

Ответ: .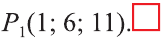

Центральная симметрия в пространстве

Если в пространстве 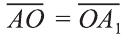, то есть точка О – середина отрезка АА₁ то точки А и А₁ называют симметричными относительно точки О.

Если в пространстве каждая точка фигуры F переходит в точку, симметричную относительно точки О (рис. 47), то такое преобразование называют симметрией относительно точки О. На рисунках 48, 49 изображёны фигуры симметричные относительно точки О. Симметрия относительно точки является движением.

Если при симметрии относительно точки О фигура F переходит в себя, то её называют центрально симметричной фигурой.

Например, диагонали параллелепипеда (рис. 50) относительно их точки пересечения О являются центрально симметричными фигурами.

Пример:

В какую точку перейдет точка A = (1; 2; 3) при симметрии относительно точки О (2; 4; 6)?

Решение:

Пусть А₁ = (х; у; z) – искомая точка. По определению точка

О – середина отрезка АА₁. Следовательно,

Из этих уравнений получаем:

.

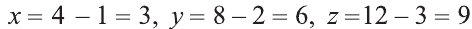
Ответ:

Симметрия относительно плоскости

Точки А и А₁ называют симметричными относительно плоскости а,

если плоскость перпендикулярна отрезку и делит его пополам (рис. 51). Фигуры F₁, и F₂ на рисунке 52 симметричны относительно

плоскости а. Очевидно, что наш силуэт и его отражение симметричны относительно плоскости зеркала (рис. 53).

Симметрия относительно плоскости а является движением.

Поэтому при симметрии относительно плоскости а отрезок переходит в равный ему отрезок, прямая – в прямую, плоскость – в плоскость.

Если при симмeтрии относительно плоскости фигура F переходит в себя, то её называют фигурой симметричной относительно плоскости.

Например, изображённый на рисунке 54 куб, есть фигура, симметричная относительно плоскости а, проходящей через его диагонали АА₁ и СС₁.

Поворот и симметрия относительно оси

Пусть в пространстве заданы точки А и А₁ и прямая l. Если перпендикуляры АК и А₁К, опущенные на прямую l, равны и образуют угол , то говорят, что точка А перешла в точку А₁ в результате поворота на угол относительно прямой l (рис. 55).

Если каждую точку фигуры F повернуть на угол относительно прямой l, то получим новую фигуру F₁ . Тогда говорят, что фигура F перешла в фигуру F₁ с помощью поворота на угол относительно прямой l. На рисунке 56 мы видим фигуры, полученные таким поворотом. Например, повернув куб, изображённый на рисунке 57, на 180° относительно прямой l, получим новый куб.

Поворот относительно прямой также является движением.

Поворот на 180° относительно прямой l называют симметрией относительно прямой l.

Центр, ось и плоскость симметрии называют элементами симметрии. Точки, симметричные точке А (х; у; z) относительно координатных плоскостей, координатных осей и начала координат, будут иметь следующие координаты:

Симметрия в природе и технике

В природе на каждом шагу можно встретить симметрию.

Например, множество живых существ, в частности тела человека и животных, листья растений и цветы устроены симметрично (рис. 58). Также в неживой природе есть элементы, например, снежинки, кристаллы соли. Молекулярное строение веществ тоже состоит из симметричных фигур. Это, конечно, неспроста, поскольку симметричные фигуры не только красивы, но и самые устойчивые.

Раз так, то можно считать, что красота и совершенство природы построены на основе симметрии. Взяв за основу природную красоту и совершенство, строители, инженеры и архитекторы создают строения и механизмы, здания и сооружения, технику и транспортные средства симметричными. В этой работе им очень помогает наука геометрия.

Подобие пространственных фигур

Пусть 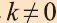и преобразование переводят фигуру F₁, в фигуру F₂. Если

при этом преобразовании для произвольных точек X₁ и Х₂ фигуры F₁ и соответствующих им точек Y₁ и Y₂ фигуры 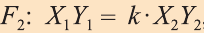, то это преобразование называют преобразованием подобия (рис. 59).

Как видим, понятие преобразования подобия в пространстве вводится также как на плоскости. Следовательно, рассматриваемые ниже виды подобия, их свойства и доказательства этих свойств подобны соответствующим на плоскости. Поэтому, мы не будем останавливаться на их доказательствах и рекомендуем провести их самостоятельно. Преобразование подобия в пространстве отображает прямую в прямую, луч в луч, отрезок в отрезок и угол в угол. Точно также это преобразование плоскость отображает в плоскость.

Если в пространстве одна из фигур перешла в другую с помощью преобразования подобия, то эти фигуры называют подобными.

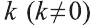
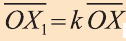
Пусть в пространстве задана фигура F, точка О и число к . Преобразование, переводящее произвольную точку X фигуры F в точку Х₁ удовлетворяющую условию , называют гомотетией относительно центра О с коэффициентом (рис. 61). Точку О называют центром гомотетии, а число коэффициентом гомотетии. Если в результате такого преобразования каждой точки фигуры F получена фигура F₁ то говорят, что фигура F гомотетична фигуре F₁.

Вы видите, что определение гомотетии в пространстве аналогично соответствующему определению на плоскости. Следовательно, все свойства и их доказательства аналогичны. Поэтому, мы не будем доказывать их и рекомендуем провести их самостоятельно.

Гомотетия относительно точки О с коэффициентом является преобразованием подобия. Гомотетия с отличным от нуля коэффициентом при = 1 отображает фигуру F в себя, а при =-1 в фигуру F₁ симметричную фигуре F относительно точки О. В остальных случаях гомотетии не сохраняет расстояния между точками, т. е. не является движением. В результате гомотетии расстояние между точками увеличивается в одно и тоже число раз, т. е. меняются измерения фигуры, но сохраняется её форма. При гомотетии а) прямая отображается в параллельную ей прямую (рис. 62.а); b) плоскость – в параллельную ей плоскость (рис. 62.b), если они не проходят через центр гомотетии.

Если же прямая или плоскость проходят через центр гомотетии, то они отображаются в себя.

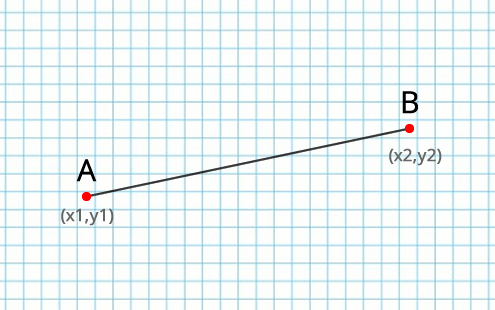
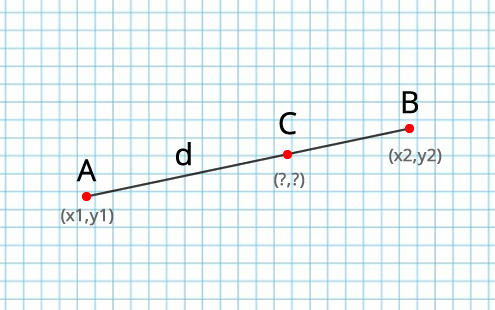
Имеем отрезок AB с координатам x1,y1 и x2, y2:

Необходимо найти координаты новой точки С, которая находится на отрезке, на определенном расстоянии от точки A.

function pointToLine($x1, $y1, $x2, $y2, $d)
{
	$Rab = sqrt(pow($x2 - $x1, 2) + pow($y2 - $y1, 2));
	$k = $d / $Rab;
	$Xc = $x1 + ($x2 - $x1) * $k;
	$Yc = $y1 + ($y2 - $y1) * $k;
	return array('x' => $Xc, 'y' => $Yc);
}

function pointToLine(x1, y1, x2, y2, d)
{
	var Rab = Math.sqrt(Math.pow(x2 - x1, 2) + Math.pow(y2 - y1, 2));
	var k = d / Rab;
	var Xc = x1 + (x2 - x1) * k;
	var Yc = y1 + (y2 - y1) * k;
	return {x: Xc, y: Yc};
}