Как найти координаты точек симметричных середине отрезка

Как найти координаты точек симметричных середине отрезка

Выясним, как связаны между собой координаты симметричных точек и рассмотрим на примерах, как найти координаты точки, симметричной данной точке.

I. Две точки A(xA;yA) и B(xB;yB) симметричны относительно точки O(xO;yO), если точка O является серединой отрезка AB.

По формулам координаты середины отрезка получаем связь координат этих точек:

    [ x_O = frac{{x_A + x_B }}{2},y_O = frac{{y_A + y_B }}{2}. ]

Координаты точек, симметричных относительно начала координат — точки O(0;0) — противоположные числа.

То есть координаты точки B, симметричной точке A относительно начала координат, отличаются от  координат точки A только знаками:

A(a;b) и B(-a;-b) — точки, симметричные относительно начала координат.

Примеры.

1) Найти точку, симметричную точке A(-3;7) относительно точки F(5; 11).

Решение:

Пусть B(xB;yB) — точка, симметричная точке A относительно точки F. Тогда

    [ x_F = frac{{x_A + x_B }}{2} ]

    [ 5 = frac{{ - 3 + x_B }}{2} ]

    [ - 3 + x_B = 5 cdot 2 ]

    [ x_B = 13, ]

    [ y_F = frac{{y_A + y_B }}{2} ]

    [ 11 = frac{{7 + y_B }}{2} ]

    [ y_B = 15. ]

Ответ: (13;15).

2) Найти точку, симметричную точке C (9;-4) относительно начала координат.

Решение:

Точка D, симметричная точке C относительно начала координат, имеет координаты, противоположные координатам точки C: D(-9;4).

Ответ: (-9;4).

II. Две точки A(xA;yA) и B(xB;yB) симметричны относительно прямой g, если эта прямая проходит через середину отрезка AB и перпендикулярна к нему.

Таким образом, чтобы найти координаты точки B, симметричной данной точке A относительно прямой g, можно:

  • Написать уравнение прямой f, перпендикулярной прямой g, проходящей через точку A.
  • Найти точку O пересечения прямых f и g.
  • Зная конец отрезка A и его середину O найти другой конец B.

Пример

Найти точку, симметричную точке A(-4;5) относительно прямой y=2x+4.

Решение:

Уравнение прямой, перпендикулярной данной прямой y=2x+4, ищем в виде y=-0,5x+b. Так как эта прямая проходит через точку A, координаты A удовлетворяют уравнению прямой:

5=-0,5·(-4)+b, откуда b=3.

Таким образом, y=-0,5x+3 — прямая, перпендикулярная прямой y=2x+4 и проходящая через точку A.

Найдём координаты точки пересечения прямых:

    [ left{ begin{array}{l} y = 2x + 4, \ y = - 0,5x + 3, \ end{array} right. Rightarrow O( - 0,4;3,2). ]

    [ x_O = frac{{x_A + x_B }}{2} ]

    [ - 0,4 = frac{{ - 4 + x_B }}{2} ]

    [ x_B = 3,2; ]

    [ y_O = frac{{y_A + y_B }}{2} ]

    [ y_B = 1,4. ]

Значит точка B(3,2;1,4) симметрична точке A(-4;5) относительно прямой y=2x+4.

Ответ: (3,2;1,4).

Координаты точек, симметричных относительно осей координат и биссектрис координатных четвертей — прямых y=x и y=-x — находятся проще:

 для точки A(x;y)
симметрия относительно:
оси Ox A1(x;-y)
оси Oy A2(-x;y)

биссектрисы I и II координатных

четвертей (прямой y=x)

 A3(y;x)

биссектрисы I b II координатных

четвертей (прямой y= -x)

 A4(-y;-x)
Источник
  1. Главная
  2. Справочники
  3. Справочник по математике 5-9 класс
  4. Координаты на плоскости
  5. Осевая и центральная симметрии

Осевая симметрия

Рассмотрим построение точки, симметричной данной точке А относительно данной прямой .

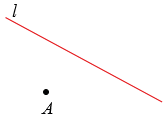
Пусть дана точка А и прямая .

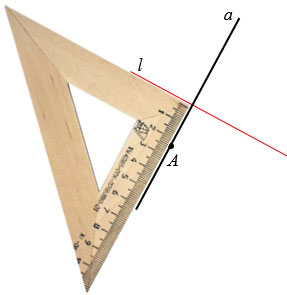
Точку симметричную точке А относительно прямой , можно построить так. Проведем через точку А прямую , перпендикулярную прямой . Для этого используем чертежный угольник. Прикладываем чертежный угольник так, как показано на рисунке ниже и проводим прямую через точку А.

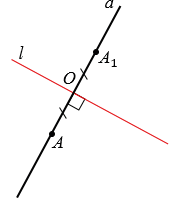
Пусть прямые и пересекаются в точке О. Отложим при помощи линейки на прямой отрезок ОА1, равный отрезку ОА.

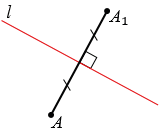
Получаем точки А и А1, которые симметричны относительно прямой .

Также можно построить фигуры, симметричные относительно прямой.

Построим треугольник А1В1С1, симметричный треугольнику АВС относительно прямой .

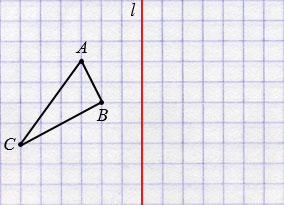
Пусть дан треугольник АВС и прямая .

Далее строим точки А1, В1 и С1, симметричные точкам А, В и С относительно прямой (алгоритм построения смотри выше), соединив которые получим треугольник А1В1С1, симметричный треугольнику АВС относительно прямой .

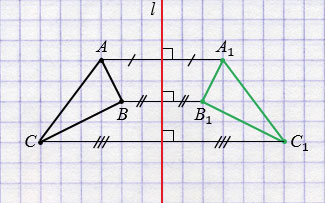
Обратите внимание, любые две фигуры, симметричные относительно прямой, равны.

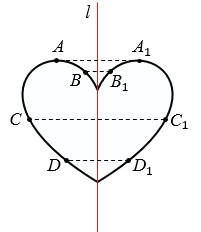
Если фигура имеет ось симметрии (прямая  ) то, все точки этой фигуры, не принадлежащие этой оси, можно разделить на пары симметричных точек.

Центральная симметрия

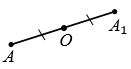
Точки М и М1 называют симметричными относительно точки О, если точка О является серединой отрезка ММ1 (смотри рисунок ниже).

Рассмотрим построение точки, симметричной данной точке М относительно данной точки О.

Пусть даны точки М и О. Точку, симметричную точке М относительно точки О, можно построит так. Проведем луч МО.

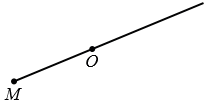
На луче МО отложим отрезок ОN , равный отрезку ОМ.

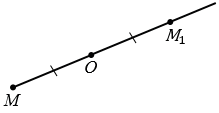
Точки М и М1, которые симметричны относительно точки О.

Также можно построить фигуры, симметричные относительно точки.

Построим треугольник А1В1С1, симметричный треугольнику АВС относительно точки О.

Пусть дан треугольник АВС и точки О.

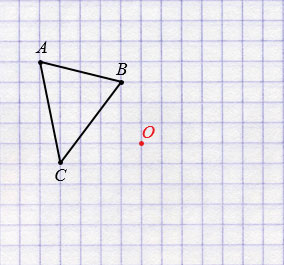
Далее строим точки А1, В1 и С1, симметричные точкам А, В и С относительно точки О (алгоритм построения смотри выше), соединив которые получим треугольник А1В1С1, симметричный треугольнику АВС относительно точки О.

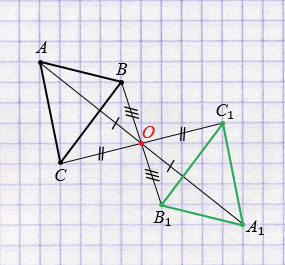
Обратите внимание, любые две фигуры, симметричные относительно точки, равны.

Рассмотрим окружность с центром в точке О. Все точки окружности можно разбить на пары точек, симметричных относительно точки О.

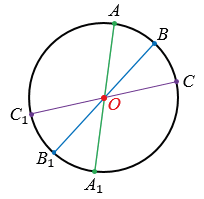
В таком случае говорят, что окружность имеет центр симметрии – точку О.

Также центр симметрии имеют такие фигуры, как отрезок, прямоугольник, эллипс.

Советуем посмотреть:

Перпендикулярные прямые

Параллельные прямые

Координатная плоскость

Координаты на плоскости


Правило встречается в следующих упражнениях:

6 класс

Номер 1251,
Мерзляк, Полонский, Якир, Учебник

Номер 1252,
Мерзляк, Полонский, Якир, Учебник

Номер 1262,
Мерзляк, Полонский, Якир, Учебник

Номер 1266,
Мерзляк, Полонский, Якир, Учебник

Номер 1267,
Мерзляк, Полонский, Якир, Учебник

Номер 1268,
Мерзляк, Полонский, Якир, Учебник

Номер 1272,
Мерзляк, Полонский, Якир, Учебник

Номер 1305,
Мерзляк, Полонский, Якир, Учебник

Номер 2,
Мерзляк, Полонский, Якир, Учебник

Номер 9,
Мерзляк, Полонский, Якир, Учебник

Источник

………………..

Там надо ответ аоаардрсм то отиррооотттьбьтиссвнлт пп

по  2 своцсту треугольников они равны

Квадрат гипотенузы равен сумме квадратов катетов

<span>Соединим точку А с точкой Ц, и точку Б с точкой Д. Получились два подобных треугольника. Обозначим половину ЦД через Х получим Х/16 равно 4/Х. Отсюда Х равен 8, а вся хорда 16 см.</span>

Источник

  • Геометрия

Предыдущий вопрос

Следующий вопрос


katr2012
3 года назад

Ответ

Проверено экспертом

Ответ дан

kirichekov

ответ:

О1 (5; – 0,5; 3,5)

пошаговое объяснение:

решение во вложении

Ответы и объяснения

  • katr2012

Не тот ответ, который тебе нужен?

Найди нужный

Источник

Добавить комментарий