Как найти координаты точек xyz

Построение ортогональных проекций точек

Положение точки в пространстве может быть задано двумя её ортогональными проекциями, например, горизонтальной и фронтальной, фронтальной и профильной. Сочетание любых двух ортогональных проекций позволяет узнать значение всех координат точки, построить третью проекцию, определить октант, в котором она находится. Рассмотрим несколько типичных задач из курса начертательной геометрии.

По заданному комплексному чертежу точек A и B необходимо:

1. Записать их координаты.
2. Достроить проекции т. A и B на плоскость П₃.
3. Определить положение точек в пространстве (октант или плоскость проекций).
4. Построить наглядное изображение точек в системе плоскостей П₁, П₂, П₃.

Определение координат точек по их проекциям

Определим сначала координаты т. A, которые можно записать в виде A (x, y, z). Горизонтальная проекция т. A – точка A’, имеющая координаты x, y. Проведем из т. A’ перпендикуляры к осям x, y и найдем соответственно A_х, A_у. Координата х для т. A равна длине отрезка A_хO со знаком плюс, так как A_х лежит в области положительных значений оси х. С учетом масштаба чертежа находим х = 10. Координата у равна длине отрезка A_уO со знаком минус, так как т. A_у лежит в области отрицательных значений оси у. С учетом масштаба чертежа у = –30. Фронтальная проекция т. A – т. A” имеет координаты х и z. Опустим перпендикуляр из A” на ось z и найдем A_z. Координата z точки A равна длине отрезка A_zO со знаком минус, так как A_z лежит в области отрицательных значений оси z. С учетом масштаба чертежа z = –10. Таким образом, координаты т. A (10, –30, –10).

Координаты т. B можно записать в виде B (x, y, z). Рассмотрим горизонтальную проекцию точки B –  т. В’. Так как она лежит на оси х, то B_x = B’ и координата B_у = 0. Абсцисса x точки B равна длине отрезка B_хO со знаком плюс. С учетом масштаба чертежа x = 30. Фронтальная проекция точки B – т. B˝ имеет координаты х, z. Проведем перпендикуляр из B” к оси z, таким образом найдем B_z. Аппликата z точки B равна длине отрезка B_zO со знаком минус, так как B_z лежит в области отрицательных значений оси z. С учетом масштаба чертежа определим значение z = –20. Таким образом, координаты B (30, 0, -20). Все необходимые построения представлены на рисунке ниже.

Построение проекций точек

Точки A и B в плоскости П₃ имеют следующие координаты: A”’ (y, z); B”’ (y, z). При этом A” и A”’ лежат одном перпендикуляре к оси z, так как координата z у них общая. Точно также на общем перпендикуляре к оси z лежат B” и B”’. Чтобы найти профильную проекцию т. A, отложим по оси у значение соответствующей координаты, найденное ранее. На рисунке это сделано с помощью дуги окружности радиуса A_уO. После этого проведем перпендикуляр из A_у до пересечения с перпендикуляром, восстановленным из точки A” к оси z. Точка пересечения этих двух перпендикуляров определяет положение A”’.

Точка B”’ лежит на оси z, так как ордината y этой точки равна нулю. Для нахождения профильной проекции т. B в данной задаче необходимо лишь провести перпендикуляр из B” к оси z. Точка пересечении этого перпендикуляра с осью z есть B”’.

Определение положения точек в пространстве

Наглядно представляя себе пространственный макет, составленный из плоскостей проекций П₁, П₂ и П₃, расположение октантов, а также порядок трансформации макета в эпюр, можно непосредственно определить, что т. A расположена в III октанте, а т. B лежит в плоскости П₂.

Другим вариантом решения данной задачи является метод исключений. Например, координаты точки A (10, -30, -10). Положительная абсцисса x позволяет судить о том, что точка расположена в первых четырех октантах. Отрицательная ордината y говорит о том, что точка находится во втором или третьем октантах. Наконец, отрицательная аппликата z указывает на то, что т. A расположена в третьем октанте. Приведенные рассуждения наглядно иллюстрирует следующая таблица.

Октанты	Знаки координат
x	y	z
1	+	+	+
2	+	–	+
3	+	–	–
4	+	+	–
5	–	+	+
6	–	–	+
7	–	–	–
8	–	+	–

Координаты точки B (30, 0, -20). Поскольку ордината т. B равна нулю, эта точка расположена в плоскости проекций П₂. Положительная абсцисса и отрицательная аппликата т. B указывают на то, что она расположена на границе третьего и четвертого октантов.

Построение наглядного изображения точек в системе плоскостей П₁, П₂, П₃

Используя фронтальную изометрическую проекцию, мы построили пространственный макет III октанта. Он представляет собой прямоугольный трехгранник, у которого гранями являются плоскости П₁, П₂, П₃, а угол (-y0x) равен 45 º. В этой системе отрезки по осям x, y, z будут откладываться в натуральную величину без искажений.

Построение наглядного изображения т. A (10, -30, -10) начнем с её горизонтальной проекции A’. Отложив по оси абсцисс и ординат соответствующие координаты, найдем точки A_х и A_у. Пересечение перпендикуляров, восстановленных из A_х и A_у  соответственно к осям x и y определяет положение т. A’. Отложив от A’ параллельно оси z в сторону её отрицательных значений отрезок AA’, длина которого равна 10, находим положение точки A.

Наглядное изображение т. B (30, 0, -20) строится аналогично – в плоскости П₂ по осям x и z нужно отложить соответствующие координаты. Пересечение перпендикуляров, восстановленных из B_х и B_z, определит положение точки B.

Содержание:

Система координат в пространстве

Декартова система координат в пространстве

Вы познакомились с декартовой системой координат на плоскости в предыдущих классах. Систему координат в пространстве введём аналогично тому, как это было сделано на плоскости. Рассмотрим три взаимно перпендикулярных оси Ох, Оу и Оz, пересекающихся в точке О, являющейся началом координат. Через каждую пару этих прямых проведём плоскости Оху, 0xz и Оуz (рис. 1). Таким образом вводится система координат в пространстве, при этом

точку О – называют началом координат, прямые Ох, Оу и Оz — осями координат, Ох – ось абсцисс, Оу – ось ординат и Оz – ось аппликат, плоскости Оху, Оуz и Охz – координатными плоскостями.

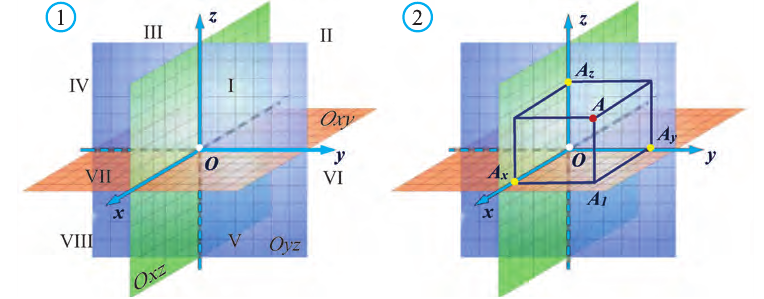
Координатные плоскости делят пространство на 8 октант (получетвертей) (рис. 1).

Пусть в пространстве задана произвольная точка А. Через эту точку проведём плоскости, перпендикулярные плоскостям Охz, Оуz и Охz (рис. 2). Одна из этих плоскостей пересечёт ось Ох в точке Ах.

Координату Ах на оси Ох называют координатой х или абсциссой точки А.

Аналогично определяют у – координату (ординату) и z- координату (аппликату) точки А.

Координаты точки А записывают в виде А (х; у; z) или короче (х; у; z). Точки, изображённые на рисунке 3, имеют следующие координаты: А (0; 5; 0), B (4; 0; 0), М (0; 5; 4), К (2; 3; 4), Р (-2; 3; -4).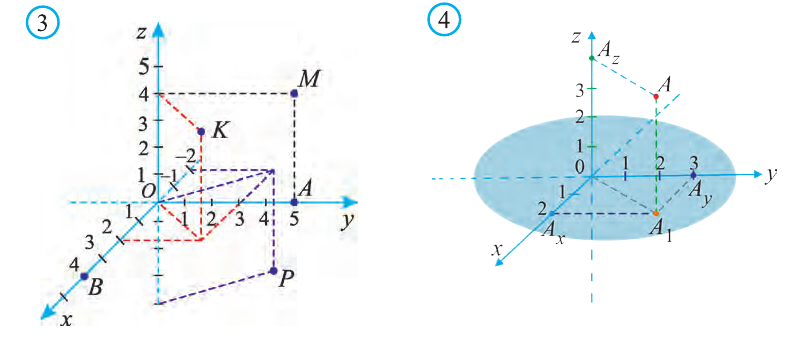

Пример:

Пусть в пространстве в декартовой системе координат

задана точка А (2; 3; 4). Где она расположена?

Решение:

От начала координат в положительном направлении осей Ох и Оу отложим отрезки ОА_х = 2 и ОА_у = 3 (рис. 4).

Через точку А_х проведём прямую, лежащую в плоскости Оху и параллельную оси Оу. А через точку Аy проведём прямую, лежащую в плоскости Оху и параллельную оси Ох. Точку пересечения этих прямых обозначим A₁ . Через точку A₁ проведём прямую, перпендикулярную плоскости Оху и на ней в положительном направлении Oz отложим отрезок АА₁ = 4. Тогда точка А (2; 3; 4) и будет искомой точкой.

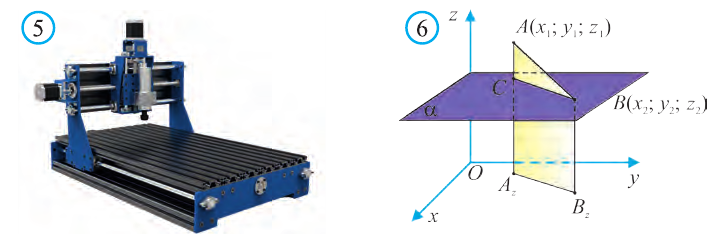
Пользуясь системой координат, созданной для современных программируемых станков и автоматизированных роботов, составляются программы, на основе которых обрабатываются металлы (рис. 5).

Расстояние между двумя точками

Пусть заданы две точки А (х₁; у₁; z₁) и B (х₂; у₂; z₂).

1.Сначала рассмотрим случай, когда прямая АВ не параллельна оси Оz (рис. 6). Через точки А и В проведём прямые, параллельные оси Оz. И пусть они пересекают плоскость Оху в точках А_z и В_z .

Координаты х и у этих точек соответственно равны координатам х и у точек А, В, а координаты z равны 0.

Теперь через точку В проведём плоскость а, параллельную плоскости Оху. Она пересечёт прямую АА_z в некоторой точке С.

По теореме Пифагора: АВ² = АС² + СВ².

Однако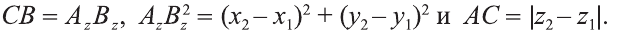

Поэтому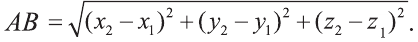

2.Пусть отрезок АВ параллелен оси Оz, тогда 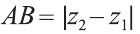и, так как

х₁= х₂ , у₁ = у₂ , мы опять приходим к вышеприведённой формуле.

Следовательно, расстояние между двумя точками А и В:

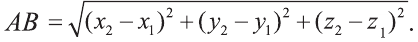(1)

Примечание. Формула (1) выражает длину диагонали прямоугольного параллелепипеда, измерения которого равны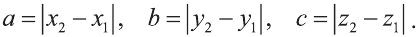

Уравнение сферы и шара

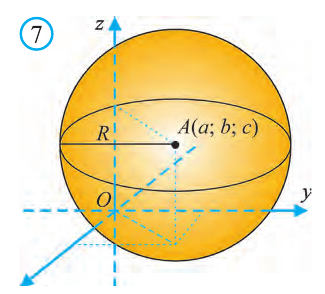
Известно, что множество всех точек М (х; у; z), расположенных на расстоянии R от данной точки А (а; Ь; с) образуют сферу (рис. 7). Тогда по формуле (1) координаты всех точек, расположенных на сфере радиуса R с центром в точке А (а; b; с), удовлетворяют равенству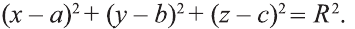

Отсюда, ясно, что неравенство для точек шара радиуса R с центром в

точке А (а; b; с) имеет вид: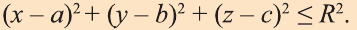

Пример:

Найдите периметр треугольника ABC с вершинами в

точках А (9; 3; -5), В (2; 10; -5), С (2; 3; 2).

Решение:

Р=АВ+АС+ВС периметр треугольника ABC. Воспользовавшись формулой 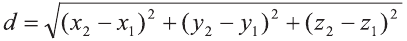расстояния между двумя точками, найдём длины сторон треугольника:

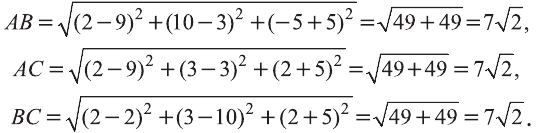
Следовательно, треугольник ABC равносторонний и его периметр .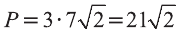

Ответ: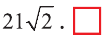

Координаты середины отрезка

Пусть А (x₁; y₁;z₁) и В (х₂; у₂; z₂) – произвольные точки, точка С (х; у; z) середина отрезка AB (рис. 8).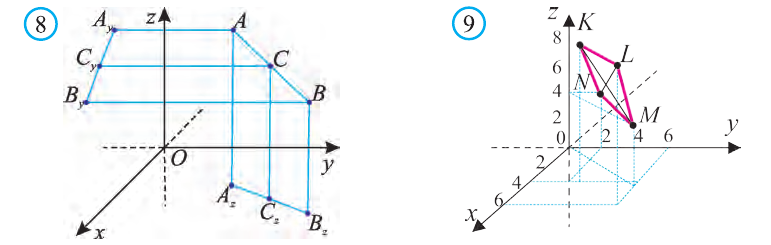

Через точки А, В и С проведём прямые, параллельные оси пересекающие плоскость Оху в точках 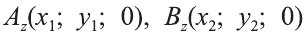и 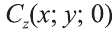. Тогда по теореме Фалеса точка С_z – середина отрезка А_zВ_z.

Отсюда по формулам нахождения координат середины отрезка на плоскости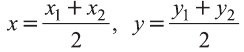

Чтобы найти координату z, нужно вместо плоскости Оху рассмотреть плоскость 0xz или Оуz.

Тогда и для z получим формулу, подобную вышеприведённой.

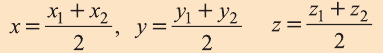
Аналогично, используя координаты концов A и B отрезка AB, по формулам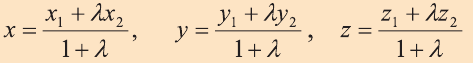

находят координаты точки Р(х1;у]; г,), делящей отрезок АВ в отношении X САР: РВ = X).

Задача 3. Докажите, что четырёхугольник МЛШЬ с вершинами М{3; 6; 4), N(0; 2; 4), К(3; 2; 8), 1(6; 6; 8) – параллелограмм (рис. 9).

Доказательство: Для решения задачи используем признак параллелограмма: Четырёхугольник, точка пересечения диагоналей которого делит их пополам, является параллелограммом.

Координаты середины отрезка МК:

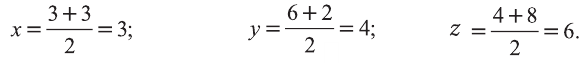
Координаты середины отрезка NL:

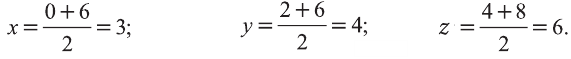
Координаты середин отрезков МК и NL равны. Это говорит о том, что отрезки пeрeсeкаются и в точке пeрeсeчeния делятся пополам. Следовательно, четырёхугольник MNLK – параллелограмм.

В переписке с известным целителем и математиком Абу Али ибн Сино Абу Райхон Беруни задаёт следующий вопрос: «Почему Аристотель и другие (философы) называют шесть сторон?»

Рассматривая шестисторонний куб, Беруни говорит о фигурах «с другим количеством сторон» и добавляет, что «шарообразные фигуры не имеют сторон.» А Ибн Сино отвечает, что «во всех случаях нужно считать, что сторон шесть, так как у каждой фигуры, независимо от её формы, есть три измерения – длина, глубина и ширина».

Здесь Ибн Сино имеет ввиду три координаты, именуемые условно «шесть сторон».

В произведении «Канон Масъуда» Беруни приводит точное математическое определение шести сторон: «Сторон шесть, так как они ограничивают движение фигур по своим измерениям. Измерений три: длина, ширина и глубина. А их в два раза больше самих измерений.»

В предыдущих книгах автор определяет положение небесных тел с помощью двух координат относительно небесной сферы – эклиптического уравнения. Либо через те же координаты, но относительно небесного экватора или горизонта. Однако при определении взаимного расположения звёзд и небесных светил придётся учитывать и случаи затмений. Вот в таких случаях появляется необходимость в третьей сферической координате. Эта необходимость привела Беруни к отказу от теории небесных координат.

Векторы в пространстве и действия над ними

Векторы в пространстве

Понятие вектора в пространстве вводят также как на плоскости.

Вектором в пространстве называют направленный отрезок. Основные понятия, относящиеся к векторам в пространстве, аналогичны этим понятиям на плоскости: длина (модуль), направление вектора, равенство векторов.

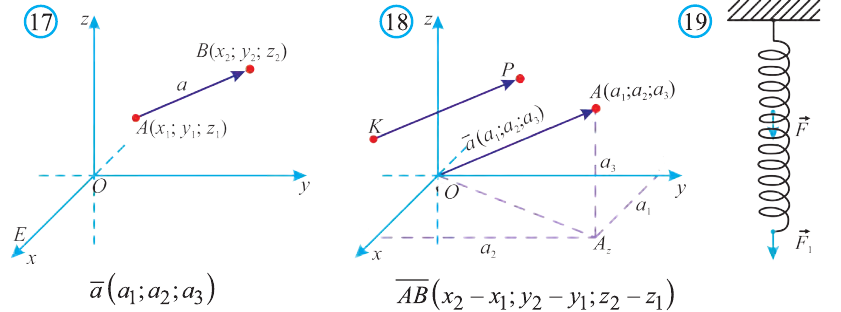
Координатами вектора с началом в точке А (х₁; у₁; z₁) и концом в точке В (х₁; у₁; z₁) называют числа 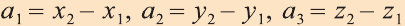, (рис. 17).

Приведем без доказательства свойства векторов, аналогичных свойствам на плоскости.

Также как на плоскости, соответствующие координаты равных векторов равны и, обратно, векторы с равными координатами равны.

Hа основании этого вектор можно обозначить как 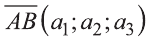или 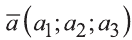или кратко 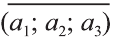(рис. 18).

Вектор можно записать и без координат 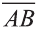(или 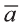). В этой записи

на первом месте начало вектора, а на втором – конец.

Вектор с координатами, равными нулю, называют нулевым вектором и обозначают 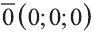или 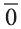, направление этого вектора не определено.

Если начало вектора расположено в начале координат О, а числа а₁,

а₂ и а₃ – координаты точки А, то есть А (а₁; а₂; а₃), то эти же числа будут

координатами вектора 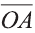: 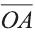(а₁; а₂; а₃).

Однако вектор в пространстве 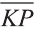с началом в точке К(с₁; с₂; с₃) и концом в точке 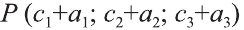будет иметь те же координаты: .

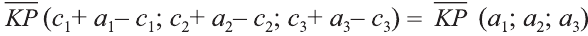Отсюда следует, что вектор можно приложить к любой точке пространства. В геометрии мы рассматриваем такие свободные векторы. Но в физике, обычно вектор связан с некоторой точкой. Например, воздействие силы приложенная к пружине F на рисунке 19 зависит от точки её приложения.

Длинной вектора называют длину направленного отрезка

изображающего его (рис. 17). Длину вектора 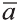записывают

так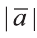. Длина вектора 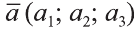, заданного координатами,

вычисляется по формуле .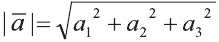

Пример:

Даны точки А (2; 7;-3),В (1; 0; 3), С (-3;-4; 5) и D (-2; 3; -1). Какие из векторов 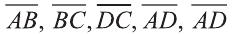и 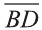равны между собой?

Решение:

У равных векторов равны соответствующие координаты. Поэтому найдём координаты векторов:

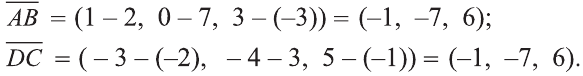
Следовательно, .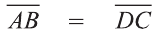

Докажите самостоятельно, что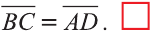

Действия над векторами в пространстве

Действия над векторами. Сложение векторов, умножение на число и их скалярное произведение определяется также как на плоскости.

Суммой векторов 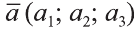и (b₁; b₂; b₃); называют вектор 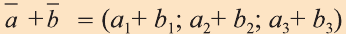(рис. 20).

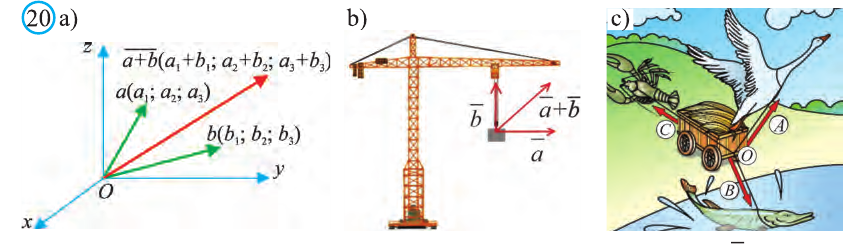
Пусть кран на рисунке 20.b движется вдоль вектора 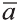, а груз относительно крана вдоль вектора 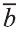. В результате груз движется вдоль вектора 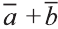. Поэтому из рисунка 20.с, на котором изображён сюжeт басни русского писателя И.А.Крылова, ясно, что герои басни не смогут сдвинуть телегу с места.

Свойства суммы векторов

Для любых векторов 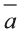, 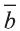и 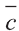имеют место следующие свойства:

a) – переместительный закон сложения векторов;

b)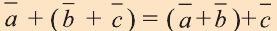 – распределительный закон сложения.

Правило треугольника сложения векторов

Для любых точек А, В и С (рис. 21):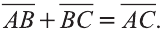

Правило параллелограмма сложения векторов

Если АВСD – параллелограмм (рис. 22), то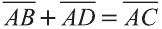

Правило многоугольника сложения векторов

Если точки А, В, С, D и Е – вершины многоугольника (рис. 23), то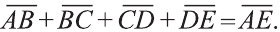

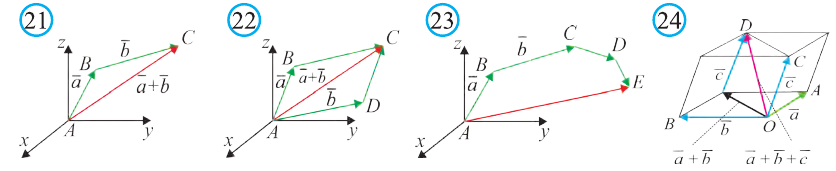
Правило параллелепипеда сложения трёх векторов, не лежащих в одной плоскости. Если АВСDА₁В₁С₁D₁ параллелепипед (рис. 24), то

.

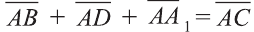Вектор ​​​​​​= (a1; a₂; a₃) – называют умножением вектора

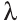(a₁; a₂; a₃) на число (рис. 25). Свойства операции умножения вектора на число.

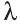Для любых векторов и и чисел и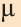

а);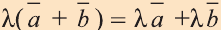

b);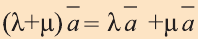

c)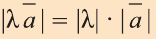 и направление вектора

совпадает с направлением вектора , если ,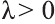

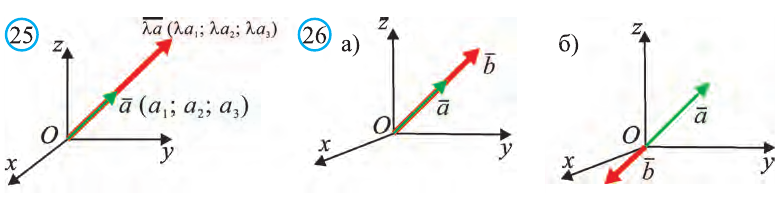
противоположно направлению вектора , если .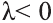

Коллинеарные и компланарные векторы

Пусть заданы ненулевые векторы и 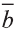. Если векторы

и сонаправлены или противоположно направлены,

то их называют коллинеарными векторами (рис. 26).

Свойство 1. Если для векторов и имеет место равенство 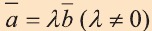, то они коллинеарны и наоборот.

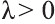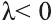Если , то векторы и сонаправлены , если, то

противоположно направлены .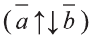

Свойство 2. Если векторы (a₁; a₂; a₃) и (b₁; b₂; b₃) коллинеарны,

то их соответствующие координаты пропорциональны:

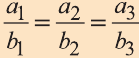и наоборот.

Пример:

Найдите вектор с началом в точке А (1; 1; 1) и концом в точке В, лежащей в плоскости Оху, коллинеарный вектору ( 1; 2; 3).

Решение:

Пусть точка В имеет координаты В (х; у; z). Так как точка В лежит в плоскости Оху, то z=0. Тогда 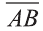(х – 1 ;у – 1; – 1).

По условию задачи векторы 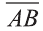(х – 1 ;у – 1; – 1) и (1, 2, 3) коллинеарны. Следовательно, их координаты пропорциональны.

Тогда получаем следующие пропорции .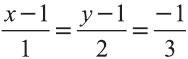

Откуда находим , .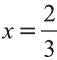

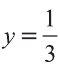Итак,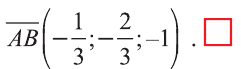

Векторы, лежащие в одной плоскости или параллельных плоскостях, называют компланарными векторами (рис. 27).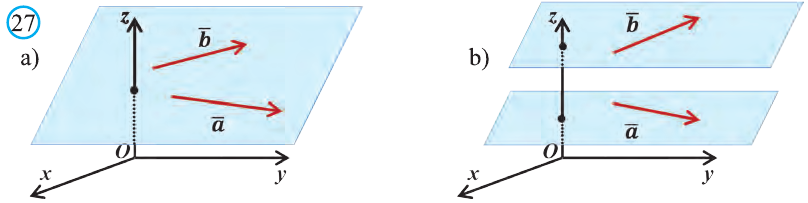

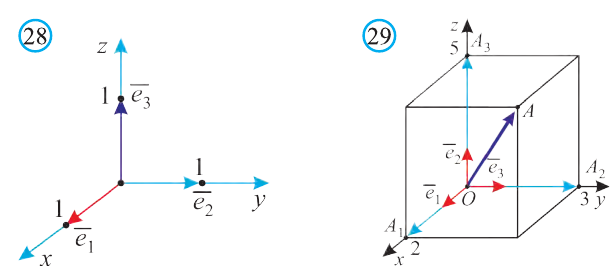
Векторы 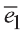(1; 0; 0), 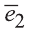(0; 1; 0) и 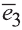(0; 0; 1) называют ортами (рис. 28).

Любой вектор 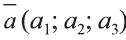можно единственным образом разложить по ортам, то есть представить в виде 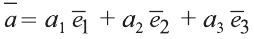(рис. 29).

Точно также, если заданы три нeкомпланарных вектора 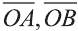и 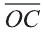, то любой вектор 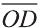можно единственным образом представить в виде:

.

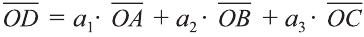Здесь 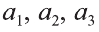некоторые действительные числа. Тогда говорят, что вектор разложен по заданным векторам.

Скалярное произведение векторов

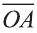Углом между ненулевыми векторами и называют угол между направленными отрезками векторов = и 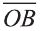=, исходящих из точки О (рис. 30).

Угол между векторами и обозначают так .

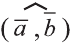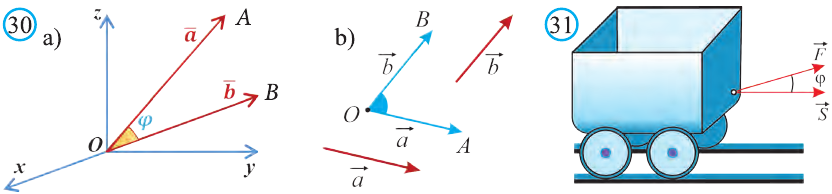
Скалярным произведением векторов и называют произведение длин этих векторов на косинус угла между ними.

Если один из векторов нулевой, то скалярное произведение этих векторов равно нулю.

Скалярное произведение обозначают 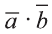или 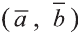. По определению 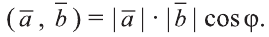(1)

Из определения следует, что если скалярное произведение векторов и равно нулю, то эти векторы перпендикулярны и наоборот.

В физике работа A, выполненная при движении тела на расстоянии 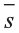, под воздействием силы 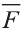(рис. 31), равна скалярному произведению силы 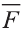на расстояние:

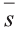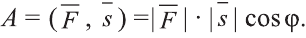
Свойство. Если 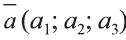и (b₁; b₂; b₃), то () =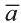

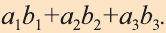
Доказательство. Приложим векторы 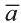и к началу

координат О (рис.32). Тогда 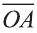= 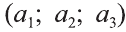и 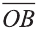= (b₁; b₂; b₃).

Если векторы неколлинеарны, то получаем треугольник АВО , для которого справедлива теорема косинусов.

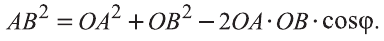
Тогда .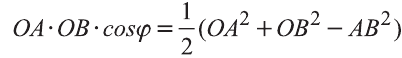

Однако, ,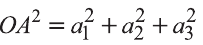

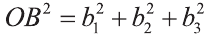
и .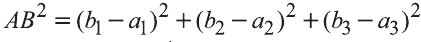

Следовательно,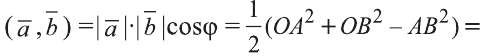

.

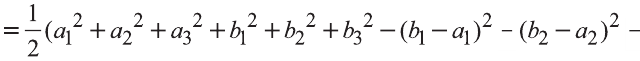
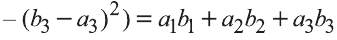Самостоятельно докажите, что и в случае, когда данные векторы коллинеарны 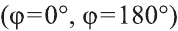, также выполняется

это равенство.

Свойства скалярного произведения векторов

1.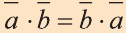 – переместительное свойство.

2.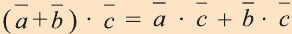 – распределительное свойство.

3.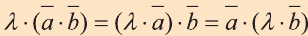 – сочетательное свойство.

4.Если векторы а и b являются сонаправленными коллинеарными

векторами, то 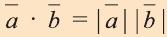, так как соs 0° = 1.

5.Если же векторы противоположно направлены, то 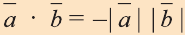, так как cos l80° = -1.

6. .

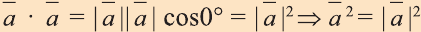7. Если вектор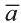 перпендикулярен вектору , то 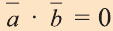. Следствия: а) Длина вектора 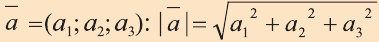; (1) b) косинус угла между векторами

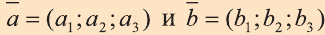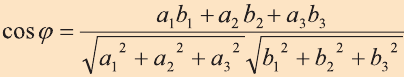: ; (2)

с) условие перпендикулярности векторов 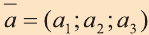и

.

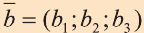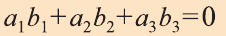(3)

Пример:

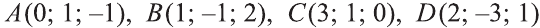– заданные точки. Найдите косинус угла между векторами .

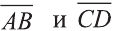Решение:

Найдём длины векторов :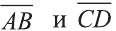

,

.

,

.

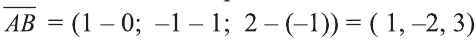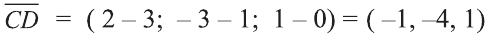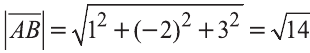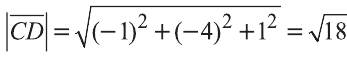Следовательно,

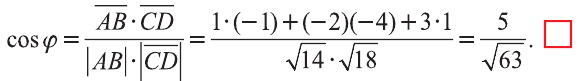
Пример:

Найдите угол между векторами .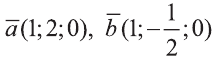

Решение:

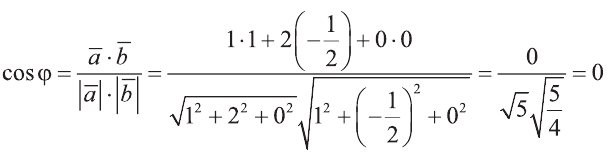Итак,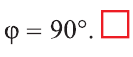

Пример:

Найдите 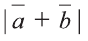, если 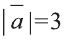, 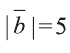и угол между векторамии равен .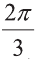

Решение:

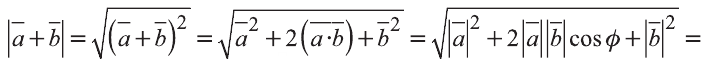
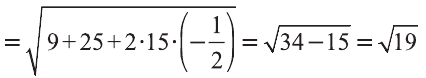
Пример:

Найдите координаты и длины векторов 1)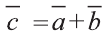; 2)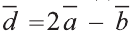, если .

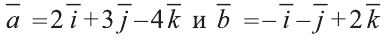Решение:

Подставим в выражения искомых векторов разложения векторов и по координатам:

1)

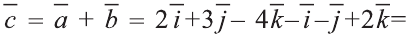
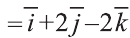. Следовательно,.

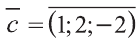Тогда.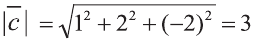

2)

.

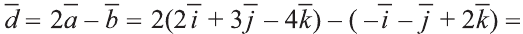
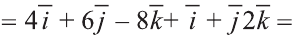
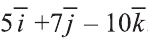Следовательно, .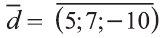

Тогда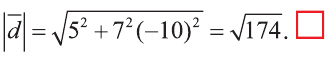

• Заказать решение задач по высшей математике

Пример:

Найдите произведение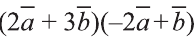, если угол между векторами и равен 30° и , .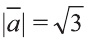

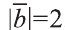Решение:

Сначала найдём поизведение векторов и :

.

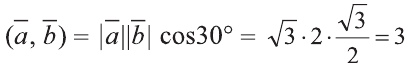Затем перемножим заданные выражения как многочлены

и, пользуясь распределительным свойством умножения

вектора на число, получим:

.

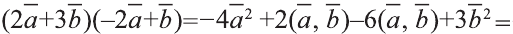
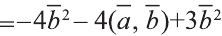Учитывая, что ,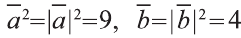

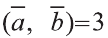найдём искомое произведение

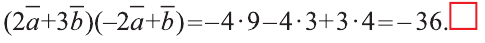
Преобразование и подобие в пространстве

Геометрические преобразования в пространстве

Если каждую точку заданной в пространстве фигуры F изменить одним и тем же способом, то получим фигуру F_1. Если при этом преобразовании различные точки первой фигуры переходят в различные точки второй, то говорят о преобразовании геометрической фигуры.

Если рассматривать все пространства как геометрическую фигуру, то также можно говорить о преобразовании геометрической фигуры.

Понятие геометрического преобразование в пространстве вводят также как на плоскости. Следовательно, свойства некоторых рассматриваeмых ниже видов преобразований и их доказательства также подобны соответствующим им на плоскости. Поэтому, мы не будем доказывать их и рекомендуем провести их самостоятельно.

Движение и параллельный перенос

Преобразование фигур, при котором сохраняются расстояния между точками, называют движением. Можно привести следующие свойства движения. При движении прямая переходит в прямую, луч – в луч, отрезок – в равный ему отрезок, угол – в равный ему угол, треугольник – в равный ему треугольник, плоскость – в плоскость, тетраэдр – в равный ему тетраэдр.

В пространстве фигуры, которые можно перевести одну в другую при некотором движении называют равными фигурами.

Простейшим примером движения является параллельный перенос.

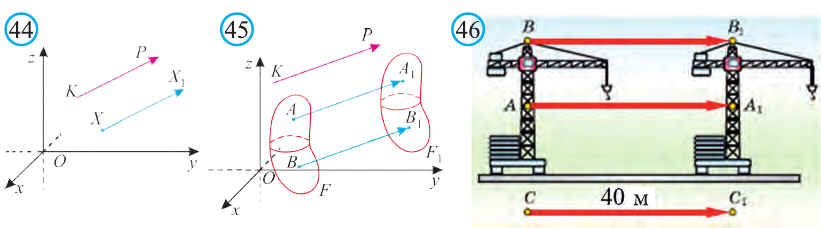
Пусть в пространстве даны вектор и произвольная точка Х

(рис. 44). Говорят, что точка Х перешла в точку X₁ параллельным

переносом на вектор , если выполняется условие 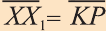. Если каждую точку фигуры F сдвинуть на вектор при помощи параллельного переноса (рис. 45), то получим фигуру F₁. Тогда говорят, что фигура F получена параллельным переносом фигуры F₁ . При параллельном переносе каждая точка фигуры F сдвигается в одном и том же направлении на одно и то же расстояние.

Каждая точка подъёмного крана, изображённого на рисунке 46, параллельно перенесена на 40 м относительно начального положения.

Ясно, что параллельный перенос является движением. Поэтому прямая переходит в прямую, луч – в луч, плоскость – в плоскость,

и т. д.

Пусть точка 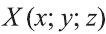фигуры F перешла в точку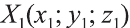

фигуры F₁ при помощи параллельного переноса

на вектор .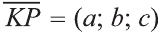

Тогда по определению получим:

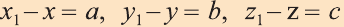или

.

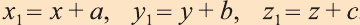Эти равенства называют формулами параллельного переноса.

Пример:

В какую точку перейдёт точка Р (-2; 4; 6) при параллельном переносе на вектор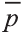 = (3; 2; 5)?

Решение:

По вышеприведённым формулам параллельного переноса: .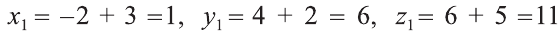

Ответ: .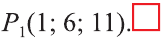

Центральная симметрия в пространстве

Если в пространстве 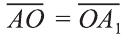, то есть точка О – середина отрезка АА₁ то точки А и А₁ называют симметричными относительно точки О.

Если в пространстве каждая точка фигуры F переходит в точку, симметричную относительно точки О (рис. 47), то такое преобразование называют симметрией относительно точки О. На рисунках 48, 49 изображёны фигуры симметричные относительно точки О. Симметрия относительно точки является движением.

Если при симметрии относительно точки О фигура F переходит в себя, то её называют центрально симметричной фигурой.

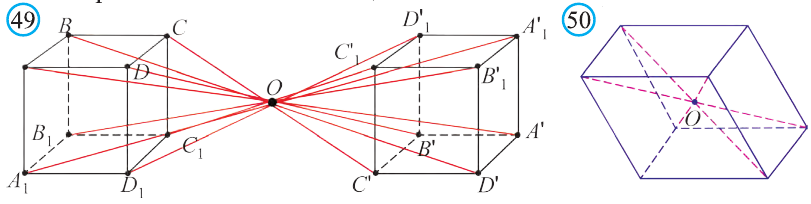
Например, диагонали параллелепипеда (рис. 50) относительно их точки пересечения О являются центрально симметричными фигурами.

Пример:

В какую точку перейдет точка A = (1; 2; 3) при симметрии относительно точки О (2; 4; 6)?

Решение:

Пусть А₁ = (х; у; z) – искомая точка. По определению точка

О – середина отрезка АА₁. Следовательно,

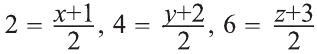
Из этих уравнений получаем:

.

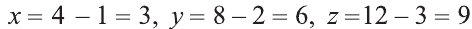Ответ: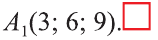

Симметрия относительно плоскости

Точки А и А₁ называют симметричными относительно плоскости а,

если плоскость перпендикулярна отрезку и делит его пополам (рис. 51). Фигуры F₁, и F₂ на рисунке 52 симметричны относительно

плоскости а. Очевидно, что наш силуэт и его отражение симметричны относительно плоскости зеркала (рис. 53).

Симметрия относительно плоскости а является движением.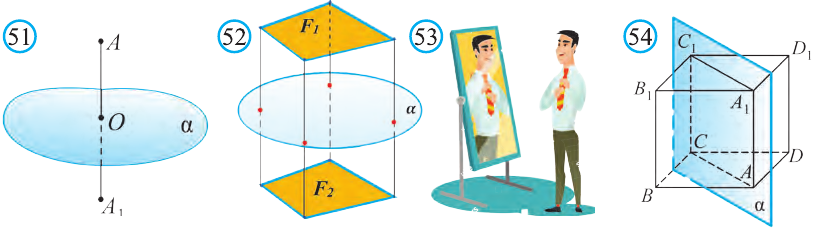

Поэтому при симметрии относительно плоскости а отрезок переходит в равный ему отрезок, прямая – в прямую, плоскость – в плоскость.

Если при симмeтрии относительно плоскости фигура F переходит в себя, то её называют фигурой симметричной относительно плоскости.

Например, изображённый на рисунке 54 куб, есть фигура, симметричная относительно плоскости а, проходящей через его диагонали АА₁ и СС₁.

Поворот и симметрия относительно оси

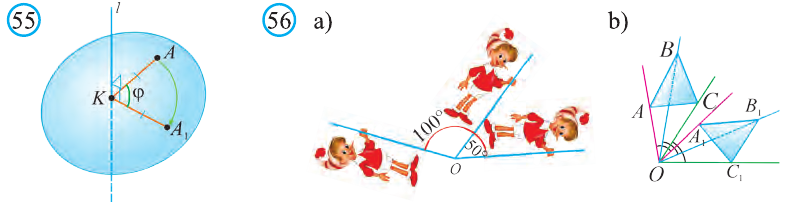
Пусть в пространстве заданы точки А и А₁ и прямая l. Если перпендикуляры АК и А₁К, опущенные на прямую l, равны и образуют угол , то говорят, что точка А перешла в точку А₁ в результате поворота на угол относительно прямой l (рис. 55).

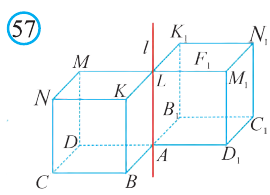
Если каждую точку фигуры F повернуть на угол относительно прямой l, то получим новую фигуру F₁ . Тогда говорят, что фигура F перешла в фигуру F₁ с помощью поворота на угол относительно прямой l. На рисунке 56 мы видим фигуры, полученные таким поворотом. Например, повернув куб, изображённый на рисунке 57, на 180° относительно прямой l, получим новый куб.

Поворот относительно прямой также является движением.

Поворот на 180° относительно прямой l называют симметрией относительно прямой l.

Центр, ось и плоскость симметрии называют элементами симметрии. Точки, симметричные точке А (х; у; z) относительно координатных плоскостей, координатных осей и начала координат, будут иметь следующие координаты:

Симметрия в природе и технике

В природе на каждом шагу можно встретить симметрию.

Например, множество живых существ, в частности тела человека и животных, листья растений и цветы устроены симметрично (рис. 58). Также в неживой природе есть элементы, например, снежинки, кристаллы соли. Молекулярное строение веществ тоже состоит из симметричных фигур. Это, конечно, неспроста, поскольку симметричные фигуры не только красивы, но и самые устойчивые.

Раз так, то можно считать, что красота и совершенство природы построены на основе симметрии. Взяв за основу природную красоту и совершенство, строители, инженеры и архитекторы создают строения и механизмы, здания и сооружения, технику и транспортные средства симметричными. В этой работе им очень помогает наука геометрия.

Подобие пространственных фигур

Пусть 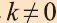и преобразование переводят фигуру F₁, в фигуру F₂. Если

при этом преобразовании для произвольных точек X₁ и Х₂ фигуры F₁ и соответствующих им точек Y₁ и Y₂ фигуры 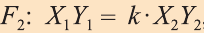, то это преобразование называют преобразованием подобия (рис. 59).

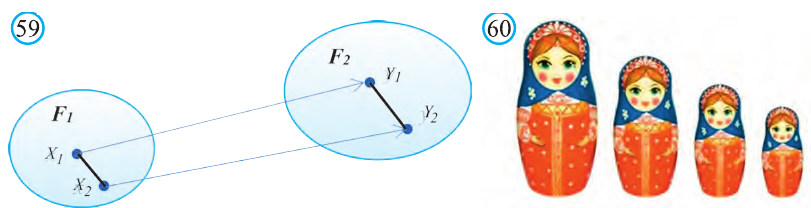
Как видим, понятие преобразования подобия в пространстве вводится также как на плоскости. Следовательно, рассматриваемые ниже виды подобия, их свойства и доказательства этих свойств подобны соответствующим на плоскости. Поэтому, мы не будем останавливаться на их доказательствах и рекомендуем провести их самостоятельно. Преобразование подобия в пространстве отображает прямую в прямую, луч в луч, отрезок в отрезок и угол в угол. Точно также это преобразование плоскость отображает в плоскость.

Если в пространстве одна из фигур перешла в другую с помощью преобразования подобия, то эти фигуры называют подобными.

Пусть в пространстве задана фигура F, точка О и число к 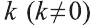. Преобразование, переводящее произвольную точку X фигуры F в точку Х₁ удовлетворяющую условию 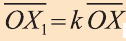, называют гомотетией относительно центра О с коэффициентом (рис. 61). Точку О называют центром гомотетии, а число коэффициентом гомотетии. Если в результате такого преобразования каждой точки фигуры F получена фигура F₁ то говорят, что фигура F гомотетична фигуре F₁.

Вы видите, что определение гомотетии в пространстве аналогично соответствующему определению на плоскости. Следовательно, все свойства и их доказательства аналогичны. Поэтому, мы не будем доказывать их и рекомендуем провести их самостоятельно.

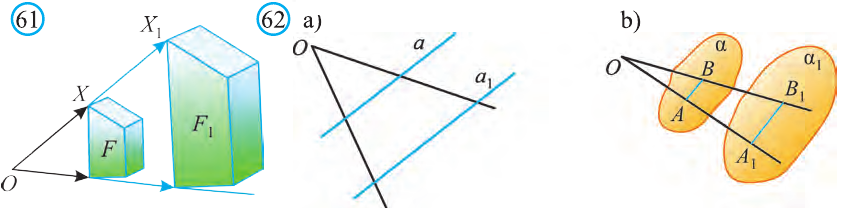
Гомотетия относительно точки О с коэффициентом является преобразованием подобия. Гомотетия с отличным от нуля коэффициентом при = 1 отображает фигуру F в себя, а при =-1 в фигуру F₁ симметричную фигуре F относительно точки О. В остальных случаях гомотетии не сохраняет расстояния между точками, т. е. не является движением. В результате гомотетии расстояние между точками увеличивается в одно и тоже число раз, т. е. меняются измерения фигуры, но сохраняется её форма. При гомотетии а) прямая отображается в параллельную ей прямую (рис. 62.а); b) плоскость – в параллельную ей плоскость (рис. 62.b), если они не проходят через центр гомотетии.

Если же прямая или плоскость проходят через центр гомотетии, то они отображаются в себя.

При введении системы координат на плоскости или в трехмерном пространстве появляется уникальная возможность описания геометрических фигур и их свойств при помощи уравнений и неравенств. Это имеет иное название – методы алгебры.

Данная статья поможет разобраться с заданием прямоугольной декартовой системой координат и с определением координат точек. Более наглядное и подробное изображение имеется на графических иллюстрациях.

Прямоугольная декартова система координат на плоскости

Чтобы ввести систему координат на плоскости, необходимо провести на плоскости две перпендикулярные прямые. Выбираем положительное направление, обозначая стрелочкой. Необходимо выбрать масштаб. Точку пересечения прямых назовем буквой O. Она считается началом отсчета. Это и называется прямоугольной системой координат на плоскости.

Прямые с началом O, имеющие направление и масштаб, называют координатной прямой или координатной осью.

Прямоугольная система координат обозначается Oxy. Координатными осями называют Ох и Оу, называемые соответственно ось абсцисс и ось ординат.

Изображение прямоугольной системы координат на плоскости.

Оси абсцисс и ординат имеют одинаковую единицу изменения и масштаб, что показано в виде штрихе в начале координатных осей. Стандартное направление Ох слева направо, а Oy – снизу вверх. Иногда используется альтернативный поворот под необходимым углом.

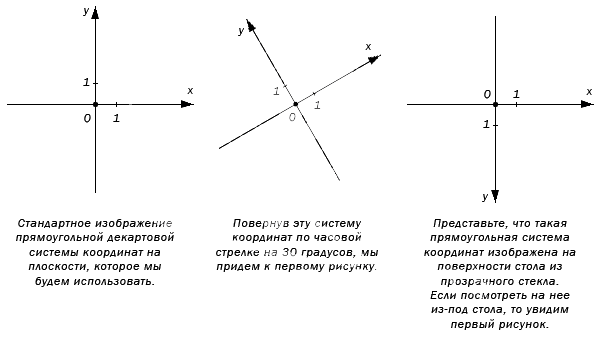
Прямоугольная система координат получила название декартовой в честь ее первооткрывателя Рене Декарта. Часто можно встретить название как прямоугольная декартовая система координат.

Прямоугольная система координат в трехмерном пространстве

Трехмерное евклидовое пространство имеет аналогичную систему, только оно состоит не из двух, а из трех Ох, Оу, Оz осей. Это три взаимно перпендикулярные прямые, где Оz имеет название ось аппликат.

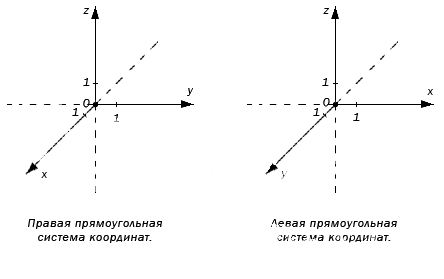
По направлению координатных осей делят на правую и левую прямоугольные системы координат трехмерного пространства.

Оси координат пересекаются в точке O, называемой началом. Каждая ось имеет положительное направление, которое указывается при помощи стрелок на осях. Если при повороте Ох против часовой стрелки на 90° ее положительное направление совпадает с положительным Оу, тогда это применимо для положительного направления Оz. Такую систему считают правой. Иначе говоря, если сравнить направление Х с большим пальцем руки, то указательный отвечает за Y, а средний за Z.

Аналогично образуется левая система координат. Обе системы совместить невозможно, так как соответствующие оси не совпадут.

Координаты точки в декартовой системе координат на плоскости

Для начала отложим точку М на координатной оси Ох. Любое действительное число xM равняется единственной точке М, расположенной на данной прямой. Если точка расположена на координатной прямой на расстоянии 2 от начала отсчета по положительному направлению, то она равна 2 , если -3, то соответственное расстояние 3. Ноль – это начало отсчета координатных прямых.

Иначе говоря, каждая точка М, расположенная на Ox, равна действительному числу xM . Этим действительным числом и является ноль, если точка M расположена в начале координат, то есть на пересечении Ox и Оу. Число длины отрезка всегда положительно, если точка удалена в положительном направлении и наоборот.

Имеющееся число xM называют координатой точки М на заданной координатной прямой.

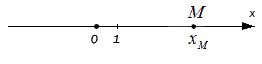
Возьмем точку как проекцию точки Mx на Ох, а как проекцию точки My на Оу. Значит, через точку М можно провести перпендикулярные осям Оx и Оу прямые, где послучим соответственные точки пересечения  Mx и My .

Тогда точка Mx на оси Ох имеет соответствующее число xM , а My на Оу – yM. На координатных осях это выглядит так:

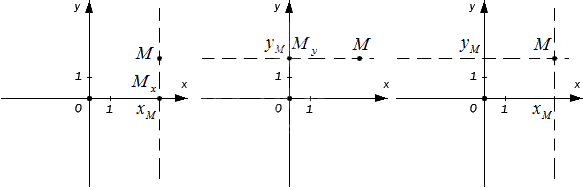
Каждая точка M на заданной плоскости в прямоугольной декартовой системе координат имеет одну соответствующую пару чисел (xM, yM), называемую ее координатами. Абсцисса M – это xM , ордината M – это yM .

Обратное утверждение также считается верным: каждая упорядоченная пара (xM, yM) имеет соответствующую заданную в плоскости точку.

Координаты точки в прямоугольной системе координат в трехмерном пространстве

Определение точки М в трехмерном пространстве. Пусть имеются Mx, My, Mz,  являющиеся проекциями точки М на соответствующие оси Ох, Оу, Оz. Тогда значения этих точек на осях Ох, Оу, Оz примут значения xM, yM, zM. Изобразим это на координатных прямых.

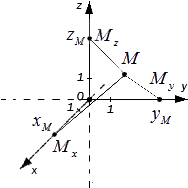
Чтобы получить проекции точки M, необходимо добавить перпендикулярные прямые Ох, Оу, Оz продолжить и изобразит в виде плоскостей, которые проходят через M. Таким образом, плоскости пересекутся в Mx, My, Mz

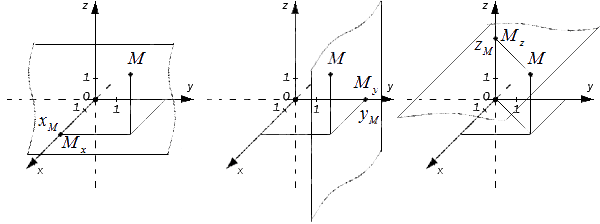
Каждая точка трехмерного пространства имеет свои данные (xM, yM, zM) , которые имеют название координаты точки M, , xM, yM, zM- это числа, называемые абсциссой, ординатой и аппликатой заданной точки M. Для данного суждения верно и обратное утверждение: каждая упорядоченная тройка действительных чисел (xM, yM, zM) в заданной прямоугольной системе координат имеет одну соответствующую точку M трехмерного пространства.

Прямоугольная система координат

Чтобы определить понятие координат точек, нам необходимо ввести систему координат, в которой мы и будем определять ее координаты. Одна и та же точка в разных системах координат может иметь различные координаты. Здесь мы будем рассматривать прямоугольную систему координат в пространстве.

Возьмем в пространстве точку $O$ и введем для нее координаты $(0,0,0)$. Назовем ее началом системы координат. Проведем через нее три взаимно перпендикулярные оси $Ox$, $Oy$ и $Oz$, как на рисунке 1. Эти оси будут называться осями абсцисс, ординат и аппликат, соответственно. Осталось только ввести масштаб на осях (единичный отрезок) – прямоугольная система координат в пространстве готова (рис. 1)

Координаты точки

Теперь разберем, как определяют в такой системе координаты любой точки. Возьмем произвольную точку $M$ (рис. 2).

Построим на координатных осях прямоугольный параллелепипед, так, что точки $O$ и $M$ противоположные его вершины (рис. 3).

«Координаты точки и координаты вектора. Как найти координаты вектора» 👇

Тогда точка $M$ будет иметь координаты $(X,Y,Z)$, где $X$ – значение на числовой оси $Ox$, $Y$ – значение на числовой оси $Oy$, а $Z$ – значение на числовой оси $Oz$.

Координаты вектора по двум точкам и формула нахождения

Чтобы узнать, как найти вектор по координатам двух точек, необходимо рассмотреть введенную нами ранее систему координат. В ней от точки $O$ по направлению оси $Ox$ отложим единичный вектор $overline{i}$, по направлению оси $Oy$ – единичный вектор $overline{j}$, а единичный вектор $overline{k}$ нужно направлять по оси $Oz$.

Для того чтобы ввести понятие координат вектора, введем следующую теорему (здесь ее доказательство мы рассматривать не будем).

Так как векторы $overline{i}$, $overline{j}$ и $overline{k}$ построены на координатных осях прямоугольной системы координат, то они, очевидно, не будут принадлежать одной плоскости. Значит любой вектор $overline{δ}$ в этой системе координат, по теореме 1, может принимать следующий вид

$overline{δ}=moverline{i}+noverline{j}+loverline{k}$ (1)

где $n,m,l∈R$.

Линейные операции над векторами