
Когда мы строим ломаную или кривую, иногда необходимо вместо привычных декартовых X,Y-координат задавать точку кривой через угол и расстояние. Ни в GDI, ни в GDI+, нет инструментов, чтобы задать координаты точки по углу от произвольной прямой и расстоянию.
Зато координаты можно очень легко посчитать. Вот этим сейчас и займемся. А потом найдем угол между двумя прямыми.
Найти координаты по углу и расстоянию
Если прямая, от которой необходимо отложить угол, параллельна оси X, формулы для нахождения координат достаточно очевидны.

Рис1. Прямая отстоит на угол от оси X
Где:
L — расстояние, или длина прямой (P1, P2)
А — угол, на который отстоит прямая (P1, P2) от прямой (P0, P1). Отрицательное значение угла означает — против часовой стрелки.
Теперь придадим прямой (P0, P1) наклон.

A (синий) — это угол, на который отстоит (P1, P2) от прямой (P0, P1);
В (красный) — угол на между прямой (P0, P1) и осью X;
C (оранжевый) — угол на между прямой (P1, P2) и осью X.
Задача сводится к нахождению угла C. Как нетрудно убедится по рисунку:
Угол А нам известен. Угол B найдем через arctan2. Функция arctan2 есть во множестве языков. Возможно, будет называться atan2.
Таким образом, функция для нахождения координат точки выглядит так:
|
// Посчитать координаты по углу и расстоянию // P0,P1 – прямая, точка считается от P1 // A – угол отклонения от (P0,P1), градусы // L – расстояние до точки function CalcPolarCoord(const P0, P1: TPointF; A, L: Single): TPointF; var B, C: Single; begin B := arctan2(p0.Y–p1.Y, p0.X–p1.x); C := A * PI/180 + B; Result.X := p1.X + cos(C) * L; Result.Y := p1.Y + sin(C) * L; end; |
И что, всегда работает? Всегда.

Найти угол по трем координатам
Рассмотрим процесс, обратный нахождению координаты по углу. Теперь будем находить угол между отрезками ломаной. Мы в плоскости работаем в декартовых координатах. Меняем мышкой координаты X, Y. А ситуация может возникнуть такая, что для предметной области важно хранить данные в полярных координатах.
Функция такая:
|
// Нахождение угла между тремя точками в градусах // Точки заданы массивом из трех элементов function CalcPolarAngle(const pnt: Array of TPointF): Single; var a1, a2: Single; begin if Length(pnt)<3 then Exit; a1 := ArcTan2(pnt[0].y–pnt[1].y, pnt[0].x–pnt[1].x) * 180/PI; a2 := ArcTan2(pnt[2].y–pnt[1].y, pnt[2].x–pnt[1].x) * 180/PI; Result := (a2 – a1); end; |
Более продвинутую функцию можно найти в статье Пересечение прямых, угол и координаты пересечения.

Друзья, спасибо за внимание!
Оставляйте комментарии. Подписывайтесь на телегу.
В группе комментариев уже потихоньку становится интересно )))
Veinar, я думаю, что существуют две точки, принадлежащие заданной прямой и находящиеся на заданном расстоянии от заданной плоскости. Не вдаваясь в подробности вычислений, могу предложить два способа решения задачи.
Первый способ заключается в том, что нужно найти плоскости, параллельные заданной и расположенные на заданном расстоянии от неё. Затем нужно найти точки пересечения заданной прямой с найденными плоскостями.
Второй способ заключается в том, что находится точка пересечения заданных прямой и плоскости. Затем находятся расстояния от точки [math](1,~0,~-1)[/math] до заданной плоскости и до найденной выше точки. Затем рассматриваются подобные треугольники, расположенные в плоскости, перпендикулярной заданной плоскости, и проходящей через заданную прямую.
Вроде бы так… 
|
26 / 26 / 3 Регистрация: 13.04.2012 Сообщений: 61 |
|
|
1 |
|
Найти координаты точки, зная расстояние до других точек24.05.2015, 00:49. Показов 12530. Ответов 1
Здравствуйте! Есть 4 точки в трехмерной системе координат: A, B, C, D. Заранее спасибо!
0 |
|
6353 / 4062 / 1509 Регистрация: 09.10.2009 Сообщений: 7,550 Записей в блоге: 4 |
|
|
24.05.2015, 11:29 |
2 |
|
А алгебру не забыли? Потому что ваша задача сводится к решению системы
1 |
|
IT_Exp Эксперт 87844 / 49110 / 22898 Регистрация: 17.06.2006 Сообщений: 92,604 |
24.05.2015, 11:29 |
|
Помогаю со студенческими работами здесь
Найти координаты точек С, если известны координаты точек А Как получить комплементарный (контрастный) цвет, зная координаты точки на окружности Составить уравнение сторон треугольника, зная координаты точки и уравнения высоты и биссектрисы Координаты вершины №1 Искать еще темы с ответами Или воспользуйтесь поиском по форуму: 2 |
Простейшие задачи аналитической геометрии на плоскости

1. Расстояние между двумя точками.
Теорема
1.
Для любых двух точек
 и
и плоскости расстояние
плоскости расстояние между ними выражается формулой:
между ними выражается формулой:
 .
.
(1.1)
Например,
если
даны точки
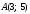 и
и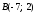 ,
,
то расстояние между ними:
 .
.
2. Площадь треугольника.
Теорема
2.
Для любых точек 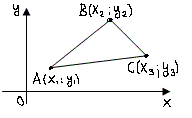
 ,
,
не лежащих на одной прямой, площадь
треугольника
 выражается формулой:
выражается формулой:
 .
.
(1.2)
Например,
найдем площадь треугольника, образованного
точками
 ,
, и
и .
.
 .
.
Замечание.
Если площадь треугольника равна нулю,
это означает, что точки лежат на одной
прямой.
3. Деление отрезка в заданном отношении.
Пусть
на плоскости дан произвольный отрезок
![]()
и
пусть
 –любая
–любая
точка этого отрезка, отличная от точек
концов. Число
 ,
,
определенное равенством ,
,
называетсяотношением,
в
котором точка
 делит отрезок
делит отрезок![]() .
.
Задача
о делении отрезка в данном отношении
состоит в том, чтобы по данному отношению
![]() и данным координатам точек
и данным координатам точек
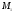 и
и
 найти координаты точки
найти координаты точки .
.
Теорема
3.
Если
точка
![]() делит отрезок
делит отрезок![]()
в
отношении 
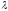 ,
,
то
координаты этой точки определяются
формулами:
 (1.3), где
(1.3), где – координаты точки
– координаты точки ,
, – координаты точки
– координаты точки .
.
Следствие:
Если
![]() – середина отрезка
– середина отрезка
 ,
,
где
 и
и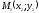 ,
,
то (1.4) (т.к.
(1.4) (т.к. ).
).
Например.
Даны точки
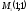 и
и .
.
Найти координаты точки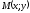 ,
,
которая в два раза ближе к ,
,
чем к
![]()
Решение:
Искомая точка
![]() делит
делит
отрезок
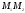 в
в
отношении
 так как
так как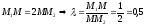 ,
,
тогда ,
,![]() ,
,
получили
 .
.
Полярные координаты
Наиболее
важной после прямоугольной системы
координат является полярная система
координат. Она состоит из некоторой
точки
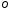 ,
,
называемойполюсом,
и исходящего из нее луча
 –полярной
–полярной
оси.
Кроме того, задается единица масштаба
для измерения длин отрезков.
Пусть
задана полярная система координат и
пусть
 – произвольная точка плоскости. Пусть
– произвольная точка плоскости. Пусть![]()
–
расстояние от точки
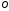 до
до
точки
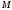 ;
; – угол, на который нужно повернуть
– угол, на который нужно повернуть
полярную ось для совмещения с лучом .
.
Полярными
координатами точки
 называются числа
называются числа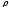 и
и .
.
При этом число считается первой координатой и называетсяполярным
считается первой координатой и называетсяполярным
радиусом,
число
 – второй координатой и называетсяполярным
– второй координатой и называетсяполярным
углом.
Обозначается
 .
.
Полярный радиус может иметь любое
неотрицательное значение:
 .
.
Обычно считают, что полярный угол
изменяется в следующих пределах: .
.
Однако в ряде случаев приходится
определять углы, отсчитываемые от
полярной оси по часовой стрелке.
Связь между полярными координатами точки и ее прямоугольными координатами.
Будем
считать, что начало прямоугольной
системы координат находится в полюсе,
а положительная полуось абсцисс совпадает
с полярной осью.
Пусть
 – в прямоугольной системе координат и
– в прямоугольной системе координат и – в полярной системе координат. Определен
– в полярной системе координат. Определен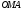 – прямоугольный треугольник с
– прямоугольный треугольник с .
.
Тогда![]() (1.5).
(1.5).
Эти формулы выражают прямоугольные
координаты через полярные.
С
другой стороны, по теореме Пифагора
 и
и![]()
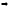
![]() (1.6)
(1.6)
– эти формулы, выражают полярные
координаты через прямоугольные.
Заметим,
что формула
 определяет два значения полярного угла
определяет два значения полярного угла ,
,
так как .
.
Из этих двух значений угла выбирают тот, при котором удовлетворяются
выбирают тот, при котором удовлетворяются
равенства .
.
Например,
найдем полярные координаты точки

 .
. .
. или
или ,
,
т.к. I
I
четверти .
.
Пример
1:
Найти точку, симметричную точке 

относительно
биссектрисы первого координатного
угла.
Решение:
Проведем
через точку А
прямую l1,
перпендикулярную биссектрисе l
первого координатного угла. Пусть
 .
.
На прямой
l1
отложим отрезок
СА1,
равный
отрезку
АС.
Прямоугольные треугольники
АСО
и
А1СО
равны
между собой (по двум катетам). Отсюда
следует, что |ОА|
= |OA1|.
Треугольники
ADO
и
ОЕА1
также равны между собой (по гипотенузе
и острому углу). Заключаем, что
|AD|
= |ОЕ|
= 4,
|OD| = |EA1|
=
2, т.е. точка имеет координаты х
= 4, у = -2,
т.е. А1(4;-2).
Отметим,
что имеет место общее утверждение: точка
A1,
симметричная точке

относительно биссектрисы первого и
третьего координатных углов, имеет
координаты
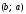 ,
,
то есть .
.
Пример
2:
Найти точку, в которой прямая, проходящая
через точки
 и
и
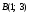 ,
,
пересечет ось
Ох.
Решение:
Координаты
искомой точки
С
есть (x;
0). А так как точки
А,
В и
С
лежат на одной прямой, то должно
выполняться условие (x2-x1)(y3-y1)-(x3-x1)(y2-y1)=0
(формула (1.2), площадь треугольника ABC
равна
нулю!), где

–
координаты точки А,
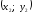 – точкиВ,
– точкиВ,
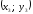 – точкиС.
– точкиС.
Получаем
 ,
,
т.е.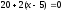 ,
,
 ,
,
 .
.
Следовательно, точка
С
имеет координаты
 ,
, ,
,
т.е. .
.
Пример
3: В
полярной системе координат заданы точки
 ,
, .
.
Найти:
а)
расстояние между точками

и
 ;
;
б)
площадь треугольника
ОМ1М2
(О
– полюс).
Решение:
а)
Воспользуемся формулами (1.1) и (1.5):

 ,
,
то
есть,
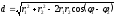 .
.
б)
пользуясь формулой для площади
треугольника со сторонами
а
и
b
и углом
 между ними (
между ними ( ),
),
находим площадь треугольника
ОМ1М2.
 .
.
На чтение 4 мин Просмотров 1.2к.
Рассмотрим первый пример. Пусть в плоскости координат задан двумя точками некий отрезок. В данном случае его длину мы можем найти, применяя теорему Пифагора.
Итак, в системе координат начертим отрезок с заданными координатами его концов (x1; y1) и (x2; y2) . На оси X и Y из концов отрезка опустим перпендикуляры. Отметим красным цветом отрезки, которые являются на оси координат проекциями от исходного отрезка. После этого перенесем параллельно к концам отрезков отрезки-проекции. Получаем треугольник (прямоугольный). Гипотенузой у данного треугольника станет сам отрезок АВ, а его катетами являются перенесенные проекции.
Вычислим длину данных проекций. Итак, на ось Y длина проекции равна y2-y1, а на ось Х длина проекции равна x2-x1. Применим теорему Пифагора: |AB|² = (y2 – y1)² + (x2 – x1)². В данном случае |AB| является длиной отрезка.
Если использовать данную схему для вычисления длины отрезка, то можно даже отрезок и не строить. Теперь высчитаем, какова длина отрезка с координатами (1;3) и (2;5). Применяя теорему Пифагора, получаем: |AB|² = (2 – 1)² + (5 – 3)² = 1 + 4 = 5. А это значит, что длина нашего отрезка равна 5:1/2.
Рассмотрим следующий способ нахождения длины отрезка. Для этого нам необходимо знать координаты двух точек в какой-либо системе. Рассмотрим данный вариант, применяя двухмерную Декартову систему координат.

Итак, в двухмерной системе координат даны координаты крайних точек отрезка. Если проведем прямые лини через эти точки, они должны быть перпендикулярными к оси координат, то получим прямоугольный треугольник. Исходный отрезок будет гипотенузой полученного треугольника. Катеты треугольника образуют отрезки, их длина равна проекции гипотенузы на оси координат. Исходя из теоремы Пифагора, делаем вывод: для того чтобы найти длину данного отрезка, нужно найти длины проекций на две оси координат.
Найдем длины проекций (X и Y) исходного отрезка на координатные оси. Их вычислим путем нахождения разницы координат точек по отдельной оси: X = X2-X1, Y = Y2-Y1.
Рассчитаем длину отрезка А, для этого найдем квадратный корень:
Если наш отрезок расположен между точками, координаты которых 2;4 и 4;1, то его длина, соответственно, равна √((4-2)²+(1-4)²) = √13 ≈ 3,61.
Этот онлайн калькулятор рассчитывает длину отрезка и координаты середины отрезка (средней точки) по декартовым координатам концов отрезка. Отрезок и средняя точка отображаются на графике, также на графике показан графический способ нахождения середины отрезка.
Эта страница существует благодаря следующим персонам
![]()
Timur
- Статья : Расчет длины отрезка и координат середины отрезка по двум точкам – Автор, Переводчик en – ru
- Калькулятор : Расчет длины отрезка и координат середины отрезка по двум точкам – Автор, Переводчик en – ru
Этот онлайн калькулятор рассчитывает длину отрезка и координаты середины отрезка по введенным декартовым координатам двух точек – концов отрезка.
Формула вычисления расстояния между двумя точками и это формула длины гипотенузы прямоугольного треугольника . Координаты середины отрезка – среднее арифметическое координат точек .
Отрезок и средняя точка отображаются на графике. Также среднюю точку можно найти построением. Для этого на графике надо построить две дуги с центрами на концах отрезка и с радиусом равным длине отрезка. Затем надо построить прямую линию между точками пересечения дуг. Эта линия пересечет исходный отрезок в середине.
Отрезком обозначают ограниченный двумя точками участок прямой. Точки – концы отрезка.
Общеизвестный факт, что каждая точка А плоскости имеет свои координаты (х, у).
В данном примере вектор AB задан координатами (х2— х1, y2— y1). Квадрат длины вектора будет равен сумме квадратов его координат. Следовательно, расстояние d между точками А и В, или, что то же самое, длина вектора АВ, вычисляется согласно формуле:
Эта формула длины отрезка предоставляет возможность рассчитывать расстояние между двумя произвольными точками плоскости, при условии, что известны координаты этих точек
Вышеуказанную формулу длины отрезка можно доказать и другим способом. В системе координат заданы координаты крайних точек отрезка координатами его концов(х1y1) и (х2,у2).
Прочертим прямые лини через эти точки перпендикулярно к осям координат, в результате имеем прямоугольный треугольник. Первоначальный отрезок является гипотенузой образовавшегося треугольника. Катеты треугольника сформированы отрезками, их длиной будет проекция гипотенузы на оси координат.
Установим длину этих проекций.
На ось у длина проекции равна y2 – y1, а на ось х длина проекции равна х2 – х1. На основании теоремы Пифагора видим, что |AB|² = (y2 – y1)² + (x2 – x1)².
В рассмотренном случае |AB| выступает длиной отрезка.
Вычислим длину отрезка АВ, для этого извлечем квадратный корень. Результатом является все та же формула длины отрезков по известным координатам конца и начала.

 Как найти площадь сектора окружности, зная координаты центра окружности и двух равноудаленных точек
Как найти площадь сектора окружности, зная координаты центра окружности и двух равноудаленных точек