Координаты – это величины, которые отображают местоположение конкретной точки в пространстве. Они определяются путем проведения геодезических измерений, к которым относится триангуляция, а также построение тахеометрического и теодолитного хода.
На плоскости координаты можно вводить неисчислимым количеством способов и через различные математические задачи создавать координатные системы. Благодаря вычислению координаты точек теодолитного хода на карту или план наносятся как эти самые пункты, так и жесткие объекты в зоне их видимости.
Содержание
- 1 Общие понятия о системах координат в геодезии
- 2 Исходные данные для расчетов
- 3 Уравнивание измерений
- 4 Вычисление дирекционных углов вершин
- 5 Решение прямой и обратной геодезической задачи
- 5.1 Создавайте будущее вместе с нами
- 6 Приращение координат и их увязка
- 7 Как вычислить координаты точек хода
- 8 Нанесение точек на план и его оформление
Общие понятия о системах координат в геодезии
Столь глубокие познания о строении и форме Земли, которые человек осваивал на протяжении веков, сегодня позволяют создавать невероятно точные координатные системы и картографические проекции.
Координатные системы заданы двумя направлениями на плоскости, а в пространстве – тремя. Осевые направления всегда перпендикулярны друг другу, а ориентированы горизонтально и вертикально. Их пересечение и определяет местоположение точки в заданной системе.

В геодезии координатные системы разделены на следующие две группы:
- Прямолинейные прямоугольные. К ним причисляют проекцию Гаусса-Крюгера, индивидуальные референцные и местные системы.
- Полярные. Это геодезические, географические, астрономические, а также геоцентрические и топоцентрические координаты.
Теодолитный ход можно считать самым распространённым плановым обоснованием. Он не требует дорогостоящего и высокоточного оборудования, но помогает создать надежную плановую основу на территориях со сложной местностью. Его развивают от пунктов государственных геодезических сетей (ГГС) и сетей сгущения с уже установленными координатами.
Вычисляются координаты точек замкнутого и разомкнутого теодолитного хода посредством нахождения дирекционных углов его сторон и решения прямой геодезической задачи. Но перед этим следует проверить, соответствуют ли измерения нормативным требованиям.
Исходные данные для расчетов
Теодолитный ход может быть проложен в виде замкнутой фигуры или ломаной линии. Это зависит от характера снимаемой местности. Он является отличной геодезической основой для многих инженерных изысканий.
По итогу проведенных измерений составляется план или карта местности, а все вычисления заносятся в специальные ведомости. В нее заносятся следующие данные:
– горизонтальные углы пунктов;
– измеренное расстояние между ними;
– координаты пункта ГГС или опорной сети;
– значение исходного дирекционного угла.

Для привязки хода к пункту ГГС или опорной сети необходимо определить местоположение одной его точки относительно этого пункта. Это можно сделать, измерив расстояние и горизонтальный примычной угол между ними. Такая процедура называется передачей координат и дирекционных углов.
Уравнивание измерений
Не существует еще методов, позволяющих без погрешностей выполнить измерения, но уравнивание позволит свести их к минимуму. Для замкнутого хода первым делом рассчитывается невязка:
(f_{beta}=sum beta _{изм}-sum beta_{теор})
где:
(sum beta _{изм}=beta _{1}+beta _{2}+…beta _{n}) – сумма углов пунктов;
(sum beta _{теор}) – теоретическая сумма, определяемая выражением:
(sum beta _{теор}=180^{circ}cdot (n-2))
(n) – количество углов.
Вычисленная невязка допустима, если соответствует требованию:
(beta _{испр}=pm 1,5sqrt{n})
Когда полученное значение не превышает допуск, то невязку разбрасываются между углами с противоположным знаком равномерно. Можно также распределить ее только между самыми короткими сторонами. Учитывая поправки и их знак, вычисляют исправленные углы:
(beta _{испр}=beta _{изм}+delta _{beta })
(delta _{beta }) – поправка.

Правильность уравнивания подтверждается следующим условием:
(sum beta _{теор}=beta _{испр})
Поскольку разомкнутый ход является ломаной линией, математические расчеты для него проводятся как для хода, в котором две исходные стороны и дирекционных угла. Для него применяют следующие выражения:
для левых углов:
(sum beta _{теор}=alpha _{кон}-alpha _{нач}+ncdot 180^{circ})
правых:
(sum beta _{теор}=alpha _{нач}-alpha _{кон}+ncdot 180^{circ})
Для упрощения дальнейших вычислений поправки могут быть распределены с целью округления десятых долей минут в углах до целых минут.
Вычисление дирекционных углов вершин
В геодезии за дирекционный угол ((alpha )) принимают угол, который начинают отсчитывать от северного направления осевого меридиана и до заданной стороны. Он измеряется от 0 до 360°. Вычислить его значение для правой стороны хода можно по формуле ниже:
(alpha _{n}=alpha _{n-1}+eta )
(eta=180^{circ} -beta _{пр.испр})
(a _{n}=alpha _{n-1}+180^{circ}-beta _{пр.испр})
Для левой стороны это выражение будет иметь такой вид:
(alpha _{n}=alpha _{n-1}+eta )
(eta=beta _{лев.исп.}-180^{circ} )
(a _{n}=alpha _{n-1}-180^{circ}+beta _{лев.исп.})
где:
(alpha _{n-1}) – дирекционный угол предыдущей стороны, а (n) – последующей;
(beta _{пр.исп.}) – значение правого исправленного угла между сторонами отрезка, а (beta _{лев.исп.})– левой стороны.

Вычисления выполнены верно при равенстве заданного α и начальной стороны теодолитного хода. Если дирекционный угол больше 360° или имеет отрицательное значение, то это говорит об ошибке в расчетах.
После дирекционных углов необходимо найти румбы – острые углы, отсчитываемые от 0 до 90°. Они берут свое начало от ближайшего окончания осевого меридиана до ориентирной линии.
| Четверть румба | Название четверти | Пределы изменения α | Формула румба | Знаки приращения | |
| ΔХ | ΔУ | ||||
| I | С.В. (северо-восток) | 0° – 90° | r = α | + | + |
| II | Ю.В. (юго-восток) | 90°-180° | r = 180° – α | – | + |
| III | Ю.З. (юго-запад) | 180°-270° | r = α – 180° | – | – |
| IV | С.З. (северо-запад) | 270°-360° | r = 360° – °α | + | – |
Таблица 1. Связь дирекционного угла и румба
Вычисление румбов и их знаков приращений зависит от четверти геодезических прямоугольных координат, в которой находится линия ориентирования.
Решение прямой и обратной геодезической задачи
Суть прямой геодезической задачи состоит в том, чтобы определить координатные значения вершины при заданных координатах соседней. Это возможно при известной горизонтальном проложении между ними и дирекционным углом линии. Для ее решения используются следующие формулы:
(Delta X=dcdot cos alpha )
(Delta Y=dcdot sin alpha )
где:
Создавайте будущее вместе с нами
Присоединяйтесь к нашей команде: мы создаем финтех-сервисы для 28 млн клиентов и опережаем рынок на 5 лет. Работаем на результат и делаем больше, чем от нас ждут.
(d)–расстояния между соседними пунктами.
(alpha ) – значение дирекционного угла.
Знаки приращений зависят от четверти, определяемой дирекционным углом направления. Координатные значения конечной точки линии равняется сумме координаты начальной и приращения между ними. Из этого следует следующие выражение:
(X_{2}=X_{1}+Delta X)
(Y_{2}=Y_{1}+Delta Y)
(X_{2}=X_{1}+d_{1-2}cdot cosalpha _{1-2})
(Y_{2}=Y_{1}+d_{1-2}cdot sinalpha _{1-2})

Стоит также упомянуть и обратную геодезическую задачу, которая позволяет определить дирекционный угол, румб и горизонтальное проложение при установленных координатах пунктов теодолитного хода. Вычисления имеют такую последовательность:
(Delta X=X_{2}-X_{1})
(Delta Y=Y_{2}-Y_{1})
определяется румб линии (r_{1-2}):
(tgr=frac{Delta Y}{Delta X})
из этого выходит, что:
(r=arctgfrac|{Delta Y}{Delta X}|)
По знакам приращения определяют четверть, в котором находится направление и по уже известному румбу вычисляют дирекционный угол. Определение горизонтального проложения будет завершающим этапом в решении обратной задачи:
(d=frac{Delta X}{cosalpha })
(d=frac{Delta Y}{sinalpha })
(d=sqrt{Delta X^2+Delta Y^2})
Приращение координат и их увязка
Приращением называют величины, на которые будут увеличены координаты предыдущей точки для вычисления последующей. В основу этих расчетов берется уже знакомая формула прямой задачи:
(Delta X=dcdot cos alpha )
(Delta Y=dcdot sin alpha )
Полученные значения также необходимо уровнять, чтобы равномерно распределить погрешности и получить наиболее точный результат. Начинают расчеты с определения невязок. Поскольку сумма проекций в сторонах многоугольной замкнутой фигуры равняется нулю, для вычисления невязок пунктов замкнутого хода используют следующую формулу:
(f_{X}=sum Delta X_{выч}-sum Delta X_{теор};sum Delta X_{теор}=0)
(f_{Y}=sum Delta Y_{выч}-sum Delta Y_{теор};sum Delta Y_{теор}=0)
(sum Delta X_{выч},sum Delta Y_{выч}) – суммы приращений, рассчитанные с учетом знаков для замкнутого и разомкнутого хода;
(sum Delta X_{теор},sum Delta Y_{теор}) – теоретические суммы приращений.
Если невязки не находятся в допуске, необходимы повторные расчеты, чтобы определить ошибку и устранить ее. В противном случае проводятся повторные измерения на участке.

Вследствие влияния погрешностей на ход, он будет разомкнут на величину , которая представляет собой абсолютную невязку в его периметре. По этому причине проверяется соответствие условию допустимости его невязок.
- Абсолютное значение:
(f_{p}=sqrt{f_{x}^2+f_{y}^2})
- Относительное
(f_{отн}=frac{f_{абс}}{P})
P – периметр хода, полученный суммированием всех его сторон.
Допустимая невязка должна удовлетворять условие 1/2000, а при соответствии выражению (|f_{отн}|leq |f_{доп}|) выполняют ее распределение с противоположным знаком. Однако перед этим рассчитывают поправки приращений, которые определяют для каждой стороны:
(delta _{x_{i}}=-frac{f_{x}d_{i}}{P});(delta _Delta {y_{i}}=-frac{f_{y}d_{i}}{P})
(delta _{x_{i}},delta _{y_{i}})– значения поправок в приращениях.
Чтобы упростить дальнейшие расчеты поправки, необходимо округлить их до 0,01 м.
Для разомкнутого хода за теоретическую сумму приращений берется разность между двумя соседними точками.
(f_{X}=sum Delta X_{выч}-sum Delta X_{теор}; sum Delta X_{теор}=x_{B}-x_{A})
(f_{Y}=sum Delta Y_{выч}-sum Delta Y_{теор}; sum Delta Y_{теор}=y_{B}-y_{A})
Для обоих ходов поправки имеют противоположный приращению знак. Уравнивание выполнено верно, если сумма исправленных приращений равна или максимально приближена к нулю.
Как вычислить координаты точек хода
Вычисляют значения координат вершин замкнутого и разомкнутого теодолитного хода сначала для опорного пункта, а потом уже для остальных его вершин.

Значение следующего пункта хода вычисляют суммированием предыдущего пункта и исправленного приращения. Это наглядно отображено в формуле:
(X_{n}=X_{n-1}+Delta X _{n-1(испр)})
(Y_{n}=Y_{n-1}+Delta Y _{n-1(испр)})
(X_{n-1},Y_{n-1}) – координатные значения предыдущего пункта
(Delta X_{теор}=x_{B}-x_{A},Delta Y_{теор}=y_{B}-y_{A}) – исправленные приращения.
В данных формулах применяется алгебраическая сумма, поэтому знаки также необходимо учитывать при расчетах. Если в конце вычислений получены координатные значения начальной точки, то они выполнены правильно.
Нанесение точек на план и его оформление
После завершения обработки измерений, которые были проведены на местности, составляется ее контурный или ситуационный план. Построение плана теодолитного хода происходит поэтапно и состоит из следующих этапов:
- Создание координатной сетки. Ход необходимо равномерно отобразить на плане, поэтому сначала определяют середину листа. Через весь лист проводят два диагональных отрезка, от которых и будет строиться сетка, состоящая из отрезков по 10 см. Допускается погрешность не более 0,2 мм. Определить их количество можно по формуле:
(N_{X}=(x_{max}-x_{min})/200)
(N_{Y}=(y_{max}-y_{min})/200)
(x_{max},y_{max}) – наибольшие значения координат, увеличенные до большего значения, которое кратное 200.
(x_{min},y_{min}) – наименьшее значение, но уменьшенное и кратное 200.
200 – длина стороны квадрата в метрах , которая в плане равна 10 см.

- Обозначение точек на плане. Лучше всего подходят для нанесения координат пунктов на план циркуль и масштабная линейка. Соседние вершины должны иметь такое же расстояние и дирекционный угол, как записано в ведомости.
- Нанесение ситуации на план. Участки снимаемой местности в процессе полевых работ отображают на специальном схематическом бланке – абрисе. В дальнейшем их используют для переноса контуров, линий и вершин точек. Ситуация изображается на планах и картах специальными обозначениями – условными знаками.
- Оформление плана в соответствии с требованиями. Все топографические материалы должны строго соответствовать нормативным документам. В частности, нужно выдерживать заданные очертания и их размеры. Должны присутствовать пояснительные надписи, легенда, а также указан масштаб.
Сегодня координаты замкнутого теодолитного хода вычисляются значительно проще, а создание всех графических материалов выполняется при помощи специализированных программ автоматически. Это значительно ускорило процесс выполнения геодезических работ и других инженерных изысканий.
Определение геодезических координат по топографической карте.
Северная
и южная линии внутренней рамки листа
топографической карты являются
параллелями, западная и восточная –
меридианами. Во всех четырех углах листа
карты подписаны значения широты и
долготы.
Между
внутренней и внешней рамками выделена
градусная рамка в виде двойной линии с
переменной заливкой белым и черным
цветами. Каждый интервал (белый или
черный) равен 1’. Этот минутный интервал
разделен с помощью точек на 10-секундные
отрезки. Если соединить аналогичные
точки на северной и южной стороне листа
получим меридиан с известной долготой.
Соответственно при соединении аналогичных
точек на западной и восточной стороне
получим параллель с известной широтой.
Чтобы
определить геодезические координаты
(широту и долготу) точки нужно через нее
провести перпендикуляры к градусной
рамке листа топографической карты (рис.
1).
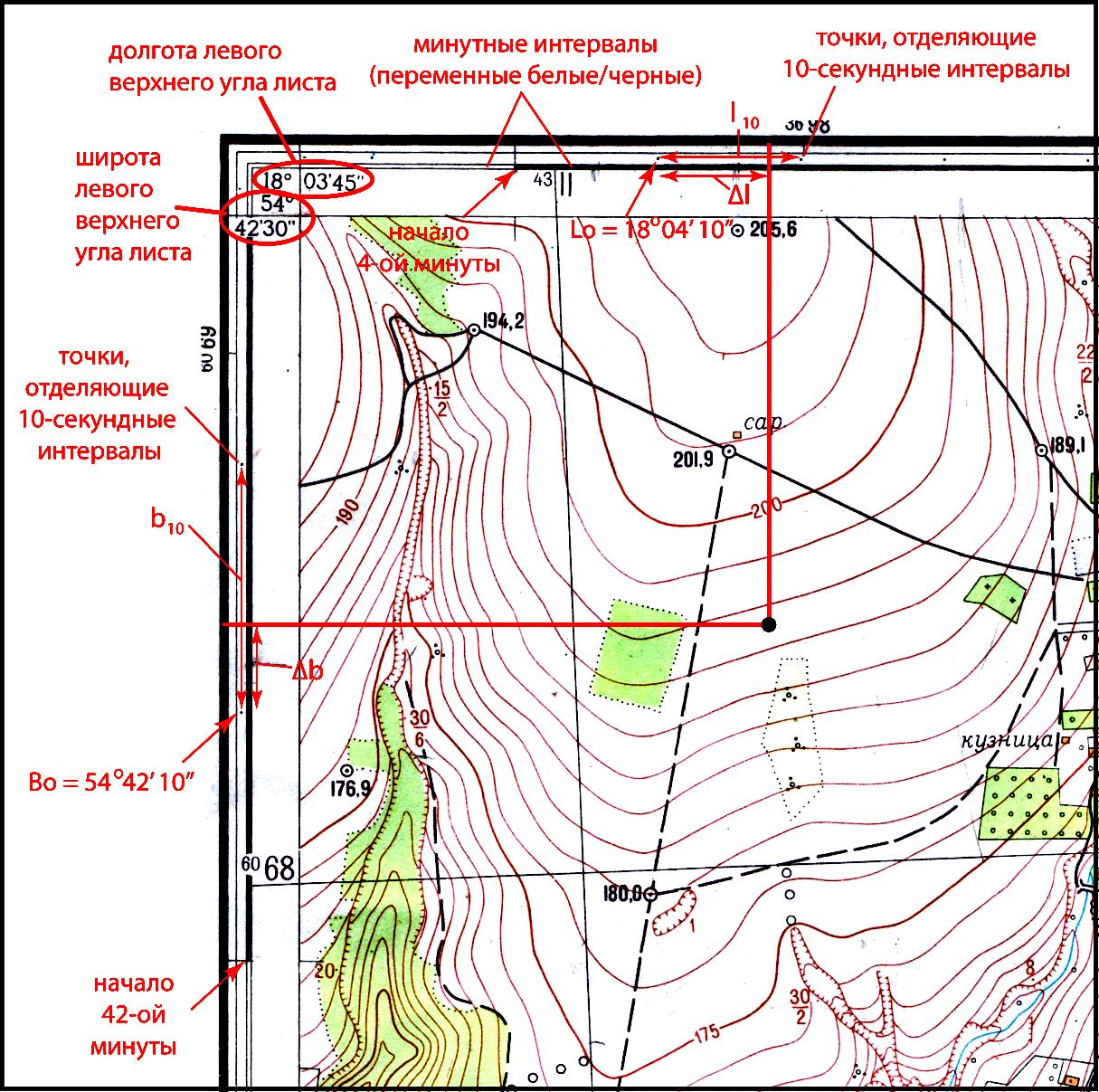
Рис.
1. Определение геодезических координат.
Проводим
перпендикуляр к западной стороне листа.
Находим пересечение с градусной рамкой.
Далее определяем широту ближайшей южной
точки, отделяющей 10-секундные интервалы
(В0).
Измеряем длину 10-секундного интервала
(b10)
и расстояние от ближайшей точки до
отметки пересечения перпендикуляра с
градусной рамкой (∆b).
Широту
заданной точки можно вычислить по
формуле B
= В0
+ (∆b
* 10’’ / b10).
Чтобы
определить долготу заданной точки,
необходимо опустить перпендикуляр на
южную сторону листа карты, определить
долготу ближайшей западной точки,
отделяющей 10-секундные интервалы (L0).
Далее процесс аналогичен предыдущему,
формула выглядит как L
= L0
+ (∆l
* 10’’ / l10).
Масштаб
– величина, характеризующая степень
уменьшения длины отрезка на местности
при его отображении на карте. На картах
масштаб указывается обязательно. Подпись
масштаба возможна в нескольких вариантах.
Численный
масштаб
представляется в виде дроби с единицей
в числителе, например, 1 : 10 000, 1 : 100 000
и т.д. Именованный масштаб
– это запись вида «в 1 сантиметре 100
метров», «в 1 сантиметре 1 километр».
Линейный
масштаб
дается в виде масштабной линейки, которая
облегчает измерение длин по топографической
карте. На топографических картах, как
правило, даются все три варианта (рис.
2).
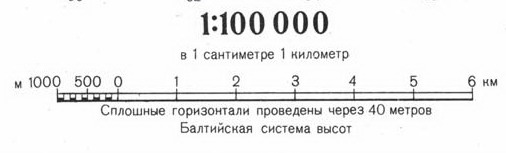
Рис.
2. – Подписи масштаба топографических
карт (сверху вниз: численный, именованный,
линейный).
К
артографическая
проекция
– математически определенный способ
изображения эллипсоида на плоскости.
В России для составления топографических
карт используют проекцию
Гаусса-Крюгера.
Это поперечно-цилиндрическая равноугольная
зональная проекция.
В
проекции Гаусса-Крюгера размер зон для
топографических карт ограничен 6-ю
градусами по долготе. Зоны располагаются
последовательно от нулевого (Гринвичского
меридиана) в направлении с запада на
восток. Т.е. 1-я зона ограничена меридианами
00
и 60
в.д., 2-я – 60
и 120
в.д., 60-я – 60
и 00
з.д.
Через
центр зоны проходит осевой
меридиан,
являющийся касательным к боковой
поверхности гипотетического цилиндра.
Таким образом, для 1-й зоны осевой меридиан
будет иметь долготу 30
в.д.,
2-й – 90
в.д. и т.д. Чтобы определить долготу
осевого меридиана по номеру зоны, можно
воспользоваться формулами:
для
восточного полушария L
= 6*n
– 3
для
западного полушария L
= 180 – 6*(n
– 30) + 3,
где
n
– номер зоны.
Прямоугольные
координаты.
На
топографических картах применяется
зональная прямоугольная система
координат. Координаты – абсцисса и
ордината – определяются в метрах. За
ось
ординат Y
принята линия экватора (рис. 3), а за ось
абсцисс X
– северное направление осевых меридианов
зон. Начало отсчета по оси ординат
смещено на 500 км к западу, чтобы исключить
отрицательные значения ординат.
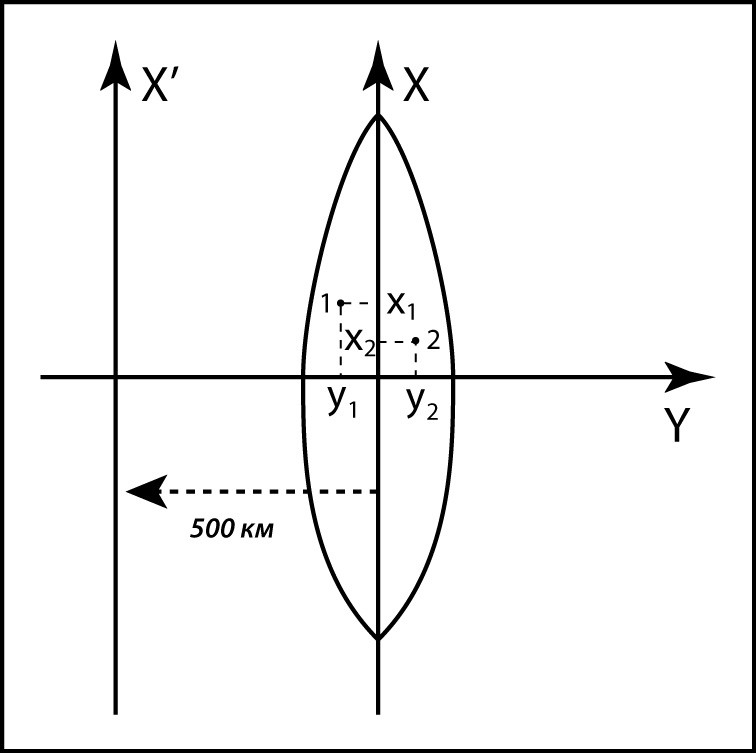
Рис.
3. Система плоских прямоугольных координат
Для
устранения неоднозначности определения
ординат, в ее состав вводится номер зоны
(первые одна или две цифры). Таким образом,
запись ординаты вида «4 312 000»
означает, что заданная точка находится
в 4-й зоне на расстоянии 312 км от смещенного
осевого меридиана (число меньше 500 км,
т.е. точка западнее осевого меридиана).
Абсцисса вида «6 066 000» означает,
что точка находится на расстоянии 6 066
км от экватора.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Актуальные цены на услуги геодезистов в Москве и Московской области в 2022 году.
Прямая геодезическая задача состоит в том, что по известным координатам начального пункта А(хА,уА), линии АВ, дирекционному углу этой линии αАВ и ее горизонтальному проложению sАВ – вычисляют координаты конечной точки В(хВ, уВ). Прямая геодезическая задача решается разными способами, один из них это онлайн решение, которым может воспользоваться любой кому лень разбираться с формулами.
Для точек, расположенных на сфероиде, решение данной задачи представляет значительные трудности. Для точек на плоскости она решается следующим образом.
Дано: Точка А( XA, YA ), SAB и αAB.
Найти: точку В( XB, YB ).
Непосредственно имеем:
ΔX = XB – XA ;
ΔY = YB – YA .
Разности ΔX и ΔY точек последующей и предыдущей называются приращениями. Они представляют собой проекции отрезка АВ на соответствующие оси координат. Их значения находим из прямоугольного прямоугольника АВС:
ΔX = SAB · cos αAB ;
ΔY = SAB · sin αAB .
Так как в этих формулах SAB всегда число положительное, то знаки приращений ΔX и ΔY зависят от знаков cos αAB и sin αAB. Для различных значений углов знаки ΔX и ΔY представлены в таблице ниже.
Таблица знаков приращений координат ΔX и ΔY
| Приращения | Четверть окружности в которую направлена линия | |||
| I (СВ) | II (ЮВ) | III (ЮЗ) | IV (СЗ) | |
| ΔX | + | – | – | + |
| ΔY | + | + | – | – |
При помощи румба, приращения вычисляют по формулам:
ΔX = SAB · cos rAB ;
ΔY = SAB · sin rAB .
Знаки приращениям дают в зависимости от названия румба.
Вычислив приращения, находим искомые координаты другой точки:
XB = XA + ΔX ;
YB = YA + ΔY .
Таким образом можно найти координаты любого числа точек по правилу: координаты последующей точки равны координатам предыдущей точки плюс соответствующие приращения. Прямая геодезическая задача чаще всего используется при вычислении координат в теодолитном ходе.
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 7 июня 2021 года; проверки требуют 3 правки.
Геодези́ческая систе́ма координа́т — система координат, используемая для определения местоположения объектов на Земле. Отсчётной поверхностью является эллипсоид вращения или Ортогональная система координат, представляющий собой референц-версию, то есть адаптированный к какой-либо территории датум, геоцентрической системы координат.
Так как форма Земли является не шаром, для которого подходили бы астрономические координаты, а эллипсоидом, у которого отвесная линия не совпадает с нормалью к его поверхности, для измерений на поверхности планеты приходится использовать не астрономические, а геодезические координаты. При составлении географических карт этим отклонением пренебрегают.
Геодезические координаты используются в геодезии и навигации, в топографической съемке и картографии, а также спутниковыми навигационными системами для определения местоположения объектов на Земле в реальном времени. Положение точки в геодезической системе координат характеризуется математическими координатами абсциссой — 





Геодезическая прямоугольная система координат (Математическая локальная)[править | править код]

Рисунок 1. Проекция приведенной широты на ось абсцисс.
В геодезии используют прямоугольную систему координат, начало 



Если система координат введена для определения положения точек на части земной поверхности, например, на территории одного государства, её начало 
Из-за неизбежных ошибок измерений при практическом задании общеземной системы возможно несовпадение её начала с центром масс Земли и повороты осей. В связи с этим существуют несколько реализаций общеземной геоцентрической системы координат, и возникает необходимость перехода от одной системы координат к другой. Задача преобразования координат возникает также при переходе от референцной системы координат к общеземной и обратно[1].
Переход от одной прямоугольной системы координат к другой при одновременном переносе начала системы и повороте осей выполняют с помощью преобразования Гельмерта. Преобразование Гельмерта это преобразование с 7 элементами, с 3 параметрами смещения 


Геодезическая эллипсоидальная система координат (Астрономическая глобальная)[править | править код]

Рисунок 2. Геодезическая эллипсоидальная система координат.
Геодезическая эллипсоидальная система координат 
Геодезическая широта 

Геодезическая долгота 



Геодезическая высота 

Формулы перехода[править | править код]

Рисунок 3. Связь геодезических прямоугольной и эллипсоидальной систем координат.
Геодезические прямоугольные и эллипсоидальные системы согласованы друг с другом. Центры этих систем совмещены, ось 


Прямой переход[править | править код]
- где
— радиус кривизны первого вертикала, равный отрезку
на рисунке 3,
— эксцентриситет.

- где
— большая полуось эллипсоида[1].
Обратный переход[править | править код]
От геодезических эллипсоидальных координат к прямоугольным выполняют следующим образом: определяют долготу 



или:
Для широты находят:
Широту 



Приведенной широтой точки 


После вычисления приведенной широты геодезическую широту находят по формуле Боуринга:
Геодезическую высоту 

Референцные (Аппроксимированные приближенные)[править | править код]
Отсчетный эллипсоид может располагаться внутри Земли по-разному. Если центр эллипсоида совмещен с центром масс Земли, а его поверхность близка к поверхности геоида, то эллипсоид называют геоцентрическим, не стоит путать с общеземным. Если эллипсоид близок к геоиду на ограниченной площади, а центр его смещен относительно центра масс, его называют референц-эллипсоидом. Референц-эллипсоид, как правило, устанавливается для использования в геодезический работах в той или иной стране, отсюда и его название (референция, то есть рекомендация)[1].
Данная система, основанная на Референц-эллипсоиде, поддерживалась и использовалась в ряде научных и прикладных задач до 1961 пунктами Лапласа и астропунктами II класса, которые были частично обращены в Геодезические сети сгущения II класса, и продолжались использоваться как экспедиционные пункты II класса преимущественно в необжитых и мало обжитых районах, как обоснования для мелкомасштабных географических съемок. После 1961 г геодезические сети II класса начинают строить в виде сплошных сетей треугольников, полностью заполняющих полигоны АГС I. Работы по созданию государственной геодезической сети были в основном закончены к 1989 году. Сеть пунктов I-го и II-го классов сплошь покрывала территорию страны. В 1990 году приказом ГУГК при Совете Министров СССР создано опытно-производственное подразделение МАГП (Московского аэрогеодезического предприятия) для производства работ с использованием спутниковых систем в соответствии с концепцией перехода топографо-геодезического производства на современные методы спутниковых определений, получившее наименование ВАГП (Верхневолжского аэрогеодезического предприятия). Результаты работ проводимых в 1991 показали не удовлетворительное состояние сети. В 1993—1995 в уравнивание включены: Космическая и Доплеровская сети (служившие основанием для Геоцентрической системы ПЗ-90). В 1996 было проведено заключительного уравнивания и к концу 1990-х, построена сеть из 134 опорных пунктов ГГС включавших 35 пунктов КГС и ДГС, покрывающая всю территорию страны при среднем расстоянии между смежными пунктами 400—500 км[6][7][8][9][10][11].
Постановлением правительства РФ от 24 ноября 2016 года за номером 1240 использование системы координат СК-42 допускается до 1 января 2021 г. Взамен вводится геоцентрическая система ГСК-2011 основанная на ПЗ-90 (являющаяся датумом общеземного элипсоида ITRF).
Земной эллипсоид[править | править код]
Эллипсоид можно задать двумя параметрами:
| Параметр | Символ |
| Большая полуось | а |
| Геометрическое сжатие | 
|
Из а и 
Список литературы[править | править код]
- Огородова Л. В. Высшая геодезия. Часть III. Теоретическая геодезия, Москва, Геодезкартиздат 2006. ISBN 5-86066-076-6[1]
- Сайт Информационно-аналитического центра координатно-временного и навигационного обеспечения. Прикладной потребительский центр ГЛОНАСС.
Ссылки[править | править код]
- https://geographiclib.sourceforge.io (включает в себя утилита CartConvert, который преобразует геодезические координаты в геоцентрические (ECEF) или в локальные декартовые (ENU) координаты. Это обеспечивает точные результаты для всех входных данных, включая точки, близкие к центру Земли.
- https://www.mathworks.com/matlabcentral/fileexchange/15285-geodetic-toolbox (Набор геодезических функций, которые решают различные задачи геодезии в среде Matlab).
См. также[править | править код]
- Геоцентрические координаты
- Статья геодезические данные
- Статья координатные системы
Примечания[править | править код]
- ↑ 1 2 3 4 5 6 Огородова Л. В. Высшая геодезия. Часть III. Теоретическая геодезия / рецензенты=В. Н. Баранов
рецензенты=А. Н. Зуева. — Москва: Геодезкартиздат, 2006. — С. 36–41. — 384 с. — ISBN 5-86066-076-6. - ↑ Geomatics Guidance Note Number 7, part 2. Coordinate Conversions and Transformations including Formulas. International Association of Oil and Gas Producers (OGP). Архивировано 6 марта 2014 года.
- ↑ Судаков С. Г. § 2. Схема построения геодезической сети СССР // Основные Геодезические Сети. — Москва: “Недра”, 1975. — С. 24—25. — 368 с.
- ↑ Яковлев Н. В. § 10. Геодезические сети. Их назначение. // Высшая геодезия. — Москва: Недра, 1989. — С. 35. — 445 с. — 8600 экз.
- ↑ Генике А. А., Побединский Г. Г. § 7.4. Создание и реконструкция городских геодезических сетей с использованием спутниковых технологий. // Глобальные спутниковые системы определения местоположения и их применение в геодезии.. — Москва: ФГУП «Картгеоцентр», 2004. — С. 249. — 352 с.
- ↑ Судаков С. Г. 1. Развитие Основных геодезических сетей в СССР // Основные Геодезические Сети. — Москва: “Недра”, 1975. — С. 9,21. — 368 с.
- ↑ Яковлев Н. В. § 18. Построение Государственной геодезической сети СССР в соответствии с основными положениями 1954—1961 гг. // Высшая геодезия. — Москва: Недра, 1989. — С. 63. — 445 с. — 8600 экз.
- ↑ Пандул И. С. 6.1. Задачи геодезической астрономии. Классификация астропунктов // Геодезическая Астрономия Применительно к решению инженерно-геодезических задач. — Санкт-Петербург: “Политехника”, 2010. — С. 162—163. — 324 с.
- ↑ Генике А. А. Побединский Г. Г. 7.3. Построение государственной геодезической сети России на основе спутниковых технологий // Глобальные спутниковые системы определения местоположения и их применение в геодезии. — Москва: ФГУП «Картгеоцентр», 2004. — С. 246,269. — 352 с.
- ↑ Ермаков В. С., Михаленко Е. Б., Загрядская Н. Н., Беляев Н. Д., Духовской Ф. Н. 2. ГОСУДАРСТВЕННЫЕ ГЕОДЕЗИЧЕСКИЕ СЕТИ // Инженерная геодезия. Геодезические сети. — Санкт-Петербург: Санкт-Петербургский государственный политехнический университет, 2003. — С. 11,16. — 40 с.
- ↑ Антонович К. М. 2 Системы координат и времени в спутниковых технологиях // Использование спутниковых радионавигационных систем в геодезии. — Москва, 2006. — Т. 1. — С. 66,67.










