Пример 8.Найти координаты точки m, изображающей комплексное число .
Решение.
Выделим действительную и мнимую часть этого числа:
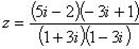
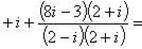
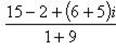
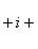
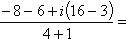
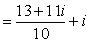
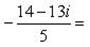
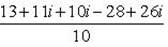
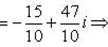
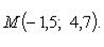
Пример 9.Найти все значения корней:
а) 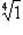 ;
;
б)  .
.
Решение.
а) Запишем комплексное число 1 в тригонометрической форме
1 = cos 0° + i sin 0°; затем по формуле Муавра, находим
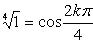

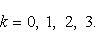
Следовательно,
б) Записав комплексное число 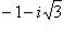 в тригонометрической форме
в тригонометрической форме
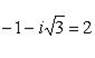
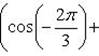

находим
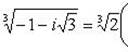

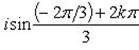
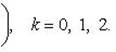
Отсюда
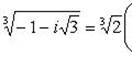
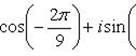

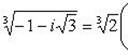
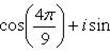
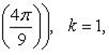
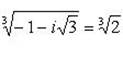
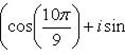
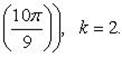
Пример 10.Изобразить корни 6 степени из 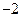 на комплексной плоскости.
на комплексной плоскости.
Решение.
Представим число 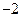 как комплексное в алгебраической форме записи, т.е. в виде
как комплексное в алгебраической форме записи, т.е. в виде 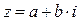 . Получим
. Получим  . Таким образом
. Таким образом  . После чего переведем его в тригонометрическую форму:
. После чего переведем его в тригонометрическую форму:  ,
, 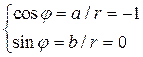 , т. е.
, т. е. 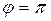 . Тогда
. Тогда 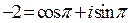 . Используем формулу для корней
. Используем формулу для корней 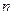 степени из комплексного числа
степени из комплексного числа 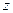 в тригонометрической форме:
в тригонометрической форме: 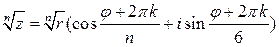 , где
, где 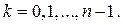 Получаем
Получаем 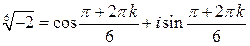 , где
, где 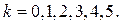
При 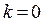 :
: 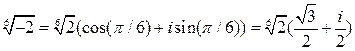 .
.
При 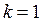 :
: 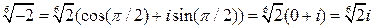 .
.
При 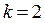 :
: 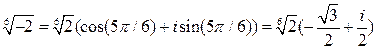 .
.
При 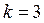 :
:  .
.
При 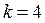 :
: 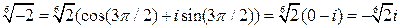 .
.
При 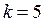 :
: 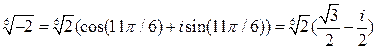 .
.
Пример 11.Решить уравнение: z6 + 1 = 0.
Решение.
Имеем 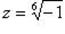 . Для вычисления всех значений
. Для вычисления всех значений  применим формулу Муавра:
применим формулу Муавра:
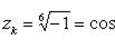
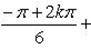
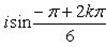
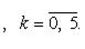
Отсюда

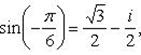
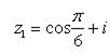
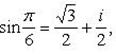
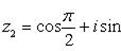
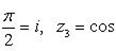
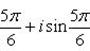
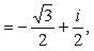
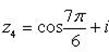
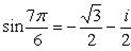
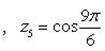
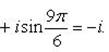
Пример 12. Доказать, что
.
Решение.
Левую часть разложим по формуле суммы кубов двух чисел:
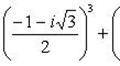
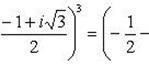

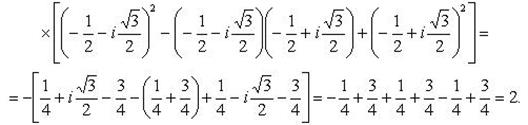
Пример 13.Найти число, сопряженное с числом
.
Решение.
Заметим, что 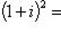
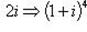
 . Тогда
. Тогда
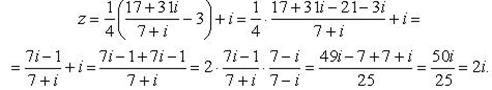
Тогда сопряженное число  .
.
Пример 14.Установить, при каких действительных значениях x и y являются противоположными следующие комплексные числа: и .
Решение.
Приведем числа z1 и z2 к алгебраической форме записи:
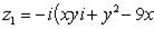
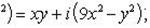
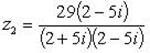
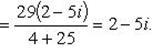
Согласно условию задачи, получаем систему:
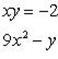
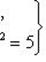 (1)
(1)
Умножим обе части первого уравнения на 5, а второго – на 2 и сложим получившиеся при этом результаты:
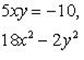
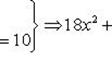
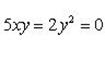 – однородное уравнение.
– однородное уравнение.
Разделим обе его части на y2, получим: 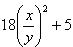
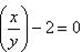 – квадратное уравнение относительно
– квадратное уравнение относительно 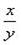 . Решив его, получим
. Решив его, получим 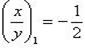 и
и 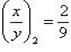 , т. е. y = -2x или
, т. е. y = -2x или 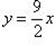 . Подставим эти значения, например, в первое уравнение из (1), получим
. Подставим эти значения, например, в первое уравнение из (1), получим 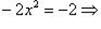
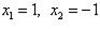 .
.
Тогда y1 = -2, y2 = 2.
Аналогично, при 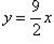 получаем
получаем 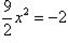 – это уравнение действительных решений не имеет.
– это уравнение действительных решений не имеет.
Ответ: {(1; -2), (-1; 2)}.
Найти координаты точки М, изображающей комплексное число. СРОЧНО
Шляхетний Вогнезiр
Ученик
(205),
на голосовании
3 месяца назад
2-3i/2i+1-i+6i-4/i+2 это 4задание
Голосование за лучший ответ
Уважаемые студенты!
Заказать решение задач по 200+ предметам можно здесь всего за 10 минут.
Изображение комплексных чисел на комплексной плоскости
Комплексное число записывается следующим образом $$z = x + iy,$$ где $x = Re z$ действительная часть, а $y = Im z$ мнимая. Для того, чтобы изобразить комплексное число нужно построить оси координат, обозначив горизонтальную $Im z$ и вертикальную $Re z$.
После этого берем значения $x$ и $y$ от данного комплексного числа и отмечаем точки соответствующие осям координат $Re z$ и $Im z$.
Иногда, требудется провести вектор от начала осей координат $(0,0)$ к точке $(x,y)$, что не является обязательным. Обычно так делают, если в условии задачи дано всего одно комплексное число.
| Пример 1 |
| Изобразите комплексные числа на комплексной плоскости $$z_1 = 2+3i, z_2 = -1+2i, z_3 = -2i.$$ |
| Решение |
|
Строим комплексную плоскость с действительной и мнимой осью $Re z$ и $Im z$. Теперь выписываем $x$ и $y$ из заданных комплексных чисел. Для $z_1 = 2+3i$ это будет $x = 2, y=3$. А для $z_2 = -1+2i$ это $x=-1, y=2$. И наконец $z_3 = -2i$ получаем $x=0, y=-2$. Теперь зная $x$ и $y$ мы можем изобразить комплексные числа на комплексной плоскости просто отметив точки. |
| Ответ |
| Изображение комплексных чисел построено |
Комплексные
числа возникли в связи с задачей решения
квадратных уравнений. Оставаясь в
множестве действительных чисел,
невозможно решить квадратное уравнение,
дискриминант которого меньше нуля.
Комплексные
числа необходимы в различных приложениях
математики. В частности, теория функций
комплексной переменной является
действенным инструментом при использовании
математических методов в различных
областях науки.
Комплексным
числом называется выражение вида
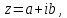
где
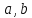 -действительные
-действительные
числа, -мнимая единица.
Итак,
комплексным числом называется
всякая упорядоченная пара
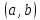 действительных
действительных
чисел
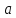 и
и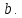 Действительное
Действительное
число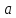 называют абсциссой комплексного числа
называют абсциссой комплексного числа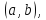 действительное
действительное
число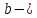 его
его
ординатой
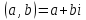
или
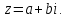
Всякое
комплексное число можно изобразить на
плоскости
 в
в
виде точки
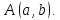 Плоскость,
Плоскость,
на которой изображаются комплексные
числа, называется плоскостью комплексного
переменного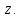
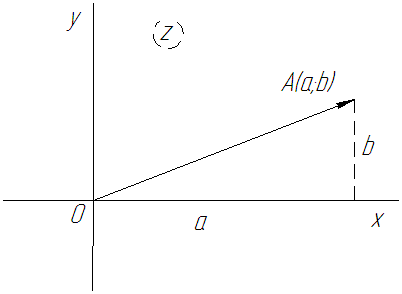
Рис.
62
Плоскость
комплексного переменного
Действительные
числа изображаются точками оси абсцисс,
мнимые числа изображаются точками оси
ординат. Поэтому ось
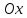 называют
называют
действительной осью, а ось ординат
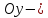 мнимой
мнимой
осью.
Соединив
точку
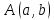 с началом координат, получим вектор
с началом координат, получим вектор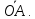 В
В
некоторых случаях удобно считать
геометрическим изображением комплексного
числа вектор
вектор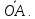 При этом действительная и мнимая части
При этом действительная и мнимая части
числа являются проекциями вектора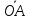 на действительную и мнимую оси.
на действительную и мнимую оси.
Обозначим
через
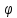
и
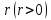 полярные координаты точки
полярные координаты точки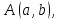 считая
считая
начало координат полюсом, а положительное
направление оси полярной
полярной
осью.
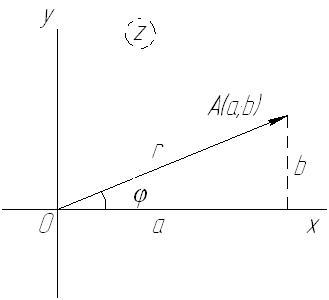
Рис.
63
Геометрическое
изображение комплексного числа
Тогда
имеют место следующие равенства

Следовательно,
комплексное число
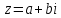 можно представить в виде
можно представить в виде
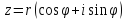
– это
есть тригонометрическая форма записи
комплексного числа
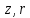 называется
называется
модулем комплексного числа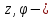 аргументом
аргументом
комплексного числа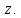
30.2. Модуль и аргумент комплексного числа
Обозначение
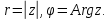
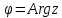 определяется
определяется
с точностью до слагаемого
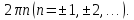
Модуль
и аргумент находятся следующим образом
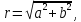
так
как

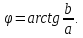
Так
как
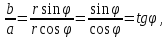
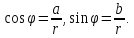
Пусть
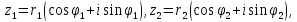
найдем
произведение этих чисел:
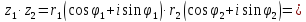
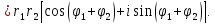
Произведение
двух комплексных чисел есть такое
комплексное число, модуль которого
равен произведению модулей сомножителей,
а аргумент равен сумме аргументов
сомножителей.
Найдем
частное двух комплексных чисел
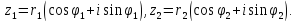
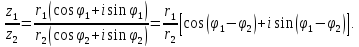
Модуль
частного двух комплексных чисел равен
частному модулей делимого и делителя,
аргумент частного равен разности
аргументов делимого и делителя.
Аргумент
комплексного числа считается положительным,
если он отсчитывается от положительного
направления оси
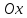 против
против
часовой стрелки, и отрицательным, если
он отсчитывается по часовой стрелке.
Аргумент
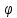 определяется
определяется
неоднозначно, а с точностью до слагаемого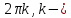 любое
любое
целое число.
30.3. Различные формы записи комплексного числа. Формула Эйлера. Алгебраические действия над комплексными числами
Форма
записи комплексного числа
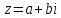 называетсяалгебраической
называетсяалгебраической
формой комплексного
числа
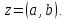 Если
Если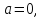 то
то
число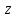 называется
называется
мнимым, если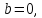 то
то
число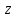 будет действительным.
будет действительным.
Два
комплексных числа
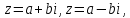 отличающиеся
отличающиеся
только знаками мнимой части, называютсякомплексно
сопряженными числами.
Комплексное
число
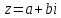 равно
равно
нулю тогда, и только тогда, когда его
действительная и мнимая части равны
нулю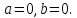
Алгебраическая
форма записи существенно облегчает
выполнение арифметических операций
над комплексными числами, как над
обычными двучленами, учитывая, что
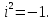
Пусть

Сложение
чисел
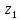 и
и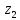 :
:
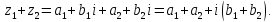
Вычитание
комплексных чисел
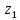 и
и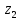 :
:
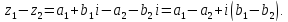
Умножение
комплексных чисел
 и
и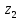 :
:
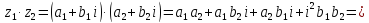
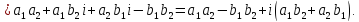
Произведение
сопряженных комплексных чисел равно
сумме квадратов их действительной и
мнимой частей
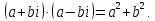
Деление
комплексных чисел
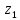 и
и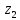 :
:
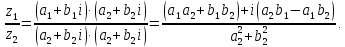
Рассмотрим
пример. Представить
комплексные числа в алгебраической
форме и выполнить операции сложения,
вычитания, умножения и деления
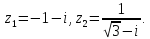
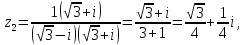
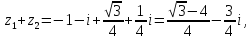
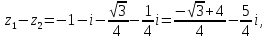
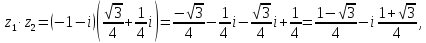
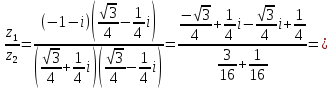
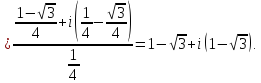
Показательная
форма записи комплексного числа.
Пусть
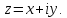 Определим
Определим
показательную функцию комплексного
переменного
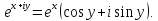
Положим
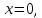 получим
получим
формулу Эйлера, выражающую показательную
функцию с мнимым показателем через
тригонометрические функции
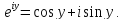
Напомним,
что комплексное число в тригонометрической
форме имеет вид
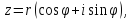
тогда,
применив к записи комплексного числа
в показательной форме, получим
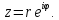
Арифметические
действия над комплексными числами в
показательной форме выполняются на
основании свойств показательной функции.
Пусть
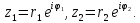
Произведение
чисел
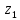 и
и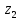
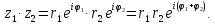
Частное
чисел
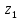 и
и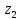 :
:
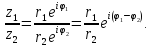
Возведение
комплексного числа в степень:
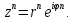
Извлечение
корня n-й
степени из комплексного числа
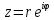 :
:
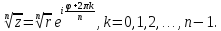
Контрольные
вопросы
-
Какие
числа называют комплексными? -
Записать
различные формы комплексного числа. -
В
каком случае применяют формулу Эйлера? -
Перечислить
алгебраические действия над комплексными
числами.
Лекция
№31. Дифференциальные уравнения
31.1.
Задачи, приводящие к составлению и
решению дифференциальных уравнений.
31.2.
Дифференциальные уравнения первого
порядка. Теорема Коши. Понятие об общем
и частном решении дифференциального
уравнения. Дифференциальные уравнения
с разделяющими переменными.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Раздел III
ОСНОВЫ ТЕОРИИ КОМПЛЕКСНЫХ ЧИСЕЛ
Глава 8. Комплексные
числа
Тема 8.1. Комплексные числа
1. Определение комплексных чисел в
алгебраической форме
Одним из основных понятий математики является понятие числа.
Это понятие прошло длительный путь развития, обогащаясь новым содержанием. Исторически
первыми возникли в практике и были введены в науку натуральные числа,
которые являются инструментом для счета количества отдельных
предметов, например количества пальцев на руке. Они образуют бесконечное множество, которое принято
обозначать буквой N.
Затем возникла необходимость во введении долей единицы и количества
этих долей (например, для измерения длин отрезков), т. е. было
введено так называемое дробное число.
Далее те же потребности измерения привели к необходимости
введения отрицательных чисел (например, если за начало отсчета
берется уровень моря, то для отметки положения горы берется положительное число
— высота горы, а для отметки положения глубины моря — отрицательное число). Целые отрицательные числа вместе с натуральными числами и числом
0 образуют множество целых чисел, обозначаемое буквой Z
Множество, состоящее из всевозможных положительных и отрицательных
целых и дробных чисел и числа Q, называется множеством рациональных
чисел и обозначается буквой Q.
Очевидно, что N ![]() Z
Z![]() Q.
Q.
Потребности практики, а также внутренние требования самой
математики, ее логического развития, показали недостаточность
множества рациональных чисел для решения различных задач. Например, дано уравнение х2
= 2,
или х = ![]() . Но не существует такого рационального
. Но не существует такого рационального
числа, квадрат которого равен 2. Такие числа получили незнание иррациональных чисел.
Поэтому появилась необходимость создать новое расширенное множество
чисел, в котором для каждой точки числовой оси находилось бы числовое значение
и в котором решалось
бы любое уравнение вида хп = а.
Такое множество получило название вещественных(действительных
) чисел и обозначается буквой R, причем Q![]() R.
R.
Развитие науки и практики показало недостаточность введенного
множества вещественных чисел.
Например,
даже такое простейшее квадратное уравнение,
как х2 + 1 = 0,
не имеет решения в множестве действительных чисел, так как не существует такого действительного числа а, что
а2 + 1 = 0. Это показывает необходимость дальнейшего расширения понятия числа. Кроме того, такие науки, как
электротехника и различные разделы физики, рассматривают величины сложной
природы, которые не могут быть охвачены
понятием вещественных чисел.
В связи с этим возникла потребность нового расширения понятия
числа.
Итальянские
математики XVI в. Дж. Кардано и Р. Бомбелли,
решая квадратные уравнения вида х2
+ а2 = 0, ввели в рассмотрение символ ![]() , который в XVIII в. петербургский
, который в XVIII в. петербургский
математик Л. Эйлер(1708-1783) обозначил через i. Формальное решение уравнения х2 + а2 = 0 при использовании
этого символа сводится к тому, что ![]() или, используя обозначение Эйлера,
или, используя обозначение Эйлера, ![]() ai.
ai.
Таким образом, возникает необходимость в расширении
множества действительных чисел до нового множества, такого, чтобы в этом множестве уравнения вида х2 + а2 = 0 имели
решения.
Ниже мы изложим краткую теорию такого расширения.
Определение 1. Комплексным
числом z называется выражение вида а+bi, a и b—действительные числа, а символ i
удовлетворяет условию i = – 1
Число а называется действительной частью комплексного
числа, bi — мнимой частью, i— мнимой единицей.
Множество комплексных чисел обозначается
буквой С.
Заметим,
что множество R действительных чисел содержится в
множестве комплексных чисел С: R ![]() C . В самом деле, всякое действительное число а можно рассматривать как
C . В самом деле, всякое действительное число а можно рассматривать как
комплексное число вида а+0i.
Комплексные
числа вида bi называются
чисто мнимыми. Они получаются из
комплексных чисел z1 = а + bi при а = 0.
Определение 2. Два
комплексных числа z1 = а + bi и z2 = с + di называются
равными, если, соответственно, равны их действительные части и коэффициенты
при мнимой единице, т. е. если а = с, b= d.
Комплексное число z = 0 + 0i называется нулем и
обозначается через 0. Оно совпадает с числом нуль множества действительных
чисел. Таким образом, z = а + bi = 0 тогда
и только тогда, когда а = 0 и b= 0, или, что то
же самое, когда а2+ b2 = 0.
Определение 3. Комплексные
числа а + bi и а — bi называются
комплексно-сопряженными.
Число, комплексно-сопряженное числу z, обозначается через ![]() . Так, если z
. Так, если z
= а + bi, то
![]() = а — bi, если же z
= а — bi, если же z
= а − bi, то ![]() = а + bi. Понятие
= а + bi. Понятие
сопряженности взаимное. Например, для комплексного числа z = = -2 + 4i комплексно-сопряженным
является комплексное число ![]() = – 2 – 4i; точно также
= – 2 – 4i; точно также
для комплексного числа -2 – 4i комплексно-сопряженным
является число -2 + 4i .
2. Геометрическая интерпретация
комплексных чисел
Комплексное число z = а + bi геометрически
можно представить точкой координатной плоскости Оху с координатами
а, b (рис. 1).
Определение 4. Плоскость,
служащая для изображения множества комплексных чисел, называется комплексной
плоскостью. Так как любое комплексное число единственным образом определяется
его действительной и мнимой частями, то каждому
комплексному числу в комплексной плоскости соответствует единственная
точка на плоскости. Очевидно, что справедливо
и обратное утверждение: каждой точке (х; у) плоскости
Оху соответствует единственное комплексное число z = х + yi.



Таким
образом, между множеством комплексных чисел
и множеством точек плоскости существует взаимно-однозначное
соответствие. При этом соответствии всякому действительному числу z = а + 0i соответствует точка А(а;
0) оси абсцисс, а всякому чисто мнимому числу z = 0 + bi — точка В(0;
b) оси ординат.
Числу z = i соответствует
точка С(0; 1) (рис. 2). Если каждой точке М комплексной
плоскости поставить в соответствие
радиус-вектор ОМ этой точки, между множеством комплексных чисел
множеством радиус-векторов можно также установить
взаимно-однозначное соответствие. Ось Ох будем называть действительной
осью, а ось Оу— мнимой.
Из определения комплексно-сопряженных чисел следует,
что числа z и ![]() на комплексной плоскости расположены симметрично относительно
на комплексной плоскости расположены симметрично относительно
действительной оси (рис. 3).
Ранее мы отметили, что квадратное уравнение ax2+ bx + c = 0, для которого
дискриминант D = b2 – 4ас < 0, в множестве R
(действительных чисел) не имеет решения, так как корень из отрицательного числа в этом множестве не имеет действительного значения. Однако в
множестве С (комплексных чисел) такое уравнение имеет два комплексно-сопряженных
решения. В самом деле, пусть дано
квадратное уравнение
ах2 + bx + c = 0.
причем D < 0.
Решения этого
уравнения
![]() ,
,
представим в виде
![]() ,
,
где уже![]() , а потому
, а потому ![]() есть некоторое
есть некоторое
действительное число.
Следовательно,
решениями квадратного уравнения будут два комплексно-сопряженных числа
![]() ,
, ![]()
![]() .
.
Пример 1. Решить
квадратное уравнение ![]() .
.
Решение. Находим:
![]() .
.
Таким образом,
решениями данного квадратного уравнения будут два комплексно-сопряженных числа
![]() и
и ![]() .
.
Итак, в
множестве комплексных чисел любое квадратное уравнение имеет решение.
3. Действия над комплексными числами
Действия над комплексными числами определяются таким образом, чтобы для частного случая
действительных чисел эти операции совпадали с известными операциями над ними.
Сумма z комплексных
чисел ![]() и
и ![]() определяется как комплексное число
определяется как комплексное число
![]() . Его обозначают
. Его обозначают ![]() .
.
Таким образом,
![]() (1)
(1)
В частности,
если ![]() , то ,
, то , ![]() поэтому
поэтому
![]() , следовательно, сумма
, следовательно, сумма
комплексно-сопряженных чисел есть число действительное. Операцию
сложения легко распространить и на сумму любого конечного числа
комплексных чисел. Так, если
![]() ,
, ![]() , …,
, …, ![]()
то
![]() . (2)
. (2)
Пример 2. Найти комплексное число z из равенства ![]() .
.
Решение. Пусть ![]() . Тогда
. Тогда
![]()
или
![]() .
.
Два комплексных числа равны тогда и только
тогда, когда соответственно равны их
действительные и мнимые части. Следовательно,
![]() х + 4 = 2;
х + 4 = 2;
у+ 1 =3.
Решив эту систему,
находим х = – 2; у = 2. Таким образом, ![]() .
.
Вычитание двух комплексных чисел определяется как операция обратная сложению. Комплексное
число ![]() называется разностью комплексных
называется разностью комплексных
чисел ![]() и
и ![]() , если
, если ![]() .
.
Разность комплексных чисел z1 и z2,
обозначается z1 – z2–
Из определения
следует, что
![]() (3)
(3)
В частности,
![]() .
.
Умножение двух
комплексных чисел ![]() и
и ![]() определяется
определяется
следующим образом:
![]() .
.
(4)
Отсюда
следует, что два комплексных числа z1 = а + b и z2 = с – di можно умножать
по правилу умножения многочленов при условии, что i2 = −1. В самом деле,
![]()
(сравните результат с определением
(1)). В частности, если ![]() то
то ![]() .
.
Пример 3. Найти произведение комплексных чисел ![]() и
и ![]()
Решение. Очевидно, что
![]()
Деление вводится как
действие, обратное умножению. Частным от деления комплексного числа ![]() на число
на число ![]() называется
называется
комплексное число ![]() такое, что
такое, что ![]() , т. е.
, т. е.
а1+ b1 i = (a3+ b3 i)∙(a2+b2 i).
Отсюда на основании равенства (4.4)
получаем:
![]() ;
; ![]() .
.
(5)
Решая систему уравнений (5) относительно
а3 и b3 находим:
![]() ,
, ![]() ,
,
причем, ![]() , так как по
, так как по
условию ![]() . Таким образом
. Таким образом
![]() . (6)
. (6)
Равенство
(6) можно получить путем умножения числителя и знаменателя дроби ![]() на число,
на число,
комплексно-сопряженное знаменателю.
Пример 3. Найти
частное от деления комплексного числа ![]() на число
на число ![]() .
.
Решение. Очевидно, что
 .
.
Возведение комплексного
числа ![]() в степень п (п
в степень п (п![]() N) рассматривается как
N) рассматривается как
частный случай умножения комплексных чисел:
![]() (п раз) (7)
(п раз) (7)
Найдем натуральные степени мнимой
единицы i. На основании равенства (4) получаем:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
,
и вообще
![]()
![]()
![]()
![]()
где п — любое
натуральное число.
Пример 4. Найти ![]() .
.
Решение. При делении
числа 59 на 4 имеем: 59 = 14 • 4 + 3, поэтому
![]() .
.
Предоставляем
проверить самостоятельно, что для комплексно-сопряженных чисел выполняются следующие
равенства:
![]() ;
; ![]() ;
; ![]() ;
;  . (8)
. (8)
3.1.
Решение алгебраических уравнений
Многочлены и алгебраические уравнения. Многочленом
(полиномом или целой рациональной функцией) п-й
степени называется функция вида
pn (z) = аn zn + аn-1zп-1 +…+a1z+ao
(9)
где z![]() C, аo,
C, аo,
а1, .. . ,аn— коэффициенты (вообще говоря, комплексные), причем ап
≠ 0, n![]() N– Уравнение
N– Уравнение
аn zn + аn-1zп-1 +…+a1z+ao = 0, аn ≠ 0, (10)
называется алгебраическим
уравнением п-й степени. Число zo для которого рn(zо)=0, называется корнем многочлена (9) или уравнения (10).
Теорема Гаусса (основная
теорема алгебры). Всякий многочлен ненулевой степени
имеет по крайней мере один корень (вообще говоря,
комплексный).
Число zo является корнем многочлена рп
(z) в том и только в том случае,
когда рп (z) делится без остатка на бином z—zo, т. е.
pп(z) =
(z—zо)·qn–1(z),
где qn–1(z) —
многочлен (n −1)-й степени. Если pn(z)
делится без
остатка на (z—zo)k, k ≥1, но не делится на (z—zo)k +1, то zo называется корнем кратности k многочлена рn(z); при этом
pп(z) = (z—zo)k qn–k (z),
где qn–k (z) ≠ 0.
Теорема Гаусса может быть уточнена следующим образом: многочлен п-й
степени имеет ровно п корней, если каждый корень считать столько раз,
какова его кратность.
Если
коэффициенты многочлена (9)—действительные числа и zo= xo + iyo — его комплексный корень, то сопряженное
число ![]() — также корень этого
— также корень этого
многочлена, причем корни z0 и ![]() имеют
имеют
одинаковую кратность.
Пусть многочлен рn(z)
имеет корни z1, z2,
z3,…, zт (т ≤ п) кpатностей соответственно k1,
k2, …km (k1+
k2+ …+km = п) Тогда
его можно
разложить на линейные множители, т. е. справедливо тождество
pп(z) = an(z—z1)k1(z—z2)k2…(z—zm)km
Если
при этом коэффициенты многочлена—действительные числа, то, объединяя скобки, соответствующие комплексно сопряженным корням, можно разложить этот многочлен в
произведение линейных и квадратичных
множителей* с действительными коэффициентами.
Пример 5. Найти корни многочлена z6 + 2z3 + 1 и разложить
его на множители.
Решение. Так как z6 + 2z3 + 1 = (z3 + 1)2, то корнями этого
многочлена являются корни 3-й степени из −1:
z1 = -1;
![]() ;
;
![]()
При этом каждый корень имеет кратность k= 2. Разложение этого многочлена на линейные множители имеет вид

Объединяя последние
две скобки в один сомножитель, получим разложение на множители с
действительными коэффициентами
z6 + 2z3 + 1 = (z +1)2(z2 − z + 1)2.
Пример 5. Решить квадратные уравнения:
1) z2 + 2z + 5 = 0; 2) 4z2
—2z + 1= 0; 3) z2+ (5−2i) z + 5(1 − i)
= 0; 4) (z + 1)4 +16 = 0;
5) z4+18z2 + 81=0.
Решение.
1) z2 + 2z + 5 = 0; D = 4 − 4∙ 5 = 4 –
20 = -16; ![]() z2 = −1
z2 = −1
+ 2i .
2) 4z2 − 2z + 1= 0; D = 4 − 4∙ 4∙
1 = 4 – 16 = -12; ![]()
![]()
3) z2+ (5−2i) z
+ 5(1 − i) = 0; D = (5−2i)2 − 4∙5(1 − i)
= 25 −20i +4i2 −20 +20i = 1;
![]()
![]() .
.
4) (z + 1)4 +16 = 0;
(z + 1)4 = −16; (z + 1)2 = ± 4i;
z + 1 = ± 2![]() = ± 2
= ± 2![]() ;
;
![]() ;
; ![]() .
.
5)
z4+18z2 + 81=0;
Обозначим t = z2
, тогда имеем
t2 +18t + 81=0; D = 182 – 4 ∙1∙81 = 324-324 = 0;
два одинаковых корня t1,2= -9
t = z2;
z2 = -9; z1,2= z3,4=
± 3i.
Ответ. 1) −1 ± 2i;
2) ![]() 3) 3 ± i; 4)
3) 3 ± i; 4) ![]() ;
;
![]() ; 5) ± 3i.
; 5) ± 3i.
4. Полярные координаты точки на плоскости
Возьмем на
плоскости произвольную точку О и некоторую ось Or проходящую через эту точку. Ось может быть
задана, например, единичным вектором ОЕ (рис. 4).
Произвольную
точку М плоскости, не совпадающую с точкой С можно задать
двумя числами: r — длиной отрезка ОМ и φ — углом, который
образует отрезок ОМ с осью ОР в положительном направлении
Числа r и φ
называются полярными координатами точки М. При этом r называется полярным радиусом точки
М, а φ— ее полярным
углом. Совокупность точки О и оси ОР образует систему
координат на плоскости, которая называется полярной системой. Точка
О называется полюсом, а ось ОР— полярной осью.
Так же, как и для декартовых координат точки, полярные
координаты точки будем заключать в круглые скобки. Так, точка М,
заданная на рис. 5, имеет полярные координаты ![]() .
.



Точка О характеризуется
условием r = 0. Полярный угол φ для этой точки не определен.
Будем считать, что полярные координаты точек плоскости изменяются в следующих пределах: ![]() ;
; ![]() .
.
Для
построения точки по полярным координатам необходимо построить луч с началом в точке О, на котором лежит искомая точка,
и на этом луче от полюса отложить отрезок, длина которого равна полярному радиусу.
Пусть на плоскости выбраны одновременно полярные и прямоугольные
системы координат таким образом, что полюс совпадает с началом декартовых
координат, а полярная ось — с положительным направлением оси абсцисс (рис.
6). Если произвольная точка М в полярной системе имеет координатами
числа r и φ , а в
прямоугольной х, у, то очевидно
![]() ;
; ![]() (11)
(11)
![]() ;
; ![]() , (12)
, (12)
Таким образом, полярные и прямоугольные координаты одной и той же точки
плоскости при указанном выборе систем координат связаны соотношениями (11)
и (12). При этом из соотношения (11) по заданным полярным координатам r и φ определяются
прямоугольные координаты, а из соотношений (12) по заданным прямоугольным координатам
хи у определяются полярные координаты.
Необходимо учесть, что из второй формулы (12) угол ср определяется не однозначно. Поэтому, вместо этого
соотношения лучше воспользоваться соотношениями
![]() ;
; ![]() .
.
Пример. Даны полярная и прямоугольная
системы координат (рис. 7). Найти: а)
полярные координаты точки ![]() ;
;
б) прямоугольные координаты точки ![]() .
.
Решение, а) Пользуясь соотношениями (12), получим
![]() ;
;
![]() ;
; ![]() .
.

Из этих соотношений следует, что точка расположена в четвертой четверти, поэтому ![]() ;
;
б) пользуясь соотношениями (11), получим ![]() ;
; ![]() . Следовательно,
. Следовательно,  .
.
5.
Тригонометрическая форма комплексного числа
Выберем на
комплексной плоскости вместе с прямоугольной и полярную систему координат таким образом, как это изображено на рис. 6 Так как произвольное комплексное число ![]() изображается
изображается
точкой, то числа х и у являются
ее прямоугольными координатами. Пусть ![]() и
и![]() — полярные координаты точки М(х;у). Полярный
— полярные координаты точки М(х;у). Полярный
радиус![]() называется
называется
модулем, или абсолютной величиной комплексного числа z и обозначается ![]() ,
,
а полярный угол ф называется аргументом комплексного
числа и обозначается arg![]() . Так как
. Так как
![]() и
и ![]() , то
, то ![]() или
или
![]() . (13)
. (13)
Правая
часть (13) называется тригонометрической формой комплексного числа.
Запись комплексного
числа z в виде ![]() называется алгебраической
называется алгебраической
формой комплексного числа. Переход от алгебраической формы записи к
тригонометрической и обратно осуществляется по формулам
![]() ;
; ![]() ;
;
![]() ;
; ![]() .
.
Пример 1. Составить
тригонометрическую форму записи комплексного числа ![]()
Решение. Имеем: ![]()
![]() ,
, ![]() .
.
По таблице
тригонометрических функций или на калькуляторе находим ![]() .
.
Следовательно, ![]() .
.
Пример 2. Доказать, что![]() .
.
Решение. На комплексной плоскости построим числа z1 и z2 (рис. 8). Неравенства, подлежащие доказательству, вытекают из известной
теоремы геометрии о сторонах треугольника (разность двух сторон треугольника
не больше третьей стороны, а сумма двух сторон не меньше третьей стороны).
Следует
заметить, что для комплексных чисел понятия «больше» и «меньше» лишены смысла,
так как эти числа, в отличие от действительных,
располагаются на плоскости, точки которой
нельзя линейно упорядочить, в то время как точки прямой могут быть
линейно упорядочены.

5.1. Действия над комплексными числами, заданными в
тригонометрической форме
Пусть даны два
комплексных числа в тригонометрической форме:
![]()
![]() (14)
(14)
Перемножая их, получим

т. е.
![]() (15)
(15)
Таким образом, при умножении комплексных чисел в
тригонометрической форме их модули
перемножаются, а аргументы складываются:
Пример 1. Дано ![]()
![]()

ВЫЧИСЛИТЬ ![]()
![]()
![]()
Решение. Применяем
формулу (15):
![]()
На комплексной плоскости числа z1 и z2 представим,
соответственно,
векторами ![]() и
и ![]() (рис. 9). Чтобы построить вектор
(рис. 9). Чтобы построить вектор ![]() изображающий комплексное число z = z1z2 надо (см.
изображающий комплексное число z = z1z2 надо (см.
равенство (11)) вектор![]() повернуть на
повернуть на
угол ![]() против часовой стрелки, затем умножить его длину на
против часовой стрелки, затем умножить его длину на
число r. Это есть
геометрическая интерпретация умножения комплексных чисел.
В частности, так как
![]() , то умножение любого
, то умножение любого
комплексного
числа z на число i с геометрической точки зрения
можно рассматривать как операцию
поворота вектора, изображающего число z, на угол ![]() в
в
положительном направлении (против движения часовой стрелки).
Разделим теперь
первое комплексное число (14) на второе:
![]()
![]() (имея i2 = -1, получим:)
(имея i2 = -1, получим:)
![]()
![]() , где
, где ![]()
Итак, ![]()
![]()
Таким
образом, при делении комплексных чисел их модули делятся, а аргументы вычитаются:

![]()
Пример 2. Дано ![]() ,
, ![]() . Вычислить
. Вычислить![]() .
.
Решение. Имеем:
![]()
![]()
Для построения вектора ![]() изображающего комплексное число
изображающего комплексное число ![]() , нужно вектор
, нужно вектор![]() изображающий комплексное число z1, повернуть на угол
изображающий комплексное число z1, повернуть на угол ![]() по часовой стрелке и уменьшить его длину
по часовой стрелке и уменьшить его длину
в r2 раз.
Деление комплексного числа z на i с геометрической
точки зрения можно
рассматривать как операцию поворота радиус-вектора точки z на угол ![]() по
по
часовой стрелке.
Возведение комплексного числа ![]() в
в
натуральную степень п рассматривается как и-кратное умножение z на самое себя:
![]()
т. е.
![]() (16)
(16)
Таким
образом, при возведении комплексного числа в степень п модуль этого числа возводится в степень п, а
аргумент умножается на п:
![]() ;
; ![]()
Формулу (16) можно записать в виде
![]() (17)
(17)
В частности, при r = 1 из равенства (17) следует формула
Муавра, имеющая широкое применение в
математике:
![]()
Пример 3. Выразите sin 4φ
и cos 4φ через sin φ и cos φ.
Решение. Применяя
формулу Муавра при п = 4, получим:
![]() (18)
(18)
Но
 (19)
(19)
Сравнивая действительные и мнимые части равенств (18) и (19), получим
![]()
![]()
Пусть п — натуральное число.
Корнем п-й степени из
комплексного числа ![]() называется
называется
комплексное число ![]() для которого wn = z. Это число
для которого wn = z. Это число
обозначается ![]()
Так как
два комплексных числа равны тогда и только тогда, когда равны их модули, а аргументы отличаются на целое число, кратное 2л, то
![]() ,
, ![]()
откуда
![]()
![]()
Таким образом,
![]() (20)
(20)
Подставляя вместо к значения 0, 1, 2, …, п – 1, получим п
различных значений корня. Для k = п, п + 1, п + 2, …
или k = -1, -2, … корни будут принимать полученные ранее значения.
Так, например, при k = 2 имеем: ![]() и при k = п +
и при k = п +
2
![]()
Читатель может проверить, что и для функции косинуса
получается то же
самое.
Пример 4. Найти все
значения ![]()
Решение. Так как 1 = l(cos 0 + i sin 0), то
![]()
Придавая
k последовательно
значения 0, 1, 2, 3, 4, соответственно, получим:
z1 = 1 при k = 0;

![]() при k = 1;
при k = 1;
![]() при k = 2;
при k = 2;
![]() при k = 3;
при k = 3;
![]() при k = 4.
при k = 4.
Дадим геометрическую интерпретацию полученных значений ![]() . Модули всех этих значений равны 1.
. Модули всех этих значений равны 1.
Следовательно, точки z1, z2, z3, z4, z5 лежат на окружности радиуса 1 с
центром в начале координат. Построив аргументы значений z1, … , z5 (рис. 10), заметим, что точки,
изображающие числа z1,…, z5, являются
вершинами правильного пятиугольника.
Исходя из формулы (20) можно показать, что геометрически точки, соответствующие различным
значениям корня n-й степени из комплексного числа ![]() располагаются в вершинах правильного
располагаются в вершинах правильного
п-угольника с центром в точке О, причем одна из вершин (соответствующая k = 0) имеет
полярные координаты![]() .
.
6. Показательная форма комплексного числа. Формула Эйлера
Найдем тригонометрическую форму комплексного числа z, если ![]() Так как в
Так как в
записи ![]() выражение
выражение
![]() есть действительная, а
есть действительная, а ![]() —
—
мнимая часть и комплексно-
сопряженные числа отличаются знаком мнимых
частей, то
![]() (21)
(21)
Функция
косинус — четная, а синус — нечетная, поэтому соотношение (21) можно записать
в виде
![]()
Из геометрических соображений можно заключить, что точка, изображающая комплексное число 1, получается
из точки, изображающей число z,
в результате ее
симметричного отображения относительно оси абсцисс. Значит,
![]()
![]()
Из правил умножения и деления комплексных чисел в тригонометрической
форме следует, что аргумент комплексного числа ведет себя так же, как
показатель степени при умножении степеней с одинаковыми основаниями: ![]() Это
Это
обстоятельство навело Л. Эйлера на
мысль представлять комплексные числа в виде
![]() (22)
(22)
где е —
основание натурального логарифма.
К комплексным числам, записанным в форме (22), применимы
правила
действий над степенью. А именно, если ![]() ,
, ![]() , то
, то
![]() откуда следуют
откуда следуют
известные нам правила:
![]() ,
, ![]()
Аналогично получаем
![]()
т. е. при делении
комплексных чисел справедливы равенства  и
и 
Далее, возведя
комплексное число (22) в степень п, получим
![]()
Следовательно, при возведении комплексного числа в
степень |zn| = |z|n,arg(zn) = n arg z.
Таким образом, представление комплексного числа в виде (22)
формально находит оправдание. Запись (22) называется показательной или экспоненциальной формой
комплексного числа.
Если z представлено в форме (22), то
комплексно-сопряженное число
![]()
Сравнивая записи
комплексного числа в известных нам формах, будем иметь ![]() При r = 1
При r = 1
![]() (23)
(23)
Это соотношение
называется тождеством Эйлера. Аналогично можно записать
![]() (24)
(24)
Путем
сложения и вычитания равенств (23) и (24), соответственно, получаем
![]()
![]()
Эти
равенства находят широкое применение в различных вопросах математики.
Пример 5. Представить в экспоненциальной форме
комплексное число ![]()
Решение. Находим ![]()
![]()
![]()
![]() Следовательно,
Следовательно,![]()
7.
Понятие функции комплексной переменной
Пусть даны
две комплексные плоскости Оху (плоскость z) и O‘uv (плоскость w).
Определение. Если каждой точке (числу) z![]() D (D — множество точек плоскости z ) по некоторому закону f ставится в соответствие единственная точка w
D (D — множество точек плоскости z ) по некоторому закону f ставится в соответствие единственная точка w ![]() Е (Е — множество точек
Е (Е — множество точек
плоскости w), то говорят, что w есть функция от z (однозначная):
w = f (z), (25)
с областью
определения D, значения которой принадлежат множеству Е (рис. 11). Т.е. говорят, что на множестве определена однозначная функция
комплексного переменного w = f(z), отображающая
множество D в множество Е. Если множество
значений функции f (z)
исчерпывает все множество Е, то
Е называется множеством значений (областью
изменения) функции f (z). В этом случае пишут
Е = f (D). (26)
Если каждому z ![]() D соответствует несколько значений w, то функция w = f(z) называется многозначной.
D соответствует несколько значений w, то функция w = f(z) называется многозначной.
Множества D и Е можно изображать на одной комплексной плоскости.

Рис. 11.
Таким образом, каждая комплексная функция реализует однозначное
в одну сторону отображение одного множества на другое. Благодаря этому комплексные функции
находят свое применение в таких науках, как гидродинамика и аэродинамика, так как с их помощью удобно описывать «историю» движения объема жидкости (или газа).


a)
б)
Рис. 12.
Раздел математики,
изучающий свойства комплексных функций, носит название теории функций
комплексной переменной.
Пример6. Во что переходит сектор Е
![]() ,
,
![]()
(рис. 12, а)
при отображении w = z2?
Имеем
arg w =
2argz < π и |w| = |z|2 < 1.
Поэтому отображенная область E ‘ представляет собой полукруг (рис. 12, б).
Далее, как правило,
будем рассматривать такие функции w = f(z), для которых множества D и Е1 являются областями. Областью комплексной плоскости называется множество точек плоскости,
обладающих свойствами открытости и связности.
Функцию w = f(z) можно
записать в виде
u + iv = f(x + iy),
т. е.
f(x + iy) = и(х; у) +
iv(x; у),
где
и = и(х;у) = Ref(z),
v = v(x;у)
= Imf(z),
(х; у) ![]() D.
D.
Функцию и(х;у)
при этом называют действительной частью функции f(z),
a v(x;y)
— мнимой.
Таким образом, задание функции комплексного переменного
равносильно заданию двух функций двух действительных переменных.
Пример 7. Найти действительную и мнимую части
функции w = z2.
Решение: Функцию w = z2 можно записать в виде и + iv = (х + iy)2,
т.е.
и + iv = х2 — у2 + i 2ху.
Отсюда следует: и = х2
—у2, v
= 2ху.
