Сегодня поговорим об единичной окружности 🧑🏫

Можно ли найти точку (её координаты) на окружности, зная координаты центра окружности, её радиус и угол поворота?🤔
Ну, конечно, можно! Записывай и запоминай общую формулу для нахождения координат точки:
x=x0+r⋅cos δ
y=y0+r⋅sin δ
x0,y0 — координаты центра окружности;
r — радиус окружности;
δ —угол поворота радиуса вектора.
Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter. Мы обязательно поправим!
Как определить координаты точки на окружности
Как найти координаты точки?
О чем эта статья:
3 класс, 4 класс, 9 класс, 11 класс, ЕГЭ/ОГЭ
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).
Понятие системы координат
Координаты — это совокупность чисел, которые определяют положение какого-либо объекта на прямой, плоскости, поверхности или в пространстве. Например, координаты вашей квартиры тоже можно записать числами — они помогут понять, где именно находится тот дом, где вы живете. С точками на плоскости та же история.
Прямоугольная система координат — это система координат, которую изобрел математик Рене Декарт, ее еще называют «декартова система координат». Она представляет собой два взаимно перпендикулярных луча с началом отсчета в точке их пересечения.
Чтобы найти координаты, нужны ориентиры, от которых будет идти отсчет. На плоскости в этой роли выступят две числовые оси.
Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курсы по профильной математике.
Чертеж начинается с горизонтальной оси, которая называется осью абсцисс и обозначается латинской буквой x (икс). Записывают ось так: Ox. Положительное направление оси абсцисс обозначается стрелкой слева направо.
Затем проводят вертикальную ось, которая называется осью ординат и обозначается y (игрек). Записывают ось Oy. Положительное направление оси ординат показываем стрелкой снизу вверх.
Оси взаимно перпендикулярны, а значит угол между ними равен 90°. Точка пересечения является началом отсчета для каждой из осей и обозначается так: O. Начало координат делит оси на две части: положительную и отрицательную.
- Координатные оси — это прямые, образующие систему координат.
- Ось абсцисс Ox — горизонтальная ось.
- Ось ординат Oy — вертикальная ось.
- Координатная плоскость — плоскость, в которой находится система координат. Обозначается так: x0y.
- Единичный отрезок — величина, которая принимается за единицу при геометрических построениях. В декартовой системе координат единичный отрезок отмечается на каждой из осей. Длина отрезка показывает сколько раз единичный отрезок и его части укладываются в данном отрезке.
Оси координат делят плоскость на четыре угла — четыре координатные четверти.
У каждой из координатных четвертей есть свой номер и обозначение в виде римской цифры. Отсчет идет против часовой стрелки:
- верхний правый угол — первая четверть I;
- верхний левый угол — вторая четверть II;
- нижний левый угол — третья четверть III;
- нижний правый угол — четвертая четверть IV;
- Если обе координаты положительны, то точка находится в первой четверти координатной плоскости.
- Если координата х отрицательная, а координата у положительная, то точка находится во второй четверти.
- Если обе координаты отрицательны, то число находится в третьей четверти.
- Если координата х положительная, а координата у отрицательная, то точка лежит в четвертой четверти.
Определение координат точки
Каждой точке координатной плоскости соответствуют две координаты.
Точка пересечения с осью Ох называется абсциссой точки А, а с осью Оу называется ординатой точки А.
Чтобы узнать координаты точки на плоскости, нужно опустить от точки перпендикуляр на каждую ось и посчитать количество единичных отрезков от нулевой отметки до опущенного перпендикуляра.
Координаты точки на плоскости записывают в скобках, первая по оси Ох, вторая по оси Оу.
Смотрим на график и фиксируем: A (1; 2) и B (2; 3).
Особые случаи расположения точек
В геометрии есть несколько особых случаев расположения точек. Лучше их запомнить, чтобы без запинки решать задачки. Вот они:
- Если точка лежит на оси Oy, то ее абсцисса равна 0. Например,
точка С (0, 2). - Если точка лежит на оси Ox, то ее ордината равна 0. Например,
точка F (3, 0). - Начало координат — точка O. Ее координаты равны нулю: O (0,0).
- Точки любой прямой, которая перпендикулярна оси абсцисс, имеют одинаковые абсциссы.
- Точки любой прямой, которая перпендикулярна оси ординат, имеют одинаковые ординаты.
- Если точка лежит на оси абсцисс, то ее координаты будут иметь вид: (x, 0).
- Если точка лежит на оси ординат, то ее координаты будут иметь вид: (0, y).
Способы нахождения точки по её координатам
Чтобы узнать, как найти точку в системе координат, можно использовать один из двух способов.
Способ первый. Как определить положение точки D по её координатам (-4, 2):
- Отметить на оси Ox, точку с координатой -4, и провести через нее прямую перпендикулярную оси Ox.
- Отметить на оси Oy, точку с координатой 2, и провести через нее прямую перпендикулярную оси Oy.
- Точка пересечения перпендикуляров и есть искомая точка D. Ее абсцисса равна -4, а ордината — 2.
Способ второй. Как определить положение точки D (-4, 2):
- Сместить прямую по оси Ox влево на 4 единицы, так как у нас
перед 4 стоит знак минус. - Подняться из этой точки параллельно оси Oy вверх на 2 единицы, так как у нас перед 2 стоит знак плюс.
Чтобы легко и быстро находить координаты точек или строить точки по координатам, скачайте готовую систему координат и храните ее в учебнике:
Как найти координату точки окружности
Как находить точки окружности
Окружность изучается в геометрии, и чтобы правильно сделать заданную задачу, нужно научиться находить точки окружности. Для этого вам понадобится список необходимых инструментов, таких как:
- простой карандаш;
- тетрадь в клеточку;
- циркуль;
- транспортир;
- шариковая или гелевая ручка.
Как найти координаты точки окружности
Прежде, чем найти точку на окружности и обозначить ее координаты, следует эту окружность построить. При построении вам встретятся еще несколько правил, в зависимости от заданных в задаче вопросов. Это может быть как хорда, на которой тоже нужно будет найти точку в окружности, она соединяет две точки. Помните, что диаметром называется хорда, которая проходит через центр окружности и соединяет две противоположные точки на ней.
Также можно найти точку на окружности, которая находится на касательной, то есть прямой, которая имеет с окружностью одну общую точку, но не пересекает ее. Если окружность пересекается прямой, то она имеет с ней две общие точки, найти на окружности их легко, так как они одновременно относятся как к окружности, так и к прямой. Для определения координат точки на окружности можно воспользоваться как формулой для прямой, так и формулой для окружности.
Как найти координаты точки на окружности или, если известно только значение радиуса R, можно по одной из его координат, либо если дано значение угла альфа. Выглядит это так:
sin alpha = y / R
cos alpha = x / R
cos alpha * cos alpha + sin alpha * sin alpha = 1
Может помочь также найти на окружности координаты точки один из многочисленных форумов, где сидят математики и помогают решить все задачки, но не только помогают, но и стараются объяснить ее.
В школе учат, как найти точки окружности, когда начинают изучать геометрию в 6 классе.
Отличников, которые знают, как найти точки на окружности и их координаты, часто могут обижать в школе, если они не дают списывать. В таких случаях будет нелишним знать, как наказать обидчика за оскорбление.
Как найти координаты точки?
О чем эта статья:
3 класс, 4 класс, 9 класс, 11 класс, ЕГЭ/ОГЭ
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).
Понятие системы координат
Координаты — это совокупность чисел, которые определяют положение какого-либо объекта на прямой, плоскости, поверхности или в пространстве. Например, координаты вашей квартиры тоже можно записать числами — они помогут понять, где именно находится тот дом, где вы живете. С точками на плоскости та же история.
Прямоугольная система координат — это система координат, которую изобрел математик Рене Декарт, ее еще называют «декартова система координат». Она представляет собой два взаимно перпендикулярных луча с началом отсчета в точке их пересечения.
Чтобы найти координаты, нужны ориентиры, от которых будет идти отсчет. На плоскости в этой роли выступят две числовые оси.
Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курсы по профильной математике.
Чертеж начинается с горизонтальной оси, которая называется осью абсцисс и обозначается латинской буквой x (икс). Записывают ось так: Ox. Положительное направление оси абсцисс обозначается стрелкой слева направо.
Затем проводят вертикальную ось, которая называется осью ординат и обозначается y (игрек). Записывают ось Oy. Положительное направление оси ординат показываем стрелкой снизу вверх.
Оси взаимно перпендикулярны, а значит угол между ними равен 90°. Точка пересечения является началом отсчета для каждой из осей и обозначается так: O. Начало координат делит оси на две части: положительную и отрицательную.
- Координатные оси — это прямые, образующие систему координат.
- Ось абсцисс Ox — горизонтальная ось.
- Ось ординат Oy — вертикальная ось.
- Координатная плоскость — плоскость, в которой находится система координат. Обозначается так: x0y.
- Единичный отрезок — величина, которая принимается за единицу при геометрических построениях. В декартовой системе координат единичный отрезок отмечается на каждой из осей. Длина отрезка показывает сколько раз единичный отрезок и его части укладываются в данном отрезке.
Оси координат делят плоскость на четыре угла — четыре координатные четверти.
У каждой из координатных четвертей есть свой номер и обозначение в виде римской цифры. Отсчет идет против часовой стрелки:
- верхний правый угол — первая четверть I;
- верхний левый угол — вторая четверть II;
- нижний левый угол — третья четверть III;
- нижний правый угол — четвертая четверть IV;
- Если обе координаты положительны, то точка находится в первой четверти координатной плоскости.
- Если координата х отрицательная, а координата у положительная, то точка находится во второй четверти.
- Если обе координаты отрицательны, то число находится в третьей четверти.
- Если координата х положительная, а координата у отрицательная, то точка лежит в четвертой четверти.
Определение координат точки
Каждой точке координатной плоскости соответствуют две координаты.
Точка пересечения с осью Ох называется абсциссой точки А, а с осью Оу называется ординатой точки А.
Чтобы узнать координаты точки на плоскости, нужно опустить от точки перпендикуляр на каждую ось и посчитать количество единичных отрезков от нулевой отметки до опущенного перпендикуляра.
Координаты точки на плоскости записывают в скобках, первая по оси Ох, вторая по оси Оу.
Смотрим на график и фиксируем: A (1; 2) и B (2; 3).
Особые случаи расположения точек
В геометрии есть несколько особых случаев расположения точек. Лучше их запомнить, чтобы без запинки решать задачки. Вот они:
- Если точка лежит на оси Oy, то ее абсцисса равна 0. Например,
точка С (0, 2). - Если точка лежит на оси Ox, то ее ордината равна 0. Например,
точка F (3, 0). - Начало координат — точка O. Ее координаты равны нулю: O (0,0).
- Точки любой прямой, которая перпендикулярна оси абсцисс, имеют одинаковые абсциссы.
- Точки любой прямой, которая перпендикулярна оси ординат, имеют одинаковые ординаты.
- Если точка лежит на оси абсцисс, то ее координаты будут иметь вид: (x, 0).
- Если точка лежит на оси ординат, то ее координаты будут иметь вид: (0, y).
Способы нахождения точки по её координатам
Чтобы узнать, как найти точку в системе координат, можно использовать один из двух способов.
Способ первый. Как определить положение точки D по её координатам (-4, 2):
- Отметить на оси Ox, точку с координатой -4, и провести через нее прямую перпендикулярную оси Ox.
- Отметить на оси Oy, точку с координатой 2, и провести через нее прямую перпендикулярную оси Oy.
- Точка пересечения перпендикуляров и есть искомая точка D. Ее абсцисса равна -4, а ордината — 2.
Способ второй. Как определить положение точки D (-4, 2):
- Сместить прямую по оси Ox влево на 4 единицы, так как у нас
перед 4 стоит знак минус. - Подняться из этой точки параллельно оси Oy вверх на 2 единицы, так как у нас перед 2 стоит знак плюс.
Чтобы легко и быстро находить координаты точек или строить точки по координатам, скачайте готовую систему координат и храните ее в учебнике:
Окружность на координатной плоскости
Окружность на плоскости — это множество точек на плоскости равноудаленных от точки центра. На рисунке данная точка обозначена C.
Окружность радиуса R с центром в начале координат представляется уравнением:
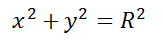
Окружность радиуса R с центром в точке C(a;b) представляется уравнением:
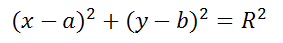
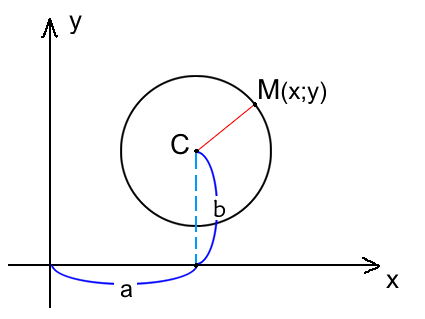
Расстояние от центра окружности С(a;b) до точки M(x;y) называется радиусом окружности R (на рисунке красная линия ).
Это уравнение можно записать в виде: 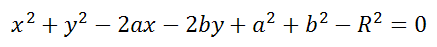
Если уравнение помножить на любое число A, то получим
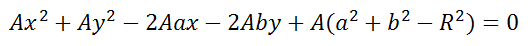
Примечание
Окружность относится к линии второго порядка, так как представляется уравнением второй степени.
Необходимые условия для этого:
1. Отсутствие в уравнение второй степени члена с произведением xy;
2. Коэффициенты при x 2 и y 2 были равны в уравнение вида: 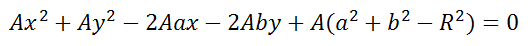
3. Если выполняется неравенство 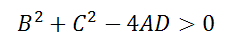
Как найти радиус и центр окружности
Уравнение Ax 2 +Bx+Ay 2 +Cy+D=0 если оно удовлетворяет примечаниям (1, 2 и 3), то тогда (a;b) и радиус R окружности можно найти по формулам:
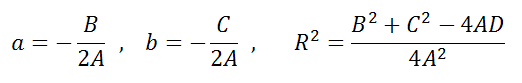
Пример 1
Уравнение 5x 2 -10x+5y 2 +20y-20=0
Здесь
A=5, B=-10, C=20, D=-20
Оно удовлетворяет примечаниям 1, 2 и выполняется неравенство
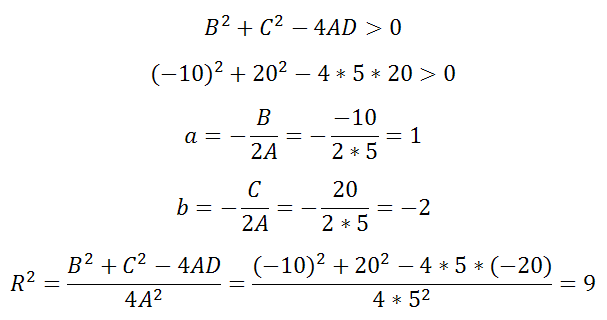
Решая, получаем что центр есть (1;-2), а радиус R=3
Анимационный график окружности
Пример 2
Уравнение второй степени x 2 +4xy+y 2 =1 не является окружностью, так как в нём есть член 4xy.
Пример 3
Уравнение второй степени 4x 2 +9y 2 =36 не представляет окружность, так как в нём коэффициенты при x 2 и y 2 не равны.
Насколько публикация полезна?
Нажмите на звезду, чтобы оценить!
Средняя оценка 4.3 / 5. Количество оценок: 4
Уравнение окружности.
Аналитическая геометрия дает единообразные приемы решения геометрических задач. Для этого все заданные и искомые точки и линии относят к одной системе координат.
В системе координат можно каждую точку охарактеризовать ее координатами, а каждую линию – уравнением с двумя неизвестными, графиком которого эта линия является. Таким образом геометрическая задача сводится к алгебраической, где хорошо отработаны все приемы вычислений.
Окружность есть геометрическое место точек с одним определенным свойством (каждая точка окружности равноудалена от одной точки, называется центром). Уравнение окружности должно отражать это свойство, удовлетворять этому условию.
Геометрическая интерпретация уравнения окружности – это линия окружности.
Если поместить окружность в систему координат, то все точки окружности удовлетворяют одному условию – расстояние от них до центра окружности должно быть одинаковым и равным окружности.
Окружность с центром в точке А и радиусом R поместим в координатную плоскость.
Если координаты центра (а;b), а координаты любой точки окружности (х; у), то уравнение окружности имеет вид:
Если квадрат радиуса окружности равен сумме квадратов разностей соответствующих координат любой точки окружности и ее центра, то это уравнение является уравнением окружности в плоской системе координат.
Если центр окружности совпадает с точкой начала координат, то квадрат радиуса окружности равен сумме квадратов координат любой точки окружности. В этом случае уравнение окружности принимает вид:
Следовательно, любая геометрическая фигура как геометрическое место точек определяется уравнением, связывающим координаты ее точек. И наоборот, уравнение, связывающее координаты х и у, определяют линию как геометрическое место точек плоскости, координаты которых удовлетворяют данному уравнению.
Примеры решения задач про уравнение окружности
Задача. Составить уравнение заданной окружности
Составьте уравнение окружности с центром в точке O (2;-3) и радиусом 4.
Решение.
Обратимся к формуле уравнения окружности:
R 2 = (x- a ) 2 + (y- b ) 2
Подставим значения в формулу.
Радиус окружности R = 4
Координаты центра окружности (в соответствии с условием)
a = 2
b = -3
Получаем:
(x — 2 ) 2 + (y — ( -3 )) 2 = 4 2
или
(x — 2 ) 2 + (y + 3 ) 2 = 16 .
Задача. Принадлежит ли точка уравнению окружности
Проверить, принадлежит ли точка A(2;3) уравнению окружности (x — 2) 2 + (y + 3) 2 = 16.
Решение.
Если точка принадлежит окружности, то ее координаты удовлетворяют уравнению окружности.
Чтобы проверить, принадлежит ли окружности точка с заданными координатами, подставим координаты точки в уравнение заданной окружности.
В уравнение ( x — 2) 2 + ( y + 3) 2 = 16
подставим, согласно условию, координаты точки А(2;3), то есть
x = 2
y = 3
Проверим истинность полученного равенства
( x — 2) 2 + ( y + 3) 2 = 16
( 2 — 2) 2 + ( 3 + 3) 2 = 16
0 + 36 = 16 равенство неверно
Таким образом, заданная точка не принадлежит заданному уравнению окружности.
Как найти координаты точки?
О чем эта статья:
3 класс, 4 класс, 9 класс, 11 класс, ЕГЭ/ОГЭ
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).
Понятие системы координат
Координаты — это совокупность чисел, которые определяют положение какого-либо объекта на прямой, плоскости, поверхности или в пространстве. Например, координаты вашей квартиры тоже можно записать числами — они помогут понять, где именно находится тот дом, где вы живете. С точками на плоскости та же история.
Прямоугольная система координат — это система координат, которую изобрел математик Рене Декарт, ее еще называют «декартова система координат». Она представляет собой два взаимно перпендикулярных луча с началом отсчета в точке их пересечения.
Чтобы найти координаты, нужны ориентиры, от которых будет идти отсчет. На плоскости в этой роли выступят две числовые оси.
Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курсы по профильной математике.
Чертеж начинается с горизонтальной оси, которая называется осью абсцисс и обозначается латинской буквой x (икс). Записывают ось так: Ox. Положительное направление оси абсцисс обозначается стрелкой слева направо.
Затем проводят вертикальную ось, которая называется осью ординат и обозначается y (игрек). Записывают ось Oy. Положительное направление оси ординат показываем стрелкой снизу вверх.
Оси взаимно перпендикулярны, а значит угол между ними равен 90°. Точка пересечения является началом отсчета для каждой из осей и обозначается так: O. Начало координат делит оси на две части: положительную и отрицательную.
- Координатные оси — это прямые, образующие систему координат.
- Ось абсцисс Ox — горизонтальная ось.
- Ось ординат Oy — вертикальная ось.
- Координатная плоскость — плоскость, в которой находится система координат. Обозначается так: x0y.
- Единичный отрезок — величина, которая принимается за единицу при геометрических построениях. В декартовой системе координат единичный отрезок отмечается на каждой из осей. Длина отрезка показывает сколько раз единичный отрезок и его части укладываются в данном отрезке.
Оси координат делят плоскость на четыре угла — четыре координатные четверти.
У каждой из координатных четвертей есть свой номер и обозначение в виде римской цифры. Отсчет идет против часовой стрелки:
- верхний правый угол — первая четверть I;
- верхний левый угол — вторая четверть II;
- нижний левый угол — третья четверть III;
- нижний правый угол — четвертая четверть IV;
- Если обе координаты положительны, то точка находится в первой четверти координатной плоскости.
- Если координата х отрицательная, а координата у положительная, то точка находится во второй четверти.
- Если обе координаты отрицательны, то число находится в третьей четверти.
- Если координата х положительная, а координата у отрицательная, то точка лежит в четвертой четверти.
Определение координат точки
Каждой точке координатной плоскости соответствуют две координаты.
Точка пересечения с осью Ох называется абсциссой точки А, а с осью Оу называется ординатой точки А.
Чтобы узнать координаты точки на плоскости, нужно опустить от точки перпендикуляр на каждую ось и посчитать количество единичных отрезков от нулевой отметки до опущенного перпендикуляра.
Координаты точки на плоскости записывают в скобках, первая по оси Ох, вторая по оси Оу.
Смотрим на график и фиксируем: A (1; 2) и B (2; 3).
Особые случаи расположения точек
В геометрии есть несколько особых случаев расположения точек. Лучше их запомнить, чтобы без запинки решать задачки. Вот они:
- Если точка лежит на оси Oy, то ее абсцисса равна 0. Например,
точка С (0, 2). - Если точка лежит на оси Ox, то ее ордината равна 0. Например,
точка F (3, 0). - Начало координат — точка O. Ее координаты равны нулю: O (0,0).
- Точки любой прямой, которая перпендикулярна оси абсцисс, имеют одинаковые абсциссы.
- Точки любой прямой, которая перпендикулярна оси ординат, имеют одинаковые ординаты.
- Если точка лежит на оси абсцисс, то ее координаты будут иметь вид: (x, 0).
- Если точка лежит на оси ординат, то ее координаты будут иметь вид: (0, y).
Способы нахождения точки по её координатам
Чтобы узнать, как найти точку в системе координат, можно использовать один из двух способов.
Способ первый. Как определить положение точки D по её координатам (-4, 2):
- Отметить на оси Ox, точку с координатой -4, и провести через нее прямую перпендикулярную оси Ox.
- Отметить на оси Oy, точку с координатой 2, и провести через нее прямую перпендикулярную оси Oy.
- Точка пересечения перпендикуляров и есть искомая точка D. Ее абсцисса равна -4, а ордината — 2.
Способ второй. Как определить положение точки D (-4, 2):
- Сместить прямую по оси Ox влево на 4 единицы, так как у нас
перед 4 стоит знак минус. - Подняться из этой точки параллельно оси Oy вверх на 2 единицы, так как у нас перед 2 стоит знак плюс.
Чтобы легко и быстро находить координаты точек или строить точки по координатам, скачайте готовую систему координат и храните ее в учебнике:
Окружность. Форма и положение.
Окружность – это замкнутая плоская линия, всякая точки которой равноудалена от одной и той же точки (O), называемой центром.
Прямые (OA, OB, OС. . . ), соединяющие центр с точками окружности – это радиусы.
Бесконечная прямая (MN), прочерченная через какие-нибудь две точки окружности – секущая. а часть ее (EF), заключенная между этими точками, называется хордой.
Всякая хорда (AD), прочерченная через центр – диаметр.
Диаметр представляет наибольшую из хорд..Всякий диаметр делит окружность и круг пополам. Таким образом, всякий диаметр разделит окружность на две полуокружности, а круг на два полукруга.
Какая-нибудь часть окружности (напр. EmF ) называется дугой.
О хорде (EF), соединяющей концы дуги, говорят, что она стягивает эту дугу.
Для определения дуги иногда применяют знак È ; напр., пишут так: ÈEmF.
Часть плоскости, ограниченная окружностью, именуют кругом.
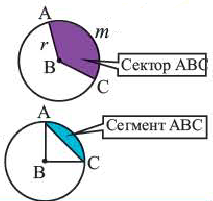
Часть круга (напр., СOB, заштрихованная на чертеже), ограниченная дугой и двумя радиусами, проведенными к концам дуги, обозначают как сектор.
Часть круга, (напр., EmF), ограниченная дугой и стягивающей ее хордой, обозначают как сегмент.
Из этого получаем:
1. Все радиусы одной окружности равны.
2. Два круга с одинаковыми радиусами будут равны.
3. Диаметр равен двум радиусам.
4. Точка, лежащая внутри круга, ближе к центру, а точка, лежащая вне круга, дальше от центра, чем точки окружности.
5. Диаметр, перпендикулярный к хорде, делит эту хорду и обе стягиваемые ею дуги пополам.
6. Дуги, заключенные между параллельными хордами, равны.
При работе с окружностями применяют следующие теоремы:
1. Теорема. Прямая и окружность не могут иметь более двух общих точек.
Из этой теоремы получаем два логично вытекающих следствия:
Никакая часть окружности не может совместиться с прямой, потому что в противном случае окружность с прямой имела бы более двух общих точек.
Линия, никакая часть которой не может совместиться с прямой, называется кривой.
Из предыдущего следует, что окружность есть кривая линия.
2. Теорема. Через всякие три точки, не лежащие на одной прямой, можно провести окружность и только одну.
Как следствие данной теоремы получаем:
Три перпендикуляра к сторонам треугольника вписанного в окружность проведенные через их середины, пересекаются в одной точке, которая является центром окружности.
Решим задачу. Требуется найти центр предложенной окружности.
Отметим на предложенной три любые точки A, B и С , начертим через них две хорды, например, AB и СB, и из середины этих хорд укажем перпендикуляры MN и PQ. Искомый центр, будучи одинаково удален от A, B и С, должен лежать и на MN, и на PQ, следовательно, он находится на пересечении этих перпендикуляров, т.е. в точке O.
[spoiler title=”источники:”]
http://skysmart.ru/articles/mathematic/kak-najti-koordinaty-tochki
http://www.calc.ru/Okruzhnost-Forma-I-Polozheniye.html
[/spoiler]
Как найти координаты точки на окружности, зная радиус и угол прямой к точке из окружности?
Михаил
Оракул
(50492),
закрыт
12 лет назад
Угол задаётся в градусах, координаты нужно получить в полярной системе.
Нужно чтобы для всех 360 градусов работало.
У меня почему-то получается точки в 300 и 60 градусах на одном и том же месте располагаются.
Дополнен 12 лет назад
*угол прямой к точке из центра окружности
Окружность — определение и вычисление с примерами решения
Определение: Кривой второго порядка называется линия, описываемая уравнением 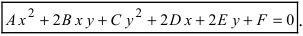
Замечание: Если коэффициенты 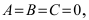
При определенных значениях параметров, входящих в это уравнение, оно дает канонические у равнения окружности, эллипса (не путать с овалом), гиперболы и параболы. Рассмотрим эти кривые второго порядка в указанной последовательности.
Определение: Окружностью называется геометрическое место точек равноудаленных от выделенной точки 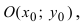 называемой центром окружности, на расстояние R, которое называется радиусом окружности.
называемой центром окружности, на расстояние R, которое называется радиусом окружности.
Получим уравнение окружности (Рис. 27). Пусть точка М(х;у) лежит на окружности:
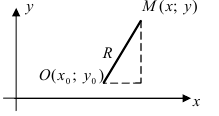
Рис. 27. Вывод уравнения окружности.
Из рисунка видно, что по теореме Пифагора 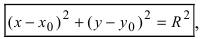 которое определяет уравнение окружности (Рис. 28):
которое определяет уравнение окружности (Рис. 28): 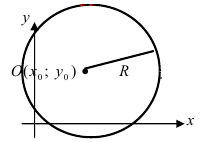
Рис. 28. Окружность. 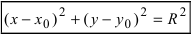
Если 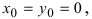 то уравнение принимает вид
то уравнение принимает вид 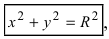 который называется каноническим уравнением окружности.
который называется каноническим уравнением окружности.
Пример:
Составить уравнение окружности, центр которой совпадает с точкой М (2; 1), прямая линия 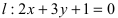 является касательной к окружности.
является касательной к окружности.
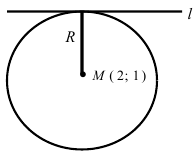
Решение:
Радиус окружности равен расстоянию от центра окружности точки М (2; 1) до прямой l, т.е.
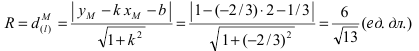
В уравнении окружности 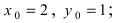 таким образом оно имеет вид:
таким образом оно имеет вид: 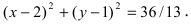
Пример:
Составить уравнение окружности, касающейся двух параллельных прямых 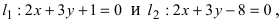 причем одной из них в т. А (1; 2).
причем одной из них в т. А (1; 2).
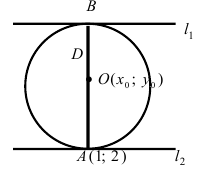
Решение:
Прежде всего определим, на какой из прямых 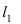 или
или 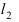 лежит точка A(1; 2). Для этого подставим ее координаты в уравнения прямых
лежит точка A(1; 2). Для этого подставим ее координаты в уравнения прямых 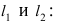
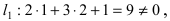 следовательно, точка A(1; 2) принадлежит линии
следовательно, точка A(1; 2) принадлежит линии 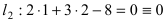 (в сокращенной форме это предложение пишут так:
(в сокращенной форме это предложение пишут так: 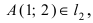 где значок
где значок 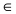 означает “принадлежит”. Таким образом, диаметр окружности D равен расстоянию от точки A(1; 2) до прямой
означает “принадлежит”. Таким образом, диаметр окружности D равен расстоянию от точки A(1; 2) до прямой 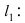
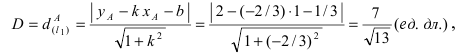
а радиус окружности 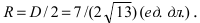 Найдём координаты центра окружности точки
Найдём координаты центра окружности точки 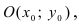 которая делит отрезок АВ пополам. Вначале составим уравнение прямой (АВ) и вычислим координаты точки
которая делит отрезок АВ пополам. Вначале составим уравнение прямой (АВ) и вычислим координаты точки 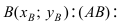 перейдем от общего уравнения прямой
перейдем от общего уравнения прямой 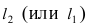 к уравнению прямой с угловым коэффициентом
к уравнению прямой с угловым коэффициентом 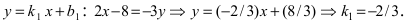 Так как прямая
Так как прямая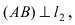 то её угловой коэффициент
то её угловой коэффициент 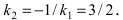 Прямая (АВ) проходит через известную точку A(1;2), следовательно,
Прямая (АВ) проходит через известную точку A(1;2), следовательно, 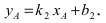 Отсюда находим
Отсюда находим 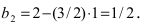 Таким образом,уравнение прямой (АВ):
Таким образом,уравнение прямой (АВ):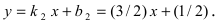
Найдем координаты точки B, которая является пересечением прямых 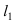 и (АВ), т.е. решим систему линейных алгебраических уравнений, составленную из уравнений прямых
и (АВ), т.е. решим систему линейных алгебраических уравнений, составленную из уравнений прямых 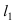 и (АВ): (В):
и (АВ): (В): 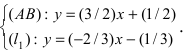 Подставим выражение для переменной у из второго у равнения в первое, получим
Подставим выражение для переменной у из второго у равнения в первое, получим 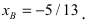 Подставив это значение во второе уравнение системы, найдем
Подставив это значение во второе уравнение системы, найдем 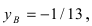 т.е.
т.е. 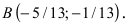
Для вычисления координат точки О применим формулы деления отрезка пополам (О): 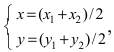 в этой формуле
в этой формуле 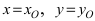 (координаты точки О),
(координаты точки О), 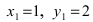 (координаты точки А),
(координаты точки А), 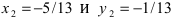 (координаты точки В), следовательно,
(координаты точки В), следовательно, 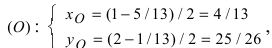 т.е. координаты точки О
т.е. координаты точки О 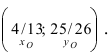
Таким образом, уравнение искомой окружности имеет вид: 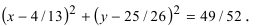
Окружность в высшей математике

которое получается из уравнения (I), если положить 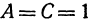 ,
, 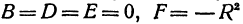 .
.
Если в формулу, выражающую расстояние между двумя точками, подставить 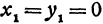 ,
, 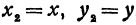 , то получим
, то получим 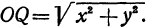 Из уравнения (1) находим, что
Из уравнения (1) находим, что 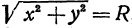 , т. е.
, т. е. 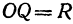 . Это значит, что все точки
. Это значит, что все точки 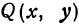 , координаты которых удовлетворяют уравнению (1), находятся на расстоянии
, координаты которых удовлетворяют уравнению (1), находятся на расстоянии 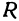 от начала координат. Следовательно, геометрическое место точек, координаты которых удовлетворяют уравнению (1), есть окружность радиуса
от начала координат. Следовательно, геометрическое место точек, координаты которых удовлетворяют уравнению (1), есть окружность радиуса  с центром в начале координат. Аналогично получаем, что уравнение
с центром в начале координат. Аналогично получаем, что уравнение 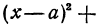
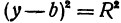 определяет окружность радиуса
определяет окружность радиуса  с центром в точке
с центром в точке 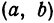 .
.
Пример:
Найдем уравнение окружности с центром в точке  и радиусом, равным 10.
и радиусом, равным 10.
Решение:
Полагая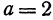 ,
, 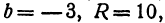 получим
получим 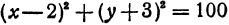 .
.
Разрешим это уравнение относительно 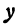 , будем иметь
, будем иметь
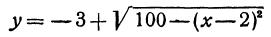
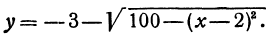
Первое из этих уравнений есть уравнение верхней половины окружности, второе—нижней.
Центральный угол. Градусная мера дуги
Дуга окружности. Если отметить на окружности точки  и
и  , то окружность разделится на две дуги: большую дугу (мажорная дуга) и меньшую дугу (минорная дуга). Если точка
, то окружность разделится на две дуги: большую дугу (мажорная дуга) и меньшую дугу (минорная дуга). Если точка 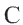 является какой-либо точкой дуги
является какой-либо точкой дуги 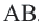 , то
, то 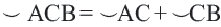 . Если точки
. Если точки  и
и  являются концами диаметра, го каждая дуга является полуокружностью.
являются концами диаметра, го каждая дуга является полуокружностью.
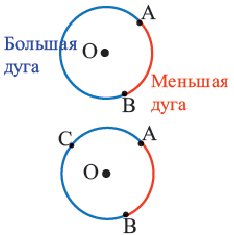
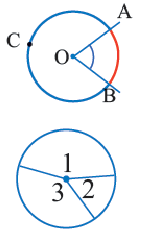
Центральный угол. Угол, вершина которого находится в центре окружности, называется центральным углом. Дугу окружности можно измерять в градусах. Градусная мера дуги равна градусной мере соответствующего центрального угла: 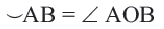
Сумма всех центральных углов окружности, не имеющих общую внутреннюю точку, равна 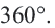
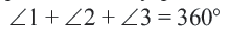
Дуги окружности и их величины

Пример: 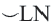 минорная дуга:
минорная дуга: 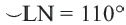
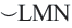 мажорная дуга:
мажорная дуга: 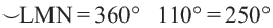
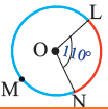
Конгруэнтные дуги
В окружности конгруэнтным центральным углам соответствуют конгруэнтные дуги и наоборот.
Если 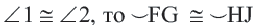
Если 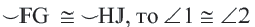
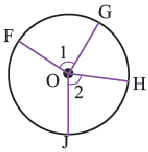
Длина дуги
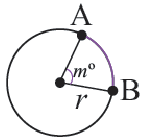
Какую часть составляет центральный угол от всей окружности, такую же часть длина дуги составляет от длины всей окружности.
Длина дуги в 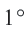 равна
равна 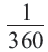 части длины окружности.
части длины окружности.
Длина дуги, соответствующей центральному углу с градусной мерой 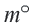 , составляет
, составляет 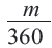 части длины окружности:
части длины окружности: 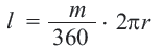
Длина дуги выражается единицами измерения длины (мм, см, м, и т.д.)
Пример №1
Длина окружности равна 72 см. Найдите длину дуги, соответствующей центральному углу 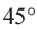 .
.
Решение:
Так как центральный угол 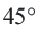 составляет
составляет 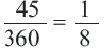 часть полного угла, то длина искомой дуги:
часть полного угла, то длина искомой дуги: 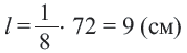
Пример №2
Найдите длину дуги, соответствующей центральному углу 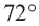 в окружности радиусом 15 см.
в окружности радиусом 15 см.
Решение: подставляя значения 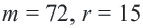 в формулу длины дуги находим:
в формулу длины дуги находим: 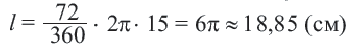
Окружность и хорда
Теорема о конгруэнтных хордах
Теорема 1. Хорды, стягивающие конгруэнтные дуги окружности, конгруэнтны.
Обратная теорема 1. Дуги, стягиваемые конгруэнтными хордами окружности, конгруэнтны.
1)Если 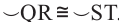 , то
, то 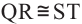
2)Если 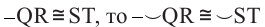
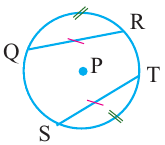
Доказательство теоремы 1:
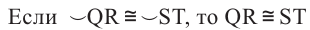

Теорема о серединном перпендикуляре хорд
Теорема 2.
Диаметр, перпендикулярный хорде, делит хорду и соответствующую дугу пополам.
Если 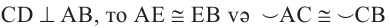
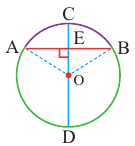
Доказательство теоремы 2.
Дано:  — центральный угол,
— центральный угол, 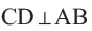
Докажите: 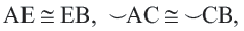
Начертите радиусы 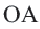 и
и 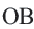 окружности.
окружности.
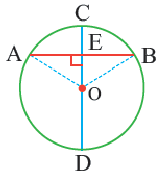
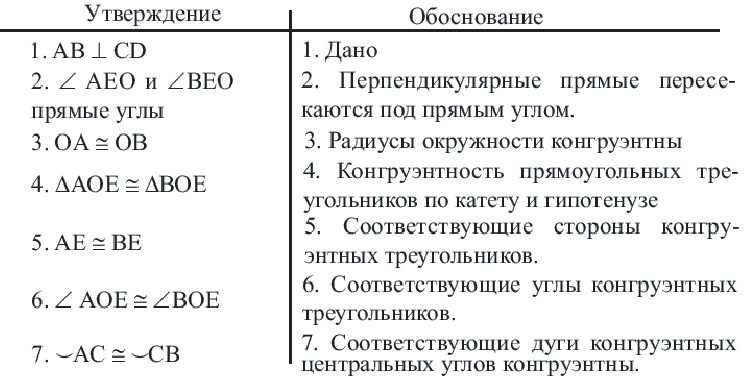
Следствие 1. Прямая, проходящая через центр окружности и перпендикулярная хорде, делит хорду и ее дугу пополам.
Следствие 2. Центр окружности расположен на серединном перпендикуляре хорды. Серединный перпендикуляр хорды проходит через центр окружности.
Пример: Найдите расстояние от центра до хорды длиной 30 единиц в окружности радиусом 17 единиц. Если 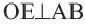 , то
, то 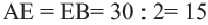 . Из
. Из 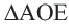 по теореме Пифагора имеем:
по теореме Пифагора имеем: 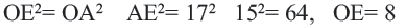
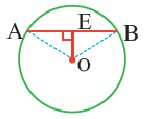
Теорема о хордах, находящихся на одинаковом расстоянии от центра окружности
Теорема 3.
Конгруэнтные хорды окружности находятся на одинаковом расстоянии от центра окружности.
Если 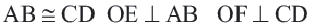 , то
, то 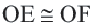
Обратная теорема 3. Хорды, находящиеся на одинаковом расстоянии от центра окружности, конгруэнтны.
Доказательство теоремы 3
Дано: Окружность с центром 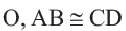
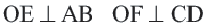
Докажите: 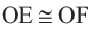
Доказательство (текстовое): Прямая, проходящая через центр окружности и перпендикулярная хорде, делит хорду и стягивающую ее дугу пополам.  и
и  — серединные перпендикуляры конгруэнтных хорд
— серединные перпендикуляры конгруэнтных хорд 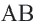 и
и 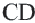 .
.  , так как они являются половиной конгруэнтных хорд. Начертим радиусы окружности
, так как они являются половиной конгруэнтных хорд. Начертим радиусы окружности 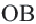 и
и 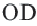 :
: 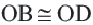 . Прямоугольные треугольники,
. Прямоугольные треугольники, 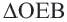 и
и 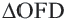 конгруэнтны (по катету и гипотенузе). Так как
конгруэнтны (по катету и гипотенузе). Так как  и
и  являются соответствующими сторонами данных треугольников, то они конгруэнтны:
являются соответствующими сторонами данных треугольников, то они конгруэнтны: 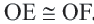 . Теорема доказана.
. Теорема доказана.
Задача. Хорды  и
и  находятся на одинаковом расстоянии от центра окружности.
находятся на одинаковом расстоянии от центра окружности. 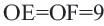 . Если радиус окружности равен 41 единице, то найдите
. Если радиус окружности равен 41 единице, то найдите 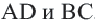 .
.
Решение: Так как хорды  и
и  находятся на одинаковом расстоянии от центра, то они конгруэнтны:
находятся на одинаковом расстоянии от центра, то они конгруэнтны: 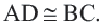
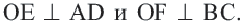 Соединим точки
Соединим точки 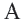 и
и 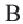 с точкой
с точкой 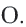 В прямоугольном треугольнике
В прямоугольном треугольнике 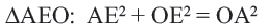
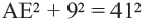 ;
; 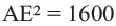 ;
; 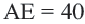 ;
; 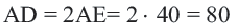
Так как 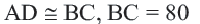
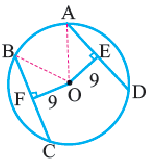
Угол, вписанный в окружность
Угол, вершина которого лежит на окружности, а стороны пересекают окружность, называется углом вписанным в окружность. Дуга, соответствующая углу, вписанному в окружность, называется дугой, на которую опирается этот угол.
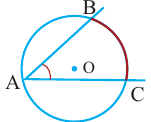
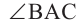 является углом вписанным в окружность с центром
является углом вписанным в окружность с центром 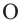 , а
, а 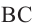 дуга, на которую опирается этот угол. Ниже показаны три разных угла, вписанных в окружность.
дуга, на которую опирается этот угол. Ниже показаны три разных угла, вписанных в окружность.
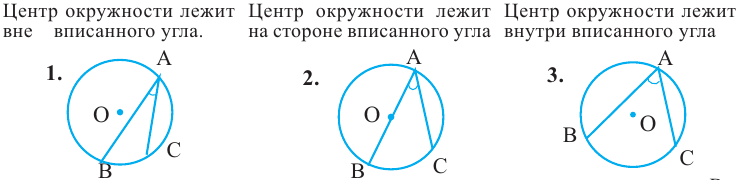
Угол, вписанный в окружность:
Теорема 1. Градусная мера угла, вписанного в окружность, равна половине градусной меры дуги, на которую он опирается. 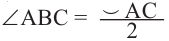
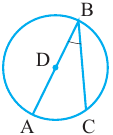
Доказательство (текстовое): 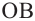 и
и 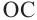 радиусы окружности и
радиусы окружности и 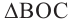 равнобедренный треугольник. Значит,
равнобедренный треугольник. Значит, 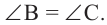 Так как
Так как 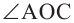 является внешним углом
является внешним углом 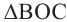 ,
, 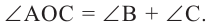 Если примем, что
Если примем, что 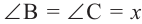 , то
, то 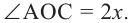 Так как градусные меры центрального угла и опирающейся на него дуги равны, то
Так как градусные меры центрального угла и опирающейся на него дуги равны, то 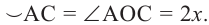 Следовательно,
Следовательно, 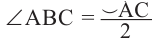 .
.
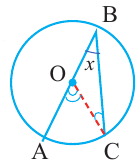
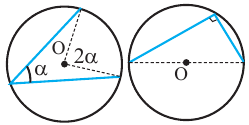
Следствие 1. Угол, вписанный в окружность, равен половине соответствующего центрального угла.
Следствие 2. Угол, вписанный в окружность и опирающийся на диаметр (полуокружность), является прямым углом.
Конгруэнтные углы, вписанные в окружность
Следствие 3. Вписанные углы, опирающиеся на одну и ту же дугу, конгруэнтны. 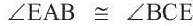 ,
, 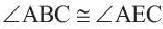 .
.
Следствие 4. Вписанные углы, опирающиеся на конгруэнтные дуги, конгруэнтны. Если 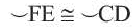 , то
, то 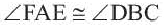 .
.
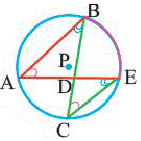

Касательная к окружности
Касательная. Признак касательной
Прямая, имеющая одну общую точку с окружностью, называется касательной. Теорема 1. Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания.
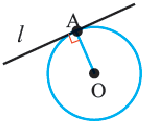
Прямая 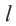 является касательной к окружности. Значит,
является касательной к окружности. Значит, 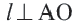 Обратная теорема (признак касательной): Прямая, проходящая через точку окружности и перпендикулярная радиусу, проведенному в эту точку, является касательной окружности.
Обратная теорема (признак касательной): Прямая, проходящая через точку окружности и перпендикулярная радиусу, проведенному в эту точку, является касательной окружности.
Прямая, касающаяся обеих окружностей, называется общей касательной этих окружностей. Окружности, касаясь друг друга изнутри или извне, могут иметь общую касательную в одной точке. Также окружности могут касаться одной касательной в разных точках.

Две окружности могут иметь несколько общих касательных или вообще не иметь общих касательных.
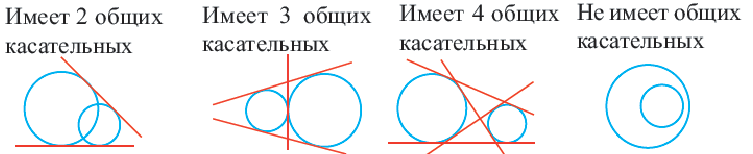
Доказательство теоремы 1. Если прямая  — касательная к окружности, значит, она имеет единственную общую точку с окружностью. Допустим, что прямая
— касательная к окружности, значит, она имеет единственную общую точку с окружностью. Допустим, что прямая  не перпендикулярна радиусу
не перпендикулярна радиусу 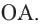 Проведем
Проведем 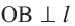 и на прямой
и на прямой  выделим отрезок
выделим отрезок 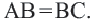 Тогда
Тогда 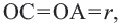 так как
так как 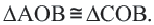 Значит, точка
Значит, точка 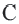 также находится на окружности. То есть прямая
также находится на окружности. То есть прямая  имеет с окружностью две общие точки, что противоречит условию. Значит,
имеет с окружностью две общие точки, что противоречит условию. Значит, 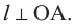
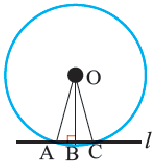
Свойства касательных, проведенных к окружности из одной точки
Теорема 2. Отрезки касательных к окружности, проведенных из одной точки, конгруэнтны, и центр окружности находится на биссектрисе угла, образованного касательными.
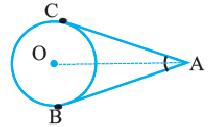
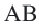 и
и 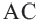 касательные, проведенные из точки
касательные, проведенные из точки 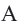 к окружности с центром
к окружности с центром 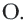
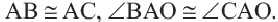
Углы, образованные секущими и касательными
Прямая, имеющая две общие точки с окружностью, называется секущей окружности.
Углы между двумя секущими
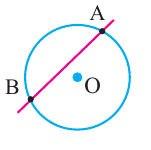
Вершина угла находится внутри окружности
Теорема. Если вершина угла, образованного двумя секущими, находится внутри окружности, то градусная мера угла равна полусумме величин дуг на которые опирается этот угол и угол вертикальный данному. 
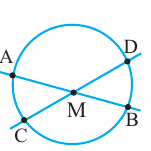
Углы между касательной и секущей
Вершина угла находится на окружности
Теорема. Если вершина угла, образованного касательной и секущей, находится на окружности, то градусная мера угла равна половине градусной меры дуги, на которую он опирается.
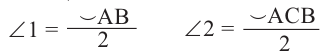
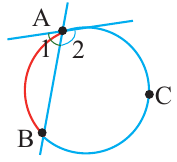
Углы, образованные касательной и секущей
Вершина угла находится вне окружности
Теорема 1.
Градусная мера угла, образованного секущей и касательной, двумя касательными, двумя секущими окружности (если вершина угла находится вне окружности), равна половине разности градусных мер дуг, находящихся между сторонами угла.
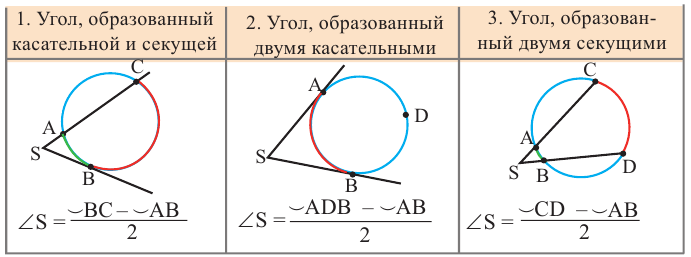
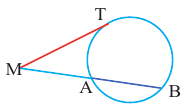
Отрезки секущих и касательных
Длина отрезков, секущих окружность
Теорема 1. При пересечении двух хорд, произведение отрезков одной хорды, полученных точкой пересечения, равно произведению отрезков второй хорды.
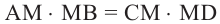
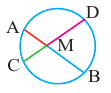
Теорема 2. Если из точки  провести две прямые, пересекающие окружность соответственно в точках
провести две прямые, пересекающие окружность соответственно в точках  и
и 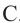 ,
, 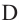 и
и 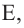 то верно равенство
то верно равенство 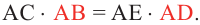
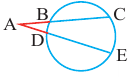
Теорема 3. Если из точки 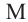 проведены прямая, которая пересекает окружность в точках
проведены прямая, которая пересекает окружность в точках  и
и  и касательная к окружности в точке
и касательная к окружности в точке 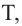 то верно равенство:
то верно равенство: 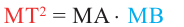
Уравнение окружности
Используя формулу расстояния между двумя точками, можно написать уравнение окружности с радиусом  и с центром в начале координат. Расстояние между центром окружности
и с центром в начале координат. Расстояние между центром окружности 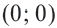 и ее любой точкой
и ее любой точкой 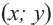 равно радиусу
равно радиусу  окружности.
окружности.
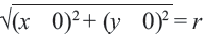 Расстояние между двумя точками
Расстояние между двумя точками
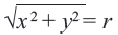 Упрощение
Упрощение
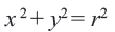 Возведение обеих частей в квадрат
Возведение обеих частей в квадрат
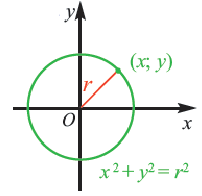
Уравнение окружности с центром в начале координат и радиусом 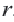 :
: 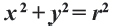
Например, уравнение окружности с центром в начале координат 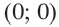 и радиусом 2 имеет вид:
и радиусом 2 имеет вид: 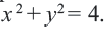
По формуле расстояния между центром окружности 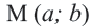 и точки
и точки 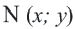 на окружности радиуса
на окружности радиуса 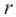 имеем
имеем 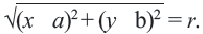 Возведя в квадрат обе части, получаем уравнение окружности с центром в точке
Возведя в квадрат обе части, получаем уравнение окружности с центром в точке 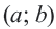 и радиусом
и радиусом 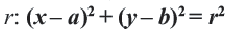
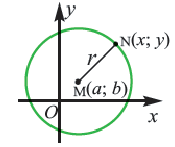
Например, уравнение окружности с центром в точке 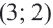 и радиусом 4 имеет вид:
и радиусом 4 имеет вид: 
Пример №3
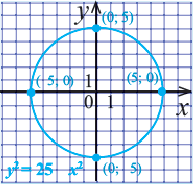
Постройте на координатной плоскости окружность, заданную уравнением 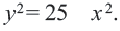
Решение: Напишем уравнение в виде 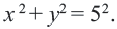 Как видно,
Как видно, 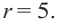
Отметим 4 точки, находящиеся на расстоянии 5 единиц от начала координат. Например, 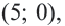
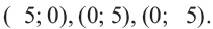 Проведем окружность через эти точки.
Проведем окружность через эти точки.
Пример №4
Точка 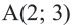 находится на окружности, центром которой является начало координат. Напишите уравнение этой окружности.
находится на окружности, центром которой является начало координат. Напишите уравнение этой окружности.
Решение: Записав координаты точки 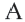 в уравнении
в уравнении 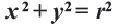 , получим:
, получим: 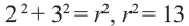 Уравнение этой окружности:
Уравнение этой окружности: 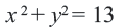
Пример №5
Найдем центр и радиус окружности, заданной уравнением 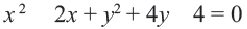
Решение: 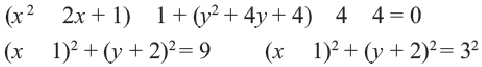
Центр окружности точка 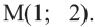 Радиус
Радиус 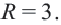
Пример №6
Мобильные телефоны работают с помощью передачи сигналов посредством спутников из одной передающей станции в другую. Компания мобильного оператора старается расположить передающую станцию так, чтобы обслуживать больше пользователей. Представим, что три больших города находятся в точках 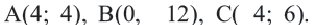 На координатной плоскости 1 единица равна расстоянию в 100 км. Передающая станция должна быть расположена в точке, находящейся на одинаковом расстоянии от этих городов. Напишите координаты этой точки и уравнение соответствующей окружности.
На координатной плоскости 1 единица равна расстоянию в 100 км. Передающая станция должна быть расположена в точке, находящейся на одинаковом расстоянии от этих городов. Напишите координаты этой точки и уравнение соответствующей окружности.
Решение: Сначала соединим эти точки и найдем точку пересечения серединных перпендикуляров сторон полученного треугольника. Эта точка 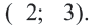 Эта точка, являясь центром окружности, показывает месторасположение станции. Расстояние между центром и любой из заданных точек является радиусом окружности,
Эта точка, являясь центром окружности, показывает месторасположение станции. Расстояние между центром и любой из заданных точек является радиусом окружности, 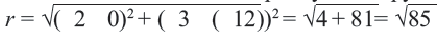
Уравнение окружности: 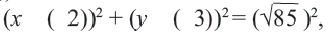
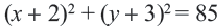
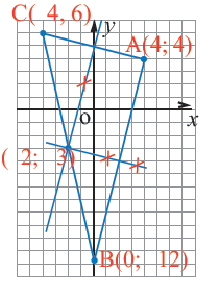
Заметка. Определив линейные уравнения, соответствующие серединным перпендикулярам, можно найти координаты центра окружности решением системы уравнений.
Координаты точек, находящихся на окружности, и тригонометрические отношения
Если точка 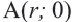 при повороте радиуса
при повороте радиуса 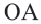 вокруг точки
вокруг точки 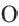 против движения часовой стрелки на угол
против движения часовой стрелки на угол 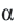 преобразуется в точку
преобразуется в точку 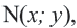 то
то 
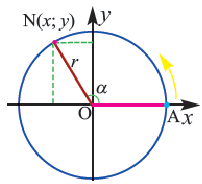
Для координат точки 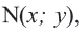 соответствующей углу поворота
соответствующей углу поворота  на окружности, верны формулы
на окружности, верны формулы 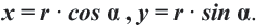 В этих формулах
В этих формулах  — угол, отсчитываемый от положительной оси
— угол, отсчитываемый от положительной оси 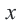 против движения часовой стрелки. Если точка
против движения часовой стрелки. Если точка 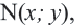 не находится на оси ординат, то
не находится на оси ординат, то 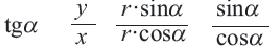 .
.
Синусы смежных углов равны, а косинусы взаимно противоположны.

Из этих формул при 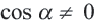 почленным делением получаем:
почленным делением получаем:
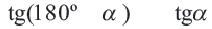
С помощью формул, приведенных выше, вычисление синуса, косинуса, тангенса для тупого угла можно свести к вычислению синуса, косинуса, тангенса острого угла, соответственно.
Сектор и сегмент
Сектор часть круга, ограниченная центральным углом, образованным двумя радиусами и соответствующей этому углу дугой. Площадь сектора, соответствующего центральному углу, составляет ту часть площади круга, которую составляет центральный угол от полного угла.
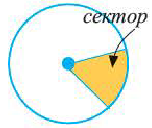
Например, часть круга, соответствующая центральному углу 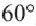 , составляет
, составляет 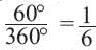 часть всего круга. Так как площадь круга
часть всего круга. Так как площадь круга 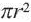 , то площадь этого сектора будет
, то площадь этого сектора будет  Сегмент часть круга, ограниченная хордой и соответствующей дугой.
Сегмент часть круга, ограниченная хордой и соответствующей дугой.
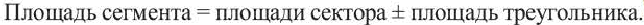
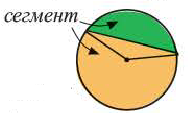
Площадь сектора
Площадь сектора: 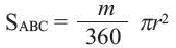
Площадь сегмента: 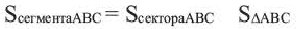
Указание: При нахождении площади сегмента, соответствующего большей дуге, к площади соответствующего сектора прибавляется площадь 
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Telegram и логотип telegram являются товарными знаками корпорации Telegram FZ-LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Если окружность задана уравнением вида
![]()
найти центр (a;b) и радиус R такой окружности несложно.
Примеры.
Определить по уравнению окружности координаты её центра и радиуса:
![]()
![]()
![]()
![]()
![]()
Решение:
![]()
a=3, b=7, R²=4.
Таким образом, центр данной окружности — точка (3;7), радиус R=2.
![]()
a=-2, b=5, R²=1. Окружность с центром в точке (-2;5) и радиусом 1.
![]()
a=0, b=-3, R²=9.
Центр окружности — (0;-3), радиус R=3.
![]()
a=6, b=0, R²=5.
Центр — в точке (6;0), радиус R=√5.
![]()
Это уравнение задаёт окружность с центром в начале координат. Центр — O(0;0), радиус R=√11.
Чтобы найти центр и радиус окружности, заданной уравнением вида
![]()
нужно дополнить его до полных квадратов, чтобы привести к привычному виду.
Для этого сначала сгруппируем слагаемые
![]()
затем прибавим и вычтем квадрат второго слагаемого из формулы квадрата разности (2ax- удвоенное произведение первого слагаемого на второе. Первое — x, второе — a)
![]()
Отсюда
![]()
![]()
При a²+b²-c>0 это уравнение задаёт окружность с радиусом
![]()
При a²+b²-c=0 уравнению удовлетворяют координаты единственной точки (a;b).
При a²+b²-c<0 нет ни одной точки, удовлетворяющей этому уравнению.
Примеры.
Найти координаты центра и радиус окружности:
![]()
![]()
![]()
Решение:
![]()
Группируем слагаемые
![]()
Выделяем в уравнении полные квадраты. В первых скобках удвоенное слагаемое 10x представляем как 10x=2·a·5 (чтобы получить 2ab для формулы a²+2ab+b²=(a+b)²). Получается, что b=5. Если прибавить и вычесть b², результат не изменится:
![]()
Аналогично
![]()
Таким образом,
![]()
![]()
![]()
Центром этой окружности является точка (-5;3), радиус R=7.
![]()
![]()
![]()
![]()
![]()
Центр окружности — точка (2,5;0), радиус R=1,5.
![]()
Разделим обе части уравнения на 3:
![]()
Далее — аналогично
![]()
![]()
![]()
![]()
![]()
Центр этой окружности лежит в точке
![]()
