Найти медиану треугольника по координатам вершин
Как найти медиану если даны координаты вершин треугольника?
Чтобы найти медиану треугольника по координатам его вершин, применим формулы координат середины отрезка и формулу расстояния между точками.
Рассмотрим нахождение медианы на конкретном примере.
 Дано: ΔABC,
Дано: ΔABC,
A(-11;12), B(3;8), C(-1;6),
AF — медиана.
Найти: AF
Решение:
1) Так как AF — медиана треугольника ABC, то F — середина BC.
По формулам координат середины отрезка:
![]()
![]()
Итак, F(1;7).
2) По формуле расстояния между точками
![]()
![]()
![]()
Ответ: 13.
Лидеры категории
Лена-пена
Искусственный Интеллект
М.И.
Искусственный Интеллект
Y.Nine
Искусственный Интеллект
•••
Для того, чтобы найти координаты точки пересечения высоты и медианы треугольника, необходимо обладать хотя бы некоторыми исходными данными:
1) координаты вершин треугольника (либо данные, позволяющие вычислить эти координаты);
2) информацией о том, из каких вершин проводится высота и медиана, координаты точки пересечения которых необходимо найти.
По этим данным находятся координаты точки медианы, которая принадлежит стороне треугольника (ее координаты равны полусуммам соответствующих координат) уравнение прямой, которая принадлежит медиана (по двум точкам вершине треугольника, из которого проведена медиана, и второй точке, принадлежащей стороне треугольника).
Далее, составляется уравнение прямой, к которой проведена высота (по двум точкам вершинам треугольника) и, имея это уравнение составляется уравнение прямой, содержащей высоту (как прямой, перпендикулярной данной и проходящей через заданную точку – вершину треугольника).
Затем уравнения медианы и высоты приравниваются друг к другу и решаются как уравнение, находится абсцисса искомой точки, а затем, после подстановки ее в уравнение медианы или высоты и ордината искомой точки.
Данный алгоритм решения задачи справедлив в случае, если треугольник задан в двумерном пространстве (т.е. на координатной плоскости).
Если же треугольник задан в трехмерном пространстве, то необходимо прежде всего составить уравнение плоскости, проходящей через вершины треугольника, а затем использовать его на последнем этапе для составления системы уравнений.
Помогите доказать методом координат. Самостоятельная работа 4. Вариант 7. № 1 ГДЗ Геометрия 9 класс Зив Б.Г. – Рамблер/класс
Помогите доказать методом координат. Самостоятельная работа 4. Вариант 7. № 1 ГДЗ Геометрия 9 класс Зив Б.Г. – Рамблер/класс
Интересные вопросы
Школа
Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?
Новости
Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?
Школа
Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?
Школа
Когда в 2018 году намечено проведение основного периода ЕГЭ?
Новости
Будет ли как-то улучшаться система проверки и организации итоговых сочинений?
Вузы
Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?
Докажите методом координат, что медианы треугольника
пересекаются в одной точке и делятся ею в отношении 2:1, считая от вершин треугольника.
ответы
Пусть А(0; 0), В(b; h), С(а; 0). Пусть BE медиана и
Рассмотрим медиану АF и точку М1 на ней такую, что
=> М и М1 совпадают. Аналогично и с медианой CG. Ч.т.д.
ваш ответ
Можно ввести 4000 cимволов
отправить
дежурный
Нажимая кнопку «отправить», вы принимаете условия пользовательского соглашения
похожие темы
Экскурсии
Мякишев Г.Я.
Досуг
Химия
похожие вопросы 5
Докажите, что треугольники подобны. Вопросы и задачи 64, Геометрия, 10-11 класс, Атанасян Л.С.
Привет. Запуталась при решении, нужна помощь знатоков!!!
Три прямые, проходящие через одну точку и не лежащие в одной (Подробнее…)
ГДЗГеометрия11 класс10 классАтанасян Л.С.
Самостоятельная работа 19.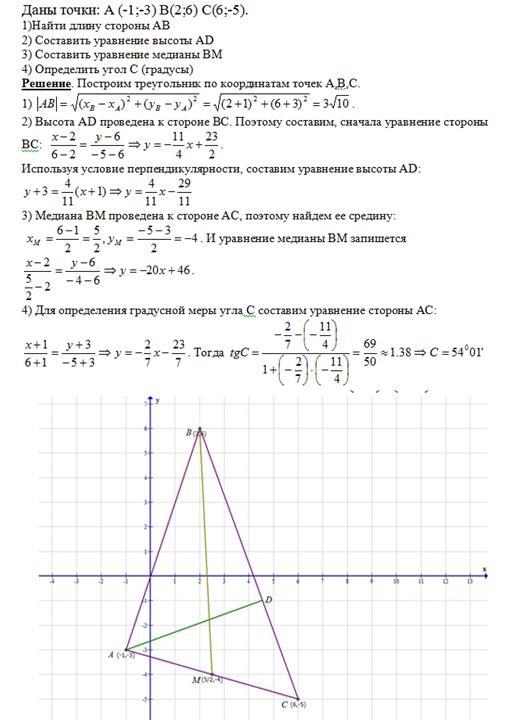 Вариант 2. № 2 ГДЗ Геометрия 9 класс Зив Б.Г. Помогите доказать, используя параллельный перенос
Вариант 2. № 2 ГДЗ Геометрия 9 класс Зив Б.Г. Помогите доказать, используя параллельный перенос
Используя параллельный перенос, докажите, что углы при основании равнобедренной трапеции равны между собой.
ГДЗЭкзаменыГеометрия9 классЗив Б. Г.
ГДЗ Тема 21 Физика 7-9 класс А.В.Перышкин Задание №476 Изобразите силы, действующие на тело.
Привет всем! Нужен ваш совет, как отвечать…
Изобразите силы, действующие на тело, когда оно плавает на поверхности жидкости. (Подробнее…)
ГДЗФизикаПерышкин А.В.Школа7 класс
Дадут ли аттестат после второй пересдачи.?
Мне сказала подруга,что аттестат не дадут после второй пересдачи,дадут только справку и всё,так ли это?
9 класс
Ребята нужны ответы на пересдачу по математике 9 класс 11 регион. Срочно!
ГИА9 класс
Как найти медиану треугольника зная его стороны.
 Медиана
Медиана
Медиана и высота треугольника – это одна из самых увлекательных и интересных тем геометрии. Термин «Медиана» означает прямую или отрезок, который соединяет вершину треугольника с его противоположной стороной. Другими словами, медиана – это линия, которая проходит из середины одной стороны треугольника в противоположную вершину этого же треугольника. Поскольку у треугольника только три вершины и три стороны, значит и медианы может быть только три.
Свойства медианы треугольника
- Все медианы треугольника пересекаются в одной точке и разделяются этой точкой в соотношении 2:1, считая от вершины. Таким образом, если нарисовать в треугольнике все три медианы, то точка их пересечения будет делить их на две части. Часть, которая располагается ближе в вершине, будет составлять 2/3 всей линии, а часть, которая располагается ближе к стороне треугольника – 1/3 линии. Пересекаются медианы в одной точке.
- Три медианы, проведенные в одном треугольнике, делят этот треугольник на 6 маленьких треугольников, чья площадь будет равна.
- Чем больше сторона треугольника, от которой исходит медиана, тем меньше эта медиана. И наоборот, самая короткая сторона имеет самую длинную медиану.
- Медиана в прямоугольном треугольнике имеет ряд собственных характеристик. Например, если вокруг такого треугольника описать окружность, которая будет проходить через все вершины, то медиана прямого угла, проведенная к гипотенузе, станет радиусом описанной окружности (то есть ее длина будет составлять расстояние от любой точки окружности до ее центра).
Уравнение длины медианы треугольника
Формула медианы исходит из теоремы Стюарта и гласит, что медиана – это квадратный корень из отношения квадратов суммы сторон треугольника, которые образуют вершину, за вычетом квадрата стороны, к которой проведена медиана к четырем. Другими словами, чтобы узнать длину медианы нужно возвести в квадрат показатели длины каждой стороны треугольника, а затем записать это в виде дроби, в числителе которой будет сумма квадратов сторон, которые образуют угол, откуда исходит медиана, минус квадрат третьей стороны. В качестве знаменателя здесь выступает цифра 4. Затем из данной дроби нужно извлечь корень квадратный, и тогда мы получим длину медианы.
В качестве знаменателя здесь выступает цифра 4. Затем из данной дроби нужно извлечь корень квадратный, и тогда мы получим длину медианы.
Точка пересечения медиан треугольника
Как мы писали выше, всем медианы одного треугольника пересекаются в одной точке. Эту точку называют центром треугольника. Он делит каждую медиану на две части, длина которым соотносится как 2:1. При этом центр треугольника является и центром описанной вокруг него окружности. А другие геометрические фигуры имеют собственные центры.
Координаты точки пересечения медиан треугольника
Чтобы найти координаты пересечения медиан одного треугольника, воспользуемся свойством центроида, согласно которому он делит каждую медиану на отрезки 2:1. Обозначаем вершины как как A(x 1 ;y 1), B(x 2 ;y 2), C(x 3 ;y 3),
и вычисляем координаты центра треугольника по формуле: x 0 = (x 1 + x 2 + x 3)/3; y 0 = (y 1 + y 2 + y 3)/3.
Площадь треугольника через медиану
Все медианы одного треугольника делят этот треугольник на 6 равных треугольников, а центр треугольника делит каждую медиану в соотношении 2:1. Поэтому если известны параметры каждой медианы, можно вычислить и площадь треугольника через площадь одного из маленьких треугольников, а затем увеличить этот показатель в 6 раз.
Поэтому если известны параметры каждой медианы, можно вычислить и площадь треугольника через площадь одного из маленьких треугольников, а затем увеличить этот показатель в 6 раз.
Медианой именуется отрезок, проведенный из вершины треугольника на середину противоположной стороны, то есть делит ее точкой пересечения пополам. Точка, в которой медиана пересекает противоположную вершине, из которой она выходит, сторону, именуется основанием. Через одну точку, называемую точкой пересечения, проходит каждая медиана треугольника. Формула длины ее может выражаться несколькими способами.
Формулы для выражения длины медианы
- Зачастую в задачах по геометрии ученикам приходится иметь дело с таким отрезком, как медиана треугольника. Формула ее длины выражается через стороны:
где a, b и c — стороны. Причем с является стороной, на которую медиана опускается. Таким образом выглядит самая простая формула. Медианы треугольника иногда требуется проводить для вспомогательных расчетов. Есть и другие формулы.
Есть и другие формулы.
- Если при расчете известны две стороны треугольника и определенный угол α, находящийся между ними, то длина медианы треугольника, опущенной к третьей стороне, будет выражаться так.
Основные свойства
- Все медианы имеют одну общую точку пересечения O и ею же делятся в отношении два к одному, если вести отсчет от вершины. Такая точка носит название центра тяжести треугольника.
- Медиана разделяет треугольник на два других, площади которых равны. Такие треугольники называются равновеликими.
- Если провести все медианы, то треугольник будет разделен на 6 равновеликих фигур, которые также будут треугольниками.
- Если в треугольнике все три стороны равны, то в нем каждая из медиан будет также высотой и биссектрисой, то есть перпендикулярна той стороне, к которой она проведена, и делит надвое угол, из которого она выходит.
- В равнобедренном треугольнике медиана, опущенная из вершины, которая находится напротив стороны, не равной никакой другой, будет также высотой и биссектрисой.

Медианы, опущенные из других вершин, равны. Это также является необходимым и достаточным условием равнобедренности. - Если треугольник является основанием правильной пирамиды, то высота, опущенная на данное основание, проецируется в точку пересечения всех медиан.
- В прямоугольном треугольнике медиана, проведенная к наибольшей стороне, равняется половине ее длины.
- Пусть O — точка пересечения медиан треугольника. Формула, приведенная ниже, будет верная для любой точки M.
- Еще одним свойством обладает медиана треугольника. Формула квадрата ее длины через квадраты сторон представлена ниже.
Свойства сторон, к которым проведена медиана
- Если соединить любые две точки пересечения медиан со сторонами, на которые они опущены, то полученный отрезок будет являться средней линией треугольника и составлять одну вторую от стороны треугольника, с которой она не имеет общих точек.
- Основания высот и медиан в треугольнике, а также середины отрезков, соединяющих вершины треугольника с точкой пересечения высот, лежат на одной окружности.

В заключение логично сказать, что одним из самых важных отрезков является именно медиана треугольника. Формула ее может использоваться при нахождении длин других его сторон.
Медиана треугольника
— это отрезок, соединяющий верщину треугольника с серединой противолежащей стороны этого треугольника.
Свойства медиан треугольника
1. Медиана разбивает треугольник на два треугольника одинаковой площади.
2. Медианы треугольника пересекаются в одной точке, которая делит каждую из них в отношении 2:1, считая от вершины. Эта точка называется центром тяжести треугольника (центроидом).
3. Весь треугольник разделяется своими медианами на шесть равновеликих треугольников.
Длина медианы проведенной к стороне:
(док-во достроением до параллелограмма и использованием равенства в параллелограмме удвоенной суммы квадратов сторон и суммы квадратов диагоналей )
Т1.
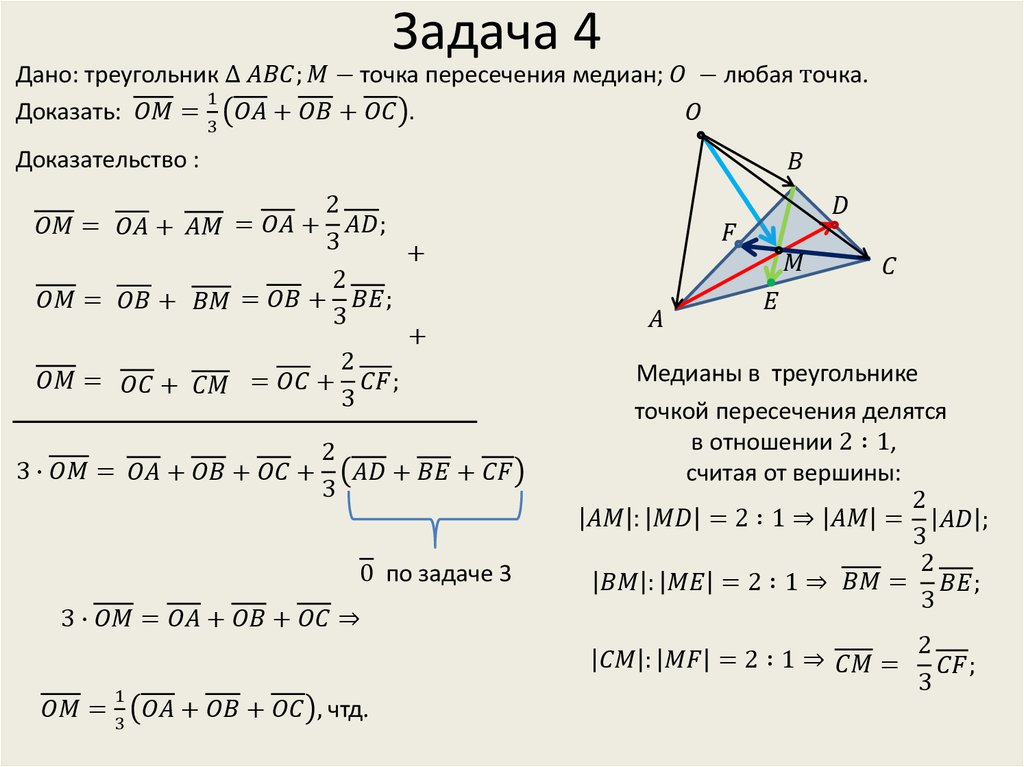
Три медианы треугольника пересекаются в одной точке М, которая делит каждую из них в отношении 2:1, считая от вершин треугольника. Дано: ∆ABC,
Дано: ∆ABC,
СС 1 , АА 1 , ВВ
1 — медианы
∆ABC
. Доказать: и
Д-во: Пусть М — точка пересечения медиан СС 1 , АА 1 треугольника ABC. Отметим A 2 — середину отрезка AM и С 2 — середину отрезка СМ. Тогда A 2 C 2 — средняя линия треугольника АМС.
Значит,А 2 С 2
|| АС
и A 2 C 2 = 0,5*АС. С 1
А 1
— средняя линия треугольника ABC. Значит, А 1
С 1
|| АС и А 1
С 1
= 0,5*АС.
Четырехугольник А 2 С 1 А 1 С 2
— параллелограмм, так как его противоположные стороны А
1
С 1
и А 2 С 2
равны и параллельны. Следовательно, А 2 М =
МА 1
и С 2 М =
МC 1 .
Это означает, что точки А 2
и M
делят медиану АА 2
на три равные части, т. е. AM = 2МА 2 . Аналогично СМ = 2MC 1
. Итак, точка М пересечения двух медиан АА 2
и CC 2
треугольника ABC делит каждую из них в отношении 2:1, считая от вершин треугольника. Совершенно аналогично доказывается, что точка пересечения медиан АА 1 и BB 1 делит каждую из них в отношении 2:1, считая от вершин треугольника.
Совершенно аналогично доказывается, что точка пересечения медиан АА 1 и BB 1 делит каждую из них в отношении 2:1, считая от вершин треугольника.
На медиане АА 1 такой точкой является точка М, следовательно, точка М
и есть точка пересечения медиан АА 1 иBB 1.
Таким образом, n
T2.
Докажите, что отрезки, которые соединяют центроид с вершинами треугольника, делят его на три равновеликие части. Дано: ∆ABC , — его медианы.
Доказать:S AMB
=S BMC
=S AMC .
Доказательство.
В,
у них общая. т.к. равны их основания и высота, проведенная из вершины М,
у них общая. Тогда
Аналогичным образом доказывается, чтоS AMB = S AMC .
Таким образом,S AMB = S AMC = S CMB .
n
Биссектриса треугольника.Теоремы связанные с биссектрисами треугольника. Формулы для нахождения биссектрис
Биссектриса угла
— луч с началом в вершине угла, делящий угол на два равных угла.
Биссектриса угла есть геометрическое место точек внутри угла, равноудалённых от сторон угла.
Свойства
1. Теорема о биссектрисе: Биссектриса внутреннего угла треугольника делит противоположную сторону в отношении, равном отношению двух прилежащих сторон
2. Биссектрисы внутренних углов треугольника пересекаются в одной точке — инцентре — центре вписанной в этот треугольник окружности.
3. Если в треугольнике две биссектрисы равны, то треугольник — равнобедренный (теорема Штейнера — Лемуса).
Вычисление длины биссектрисы
l c — длина биссектрисы, проведённой к стороне c,
a,b,c — стороны треугольника против вершин A,B,C соответственно,
p — полупериметр треугольника,
a l ,b l — длины отрезков, на которые биссектриса l c делит сторону c,
α,β,γ — внутренние углы треугольника при вершинах A,B,C соответственно,
h c — высота треугольника, опущенная на сторону c.
Метод площадей.
Характеристика метода.
Из названия следует, что главным объектом данного метода является площадь.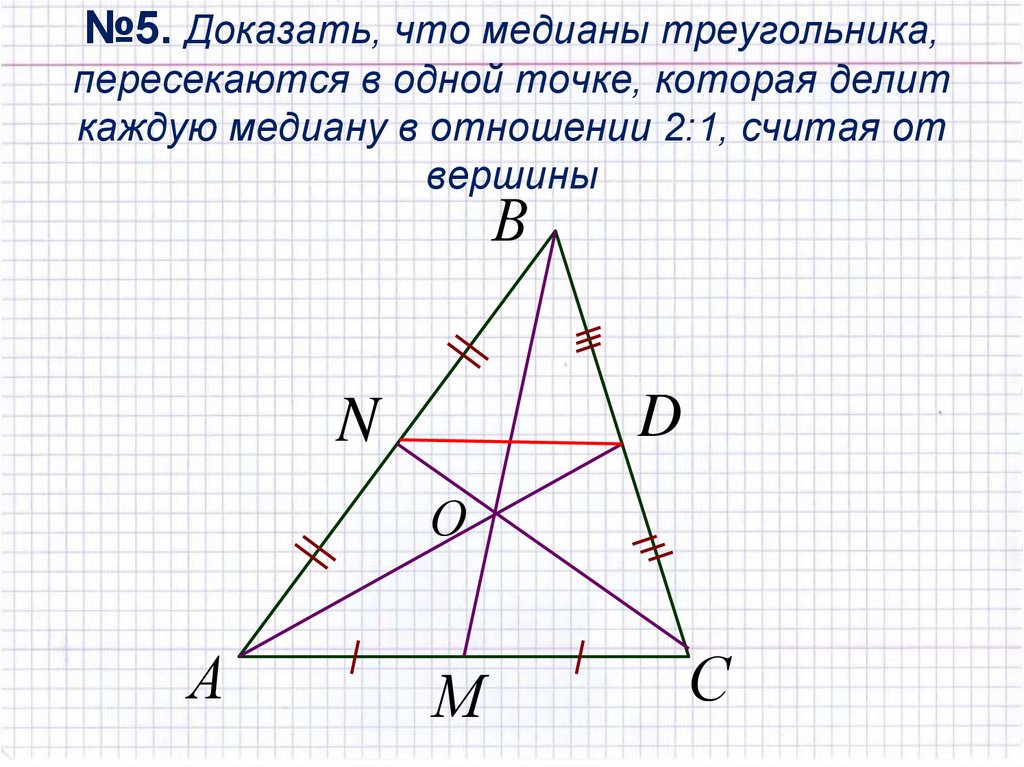 Для ряда фигур, например для треугольника, площадь довольно просто выражается через разнообразные комбинации элементов фигуры (треугольника). Поэтому весьма эффективным оказывается прием, когда сравниваются различные выражения для площади данной фигуры. В этом случае возникает уравнение, содержащее известные и искомые элементы фигуры, разрешая которое мы определяем неизвестное. Здесь и проявляется основная особенность метода площадей – из геометрической задачи он «делает» алгебраическую, сводя все к решению уравнения (а иногда системы уравнений).
Для ряда фигур, например для треугольника, площадь довольно просто выражается через разнообразные комбинации элементов фигуры (треугольника). Поэтому весьма эффективным оказывается прием, когда сравниваются различные выражения для площади данной фигуры. В этом случае возникает уравнение, содержащее известные и искомые элементы фигуры, разрешая которое мы определяем неизвестное. Здесь и проявляется основная особенность метода площадей – из геометрической задачи он «делает» алгебраическую, сводя все к решению уравнения (а иногда системы уравнений).
1) Метод сравнения: связан с большим кол-вом формул S одних и тех же фигур
2) Метод отношения S: основан на след опорных задачах:
Теорема Чевы
Пусть точки A»,B»,C» лежат на прямых BC,CA,AB треугольника. Прямые AA»,BB»,CC» пересекаются в одной точке тогда и только тогда, когда
Доказательство.
Обозначим через точку пересечения отрезков и . Опустим из точек С и А перпендикуляры на прямую ВВ 1 до пересечения с ней в точках Kи L соответственно (см.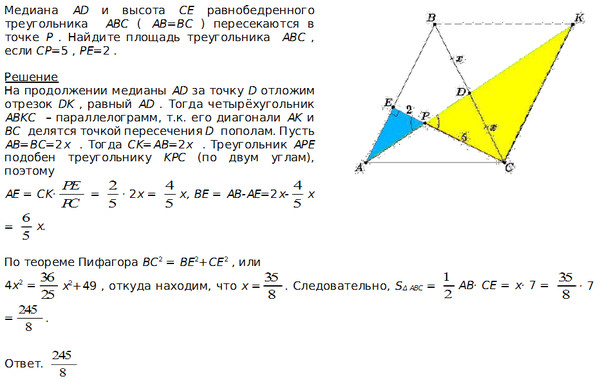 рисунок).
рисунок).
Поскольку треугольники и имеют общую сторону , то их площади относятся как высоты, проведенные на эту сторону, т.е. AL иCK:
Последнее равенство справедливо, так как прямоугольные треугольники и подобны по острому углу.
Аналогично получаем и
Перемножим эти три равенства:
что и требовалось доказать.
Замечание. Отрезок (или продолжение отрезка), соединяющий вершину треугольника с точкой, лежащей на противоположной стороне или ее продолжении, называется чевианой.
Теорема (обратная теорема Чевы)
. Пусть точки A»,B»,C» лежат на сторонах BC,CA и AB треугольника ABC соответственно. Пусть выполняется соотношение
Тогда отрезки AA»,BB»,CC» и пересекаются в одной точке.
Теорема Менелая
Теорема Менелая. Пусть прямая пересекает треугольник ABC, причем C 1 – точка ее пересечения со стороной AB, A 1 – точка ее пересечения со стороной BC, и B 1 – точка ее пересечения с продолжением стороны AC. Тогда
Доказательство
. Проведем через точку C прямую, параллельную AB. Обозначим через K ее точку пересечения с прямой B 1 C 1 .
Проведем через точку C прямую, параллельную AB. Обозначим через K ее точку пересечения с прямой B 1 C 1 .
ТреугольникиAC 1 B 1 иCKB 1 подобны (∟C 1 AB 1 = ∟KCB 1 , ∟AC 1 B 1 = ∟CKB 1). Следовательно,
ТреугольникиBC 1 A 1 иCKA 1 такжеподобны (∟BA 1 C 1 =∟KA 1 C, ∟BC 1 A 1 =∟CKA 1). Значит,
Из каждого равенства выразим CK:
Откуда что и требовалось доказать.
Теорема (обратная теорема Менелая).
Пусть дан треугольник ABC. Пусть точка C 1 лежит на стороне AB, точка A 1 – на стороне BC, а точка B 1 – на продолжении стороны AC, причем выполняется соотношение
Тогда точки A 1 ,B 1 и C 1 лежат на одной прямой.
Высоты Медианы и биссектрисы углов
Точно так же, как существуют специальные имена для особых типов треугольников, существуют специальные имена для особых отрезков внутри треугольников. Разве это не особенное?
База и высота
Каждый треугольник имеет три оснований (любая из его сторон) и три высот (высот). Каждая высота представляет собой перпендикулярный отрезок от вершины к противоположной стороне (или продолжение противоположной стороны) (рис. 1).
Каждая высота представляет собой перпендикулярный отрезок от вершины к противоположной стороне (или продолжение противоположной стороны) (рис. 1).
Рисунок 1 Три основания и три высоты одного и того же треугольника.
Высоты иногда могут совпадать со стороной треугольника или иногда могут пересекаться с расширенным основанием за пределами треугольника. На рисунке 2 AC — это высота основания BC , а BC — высота основания AC .
Рисунок 2 В прямоугольном треугольнике каждый катет может служить высотой.
На рис. 3, AM — высота до базы BC .
Рисунок 3 Высота тупоугольного треугольника.
Интересно отметить, что в любом треугольнике три прямые, содержащие высоты, пересекаются в одной точке (рис. 4).
Рисунок 4 Три линии, содержащие высоты, пересекаются в одной точке,
, который может быть или не быть внутри треугольника.
Медиана
А медиана в треугольнике — это отрезок, проведенный от вершины к середине противоположной стороны. Каждый треугольник имеет три медианы. На рисунке 5 E является средней точкой BC . Следовательно, БЭ = ЭК . AE является медианой Δ ABC.
Рисунок 5 Медиана треугольника.
В каждом треугольнике три медианы сходятся в одной точке внутри треугольника (рис. 6).
Рисунок 6 Три медианы сходятся в одной точке внутри треугольника.
Биссектриса угла
Биссектриса угла в треугольнике — это отрезок, проведенный из вершины, которая делит пополам (разрезает пополам) этот угол при вершине. У каждого треугольника есть три биссектрисы угла. На рисунке , представляет собой биссектрису угла в Δ ABC.
Рисунок 7 Биссектриса угла.
В каждом треугольнике три биссектрисы угла пересекаются в одной точке внутри треугольника (рис. 8).
Рисунок 8 Биссектрисы трех углов пересекаются в одной точке внутри треугольника.
Как правило, высоты, медианы и биссектрисы являются разными отрезками. Однако в некоторых треугольниках они могут быть одними и теми же сегментами. На рисунке можно доказать, что высота, проведенная из угла при вершине равнобедренного треугольника, является медианой, а также биссектрисой угла.
Рисунок 9 Высота, проведенная из угла при вершине равнобедренного треугольника.
Пример 1: На основании маркировки на рисунке 10 назовите высоту Δ QRS, назовите медиану Δ QRS, и назовите биссектрису угла Δ QRS .
Рисунок 10 Нахождение высоты, медианы и биссектрисы угла.
RT является высотой до основания QS , потому что RT ⊥ QS .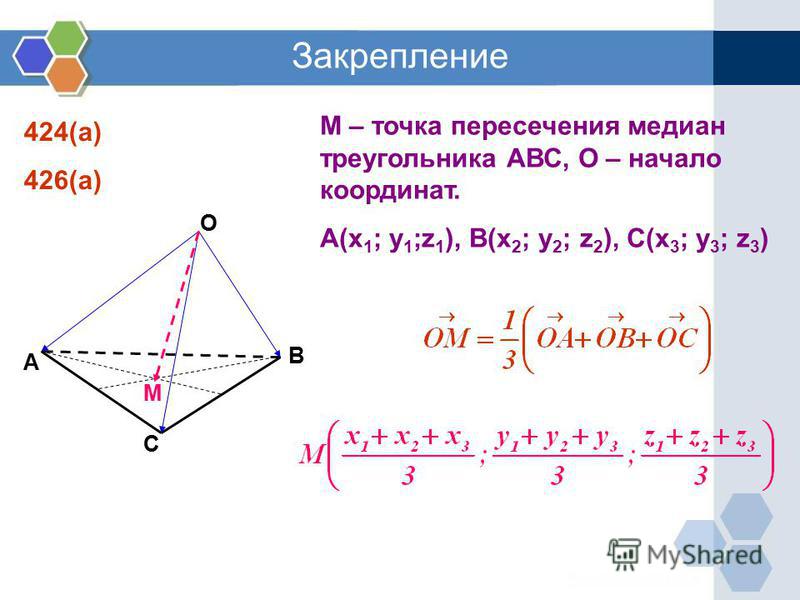
SP является медианой базы QR , поскольку P является средней точкой QR .
QU является биссектрисой угла Δ QRS , поскольку делит пополам ∠ RQS.
Калькулятор формул для уравнений равнобедренного треугольника
Изменить уравнение
Выберите, чтобы найти другое неизвестное
Разносторонний треугольник:
Стороны не имеют одинаковой длины
Нет равных углов
Уравнения разностороннего треугольника
Эти уравнения применимы к любому типу треугольника. Сокращенные
уравнений для равностороннего, прямого и равнобедренного треугольников приведены ниже.
| Perimeter | |
| Semiperimeter | |
| Area | |
| Area | |
| Base | |
| Height | |
| Angle Bisector стороны a | |
| Биссектриса угла стороны b | |
| Биссектриса угла стороны c | |
| Median of side a | |
| Median of side b | |
| Median of side c | |
| Altitude of side a | |
| Altitude of side b | |
| Высота стороны c | |
| Радиус описанной окружности | |
| Радиусы вписанной окружности |
9 20003 .
| Длина стороны A | |
| Периметр | |
| Полупериметр | |
| Площадь | |
| Высота 6 | |
| Median | |
| Angle Bisector | |
| Circumscribed Circle Radius | |
| Inscribed Circle Radius |
Right Triangle:
One angle is equal to 90 degrees
Уравнения прямоугольного треугольника
| Теорема Пифагора | |
| Периметр | |
| Semiperimeter | |
| Area | |
| Altitude of a | |
| Altitude of b | |
| Altitude of c | |
| Angle Bisector of a | |
| Биссектриса угла b | |
| Биссектриса угла c | |
| Медиана |
| Median of b | |
| Median of c | |
| Inscribed Circle Radius | |
| Circumscribed Circle Radius |
7
Isosceles Triangle:
Two sides have equal length
Two angles are равно
Уравнения равнобедренного треугольника
| Периметр | ||||
| Полупериметр | ||||
| Area | ||||
| Altitudes of sides a and c | ||||
| Altitude of side b | ||||
| Median of sides a and c | ||||
| Median of side b | ||||
| Биссектриса угла сторон a и c | ||||
| Биссектриса угла стороны b | ||||
| Радиус описанной окружности | 9167 | 0169 | Inscribed Circle Radius |
Where
= = .
| P | = | Perimeter |
| s | = | Semiperimeter |
| a | = | Length of side a |
| b | = | Длина стороны b |
| c | = | Длина стороны c |
| h | 9016 Высота над уровнем моря0172 | |
| m | = | Median |
| A | = | Angle A |
| B | = | Angle B |
| C | = | Angle C |
| T | = | Угол бисектор |
| R | = | RIGHTRED RADIUS |
| R | ||
| R | ||
| R | ||
| R | ||
| R | = | |
| R | = | |
| r | = | |
| r | = |
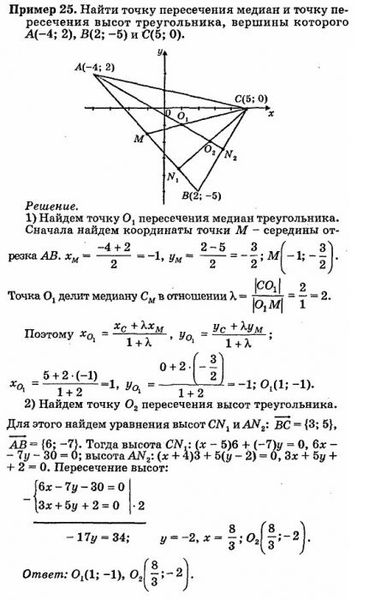
Пример 1:
Построить треугольник, вершины которого находятся в точках А (2; 4), В (-3; 2), С (-3; -4). Найти:
1) уравнения сторон треугольника АВС;
2) координаты точки пересечения медиан;
3) длину и уравнение высоты, опущенной из вершины А;
4) площадь треугольника.
Решение от преподавателя:

Уравнение, прямой проходящей через две точки
1) Уравнения сторон треугольника АВС

2) Координаты точки пересечения медиан
Медиана – отрезок, соединяющий вершину треугольника с серединой противоположной стороны.
Координаты т. E как середины отрезка ВС.

Уравнение АЕ

Координаты т. К как середины отрезка АВ.

Уравнение СК

3) Длина и уравнение высоты, опущенной из вершины А
Расстояние от точки до прямой

Уравнение прямой, проходящей через точку перпендикулярно другой прямой

Уравнение AN

4) Площадь треугольника

Длина ВС

Пример 2:

Решение от преподавателя:


Пример 3:
По координатам вершин треугольника ABC найти:
- периметр треугольника;
- уравнения сторон AB и BC;
- уравнение высоты AD; угол ABC;
- площадь треугольника.
Сделать чертеж.
А(1; 2); В (–1; 2); С(3; 0).
Решение от преподавателя:





Пример 4:
Даны координаты вершин треугольникаА, В, С.
Требуется найти:
1) уравнение и длину стороны ВС;
2) уравнение и длину высоты, проведённой из вершиныА;
3) уравнение медианы, проведённой из вершиныА;
4) площадь треугольника.
Сделать чертёж.
А(4;-3), B(-2;-1), C(3;-2).
Решение от преподавателя:


Пример 5:

![]()
Решение от преподавателя:
1) ![]()
2)
3) Находим координаты точки М – середины стороны ВС:
![]()
Определяем длину медианы АМ:
![]()
4) Составляем уравнение медианы – прямой АМ:

5) Если ВН – высота, проведенная из вершины В к стороне АС, то, поскольку ВН проходит через точку В перпендикулярно вектору ![]() , то составляем уравнение высоты по формуле
, то составляем уравнение высоты по формуле ![]() , где (a,b) – координаты вектора перпендикулярного искомой прямой,
, где (a,b) – координаты вектора перпендикулярного искомой прямой, ![]() – координаты точки, принадлежащей этой прямой. Находим координаты вектора АС:
– координаты точки, принадлежащей этой прямой. Находим координаты вектора АС:
![]()
и подставляем в формулу, ![]() ,
,
![]()
6) Длину высоты ВН находим как расстояние от точки В до прямой АС:

7) Площадь треугольника АВС:

8) Находим угол ВАС треугольника:

9) Составляем уравнение прямой, проходящей через т.А параллельно ВС:

Ответ:

Пример 6:

Решение от преподавателя:
- Уравнение прямой
Прямая, проходящая через точки A1(x1; y1) и A2(x2; y2), представляется уравнениями:
Уравнение прямой AB
Каноническое уравнение прямой:
или
или
y = -3/7x + 16/7 или 7y + 3x – 16 = 0 - Обозначим середину стороны AB буквой М. Тогда координаты точки M найдем по формулам деления отрезка пополам.


M(3;1)
Уравнение медианы CM найдем, используя формулу для уравнения прямой, проходящей через две заданные точки. Медиана CМ проходит через точки C(-8;2) и М(3;1), поэтому:
Каноническое уравнение прямой:
или
или
y = -1/11x + 14/11 или 11y + x – 14 = 0 - Уравнение высоты через вершину C
Прямая, проходящая через точку N0(x0;y0) и перпендикулярная прямой Ax + By + C = 0 имеет направляющий вектор (A;B) и, значит, представляется уравнениями:
Найдем уравнение высоты через вершину C
y = 7/3x + 62/3 или 3y -7x – 62 = 0 - уравнение параллельной прямой AB, проходящей через точку (-8,2)
Уравнение прямой AB: y = -3/7x + 16/7
Уравнение KN параллельно AB находится по формуле:
y – y0 = k(x – x0)
Подставляя x0 = -8, k = -3/7, y0 = 2 получим:
y-2 = -3/7(x-(-8))
или
y = -3/7x – 10/7 или 7y + 3x +10 = 0
Пример 7:

Даны координаты вершин треугольника: A(1,1), B(4,13), C(10,5).
Решение от преподавателя:
4) Уравнение высоты через вершину C
Прямая, проходящая через точку N0(x0;y0) и перпендикулярная прямой Ax + By + C = 0 имеет направляющий вектор (A;B) и, значит, представляется уравнениями: 
Найдем уравнение высоты через вершину C 
y = -1/4x + 15/2 или 4y +x -30 = 0
Данное уравнение можно найти и другим способом. Для этого найдем угловой коэффициент k1 прямой AB.
Уравнение AB: y = 4x -3, т.е. k1 = 4
Найдем угловой коэффициент k перпендикуляра из условия перпендикулярности двух прямых: k1*k = -1.
Подставляя вместо k1 угловой коэффициент данной прямой, получим:
4k = -1, откуда k = -1/4
Так как перпендикуляр проходит через точку C(10,5) и имеет k = -1/4,то будем искать его уравнение в виде: y-y0 = k(x-x0).
Подставляя x0 = 10, k = -1/4, y0 = 5 получим:
y-5 = -1/4(x-10)
или
y = -1/4x + 15/2 или 4y + x – 30 = 0
Найдем точку пересечения с прямой AB:
Имеем систему из двух уравнений:
y -4x +3 = 0
4y + x – 30 = 0
Из первого уравнения выражаем y и подставим во второе уравнение.
Получаем:
x = 42/17
y = 117/17
D(42/17;117/17)
Длина высоты треугольника, проведенной из вершины C
Расстояние d от точки M1(x1;y1) до прямой Ax + By + С = 0 равно абсолютному значению величины: 
Найдем расстояние между точкой C(10;5) и прямой AB (y -4x +3 = 0) 

5,7) Уравнение медианы треугольника
Обозначим середину стороны BC буквой Е. Тогда координаты точки Е найдем по формулам деления отрезка пополам. 

Е(7;9)
Уравнение медианы AЕ найдем, используя формулу для уравнения прямой, проходящей через две заданные точки A(1;1) иЕ(7;9), поэтому:
Каноническое уравнение прямой: 
или 
или
y = 4/3x -1/3 или 3y -4x +1 = 0
Найдем длину медианы.
Расстояние между двумя точками выражается через координаты формулой: 
6) CD–диаметр окружности. Центр окружности точка О лежит в середине отрезка CD


Уравнение окружности (x-x0)2+(y-y0)2=r2
(x-106/17)2+(y-101/17)2=256/17
8) Уравнение прямой, параллельной CD, проходящей через точку A
Так как прямая проходит через точку А(1,1) и имеет k = -1/4, ( так как уравнение CD:y = -1/4x + 15/2 или 4y + x – 30 = 0 ),
то будем искать уравнение в виде: y-y0 = k(x-x0).
Подставляя x0 = 1, k = -1/4, y0 = 1получим:
y-1 = -1/4(x-1)
или
y = -1/4x + ¼+1 или 4y + x – 5 = 0
Пример 8:

Решение от преподавателя:
Точка D – середина стороны АВ , ее координаты равны полусумме координат А и В. Получим D(1, -1)
Пример 9:
Даны координаты вершин треугольника АВС: А (3,-2), В (-5,-4), С (-1,6).
Найдите: 1) уравнения сторон треугольника АВ, ВС и АС;
2) периметр (сумму длин) треугольника;
3) уравнение высоты СН;
4) расстояние d от точки С до прямой АВ;
5) сделайте чертеж.
Решение от преподавателя:
Решение.

1) уравнения сторон треугольника АВ, ВС и АС
Уравнение, прямой проходящей через две точки

2) периметр (сумму длин) треугольника
Расстояние между двумя точками

3) уравнение высоты СН
Уравнение прямой, проходящей через точку перпендикулярно другой прямой

4) расстояние d от точки С до прямой АВ
Расстояние от точки до прямой

Пример 10:
Даны вершины A (x1; y1), B (x2; y2), C (x3; y3) треугольника.
Найти: 1) уравнение стороны AB;
2) уравнение медианы, проведенной из вершины C;
3) уравнение высоты, проведенной из вершины C ;
4) уравнение прямой, проходящей через вершину C параллельно стороне AB .
A (6; 0), B (2; − 6), C (−3; −9).
Решение от преподавателя:






Пример 11:

Решение от преподавателя:




Пример 12:
Дан треугольник с координатами вершин ![]() найти:
найти:
а) длину стороны AB;
б) косинус угла ABC;
в) площадь треугольника ABC (через векторное произведение);
Решение от преподавателя:

Пример 13:

Решение от преподавателя:
Даны координаты вершин треугольника: A(6,0), B(2,-6), C(-3,-9).
1) Уравнение прямой
Прямая, проходящая через точки A1(x1; y1) и A2(x2; y2), представляется уравнениями: 
Уравнение прямой AB
Каноническое уравнение прямой: 
или 
или
y = 3/2x -9 или 2y -3x +18 = 0
2) Уравнение медианы треугольника
Обозначим середину стороны AB буквой М. Тогда координаты точки M найдем по формулам деления отрезка пополам. 

M(4;-3)
Уравнение медианы CM найдем, используя формулу для уравнения прямой, проходящей через две заданные точки. Медиана CМ проходит через точки C(-3;-9) и М(4;-3), поэтому:
Каноническое уравнение прямой: 
или 
или
y = 6/7x -45/7 или 7y -6x +45 = 0
3) Уравнение высоты через вершину C
Прямая, проходящая через точку N0(x0;y0) и перпендикулярная прямой Ax + By + C = 0 имеет направляющий вектор (A;B) и, значит, представляется уравнениями: 
Найдем уравнение высоты через вершину C 
y = -2/3x -11 или 3y +2x + 33 = 0
4) Уравнение прямой, параллельной AB, проходящей через С(-3,-9)
Уравнение прямой AB: 2y -3x +18 = 0
Уравнение СN параллельно AB находится по формуле:

Или 2y -3x +9 = 0
Пример 14:
Даны вершины треугольника А(8,1), В(0,3), С(-2,-3). Напишите уравнения стороны AB, медианы AD, высоты BE.
Решение от преподавателя:
Даны координаты вершин треугольника: A(8,1), B(0,3), C(-2,-3).
1) Уравнение прямой (АВ)
Прямая, проходящая через точки A1(x1; y1) и A2(x2; y2), представляется уравнениями: 
Уравнение прямой AB

или 
или
4y + x – 12 = 0
2)Уравнение медианы (АD)
Обозначим середину стороны BC буквой М. Тогда координаты точки M найдем по формулам деления отрезка пополам. 

M(-1;0)
Уравнение медианы AM найдем, используя формулу для уравнения прямой, проходящей через две заданные точки. Медиана AМ проходит через точки A(8;1) и М(-1;0), поэтому: 
или 
или
y = 1/9x + 1/9 или 9y -x – 1 = 0
3) Уравнение высоты через вершину B
Найдем уравнение высоты через вершину B
Для этого найдем угловой коэффициент k1 прямой AC.
Уравнение прямой AC
уравнение прямой, проходящей через 2 точки: 
или 
или
y = 2/5x -11/5 т.е. k1 = 2/5
Найдем угловой коэффициент k перпендикуляра из условия перпендикулярности двух прямых: k1*k = -1.
Подставляя вместо k1 угловой коэффициент данной прямой, получим:
2/5k = -1, откуда k = -5/2
Так как перпендикуляр проходит через точку B(0,3) и имеет k = -5/2,то будем искать его уравнение в виде: y-y0 = k(x-x0).
Подставляя x0 = 0, k = -5/2, y0 = 3 получим:
y-3 = -5/2(x-0)
или
y = -5/2x + 3 или 2y + 5x – 6 = 0 – уравнение (ВЕ)
Пример 15:
Дан треугольник АВС. Найти:
а) величину угла А;
б) уравнение стороны АС;
в) уравнение высоты и медианы, опущенных из вершины В.
Сделать чертеж.
А(-1,2); В(1,3); С(3,-4).
Решение от преподавателя:



Пример 16:
Треугольник задан вершинами А(-6; -2); В(4; 8); С(2; -8). Найти:
а) уравнение прямой BN, параллельной стороне АС;
б) уравнение медианы CD;
в) уравнение высоты АЕ;
Решение от преподавателя:
а) уравнение прямой BN, параллельной стороне АС;
Уравнение прямой AC:
Каноническое уравнение прямой:![]()
или![]()
или
y = -3/4x -13/2 или 4y + 3x +26 = 0
Уравнение BN параллельно AC находится по формуле:
y – y0 = k(x – x0)
Подставляя x0 = 4, k = -3/4, y0 = 8 получим:
y-8 = -3/4(x-4)
или
y = -3/4x + 11 или 4y + 3x – 44 = 0
б) уравнение медианы CD;
Обозначим середину стороны AB буквой М. Тогда координаты точки M найдем по формулам деления отрезка пополам.![]()
![]()
M(-1;3)
Уравнение медианы CM найдем, используя формулу для уравнения прямой, проходящей через две заданные точки. Медиана CМ проходит через точки C(2;-8) и М(-1;3), поэтому:
Каноническое уравнение прямой:![]()
или![]()
или
y = -11/3x -2/3 или 3y + 11x +2 = 0
в) уравнение высоты АЕ;
Прямая, проходящая через точку Е0(x0;y0) и перпендикулярная прямой Ax + By + C = 0 имеет направляющий вектор (A;B) и, значит, представляется уравнениями:![]()
Найдем уравнение высоты через вершину A![]()
y = -1/8x – 11/4 или 8y +x + 22 = 0
Пример 17:
A(1, 2), В(5, 8), С(11, 3).

Решение от преподавателя:


Пример 18:
В ∆ABC вершины имеют координаты точки А (-3;4), точки В (-4;-3), точки С (8;1).
Составить уравнения стороны (AB), высоты (ВК) и медианы (CМ).
Решение от преподавателя:
Уравнение прямой AB
Каноническое уравнение прямой:![]()
или![]()
или
x +4 = 0 или x = -4
Уравнение прямой AC
Каноническое уравнение прямой:![]()
или![]()
или
y = -1/4x + 3 или 4y + x – 12 = 0
Найдем уравнение высоты через вершину B![]()
y = 4x + 13 или y -4x – 13 = 0
Уравнение медианы CM найдем, используя формулу для уравнения прямой, проходящей через две заданные точки. Медиана CМ проходит через точки C(8;1) и М(-4;1/2), поэтому:
Каноническое уравнение прямой:
или
или
y = 1/24x + 2/3 или 24y -x – 16 = 0
Пример 19:
Дан треугольник ABC с координатами вершин A(-5;-3; 2), B(-2;-6;-3) и C(-2; 2;-1).
Найти:
а) длину стороны АВ;
б) косинус угла ABC;
в) площадь треугольника АВС (через векторное произведение).
Решение от преподавателя:

