Координатный луч изображается по той же схеме, но существенно отличается. Мы ставим точку отсчета и отмеряем единичный отрезок.
Данная статья посвящена разбору таких понятий, как координатный луч и координатная прямая. Мы остановимся на каждом понятии и подробно рассмотрим примеры. Благодаря этой статье вы сможете освежить свои знания или ознакомиться с темой без помощи преподавателя.
Координатный луч
Для того, чтобы определить понятие координатного луча, следует иметь представление о том, что такое луч.
Луч – это геометрическая фигура, которая имеет начало отсчета координатного луча и направление движения. Прямую обычно изображают горизонтально, указывая направление направо.
На примере мы видим, что O является началом луча.

Координатный луч изображается по той же схеме, но существенно отличается. Мы ставим точку отсчета и отмеряем единичный отрезок.

Единичный отрезок – это расстояние от 0 до точки, выбранной для измерения.

От конца единичного отрезка нужно отложить несколько штрихов и сделать разметку.
Благодаря манипуляциям, которые мы проделали с лучом, он стал координатным. Подпишите штрихи натуральными числами в последовательности от 1 – например, 2, 3, 4, 5…
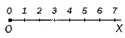
Координатный луч – это шкала, которая может длиться до бесконечности.
Зачастую его изображают лучом с началом в точке O, и откладывают единственный единичный отрезок. Пример указан на рисунке.

Мы в любом случае сможем продолжить шкалу до того числа, которое нам необходимо. Вы можете записывать числа как удобно – под лучом или над ним.
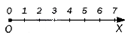
Для отображений координат луча могут использоваться как заглавные, как и строчные буквы.
Координатная прямая
Принцип изображения координатной прямой практически не отличается от изображения луча. Все просто – прочертите луч и дополните до прямой, придав положительное направление, которое указывается стрелочкой.

Проведите луч в противоположную сторону, дополнив его до прямой

Отложите единичные отрезки по примеру, указанному выше
С левой стороны запишите натуральные числа 1, 2, 3, 4, 5… с противоположным знаком. Обратите внимание на пример.

Вы можете отметить только начало отсчета и единичные отрезки. Смотрите на примере, как это будет выглядеть.

Координатная прямая – это прямая, которая изображается с определенной точкой отсчета, которая принимается за 0, единичным отрезком и заданным направлением движения.
Соответствие между точками координатной прямой и действительными числами
Координатная прямая может содержать множество точек. Они напрямую связаны с действительными числами. Это можно определить, как взаимно однозначное соответствие.
Каждой точке на координатной прямой соответствует единственное действительное число, а каждому действительному числу соответствует единственная точка на координатной прямой.
Для того, чтобы лучше понять правило, следует отметить точку на координатной прямой и посмотреть, какое натуральное число соответствует отметке. Если эта точка совпадает с началом отсчета, она будет отмечена нулем. Если точка не совпадает с началом отсчета, мы откладываем нужное количество единичных отрезков до тех пор, пока не достигнем указанной отметки. Число, записанное под ней, и будет соответствовать данной точке. На примере, указанном внизу, мы покажем вам это правило наглядно.

Если мы не можем найти точку, откладывая единичные отрезки, следует отмечать также точки, составляющие одну десятую, сотую или тысячную долю единичного отрезка. На примере можно подробно рассмотреть данное правило.
Отложив несколько подобных отрезков, мы сможем получить не только целое, но и дробное число – как положительное, так и отрицательное.
Отмеченные отрезки помогут нам отыскать на координатной прямой необходимую точку. Это могут быть как целые, так и дробные числа. Однако на прямой существуют точки, которые очень сложно найти с помощью единичных отрезков. Этим точкам соответствуют десятичные дроби. Для того, чтобы искать подобную точку, придётся откладывать единичный отрезок, десятую, сотую, тысячную, десятитысячную и другие его доли. Одной точке координатной прямой отвечает иррациональное число π (=3,141592…).
Множество действительных чисел включается в себя все числа, которые можно записать в виде дроби. Это позволяет выявить правило.
Каждой точке координатной прямой соответствует конкретное действительное число. Разные точки определяют разные действительные числа.
Это соответствие однозначно –каждой точке соответствует определенное действительное число. Но это работает также и в обратном направлении. Мы также можем указать определенную точку на координатной прямой, которая будет относиться конкретному действительному числу. Если число не является целым, то нам необходимо отметить несколько единичных отрезков, а также десятых, сотых долей в заданном направлении. Например, числу 400350 отвечает точка на координатной прямой, в которую из начала отсчета можно попасть, отложив в положительном направлении 400 единичных отрезков, 3 отрезка, составляющих десятую долю единичного, и 5 отрезков – тысячную долю.
Согласно правилу,
Каждой точке на координатной прямой отвечает действительное число, и каждое действительное число отмечается в виде точки на координатной прямой.
Благодаря этому утверждению координатную прямую зачастую определяют как числовую.
Следует отметить, что знак, стоящий перед числом, зависит от размещения точки на прямой. Точкам, лежащим правее начала отсчета, соответствуют положительные числа, а точкам, лежащим левее, – отрицательные.
Координаты точек на координатной прямой
Число, соответствующее точке на координатной прямой, называется координатой этой точки.
Ранее было отмечено, что к каждому числу относится единственная точка на прямой. Можно сказать, что координата точки определяет ее положение на прямой. Именно координата задает эту точку.
Перед тем, как завершить статью, следует упомянуть о принятых обозначениях координаты точки. Координату принято записывать в круглых скобках справа от буквы, которой обозначена точка. Например, если точка M имеет координату – 6, то можно записать как M(-6) , а запись вида M(53+7) значит, что координатой является 53+7
Введение
Вот такие отметки на дороге (рис. 1) выполняют сразу три функции.

Рис. 1. Отметки на дороге
- Измерение расстояний. Мы знаем, на сколько мы удалились от города. Или от другой подобной отметки.
- Адрес, имя. Мы знаем, где находимся. По телефону легко передать числовой адрес нашего места.
- Направление. Глядя на эти отметки, легко понять, в какой стороне находится город – начало отсчета.
Где ещё числа помогают нам ориентироваться? В кинотеатре. В зрительном зале все ряды и все кресла пронумерованы. И на нашем билете написаны номер ряда и номер места. С помощью двух этих чисел мы легко находим свое место (рис. 2).

Рис. 2. Место в кинотеатре
Раньше дома не имели номеров. Вы приезжаете в город и ищете дом купца Елисеева. Когда людей и домов не очень много, то это не очень трудно. Особенно, если вы ищете дом известного человека (рис. 3).

Рис. 3. Дом без номера
Но в современном городе с сотнями тысяч и миллионами жителей ориентироваться нам помогает нумерация домов (рис. 4).

Рис. 4. Нумерация домов
Но вернемся к дороге. Представьте, что вы вдруг оказались на дороге перед отметкой ![]() (рис. 5).
(рис. 5).

Рис. 5. Отметка ![]()
Понятно ли, где вы находитесь? Пока нет. Нужно знать еще вот что:
- В каких единицах это измерено: может, это километры, может, версты, а может, мы в Англии и это мили.
- Точка отсчета. А в какой стороне начало, город от которого отсчитывается? В какую сторону увеличиваются эти отметки?
Когда нам будут известны эти две вещи, то мы точно будем знать, где находимся.
Координатная (числовая) прямая
Моделью дороги в математике является прямая.
Две идеи (присвоить точкам имена и измерять расстояния) объединяются в одну – координатная (или числовая) прямая. Можно имена присваивать буквенные. Там даже функцию порядка можно сохранить – за ![]() идет
идет ![]() , за
, за ![]() идет
идет ![]() и т.д. Но с измерением расстояний тут не понятно, как поступить. Поэтому удобнее присвоить точкам на прямой числовые имена.
и т.д. Но с измерением расстояний тут не понятно, как поступить. Поэтому удобнее присвоить точкам на прямой числовые имена.
Для этого требуется три действия.
- Отмечаем точку, относительно которой все будет считаться, начало отсчета. Самое разумное – поставить там отметку ноль, ведь если мы находимся в этой точке, то расстояние до начала отсчета равно нулю (рис. 6).

Рис. 6. Начало отсчета
- Выбираем единицы, в которых будем измерять. Для этого нужно указать длину отрезка, которую мы будем считать единичной (рис. 7).

Рис. 7. Единичный отрезок
- Выбираем направления, куда будут увеличиваться отметки. Отметим его стрелкой. Координатная прямая готова (рис. 8).

Рис. 8. Координатная прямая
Теперь каждой точке соответствует число, адрес этой точки. Это число называют координатой.
Модель дороги
Когда мы говорим «модель дороги в математике – прямая», может возникнуть резонный вопрос: но дорога далеко не всегда бывает прямой, она может быть какой угодно формы (рис. 9).

Рис. 9. Извилистая дорога
Уточним: мы говорим о модели дороги в том случае, если речь идёт не об удобстве, а только о расстоянии и порядке.
Если мы можем двигаться исключительно по дороге (не можем срезать и т.п.), то нам неважно, какой формы дорога: за столбом с номером ![]() будет идти столб с номером
будет идти столб с номером ![]() и т.д. Таким образом, для описания движения автомобиля, например, дорогу можно «выпрямить» и рассматривать модель – прямую
и т.д. Таким образом, для описания движения автомобиля, например, дорогу можно «выпрямить» и рассматривать модель – прямую
Координатная плоскость
В жизни мы часто сталкиваемся с ситуациями, когда упорядочивания по одному параметру недостаточно.
Например, в кинотеатре места занумерованы не от ![]() до нескольких тысяч (что значительно усложнило бы поиск места зрителем), а обозначены номером ряда и номером места в этом ряду. Таким образом, каждому месту мы ставим в соответствие две координаты (а не одну) – ряд и место (рис. 10).
до нескольких тысяч (что значительно усложнило бы поиск места зрителем), а обозначены номером ряда и номером места в этом ряду. Таким образом, каждому месту мы ставим в соответствие две координаты (а не одну) – ряд и место (рис. 10).

Рис. 10. Ряд и место
В этом случае нам уже не будет хватать координатной прямой, понадобится координатная плоскость.
Посмотреть урок про координатную плоскость можно по ссылке: Координатная плоскость.
Определение координат точки
Давайте потренируемся определять эти координаты для разных точек.
Определим координату точки ![]() (рис. 11).
(рис. 11).

Рис. 11. Точка ![]()
Для этого измерим, сколько раз единичный отрезок уложится от начала отсчета ![]() до точки
до точки ![]() .
. ![]() раза. Точке
раза. Точке ![]() соответствует число
соответствует число ![]() . Или точка
. Или точка ![]() имеет координату
имеет координату ![]() (рис. 12).
(рис. 12).

Рис. 12. Координата точки ![]()
Иногда координату записывают в скобках после названия точки (рис. 13).

Рис. 13. Запись координаты
Определим координату точки ![]() (рис. 14).
(рис. 14).

Рис. 14. Точка ![]()
Единичный отрезок поместился ![]() раз. Координата
раз. Координата ![]() (рис. 15).
(рис. 15).

Рис. 15. Координата точки ![]()
Можно поступить наоборот: найти точку по ее координате. Точка ![]() имеет координату
имеет координату ![]() . Тогда от нуля нужно отложить
. Тогда от нуля нужно отложить ![]() целых единичных отрезков и
целых единичных отрезков и ![]() (рис. 16).
(рис. 16).

Рис. 16. Расположение точки ![]()
Пусть теперь точка левее начала отсчета. Точка ![]() . Отрезок укладывается
. Отрезок укладывается ![]() раза. Но координата
раза. Но координата ![]() уже занята для точки
уже занята для точки ![]() справа (рис. 17).
справа (рис. 17).

Рис. 17. Расположение точки ![]()
Да и все остальные положительные числа уже использованы для координат тех точек, что находятся справа от нуля.
Но у нас остались еще отрицательные числа. Их и будем использовать для таких точек. То есть точка ![]() имеет координату
имеет координату ![]() .
.
Две координаты, отличающиеся только знаками (то есть противоположные числа), соответствуют точкам, симметричным относительно начала координат. Например, ![]() и
и ![]() соответствуют двум симметричным точкам
соответствуют двум симметричным точкам ![]() и
и ![]() (рис. 18).
(рис. 18).

Рис. 18. Симметричные точки
Названия числовых прямых
Если числовых прямых две или больше, то, чтобы отличать одну от другой, их обозначают буквами, ![]() ,
, ![]() ,
, ![]() и т.д. Например, в прямоугольной системе координат на плоскости две оси. Их обозначают обычно
и т.д. Например, в прямоугольной системе координат на плоскости две оси. Их обозначают обычно ![]() и
и ![]() . В нашем случае, хоть прямая и одна, ее все равно обычно обозначают буквой
. В нашем случае, хоть прямая и одна, ее все равно обычно обозначают буквой ![]() . Кроме того, чтобы не откладывать каждый раз единичные отрезки до нужной точки, на прямой часто сразу ставят несколько отметок, соответствующих целым числам.
. Кроме того, чтобы не откладывать каждый раз единичные отрезки до нужной точки, на прямой часто сразу ставят несколько отметок, соответствующих целым числам.
Определение
Итак, координатная прямая (числовая прямая) – это прямая, на которой выбраны начало отсчета, направление, масштаб (единичный отрезок).
Каждой точке соответствует число, которое называют координатой. Координата является адресом точки. По этой координате можно точно найти, где находится точка, как дом по адресу. И, наоборот, по точке можно однозначно сказать, какая у нее координата (рис. 19).

Рис. 19. Координатная прямая
Использование координатной прямой
Итак, когда же мы используем координатную прямую? Представьте, что вам по телефону нужно объяснить, где находятся эти точки на прямой (рис. 20).

Рис. 20. Точки на прямой
Мы можем взять линейку, измерить все расстояния между точками и передать по телефону.
А теперь, пусть это числовая прямая. Теперь у каждой точки есть координата, ее можно продиктовать по телефону, а на том конце ваш собеседник по этим координатам может точно так же расставить точки (рис. 21).

Рис. 21. Точки на координатной прямой
Сравнение чисел и арифметические операции с помощью числовой прямой
Итак, у нас каждой точке соответствует число и наоборот. Но соответствие распространяется и дальше – на сравнение чисел и на арифметические операции.
То, что ![]() , означает, что точка с большой координатой находится правее (рис. 22).
, означает, что точка с большой координатой находится правее (рис. 22).

Рис. 22. Сравнение координат
Прибавить к числу ![]() положительное число
положительное число ![]() на прямой будет означать, что от исходной точки с координатой
на прямой будет означать, что от исходной точки с координатой ![]() отступить вправо на
отступить вправо на ![]() единичных отрезка. Придем в точку
единичных отрезка. Придем в точку ![]() (рис. 23).
(рис. 23).

Рис. 23. Сложение положительных чисел
Прибавить отрицательное число (вычесть положительное) означает сдвиг влево (рис. 24).

Рис. 24. Вычитание
Свойство противоположных чисел: их сумма равна нулю. Двум противоположным числам соответствуют симметричные относительно нуля точки. Например, ![]() и
и ![]() . Можно к
. Можно к ![]() прибавить
прибавить ![]() , то есть сдвинуться на
, то есть сдвинуться на ![]() единиц вправо, придем в точку ноль. Или, наоборот, от точки
единиц вправо, придем в точку ноль. Или, наоборот, от точки ![]() можно сдвинуться на
можно сдвинуться на ![]() единиц влево (прибавить отрицательное число
единиц влево (прибавить отрицательное число ![]() или вычесть
или вычесть ![]() ) (рис. 25).
) (рис. 25).

Рис. 25. Свойство противоположных чисел
Задача
Замена в задаче чисел точками, а сложения – сдвигом может облегчить решение. Чему равна сумма бесконечного числа слагаемых: ![]() ?
?
Решение
Изобразим точку ![]() на прямой. Она находится посредине между
на прямой. Она находится посредине между ![]() и
и ![]() (рис. 26).
(рис. 26).

Рис. 26. Расположение точки ![]()
Добавить одну четвертую – значит найти точку, сдвинутую на ![]() единичного отрезка вправо, то есть на половину оставшегося до единицы (рис. 27).
единичного отрезка вправо, то есть на половину оставшегося до единицы (рис. 27).

Рис. 27. Добавили ![]()
Добавим к нему ![]() , то есть еще движемся вправо на
, то есть еще движемся вправо на ![]() , половину оставшегося отрезка (рис. 28).
, половину оставшегося отрезка (рис. 28).

Рис. 28. Добавили ![]()
Этот процесс будет продолжаться до бесконечности, но новая точка всегда будет левее единицы, но все ближе и ближе к ней.
То есть сумма становится всё ближе к единице, но не превосходит ее. Поэтому такую бесконечную сумму считают равной единице: ![]() .
.
Заключение
Мы выяснили, что числовая прямая устанавливает соответствие между точками и числами. Такое взаимно-однозначное соответствие позволяет заменить работу с точками на работу с числами или наоборот. Переход от одних объектов к другим часто позволяет упростить задачу, облегчить понимание.
- Зубарева И.И., Мордкович А.Г. Математика. 6 класс. М.: ИОЦ «Мнемозина», 2014.
- Дорофеев Г.В., Петерсон Л.Г. Математика. 6 класс. Учебник в 3 частях. Ч. 2. М. «Просвещение», 2010.
- Виленкин Н.Я. и др. Математика. Учебник для 6 класса. М.: ИОЦ «Мнемозина», 2013.
Рекомендованные ссылки на ресурсы сети Интернет
- Yaklass.ru (Источник).
- Math-prosto.ru (Источник).
- School-assistant.ru (Источник).
Домашнее задание
- Укажите координату точки
 (рис. 1).
(рис. 1).

Рис. 1. Иллюстрация к заданию
Координатный луч с положительными числами дополним противоположным ему лучом и нанесём на него такие же деления. Получим координатную прямую.

Координатная прямая — это прямая с указанными на ней началом отсчёта (O )((0)), направлением и единичным отрезком.
Точка (O)( (0)) — начало отсчёта. Справа от неё отмечают положительные числа, а слева — отрицательные числа. Стрелочка указывает положительное направление отсчёта на координатной прямой.
Около стрелочки часто ставят букву (x), (y), (z) или другую букву латинского алфавита. В таких случаях говорят: ось (x), ось (y), ось (z) соответственно.

На координатной прямой важно расположение точек.
Говорят: «Точка (P) расположена слева от точки (O)». «Точка (P) расположена справа от точки (K)».
Число, показывающее положение точки на прямой, называют координатой точки.

Обрати внимание!
Единичный отрезок может быть разным на двух координатных прямых.
В данном случае единичный отрезок равен (4) клеточкам, и одной клеточке соответствует (0,25) единичного отрезка.
Запишем координаты точек (M), (K), (P), (T), (F).
M−1,5;K−1;P12;T2;F2,25.
Похоже, вы используете блокировщик рекламы. Наш сайт существует и развивается
только за счет дохода от рекламы.
Пожалуйста, добавьте нас в исключения блокировщика.


на главную
Как найти координаты точки
Поддержать сайт![]()
Каждой точке координатной плоскости соответствуют две координаты.
Координаты точки на плоскости — это пара чисел, в которой на
первом месте стоит
абсцисса, а на
втором —
ордината точки.

Рассмотрим как в системе координат (на координатной плоскости):
- находить координаты точки;
- найти положение точки.
Чтобы найти координаты точки на плоскости, нужно опустить из этой точки
перпендикуляры на оси координат.
Точка пересечения с осью «x» называется абсциссой точки «А»,
а с осью y называется ординатой точки «А».

Обозначают координаты точки, как указано выше (·) A (2; 3).
Пример (·) A (2; 3) и (·) B (3; 2).

Запомните!
![]()
На первом месте записывают абсциссу (координату по оси «x»), а на втором —
ординату (координату по оси «y») точки.
Особые случаи расположения точек
- Если точка лежит на оси «Oy»,
то её абсцисса равна 0. Например,
точка С (0, 2). - Если точка лежит на оси «Ox», то её ордината равна 0.
Например,
точка F (3, 0). - Начало координат — точка O имеет координаты, равные нулю O (0,0).

- Точки любой прямой перпендикулярной оси абсцисс, имеют одинаковые абсциссы.

- Точки любой прямой перпендикулярной оси ординат, имеют одинаковые ординаты.

- Координаты любой точки, лежащей на оси абсцисс имеют вид (x, 0).

- Координаты любой точки, лежащей на оси ординат имеют вид (0, y).

Как найти положение точки по её координатам
Найти точку в системе координат можно двумя способами.
Первый способ
Чтобы определить положение точки по её координатам,
например, точки D (−4 , 2), надо:
- Отметить на оси «Ox», точку с координатой
«−4», и провести через неё прямую перпендикулярную оси «Ox». - Отметить на оси «Oy»,
точку с координатой 2, и провести через неё прямую перпендикулярную
оси «Oy». - Точка пересечения перпендикуляров (·) D — искомая точка.
У неё абсцисса равна «−4», а ордината равна 2.
Второй способ
Чтобы найти точку D (−4 , 2) надо:
- Сместиться по оси «x» влево на
4 единицы, так как у нас
перед 4
стоит «−». - Подняться из этой точки параллельно оси y вверх на 2 единицы, так
как у нас перед 2 стоит «+».

Чтобы быстрее и удобнее было находить координаты точек или строить точки по координатам на
листе формата A4 в клеточку, можно скачать и использовать
готовую систему координат на нашем сайте.
Ваши комментарии
Важно!

Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
Координаты на прямой:
Если на прямой задано направление, то такую прямую называют направленной, а выбранное направление—положительным. Например, на горизонтальной прямой можно отметить направление вправо, тогда будем говорить, что направленная прямая имеет положительное направление вправо. Можно с таким же правом считать положительным и направление влево. Направление прямой будем указывать стрелкой (рис. 1).
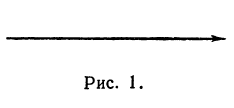
Выберем на направленной прямой точку, которую назовем началом отсчета или началом координат, и будем обозначать ее буквой О. Кроме того, выберем отрезок, длину которого будем считать единицей длины. Этот отрезок назовем единицей масштаба.
Определение: Прямая линия, на которой указаны: начало отсчета, единица масштаба и направление отсчета, называется осью координат.
Рассмотрим отрезок, расположенный на оси координат. Если одну из точек, ограничивающих отрезок, назовем началом отрезка, а другую—его концом, то отрезок будем называть направленным отрезком. Направленный отрезок обозначают двумя буквами, например: АВ, СМ, КР, причем на первом месте ставят букву, обозначающую начало, на втором— букву, обозначающую конец. Таким образом, запись АВ показывает, что начало отрезка есть точка А, а конец — точка В. Направление отрезка считается от начала к концу.
Если направление отрезка совпадает с направлением оси, то отрезок называют положительно направленным: если же его направление противоположно направлению оси, то—отрицательно направленным. Таким образом, отрезки АВ и ВА имеют противоположные направления. Это записывают так:

Отметим, что положительный отрезок может находиться в любом месте координатной оси, только его направление должно совпадать с направлением оси.
Сложение направленных отрезков производится по следующему правилу: Для того чтобы сложить два направленных отрезка, нужно к концу первого приложить начало второго; тогда отрезок, имеющий началом начало первого отрезка и концом конец второго, называют суммой двух направленных отрезков.
Из этого определения вытекает, что сумма отрезков АВ и ВС равна отрезку АС при любом расположении точек А, В, С, т. е. всегда:

(рис. 2 и 3).
Координатным отрезком точки А называется направленный отрезок, имеющий начало в точке О (т. е. в начале координат), а концом — рассматриваемую точку А.

Всякий направленный отрезок, лежащий на оси, можно выразить через координатные отрезки его начала и конца. В самом деле, рассмотрим направленный отрезок АВ. На основании равенства (2) можно написать
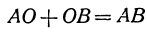
(здесь вместо точки В поставлена точка О, а вместо точки С точка В) или
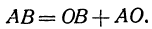
Отрезок ОВ есть координатный отрезок (его начало есть точка О), но отрезок АО не является координатным, посколькуего начало не является началом координат. Но в силу равенства (1)

поэтому можно написать

Получен следующий результат:
Направленный отрезок равен разности координатного отрезка его конца и координатного отрезка его начала.
Это верно для любого отрезка, лежащего на координатной оси. Теперь дадим одно из самых важных определений:
Координатой точки на координатной оси называется число, равное по абсолютной величине длине координатного отрезка этой точки и по знаку совпадающее со знаком координатного отрезка.
Точку А, имеющую координатной число 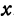 , будем обозначать
, будем обозначать 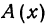 .
.

Указанные на рис. 4 точки имеют следующие координаты: 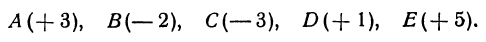 Будем также писать
Будем также писать

Если даны точки 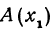 и
и 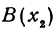 , то на основании формул (3) и (4) получим
, то на основании формул (3) и (4) получим

т. е. направленный отрезок равен разности координат его конца и начала. Отсюда сразу получаем, что длина отрезка равна абсолютной величине разности координат его конца и начала.
Длину отрезка будем обозначать, пользуясь знаком | |, т. е. знаком абсолютной величины. Таким образом, длина отрезка АВ будет записываться так:
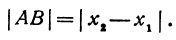
- Заказать решение задач по высшей математике
Пример:
Если даны точки 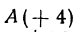 ,
,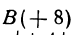 , то отрезок
, то отрезок 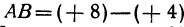 , а его длина
, а его длина 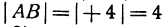 . Если даны точки
. Если даны точки 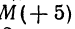 и
и 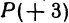 , то отрезок
, то отрезок 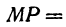
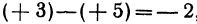 , а его длина
, а его длина 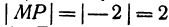 . Даны две точки:
. Даны две точки: 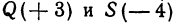 . Длина отрезка
. Длина отрезка 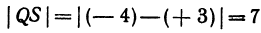 . Даны две точки
. Даны две точки 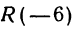 и
и 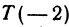 ; отрезок
; отрезок 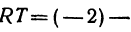
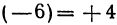 , а его длина |
, а его длина | 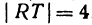 .
.
Пример:
Начало отрезка АВ находится в точке 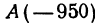 , а конец—в точке
, а конец—в точке 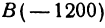 ; найти его направление и длину. Отрезок
; найти его направление и длину. Отрезок 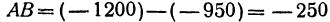 . Так как он получился отрицательным, то его направление противоположно направлению оси. Его длина равна
. Так как он получился отрицательным, то его направление противоположно направлению оси. Его длина равна 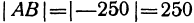 .
.
Пример:
На координатной оси даны две точки: 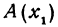 и
и 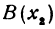 . Найти точку С, лежащую между ними и делящую отрезок АВ в отношении
. Найти точку С, лежащую между ними и делящую отрезок АВ в отношении 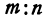 . Чтобы найти точку, надо найти ее координату. По условию задачи должно быть
. Чтобы найти точку, надо найти ее координату. По условию задачи должно быть

Обозначая координату искомой точки С через 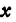 и выражая отрезки через координаты, т. е. применяя формулу (5), получим, что
и выражая отрезки через координаты, т. е. применяя формулу (5), получим, что 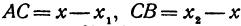 . Подставляя эти выражения в равенство (6), будем иметь
. Подставляя эти выражения в равенство (6), будем иметь
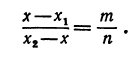
Решая последнее уравнение относительно 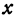 , найдем:
, найдем:
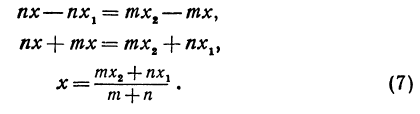
Это и есть координата искомой точки.
Пример:
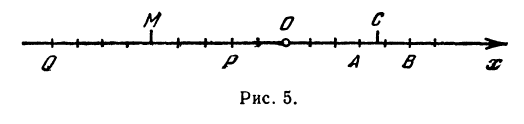
Найти точку С, делящую отрезок АВ в отношении 1:2, если даны начало отрезка  и конец
и конец 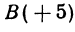 (рис. 5).
(рис. 5).
Решение:
Здесь 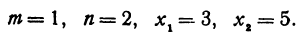 Применяя формулу (7), получим
Применяя формулу (7), получим
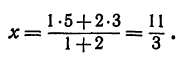
Пример:
Найти точку 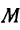 , делящую расстояние между точками
, делящую расстояние между точками 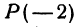 и
и 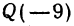 в отношении 3:4 (рис. 5). Здесь
в отношении 3:4 (рис. 5). Здесь 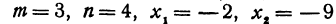 . По формуле (7) находим
. По формуле (7) находим
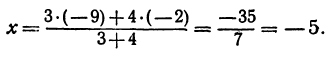
Решение:
Если 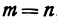 , т. е. точка
, т. е. точка  делит отрезок
делит отрезок 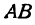 пополам, тогда формула (7) перепишется так:
пополам, тогда формула (7) перепишется так:

Таким образом, координата точки, делящей отрезок пополам, равна средней арифметической координат его начала и конца.
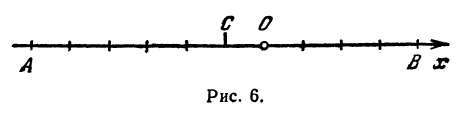
Пример:
Найдем середину отрезка, заключенного между точками 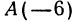 и
и 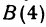 (рис.6).
(рис.6).
Решение:
Применяя формулу (8), получим, 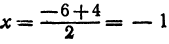
- Координаты на плоскости
- Линейная функция
- Квадратичная функция
- Тригонометрические функции
- Элементы матричного анализа
- Уравнение линии
- Функции нескольких переменных
- Комплексные числ
