Как найти координаты точки на дуге - Сайт, где вы сможете решить свои вопросы

Как найти координаты точек на дуге зная координаты точек хорды?

Добрый день друзья!
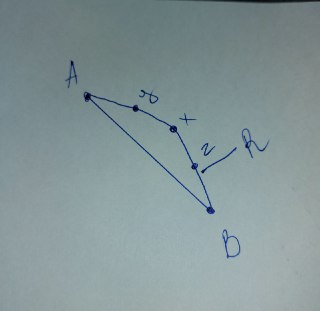
Помогите решить такую задачу. Есть координаты точек отрезка АВ, через который проходит окружность, то есть по сути это координаты хорды. Знаем также радиус окружности R. Как найти координаты промежуточных точек на дуге, которые делят дугу на 1/4, 1/2 и 3/4?
Заранее спасибо!

Вопрос задан

более двух лет назад
2022 просмотра

По теореме Пифагора находим расстояние от центра до хорды: d = sqrt(R² − [(x2−x1)² + (y2−y1)²]/4).
Находим середину отрезка AB (назовём её (x3, y3)). Находим направляющий вектор отрезка AB (x4,y4) = ((x2−x1)/|AB|, (y2−y1)/|AB|), и есть два варианта центра — (x0,y0) = (x3±d·y4, y3∓d·x4).
А дальше через atan2 получаем углы, упорядочиваем их и через углы получаем сколько угодно точек.

Пригласить эксперта

Надо найти угол сектора для этих точек(начальный-конечный):
x = r*cos(fi)
y = r*sin(fi)
поделить его как надо и найти координаты точек
подразумевается что центр окружности в нулевых координатах.

найти координаты центра (центр может быть как по одну, так и по другую сторону отрезка)
найти угол от оси X к точке А
найти угол от оси X к точке B
найти угол от оси X к искомой точке на дуге.
Длина дуги пропорциональна углу. Поэтому 1/2 длины находится на 1/2 угла: угол_к_В + (угол_к_А - угол_к_В) / 2
найти координаты точки, исходя из центра, угла и радиуса

картинка

Показать ещё
Загружается…

16 мая 2023, в 01:43

2000 руб./за проект

16 мая 2023, в 00:11

300 руб./за проект

16 мая 2023, в 00:11

20000 руб./за проект

Минуточку внимания

Источник

$begingroup$

i have arc A ,i know startangle,endangle,startPoint,Endpoint,centre,radius of arc and i have point B, i like to find point B lies or not in arc A , i need formula or algorithum for this

asked Oct 6, 2010 at 10:33

$endgroup$

$begingroup$

Assuming you’re talking about an arc of a circle, the first question to ask is whether the point lies on the circle. This just means that the distance from the center of the circle to your point is equal to the radius. Then find out the angle between the radius to your point and, say, a horizontal line, and figure out whether the point is within the bounds of the arc.

answered Oct 6, 2010 at 11:59

$endgroup$

$begingroup$

There is a simple test in cases where the arc does not sweep 180 degrees…

After determining if the point lies on the arc, the next step is to calculate the distance between the two arc endpoints. On a short arc, the point in question will be within this distance of both endpoints. On a long arc, the point will not be within this distance of both points (none, one, or the other, but not both).

answered Oct 11, 2018 at 13:10

$endgroup$

Not the answer you’re looking for? Browse other questions tagged

.

Источник

1 / 1 / 0

Регистрация: 28.12.2013

Сообщений: 86

Получить точку на окружности, зная исходную точку и длину дуги

04.07.2018, 15:29. Показов 3316. Ответов 6

Есть окружность с известными координатами центра и радиусом. Известна точка на этой окружности и длина дуги, которую нужно отложить от этой точки, чтобы получить искомую. Каким образом это сделать? Подскажите формулу пожалста

Programming

Эксперт

94731 / 64177 / 26122

Регистрация: 12.04.2006

Сообщений: 116,782

04.07.2018, 15:29

Ответы с готовыми решениями:

Найти точку координат на окружности имея начальную точку и расстояние
Здравствуйте.

Есть точка с известными координатами A(a, b, c) и есть точка с неизвестными…

Нарисовать часть окружности зная диаметр, стартовую точку, стартовый и конечный углы
Необходимо нарисовать часть окружности.
Известен радиус, Начальный угол, Конечный угол и Стартовая…

Получить точку на окружности (на хорде) между заданными точками и координаты пересечения окружности с прямой
Дано:
Координаты двух точек на плоскости (в них требуется вписать окружность) (t1, t2)
Радиус…

Найти длину окружности, которая проходит через точку A и центр которой находится в точке B
Помогите, пожалуйста, с заданием:( 3. Составьте программу для решения задачи: найдите длину…

Диссидент

27462 / 17151 / 3780

Регистрация: 24.12.2010

Сообщений: 38,627

04.07.2018, 15:51

Сообщение было отмечено stokkato как решение

Решение

Если центр окружности находится в точке (x0, y0)
x = x0 + Rcos(2*pi*d/R)
y = y0 + Rsin(2*pi*d/R)
Дуга откладывается против часовой стрелки

Почетный модератор

64285 / 47584 / 32739

Регистрация: 18.05.2008

Сообщений: 115,182

04.07.2018, 16:54

Сообщение от Байт

Дуга откладывается против часовой стрелки

От чего?

Добавлено через 4 минуты
По моему нужно определить угол между положительным направлением оси ОХ(u1), угол, стягиваемый дугой(u2), потом считать
x=x0+R*cos(u1+u2);
y=y0+R*sin(u1+u2);
Или нет?

Диссидент

27462 / 17151 / 3780

Регистрация: 24.12.2010

Сообщений: 38,627

04.07.2018, 17:06

Сообщение от Puporev

Или нет?

Да, вы правы. У вас получается более общий подход.
Можно зафиксировать систему координат, а можно подобрать ее под окружность и начальную точку. То, что предложил я, является как бы смесью этих подходов.
Надеюсь, ТС с этим разберется. Если же нет, придется нам ему помочь

1 / 1 / 0

Регистрация: 28.12.2013

Сообщений: 86

05.07.2018, 10:45

[ТС]

Это все хорошо, но мне нужно откладывать дугу не от начала координат, а от конкретной точки. И в каком положении относительно начала координат она находится я получается сначала должен определить?

Почетный модератор

64285 / 47584 / 32739

Регистрация: 18.05.2008

Сообщений: 115,182

05.07.2018, 11:17

Я немного не точно написал.
1.Нужно определить угол между положительным направлением оси ОХ и направлением от центра окружности на первую точку(u1).
2.Определить угол, стягиваемый дугой(u2).
3.Потом считать
x=x0+R*cos(u1+u2);
y=y0+R*sin(u1+u2);

1 / 1 / 0

Регистрация: 28.12.2013

Сообщений: 86

05.07.2018, 11:42

[ТС]

Понятно, спасибо!

Источник

Для нахождения координат точки эллипса по углу существует простое и элегантное решение. Понимаю, что для маститого математика это решение является очевидным. Однако, для меня в то далекое время, когда инет был диким, связь модемной, а я сильно молодым, это таковым не являлось.

ВНИМАНИЕ! Если Вы искали как найти координаты точки по углу от произвольной прямой и совсем не подразумевали эллипс, то Вам сюда.

Калькулятор точки на эллипсе

Давайте посмотрим, как это выглядит на практике. Потом теория. Оранжевый маркер отвечает за угол, на основании которого считаем координаты. Красный — параметрический угол, о котором ниже.

Маркеры кликабельны и таскабельны.

Если есть вопросы, предложения по калькулятору или заметили ошибку, буду очень рад обратной связиx

Эллипс:

a:
b:

Углы (град.):

Get a better browser, bro…

Параметрическое уравнение эллипса

Обратимся, как обычно, к Википедии. Находим там следующее:

Каноническое уравнение эллипса может быть параметризовано:

(1) Параметрическое уравнение эллипса

Очевидно, что t — это угол, и это не «наш» угол. Это какой-то другой угол, который функционально связан с «нашим». «Нашим» называю угол, от которого требуется посчитать координаты.

Таким образом, задача нахождения координат точки эллипса по углу сводится к задаче нахождения угла t, зависящим от требуемого. Нахождением этой зависимости и займемся.

Подготовка

Рис.1. Построение эллипса

У нас есть эллипс, описанный двумя полуосями a и b. Представим две окружности, имеющих общий центр. Меньшая окружность (зеленая) имеет радиус b. Большая окружность (синяя) имеет радиус a.

Проведем прямую из общего центра [X₀;Y₀] в произвольную точку плоскости [X;Y]. В результате пересечения с этими окружностями получаются две точки [X₁;Y₁] и [X₂;Y₂].

α – угол между прямой и осью X.

Малая окружность	X₁ = b × cos α	Y₁ = b × sin α
Большая окружность	X₂ = a × cos α	Y₂ = a × sin α

Таблица 1. Координаты точек пересечения прямой с окружностями

Нахождение зависимости

Рис.2. Угол β для точки эллипса [X’;Y’]

Используя уравнение (1) посчитаем координаты точки на эллипсе [X’;Y’] для угла α. Проведем прямую из центра [X₀;Y₀] в точку [X’;Y’]. Угол β – угол между этой прямой и осью X.

Задача сводится к тому, чтобы найти такой α, при котором β был бы равен интересующему нас углу. Таким образом, угол α будет являться параметром в уравнении (1) для требуемого угла β.

Найдем зависимость между получившимся углом β и углом α. На рисунке видно, что прилегающий к углу катет (синий) равен ранее рассчитанному X2, а противолежащий (зеленый) равен Y1:

X’ = X₂ = a × cos α

Y’ = Y₁ = b × sin α

Опыт показывает, что тут зачастую возникает легкий ступор. Возможно, рисунок вводит в некое заблуждение. Видим треугольник, и если с синим катетом вопросов нет, то с зеленым — масса. Почему синус от α? Угол «вона где», тут синус вообще не от того угла и т.д.

Смотрим на пересечение прямой и малой (зеленой) окружности. Зеленый катет прилетает именно оттуда. Именно так координату Y’ и рассчитывали, согласно уравнению(1). Рисунок — это иллюстрация, не метод решения.

Тангенс угла β в этом случае равен:

(3) Тангенс угла β

Используя формулу тангенса произведем дальнейшие преобразования:

(4) Зависимость тангенса α от тангенса β

Таким образом, видим прямую зависимость угла α, который нужен нам в качестве параметра в уравнении(1), от угла β, координаты точки от которого хотим получить.

Нахождение координат

Угол α находим через арктангенс. В Delphi (и не только) для этих целей используется функция ArcTan2 из модуля math. Она корректно возвращает знак ± угла в зависимости от квадранта, а также предусмотрительно нечувствительна к возможным коллизиям, типа деления на 0.

Находим синус и косинус от требуемого угла β и подставляем в параметры функции ArcTan2, согласно последней формуле (4):

//– находим параметр (некий угол) для уравнения —

SinCos(Angle,sn,cs);

t := ArcTan2(a*sn, b*cs);

Получившийся в результате вызова ArcTan2 угол есть ничто иное, как параметр t в параметрическом уравнении (1). Подставив его в уравнение, находим координаты точки на эллипсе, отстоящей на заданный угол от оси X.

О параметре

Практический смысл параметра t состоит в том, что это угол окружности до «сплющивания». Этот тот угол окружности, который будет соответствовать точке эллипса при заданном угле. Попытаюсь на практике показать.

В JavaScript’е нет понятия эллипс. Тем более нет понятия дуги эллипса. Но можно нарисовать окружность (через дугу) и «сплющить». Может быть такой номер пройдет и с дугой?

// рисует дугу эллипса

function drawArcEllipse(ctx, center, a, b, start, finish,

colorLine=‘none’, widthLine=0.0, angle=0.0) {

if (a==0.0) return;

var t1 = start;

var t2 = finish;

ctx.beginPath();

// сохраняем контекст

ctx.save();

// перемещение координат в центр эллипса

ctx.translate(center.x, center.y);

// поворот плоскости на угол, если требуется

if (angle!=0.0) ctx.rotate(angle);

// сжимаем по вертикали

ctx.scale(1, b/a);

// рисуем дугу

ctx.arc(0, 0, a, t1, t2);

// восстанавливает контекст

ctx.restore();

if (colorLine!=‘none’)

ctx.strokeStyle = colorLine;

if (widthLine>0.0)

ctx.lineWidth = widthLine;

ctx.stroke();

ctx.closePath();

}

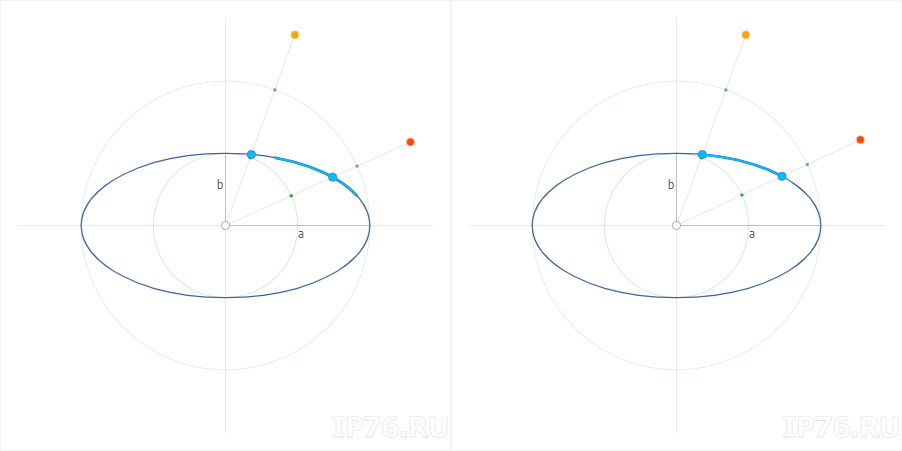
Рис.3. Использование параметра эллипса

На рисунке слева видим, что дуга расположена совершенно неправильно. Очевидно, что надо использовать какие-то другие углы. Вот тут на помощь приходит параметр эллипса. Это как раз тот самый угол, который обеспечивает «попадание» в нужный нам угол при «сплющивании» окружности.

Перепишем функцию с учетом нахождения параметра:

// рисует дугу эллипса

function drawArcEllipse(ctx, center, a, b, start, finish,

colorLine=‘none’, widthLine=0.0, angle=0.0) {

if (a==0.0) return;

var sn = Math.sin(start);

var cs = Math.cos(start);

var t1 = Math.atan2(a*sn, b*cs);

sn = Math.sin(finish);

cs = Math.cos(finish);

var t2 = Math.atan2(a*sn, b*cs);

ctx.beginPath();

// сохраняем контекст

ctx.save();

// перемещение координат в центр эллипса

ctx.translate(center.x, center.y);

// поворот плоскости на угол, если требуется

if (angle!=0.0) ctx.rotate(angle);

// сжимаем по вертикали

ctx.scale(1, b/a);

// рисуем дугу

ctx.arc(0, 0, a, t1, t2);

// восстанавливает контекст

ctx.restore();

if (colorLine!=‘none’)

ctx.strokeStyle = colorLine;

if (widthLine>0.0)

ctx.lineWidth = widthLine;

ctx.stroke();

ctx.closePath();

}

На рисунке справа видим, что все встало на свои места. Идеальная дуга )

Координаты точки наклонного эллипса

Перенесено в отдельную статью.

Практика

Две функции. Первая находит параметр t по углу. Вторая производит расчет координат. Из второй не вызываю первую, т.к. получится двойное вычисление полуосей. Код не настолько велик, чтобы его нельзя было продублировать.

//******************************************************************

// Найти угол, который будет использован в расчете точки на элипсе

// Т.е. тот самый параметр t в параметрическом уравнении эллипса:

// x = a * cos t

// y = b * sin t

//******************************************************************

function GetEllipseAngleParam(ARect : TRectF;

Angle : Extended) : Extended;

var sn,cs : Extended; // синус/косинус

a,b : Extended; // полуоси по X/Y

begin

a := ARect.Width/2;

b := ARect.Height/2;

SinCos(Angle,sn,cs);

result := ArcTan2(a * sn, b * cs);

end;

//********************************************************************

// Найти координату точки на эллипсе по углу отклонения

//********************************************************************

function CalcEllipsePointCoord(ARect : TRectF;

Angle : extended) : TPointF;

var sn,cs : Extended; // синус/косинус

a,b : Extended; // полуоси по X/Y

cnt : TPointF; // центр

t : Extended; // параметр для уравнения эллипса

begin

// инициализация полуосей

a := ARect.Width/2;

b := ARect.Height/2;

// центр эллипса

cnt := ARect.CenterPoint;

// находим параметр (некий угол) для уравнения

SinCos(Angle,sn,cs);

t := ArcTan2(a * sn, b * cs);

// считаем результат по параметрическому уравнению

SinCos (t, sn, cs);

result.X := cnt.x + a * cs;

result.Y := cnt.Y + b * sn;

end;

Скачать исходник + исполнямый файл

Друзья, спасибо за внимание!

Надеюсь, материал после правок стал понятней.

Подписывайтесь на телегу.

Если есть вопросы, с удовольствием отвечу )

Источник

Определить углы радиусов, угол радиуса к точке и убедиться, что этот угол там, где надо угол 🙂

Основной вопрос – любая точка на окружности в принципе на этой дуге… Только одна дуга (на рисунке) – сверху, вторая – снизу 🙂 Тут уж решайте сами, принадлежность какой дуге нужна…

Update

С учетом изменения условия в комментариях – находите угол между векторами (x-x0,y-y0) и (x1-x0,y1-y0) – из центра к вашей точке и к точке (x1,y1) – например, вычисляя скалярное произведение – и смотрите, меньше ли он указанного вами раствора (последнее ваше значение – 45 градусов).

Если меньше – попадает, если больше – нет…

Собственно, вот:

Или даже

Только тут неплохо бы убедиться, что расстояния от точек до центра и правда равны радиусу…

Источник

Как найти координаты точек на дуге зная координаты точек хорды?

Минуточку внимания

Not the answer you’re looking for? Browse other questions tagged .

Получить точку на окружности, зная исходную точку и длину дуги

Решение

Калькулятор точки на эллипсе

Параметрическое уравнение эллипса

Подготовка

Нахождение зависимости

Нахождение координат

О параметре

Координаты точки наклонного эллипса

Практика

Вам также может понравиться

Как найти ide controller драйвер

Как найти телефон который пропал

Как перепрошить телефон чтобы его не нашли

Добавить комментарий Отменить ответ

Not the answer you’re looking for? Browse other questions tagged

.