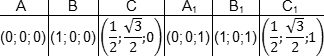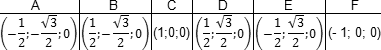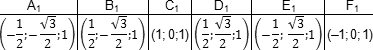Тема .
Стереометрия в координатах
Вспоминай формулы по каждой теме
Решай новые задачи каждый день
Вдумчиво разбирай решения
ШКОЛКОВО.
Готовиться с нами – ЛЕГКО!
Подтемы раздела
стереометрия в координатах
Решаем задачи
Показать ответ и решение
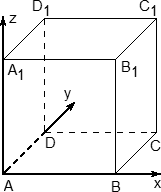
Пусть ребро тетраэдра равно .
В основании лежит равносторонний треугольник со стороной высота в этом треугольнике
Проекция точки на плоскость
это точка пересечения медиан(точка
), и она делит медиану
в
отношении от вершины. Найдём
по теореме Пифагора для
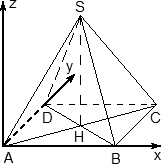
Введём прямоугольную систему координат(см. рисунок).
Точка – начало координат,
Ось направим вдоль вектора
,
Ось лежит в плоскости
и направлена в полуплоскость с точкой
перпендикулярно
,
Ось направим в полупространство, содержащее точку
, перпендикулярно векторам
и
.
Запишем координаты всех точек.
,
,
,
,
.
Так как
а) Найдем угол между прямыми и
, как угол между направляющими векторами
Найдём угол между векторами по следующей формуле
Замечание. При вычислении скалярного произведения мы воспользовались свойством ассоциативности
Отсюда следует ответ
б) Из условия, что ребро тетраэдра равно , получаем, что
.
Параметрически зададим уравнение прямой через начальную точку и направляющий вектор этой
прямой.
Параметрически зададим уравнение прямой через начальную точку и направляющий вектор этой
прямой.
Решим базовую задачу расстояния между прямыми(см. методичку задача №7), получим ответ.
Ответ:
а) б) 2
Показать ответ и решение
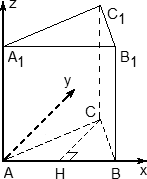
Пусть .
В основании лежит квадрат со стороной диагональ
Проекция точки на плоскость
это точка пересечения диагоналей(точка
). Найдём
по теореме
Пифагора для
Введём прямоугольную систему координат(см. рисунок).
Точка – начало координат,
Ось направим вдоль вектора
,
Ось направим вдоль вектора
,
Ось направим в полупространство, содержащее точку
, перпендикулярно векторам
и
.
Запишем координаты некоторых точек точек.
,
,
,
,
,
— середина стороны
.
Так как – точка пересечения медиан,
, тогда координаты точки
можно найти следующим
образом
а) Заметим, что
Получаем, что
б) По условию . Найдём координаты точки
.
Найдем длину вектора и получим ответ.
Ответ:
Показать ответ и решение
В основании лежит равносторонний треугольник со стороной высота в этом треугольнике
.
Проекция точки на плоскость
это точка пересечения медиан(точка
), и она делит медиану
в
отношении от вершины. Найдём
по теореме Пифагора для
Введём прямоугольную систему координат(см. рисунок).
Точка – начало координат,
Ось направим вдоль вектора
,
Ось лежит в плоскости
и направлена в полуплоскость с точкой
перпендикулярно
,
Ось направим в полупространство, содержащее точку
, перпендикулярно векторам
и
.
Запишем координаты некоторых точек точек.
,
,
,
,
Так как
а) Докажем перпендикулярность прямых через перпендикулярность их направляющих векторв.
Найдем скалярное произведение .
Замечание. При вычислении скалярного произведения мы воспользовались свойством ассоциативности
Следовательно, прямые перпендикулярны ч.т.д.
б) Параметрически зададим уравнение прямой через начальную точку и направляющий вектор этой
прямой.
Решим базовую задачу расстояния между точкой и прямой(см. методичку задача №5), получим ответ.
Показать ответ и решение
Введём прямоугольную систему координат(см. рисунок).
Точка – начало координат,
Ось направим вдоль вектора
,
Ось направим вдоль вектора
,
Ось направим вдоль вектора
.
Найдем координаты всех точек
Способ 1.
а) Найдём уравнение плоскости
, подставляя координаты точек:
Пусть . Тогда из первого уравнения
, из второго уравнения
, из третьего
.
Получим уравнение: . Подставим координаты точки
и проверим, выполняется ли
равенство:
Равенство верно, значит, тока принадлежит плоскости
б) Найдём уравнение плоскости , подставив соответствующие точки в уравнение плоскости
:
Пусть , тогда из первого уравнения
. Из второго и третьего уравнений
. Получим уравнение
, вектор нормали этой плоскости
. Вектор нормали плоскости
с уравнением
равен
. Угол между плоскостями равен углу между соответствующими им нормалями:
. Получим ответ
.
Способ 2
а) Параметрически зададим плоскость через начальную точку и два направляющих вектора плоскости.
Заметим, что при подстановке в уравнение плоскости, получаем точку
:
Следовательно, точка принадлежит плоскости
ч.т.д.
б) Параметрически зададим плоскость через начальную точку и два направляющих вектора
плоскости
Найдем угол между двумя заданными плоскостями(см. базовая задача №10 из методички), получим
ответ.
Ответ:
Показать ответ и решение
Введём прямоугольную систему координат(см. рисунок).
Точка – начало координат,
Ось направим вдоль вектора
,
Ось лежит в плоскости
и направлена в полуплоскость с точкой
перпендикулярно
,
Ось направим вдоль вектора
.
Пусть , а
. Найдём координаты некоторых точек
a) Докажем перпендикулярность прямых через перпендикулярность их направляющих векторв.
б) Из условия ,
следует, что
.
Способ 1.
Найти расстояние между скрещивающимися прямыми то же самое , что и найти расстояние от любой точки на одной
прямой до плоскости, проходящей, через вторую прямую, параллельной первой.
Пусть — плоскость, проходящая через
параллельно
. Тогда если провести
(вдоль
направления оси ) и
, то
Найдём координаты точки
Найдём уравнение плоскости :
Из первого и второго уравнения следует, что Пусть
, тогда
из второго уравнения. Из третьего
уравнения . Домножим все коэффициенты уравнения на
и получим плоскость
с уравнением
. Вектор нормали
, его длина равна
Найдём расстояние от точки
до
плоскости :
Способ 2.
Параметрически зададим уравнение прямой через начальную точку и направляющий вектор прямой.
Параметрически зададим уравнение прямой через начальную точку и направляющий вектор прямой.
Найдем расстояние между скрещивающимися прямыми(см. базовая задача №7 из методички), получим
ответ.
Ответ:
Показать ответ и решение
Введём прямоугольную систему координат(см. рисунок).
Точка – начало координат,
Ось направим вдоль вектора
,
Ось лежит в плоскости
и направлена в полуплоскость с точкой
перпендикулярно
,
Ось направим в верхнее полупространство перпендикулярно векторам
и
.
По теоереме косинусов для треугольника :
Пусть точка – центр описанной окружности равностроннего треугольника, тогда
По теореме
Пифагора для треугольника :
Найдем координаты всех точек.
a) Докажем перпендикулярность прямый через перпендикулярность их направляющих векторв.
Найдем их скалярное произведение
б) Найдем косинус угла между прямыми, как косинус угла между их направляющими векторами.
Подставляем найденные значения в уравнение с косинусом
Ответ:
Показать ответ и решение
Введём прямоугольную систему координат(см. рисунок).
Точка – начало координат,
Ось направим вдоль вектора
,
Ось направим вдоль вектора
,
Ось направим в полупространоство, содержащее точку
, перпендикулярно векторам
и
.
По теореме Пифагора для
По теореме Пифагора для (
-проекция точки
на плоскость
)
Найдём координаты некоторых точек
,
,
,
,
.
Параметрически зададим уравнение прямой через начальную точку и направляющий вектор прямой:
Способ 1
а) Найдём уравнение плоскости
, подставив координаты точек:
Вычтя из второго уравнения 4 раза первое, получим . То есть плоскость
имеет уравнение вида
.
Проведём
. Найдём координаты точки
. Поскольку
, то
—
равносторонний, и тогда по теореме о пропорциональных отрезках . Получим, что
. Подставив координаты этой точки в уравнение плоскости
, получим верное равенство. Значит, точка
. Значит,
, которая параллельна
. Значит,
.
б) Так как , то проведём
, где
— точка пересечения плоскости
с ребром
. По
теореме Пифагора То есть
А по теореме о пропорциональных
отрезках для угла и параллельных секущих
и
:
. Тогда
Уравнение плоскости легко понять, учитывая то, что его вектор нормали направлен вдоль оси
, и плоскость
проходит через начало координат: . Вектор нормали будет
.
Тогда расстояние от точки до плоскости вычисляется по формуле
Замечание. Расстоянием от точки до такой плоскости будет модуль третьей координаты этой точки, поскольку отрезок,
соединяющий точку и плоскость будет идти вдоль вектора нормали.
Способ 2
Параметрически зададим уравнение плоскости через начальную точку и 2 направляющих вектора этой
плоскости.
Попробуем найти точки пересечения плоскости и прямой
Если у системы нет решений, значит нет точек пересечения, следовательно, прямая и плоскость параллельны.
ч.т.д.
б) Найдем уравнение прямой
Найдем точку в пересечении
и
Откуда
Подставим найденное значение в уравнение прямой
Заметим, что модуль значения по координате это и есть расстояние точки до плоскости
Тогда
Ответ:
Показать ответ и решение
Введём прямоугольную систему координат(см. рисунок).
Точка – начало координат,
Ось направим вдоль вектора
,
Ось направим вдоль вектора
,
Ось направим в полупространство, содержащее точку
, перпендикулярно векторам
и
.
Найдем координаты некоторых точек
,
,
,
,
а) Параметрически зададим уравнение прямой через начальную точку и направляющий вектор
прямой:
По обратной ТТП для плоскости , наклонной
и прямой
, перпендикулярной наклонной, получаем, что
— проекция
точка
принадлежит прямой
Найдем вектор
Тогда из условия
Получаем, что
Следовательно, – середина
. ч.т.д.
б) Параметрически зададим уравнение прямой через начальную точку и направляющий вектор
прямой:
Параметрически зададим уравнение прямой через начальную точку и направляющий вектор прямой:
Пусть – искомое расстояние.
принадлежат
соответственно.
,
Тогда имеем следующее
Можем найти
Найдём длину вектора
Ответ:
Показать ответ и решение
Введём прямоугольную систему координат(см. рисунок).
Точка – начало координат,
Ось направим вдоль вектора
,
Ось лежит в плоскости
и направлена в полуплоскость с точкой
перпендикулярно
,
Ось направим вдоль вектора
.
Пусть , угол между осью
и прямой
, направленный в полуплоскость, содержащую
отрицательное направление оси (как на картинке), равняется
.
Найдём координаты всех точек:
,
,
,
,
а) Найдём вектора :
Так как :
В силу того, что – длины сторон треугольника
.
Тогда . Получаем, что ось
совпадает с
. Отсюда следует, что угол между
и
равняется углу между и
, равняется
. Треугольник
прямоугольный с прямым углом
.
ч.т.д.
б) По теоереме косинусов для :
Применяя три раза теорему Пифагора для , получим равенства
Следовательно, объем пирамиды равен
Введение системы координат
30 мая 2011
Метод координат — это, конечно, очень хорошо, но в настоящих задачах C2 никаких координат и векторов нет. Поэтому их придется вводить. Да-да, вот так взять и ввести: указать начало отсчета, единичный отрезок и направление осей x, y и z.
Самое замечательное свойство этого метода заключается в том, что не имеет никакого значения, как именно вводить систему координат. Если все вычисления будут правильными, то и ответ будет правильным.
Тем не менее, приведу некоторые рекомендации, как лучше ввести систему координат для самых часто встречающихся в задаче C2 многогранников. С указанием конкретных точек. Во всех случаях упор делается на минимизацию объема вычислений.
Координаты куба
Если в задаче C2 будет куб — считайте, что вам повезло. Это самый простой многогранник, все двугранные углы которого равны 90°.
Система координат также вводится очень просто:
- Начало координат — в точке A;
- Чаще всего ребро куба не указано, поэтому принимаем его за единичный отрезок;
- Ось x направляем по ребру AB, y — по ребру AD, а ось z — по ребру AA1.
Обратите внимание: ось z направляется вверх! После двумерной системы координат это несколько непривычно, но на самом деле очень логично.
Итак, теперь у каждой вершины куба есть координаты. Соберем их в таблицу — отдельно для нижней плоскости куба:
| Точка | A | B | C | D |
| Координаты | (0; 0; 0) | (1; 0; 0) | (1; 1; 0) | (0; 1; 0) |
И для верхней:
| Точка | A1 | B1 | C1 | D1 |
| Координаты | (0; 0; 1) | (1; 0; 1) | (1; 1; 1) | (0; 1; 1) |
Несложно заметить, что точки верхней плоскости отличаются соответствующих точек нижней только координатой z. Например, B = (1; 0; 0), B1 = (1; 0; 1). Главное — не запутаться!
Координаты трехгранной призмы
Призма — это уже намного веселее. При правильном подходе достаточно знать координаты только нижнего основания — верхнее будет считаться автоматически.
В задачах C2 встречаются исключительно правильные трехгранные призмы (прямые призмы, в основании которых лежит правильный треугольник). Для них система координат вводится почти так же, как и для куба. Кстати, если кто не в курсе, куб — это тоже призма, только четырехгранная.
Итак, поехали! Вводим систему координат:
- Начало координат — в точке A;
- Сторону призмы принимаем за единичный отрезок, если иное не указано в условии задачи;
- Ось x направляем по ребру AB, z — по ребру AA1, а ось y расположим так, чтобы плоскость OXY совпадала с плоскостью основания ABC.
Здесь требуются некоторые пояснения. Дело в том, что ось y НЕ совпадает с ребром AC, как многие считают. А почему не совпадает? Подумайте сами: треугольник ABC — равносторонний, в нем все углы по 60°. А углы между осями координат должны быть по 90°, поэтому сверху картинка будет выглядеть так:
Надеюсь, теперь понятно, почему ось y не пойдет вдоль AC. Проведем в этом треугольнике высоту CH. Треугольник ACH — прямоугольный, причем AC = 1, поэтому AH = 1 · cos A = cos 60°; CH = 1 · sin A = sin 60°. Эти факты нужны для вычисления координат точки C.
Теперь взглянем на всю призму вместе с построенной системой координат:
Получаем следующие координаты точек:
Как видим, точки верхнего основания призмы снова отличаются от соответствующих точек нижнего лишь координатой z. Основная проблема — это точки C и C1. У них есть иррациональные координаты, которые надо просто запомнить. Ну, или понять, откуда они возникают.
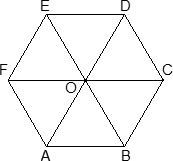
Координаты шестигранной призмы
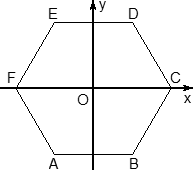
Шестигранная призма — это «клонированная» трехгранная. Можно понять, как это происходит, если взглянуть на нижнее основание — обозначим его ABCDEF. Проведем дополнительные построения: отрезки AD, BE и CF. Получилось шесть треугольников, каждый из которых (например, треугольник ABO) является основанием для трехгранной призмы.
Теперь введем собственно систему координат. Начало координат — точку O — поместим в центр симметрии шестиугольника ABCDEF. Ось x пойдет вдоль FC, а ось y — через середины отрезков AB и DE. Получим такую картинку:
Обратите внимание: начало координат НЕ совпадает с вершиной многогранника! На самом деле, при решении настоящих задач вы обнаружите, что это очень удобно, поскольку позволяет значительно уменьшить объем вычислений.
Осталось добавить ось z. По традиции, проводим ее перпендикулярно плоскости OXY и направляем вертикально вверх. Получим итоговую картинку:
Запишем теперь координаты точек. Предположим, что все ребра нашей правильной шестигранной призмы равны 1. Итак, координаты нижнего основания:
Координаты верхнего основания сдвинуты на единицу по оси z:
Координаты четырехугольной пирамиды
Пирамида — это вообще очень сурово. Мы разберем только самый простой случай — правильную четырехугольную пирамиду, все ребра которой равны единице. Однако в настоящих задачах C2 длины ребер могут отличаться, поэтому ниже приведена и общая схема вычисления координат.
Итак, правильная четырехугольная пирамида. Это такая же, как у Хеопса, только чуть поменьше. Обозначим ее SABCD, где S — вершина. Введем систему координат: начало в точке A, единичный отрезок AB = 1, ось x направим вдоль AB, ось y — вдоль AD, а ось z — вверх, перпендикулярно плоскости OXY. Для дальнейших вычислений нам потребуется высота SH — вот и построим ее. Получим следующую картинку:
Теперь найдем координаты точек. Для начала рассмотрим плоскость OXY. Здесь все просто: в основании лежит квадрат, его координаты известны. Проблемы возникают с точкой S. Поскольку SH — высота к плоскости OXY, точки S и H отличаются лишь координатой z. Собственно, длина отрезка SH — это и есть координата z для точки S, поскольку H = (0,5; 0,5; 0).
Заметим, что треугольники ABC и ASC равны по трем сторонам (AS = CS = AB = CB = 1, а сторона AC — общая). Следовательно, SH = BH. Но BH — половина диагонали квадрата ABCD, т.е. BH = AB · sin 45°. Получаем координаты всех точек:
Вот и все с координатами пирамиды. Но не с координатами вообще. Мы рассмотрели лишь самые распространенные многогранники, однако этих примеров достаточно, чтобы самостоятельно вычислить координаты любых других фигур. Поэтому можно приступать, собственно, к методам решения конкретных задач C2.
Смотрите также:
- Четырехугольная пирамида в задаче C2
- Метод координат в пространстве
- Сложение и вычитание дробей
- Не пишите единицы измерения в задаче B12
- Как решать простейшие логарифмические уравнения
- Задача B4: транзит нефти
План урока:
Прямоугольная система координат
Координаты вектора
Координаты середины отрезка
Вычисление длины векторов и расстояния между точками
Коллинеарность векторов
Определение компланарности векторов
Скалярное произведение векторов
Прямоугольная система координат
В планиметрии мы уже рассматривали прямоугольную систему координат. Ее образовывали 2 перпендикулярные друг другу оси – Ох и Оу. С ее помощью можно было определить положение любой точки на координатной плоскости, просто указав две ее координаты – абсциссу х и ординату у.
В стереометрии необходимо определять положение точки уже не на плоскости, а в пространстве. Для этого добавляется третья ось Оz, которую ещё называют осью апликат. Каждые пара осей образует свою отдельную координатную плоскость, всего получается три таких плос-ти: Оху, Охz и Oуz.
Точка О именуется началом координат. Она делит каждую ось на два луча, один из которых – это положительная полуось, а второй – отрицательная полуось.
Для каждой точки в пространстве можно указать три координаты, однозначно определяющие ее положение в пространстве. Пусть в пространстве есть некоторая точка М. Опустим из нее перпендикуляры на координатные плоскости. В свою очередь из этих проекций точки М опустим перпендикуляры уже на координатные оси. В результате будет построен прямоугольный параллелепипед. Измерения этого параллелепипеда и будут координатами точки М:
Если точка M находится в одной из координатных плоскостей, то одна из ее координат будет нулевой. Например, если М принадлежит плоскости Охz, то нулю будет равна координата у. Если же точка располагается на одной из координатных осей, то у нее уже две координаты будут нулевыми. Так, если точка находится на оси Ох, то только координата х может быть ненулевой, а у и z окажутся нулевыми координатами.
На показанном рисунке ребра параллелепипеда лежат на положительных полуосях, поэтому все координаты положительны. Если же какие-то ребра будут лежать на отрицательных полуосях, то и соответствующие координаты будут отрицательными.
Координаты вектора
Введем в пространстве прямоугольную систему коорд-т, а далее от ее начала отложим вектора i, j и k, которые соответственно будут лежать на координатных осях Ох, Оу и Оz, и длина которых составит единицу. Эти вектора именуют координатными векторами, единичными векторами или просто ортами.
Ясно, что орты находятся в разных плоскостях, то есть они образуют тройку некомпланарных векторов. Это означает, что любой вектор а в пространстве можно разложить на орты:
где х, у и z – какие-то действительные числа. Они как раз и считаются координатами вектора а. Записываются коорд-ты вектора в фигурных скобках. На следующем рисунке показан вектор а{3; – 2; – 4}.
Задание. Разложите на орты вектор
Если начало вектора ОМ располагается в начале системы координат О, то вектор ОМ именуют радиус-вектором. В таком случае коорд-ты точки конца вектора, то есть точки М, совпадают с коорд-тами самого вектора ОМ.
Это свойство радиус-вектора мы уже изучали в 9 классе в планиметрии, и в стереометрии оно сохраняется.
Задание. О – начало координат, а точка М имеет коорд-ты (2; 5; – 3). Найдите коорд-ты вектора ОМ.
Решение. Всё очень просто – коорд-ты вектора будут совпадать с коорд-тами его конца, так его начало совпадает с началом коорд-т:
Также в стереометрии остаются справедливыми ещё несколько правил, которые были доказаны в курсе планиметрии:
Задание. Найдите сначала сумму, а потом разность векторов а{3; 7; 5} и b{2; 4; 6}.
Решение. Будем обозначать коорд-ты векторов через индексы. Например, коорд-ты вектора а – это ха, уа и zа. Пусть сумма векторов будет вектором с, а их разность – вектором d. Для вычисления суммы надо складывать соответствующие координаты:
Для вычисления разности надо из коорд-т вектора а вычитать коорд-ты вектора b:
Задание. Вычислите коорд-ты вектора р, зная, что:
Решение. Для вычисления координат надо в выражении для вектора р сами векторы заменить на их координаты:
Получается, что вектор p имеет координаты {0; – 2; 3}.
Теперь мы можем доказать ещё одно утверждение, уже известное из курса планиметрии:
Действительно, пусть есть некоторый вектор АВ, причем коорд-ты точек А и В известны. Построим радиус-вектора OА и OВ:
Координаты радиус-векторов будут совпадать с координатами их концов:
ч. т. д.
Задание. Определите коорд-ты вектора CD, если даны коорд-ты точек С и D: С(3; 8; – 5) и D(5; 4; 1).
Решение. Здесь надо просто из коорд-т точки D, являющейся концом вектора, вычесть коорд-ты точки С:
Задание. От точки K(10; 6; 13) отложен вектор m{3; 2; 5}, конец совпал в точку H. Найдите коорд-ты точки H.
Решение. Коорд-ты вектора m и его концов связаны формулами:
Координаты середины отрезка
Пусть в пространстве есть отрезок АВ, и координаты его концов известны. Точка М – середина этого отрезка. Как вычислить ее координаты? Рассмотрим взаимосвязь векторов АМ, МВ и АВ:
Раз М – середина АВ, то вектора АМ и МВ имеют равные длины, и при этом они находятся на одной прямой. Значит, эти вектора равны и потому у них одинаковые коорд-ты:
Аналогично можно получить аналогичные формулы для коорд-т у и z:
Рассмотрим несколько задач на координаты точек.
Задание. Найдите коорд-ты середины отрезка, соединяющего точки А(3; 7; 12) и В(1; 5; – 4).
Решение. Просто используем только что выведенные формулы. Середину также обозначаем буквой М:
Задание. Известно, что K середина отрезка CD. Даны координаты точек С и K: С(12; 9; – 3) и K(15; 7; 3). Найдите коорд-ты D.
Решение. Сначала запишем формулу для коорд-ты х:
Вычисление длины векторов и расстояния между точками
Рассмотрим радиус-вектор ОМ с коорд-тами {x; у; z}. Попытаемся найти его длину. Мы можем построить прямоугольный параллелепипед, в котором этот вектор окажется диагональю:
Напомним, что квадрат длины диагонали в прямоугольном параллелепипеде равен сумме квадратов его измерений. Но в полученном параллелепипеде измерения – это коорд-ты х, у и z, поэтому можно записать:
Так как равные вектора имеют как одинаковы и коорд-ты, и длина, то ясно, что каждый вектор с коорд-тами {x; y; z} будет равен рассмотренному радиус-вектору, а значит и его длина будет рассчитываться по такой же формуле.
Задание. Найдите длину вектора m{– 2; 9; 6}.
Решение. Просто используем формулу:
Рассмотрим отрезок АВ с известными коорд-тами его концов. Можно построить вектор АВ, его коорд-ты будут определяться так:
Задание. Найдите расстояние между точкой K(10; 15; 5) и M(16; 21; – 2).
Решение. Просто подставляем коорд-ты точек в формулу:
Задание. Найдите длину медианы KM в ∆ KPN, если известны коорд-ты его вершин: P(2; 5; 8), N (6; 9; 12) и K(16; 11; 13).
Решение. Для нахождения длины медианы достаточно знать коорд-ты ее концов. Коорд-ты K уже известны, а M – середина PN, что позволяет вычислить и ее коорд-ты:
Коллинеарность векторов
Напомним, что если два вектора а и b коллинеарны друг другу, то должно существовать такое число k, что
Полученное отношение (1) является одновременно и признаком коллинеарных векторов, и их свойством. Слово «признак» означает, что любые вектора, чьи координаты соответствуют условию (1), будут коллинеарны. Слово «свойство» означает обратное – если известно, что вектора коллинеарны, то для них обязательно выполняется условие (1). В таких случаях в математике может использоваться словосочетание «тогда и только тогда»:
Очень важно то, что это правило действует только в случае, если все коорд-ты векторов ненулевые. Теперь рассмотрим случай, когда какие-то коорд-ты вектора b (одна или две из них) равны нулю. Например, пусть
В результате мы выяснили, что если коорд-та одного вектора нулевая, то и у любого вектора, коллинеарному ему, эта же коорд-та также должна быть нулевой. Особняком стоит случай с нулевым вектором с коорд-тами {0; 0; 0}. Он условно признается коллинеарным любому вектору.
Задание. Выясните, какие из этих пар векторов коллинеарны:
Решение. В первом задании просто делим друг на друга соответствующие коорд-ты и находим значение коэффициента k:
Значение коэффициента k оказалось одинаковым для каждой пары коорд-т, значит, вектора коллинеарны.
Повторяем эти действия в задании б):
На этот раз коэффициенты k оказались различными, значит, вектора неколлинеарны.
В задании в) у вектора е коорд-та z нулевая. Значит, если и у вектора f, если он коллинеарен z, эта координата должна быть нулевой, но это не так. Значит, вектора e и f неколлинеарны.
В задании г) снова указаны вектора с нулевыми коорд-тами. Но у обоих векторов коорд-та z нулевая, поэтому они могут быть коллинеарными. Однако необходимо проверить, что отношение ненулевых координат одинаково:
Коэффициент k получился одинаковым, поэтому вектора коллинеарны.
В последнем задании д) вектор n – нулевой, ведь все его коорд-ты нулевые. Нулевой вектор всегда коллинеарен другим векторам, в том числе и в этом задании.
Ответ: а) да; б) нет; в) нет; г) да; д) да.
Задание. Выясните, располагаются ли на одной прямой точки А(3; 5; 12), В(5; 7; 16) и С(0; 2; 6).
Решение. Ясно, что если эти точки находятся на одной прямой, то вектора АВ и ВС будут коллинеарными. Если же эти вектора неколлинеарны, то и точки должны находиться на разных прямых.
Сначала вычислим коорд-ты векторов АВ и ВС:
Теперь проверяем, коллинеарны ли эти вектора:
Коэффициенты k одинаковы, а потому АВ и ВС – коллинеарные векторы. Значит, точки А, В и С находятся на одной прямой.
Определение компланарности векторов
Пусть у нас есть три вектора с известными коорд-тами:
Как определить, компланарны ли эти вектора, то есть располагаются ли они в одной плоскости? Если эти вектора компланарны, то, по признаку компаланарности, вектор а можно разложить на вектора b и с:
где х и y – некоторые числа. Но если такое разложение существует, то коорд-ты векторов а, b и с будут связаны равенствами:
Получили систему из 3 уравнений с двумя неизвестными (х и y). Если такая система имеет решение, то вектора компланарны. Если же решения нет, то вектора не компланарны.
Задание. Определите, компланарны ли вектора
Имеем систему с тремя уравнениями. Из последних двух уравнений очевидно, что его решением может быть только пара чисел:
Значит, рассмотренная тройка векторов компланарна.
Задание. Располагаются ли в одной плос-ти вектора:
Решение. Нам надо проверить компаланарность векторов, поэтому действуем также, как и в предыдущей задаче. Если вектора компланарны, то существует разложение:
Получилось неверное равенство. Это означает, что у системы уравнений решения нет, и потому тройка векторов некомпланарна.
Скалярное произведение векторов
В 9 классе мы уже изучали скалярное произведение векторов.
Для нахождения угла между векторами необходимо отложить их от одной точки, тогда они образуют такой угол.
Задание. Угол между векторами с и d составляет 60°, а их длины соответственно равны 5 и 6. Найдите их скалярное произведение.
Решение. Здесь для расчета просто перемножаем длины векторов и косинус 60°:
Напомним несколько уже известных нам фактов о скалярном произведении, остающихся верными и в стереометрии:
Формула для расчета скалярного произведения по коорд-там векторов, используемая в стереометрии, несколько отличается от формулы из курса планиметрии. Напомним, что в планиметрии произведение векторов а{xа; уа} и b{хb; yb} можно было рассчитать так:
Задание. Вычислите скалярное произведение векторов:
На практике скалярное произведение обычно используется для расчета углов между векторами, а также отрезками и прямыми. Рассмотрим несколько задач.
Задание. Вычислите угол между векторами:
Теперь через скалярное произведение возможно рассчитать косинус искомого нами угла, а затем и сам угол, который мы обозначим как α:
Задание. Рассчитайте углы в ∆АВС, зная коорд-ты его вершин: А(1; – 1; 3), В(3; – 1; 1) и С(– 1; 1; 3).
Решение. Чтобы найти ∠В, необходимо просто рассчитать угол между векторами ВС и ВА также, как это сделано в предыдущей задаче. Но сначала найдем коорд-ты векторов ВС и ВА и их длины:
Далее рассчитываем скалярное произведение векторов:
Теперь найдем угол А, который представляет собой угол между векторам AВ и AС. Вектор AВ – это вектор, противоположный ВA, то у него та же длина, но противоположный знак у коорд-т:
Задание. В прямоугольном параллелепипеде АВСDA1B1C1D1 ребра имеют длину:
AB = 1
BC = 2
BB1 = 2
Рассчитайте угол между векторами DB1 и BC1.
Решение. Введем систему коорд-т Охуz и расположим в нем параллелепипед следующим образом:
При этом построении граничные точки векторов будут иметь следующие коорд-ты:
Находим коорд-ты векторов, а также их длины:
Рассчитываем скалярное произведение DB1 и BC1:
Получили ноль. Из этого вытекает, что вектора перпендикулярны, то есть искомый нами угол составляет 90°.
Ответ: 90°
Сегодня мы научились использовать координаты для решения стереометрических задач. Почти все формулы, используемые в методе координаты, аналогичны тем формулам, которые были выведены ещё в курсе планиметрии. Надо лишь учитывать существование ещё одной, третьей координаты z.
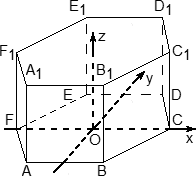
Представьте, перед вам нарисованный куб с осями координат, направленным по трем ребрам, выходящим из одной вершины. За единицу масштаба берем ребро куба и обозначим вершины буквами $%A$%, $%B$%, $%C$%, $%D$%, $%A_1$%, $%B_1$%, $%C_1$% и $%D_1$%. Нужно:
- Найти координаты всех вершин куба.
- Найти координаты середины ребра $%CC_1$%.
- Найти, чему равно расстояние от вершины $%(0;0;0)$% куба до точки пересечения диагоналей грани $%BB_1C_1C$%.
Здесь не сказано, какая из вершин принята за начало координат а также не указан порядок выбора осей, что создаёт неоднозначность в ответах на некоторые из пунктов. Координаты вершин всегда имеют вид 000, 001, 010, 011, 100, 101, 110, 111 (пишу для простоты без скобок и промежуточных запятых). Для всего остального требуются уточнения, хотя там всё в принципе просто.
(15 Мар ’15 12:02)
falcao
@falcao, начало координат-точка А. Оси x,y,z соответствуют ребрам AB, AD, AA1
1
Тогда все координаты непосредственно видны из рисунка: B(1;0;0), D(0;1;0), C(1;1;0), C1(1;1;1). Середина ребра соответствует полусумме координат: (1;1;1/2). В пункте 3 берётся середина грани, координаты (1;1/2;1/2). Расстояние до нуля — корень из суммы квадратов, то есть $%sqrt{3/2}=sqrt6/2$%.
(15 Мар ’15 12:34)
falcao
Тригонометрия
Найти координаты точки на единичной окружности, полученной поворотом точки ( Aleft( 1;0 right) ) на ( -225<>^circ ) .
Окружность единичная с центром в точке ( left( 0;0 right) ) , значит, мы можем воспользоваться упрощёнными формулами:
( beginx=cos beta =cos (-225<>^circ )\y=sin beta =sin (-225<>^circ )end ) .
Можно заметить, что ( -225<>^circ =-360<>^circ +135<>^circ ; -225<>^circ =-180<>^circ -45<>^circ ) . Изобразим рассматриваемый пример на рисунке:
Радиус ( <_<1>>W ) образует с осью ( x ) углы, равные ( 45<>^circ ) и ( 135<>^circ ) . Зная, что табличные значения косинуса и синуса ( 45<>^circ ) равны ( displaystyle dfrac<sqrt<2>> <2>) , и определив, что косинус здесь принимает отрицательное значение, а синус положительное, имеем:
Подробней подобные примеры разбираются при изучении формул приведения тригонометрических функций в теме “Формулы тригонометрии”.
Таким образом, искомая точка имеет координаты ( left( -dfrac<sqrt<2>><2>;dfrac<sqrt<2>> <2>right) ) .
10.V-3. Поворот точки вокруг начала координат-2
Алгебра. 10 класс. Тригонометрия. Тест 3.
Вариант 1.
1. Найти координаты точки единичной окружности, полученной поворотом точки (1; 0) на угол 3π/2±π.
A) (0; -1); B) (0; 1); C) (1; 0); D) (-1; 0).
2. Найти координаты точки единичной окружности, полученной поворотом точки (1; 0) на угол π/6±π.
3. Найти координаты точки единичной окружности, полученной поворотом точки (1; 0) на угол π+πk, где kϵZ.
A) (-1; 0); (1; 0); B) (0; -1); (1; 0); C) (1; 0); (0; 1); D) (0; -1); (-1; 0).
4. Записать все углы, на которые нужно повернуть точку Р(1; 0), чтобы в результате получить
A) 3π/4+2πk, kϵZ; B) -π/4+2πk, kϵZ; C) π/4+2πk, kϵZ; D) 7π/4+2πk, kϵZ.
5. Записать все углы, на которые нужно повернуть точку Р(1; 0), чтобы в результате получались
A) π/6+πk, kϵZ; B) π/3+2πk, kϵZ; C) -π/3+πk, kϵZ; D) -π/6+2πk, kϵZ.
6. При повороте точки Р(1; 0) вокруг начала координат получены углы α=π/2+πk, kϵZ. Записать те из них, которые принадлежат отрезку [-5π; -7π/2].
A) -9π/2; -4π; B) -9π/2; -7π/2; C) -7π/2; D) -5π; -9π/2.
7. Точке М единичной окружности соответствует бесконечное множество действительных чисел ±5π/6+2πk, где kϵZ. Записать те из них, которые принадлежат отрезку [3π; 9π/2].
A) 19π/6; B) 17π/6; C) 4π; D) 13π/6.
8. Точке М единичной окружности соответствует бесконечное множество действительных чисел ±π/3+πk, где kϵZ. Записать те из них, которые принадлежат отрезку [-2π; -π/2].
A) -5π/3; -4π/3; B) -4π/3; -2π/3; C) -5π/3; -4π/3; -2π/3; D) -2π; -4π/3; -2π/3.
Вариант 2.
1. Найти координаты точки единичной окружности, полученной поворотом точки (1; 0) на угол π/2±π.
A) (0; -1); B) (0; 1); C) (1; 0); D) (-1; 0).
2. Найти координаты точки единичной окружности, полученной поворотом точки (1; 0) на угол π/3±π.
3. Найти координаты точки единичной окружности, полученной поворотом точки (1; 0) на угол -π+πk, где kϵZ.
A) (-1; 0); (0; -1); B) (0; -1); (1; 0); C) (1; 0); (0; 1); D) (1; 0); (-1; 0).
4. Записать все углы, на которые нужно повернуть точку Р(1; 0), чтобы в результате получить
A) 5π/6+2πk, kϵZ; B) π/6+2πk, kϵZ; C) -π/6+2πk, kϵZ; D) 5π/3+2πk, kϵZ.
5. Записать все углы, на которые нужно повернуть точку Р(1; 0), чтобы в результате получались
A) -π/4+πk, kϵZ; B) π/4+πk, kϵZ; C) -π/8+πk, kϵZ; D) -π/6+2πk, kϵZ.
6. При повороте точки Р(1; 0) вокруг начала координат получены углы α=πk, kϵZ. Записать те из них, которые принадлежат отрезку [4π; 11π/2].
A) 9π/2; 5π; B) 4π; 9π/2; C) 4π; 5π; D) 5π.
7. Точке М единичной окружности соответствует бесконечное множество действительных чисел -π/4+2πk, где kϵZ. Записать те из них, которые принадлежат отрезку [-9π/2; -3π].
A) -13π/4; B) -19π/4; C) -15π/4; D) -17π/4.
8. Точке М единичной окружности соответствует бесконечное множество действительных чисел ±2π/3+2πk, где kϵZ. Записать те из них, которые принадлежат отрезку [-5π; -7π/2].
A) -16π/3; B) -14π/3; C) -13π/3; D) -3π; -14π/3.
Вариант 3.
1. Найти координаты точки единичной окружности, полученной поворотом точки (1; 0) на угол -π/2±π.
A) (0; 1); B) (0; -1); C) (1; 0); D) (-1; 0).
2. Найти координаты точки единичной окружности, полученной поворотом точки (1; 0) на угол 3π/4±π.
3. Найти координаты точки единичной окружности, полученной поворотом точки (1; 0) на угол -3π/2+πk, где kϵZ.
A) (-1; 0); (0; -1); B) (0; 1); (0; -1); C) (1; 0); (0; 1); D) (1; 0); (-1; 0).
4. Записать все углы, на которые нужно повернуть точку Р(1; 0), чтобы в результате получить
A) 5π/3+2πk, kϵZ; B) π/3+2πk, kϵZ; C) π/6+2πk, kϵZ; D) 7π/6+2πk, kϵZ.
5. Записать все углы, на которые нужно повернуть точку Р(1; 0), чтобы в результате получались
A) -π/6+πk, kϵZ; B) -π/4+πk, kϵZ; C) -π/3+πk, kϵZ; D) π/6+2πk, kϵZ.
6. При повороте точки Р(1; 0) вокруг начала координат получены углы α=5π/6+2πk, kϵZ. Записать те из них, которые принадлежат отрезку [-6π; -4π].
A) -5π; B) -29π/6; C) -25π/6; D) -31π/6.
7. Точке М единичной окружности соответствует бесконечное множество действительных чисел ±π/4+2πk, где kϵZ. Записать те из них, которые принадлежат отрезку [-5π; -3π].
A) -17π/4; B) -15π/4; C) -15π/4; -17π/4; D) -13π/4; -15π/4.
8. Точке М единичной окружности соответствует бесконечное множество действительных чисел π/4+πk/2, где kϵZ. Записать те из них, которые принадлежат отрезку [5π; 13π/2].
A) 21π/4; 23π/4; 25π/4; B) 21π/4; 23π/4; C) 23π/4; 25π/4; D) 23π/4.
Вариант 4.
1. Найти координаты точки единичной окружности, полученной поворотом точки (1; 0) на угол -3π/2±π.
A) (-1; 0); B) (0; 1); C) (1; 0); D) (0; -1).
2. Найти координаты точки единичной окружности, полученной поворотом точки (1; 0) на угол 5π/6±π.
3. Найти координаты точки единичной окружности, полученной поворотом точки (1; 0) на угол 3π/2+πk, где kϵZ.
A) (-1; 0); (0; -1); B) (0; -1); (0; 1); C) (1; 0); (0; 1); D) (1; 0); (-1; 0).
4. Записать все углы, на которые нужно повернуть точку Р(1; 0), чтобы в результате получить
A) π/3+2πk, kϵZ; B) -π/3+2πk, kϵZ; C) 2π/3+2πk, kϵZ; D) π/6+2πk, kϵZ.
5. Записать все углы, на которые нужно повернуть точку Р(1; 0), чтобы в результате получались
A) π/6+πk, kϵZ; B) -π/4+πk, kϵZ; C) π/3+πk, kϵZ; D) π/4+πk, kϵZ.
6. При повороте точки Р(1; 0) вокруг начала координат получены углы α=π/3+2πk, kϵZ. Записать те из них, которые принадлежат отрезку [-5π/2; -π].
A) -5π/3; B) -π/3; -4π/3; C) -2π/3; D) -4π/3.
7. Точке М единичной окружности соответствует бесконечное множество действительных чисел ±π/3+2πk, где kϵZ. Записать те из них, которые принадлежат отрезку [-2π; -π/2].
A) -π/3; B) -2π/3; C) -4π/3; D) -5π/3.
8. Точке М единичной окружности соответствует бесконечное множество действительных чисел π/4+πk/2, где kϵZ. Записать те из них, которые принадлежат отрезку [-7π/2; -5π/2].
A) -13π/4; B) -13π/4; -11π/4; C) -11π/4; D) -3π.
Поворот точки вокруг начала координат
Рассмотрим на координатной плоскости окружность радиуса 1 с центром в начале координат. Ее называют единичной окружностью. Введем понятие поворота точки единичной окружности во круг начала координат на угол α радиан, где α – любое действительное число.
1. 1. Пусть α>0. Предположим, что точка, двигаясь поединичной окружности от точки Р против часовой стрелки, прошла путь длиной α (рис. 1). Конечную точку пути обозначим М.
В этом случае будем говорить, что точка М получена из точки Р поворотом вокруг начала координат на угол α радиан.
Частные случаи решения уравнений tg x = a
| Уравнение | Решение |
| tg x = – 1 | |
| tg x = 0 | |
| tg x = 1 | |
20(1). Вопрос: Определение производной, правила дифференцирования, примеры.
Ответ: Производная функции − одно из основных понятий математики, а в математическом анализе производная наряду с интегралом занимает центральное место. Процесс нахождения производной называется дифференцированием. Обратная операция − восстановление функции по известной производной − называется интегрированием.
Производная функции в некоторой точке характеризует скорость изменения функции в этой точке.
1. Вопрос: Аксиомы стереометрии. Следствия из аксиом (доказать одно из них).
Ответ: А1. Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна.
| А В (точки А, В, С лежат в плоскости ) С |
А2. Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости
| АB Прямая АВ лежит в плоскости |
Замечание. Если прямая и плоскость имеют только одну общую точку, то говорят, что они пересекаются.
| а = М Прямая а и плоскость пересекаются в точке М. |
А3. Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей.
| = a и пересекаются по прямой а. |
Следствие 1. Через прямую и не лежащую на ней точку проходит плоскость, и притом только одна.
1) Рассмотрим прямую a и точку A, которая не находится на этой прямой.
2) На прямой a выберем точки B и C.
3) Так как все 3 точки не находятся на одной прямой, из второй аксиомы следует, что через точки A, B, Cи можно провести одну единственную плоскостьα.
4) Точки прямой a, B и C, лежат на плоскостиα, поэтому из третьей аксиомы следует, что плоскость проходит через прямую a и, конечно, через точку A.
Следствие 2. Через две пересекающиеся прямые проходит плоскость, и притом только одна.
2. Вопрос: Теорема о параллельности трех прямых (формулировка и доказательство).
Ответ: Две прямые, параллельные третьей прямой, параллельны.
Выберем точку M на прямой b.
Через точку M и прямую a, которая не содержит эту точку, можно провести только одну плоскость α (Через прямую и не лежащую на ней точку можно провести только одну плоскость).
Возможны два случая:
1) прямая b пересекает плоскость α или 2) прямая b находится в плоскости α.
Пусть прямая b пересекает плоскость α.
Значит, прямая c, которая параллельна прямой b, тоже пересекает плоскость α. Так как a∥c, то получается, что a тоже пересекает эту плоскость. Но прямая a не может одновременно пересекать плоскость α и находиться в плоскости α. Получаем противоречие, следовательно, предположение, что прямая b пересекает плоскость α, является неверным.
Значит, прямая b находится в плоскости α.
Теперь нужно доказать, что прямые a и b параллельны.
Пусть у прямых a и b есть общая точка L.
Это означает, что через точку L проведены две прямые a и b, которые параллельны прямой c. Но по теореме (Через любую точку пространства вне данной прямой можно провести прямую, параллельную данной прямой, и при том только одну.) это невозможно. Поэтому предположение неверное, и прямые a и b не имеют общих точек.
Так как прямые a и b находятся в одной плоскости α и у них нет общих точек, то они параллельны.
3. Вопрос: Параллельные прямые в пространстве(определение). Теорема о параллельных прямых.
Ответ: Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.
Теорема о параллельных прямых: Через любую точку пространства, не лежащую на данной прямой проходит прямая, параллельная данной, и притом только одна.
4. Вопрос: Параллельность прямой и плоскости(определение). Признак параллельности прямой и плоскости.
Ответ: Прямая и плоскость называются параллельными, если они не имеют общих точек.
Признак параллельности прямой и плоскости:Если прямая, не лежащая в плоскости, параллельна некоторой прямой, лежащей в этой плоскости, то прямая параллельна самой плоскости.
5. Вопрос: Расположение прямых в пространстве(виды). Признак скрещивающихся прямых.
Ответ:
Признак скрещивающихся прямых: Если одна из двух прямых лежит на плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые скрещиваются.
6. Вопрос: Углы с сонаправленными сторонами. Определение, теорема.
7. Вопрос: Признак параллельности двух плоскостей.
Ответ: Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то плоскости параллельны.
8. Вопрос: Свойства параллельности плоскостей(доказать одно из них)
Ответ: Всего 3 свойства.
С1:Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны.
Пусть даны параллельные плоскости и и плоскость , которая пересекает плоскости и по прямым а и b соответственно (Рис. 1.).
Прямые а и b лежат в одной плоскости, а именно в плоскости γ. Докажем, что прямые а и b не пересекаются.
Если бы прямые а и b пересекались, то есть имели бы общую точку, то эта общая точка принадлежала бы двум плоскостям и , и , что невозможно, так как они параллельны по условию.
Итак, прямые а и b параллельны, что и требовалось доказать.
С2: Отрезки параллельных прямых, заключенные между параллельными плоскостями, равны.
Пусть даны параллельные плоскости и и параллельные прямые АВ и СD, которые пересекают эти плоскости (Рис. 2.). Докажем, что отрезки АВ и СD равны.
Две параллельные прямые АВ и СD образуют единственную плоскость γ, γ = АВDС. Плоскость γ пересекает параллельные плоскости и по параллельным прямым (по первому свойству). Значит, прямые АС и ВD параллельны.
Прямые АВ и СD также параллельны (по условию). Значит, четырехугольник АВDС – параллелограмм, так как его противоположные стороны попарно параллельны.
Из свойств параллелограмма следует, что отрезки АВ и СD равны, что и требовалось доказать.
С3: Параллельные плоскости рассекают стороны угла на пропорциональные части.
Пусть нам даны параллельные плоскости и , которые рассекают стороны угла А (Рис. 3.). Нужно доказать, что .
Параллельные плоскости и рассечены плоскостью угла А. Назовем линию пересечения плоскости угла А и плоскости – ВС, а линию пересечения плоскости угла А и плоскости – В1С1. По первому свойству, линии пересечения ВС и В1С1 параллельны.
.
9. Вопрос: Тетраэдр и параллелепипед. Определения. Свойства параллелепипеда.
Ответ: Тетраэдр – поверхность, составленная из четырёх треугольников DАВ, DВС, DАС и АВС.
| АВС, DАС, DВС, DАВ – грани. отрезки DА, DВ, АВ и т.д. – рёбра. точки А, В, С и т.д. – вершины. Рёбра АD и ВС – противоположные. Считается АВС – основание, остальные грани – боковые. |
Параллелепипед. АВСDA1B1C1D1: поверхность, составленная из двух равных параллелограммов АВСD и A1B1C1D1, лежащих в параллельных плоскостях и четырёх параллелограммов.
| все параллелограммы – грани, их стороны – рёбра, их вершины – вершины параллелепипеда. Считается: АВСD и A1B1C1D1 – основания, остальные грани – боковые. | |
| рис. 29 | Отрезок, соединяющий противоположные вершины, называется диагональю параллелепипеда: A1C, D1B, AC1, DB1. |
Свойства:
1. Противоположные грани параллелепипеда параллельны и равны.
Для любой пары противолежащих граней параллелепипеда имеем: соответствующие углы равны (например, , и т. д.); соответствующие стороны равны и параллельны ( и , и и т. д. как противолежащие стороны параллелограммов). Отсюда и их плоскости параллельны.
2. Диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам.
10. Вопрос: Признак перпендикулярности прямой и плоскости.
Ответ:Если прямая, пересекающая плоскость, перпендикулярна двум прямым в этой плоскости, проходящим через точку пересечения данной прямой и плоскости, то она перпендикулярна плоскости.
11. Вопрос: Теорема о трёх перпендикулярах.
Ответ: Если прямая, проведенная на плоскости через основание наклонной, перпендикулярна ее проекции, то она перпендикулярна наклонной. И обратно: Если прямая на плоскости перпендикулярна наклонной, то она перпендикулярна и проекции наклонной.
12. Вопрос: Признак перпендикулярности двух плоскостей.
Ответ: Если плоскость проходит через прямую, перпендикулярную другой плоскости, то эти плоскости перпендикулярны.
13. Вопрос: Призма. Основные элементы, Sбок, Sполн, Vпризмы.
Ответ: Призма — это многогранник, две грани которого являются равными многоугольниками, находящимися в параллельных плоскостях, а остальные грани — параллелограммами.
14. Вопрос: Пирамида. Основные элементы, Sбок, Sполн, Vпирамиды.
Ответ: Пирамида – многогранник, одна из граней которого (называется основанием) – произвольный многоугольник, а остальные грани соединяются в одной точке(вершине).
15. Вопрос: Усечённаяпирамида. Основные элементы, Sбок, Sполн.
Ответ: Усечённой пирамидой называется часть пирамиды, заключенная между её основанием и сечением пирамиды, параллельным основанию.
16. Вопрос: Двугранный угол. Градусная мера двугранного угла.
Ответ: Двугранный угол – это фигура, образованная двумя полуплоскостями, исходящими из одной прямой.Двугранный угол измеряется величиной своего линейного угла.Чтобы найти величину двугранного угла или угла между плоскостями, нужно построить линейный угол и найти величину этого линейного угла.
17. Вопрос: Прямоугольный параллелепипед. Свойства прямоугольного параллелепипеда (доказать одно из них).
Ответ: Прямоугольный параллелепипед – многогранник с шестью гранями, каждая из которых является в общем случае прямоугольником. Противолежащие грани параллелепипеда равны.
Свойства прямоугольного параллелепипеда:
С1:В прямоугольном параллелепипеде все шесть граней прямоугольники.
С2: Боковые ребра перпендикулярны основанию. Значит, все боковые грани прямоугольного параллелепипеда – прямоугольники.
С3: Все двугранные углы прямоугольного параллелепипеда прямые.
Рассмотрим, например, двугранный угол прямоугольного параллелепипеда с ребром АВ, т. е. двугранный угол между плоскостями АВВ1 и АВС.
АВ – ребро, точка А1 лежит в одной плоскости – в плоскости АВВ1, а точка D в другой – в плоскости А1В1С1D1. Тогда рассматриваемый двугранный угол можно еще обозначить следующим образом: ∠А1АВD.
Возьмем точку А на ребре АВ. АА1 – перпендикуляр к ребру АВ в плоскости АВВ1, AD перпендикуляр к ребру АВ в плоскости АВС. Значит, ∠А1АD –линейныйуголданногодвугранногоугла. ∠А1АD = 90°, значит, двугранныйуголприребреАВравен 90°.
∠(АВВ1, АВС) = ∠(АВ) = ∠А1АВD= ∠А1АD = 90°.
Аналогично доказывается, что любые двугранные углы прямоугольного параллелепипеда прямые.
18. Вопрос: Понятие многогранника. Виды. Примеры.
Ответ: Если поверхности геометрических тел составлены из многоугольников, то такие тела называются многогранниками.
19. Вопрос: Правильная пирамида. Определение, Sбок.
Ответ: Пирамида называется правильной, если её основанием является правильный многоугольник, при этом вершина такой пирамиды проецируется в центр ее основания.
20. Вопрос: Симметрия в пространстве. Правильные многогранники.
Ответ: Точки А и A1 называются симметричными относительно точки О (центра симметрии), если О – середина отрезка AA1. Точка О симметрична сама себе.
Точки А и A1 называются симметричными относительно прямой а (ось симметрии) если прямая а проходит через середину отрезка AA1 и перпендикулярна ему. Каждая точка прямой a симметрична сама себе.
Точки А и A1 называются симметричными относительно плоскости a (плоскость симметрии) если плоскость a проходит через середину отрезка AA1 и перпендикулярна ему. Каждая точка плоскости a симметрична сама себе.
21. Вопрос: Уравнение сферы. Взаимное расположение сферы и плоскости.
Взаимное расположение сферы и плоскости:
1. Плоскость не пересекает сферу;
2. Плоскость касается сферы;
3. Плоскость пересекает сферу.
22. Вопрос: Касательная плоскость к сфере. Свойство с доказательством.
Ответ: Радиус сферы, проведённый в точку касания сферы и плоскости, перпендикулярен к касательной плоскости.
Свойство: Если радиус сферы перпендикулярен к плоскости, проходящей через его конец, лежащий на сфере, то эта плоскость является касательной к сфере.
Доказательство: Из условия свойства следует, что данный радиус является перпендикуляром, проведенным из центра сферы к данной плоскости. Поэтому расстояние от центра сферы до плоскости равно радиусу сферы, и, следовательно, сфера и плоскость имеют только одну общую точку. Это и означает, что данная плоскость является касательной к сфере.
23. Вопрос: Цилиндр. Основные элементы, Sбок, Sполн, Vцилиндра.
Ответ: Цилиндр – тело, которое состоит из двух кругов, лежащих в параллельных плоскостях и всех отрезков, соединяющих соответствующие линии этих кругов.
Sбок=2πrh, r– радиус, h– высота;
24. Вопрос: Конус. Основные элементы, Sбок, Sполн, Vконуса.
Ответ: Конусом называется тело, которое состоит из круга, точки и всех отрезков, соединяющих эту точку с точкой круга. Круг называется основанием, а отрезки – образующими. Точка называется вершиной, а высота конуса перпендикуляр, проведённый из вершины конуса к основанию.
25. Вопрос:Шар и сфера, основные элементы, Sсферы, Vшара.
Ответ: Сфера – геометрическое место точек в пространстве, равноудалённых от некоторой заданной точки (центра сферы). Расстояние между любой точкой сферы и её центром называется радиусом. Геометрическое тело, ограниченное сферой, называется шаром.
[spoiler title=”источники:”]
http://poisk-ru.ru/s16092t8.html
[/spoiler]