Похоже, вы используете блокировщик рекламы. Наш сайт существует и развивается
только за счет дохода от рекламы.
Пожалуйста, добавьте нас в исключения блокировщика.


на главную
Как найти координаты точки
Поддержать сайт![]()
Каждой точке координатной плоскости соответствуют две координаты.
Координаты точки на плоскости — это пара чисел, в которой на
первом месте стоит
абсцисса, а на
втором —
ордината точки.

Рассмотрим как в системе координат (на координатной плоскости):
- находить координаты точки;
- найти положение точки.
Чтобы найти координаты точки на плоскости, нужно опустить из этой точки
перпендикуляры на оси координат.
Точка пересечения с осью «x» называется абсциссой точки «А»,
а с осью y называется ординатой точки «А».

Обозначают координаты точки, как указано выше (·) A (2; 3).
Пример (·) A (2; 3) и (·) B (3; 2).

Запомните!
![]()
На первом месте записывают абсциссу (координату по оси «x»), а на втором —
ординату (координату по оси «y») точки.
Особые случаи расположения точек
- Если точка лежит на оси «Oy»,
то её абсцисса равна 0. Например,
точка С (0, 2). - Если точка лежит на оси «Ox», то её ордината равна 0.
Например,
точка F (3, 0). - Начало координат — точка O имеет координаты, равные нулю O (0,0).

- Точки любой прямой перпендикулярной оси абсцисс, имеют одинаковые абсциссы.

- Точки любой прямой перпендикулярной оси ординат, имеют одинаковые ординаты.

- Координаты любой точки, лежащей на оси абсцисс имеют вид (x, 0).

- Координаты любой точки, лежащей на оси ординат имеют вид (0, y).

Как найти положение точки по её координатам
Найти точку в системе координат можно двумя способами.
Первый способ
Чтобы определить положение точки по её координатам,
например, точки D (−4 , 2), надо:
- Отметить на оси «Ox», точку с координатой
«−4», и провести через неё прямую перпендикулярную оси «Ox». - Отметить на оси «Oy»,
точку с координатой 2, и провести через неё прямую перпендикулярную
оси «Oy». - Точка пересечения перпендикуляров (·) D — искомая точка.
У неё абсцисса равна «−4», а ордината равна 2.
Второй способ
Чтобы найти точку D (−4 , 2) надо:
- Сместиться по оси «x» влево на
4 единицы, так как у нас
перед 4
стоит «−». - Подняться из этой точки параллельно оси y вверх на 2 единицы, так
как у нас перед 2 стоит «+».

Чтобы быстрее и удобнее было находить координаты точек или строить точки по координатам на
листе формата A4 в клеточку, можно скачать и использовать
готовую систему координат на нашем сайте.
Ваши комментарии
Важно!

Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
- Главная
- Справочники
- Справочник по математике 5-9 класс
- Координаты на плоскости
- Координатная плоскость
Указать положение точки на плоскости можно с помощью координат. Для этого проведем на плоскости две перпендикулярные координатные прямые так, чтобы их начала отсчета совпадали.
Эти прямые называют осями координат, точку их пересечения О – начало отсчета.
Горизонтальная ось – ось абсцисс, обозначают буквой  , поэтому еще называют ось
, поэтому еще называют ось  , пишут:
, пишут: 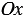 .
.
Вертикальная ось – ось ординат, обозначают буквой  , поэтому еще называют ось
, поэтому еще называют ось  , пишут:
, пишут: 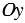 .
.
Оси  и
и  вместе образуют прямоугольную систему координат на плоскости. Плоскость, на которой выбрана система координат, называют координатной плоскостью.
вместе образуют прямоугольную систему координат на плоскости. Плоскость, на которой выбрана система координат, называют координатной плоскостью.
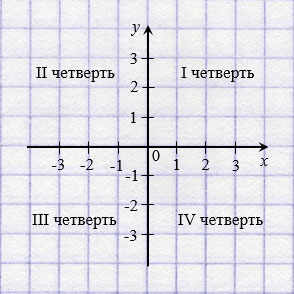
Координатные оси разбивают плоскость на четыре части, которые называют координатными четвертями и нумеруют так, как показано на рисунке ниже.
Отметим на координатной плоскости точку А. Проведем через нее прямую АВ, перпендикулярную оси абсцисс (АВ 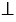
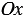 ), и прямую АС, перпендикулярную оси ординат (АС
), и прямую АС, перпендикулярную оси ординат (АС 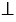
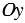 ).
).
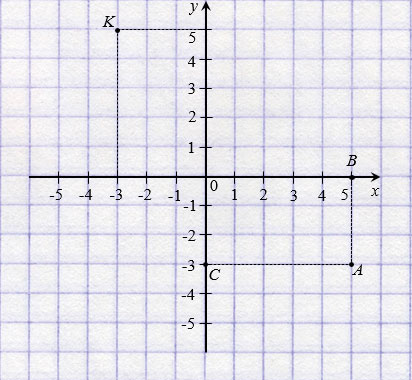
Точка В на оси  имеет координату 5, а точка С на оси
имеет координату 5, а точка С на оси  – координату
– координату  3 . Число 5 называют абсциссой точки А, число
3 . Число 5 называют абсциссой точки А, число  3 – ординатой точки А. Числа 5 и
3 – ординатой точки А. Числа 5 и  3 однозначно определяют положение точки А на координатной плоскости, поэтому их называют координатами точки А и записывают: А(5;
3 однозначно определяют положение точки А на координатной плоскости, поэтому их называют координатами точки А и записывают: А(5;  3).
3).
Обратите внимание, записывая координаты точки, абсциссу всегда ставят на первое место, а ординату – на второе. Если числа 5 и  3 поменять местами, то получим координаты другой точки – точки К(
3 поменять местами, то получим координаты другой точки – точки К( 3; 5) (смотри рисунок выше).
3; 5) (смотри рисунок выше).
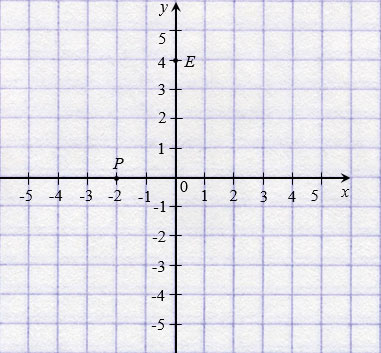
У начала координат абсцисса и ордината равны нулю, записывают так: О(0; 0). Если точка лежит на оси абсцисс, то ее ордината равна нулю, а если на оси ординат, то нулю равна ее абсцисса. На рисунке ниже: Р( 2; 0); Е(0; 4).
2; 0); Е(0; 4).
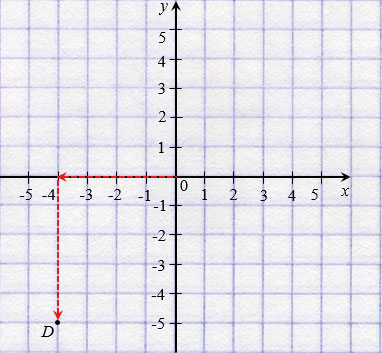
Чтобы попасть в точку D с координатами ( 4;
4;  5), нужно сначала пройти по оси
5), нужно сначала пройти по оси  от начала отсчета влево на 4 единицы, а потом – на 5 единиц вниз.
от начала отсчета влево на 4 единицы, а потом – на 5 единиц вниз.
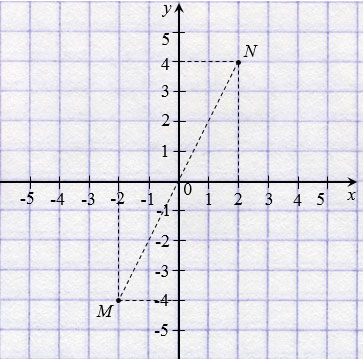
Две точки с противоположными абсциссами и ординатами симметричны относительно начала координат.
На рисунке ниже точки N(2; 4) и М( 2;
2;  4) симметричны относительно начала координат.
4) симметричны относительно начала координат.
Две точки, имеющие равные ординаты и противоположные абсциссы, симметричны относительно оси ординат.
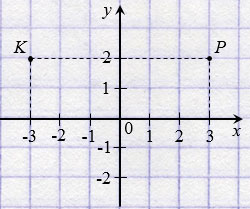
На рисунке ниже точки Р(3; 2) и К( 3; 2) симметричны относительно оси ординат.
3; 2) симметричны относительно оси ординат.
Две точки, имеющие равные абсциссы и противоположные ординаты, симметричны относительно оси абсцисс.
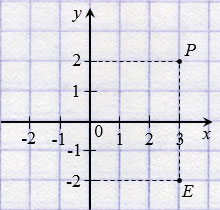
На рисунке ниже точки Р(3; 2) и Е(3;  2) симметричны относительно оси абсцисс.
2) симметричны относительно оси абсцисс.
Советуем посмотреть:
Перпендикулярные прямые
Осевая и центральная симметрии
Параллельные прямые
Координаты на плоскости
Правило встречается в следующих упражнениях:
6 класс
Номер 1308,
Мерзляк, Полонский, Якир, Учебник
Номер 1311,
Мерзляк, Полонский, Якир, Учебник
Номер 1339,
Мерзляк, Полонский, Якир, Учебник
Задание 1391,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1402,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1462,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1531,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1534,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1536,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1542,
Виленкин, Жохов, Чесноков, Шварцбург, Учебник
7 класс
Номер 776,
Мерзляк, Полонский, Якир, Учебник
Номер 819,
Мерзляк, Полонский, Якир, Учебник
Номер 824,
Мерзляк, Полонский, Якир, Учебник
Номер 825,
Мерзляк, Полонский, Якир, Учебник
Номер 830,
Мерзляк, Полонский, Якир, Учебник
Номер 840,
Мерзляк, Полонский, Якир, Учебник
Номер 858,
Мерзляк, Полонский, Якир, Учебник
Номер 926,
Мерзляк, Полонский, Якир, Учебник
Номер 991,
Мерзляк, Полонский, Якир, Учебник
Номер 1212,
Мерзляк, Полонский, Якир, Учебник
8 класс
Номер 6,
Мерзляк, Полонский, Якир, Учебник
Номер 322,
Мерзляк, Полонский, Якир, Учебник
Номер 327,
Мерзляк, Полонский, Якир, Учебник
Номер 330,
Мерзляк, Полонский, Якир, Учебник
Номер 333,
Мерзляк, Полонский, Якир, Учебник
Номер 343,
Мерзляк, Полонский, Якир, Учебник
Номер 353,
Мерзляк, Полонский, Якир, Учебник
Номер 356,
Мерзляк, Полонский, Якир, Учебник
Номер 366,
Мерзляк, Полонский, Якир, Учебник
Номер 375,
Мерзляк, Полонский, Якир, Учебник
Как найти координаты точки?

О чем эта статья:
3 класс, 4 класс, 9 класс, 11 класс, ЕГЭ/ОГЭ
Понятие системы координат
Координаты — это совокупность чисел, которые определяют положение какого-либо объекта на прямой, плоскости, поверхности или в пространстве. Например, координаты вашей квартиры тоже можно записать числами — они помогут понять, где именно находится тот дом, где вы живете. С точками на плоскости та же история.
Прямоугольная система координат — это система координат, которую изобрел математик Рене Декарт, ее еще называют «декартова система координат». Она представляет собой два взаимно перпендикулярных луча с началом отсчета в точке их пересечения.
Чтобы найти координаты, нужны ориентиры, от которых будет идти отсчет. На плоскости в этой роли выступят две числовые оси.
Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курсы по профильной математике.
Чертеж начинается с горизонтальной оси, которая называется осью абсцисс и обозначается латинской буквой x (икс). Записывают ось так: Ox. Положительное направление оси абсцисс обозначается стрелкой слева направо.
Затем проводят вертикальную ось, которая называется осью ординат и обозначается y (игрек). Записывают ось Oy. Положительное направление оси ординат показываем стрелкой снизу вверх.
Оси взаимно перпендикулярны, а значит угол между ними равен 90°. Точка пересечения является началом отсчета для каждой из осей и обозначается так: O. Начало координат делит оси на две части: положительную и отрицательную.
- Координатные оси — это прямые, образующие систему координат.
- Ось абсцисс Ox — горизонтальная ось.
- Ось ординат Oy — вертикальная ось.
- Координатная плоскость — плоскость, в которой находится система координат. Обозначается так: x0y.
- Единичный отрезок — величина, которая принимается за единицу при геометрических построениях. В декартовой системе координат единичный отрезок отмечается на каждой из осей. Длина отрезка показывает сколько раз единичный отрезок и его части укладываются в данном отрезке.
Оси координат делят плоскость на четыре угла — четыре координатные четверти.
У каждой из координатных четвертей есть свой номер и обозначение в виде римской цифры. Отсчет идет против часовой стрелки:
- верхний правый угол — первая четверть I;
- верхний левый угол — вторая четверть II;
- нижний левый угол — третья четверть III;
- нижний правый угол — четвертая четверть IV;
- Если обе координаты положительны, то точка находится в первой четверти координатной плоскости.
- Если координата х отрицательная, а координата у положительная, то точка находится во второй четверти.
- Если обе координаты отрицательны, то число находится в третьей четверти.
- Если координата х положительная, а координата у отрицательная, то точка лежит в четвертой четверти.
Определение координат точки
Каждой точке координатной плоскости соответствуют две координаты.
Точка пересечения с осью Ох называется абсциссой точки А, а с осью Оу называется ординатой точки А.
Чтобы узнать координаты точки на плоскости, нужно опустить от точки перпендикуляр на каждую ось и посчитать количество единичных отрезков от нулевой отметки до опущенного перпендикуляра.
Координаты точки на плоскости записывают в скобках, первая по оси Ох, вторая по оси Оу.
Смотрим на график и фиксируем: A (1; 2) и B (2; 3).
Особые случаи расположения точек
В геометрии есть несколько особых случаев расположения точек. Лучше их запомнить, чтобы без запинки решать задачки. Вот они:
- Если точка лежит на оси Oy, то ее абсцисса равна 0. Например,
точка С (0, 2). - Если точка лежит на оси Ox, то ее ордината равна 0. Например,
точка F (3, 0). - Начало координат — точка O. Ее координаты равны нулю: O (0,0).
- Точки любой прямой, которая перпендикулярна оси абсцисс, имеют одинаковые абсциссы.
- Точки любой прямой, которая перпендикулярна оси ординат, имеют одинаковые ординаты.
- Если точка лежит на оси абсцисс, то ее координаты будут иметь вид: (x, 0).
- Если точка лежит на оси ординат, то ее координаты будут иметь вид: (0, y).
Способы нахождения точки по её координатам
Чтобы узнать, как найти точку в системе координат, можно использовать один из двух способов.
Способ первый. Как определить положение точки D по её координатам (-4, 2):
- Отметить на оси Ox, точку с координатой -4, и провести через нее прямую перпендикулярную оси Ox.
- Отметить на оси Oy, точку с координатой 2, и провести через нее прямую перпендикулярную оси Oy.
- Точка пересечения перпендикуляров и есть искомая точка D. Ее абсцисса равна -4, а ордината — 2.
Способ второй. Как определить положение точки D (-4, 2):
- Сместить прямую по оси Ox влево на 4 единицы, так как у нас
перед 4 стоит знак минус. - Подняться из этой точки параллельно оси Oy вверх на 2 единицы, так как у нас перед 2 стоит знак плюс.
Чтобы легко и быстро находить координаты точек или строить точки по координатам, скачайте готовую систему координат и храните ее в учебнике:
Урок на тему “Метод областей”. 11-й класс
Класс: 11
Презентация к уроку
«Считай несчастным тот день и тот час,
вк оторый ты не усвоил ничего нового и ничего
не прибавил к своему образованию».
Я.А Коменский
Тип урока: урок-обобщения и систематизации знаний учащихся.
Цели урока:
- создать условия для систематизации, обобщения знаний и умений обучающихся по применению различных методов решения неравенств;
- воспитание нравственных качеств личности, таких как ответственность, аккуратность, дисциплинированность;
- воспитание культуры общения.
- развитие у учащихся умений выделять главное, существенное в изучаемом материале, обобщать изучаемые факты, логически излагать свои мысли;
- развитие психических процессов, таких как память, внимание, мышление, а также наблюдательности, активности, самостоятельности.
Задачи:
- формировать умение классифицировать неравенства по методам решения;
- закрепить навыки решения неравенств различными методами;
- отрабатывать навыки самоконтроля с целью подготовки к итоговой аттестации;
- воспитывать чувство коллективизма, ответственности.
Оборудование:
- Компьютер
- Мультимедийный проектор, звуковые колонки
- Программа «MicrosoftPowerPoint 2003»
Методы обучения:
- частично-поисковый метод,
- репродуктивный,
- обобщающий.
План урока.
План урока рассчитан на 2 учебных часа (90 мин)
- Организационный момент.
- Вступительное слово учителя.
- Повторение теории.
- Решение неравенств различными методами (варианты ЕГЭ)
- Самостоятельная работа с самопроверкой.
- Итог урока.
- Рефлексия.
Ход урока
I. Организационный момент
«То, что мы знаем, – ограничено, а то чего
мы не знаем, – бесконечно».
Приветствие учащихся.Ученики под руководством учителя проверяют наличие дневника, рабочей тетради, инструментов, отмечаются отсутствующие, проверяется готовность класса к уроку, учитель психологически настраивает детей на работу на уроке.Формулируется тема и цели урока. Знакомство с этапами урока.
II. Вступительное слово учителя
Для успешного исследования многих задач повышенной сложности полезно уметь строить не только графики функций, но и множества точек плоскости, координаты которых удовлетворяют заданным уравнениям, неравенствам или их системам. Эффективно строить на координатной плоскости такие множества позволяет метод областей. Это весьма полезный прием можно назвать обобщающим методом интервалов.
Метод областей особенно полезен при решении уравнений или неравенств с параметром. Применение метода интервалов в таких случаях затруднено, так как взаимное расположение точек, отмечаемых на числовой оси, может изменяться в зависимости от значений параметра. Это означает необходимость сравнивать их между собой и рассматривать различные случаи. В этой ситуации нам может помочь метод областей.

III. Повторение теории
Метод интервалов на координатной прямой и метод областей на координатной плоскости.
Точка х=а разбивает числовую прямую на два множества, задаваемые неравенствами x a

Всякая действительная кривая на координатной плоскости, заданная уравнением F(x;y)=0 разбивает координатную плоскость на конечное число областей, в каждой из которых для всех точек области выполняется только одно из неравенств: F(x;y)>0 или F(x;y) kx+p или y c

Решением системы неравенств с двумя переменными являются координаты точек пересечения множеств, удовлетворяющих одному из неравенств системы

Уравнение y= k(x-x0) + y0 задает множество прямых, проходящих через точку с координатами (x0,y0).
При изменении значений параметра прямые y= k(x-x0) + y0 «поворачиваются» вокруг данной точки. При увеличении параметра прямая поворачивается «против часовой стрелки», при уменьшении – «по часовой стрелке».

Уравнение y=kx+p при фиксированном значении параметра k = k0 задает семейство прямых, параллельных прямой y=kx+p проходящей через начало координат

Если точка с координатами  лежит «выше» прямой заданной уравнением y=kx+p, то ее координаты удовлетворяют неравенству , если же точка лежит «ниже», то неравенству
лежит «выше» прямой заданной уравнением y=kx+p, то ее координаты удовлетворяют неравенству , если же точка лежит «ниже», то неравенству

Задача
Пусть M – множество точек плоскости с координатами (x; y) таких, что числа x, y, 6-2x являются сторонами некоторого треугольника. Найдите его площадь.
Если три числа являются сторонами некоторого треугольника, то это числа положительные и каждое из них меньше суммы двух других чисел. Поэтому, координаты точек, удовлетворяющих условию задачи, будут задаваться системой линейных неравенств с двумя переменными:

Геометрическое место точек на плоскости
Множество точек плоскости, равноудаленных от данной точки на расстояние, равное положительной величине R, называется окружностью.
Уравнением окружности называется уравнение вида

Множество точек, удаленных от данной точки на положительное расстояние, меньшее R, называется кругом. Круг задается неравенством

Множество точек, лежащих вне круга, задается неравенством


Геометрическое место точек на плоскости
Квадратным трехчленом относительно переменной, называется выражение

Графиком квадратного трехчлена является кривая, называемая параболой.
Расположение параболы зависит от знака старшего коэффициента и знака дискриминанта квадратного трехчлена

Парабола разбивает плоскость на часть, лежащую «над» параболой и лежащую «под» параболой. Первая задается неравенством

, а вторая – 

Метод областей при решении задач с параметрами
1. Свойства функций
2. Графический прием
Параметр – «равноправная» переменная Þ отведем ему координатную ось, т.е. задачу с параметром будем рассматривать как функцию f(x ;a) >0
Общие признаки задач подходящих под рассматриваемый метод:
- В задаче дан один параметр а и одна переменная х
- Они образуют некоторые аналитические выражения F(x;a), G(x;a)
- Графики уравнений F(x;a)=0,G(x;a)=0 строятся несложно
- Строим графический образ
- Пересекаем полученный график прямыми, перпендикулярными параметрической оси
- «Считываем» нужную информацию
Обобщенный метод областей («переход» метода интервалов с прямой на плоскость)
Неравенства с одной переменной
Неравенства с двумя переменной
- ОДЗ
- Граничные линии
- Координатная плоскость
- Знаки в областях
- Ответ по рисунку
IV. Решение неравенств
Пример №1
Найти все значения параметра p, при каждом из которых множество решений неравенства не содержит ни одного решения неравенства
Применим обобщенный метод областей.
1. Построим граничные линии
2. Определяем знаки в полученных областях и получаем решение 1 неравенства
3. Из полученного множества исключим решение 

Пример № 2
При каких значениях параметра а система неравенств не имеет решений.
1. Рассмотрим 1 неравенство и получаем
2. Рассмотрим 2 неравенство и получаем
3. Заметим, что исходная система неравенств равносильна системе:
4. Изобразим систему неравенств в виде плоской фигуры на координатной плоскости. Для этого введём параметрическую плоскость Oax

5. Мы получили плоскую фигуру, множество точек которой является решением системы.
Таким образом, отвечая на вопрос задачи, решений системы нет при

Пример №3
При каких положительных значениях параметраа система уравнений имеет ровно 4 решения.
1. Запишем систему в следующем виде:
2. Построим график 1 уравнения.
3. Построим график 2 уравнения – семейство окружностей с центром в точке (2; 0) и радиусом а.

Ответ: при 
V. Самостоятельная работа с самопроверкой
На координатной плоскости изобразите множество точек, удовлетворяющих неравенству

1. ОДЗ: 
2. Строим граничные линии:

3. Они разбивают плоскость на восемь областей, определяя знаки подстановкой в отдельных точках, получаем решение.

Ответ: заштрихованная область на рисунке
На координатной плоскости изобразите множество точек, координаты которых удовлетворяют неравенству

- На координатной плоскости нарисуем линии определённые равенствами x-y=0 и xy-1=0, которые разбивают плоскость на несколько областей.
- Определяем знаки в областях.

Ответ: заштрихованная область на рисунке
VI. Итог урока
(подвожу итог, комментирую работу учащихся, сообщаю оценки за урок.)
VII. Рефлексия.
Ребята. На этом урок окончен. Спасибо за урок!
Литература.
- П. И. Горнштейн, В.Б.Полонский, М.С.Якир. Задачи с параметрами. 3-е издание, дополненное и переработанное. — М.: Илскса, Харьков: Гимназия, 2005,- 328 с.
- Черкасов О. Ю., Якушев А. Г. Математика: интенсивный курс подготовки к экзамену.
- Экзаменационные материалы для подготовки к ЕГЭ-2007. Математика. М.: ООО «РУСТЕСТ», 2006. – 108с. Сост. – Клово А.Г.
- Задачи с параметром и другие сложные задачи. Козко А.И., Чирский В.Г. М.: МЦНМО, 2007. – 296с.
- ЕГЭ 2011. Математика. Задача С5. Козко А.И., Панферов В.С., Сергеев И.Н., Чирский В.Г.
Координаты точки пересечения двух прямых – примеры нахождения
Для того, чтобы решить геометрическую задачу методом координат, необходима точка пересечения, координаты которой используются при решении. Возникает ситуация, когда требуется искать координаты пересечения двух прямых на плоскости или определить координаты тех же прямых в пространстве. Данная статья рассматривает случаи нахождения координат точек, где пересекаются заданные прямые.
Точка пересечения двух прямых – определение
Необходимо дать определение точкам пересечения двух прямых.
Раздел взаимного расположения прямых на плоскости показывает, что они могут совпадать , быть параллельными, пересекаться в одной общей точке или скрещивающимися. Две прямые, находящиеся в пространстве, называют пересекающимися, если они имеют одну общую точку.
Определение точки пересечения прямых звучит так:
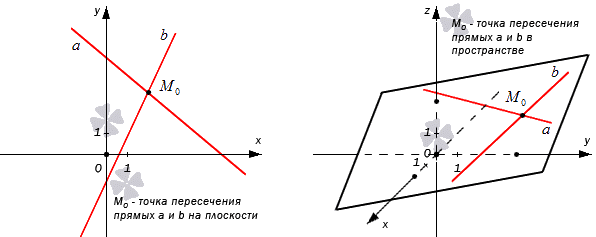
Точка, в которой пересекаются две прямые, называют их точкой пересечения. Иначе говоря, что точка пересекающихся прямых и есть точка пересечения.
Рассмотрим на рисунке, приведенном ниже.
Нахождение координат точки пересечения двух прямых на плоскости
Перед нахождением координат точки пересечения двух прямых, необходимо рассмотреть предлагаемый ниже пример.
Если на плоскости имеется система координат О х у , то задаются две прямые a и b . Прямой a соответствует общее уравнение вида A 1 x + B 1 y + C 1 = 0 , для прямой b – A 2 x + B 2 y + C 2 = 0 . Тогда M 0 ( x 0 , y 0 ) является некоторой точкой плоскости необходимо выявить , будет ли точка М 0 являться точкой пересечения этих прямых.
Чтобы решить поставленную задачу, необходимо придерживаться определения. Тогда прямые должны пересекаться в точке, координаты которой являются решением заданных уравнений A 1 x + B 1 y + C 1 = 0 и A 2 x + B 2 y + C 2 = 0 . Значит, координаты точки пересечения подставляются во все заданные уравнения. Если они при подстановке дают верное тождество, тогда M 0 ( x 0 , y 0 ) считается их точкой пересечения.
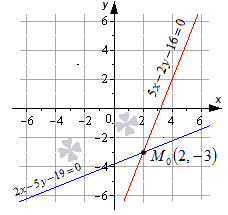
Даны две пересекающиеся прямые 5 x – 2 y – 16 = 0 и 2 x – 5 y – 19 = 0 . Будет ли точка М 0 с координатами ( 2 , – 3 ) являться точкой пересечения.
Чтобы пересечение прямых было действительным, необходимо, чтобы координаты точки М 0 удовлетворяли уравнениям прямых. Это проверяется при помощи их подстановки. Получаем, что
5 · 2 – 2 · ( – 3 ) – 16 = 0 ⇔ 0 = 0 2 · 2 – 5 · ( – 3 ) – 19 = 0 ⇔ 0 = 0
Оба равенства верные, значит М 0 ( 2 , – 3 ) является точкой пересечения заданных прямых.
Изобразим данное решение на координатной прямой рисунка, приведенного ниже.
Ответ: заданная точка с координатами ( 2 , – 3 ) будет являться точкой пересечения заданных прямых.
Пересекутся ли прямые 5 x + 3 y – 1 = 0 и 7 x – 2 y + 11 = 0 в точке M 0 ( 2 , – 3 ) ?
Для решения задачи необходимо подставить координаты точки во все уравнения. Получим, что
5 · 2 + 3 · ( – 3 ) – 1 = 0 ⇔ 0 = 0 7 · 2 – 2 · ( – 3 ) + 11 = 0 ⇔ 31 = 0
Второе равенство не является верным, значит, что заданная точка не принадлежит прямой 7 x – 2 y + 11 = 0 . Отсюда имеем, что точка М 0 не точка пересечения прямых.
Чертеж наглядно показывает, что М 0 – это не точка пересечения прямых. Они имеют общую точку с координатами ( – 1 , 2 ) .
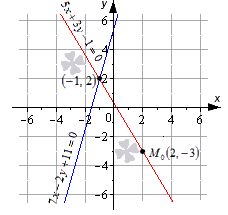
Ответ: точка с координатами ( 2 , – 3 ) не является точкой пересечения заданных прямых.
Переходим к нахождению координат точек пересечения двух прямых при помощи заданных уравнений на плоскости.
Задаются две пересекающиеся прямые a и b уравнениями вида A 1 x + B 1 y + C 1 = 0 и A 2 x + B 2 y + C 2 = 0 , расположенных в О х у . При обозначении точки пересечения М 0 получим, что следует продолжить поиск координат по уравнениям A 1 x + B 1 y + C 1 = 0 и A 2 x + B 2 y + C 2 = 0 .
Из определения очевидно, что М 0 является общей точкой пересечения прямых. В этом случае ее координаты должны удовлетворять уравнениям A 1 x + B 1 y + C 1 = 0 и A 2 x + B 2 y + C 2 = 0 . Иными словами это и есть решение полученной системы A 1 x + B 1 y + C 1 = 0 A 2 x + B 2 y + C 2 = 0 .
Значит, для нахождения координат точки пересечения , необходимо все уравнения добавить в систему и решить ее.
Заданы две прямые x – 9 y + 14 = 0 и 5 x – 2 y – 16 = 0 на плоскости. необходимо найти их пересечение.
Данные по условию уравнения необходимо собрать в систему, после чего получим x – 9 y + 14 = 0 5 x – 2 y – 16 = 0 . Чтобы решить его, разрешается первое уравнение относительно x , подставляется выражение во второе:
x – 9 y + 14 = 0 5 x – 2 y – 16 = 0 ⇔ x = 9 y – 14 5 x – 2 y – 16 = 0 ⇔ ⇔ x = 9 y – 14 5 · 9 y – 14 – 2 y – 16 = 0 ⇔ x = 9 y – 14 43 y – 86 = 0 ⇔ ⇔ x = 9 y – 14 y = 2 ⇔ x = 9 · 2 – 14 y = 2 ⇔ x = 4 y = 2
Получившиеся числа являются координатами, которые необходимо было найти.
Ответ: M 0 ( 4 , 2 ) является точкой пересечения прямых x – 9 y + 14 = 0 и 5 x – 2 y – 16 = 0 .
Поиск координат сводится к решению системы линейных уравнений. Если по условию дан другой вид уравнения, тогда следует привести его к нормальному виду.
Определить координаты точек пересечения прямых x – 5 = y – 4 – 3 и x = 4 + 9 · λ y = 2 + λ , λ ∈ R .
Для начала необходимо привести уравнения к общему виду. Тогда получаем, что x = 4 + 9 · λ y = 2 + λ , λ ∈ R преобразуется таким образом:
x = 4 + 9 · λ y = 2 + λ ⇔ λ = x – 4 9 λ = y – 2 1 ⇔ x – 4 9 = y – 2 1 ⇔ ⇔ 1 · ( x – 4 ) = 9 · ( y – 2 ) ⇔ x – 9 y + 14 = 0
После чего беремся за уравнение канонического вида x – 5 = y – 4 – 3 и преобразуем. Получаем, что
x – 5 = y – 4 – 3 ⇔ – 3 · x = – 5 · y – 4 ⇔ 3 x – 5 y + 20 = 0
Отсюда имеем, что координаты – это точка пересечения
x – 9 y + 14 = 0 3 x – 5 y + 20 = 0 ⇔ x – 9 y = – 14 3 x – 5 y = – 20
Применим метод Крамера для нахождения координат:
∆ = 1 – 9 3 – 5 = 1 · ( – 5 ) – ( – 9 ) · 3 = 22 ∆ x = – 14 – 9 – 20 – 5 = – 14 · ( – 5 ) – ( – 9 ) · ( – 20 ) = – 110 ⇒ x = ∆ x ∆ = – 110 22 = – 5 ∆ y = 1 – 14 3 – 20 = 1 · ( – 20 ) – ( – 14 ) · 3 = 22 ⇒ y = ∆ y ∆ = 22 22 = 1
Ответ: M 0 ( – 5 , 1 ) .
Имеется еще способ для нахождения координат точки пересечения прямых, находящихся на плоскости. Он применим, когда одна из прямых задается параметрическими уравнениями, имеющими вид x = x 1 + a x · λ y = y 1 + a y · λ , λ ∈ R . Тогда вместо значения x подставляется x = x 1 + a x · λ и y = y 1 + a y · λ , где получим λ = λ 0 , соответствующее точке пересечения, имеющей координаты x 1 + a x · λ 0 , y 1 + a y · λ 0 .
Определить координаты точки пересечения прямой x = 4 + 9 · λ y = 2 + λ , λ ∈ R и x – 5 = y – 4 – 3 .
Необходимо выполнить подстановку в x – 5 = y – 4 – 3 выражением x = 4 + 9 · λ , y = 2 + λ , тогда получим:
4 + 9 · λ – 5 = 2 + λ – 4 – 3
При решении получаем, что λ = – 1 . Отсюда следует, что имеется точка пересечения между прямыми x = 4 + 9 · λ y = 2 + λ , λ ∈ R и x – 5 = y – 4 – 3 . Для вычисления координат необходимо подставить выражение λ = – 1 в параметрическое уравнение. Тогда получаем, что x = 4 + 9 · ( – 1 ) y = 2 + ( – 1 ) ⇔ x = – 5 y = 1 .
Ответ: M 0 ( – 5 , 1 ) .
Для полного понимания темы, необходимо знать некоторые нюансы.
Предварительно необходимо понять расположение прямых. При их пересечении мы найдем координаты, в других случаях решения существовать не будет. Чтобы не делать эту проверку, можно составлять систему вида A 1 x + B 1 y + C 1 = 0 A 2 x + B 2 + C 2 = 0 При наличии решения делаем вывод о том, что прямые пересекаются. Если решение отсутствует, то они параллельны. Когда система имеет бесконечное множество решений, тогда говорят, что они совпадают.
Даны прямые x 3 + y – 4 = 1 и y = 4 3 x – 4 . Определить, имеют ли они общую точку.
Упрощая заданные уравнения, получаем 1 3 x – 1 4 y – 1 = 0 и 4 3 x – y – 4 = 0 .
Следует собрать уравнения в систему для последующего решения:
1 3 x – 1 4 y – 1 = 0 1 3 x – y – 4 = 0 ⇔ 1 3 x – 1 4 y = 1 4 3 x – y = 4
Отсюда видно, что уравнения выражаются друг через друга, тогда получим бесконечное множество решений. Тогда уравнения x 3 + y – 4 = 1 и y = 4 3 x – 4 определяют одну и ту же прямую. Поэтому нет точек пересечения.
Ответ: заданные уравнения определяют одну и ту же прямую.
Найти координаты точки пересекающихся прямых 2 x + ( 2 – 3 ) y + 7 = 0 и 2 3 + 2 x – 7 y – 1 = 0 .
По условию возможно такое, прямые не будут пересекаться. Необходимо составить систему уравнений и решать. Для решения необходимо использовать метод Гаусса, так как с его помощью есть возможность проверить уравнение на совместимость. Получаем систему вида:
2 x + ( 2 – 3 ) y + 7 = 0 2 ( 3 + 2 ) x – 7 y – 1 = 0 ⇔ 2 x + ( 2 – 3 ) y = – 7 2 ( 3 + 2 ) x – 7 y = 1 ⇔ ⇔ 2 x + 2 – 3 y = – 7 2 ( 3 + 2 ) x – 7 y + ( 2 x + ( 2 – 3 ) y ) · ( – ( 3 + 2 ) ) = 1 + – 7 · ( – ( 3 + 2 ) ) ⇔ ⇔ 2 x + ( 2 – 3 ) y = – 7 0 = 22 – 7 2
Получили неверное равенство, значит система не имеет решений. Делаем вывод, что прямые являются параллельными. Точек пересечения нет.
Второй способ решения.
Для начала нужно определить наличие пересечения прямых.
n 1 → = ( 2 , 2 – 3 ) является нормальным вектором прямой 2 x + ( 2 – 3 ) y + 7 = 0 , тогда вектор n 2 → = ( 2 ( 3 + 2 ) , – 7 – нормальный вектор для прямой 2 3 + 2 x – 7 y – 1 = 0 .
Необходимо выполнить проверку коллинеарности векторов n 1 → = ( 2 , 2 – 3 ) и n 2 → = ( 2 ( 3 + 2 ) , – 7 ) . Получим равенство вида 2 2 ( 3 + 2 ) = 2 – 3 – 7 . Оно верное, потому как 2 2 3 + 2 – 2 – 3 – 7 = 7 + 2 – 3 ( 3 + 2 ) 7 ( 3 + 2 ) = 7 – 7 7 ( 3 + 2 ) = 0 . Отсюда следует, что векторы коллинеарны. Значит, прямые являются параллельными и не имеют точек пересечения.
Ответ: точек пересечения нет, прямые параллельны.
Найти координаты пересечения заданных прямых 2 x – 1 = 0 и y = 5 4 x – 2 .
Для решения составляем систему уравнений. Получаем
2 x – 1 = 0 5 4 x – y – 2 = 0 ⇔ 2 x = 1 5 4 x – y = 2
Найдем определитель основной матрицы. Для этого 2 0 5 4 – 1 = 2 · ( – 1 ) – 0 · 5 4 = – 2 . Так как он не равен нулю, система имеет 1 решение. Отсюда следует, что прямые пересекаются. Решим систему для нахождения координат точек пересечения:
2 x = 1 5 4 x – y = 2 ⇔ x = 1 2 4 5 x – y = 2 ⇔ x = 1 2 5 4 · 1 2 – y = 2 ⇔ x = 1 2 y = – 11 8
Получили, что точка пересечения заданных прямых имеет координаты M 0 ( 1 2 , – 11 8 ) .
Ответ: M 0 ( 1 2 , – 11 8 ) .
Нахождения координат точки пересечения двух прямых в пространстве
Таким же образом находятся точки пересечения прямых пространства.
Когда заданы прямые a и b в координатной плоскости О х у z уравнениями пересекающихся плоскостей, то имеется прямая a , которая может быть определена при помощи заданной системы A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 1 = 0 а прямая b – A 3 x + B 3 y + C 3 z + D 3 = 0 A 4 x + B 4 y + C 4 z + D 4 = 0 .
Когда точка М 0 является точкой пересечения прямых, тогда ее координаты должны быть решениями обоих уравнений. Получим линейные уравнения в системе:
A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 A 3 x + B 3 y + C 3 z + D 3 = 0 A 4 x + B 4 y + C 4 z + D 4 = 0
Рассмотрим подобные задания на примерах.
Найти координаты точки пересечения заданных прямых x – 1 = 0 y + 2 z + 3 = 0 и 3 x + 2 y + 3 = 0 4 x – 2 z – 4 = 0
Составляем систему x – 1 = 0 y + 2 z + 3 = 0 3 x + 2 y + 3 = 0 4 x – 2 z – 4 = 0 и решим ее. Чтобы найти координаты, необходимо решать через матрицу. Тогда получим основную матрицу вида A = 1 0 0 0 1 2 3 2 0 4 0 – 2 и расширенную T = 1 0 0 1 0 1 2 – 3 4 0 – 2 4 . Определяем ранг матрицы по Гауссу.
1 = 1 ≠ 0 , 1 0 0 1 = 1 ≠ 0 , 1 0 0 0 1 2 3 2 0 = – 4 ≠ 0 , 1 0 0 1 0 1 2 – 3 3 2 0 – 3 4 0 – 2 4 = 0
Отсюда следует, что ранг расширенной матрицы имеет значение 3 . Тогда система уравнений x – 1 = 0 y + 2 z + 3 = 0 3 x + 2 y + 3 = 0 4 x – 27 – 4 = 0 в результате дает только одно решение.
Базисный минор имеет определитель 1 0 0 0 1 2 3 2 0 = – 4 ≠ 0 , тогда последнее уравнение не подходит. Получим, что x – 1 = 0 y + 2 z + 3 = 0 3 x + 2 y + 3 = 0 4 x – 2 z – 4 = 0 ⇔ x = 1 y + 2 z = – 3 3 x + 2 y – 3 . Решение системы x = 1 y + 2 z = – 3 3 x + 2 y = – 3 ⇔ x = 1 y + 2 z = – 3 3 · 1 + 2 y = – 3 ⇔ x = 1 y + 2 z = – 3 y = – 3 ⇔ ⇔ x = 1 – 3 + 2 z = – 3 y = – 3 ⇔ x = 1 z = 0 y = – 3 .
Значит, имеем, что точка пересечения x – 1 = 0 y + 2 z + 3 = 0 и 3 x + 2 y + 3 = 0 4 x – 2 z – 4 = 0 имеет координаты ( 1 , – 3 , 0 ) .
Ответ: ( 1 , – 3 , 0 ) .
Система вида A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 A 3 x + B 3 y + C 3 z + D 3 = 0 A 4 x + B 4 y + C 4 z + D 4 = 0 имеет только одно решение. Значит, прямые a и b пересекаются.
В остальных случаях уравнение не имеет решения, то есть и общих точек тоже. То есть невозможно найти точку с координатами, так как ее нет.
Поэтому система вида A 1 x + B 1 y + C 1 z + D 1 = 0 A 2 x + B 2 y + C 2 z + D 2 = 0 A 3 x + B 3 y + C 3 z + D 3 = 0 A 4 x + B 4 y + C 4 z + D 4 = 0 решается методом Гаусса. При ее несовместимости прямые не являются пересекающимися. Если решений бесконечное множество, то они совпадают.
Можно произвести решение при помощи вычисления основного и расширенного ранга матрицы, после чего применить теорему Кронекера-Капелли. Получим одно, множество или полное отсутствие решений.
Заданы уравнения прямых x + 2 y – 3 z – 4 = 0 2 x – y + 5 = 0 и x – 3 z = 0 3 x – 2 y + 2 z – 1 = 0 . Найти точку пересечения.
Для начала составим систему уравнений. Получим, что x + 2 y – 3 z – 4 = 0 2 x – y + 5 = 0 x – 3 z = 0 3 x – 2 y + 2 z – 1 = 0 . решаем ее методом Гаусса:
1 2 – 3 4 2 – 1 0 – 5 1 0 – 3 0 3 – 2 2 1
1 2 – 3 4 0 – 5 6 – 13 0 – 2 0 – 4 0 – 8 11 – 11
1 2 – 3 4 0 – 5 6 – 13 0 0 – 12 5 6 5 0 0 7 5 – 159 5
1 2 – 3 4 0 – 5 6 – 13 0 0 – 12 5 6 5 0 0 0 311 10
Очевидно, что система не имеет решений, значит прямые не пересекаются. Точки пересечения нет.
Ответ: нет точки пересечения.
Если прямые заданы при помощи кононических или параметрических уравнений, нужно привести к виду уравнений пересекающихся плоскостей, после чего найти координаты.
Заданы две прямые x = – 3 – λ y = – 3 · λ z = – 2 + 3 · λ , λ ∈ R и x 2 = y – 3 0 = z 5 в О х у z . Найти точку пересечения.
Задаем прямые уравнениями двух пересекающихся плоскостей. Получаем, что
x = – 3 – λ y = – 3 · λ z = – 2 + 3 · λ ⇔ λ = x + 3 – 1 λ = y – 3 λ = z + 2 3 ⇔ x + 3 – 1 = y – 3 = z + 2 3 ⇔ ⇔ x + 3 – 1 = y – 3 x + 3 – 1 = z + 2 3 ⇔ 3 x – y + 9 = 0 3 x + z + 11 = 0 x 2 = y – 3 0 = z 5 ⇔ y – 3 = 0 x 2 = z 5 ⇔ y – 3 = 0 5 x – 2 z = 0
Находим координаты 3 x – y + 9 = 0 3 x + z + 11 = 0 y – 3 = 0 5 x – 2 z = 0 , для этого посчитаем ранги матрицы. Ранг матрицы равен 3 , а базисный минор 3 – 1 0 3 0 1 0 1 0 = – 3 ≠ 0 , значит, что из системы необходимо исключить последнее уравнение. Получаем, что
3 x – y + 9 = 0 3 x + z + 11 = 0 y – 3 = 0 5 x – 2 z = 0 ⇔ 3 x – y + 9 = 0 3 x + z + 11 = 0 y – 3 = 0
Решим систему методом Крамер. Получаем, что x = – 2 y = 3 z = – 5 . Отсюда получаем, что пересечение заданных прямых дает точку с координатами ( – 2 , 3 , – 5 ) .
[spoiler title=”источники:”]
http://urok.1sept.ru/articles/664756
http://zaochnik.com/spravochnik/matematika/prjamaja-ploskost/koordinaty-tochki-peresechenija-dvuh-prjamyh-prime/
[/spoiler]
Содержание:
Система координат в пространстве
Декартова система координат в пространстве
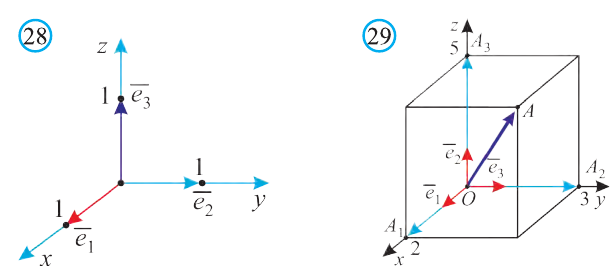
Вы познакомились с декартовой системой координат на плоскости в предыдущих классах. Систему координат в пространстве введём аналогично тому, как это было сделано на плоскости. Рассмотрим три взаимно перпендикулярных оси Ох, Оу и Оz, пересекающихся в точке О, являющейся началом координат. Через каждую пару этих прямых проведём плоскости Оху, 0xz и Оуz (рис. 1). Таким образом вводится система координат в пространстве, при этом
точку О – называют началом координат, прямые Ох, Оу и Оz — осями координат, Ох – ось абсцисс, Оу – ось ординат и Оz – ось аппликат, плоскости Оху, Оуz и Охz – координатными плоскостями.
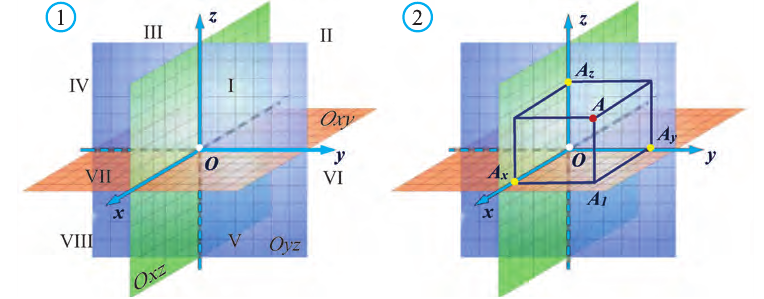
Координатные плоскости делят пространство на 8 октант (получетвертей) (рис. 1).
Пусть в пространстве задана произвольная точка А. Через эту точку проведём плоскости, перпендикулярные плоскостям Охz, Оуz и Охz (рис. 2). Одна из этих плоскостей пересечёт ось Ох в точке Ах.
Координату Ах на оси Ох называют координатой х или абсциссой точки А.
Аналогично определяют у – координату (ординату) и z- координату (аппликату) точки А.
Координаты точки А записывают в виде А (х; у; z) или короче (х; у; z). Точки, изображённые на рисунке 3, имеют следующие координаты: А (0; 5; 0), B (4; 0; 0), М (0; 5; 4), К (2; 3; 4), Р (-2; 3; -4). 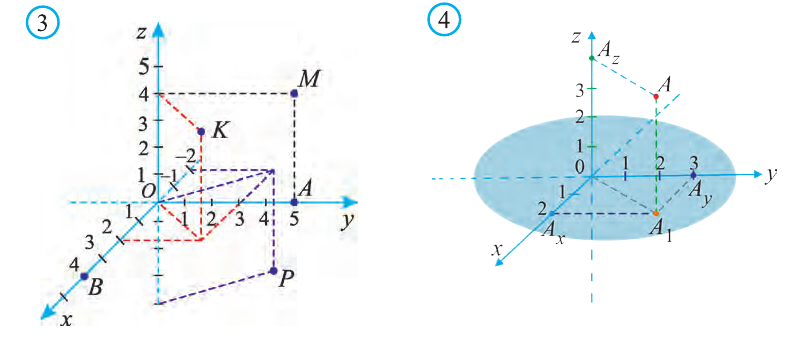
Пример:
Пусть в пространстве в декартовой системе координат
задана точка А (2; 3; 4). Где она расположена?
Решение:
От начала координат в положительном направлении осей Ох и Оу отложим отрезки ОАх = 2 и ОАу = 3 (рис. 4).
Через точку Ах проведём прямую, лежащую в плоскости Оху и параллельную оси Оу. А через точку Аy проведём прямую, лежащую в плоскости Оху и параллельную оси Ох. Точку пересечения этих прямых обозначим A1 . Через точку A1 проведём прямую, перпендикулярную плоскости Оху и на ней в положительном направлении Oz отложим отрезок АА1 = 4. Тогда точка А (2; 3; 4) и будет искомой точкой. 
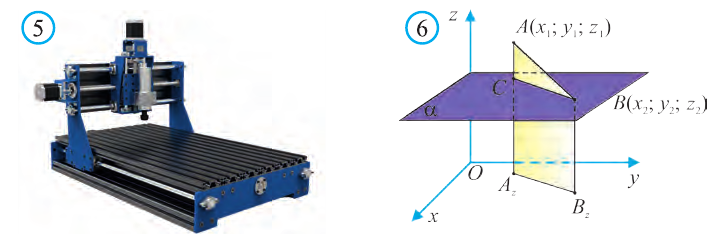
Пользуясь системой координат, созданной для современных программируемых станков и автоматизированных роботов, составляются программы, на основе которых обрабатываются металлы (рис. 5).
Расстояние между двумя точками
Пусть заданы две точки А (х1; у1; z1) и B (х2; у2; z2).
1.Сначала рассмотрим случай, когда прямая АВ не параллельна оси Оz (рис. 6). Через точки А и В проведём прямые, параллельные оси Оz. И пусть они пересекают плоскость Оху в точках Аz и Вz .
Координаты х и у этих точек соответственно равны координатам х и у точек А, В, а координаты z равны 0.
Теперь через точку В проведём плоскость а, параллельную плоскости Оху. Она пересечёт прямую ААz в некоторой точке С.
По теореме Пифагора: АВ2 = АС2 + СВ2.
Однако 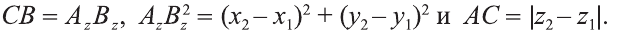
Поэтому 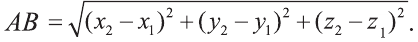
2.Пусть отрезок АВ параллелен оси Оz, тогда 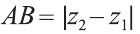 и, так как
и, так как
х1= х2 , у1 = у2 , мы опять приходим к вышеприведённой формуле.
Следовательно, расстояние между двумя точками А и В:
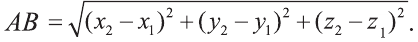 (1)
(1)
Примечание. Формула (1) выражает длину диагонали прямоугольного параллелепипеда, измерения которого равны 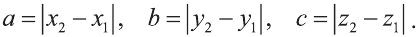
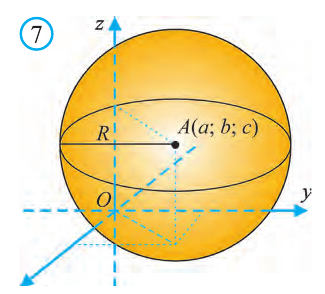
Уравнение сферы и шара
Известно, что множество всех точек М (х; у; z), расположенных на расстоянии R от данной точки А (а; Ь; с) образуют сферу (рис. 7). Тогда по формуле (1) координаты всех точек, расположенных на сфере радиуса R с центром в точке А (а; b; с), удовлетворяют равенству 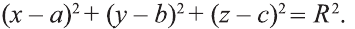
Отсюда, ясно, что неравенство для точек шара радиуса R с центром в
точке А (а; b; с) имеет вид: 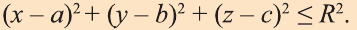
Пример:
Найдите периметр треугольника ABC с вершинами в
точках А (9; 3; -5), В (2; 10; -5), С (2; 3; 2).
Решение:
Р=АВ+АС+ВС периметр треугольника ABC. Воспользовавшись формулой 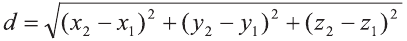 расстояния между двумя точками, найдём длины сторон треугольника:
расстояния между двумя точками, найдём длины сторон треугольника:
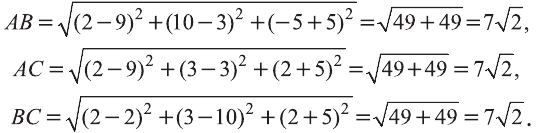
Следовательно, треугольник ABC равносторонний и его периметр 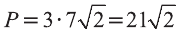 .
.
Ответ: 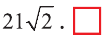
Координаты середины отрезка
Пусть А (x1; y1;z1) и В (х2; у2; z2) – произвольные точки, точка С (х; у; z) середина отрезка AB (рис. 8). 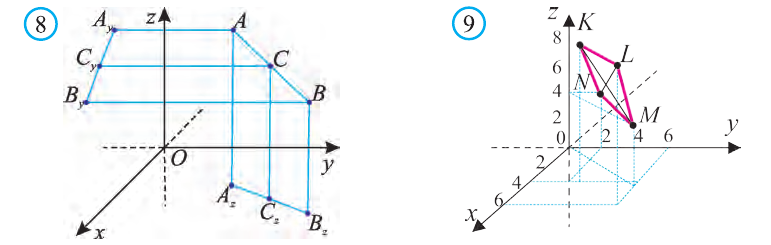
Через точки А, В и С проведём прямые, параллельные оси пересекающие плоскость Оху в точках 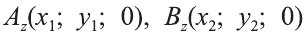 и
и 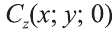 . Тогда по теореме Фалеса точка Сz – середина отрезка АzВz.
. Тогда по теореме Фалеса точка Сz – середина отрезка АzВz.
Отсюда по формулам нахождения координат середины отрезка на плоскости 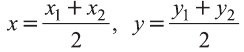
Чтобы найти координату z, нужно вместо плоскости Оху рассмотреть плоскость 0xz или Оуz.
Тогда и для z получим формулу, подобную вышеприведённой.
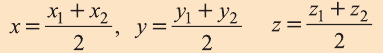
Аналогично, используя координаты концов A и B отрезка AB, по формулам 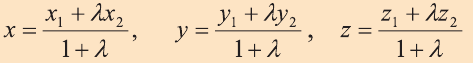
находят координаты точки Р(х1;у]; г,), делящей отрезок АВ в отношении X САР: РВ = X).
Задача 3. Докажите, что четырёхугольник МЛШЬ с вершинами М{3; 6; 4), N(0; 2; 4), К(3; 2; 8), 1(6; 6; 8) – параллелограмм (рис. 9).
Доказательство: Для решения задачи используем признак параллелограмма: Четырёхугольник, точка пересечения диагоналей которого делит их пополам, является параллелограммом.
Координаты середины отрезка МК:
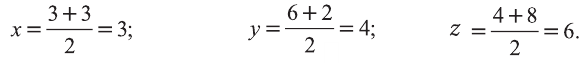
Координаты середины отрезка NL:
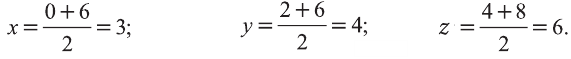
Координаты середин отрезков МК и NL равны. Это говорит о том, что отрезки пeрeсeкаются и в точке пeрeсeчeния делятся пополам. Следовательно, четырёхугольник MNLK – параллелограмм.
В переписке с известным целителем и математиком Абу Али ибн Сино Абу Райхон Беруни задаёт следующий вопрос: «Почему Аристотель и другие (философы) называют шесть сторон?»
Рассматривая шестисторонний куб, Беруни говорит о фигурах «с другим количеством сторон» и добавляет, что «шарообразные фигуры не имеют сторон.» А Ибн Сино отвечает, что «во всех случаях нужно считать, что сторон шесть, так как у каждой фигуры, независимо от её формы, есть три измерения – длина, глубина и ширина».
Здесь Ибн Сино имеет ввиду три координаты, именуемые условно «шесть сторон».
В произведении «Канон Масъуда» Беруни приводит точное математическое определение шести сторон: «Сторон шесть, так как они ограничивают движение фигур по своим измерениям. Измерений три: длина, ширина и глубина. А их в два раза больше самих измерений.»
В предыдущих книгах автор определяет положение небесных тел с помощью двух координат относительно небесной сферы – эклиптического уравнения. Либо через те же координаты, но относительно небесного экватора или горизонта. Однако при определении взаимного расположения звёзд и небесных светил придётся учитывать и случаи затмений. Вот в таких случаях появляется необходимость в третьей сферической координате. Эта необходимость привела Беруни к отказу от теории небесных координат.
Векторы в пространстве и действия над ними
Векторы в пространстве
Понятие вектора в пространстве вводят также как на плоскости.
Вектором в пространстве называют направленный отрезок. Основные понятия, относящиеся к векторам в пространстве, аналогичны этим понятиям на плоскости: длина (модуль), направление вектора, равенство векторов.
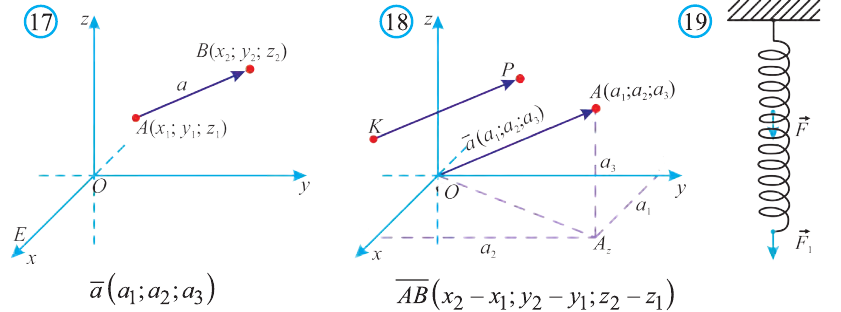
Координатами вектора с началом в точке А (х1; у1; z1) и концом в точке В (х1; у1; z1) называют числа 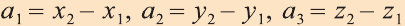 , (рис. 17).
, (рис. 17).
Приведем без доказательства свойства векторов, аналогичных свойствам на плоскости.
Также как на плоскости, соответствующие координаты равных векторов равны и, обратно, векторы с равными координатами равны.
Hа основании этого вектор можно обозначить как 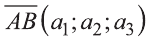 или
или 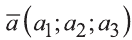 или кратко
или кратко 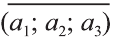 (рис. 18).
(рис. 18).
Вектор можно записать и без координат 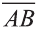 (или
(или 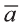 ). В этой записи
). В этой записи
на первом месте начало вектора, а на втором – конец.
Вектор с координатами, равными нулю, называют нулевым вектором и обозначают 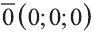 или
или 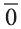 , направление этого вектора не определено.
, направление этого вектора не определено.
Если начало вектора расположено в начале координат О, а числа а1,
а2 и а3 – координаты точки А, то есть А (а1; а2; а3), то эти же числа будут
координатами вектора 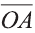 :
: 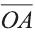 (а1; а2; а3).
(а1; а2; а3).
Однако вектор в пространстве 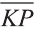 с началом в точке К(с1; с2; с3) и концом в точке
с началом в точке К(с1; с2; с3) и концом в точке 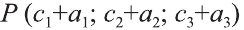 будет иметь те же координаты:
будет иметь те же координаты: 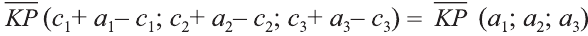 .
.
Отсюда следует, что вектор можно приложить к любой точке пространства. В геометрии мы рассматриваем такие свободные векторы. Но в физике, обычно вектор связан с некоторой точкой. Например, воздействие силы приложенная к пружине F на рисунке 19 зависит от точки её приложения.
Длинной вектора называют длину направленного отрезка
изображающего его (рис. 17). Длину вектора 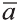 записывают
записывают
так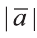 . Длина вектора
. Длина вектора 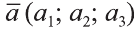 , заданного координатами,
, заданного координатами,
вычисляется по формуле 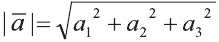 .
.
Пример:
Даны точки А (2; 7;-3),В (1; 0; 3), С (-3;-4; 5) и D (-2; 3; -1). Какие из векторов 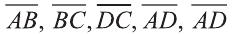 и
и 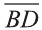 равны между собой?
равны между собой?
Решение:
У равных векторов равны соответствующие координаты. Поэтому найдём координаты векторов:
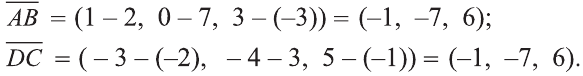
Следовательно, 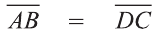 .
.
Докажите самостоятельно, что 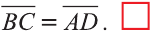
Действия над векторами в пространстве
Действия над векторами. Сложение векторов, умножение на число и их скалярное произведение определяется также как на плоскости.
Суммой векторов 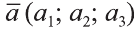 и
и  (b1; b2; b3); называют вектор
(b1; b2; b3); называют вектор 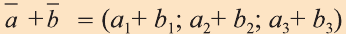 (рис. 20).
(рис. 20).
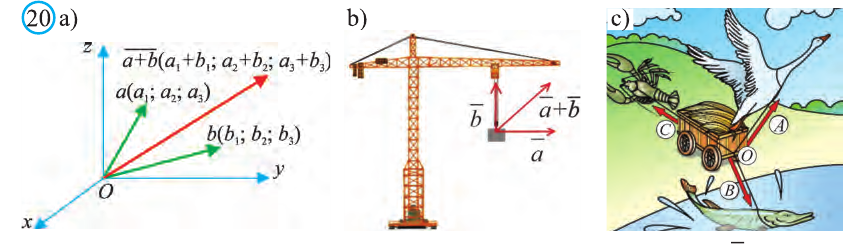
Пусть кран на рисунке 20.b движется вдоль вектора 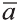 , а груз относительно крана вдоль вектора
, а груз относительно крана вдоль вектора 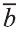 . В результате груз движется вдоль вектора
. В результате груз движется вдоль вектора 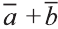 . Поэтому из рисунка 20.с, на котором изображён сюжeт басни русского писателя И.А.Крылова, ясно, что герои басни не смогут сдвинуть телегу с места.
. Поэтому из рисунка 20.с, на котором изображён сюжeт басни русского писателя И.А.Крылова, ясно, что герои басни не смогут сдвинуть телегу с места.
Свойства суммы векторов
Для любых векторов 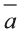 ,
,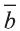 и
и 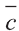 имеют место следующие свойства:
имеют место следующие свойства:
a) – переместительный закон сложения векторов;
– переместительный закон сложения векторов;
b)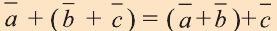 – распределительный закон сложения.
– распределительный закон сложения.
Правило треугольника сложения векторов
Для любых точек А, В и С (рис. 21): 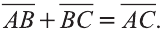
Правило параллелограмма сложения векторов
Если АВСD – параллелограмм (рис. 22), то 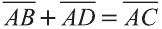
Правило многоугольника сложения векторов
Если точки А, В, С, D и Е – вершины многоугольника (рис. 23), то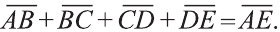
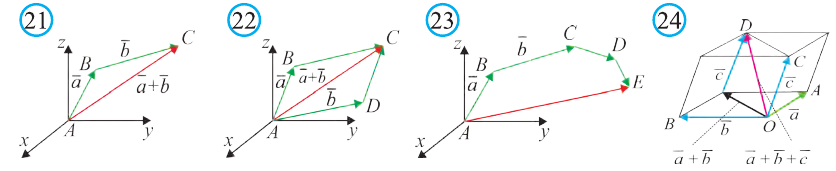
Правило параллелепипеда сложения трёх векторов, не лежащих в одной плоскости. Если АВСDА1В1С1D1 параллелепипед (рис. 24), то
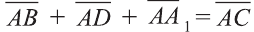 .
.
Вектор 
 = (
= ( a1;
a1;  a2;
a2;  a3) – называют умножением вектора
a3) – называют умножением вектора
 (a1; a2; a3) на число
(a1; a2; a3) на число 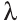 (рис. 25). Свойства операции умножения вектора на число.
(рис. 25). Свойства операции умножения вектора на число.
Для любых векторов  и
и  и чисел
и чисел 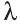 и
и 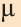
а)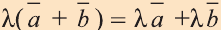 ;
;
b)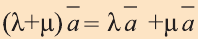 ;
;
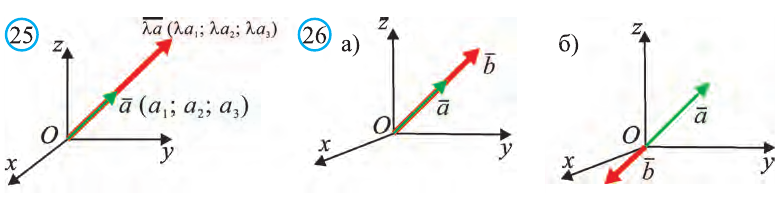
c)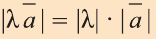 и направление вектора
и направление вектора 

совпадает с направлением вектора  , если
, если 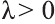 ,
,
противоположно направлению вектора  , если
, если 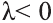 .
. 
Коллинеарные и компланарные векторы
Пусть заданы ненулевые векторы  и
и 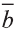 . Если векторы
. Если векторы
 и
и  сонаправлены или противоположно направлены,
сонаправлены или противоположно направлены,
то их называют коллинеарными векторами (рис. 26).
Свойство 1. Если для векторов  и
и  имеет место равенство
имеет место равенство 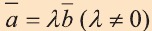 , то они коллинеарны и наоборот.
, то они коллинеарны и наоборот.
Если 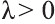 , то векторы
, то векторы  и
и  сонаправлены
сонаправлены  , если
, если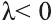 , то
, то
противоположно направлены 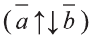 .
.
Свойство 2. Если векторы  (a1; a2; a3) и
(a1; a2; a3) и  (b1; b2; b3) коллинеарны,
(b1; b2; b3) коллинеарны,
то их соответствующие координаты пропорциональны:
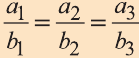 и наоборот.
и наоборот.
Пример:
Найдите вектор с началом в точке А (1; 1; 1) и концом в точке В, лежащей в плоскости Оху, коллинеарный вектору  ( 1; 2; 3).
( 1; 2; 3).
Решение:
Пусть точка В имеет координаты В (х; у; z). Так как точка В лежит в плоскости Оху, то z=0. Тогда 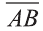 (х – 1 ;у – 1; – 1).
(х – 1 ;у – 1; – 1).
По условию задачи векторы 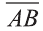 (х – 1 ;у – 1; – 1) и
(х – 1 ;у – 1; – 1) и  (1, 2, 3) коллинеарны. Следовательно, их координаты пропорциональны.
(1, 2, 3) коллинеарны. Следовательно, их координаты пропорциональны.
Тогда получаем следующие пропорции 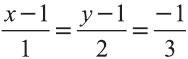 .
.
Откуда находим 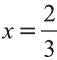 ,
, 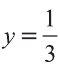 .
.
Итак,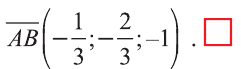
Векторы, лежащие в одной плоскости или параллельных плоскостях, называют компланарными векторами (рис. 27). 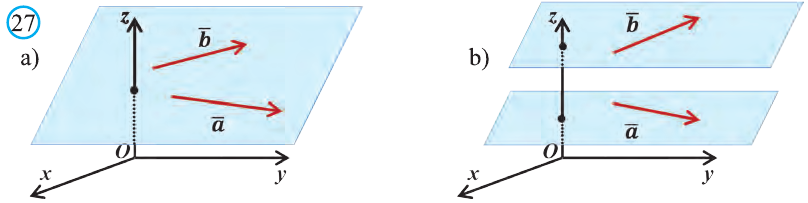
Векторы 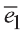 (1; 0; 0),
(1; 0; 0), 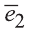 (0; 1; 0) и
(0; 1; 0) и 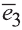 (0; 0; 1) называют ортами (рис. 28).
(0; 0; 1) называют ортами (рис. 28).
Любой вектор 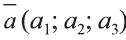 можно единственным образом разложить по ортам, то есть представить в виде
можно единственным образом разложить по ортам, то есть представить в виде 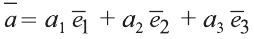 (рис. 29).
(рис. 29).
Точно также, если заданы три нeкомпланарных вектора 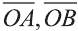 и
и 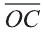 , то любой вектор
, то любой вектор 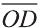 можно единственным образом представить в виде:
можно единственным образом представить в виде:
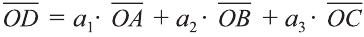 .
.
Здесь 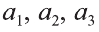 некоторые действительные числа. Тогда говорят, что вектор разложен по заданным векторам.
некоторые действительные числа. Тогда говорят, что вектор разложен по заданным векторам.
Скалярное произведение векторов
Углом между ненулевыми векторами  и
и  называют угол между направленными отрезками векторов
называют угол между направленными отрезками векторов 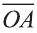 =
=  и
и 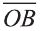 =
= , исходящих из точки О (рис. 30).
, исходящих из точки О (рис. 30).
Угол между векторами  и
и  обозначают так
обозначают так 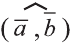 .
.
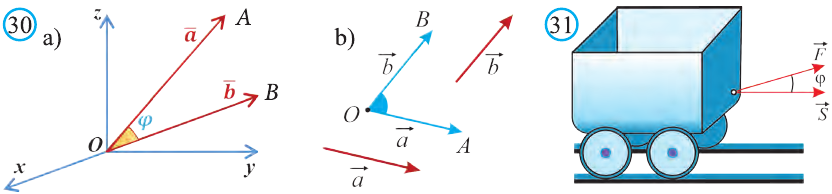
Скалярным произведением векторов  и
и  называют произведение длин этих векторов на косинус угла между ними.
называют произведение длин этих векторов на косинус угла между ними.
Если один из векторов нулевой, то скалярное произведение этих векторов равно нулю.
Скалярное произведение обозначают 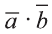 или
или 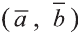 . По определению
. По определению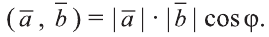 (1)
(1)
Из определения следует, что если скалярное произведение векторов  и
и  равно нулю, то эти векторы перпендикулярны и наоборот.
равно нулю, то эти векторы перпендикулярны и наоборот.
В физике работа A, выполненная при движении тела на расстоянии 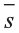 , под воздействием силы
, под воздействием силы 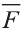 (рис. 31), равна скалярному произведению силы
(рис. 31), равна скалярному произведению силы 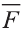 на расстояние
на расстояние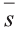 :
: 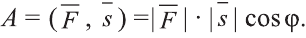
Свойство. Если 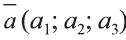 и
и  (b1; b2; b3), то (
(b1; b2; b3), то (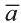
 ) =
) = 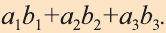
Доказательство. Приложим векторы 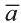 и
и  к началу
к началу
координат О (рис.32). Тогда 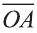 =
= 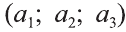 и
и 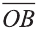 = (b1; b2; b3).
= (b1; b2; b3).
Если векторы неколлинеарны, то получаем треугольник АВО , для которого справедлива теорема косинусов.
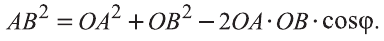
Тогда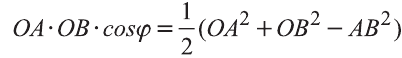 .
.
Однако, 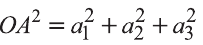 ,
,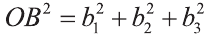
и 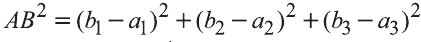 .
.
Следовательно,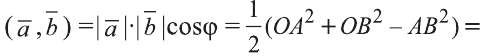
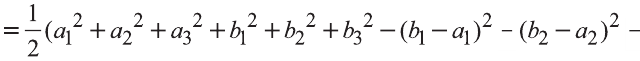
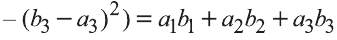 .
.
Самостоятельно докажите, что и в случае, когда данные векторы коллинеарны 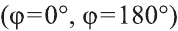 , также выполняется
, также выполняется
это равенство. 
Свойства скалярного произведения векторов
1.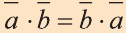 – переместительное свойство.
– переместительное свойство.
2.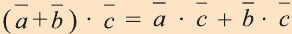 – распределительное свойство.
– распределительное свойство.
3.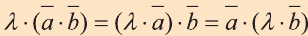 – сочетательное свойство.
– сочетательное свойство.
4.Если векторы а и b являются сонаправленными коллинеарными
векторами, то 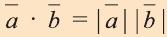 , так как соs 0° = 1.
, так как соs 0° = 1.
5.Если же векторы противоположно направлены, то 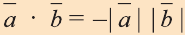 , так как cos l80° = -1.
, так как cos l80° = -1.
6. 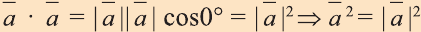 .
.
7. Если вектор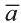 перпендикулярен вектору
перпендикулярен вектору  , то
, то 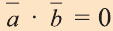 . Следствия: а) Длина вектора
. Следствия: а) Длина вектора 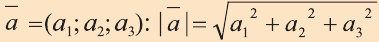 ; (1) b) косинус угла между векторами
; (1) b) косинус угла между векторами
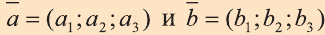 :
: 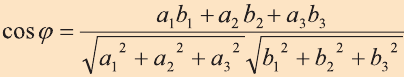 ; (2)
; (2)
с) условие перпендикулярности векторов 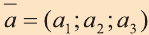 и
и
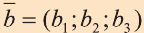 .
.
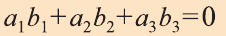 (3)
(3)
Пример:
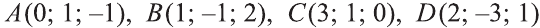 – заданные точки. Найдите косинус угла между векторами
– заданные точки. Найдите косинус угла между векторами 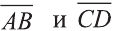 .
.
Решение:
Найдём длины векторов 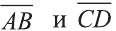 :
:
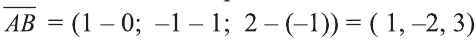 ,
,
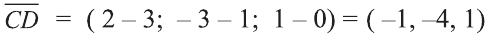 .
.
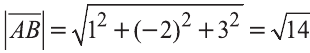 ,
,
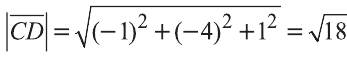 .
.
Следовательно,
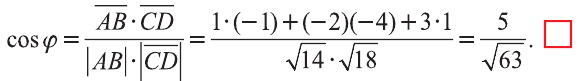
Пример:
Найдите угол между векторами 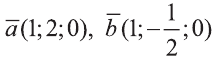 .
.
Решение:
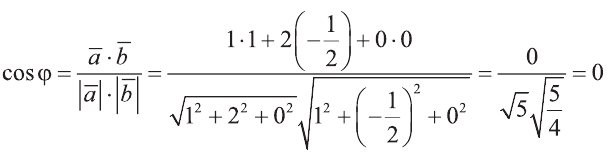 Итак,
Итак, 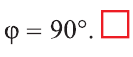
Пример:
Найдите 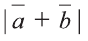 , если
, если 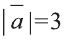 ,
, 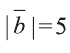 и угол между векторами
и угол между векторами и
и  равен
равен 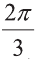 .
.
Решение:
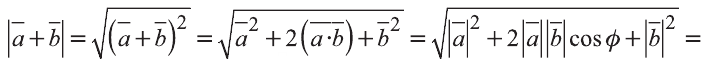
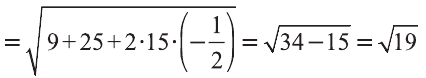
Пример:
Найдите координаты и длины векторов 1)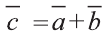 ; 2)
; 2)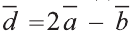 , если
, если 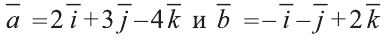 .
.
Решение:
Подставим в выражения искомых векторов разложения векторов  и
и  по координатам:
по координатам:
1)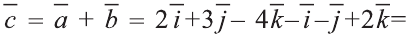
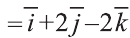 . Следовательно,
. Следовательно,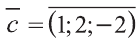 .
.
Тогда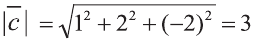 .
.
2)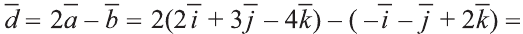
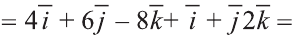
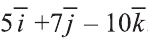 .
.
Следовательно, 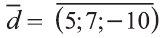 .
.
Тогда 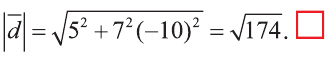
- Заказать решение задач по высшей математике
Пример:
Найдите произведение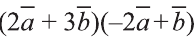 , если угол между векторами
, если угол между векторами  и
и  равен 30° и
равен 30° и 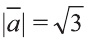 ,
, 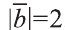 .
.
Решение:
Сначала найдём поизведение векторов  и
и  :
:
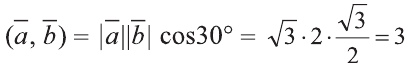 .
.
Затем перемножим заданные выражения как многочлены
и, пользуясь распределительным свойством умножения
вектора на число, получим:
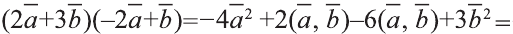
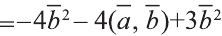 .
.
Учитывая, что 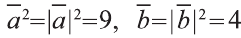 ,
,
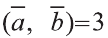 найдём искомое произведение
найдём искомое произведение
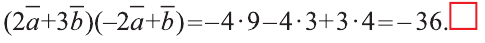
Преобразование и подобие в пространстве
Геометрические преобразования в пространстве
Если каждую точку заданной в пространстве фигуры F изменить одним и тем же способом, то получим фигуру F1. Если при этом преобразовании различные точки первой фигуры переходят в различные точки второй, то говорят о преобразовании геометрической фигуры.
Если рассматривать все пространства как геометрическую фигуру, то также можно говорить о преобразовании геометрической фигуры.
Понятие геометрического преобразование в пространстве вводят также как на плоскости. Следовательно, свойства некоторых рассматриваeмых ниже видов преобразований и их доказательства также подобны соответствующим им на плоскости. Поэтому, мы не будем доказывать их и рекомендуем провести их самостоятельно.
Движение и параллельный перенос
Преобразование фигур, при котором сохраняются расстояния между точками, называют движением. Можно привести следующие свойства движения. При движении прямая переходит в прямую, луч – в луч, отрезок – в равный ему отрезок, угол – в равный ему угол, треугольник – в равный ему треугольник, плоскость – в плоскость, тетраэдр – в равный ему тетраэдр.
В пространстве фигуры, которые можно перевести одну в другую при некотором движении называют равными фигурами.
Простейшим примером движения является параллельный перенос.
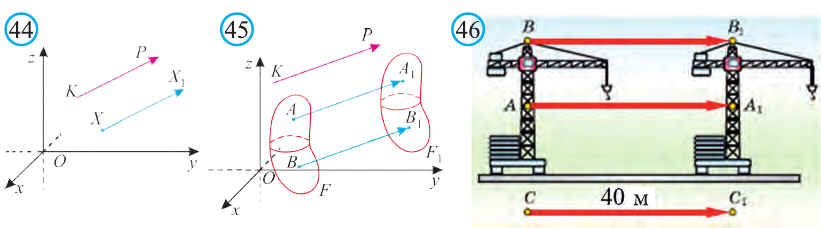
Пусть в пространстве даны вектор и произвольная точка Х
и произвольная точка Х
(рис. 44). Говорят, что точка Х перешла в точку X1 параллельным
переносом на вектор  , если выполняется условие
, если выполняется условие 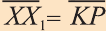 . Если каждую точку фигуры F сдвинуть на вектор
. Если каждую точку фигуры F сдвинуть на вектор  при помощи параллельного переноса (рис. 45), то получим фигуру F1. Тогда говорят, что фигура F получена параллельным переносом фигуры F1 . При параллельном переносе каждая точка фигуры F сдвигается в одном и том же направлении на одно и то же расстояние.
при помощи параллельного переноса (рис. 45), то получим фигуру F1. Тогда говорят, что фигура F получена параллельным переносом фигуры F1 . При параллельном переносе каждая точка фигуры F сдвигается в одном и том же направлении на одно и то же расстояние.
Каждая точка подъёмного крана, изображённого на рисунке 46, параллельно перенесена на 40 м относительно начального положения.
Ясно, что параллельный перенос является движением. Поэтому прямая переходит в прямую, луч – в луч, плоскость – в плоскость,
и т. д.
Пусть точка 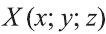 фигуры F перешла в точку
фигуры F перешла в точку 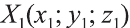
фигуры F1 при помощи параллельного переноса
на вектор 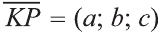 .
.
Тогда по определению получим:
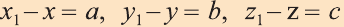 или
или
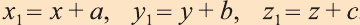 .
.
Эти равенства называют формулами параллельного переноса.
Пример:
В какую точку перейдёт точка Р (-2; 4; 6) при параллельном переносе на вектор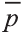 = (3; 2; 5)?
= (3; 2; 5)?
Решение:
По вышеприведённым формулам параллельного переноса: 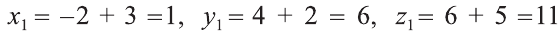 .
.
Ответ: 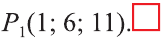 .
.
Центральная симметрия в пространстве
Если в пространстве 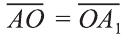 , то есть точка О – середина отрезка АА1 то точки А и А1 называют симметричными относительно точки О.
, то есть точка О – середина отрезка АА1 то точки А и А1 называют симметричными относительно точки О.
Если в пространстве каждая точка фигуры F переходит в точку, симметричную относительно точки О (рис. 47), то такое преобразование называют симметрией относительно точки О. На рисунках 48, 49 изображёны фигуры симметричные относительно точки О. Симметрия относительно точки является движением.
Если при симметрии относительно точки О фигура F переходит в себя, то её называют центрально симметричной фигурой.

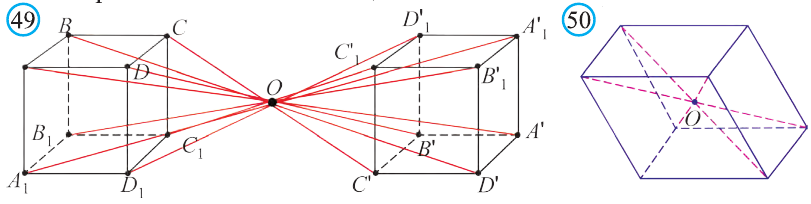
Например, диагонали параллелепипеда (рис. 50) относительно их точки пересечения О являются центрально симметричными фигурами.
Пример:
В какую точку перейдет точка A = (1; 2; 3) при симметрии относительно точки О (2; 4; 6)?
Решение:
Пусть А1 = (х; у; z) – искомая точка. По определению точка
О – середина отрезка АА1. Следовательно,
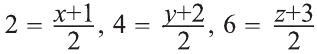
Из этих уравнений получаем:
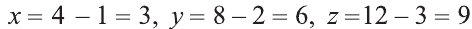 .
.
Ответ: 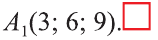
Симметрия относительно плоскости
Точки А и А1 называют симметричными относительно плоскости а,
если плоскость перпендикулярна отрезку и делит его пополам (рис. 51). Фигуры F1, и F2 на рисунке 52 симметричны относительно
плоскости а. Очевидно, что наш силуэт и его отражение симметричны относительно плоскости зеркала (рис. 53).
Симметрия относительно плоскости а является движением. 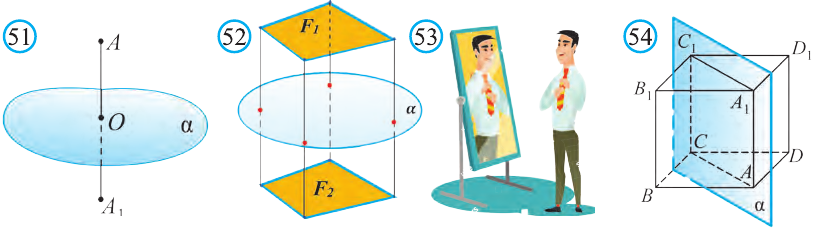
Поэтому при симметрии относительно плоскости а отрезок переходит в равный ему отрезок, прямая – в прямую, плоскость – в плоскость.
Если при симмeтрии относительно плоскости фигура F переходит в себя, то её называют фигурой симметричной относительно плоскости.
Например, изображённый на рисунке 54 куб, есть фигура, симметричная относительно плоскости а, проходящей через его диагонали АА1 и СС1.
Поворот и симметрия относительно оси
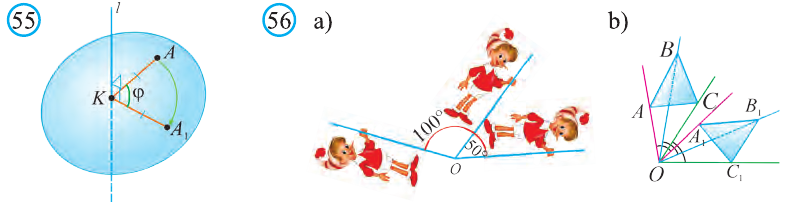
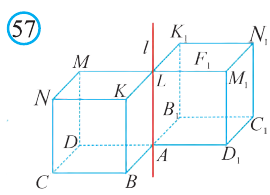
Пусть в пространстве заданы точки А и А1 и прямая l. Если перпендикуляры АК и А1К, опущенные на прямую l, равны и образуют угол  , то говорят, что точка А перешла в точку А1 в результате поворота на угол
, то говорят, что точка А перешла в точку А1 в результате поворота на угол  относительно прямой l (рис. 55).
относительно прямой l (рис. 55).
Если каждую точку фигуры F повернуть на угол  относительно прямой l, то получим новую фигуру F1 . Тогда говорят, что фигура F перешла в фигуру F1 с помощью поворота на угол
относительно прямой l, то получим новую фигуру F1 . Тогда говорят, что фигура F перешла в фигуру F1 с помощью поворота на угол  относительно прямой l. На рисунке 56 мы видим фигуры, полученные таким поворотом. Например, повернув куб, изображённый на рисунке 57, на 180° относительно прямой l, получим новый куб.
относительно прямой l. На рисунке 56 мы видим фигуры, полученные таким поворотом. Например, повернув куб, изображённый на рисунке 57, на 180° относительно прямой l, получим новый куб.
Поворот относительно прямой также является движением.
Поворот на 180° относительно прямой l называют симметрией относительно прямой l.
Центр, ось и плоскость симметрии называют элементами симметрии. Точки, симметричные точке А (х; у; z) относительно координатных плоскостей, координатных осей и начала координат, будут иметь следующие координаты:

Симметрия в природе и технике

В природе на каждом шагу можно встретить симметрию.
Например, множество живых существ, в частности тела человека и животных, листья растений и цветы устроены симметрично (рис. 58). Также в неживой природе есть элементы, например, снежинки, кристаллы соли. Молекулярное строение веществ тоже состоит из симметричных фигур. Это, конечно, неспроста, поскольку симметричные фигуры не только красивы, но и самые устойчивые.
Раз так, то можно считать, что красота и совершенство природы построены на основе симметрии. Взяв за основу природную красоту и совершенство, строители, инженеры и архитекторы создают строения и механизмы, здания и сооружения, технику и транспортные средства симметричными. В этой работе им очень помогает наука геометрия.
Подобие пространственных фигур
Пусть 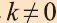 и преобразование переводят фигуру F1, в фигуру F2. Если
и преобразование переводят фигуру F1, в фигуру F2. Если
при этом преобразовании для произвольных точек X1 и Х2 фигуры F1 и соответствующих им точек Y1 и Y2 фигуры 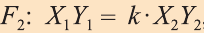 , то это преобразование называют преобразованием подобия (рис. 59).
, то это преобразование называют преобразованием подобия (рис. 59).
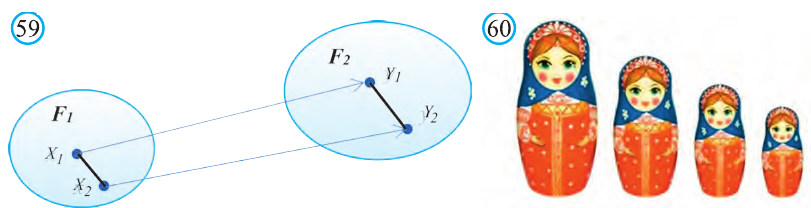
Как видим, понятие преобразования подобия в пространстве вводится также как на плоскости. Следовательно, рассматриваемые ниже виды подобия, их свойства и доказательства этих свойств подобны соответствующим на плоскости. Поэтому, мы не будем останавливаться на их доказательствах и рекомендуем провести их самостоятельно. Преобразование подобия в пространстве отображает прямую в прямую, луч в луч, отрезок в отрезок и угол в угол. Точно также это преобразование плоскость отображает в плоскость.
Если в пространстве одна из фигур перешла в другую с помощью преобразования подобия, то эти фигуры называют подобными.
Пусть в пространстве задана фигура F, точка О и число к 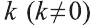 . Преобразование, переводящее произвольную точку X фигуры F в точку Х1 удовлетворяющую условию
. Преобразование, переводящее произвольную точку X фигуры F в точку Х1 удовлетворяющую условию 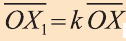 , называют гомотетией относительно центра О с коэффициентом
, называют гомотетией относительно центра О с коэффициентом  (рис. 61). Точку О называют центром гомотетии, а число
(рис. 61). Точку О называют центром гомотетии, а число  коэффициентом гомотетии. Если в результате такого преобразования каждой точки фигуры F получена фигура F1 то говорят, что фигура F гомотетична фигуре F1.
коэффициентом гомотетии. Если в результате такого преобразования каждой точки фигуры F получена фигура F1 то говорят, что фигура F гомотетична фигуре F1.
Вы видите, что определение гомотетии в пространстве аналогично соответствующему определению на плоскости. Следовательно, все свойства и их доказательства аналогичны. Поэтому, мы не будем доказывать их и рекомендуем провести их самостоятельно.
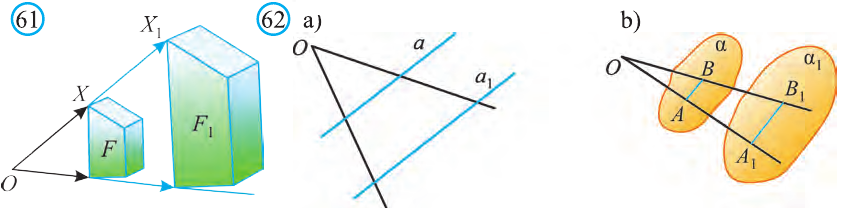
Гомотетия относительно точки О с коэффициентом  является преобразованием подобия. Гомотетия с отличным от нуля коэффициентом
является преобразованием подобия. Гомотетия с отличным от нуля коэффициентом  при
при  = 1 отображает фигуру F в себя, а при
= 1 отображает фигуру F в себя, а при  =-1 в фигуру F1 симметричную фигуре F относительно точки О. В остальных случаях гомотетии не сохраняет расстояния между точками, т. е. не является движением. В результате гомотетии расстояние между точками увеличивается в одно и тоже число
=-1 в фигуру F1 симметричную фигуре F относительно точки О. В остальных случаях гомотетии не сохраняет расстояния между точками, т. е. не является движением. В результате гомотетии расстояние между точками увеличивается в одно и тоже число  раз, т. е. меняются измерения фигуры, но сохраняется её форма. При гомотетии а) прямая отображается в параллельную ей прямую (рис. 62.а); b) плоскость – в параллельную ей плоскость (рис. 62.b), если они не проходят через центр гомотетии.
раз, т. е. меняются измерения фигуры, но сохраняется её форма. При гомотетии а) прямая отображается в параллельную ей прямую (рис. 62.а); b) плоскость – в параллельную ей плоскость (рис. 62.b), если они не проходят через центр гомотетии.
Если же прямая или плоскость проходят через центр гомотетии, то они отображаются в себя.
- Иррациональные числа
- Действительные числа
- Решение уравнений высших степеней
- Системы неравенств
- Уравнения и неравенства
- Уравнения и неравенства содержащие знак модуля
- Уравнение
- Метод математической индукции
Привет, мой друг, тебе интересно узнать все про координаты точки, тогда с вдохновением прочти до конца. Для того чтобы лучше понимать что такое
координаты точки , настоятельно рекомендую прочитать все из категории Арифметика.
каждой точке координатной плоскости соответствуют две координаты.
координаты точки на плоскости – это пара чисел, в которой на первомместе стоит абсцисса,
а на втором – ордината точки.

Рассмотрим как в системе координат (на координатной плоскости):
- находить координаты точки;
- найти положение точки.
Чтобы найти координаты точки на плоскости, нужно опустить из этой точки перпендикуляры на оси координат.
Точка пересечения с осью x называется абсциссой точки А, а с осью y называется ординатой точки А.
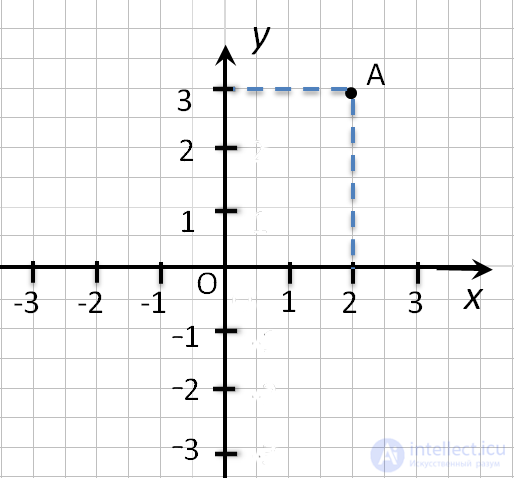
Обозначают координаты точки, как указано выше (•) A (2; 3).
Пример (•) A (2; 3) и (•) B (3; 2).
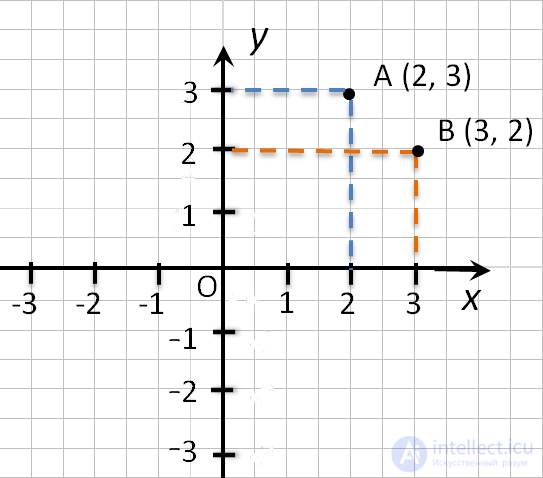




На первом месте записывают абсциссу (координату по оси x), а на втором – ординату (координату по оси y) точки.
Особые случаи расположения точек
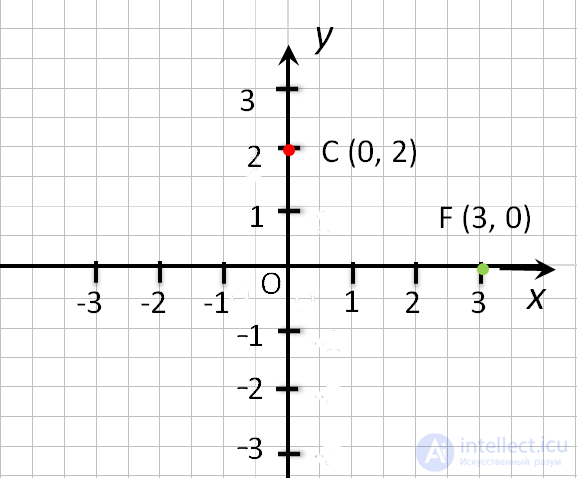
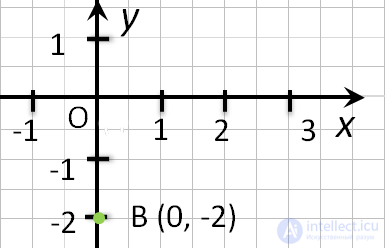
- Если точка лежит на оси Oy, то ее абсцисса равна 0 . Об этом говорит сайт https://intellect.icu . Например, точка С (0, 2).
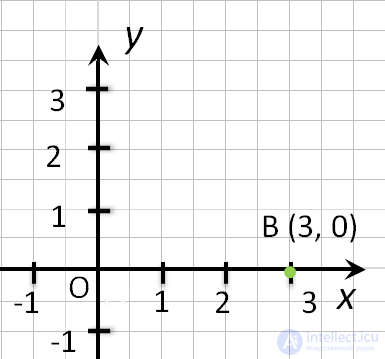
- Если точка лежит на оси Ox, то ее ордината равна 0. Например, точка F (3, 0).
- Начало координат – точка O имеет координаты, равные нулю O (0,0).
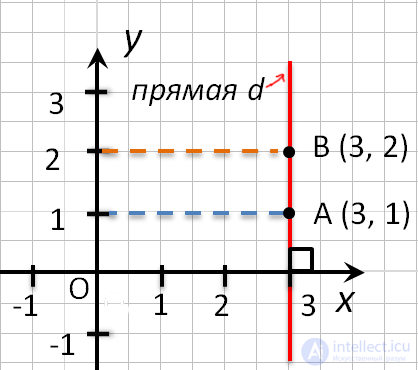
- Точки любой прямой перпендикулярной оси абсцисс, имеют одинаковые абсциссы.
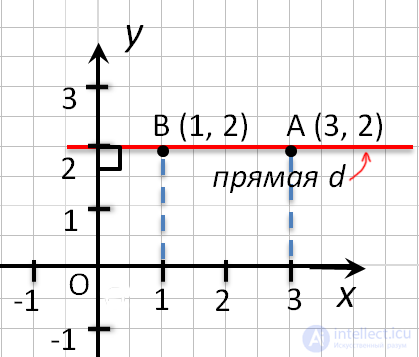
- Точки любой прямой перпендикулярной оси ординат, имеют одинаковые ординаты.
- Координаты любой точки, лежащей на оси абсцисс имеют вид (x, 0).
- Координаты любой точки, лежащей на оси ординат имеют вид (0, y).
Как найти положение точки по ее координатам
Найти точку в системе координат можно двумя способами.
Первый способ
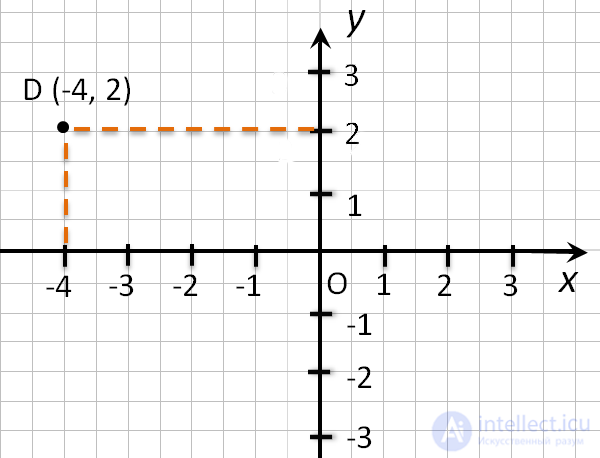
Чтобы определить положение точки по ее координатам, например, точки D (-4 , 2), надо:
- Отметить на оси Ox, точку с координатой (-4), и провести через нее прямую перпендикулярную оси 0x.
- Отметить на оси Oy, точку с координатой (2), и провести через нее прямую перпендикулярную оси 0y.
- Точка пересечения перпендикуляров (•) D – искомая точка. У нее абсцисса равна (-4), а ордината равна (2).
Второй способ
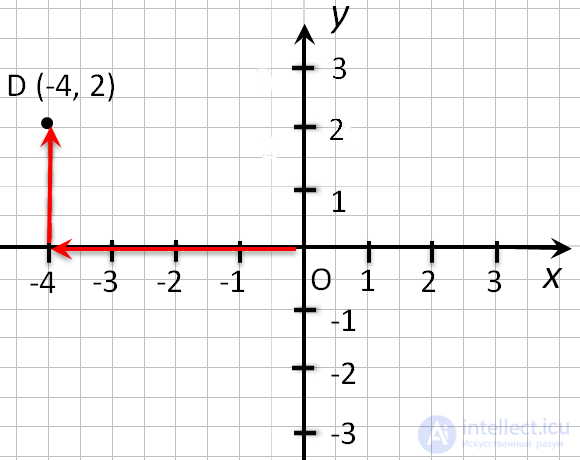
Чтобы найти точку D (-4 , 2) надо:
- Сместиться по оси x влево на 4 единицы, так как у нас перед 4 стоит «-».
- Подняться из этой точки параллельно оси y вверх на 2 единицы, так как у нас перед 2 стоит «+».
Чтобы быстрее и удобнее было находить координаты точек или строить точки по координатам на листе формата A4 в клеточку, можно скачать и использовать готовую систему координат на нашем сайте.
Как ты считаеешь, будет ли теория про координаты точки улучшена в обозримом будующем? Надеюсь, что теперь ты понял что такое координаты точки
и для чего все это нужно, а если не понял, или есть замечания,
то нестесняся пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории
Арифметика
Из статьи мы узнали кратко, но емко про координаты точки








