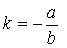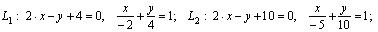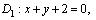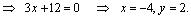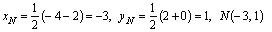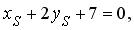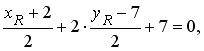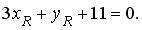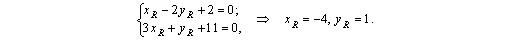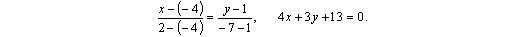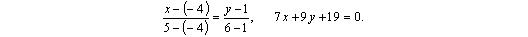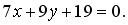Как найти координаты точки пересечения диагоналей ромба

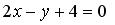
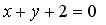
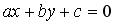
Пример 1. Вычислить координаты вершин ромба, если известны уравнения двух его сторон: и и уравнение одной из его диагоналей: . Решение. Выясним взаимное расположение известных сторон ромба. Угловой коэффициент k прямой определяется по формуле:

.

Стороны параллельны, так как имеют одинаковый угловой коэффициент:

.

Для построения рисунка (рис. 4.1) запишем уравнения в отрезках для данных прямых:

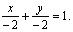
Наметим план решения: 1) находим вершины ромба P и Q ; 2) находим точку пересечения диагоналей ромба N ; 3) через точку N проводим диагональ D 2 ; 4) находим оставшиеся вершины ромба R и S .1) Так как точка P является точкой пересечения прямых L 2 и D 1 , то ее координаты находим из системы уравнений:

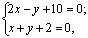
Из рис. 4.1 сразу находим координаты точки Q (- 2, 0) . 2) Так как диагонали ромба в точке пересечения делятся пополам, то точка 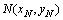является серединой отрезка PQ , поэтому ее координаты — полусумма соответствующих координат точек P и Q :

.

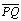
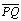
3) Так как диагонали ромба взаимно перпендикулярны, то прямая D 2 перпендикулярна вектору. Найдем его координаты:

= — 2 — (- 4); 0 — 2 = {2; — 2}.

По формуле (3.1) находим уравнение диагонали D 2 как уравнение прямой, проходящей через точку N (- 3, 1) перпендикулярно вектору 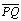= {2; — 2}:

2( x — (- 3)) + (- 2)( y — 1) = 0, x — y + 4 = 0.

4) Вершины ромба R и S — точки пересечения прямых L 2 и D 2 , L 1 и D 2 , соответственно, находим из уравнений:

, , , .

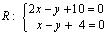
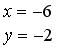
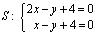
Ответ: P (- 4, 2) R (- 6, — 2), Q (- 2, 0), S (0, 4).

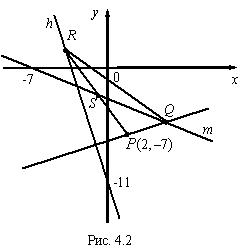
Пример 2. Составить уравнения сторон треугольника, зная одну его вершину P (2, — 7), уравнения высоты 3 x + y + 11 = 0 и медианы x + 2 y + 7 = 0, проведенных из разных вершин. Решение. Для построения рисунка (рис. 4.2) приведем уравнения данных прямых к уравнениям в отрезках:

h : 3 x + y + 11 = 0, m : x + 2 y + 7 = 0 ,

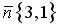
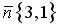
План решения:1) находим уравнение прямой PQ ;2) находим координаты точки R ;3) находим уравнения прямых RP и RQ .1) Находим нормальный вектор прямой h :. Уравнение стороны PQ , проходящей через точку P (2, — 7) параллельно вектору, запишем в виде:

, x — 3 y — 23 = 0 .

Находим координаты точки Q — точки пересечения прямых PQ и m :

x = 5 , y = — 6.

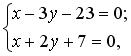
2) По свойству медианы треугольника PQR точка S ( x S , y S ) является серединой отрезка RP . Следовательно:

, .

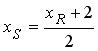
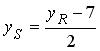
Точка S лежит на медиане m , значит,

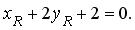
Точка R лежит на высоте h , значит,

Из последних двух уравнений определяем координаты точки R , решая систему:

3) Используя формулу (3.4), составим уравнение прямой RP , проходящей через две заданные точки R и P :

Аналогично, составим уравнение прямой RQ :

Ответ: x — 3 y — 23 = 0, ,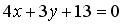

1) Обозначим вершины ромба буквами латинского алфавита A, B, C и D для удобства обсуждения. Точку пересечения диагоналей традиционно обозначают буквой O. Длину ребра ромба обозначим буквой a. Величину угла BCD, который равен углу BAD, обозначим α.

.

2) Найдем величину короткой диагонали. Так как диагонали пересекаются под прямым углом, то треугольник COD является прямоугольным. Половина короткой диагонали OD является катетом этого треугольника и может быть найдена через гипотенузу CD, а также угол OCD.

Диагонали ромба являются также биссектрисами его углов, поэтому угол OCD равен α/2.

Таким образом, OD = BD/2 = CD*sin (α/2). То есть, короткая диагональ BD = 2a*sin (α/2).

3) Аналогичным образом, из того, что треугольник COD прямоугольный, можем выразить величину OC (а это половина длинной диагонали).

OC = AC/2 = CD*cos (α/2)

Величина длинной диагонали выражается следующим образом: AC = 2a*cos (α/2)

Электронная библиотека

Пример 1. Вычислить координаты вершин ромба, если известны уравнения двух его сторон: и и уравнение одной из его диагоналей: . Решение. Выясним взаимное расположение известных сторон ромба. Угловой коэффициент k прямой определяется по формуле:

Стороны параллельны, так как имеют одинаковый угловой коэффициент:

Для построения рисунка (рис. 4.1) запишем уравнения в отрезках для данных прямых:

Наметим план решения: 1) находим вершины ромба P и Q ; 2) находим точку пересечения диагоналей ромба N ; 3) через точку N проводим диагональ D 2 ; 4) находим оставшиеся вершины ромба R и S .1) Так как точка P является точкой пересечения прямых L 2 и D 1 , то ее координаты находим из системы уравнений:

Из рис. 4.1 сразу находим координаты точки Q (- 2, 0) . 2) Так как диагонали ромба в точке пересечения делятся пополам, то точка является серединой отрезка PQ , поэтому ее координаты — полусумма соответствующих координат точек P и Q :

3) Так как диагонали ромба взаимно перпендикулярны, то прямая D 2 перпендикулярна вектору . Найдем его координаты:

По формуле (3.1) находим уравнение диагонали D 2 как уравнение прямой, проходящей через точку N (- 3, 1) перпендикулярно вектору = <2; — 2>:

2( x — (- 3)) + (- 2)( y — 1) = 0, x — y + 4 = 0.

4) Вершины ромба R и S — точки пересечения прямых L 2 и D 2 , L 1 и D 2 , соответственно, находим из уравнений:

Ответ: P (- 4, 2) R (- 6, — 2), Q (- 2, 0), S (0, 4).

Пример 2. Составить уравнения сторон треугольника, зная одну его вершину P (2, — 7), уравнения высоты 3 x + y + 11 = 0 и медианы x + 2 y + 7 = 0, проведенных из разных вершин. Решение. Для построения рисунка (рис. 4.2) приведем уравнения данных прямых к уравнениям в отрезках:

h : 3 x + y + 11 = 0, m : x + 2 y + 7 = 0 ,

План решения:1) находим уравнение прямой PQ ;2) находим координаты точки R ;3) находим уравнения прямых RP и RQ .1) Находим нормальный вектор прямой h : . Уравнение стороны PQ , проходящей через точку P (2, — 7) параллельно вектору , запишем в виде:

Находим координаты точки Q — точки пересечения прямых PQ и m :

2) По свойству медианы треугольника PQR точка S ( x S , y S ) является серединой отрезка RP . Следовательно:

Точка S лежит на медиане m , значит,

Точка R лежит на высоте h , значит,

Из последних двух уравнений определяем координаты точки R , решая систему: 3) Используя формулу (3.4), составим уравнение прямой RP , проходящей через две заданные точки R и P : Аналогично, составим уравнение прямой RQ : Ответ: x — 3 y — 23 = 0, ,

Уравнение ромба в декартовой системе координат

Составление и решение уравнений многоугольников

Скачать:

Вложение	Размер
составление и решение уравнений многоугольников	124.82 КБ

Предварительный просмотр:

Автор работы: Шпакова Маргарита Андреевна, г.о. Тольятти, МБУ СОШ

Научный руководитель: Владимирова Ольга Ивановна, учитель математики первой категории МБУ СОШ № 58.

В школьном курсе математики учащиеся часто встречаются с алгебраическими уравнениями, уравнениями прямых, уравнениями окружностей, квадратными уравнениями и т.д. Что собой представляют уравнения многоугольников, учащиеся не знают.

Как, например, выглядит уравнение треугольника? Можно ли по фигуре на плоскости составить уравнение? Можно ли рассчитать площадь фигуры по заданному уравнению? Можно ли по заданному уравнению определить, что за многоугольник? Решение этих вопросов меня и заинтересовало. В них есть проблема моей исследовательской работы.

Цель работы: изучить и исследовать на примерах методы, которые дают возможность получить уравнение с модулем любого выпуклого многоугольника на плоскости, координаты вершин которого известны. Найти взаимосвязь площади фигуры от ее уравнения.

Основные ЗАДАЧИ исследования:

1. Познакомиться с некоторыми видами уравнений прямых на плоскости (уравнение прямой в отрезках, уравнение прямой, проходящей через две различные точки на плоскости);
2. Научиться составлять уравнение прямой через заданную точку и параллельную другой прямой;
3. Научиться составлять уравнение прямой, проходящей через две заданные точки;
4. Научиться по уравнению строить многоугольник на плоскости и наоборот, по чертежу составлять уравнение многоугольника;
5. Изучить метод областей при решении уравнений, содержащих знак модуля.

Как известно из курса геометрии, любая прямая на координатной плоскости может быть задана уравнением вида

Подобное уравнение называют линейным. Уравнение такого вида называют также общим уравнением прямой на плоскости.

Если ax+by+c = 0 – уравнение некоторой прямой m, то уравнение ax+by+c = p, где р ≠ 0, задает прямую m`, параллельную m. Это следует из того, что данные два уравнения не имеют общих решений, а значит, прямые не имеют общих точек.

У параллельных прямых

Пример1 . Составим уравнение прямой, проходящей через точку М (1;-2) и параллельной прямой 3x-4y+5=0

Подставляя координаты точки М в левую часть уравнения, получаем значение 16. Значит, искомым уравнением прямой будет 3x+4y+5=16 или окончательно 3x+4y-11=0.

Пусть известны координаты двух точек М 1 (x 1 ;y 2 ), М 2 (x 2 ;y 2 ), лежащих на данной прямой. Составим уравнение прямой, проходящей через две заданные точки:

(x-x 1 )(y 2 -y 1 )-(y-y 1 )(x 2 -x 1 )=0

Пример 2 . Составим уравнение прямой, проходящей через точку М 1 (3;1) и М 2 (2;2).

Получаем такое уравнение (x-3)(2-1)-(y-1)(2-3)=0

после преобразований выходит х+у-4=0.

Если известны координаты (а;0) и (0;b) точек пересечения прямой с осями Ох и Оу, то для этой прямой проще всего записать уравнение в отрезках + = 1.

Рассмотрим на координатной плоскости ху треугольник с вершинами в точках А (х 1 ;у 1 ), В (х 2 ;у 2 ), С (х 3 ;у 3 ). Уравнение прямой, на которой лежит сторона АВ этого треугольника, можно записать в виде

(x-x 1 )(y 2 -y 1 )-(y-y 1 )(x 2 -x 1 )=0.

Подставим координаты третьей вершины С (х 3 ;у 3 ) в левую часть этого уравнения,

получим некоторое значение

q=(x 3 -x 1 )(y 2 -y 1 )-(y 3 -y 1 )(x 2 -x 1 )

Чтобы понять геометрический смысл числа q, заметим, что уравнение

(х-х 1 )(у 2 -у 1 )-(у-у 1 )(х 2 -х 1 )=q задает прямую, параллельную стороне АВ данного треугольника. Поэтому для каждой точки этой прямой результат подстановки ее координат в левую часть уравнения тот же, что и для точки C (х 3 ;у 3 ), и дает число q. Значит, то же значение получится и для точки С 1 (х 4 ;у 1 ) пересечения упомянутой прямой с прямой у=у 1 , параллельной оси абсцисс и проходящей через вершину A треугольника. Но в этой точке

(х-х 1 )(у 2 -у 1 )-(у-у 2 )(х 2 -х 1 ) = (х 4 -х 1 )(у 2 -у 1 ). Геометрический смысл последнего выражения понять уже несложно: |(х 4 -х 1 )(у 2 -у 1 )| площадь параллелограмма со сторонами АВ и АС 1 . Длина стороны АС 1 равна |х 4 -х 1 |, а длина высоты параллелограмма, опущенной из вершины B на эту сторону, есть |у 2 -у 1 |. Поэтому |q| есть площадь ΔАВС 1 , но она такая же, что и у ΔАВС. В результате приходим к следующей формуле для площади треугольника

S = |(x 3 -x 1 )(y 2 -y 1 )-(y 3 -y 1 )(x 2 -x 1 )|. (3, стр. 169).

Если треугольник задан в декартовой системе координат и имеет своими вершинами точки А (х 1 ;у 1 ), В (х 2 ;у 2 ), С (х 3 ;у 3 ), то можно составить уравнение треугольника:

|(x-x 1 )(y 2 -y 1 )-(y-y 1 )(x 2 -x 1 )| + |(x-x 2 )(y 3 -y 2 )-(y-y 2 )(x 3 -x 2 )| +

+ |(x-x 3 )(y 1 -y 3 )–(y-y 3 )(x 1 -x 3 )| = 2S, где

S = |(x 3 -x 1 )(y 2 -y 1 )-(y 3 -y 1 )(x 2 -x 1 )|.

Пример 3 . Составим уравнение треугольника, изображенного на рисунке. Для этого составим уравнения прямых, которые являются его сторонами, по формуле

(x-x 1 )(y 2 -y 1 )-(y-y 1 )(x 2 -x 1 )=0, задающей уравнение прямой по двум ее точкам. При этом допустимым считаем раскрытие скобок и приведение подобных слагаемых и недопустимым – умножение обеих частей уравнения на некоторое число (за исключением -1) .

Уравнения сторон имеют вид: х-у+1=0, х+у-1=0, 2у=0. Сложив модули левых частей этих уравнений, и приравняв полученное выражение к удвоенной площади ΔАВС, равной в данном случае 1, приходим к искомому уравнению |x-y+1|+|x+y-1|+2|y|=2.

Описанный метод дает возможность получить уравнение любого выпуклого многоугольника на плоскости, координаты вершин которого известны.

Уравнение квадрата, ромба

Пример 4 . Составить уравнение квадрата:

|x-1| + |y-1| + |x| + |y| = 1. Площадь равна 1.

Пример 5 . Составить уравнение ромба:

Через точки с координатами (1;0), (0;1) уравнение прямой: x +y -1 = 0.

Через точки с координатами (-1;0), (0;1) уравнение прямой: x – y + 1 = 0.

Через точки с координатами (-1;0), (0;-1) уравнение прямой: x + y + 1 = 0.

Через точки с координатами (0;-1), (1;0) уравнение прямой: -x + y + 1 = 0.

Получили: | x + y – 1| + | x – y + 1| + | x + y + 1| + | -x + y + 1 | = 4.

Этот же ромб имеет другое уравнение: |х| + |у| = 1, которое лучше решать «методом областей». Площадь ромба равна 2.

Пример 6 . Докажите, что уравнения: |x + y| + |x – y| = 2 и |x + 1| + |y + 1| + |x -1| +|y – 1| =4 относятся к одному квадрату.

Первое уравнение лучше решать «методом областей», где вся плоскость разбивается прямыми у =-х и у=х на четыре области, значит, искомая фигура четырехугольник, стороны которого параллельны осям координат. Из уравнений каждой области у=1, х=1и т.д. понимаем, что это квадрат, площадь которого равна 4.

Второе уравнение наглядно изображено, подтверждая первое.

Пример 7. Определить вид многоугольника по уравнениям:

|х| + 3|у| = 6; |х-3| + |у+3| = 3; |х-1| + 7|у| = 1.

Во всех случаях даны уравнения ромба .

Пример 8 . Изобразить на плоскости многоугольник по данному уравнению: |x|+|y|+|x+y|=4.

Из данного уравнения следует, что х=0, у=0, х= -у –прямые, которые разбивают плоскость на несколько областей.

Найдем уравнение прямой, стороны многоугольника, в каждой из областей:

Проанализируем расположение квадрата на координатной плоскости.

В общем случае уравнение квадрата в декартовой (прямоугольной) системе координат принимает вид:

где точка О`(a;b) – точка пересечения диагоналей квадрата;

d – длина диагонали квадрата.

В частном случае, когда точка О(0;0) – начала координат, является одновременно и точкой пересечения диагоналей квадрата, уравнение квадрата принимает вид:

где d– длина диагонали квадрата.

Одно из уравнений квадрата можно записать так
|x| + |y| = a
обычно так рисуют ромб, но это квадрат

Вопрос:
Как выглядит уравнение квадрата, если его положить на сторону? Иными словами, стороны квадрата должны быть параллельны осям координат.

Найти уравнение вершин ромба, если известны уравнения двух его его сторон x + 2y = 4, x + 2y = 10 и уравнение одной из его диагоналей y = x + 2?

Математика | 10 – 11 классы

Найти уравнение вершин ромба, если известны уравнения двух его его сторон x + 2y = 4, x + 2y = 10 и уравнение одной из его диагоналей y = x + 2.

Уже из формы задания сторон видно, что заданы две параллельные стороны (коэффициенты при х и у пропорциональны).

А) нужно найти точки пересечения диагонали с этими сторонами — это будут две вершины.

б) найти середину диагонали : (1 ; 3)

в) найти уравнение второй диагонали (прямой, проходящей через середину и перпендикулярной заданной диагонали) : y = – x + 4

г) найти точки пересечения ее со сторонами — это будут две другие вершины :

Составить уравнение сторон квадрата, если известны координаты вершины А( – 2 ; 10) и уравнения диагоналей АС : 5х + 4y – 30 = 0, BD : 4x – 5y + 17 = 0?

Составить уравнение сторон квадрата, если известны координаты вершины А( – 2 ; 10) и уравнения диагоналей АС : 5х + 4y – 30 = 0, BD : 4x – 5y + 17 = 0.

Высоты, проведенные из одной вершины ромба, образуют угол, равный 40 градусов?

Высоты, проведенные из одной вершины ромба, образуют угол, равный 40 градусов.

Найдите : а)углы ромба ; б)углы, которые сторона ромба образует с диагоналями ;

Известны уравнения стороны АВ треугольника АВС 4x + y = 12, его высот BH 5x + 4y = 12 и АМ x + y = 6?

Известны уравнения стороны АВ треугольника АВС 4x + y = 12, его высот BH 5x + 4y = 12 и АМ x + y = 6.

Найти уравнения двух других сторон треугольника АВС.

Даны координаты вершин : треуг?

Даны координаты вершин : треуг.

АВС А(3, 1), В( – 13, – 11), С( – 6, 13).

Найти : а) длину стороны BC , б) уравнение стороны BC , в) уравнение высоты, проведённой из вершины A , г) расстояние от вершины B до стороны АС , д) уравнение медианы ВD .

Найти координаты всех вершин параллелограмма если известны координаты одной из вершин A(8, – 5) и уравнения двух его сторон : 3x + 6y = – 69 – 6x + 9y + 30 = 0?

Найти координаты всех вершин параллелограмма если известны координаты одной из вершин A(8, – 5) и уравнения двух его сторон : 3x + 6y = – 69 – 6x + 9y + 30 = 0.

Расстояние от точки пересечения диагоналей ромба до одной из его сторон равно 10, а одна из диагоналей ромба равна 40?

Расстояние от точки пересечения диагоналей ромба до одной из его сторон равно 10, а одна из диагоналей ромба равна 40.

Найдите углы ромба.

Записать координаты вершин А, В, С параллелограмма ABCD, найти координаты вершины D и точки О (пересечения диагоналей параллелограмма)?

Записать координаты вершин А, В, С параллелограмма ABCD, найти координаты вершины D и точки О (пересечения диагоналей параллелограмма).

Записать уравнение стороны АВ и высоты СН.

Даны вершины треугольника АВС : А(–3 ; 1), В(2 ; 4), С(3 ; –1)?

Даны вершины треугольника АВС : А(–3 ; 1), В(2 ; 4), С(3 ; –1).

Найти : а) уравнения сторон треугольника ; б) длины сторон ; в) уравнение высоты АК ; г) уравнения медианы АЕ ; д) уравнение прямой, проходящей через вершину В параллельно стороне АС.

Найдите углы ромба и углы, которые сторона ромба образует с диагоналями, учитывая что одна из диагоналей равна стороне ромба?

Найдите углы ромба и углы, которые сторона ромба образует с диагоналями, учитывая что одна из диагоналей равна стороне ромба.

Дан ромб со стороной 5 см и одной из диагоналей равной 6 см?

Дан ромб со стороной 5 см и одной из диагоналей равной 6 см.

Найти площадь и периметр ромба.

На этой странице сайта, в категории Математика размещен ответ на вопрос Найти уравнение вершин ромба, если известны уравнения двух его его сторон x + 2y = 4, x + 2y = 10 и уравнение одной из его диагоналей y = x + 2?. По уровню сложности вопрос рассчитан на учащихся 10 – 11 классов. Чтобы получить дополнительную информацию по интересующей теме, воспользуйтесь автоматическим поиском в этой же категории, чтобы ознакомиться с ответами на похожие вопросы. В верхней части страницы расположена кнопка, с помощью которой можно сформулировать новый вопрос, который наиболее полно отвечает критериям поиска. Удобный интерфейс позволяет обсудить интересующую тему с посетителями в комментариях.

даны уравнения двух сторон ромба 2x+y-2=0 и 2x+y-8=0 и ур-е его диагонали x+y-4=0. найти координаты вершин

даны уравнения двух сторон ромба 2x+y-2=0 и 2x+y-8=0 и ур-е его диагонали x+y-4=0. найти координаты вершин

ПОМОГИТЕ ПОЖАЛУЙСТА РЕШИТЬ. ))
нужно само решение)

я получила 2 точки с координатами, вершины из которых идет диагональ, как найти остальные точки? так то их видно и найти можно, но как это записать правильно? нужно точное решение (

Избыточное количество уравнений
х=4-у
Первые вершины:
8-2у+у-2=0 6-у=0 у=6
и. т. д
Далее рисуешь по координатам и находишь остальные точки

[spoiler title=”источники:”]

http://4apple.org/uravnenie-romba-v-dekartovoj-sisteme-koordinat/

http://matematika.my-dict.ru/q/3647007_najti-uravnenie-versin-romba-esli-izvestny/

http://sprashivalka.com/tqa/q/26537739

[/spoiler]

Вы находитесь на странице вопроса 1. Как найти точку пересечения диагоналей у ромба? из категории Геометрия.
Уровень сложности вопроса рассчитан на учащихся 10 – 11 классов. На странице
можно узнать правильный ответ, сверить его со своим вариантом и обсудить
возможные версии с другими пользователями сайта посредством обратной связи.
Если ответ вызывает сомнения или покажется вам неполным, для проверки
найдите ответы на аналогичные вопросы по теме в этой же категории, или создайте
новый вопрос, используя ключевые слова: введите вопрос в поисковую строку,
нажав кнопку в верхней части страницы.