В данном разделе продолжим изучение темы уравнения прямой в пространстве с позиции стереометрии. Это значит, что мы будем рассматривать прямую линию в трехмерном пространстве как линию пересечения двух плоскостей.
Согласно аксиомам стереометрии, если две плоскости не совпадают и имеют одну общую точку, то они также имею одну общую прямую, на которой лежат все точки, которые являются общими для двух плоскостей. Используя уравнения двух пересекающихся плоскостей, мы можем определить прямую линию в прямоугольной системе координат.
По ходу рассмотрения темы приведем многочисленные примеры, ряд графических иллюстраций и развернутых решений, необходимых для лучшего усвоения материала.
Уравнения двух плоскостей, задающих прямую линию в пространстве
Пусть даны две плоскости, которые не совпадают между собой и пересекаются. Обозначим их как плоскость α и плоскость β. Разместим их в прямоугольной системе координат Oхуz трехмерного пространства.
Как мы помним, любую плоскость в прямоугольной системе координат задает общее уравнение плоскости вида Ax+By+Cz+D=0. Будем считать, что плоскости α соотвествует уравнение A1x+B1y+C1z+D1=0, а плоскости β уравнение A2x+B2y+C2z+D2=0. В этом случае нормальные вектора плоскостей α и β n1→=(A1, B1, C1) и n2→=(A2, B2, C2) не коллинеарны, так как плоскости не совпадают между собой и е размещаются параллельно друг другу. Запишем это условие следующим образом:
n1→≠λ·n2→⇔A1, B1, C1≠λ·A2, λ·B2, λ·C2 , λ∈R
Чтобы освежить в памяти материал по теме «Параллельность плоскостей», смотрите соответствующий раздел нашего сайта.
Линию пересечения плоскостей обозначим буквой a. Т.е. a=α∩β. Эта прямая представляет собой множество точек, которые являются общими для обеих плоскостей α и β. Это значит, что все точки прямой линии a удовлетворяют обоим уравнениям плоскости A1x+B1y+C1z+D1=0 и A2x+B2y+C2z+D2=0. Фактически, они являются частным решением системы уравнений A1x+B1y+C1z+D1=0A2x+B2y+C2z+D2=0.
Общее решение системы линейных уравнений A1x+B1y+C1z+D1=0A2x+B2y+C2z+D2=0 определяет координаты всех точек линии, по которой происходит пересечение двух плоскостей α и β. Это значит, что с его помощью мы можем определить положение прямой в прямоугольной системе координат Oxyz.
Рассмотрим описанную теорию еще раз, теперь уже на конкретном примере.
Прямая Ox – это прямая, по которой пересекаются координатные плоскости Oxy и Oxz. Зададим плоскость Oxy уравнением z=0, а плоскость Oxz уравнением у=0. Такой подход мы подробно разобрали в разделе «Неполное общее уравнение плоскости», так что, в случае затруднений, можно обратиться к этому материалу повторно. В этом случае координатная прямая Ox определяется в трехмерной системе координат системой из двух уравнений вида y=0z=0.
Нахождение координат точки, лежащей на прямой, по которой пересекаются плоскости
Рассмотрим задачу. Пусть в трехмерном пространстве задана прямоугольная система координат Oхуz. Линия, по которой пересекаются две плоскости a, задана системой уравнений A1x+B1y+C1z+D1=0A2x+B2y+C2z+D2=0. Дана точка трехмерного пространства M0 x0, y0, z0.
Давайте определим, принадлежит ли точка M0 x0, y0, z0 заданной прямой линии a.
Для того, чтобы получить ответ на вопрос задачи, подставим координаты точки М0 в каждое из двух уравнений плоскости. Если в результате подстановки оба уравнения превратятся в верные равенства A1x0+B1y0+C1z0+D1=0 и A2x0+B2y0+C2z0+D2=0, то точка М0 принадлежит каждой из плоскостей и принадлежит заданной линии. Если хотя бы одно из равенств A1x0+B1y0+C1z0+D1=0 и A2x0+B2y0+C2z0+D2=0 окажется неверным, то точка М0 не принадлежит прямой линии.
Рассмотрим решение примера
Прямая линия задана в пространстве уравнениями двух пересекающихся плоскостей вида 2x+3y+1=0x-2y+z-3=0. Определите, принадлежат ли точки M0(1, -1, 0) и N0(0, -13, 1) прямой линии пересечения плоскостей.
Решение
Начнем с точки М0. Подставим ее координаты в оба уравнения системы 2·1+3·(-1)+1=01-2·(-1)+0-3=0⇔0=00=0.
В результате подстановки мы получили верные равенства. Это значит, что точка М0 принадлежит обеим плоскостям и расположена на линии их пересечения.
Подставим в оба уравнения плоскости координаты точки N0(0, -13, 1). Получаем 2·0+3·-13+1=00-2·-13+1-3=0⇔0=0-113=0.
Как вы видите, второе уравнение системы превратилось в неверное равенство. Это значит, что точка N0 не принадлежит заданной прямой.
Ответ: точка М0 принадлежит прямой линии, а точка N0 не принадлежит.
Теперь предлагаем вам алгоритм нахождения координат некоторой точки, принадлежащей прямой линии, если прямая в пространстве в прямоугольной системе координат Oxyz определяется уравнениями пересекающихся плоскостей A1x+B1y+C1z+D1=0A2x+B2y+C2z+D2=0.
Количество решений системы из двух линейных уравнений с темя неизвестными A1x+B1y+C1z+D1=0A2x+B2y+C2z+D2=0 бесконечно. Любое из этих решений может стать решением задачи.
Приведем пример.
Пусть в трехмерном пространстве задана прямая линия уравнениями двух пересекающихся плоскостей вида x+3z+7=02x+3y+3z+2=0. Найдите координаты любой из точек этой прямой.
Решение
Перепишем систему уравнений x+3z+7=02x+3y+3z+2=0⇔x+0y+3z=-72x+3y+3z=-2.
Возьмем отличный от нуля минор второго порядка в качестве базисного минора основной матрицы системы 1023=3≠0. Это значит, что z – это свободная неизвестная переменная.
Перенесем слагаемые, содержащие свободную неизвестную переменную z в правые части уравнений:
x+0y+3z=-72x+3y+3z=-2⇔x+0y=-7-3z2x+3y=-2-3z
Введем произвольное действительное число λ и примем, что z=λ.
Тогда x+0y=-7-3z2x+3y=-2-3z⇔x+0y=-7-3λ2x+3y=-2-3λ.
Для решения полученной системы уравнений применим метод Крамера:
∆=1023=1·3-0·1=2∆x=-7-3λ0–3λ3=-7-3λ·3-0·(-2-3λ)=21-9λ⇒x=∆x∆=-7-3λ∆y=1-7-3λ2-2-3λ=1·-2-3λ–7-3λ·=12+3λ⇒y=∆y∆=4+λ
Общее решение системы уравнений x+3z+7=02x+3y+3z+2=0 будет иметь вид x=-7-3λy=4+λz=λ, где λ∈R.
Для получения частного решения системы уравнений, которое даст нам искомые координаты точки, принадлежащей заданной прямой, нам необходимо взять конкретное значение параметра λ . Если λ=0, то x=-7-3·0y=4+0z=0⇔x=-7y=4z=0.
Это позволяет нам получить координаты искомой точки -7, 4, 0.
Проверим верность найденных координат точки методом подстановки их в исходные уравнения двух пересекающихся плоскостей -7+3·0+7=02·(-7)+3·4+3·0+2=0⇔0=00=0.
Ответ: -7, 4, 0
Направляющий вектор прямой, по которой пересекаются две плоскости
Давайте рассмотрим, как определить координаты направляющего вектора прямой, которая задана уравнениями двух пересекающихся плоскостей A1x+B1y+C1z+D1=0 и A2x+B2y+C2z+D2=0. В прямоугольной системе координат 0хуz направляющий вектор прямой неотделим от прямой линии.
Как мы знаем, прямая перпендикулярна по отношению к плоскости в том случае, когда она перпендикулярна по отношению к любой прямой, лежащей в данной плоскости. Исходя из вышесказанного, нормальный вектор плоскости перпендикулярен любому ненулевому вектору, лежащему в данной плоскости. Эти два факта помогут нам в нахождении направляющего вектора прямой.
Плоскости α и β пересекаются по линии a. Направляющий вектор a→ прямой линии a расположен перпендикулярно по отношению к нормальному вектору n1→=(A1, B1, C1) плоскости A1x+B1y+C1z+D1=0 и нормальному вектору n2→=(A2, B2, C2) плоскости A2x+B2y+C2z+D2=0.
Направляющий вектор прямой a представляет собой векторное произведение векторов n→1=(A1, B1, C1) и n2→=A2, B2, C2.
a→=n→1×n2→=i→j→k→A1B1C1A2B2C2
Зададим множество всех направляющих векторов прямой как λ·a→=λ·n1→×n2→, где λ – это параметр, который может принимать любые действительные значения, отличные от нуля.
Пусть прямая в пространстве в прямоугольной системе координат Oхуz задана уравнениями двух пересекающихся плоскостей x+2y-3z-2=0x-z+4=0. Найдем координаты любого направляющего вектора этой прямой.
Решение
Плоскости x+2y-3z-2=0 и x-z+4=0 имеют нормальные векторы n1→=1, 2, -3 и n2→=1, 0, -1. Примем за направляющий вектор прямой линии, являющейся пересечением двух заданных плоскостей, векторное произведение нормальных векторов:
a→=n→1×n2→=i→j→k→12-310-1=i→·2·(-1)+j→·(-3)·1+k→·1·0–k→·2·1-j→·1·(-1)-i→·(-3)·0=-2·i→-2j→-2k→
Запишем ответ в координатной форме a→=-2, -2, -2. Тем, кто не помнит, как это делается, рекомендуем обратиться к теме «Координаты вектора в прямоугольной системе координат».
Ответ: a→=-2, -2, -2
Переход к параметрическим и каноническим уравнениям прямой в пространстве
Для решения ряда задач проще использовать параметрические уравнения прямой в пространстве вида x=x1+ax·λy=y1+ay·λz=z1+az·λ или канонические уравнения прямой в пространстве вида x=x1+ax·λy=y1+ay·λz=z1+az·λ. В этих уравнениях ax, ay, az – координаты направляющего вектора прямой, x1, y1, z1 – координаты некоторой точки прямой, а λ – параметр, принимающий произвольные действительные значения.
От уравнения прямой вида A1x+B1y+C1z+D1=0A2x+B2y+C2z+D2=0 можно перейти к каноническим и параметрическим уравнениям прямой линии в пространстве. Для записи канонических и параметрических уравнений прямой нам понадобятся навыки нахождения координат некоторой точки прямой, а также координат некоторого направляющего вектора прямой, заданной уравнениями двух пересекающихся плоскостей.
Рассмотрим написанное выше на примере.
Зададим прямую линию в трехмерной системе координат уравнениями двух пересекающихся плоскостей 2x+y-z-1=0x+3y-2z=0. Напишем канонические и параметрические уравнения этой прямой.
Решение
Найдем координаты направляющего вектора прямой, который является векторным произведением нормальных векторов n1→=2, 1, -1 плоскости 2x+y-z-1=0и n2→=(1, 3, -2) плоскости x+3y-2z=0:
a→=n1→×n2→=i→j→k→21-113-2=i→·1·(-2)+j→·(-1)·1+k→·2·3–k→·1·1-j→·2·(-2)-i→·(-1)·3=i→+3·j→+5·k→
Координаты направляющего вектора прямой a→=(1, 2, 5).
Следующим шагом является определение координат некоторой точки заданной прямой линии, которыми является одно из решений системы уравнений: 2x+y-z-1=0x+3y-2z=0⇔2x+y-z=1x+3y-2z=0.
Возьмем в качестве минорной матрицы системы определитель 2113=2·3-1·1=5 , который отличен от нуля. В этом случае переменная z является свободной. Перенесем слагаемые с ней в правые части каждого уравнения и придаем переменной произвольное значение λ:
2x+y-z=1x+3y-2z=0⇔2x+y=1+zx+3y=2z⇔2x+y=1+λx+3y=2λ, λ∈R
Применяем для решения полученной системы уравнений метод Крамера:
∆=2113=2·3-1·1=5∆x=1+λ12λ3=(1+λ)·3-1·2λ=3+λ⇒x=∆x∆=3+λ5=35+15·λ∆y=21+λ12λ=2·2λ-(1+λ)·1=-1+3λ⇒y=∆y∆=-1+3λ5=-15+35·λ
Получаем: 2x+y-z-1=0x+3y-2z=0⇔x=35+15y=-15+35z=λ
Примем λ=2 для того, чтобы получить координаты точки прямой линии: x1=35+15·2y1=-15+35·2z1=2⇔x1=1y1=1z1=2. Теперь мы имеем достаточно данных для того, чтобы записать канонические и параметрические уравнения данной прямой в пространстве: x-x1ax=y-y1ay=z-z1az⇔x-11=y-13=z-25x=x1+ax·λy=y1+ay·λz=z1+az·λ⇔x=1+1·λy=1+3·λz=2+5·λ⇔x=1+λy=1+3·λz=2+5·λ
Ответ: x-11=y-13=z-25 и x=1+λy=1+3·λz=2+5·λ
Данная задача имеет еще один способ решения.
Нахождение координат некоторой точки прямой проводится при решении системы уравнений A1x+B1y+C1z+D1=0A2x+B2y+C2z+D2=0.
В общем случае ее решения можно записать в виде искомых параметрических уравнений прямой в пространстве x=x1+ax·λy=y1+ay·λz=z1+az·λ.
Получение канонических уравнений проводится следующим образом: решаем каждое из полученных уравнений относительно параметра λ, приравниваем правые части равенства.
x=x1+ax·λy=y1+ay·λz=z1+az·λ⇔λ=x-x1axλ=y-y1ayλ=z-z1az⇔x-x1ax=y-y1ay=z-z1az
Применим данный способ к решению задачи.
Зададим положение прямой линии уравнениями двух пересекающихся плоскостей 2x+y-z-1=0x+3y-2z=0. Напишем параметрическое и каноническое уравнения для этой прямой линии.
Решение
Решение системы из двух уравнений с тремя неизвестными проводится аналогично тому, как мы делали это в предыдущем примере. Получаем: 2x+y-z-1=0x+3y-2z=0⇔x=35+15·λy=-15+35·λz=λ.
Это параметрические уравнения прямой в пространстве.
Канонические уравнения получаем следующим образом: x=35+15·λy=-15+35·λz=λ⇔λ=x-3515λ=y+1535λ=z1⇔x-3515=y+1535=z1
Полученные в обоих примерах уравнения отличаются внешне, однако они эквивалентны, так как определяют одно и то же множество точек трехмерного пространства, а следовательно и одну и ту же прямую линию.
Ответ: x-3515=y+1535=z1 и x=35+15·λy=-15+35·λz=λ
Л
пересечения двух плоскостей – прямая
линия. Рассмотрим сначала частный случай
(рис. 3.9), когда одна из пересекающихся
плоскостей параллельна горизонтальной
плоскости проекций (α ׀׀
π1,
f0α
׀׀Х).
В этом случае линия пересечения а,
принадлежащая плоскости α,
будет также параллельна плоскости π1,
(рис. 3.9. а) т.
е. будет совпадать с горизонталью
пересекающихся плоскостей (а ≡ h).
Если одна из
плоскостей параллельна фронтальной
плоскости проекций (рис. 3.9. б), то линия
пересечения а, принадлежащая этой
плоскости, будет параллельна плоскости
π2
и будет совпадать с фронталью
пересекающихся
плоскостей (а ≡ f).
а)
б)
Рис. 3.9. Частный
случай пересечения плоскости общего
положения с плоскостями: а) горизонтального
уровня; б) фронтального уровня
Пример построения
точки пересечения (К) прямой а (АВ) с
плоскостью α (DEF)
показан на рис. 3.10. Для этого прямая а
заключена в произвольную плоскость β
и определена линия пересечения плоскостей
α и β.
В рассматриваемом
примере прямые АВ и MN
принадлежат одной плоскости β и
пересекаются в точке К, а т. к. прямая MN
принадлежит заданной плоскости α (DEF),
то точка К является и точкой пересечения
прямой а (АВ) с плоскостью α. (рис. 11).
Рис. 3.10. Построение
точки пересечения прямой с плоскостью
Для решения подобной
задачи на комплексном чертеже необходимо
уметь находить точку пересечения прямой
общего положения с плоскостью общего
положения.
Рассмотрим пример
нахождения точки пересечения прямой
АВ c
плоскостью треугольника DEF
представленный на рис. 3.11.
Для нахождения
точки пересечения через фронтальную
проекцию прямой А2В2
проведена фронтально-проецирующая
плоскость β которая пересекла треугольник
в точках M
и N.
На фронтальной плоскости проекций (π2)
эти точки представлены проекциями M2,
N2.
Из условия принадлежности прямой
плоскости на горизонтальной плоскости
проекций (π1)
находятся горизонтальные проекции
полученных точек M1
N1.
В пересечении горизонтальных проекций
прямых А1В1
и M1N1
образуется горизонтальная проекция
точки их пересечения (К1).
По линии связи и условиям принадлежности
на фронтальной плоскости проекций
находится фронтальная проекция точки
пересечения (К2).
В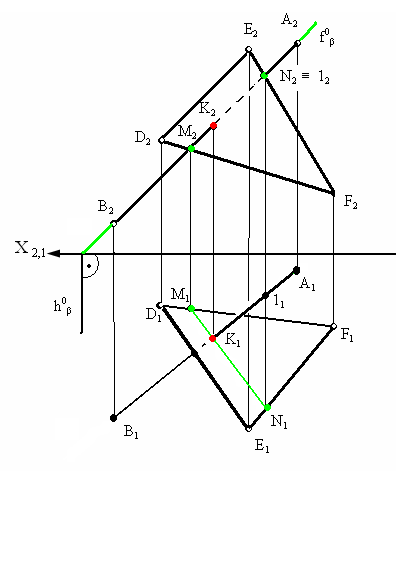
отрезка АВ относительно треугольника
DEF
определена методом конкурирующих
точек.
На плоскости π2
рассмо- трены две точки NEF
и
Рис. 3.11. Пример
определения точки
пересечения прямой
и плоскости
1АВ.
По горизонтальным проекциям этих
точек можно установить, что точка N
рас- положена ближе к наблюда-
телю (YN>Y1
), чем точка 1 (направление луча
зрения параллельно S).
Следовательно, прямая АВ, т. е. часть
прямой АВ (К1)
закрыта плоскостью DEF
на плоскости π2
(ее проекция К212
показана штриховой линией). Аналогично
установлена видимость на плоскости
π1.
Вопросы для
самоконтроля
-
В чем заключается
сущность метода конкурирующих точек
? -
Свойства прямой.
-
Каков алгоритм
определения точки пересечения прямой
и плоскости ? -
Каков алгоритм
определения линии пересечения плоскостей
? -
Какие задачи
называются позиционными ? -
Сформулируйте
условия принадлежности прямой плоскости.
Соседние файлы в папке Лекции нг
- #
- #
- #
- #
- #
- #
- #
- #
Линия пересечения плоскостей онлайн
С помощю этого онлайн калькулятора можно найти линию пересечения плоскостей. Дается подробное решение с пояснениями. Для нахождения уравнения линии пересечения плоскостей введите коэффициенты в уравнения плоскостей и нажимайте на кнопку “Решить”. Теоретическую часть и численные примеры смотрите ниже.
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Линия пересечения плоскостей − теория, примеры и решения
Две плоскости в пространстве могут быть параллельными, могут совпадать или пересекаться. В данной статье мы определим взаимное расположение двух плоскостей, и если эти плоскости пересекаются, выведем уравнение линии пересечения плоскостей.
Пусть задана декартова прямоугольная система координат Oxyz и пусть в этой системе координат заданы плоскости α1 и α2:
| α1: A1x+B1y+C1z+D1=0, | (1) |
| α2: A2x+B2y+C2z+D2=0, | (2) |
где n1={A1, B1, C1} и n2={A2, B2, C2} − нормальные векторы плоскостей α1 и α2, соответственно.
Найдем уравнение линии пересеченя плоскостей α1 и α2. Для этого рассмотрим следующие случаи:
1. Нормальные векторы n1 и n2 плоскостей α1 и α2 коллинеарны (Рис.1).
Поскольку векторы n1 и n2 коллинеарны, то существует такое число λ≠0, что выполнено равенство n1=λn2, т.е. A1=λA2, B1=λB2, C1=λC2.
Умножив уравнение (2) на λ, получим:
| α2: A1x+B1y+C1z+λD2=0, | (3) |
Если выполненио равенство D1=λD2, то плоскости α1 и α2 совпадают, если же D1≠λD2то плоскости α1 и α2 параллельны, то есть не пересекаются.
2. Нормальные векторы n1 и n2 плоскостей α1 и α2 не коллинеарны (Рис.2).
Если векторы n1 и n2 не коллинеарны, то решим систему линейных уравнений (1) и (2). Для этого переведем свободные члены на правую сторону уравнений и составим соответствующее матричное уравнение:
Как решить уравнение (4) посмотрите на странице Метод Гаусса онлайн или Метод Жоржана-Гаусса онлайн.
Так как в системе линейных уравнений (4) векторы n1={A1, B1, C1} и n2={A2, B2, C2} не коллинеарны, то решение этой системы линейных уравнений имеет следующий вид:
где x0, y0, z0, m, p, l действительные числа, а t − переменная.
Равенство (5) можно записать в следующем виде:
Мы получили параметрическое уравнение прямой, которое является линией пересечения плоскостей α1 и α2. Полученное уравнение прямой можно записать в каноническом виде:
Пример 1. Найти линию пересечения плоскостей α1 и α2:
Решение. Определим, сначала, взаимное расположение данных плоскостей. Плоскость α1 имеет нормальный вектор n1={A1, B1, C1}={1, 2, 1}. Плоскость α2 имеет нормальный вектор n2={A2, B2, C2}={2, 9, −5}.
Поскольку направляющие векторы n1 и n2 неколлинеарны, то плолскости α1 и α2 пересекаются.
Для нахождения линии пересечения влоскостей α1 и α2 нужно решить систему линейных уравнений (7) и (8). Для этого составим матричное уравнение этой системы:
Решим систему линейных уравнений (9) отностительно x, y, z. Для решения системы, построим расширенную матрицу:
Обозначим через aij элементы i-ой строки и j-ого столбца.
Первый этап. Прямой ход Гаусса.
Исключим элементы 1-го столбца матрицы ниже элемента a11. Для этого сложим строку 2 со строкой 1, умноженной на −2:
Второй этап. Обратный ход Гаусса.
Исключим элементы 2-го столбца матрицы выше элемента a22. Для этого сложим строку 1 со строкой 2, умноженной на −2/5:
Делим каждую строку матрицы на соответствующий ведущий элемент (если ведущий элемент существует):
Получим решение:
где t− произвольное действительное число.
Запишем (11) в следующем виде:
Получили уравнение линии пересечения плоскостей α1 и α2 в параметрическом виде. Запишем ее в каноническом виде.
Из равентсв выше получим каноническое уравнение прямой:
Ответ. Уравнение линии пересечения плоскостей α1 и α2имеет вид:
Пример 2. Найти линию пересечения плоскостей α1 и α2:
Решение. Определим, сначала, взаимное расположение данных плоскостей. Плоскость α1 имеет нормальный вектор n1={A1, B1, C1}={1, 2, 7}. Плоскость α2 имеет нормальный вектор n2={A2, B2, C2}={2, 4, 14}.
Поскольку направляющие векторы n1 и n2 коллинеарны (n1 можно получить умножением n2 на число 1/2), то плоскости α1 и α2 параллельны или совпадают.
При умножении уравнения на ненулевое число уравнение не изменяется. Преобразуем уравнение плоскости α2 умножив на число 1/2:
Так как нормальные векторы уравнений (14) и (16) совпадают, а свободные члены разные, то плоскости α1 и α2 не совпадают. Следовательно они параллельны, т.е. не пересекаются.
Пример 3. Найти линию пересечения плоскостей α1 и α2:
Решение. Определим, сначала, взаимное расположение данных плоскостей. Плоскость α1 имеет нормальный вектор n1={A1, B1, C1}={5, −2, 3}. Плоскость α2 имеет нормальный вектор n2={A2, B2, C2}={15, −6, 9}.
Поскольку направляющие векторы n1 и n2 коллинеарны (n1 можно получить умножением n2 на число 1/3), то плоскости α1 и α2 параллельны или совпадают.
При умножении уравнения на ненулевое число уравнение не изменяется. Преобразуем уравнение плоскости α2 умножив на число 1/3:
Так как нормальные векторы уравнений (17) и (19) совпадают, и свободные члены равны, то плоскости α1 и α2 совпадают.
Пересечение двух плоскостей
Пересечение двух плоскостей общего положения представляет собой прямую линию, поэтому для ее определения достаточно найти две
точки, принадлежащие одновременно каждой из двух заданных плоскостей – так называемые общие точки.
Чтобы найти общие точки, достаточно ввести одну или две вспомогательные секущие плоскости γ1
и γ2.
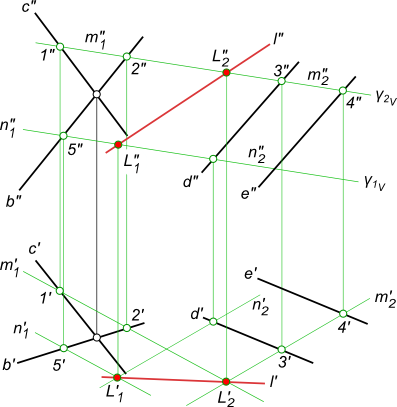
Найти пересечение двух плоскостей общего положения линию l, если плоскости заданны пересекающимися прямыми b c и
параллельными прямыми d e.
Пересечение двух плоскостей
Вспомогательная плоскость γ1 пересекает заданные плоскости по прямым n1 и n2, которые пересекаясь между собой дают первую точку искомой линии.
Вспомогательная плоскость γ2 пересекает заданные плоскости по прямым m1 и m2, которые пересекаясь между собой дают вторую точку искомой линии.
Проведя через найденные точки L1 и L2 прямую линию получаем искомое, пересечение двух плоскостей – линию l.
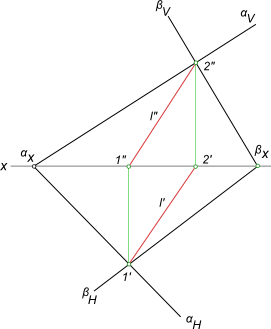
Определить линию пересечения l плоскостей заданных следами αH,
αV и βH, βV.
Пересечение двух плоскостей
Задача на пересечение плоскостей заданных следами αH,
αV и βH, βV.
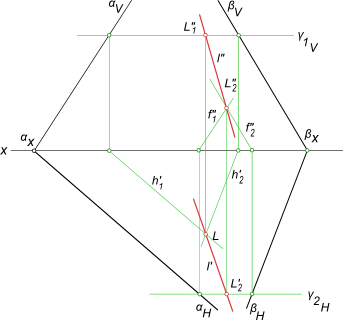
Пересечение двух плоскостей
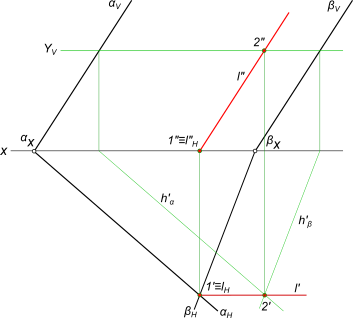
Задача на пересечение плоскостей заданных следами αH,
αV и βH, βV причем αV ║ βV.
Пересечение двух плоскостей
Пересечение двух плоскостей, заданных треугольниками ABC и DEF.
Пересечение двух плоскостей
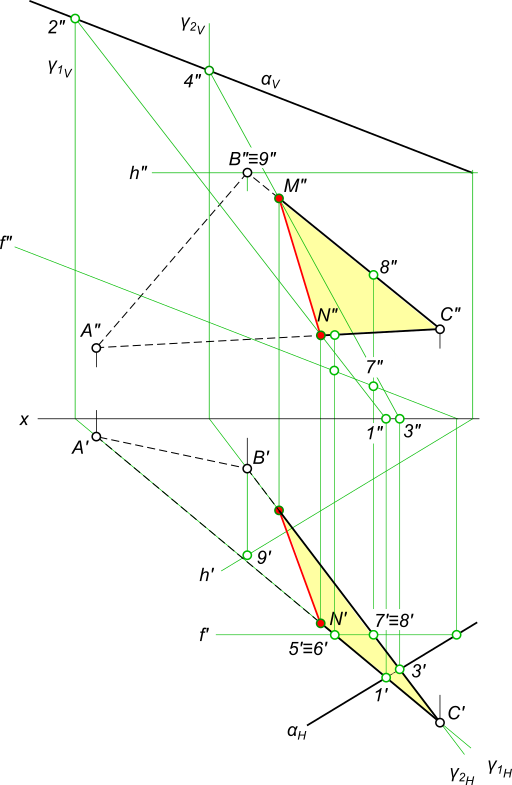
Вспомогательная плоскость γ1 пересекает заданные плоскости по прямым 1-2 и DE, которые пересекаясь между собой дают первую точку искомой линии – точка M.
Вспомогательная плоскость γ2 пересекает заданные плоскости по прямым 3-4 и AC, которые пересекаясь между собой дают вторую точку искомой линии – точка N.
Соединяем точки MN прямой линией получаем искомую линию l пересечения двух плоскостей.
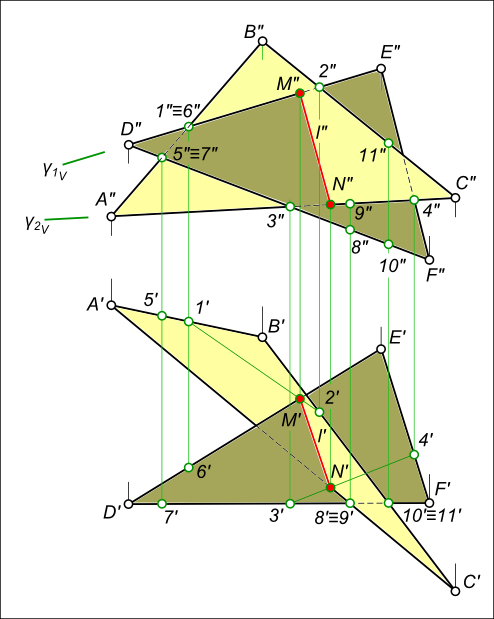
Определение видимости пересекающихся плоскостей на плоскостях проекций выполняем, используя Конкурирующие точки:
на фронтальной плоскости проекций – 1″≡6″; 1`, 6` и 5″≡ 7″; 5`, 7` – будет видна вершина D с прилегающими сторонами до линии пересечения.
на горизонтальной плоскости проекций – 8`≡9`; 8″, 9″ и 10`≡ 11`; 10″, 11″ – будет видна вершина C с прилегающими сторонами до линии пересечения.
Построить линию пересечения двух плоскостей треугольник ABC и α(αH, αV)
Пересечение двух плоскостей
Графическая работа 1 представляет задачу на пересечение двух плоскостей заданных треугольником и ромбом
+
В задаче необходимо найти линию пересечения двух плоскостей и определить натуральную величину одной из них методом плоскопараллельного перемещения.
Для решения такой классической задачи по начертательной геометрии необходимо знать следующий теоретический материал:
— нанесение проекций точек пространства на комплексный чертеж по заданным координатам;
— способы задания плоскости на комплексном чертеже, плоскости общего и частного положения;
— главные линии плоскости;
— определение точки пересечения прямой линии с плоскостью (нахождение «точки встречи»);
— метод плоскопараллельного перемещения для определения натуральной величины плоской фигуры;
— определение видимости на чертеже прямых линий и плоскостей с помощью конкурирующих точек.
Порядок решения Задачи
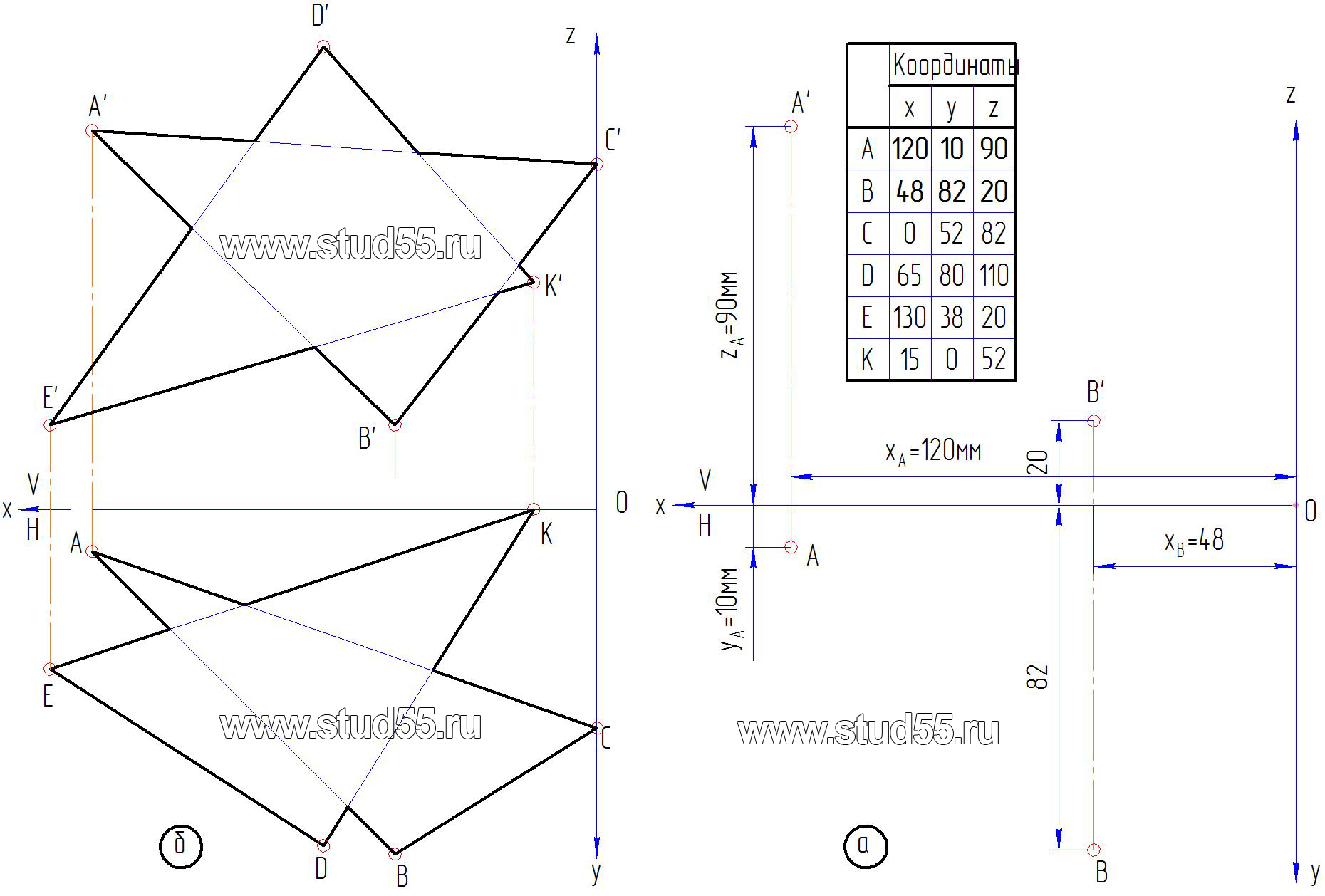
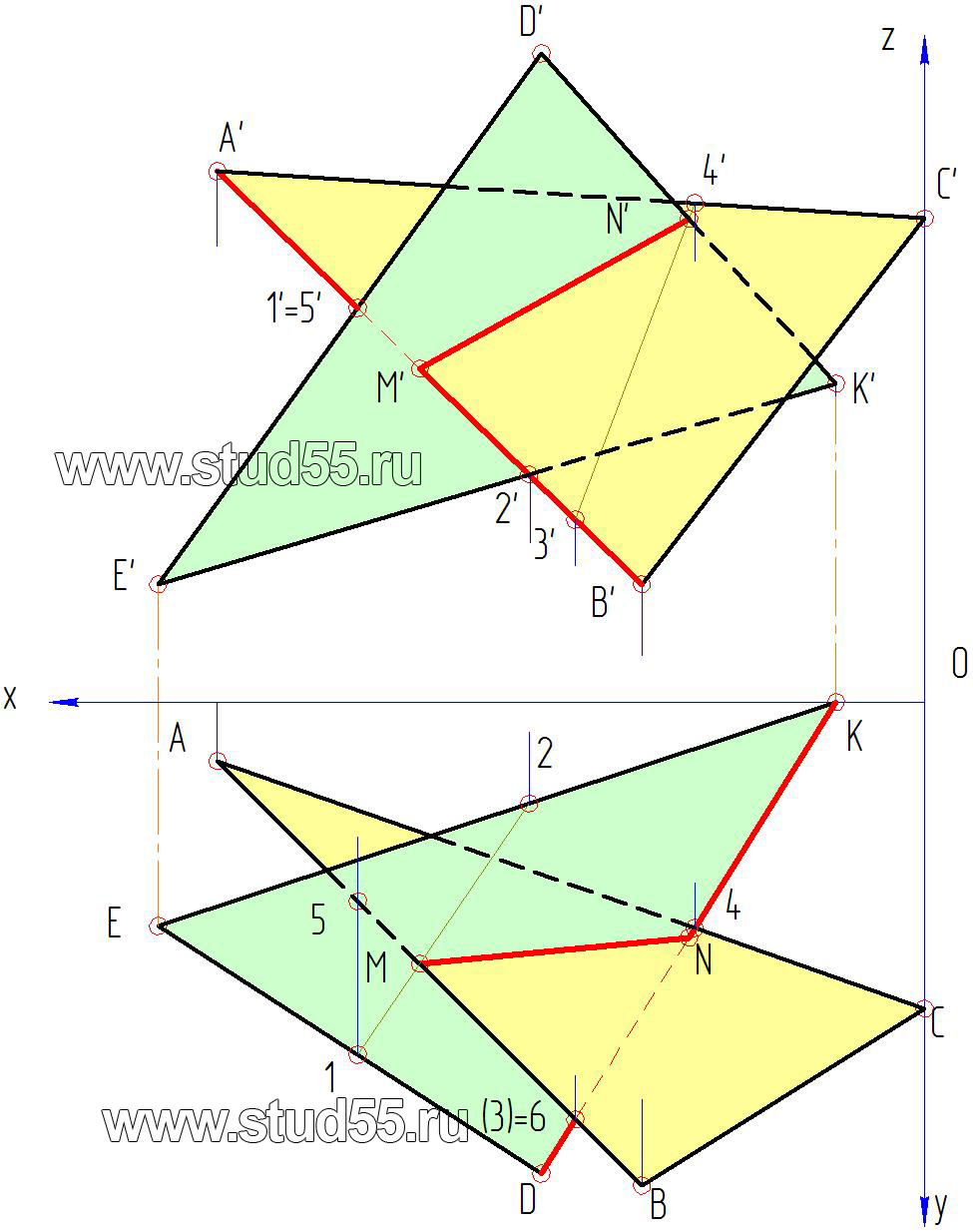
1. Согласно варианту Задания по координатам точек наносим на комплексный чертеж две плоскости, заданные в виде треугольников ABC (A’, B’, C’; A, B, C) и DKE (D’, K’, E’; D, K, Е) (рис.1.1).
Рис.1.1
2. Для нахождения линии пересечения воспользуемся методом проецирующей плоскости. Суть его в том, что берется одна сторона (линия) первой плоскости (треугольника) и заключается в проецирующую плоскость. Определяется точка пересечения этой линии с плоскостью второго треугольника. Повторив эту задачу еще раз, но для прямой второго треугольника и плоскости первого треугольника, определим вторую точку пересечения. Так как полученные точки одновременно принадлежат обеим плоскостям, они должны находиться на линии пересечения этих плоскостей. Соединив эти точки прямой, будем иметь искомую линию пересечения плоскостей.
3. Задача решается следующим образом:
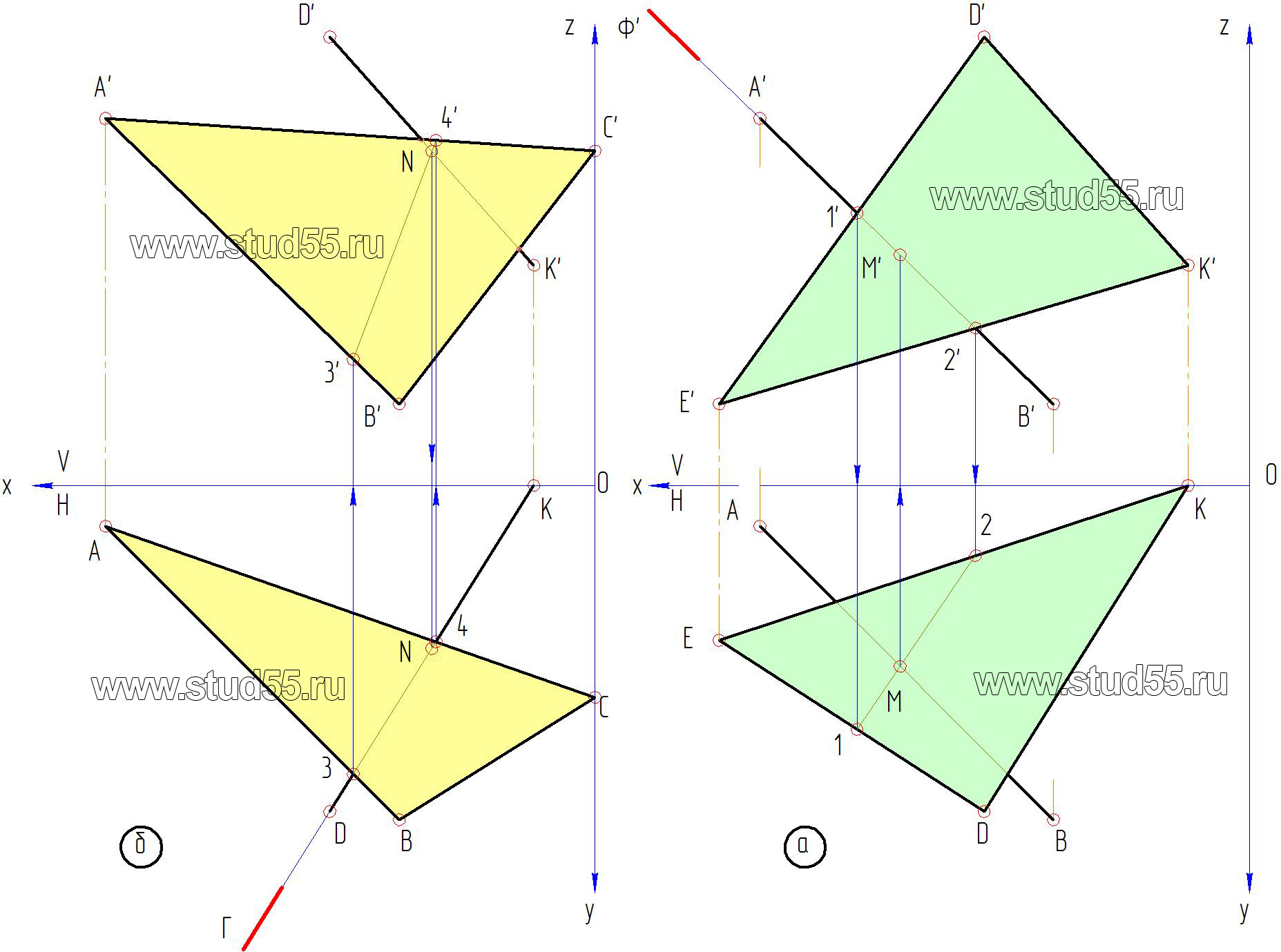
а) заключаем в проецирующую плоскость Ф(Ф’) сторону AB(A’B’) первого треугольника во фронтальной плоскости проекций V. Отмечаем точки пересечения проецирующей плоскости со сторонами DK и DE второго треугольника, получая точки 1(1’) и 2 (2’). Переносим их по линиям связи на горизонтальную плоскость проекций H на соответствующие стороны треугольника, точка 1(1) на стороне DE и точка 2(2) на стороне DK.
Рис.1.2
б) соединив проекции точек 1 и 2, будем иметь проекцию проецирующей плоскости Ф. Тогда точка пересечения прямой АВ с плоскостью треугольника DKE определится (согласно правилу) вместе пересечения проекции проецирующей плоскости 1-2 и одноименной проекции прямой AB. Таким образом, получили горизонтальную проекцию первой точки пересечения плоскостей – M, по которой определяем (проецируем по линиям связи) её фронтальную проекцию – M’ на прямой A’B’(рис.1.2.а);
в) аналогичным путем находим вторую точку. Заключаем в проецирующую плоскость Г(Г) сторону второго треугольника DK(DK). Отмечаем точки пересечения проецирующей плоскости со сторонами первого треугольника AC и BC во горизонтальной проекции, получая проекции точек 3 и 4. Проецируем их на соответствующие стороны в фронтальной плоскости, получаем 3’ и 4’. Соединив их прямой, имеем проекцию проецирующей плоскости. Тогда вторая точка пересечения плоскостей будет в месте пересечения линии 3’-4’ со стороной треугольника D’K’, которую заключали в проецирующую плоскость. Таким образом, получили фронтальную проекцию второй точки пересечения – N’, по линии связи находим горизонтальную проекцию – N (рис.1.2.б).
г) соединив полученные точки MN(MN) и (M’N’) на горизонтальной и фронтальной плоскостях, имеем искомую линию пересечения заданных плоскостей.
4. С помощью конкурирующих точек определяем видимость плоскостей. Возьмем пару конкурирующих точек, например, 1’=5’ во фронтальной проекции. Спроецируем их на соответствующие стороны в горизонтальную плоскость, получим 1 и 5. Видим, что точка 1, лежащая на стороне DЕ имеет большую координату до оси x, чем точка 5, лежащая на стороне AВ. Следовательно, согласно правилу, большей координаты, точка 1 и сторона треугольника D’Е’ во фронтальной плоскости будут видимые. Таким образом, определяется видимость каждой стороны треугольника в горизонтальной и фронтальной плоскостях. Видимые линии на чертежах проводятся сплошной контурной линией, а не видимые — штриховой линией. Напомним, что в точках пересечения плоскостей (M—N и M’-N’) будет происходить смена видимости.
Рис.1.3
Рис.1.4.
На эпюре дополнительно показано определение видимости в горизонтальной плоскости с использованием конкурирующих точек 3 и 6 на прямых DK и АВ.
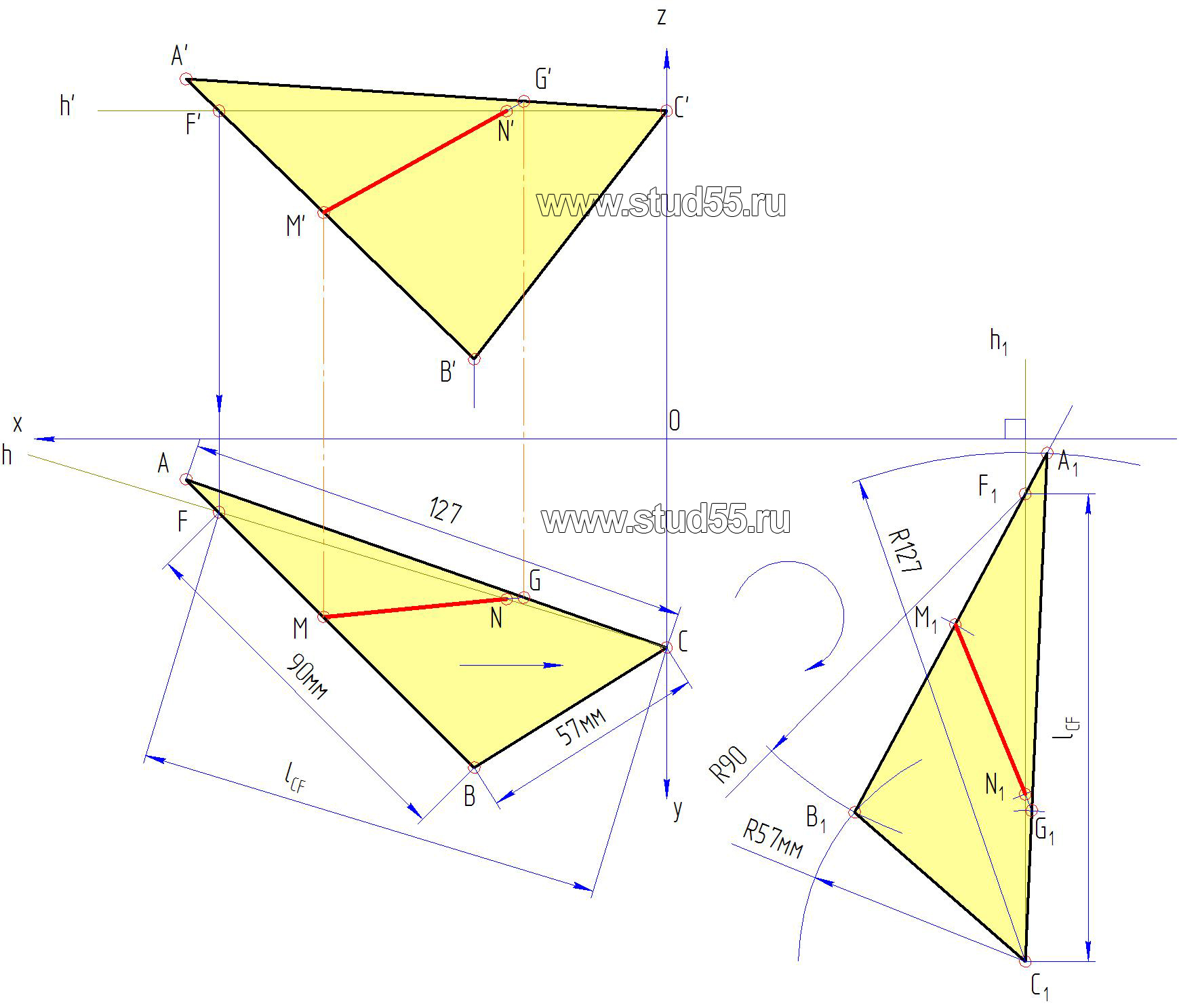
5. Методом плоскопараллельного перемещения определяем натуральную величину плоскости треугольника ABC, для чего:
а) в указанной плоскости через точку С(С) проводим фронталь C—F (С-F и C’-F’);
б) на свободном поле чертежа во горизонтальной проекции берем (отмечаем) произвольную точку С1, считая, что это одна из вершин треугольника (конкретно вершина C). Из нее восстанавливаем перпендикуляр к фронтальной плоскости (через ось х);
Рис.1.5
в) плоскопараллельным перемещением переводим горизонтальную проекцию треугольника ABC, в новое положение A1B1C1 таким образом, чтобы в фронтальной проекции он занял проецирующее положение (преобразовался в прямую линию). Для этого: на перпендикуляре от точки С1, откладываем фронтальную проекцию горизонтали C1—F1 (длина lCF) получаем точку F1. Раствором циркуля из точки F1 величиною F-A делаем дуговую засечку, а из точки C1 — засечку величиной CA, тогда в пересечении дуговых линий получаем точку A1 (вторая вершина треугольника);
— аналогично получаем точку B1 (из точки C1 делаем засечку величиной C—B (57мм), а из точки F1 величиной F—B (90мм).Заметим, что при правильном решении три точки A1 F’1 и B’1 должны лежать на одной прямой (сторона треугольника A1—B1)две другие стороны С1—A1 и C1—B1 получаются путем соединения их вершин;
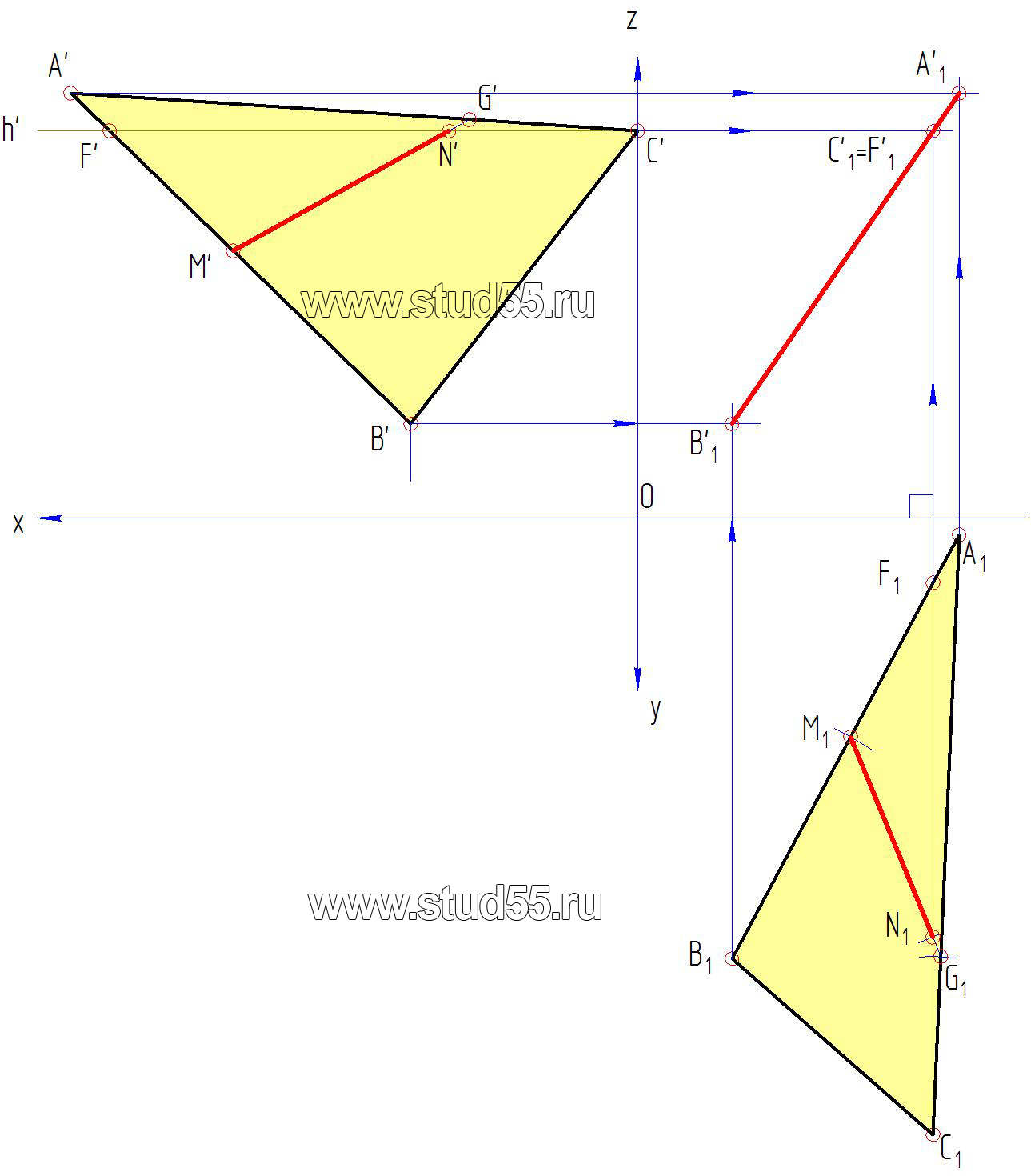
г) из метода вращения следует, что при перемещении или вращении точки в какой-то плоскости проекций — на сопряженной плоскости проекция этой точки должна двигаться по прямой линии, в нашем конкретном случае по прямой параллельной оси х. Тогда проводим из точек A’B’C’ фронтальной проекции эти прямые (их называют плоскостями вращения точек), а из фронтальных проекций перемещенных точек A1 В1 C1 восстановим перпендикуляры (линии связи) (рис.1.6).
Рис.1.6
Пересечения указанных линий с соответствующими перпендикулярами дает новые положения фронтальной проекции треугольника ABC, конкретно A’1В’1C’1 который должен стать проецирующим (прямой линией), поскольку горизонталь h1 мы провели перпендикулярно фронтальной плоскости проекций (рис.1.6);
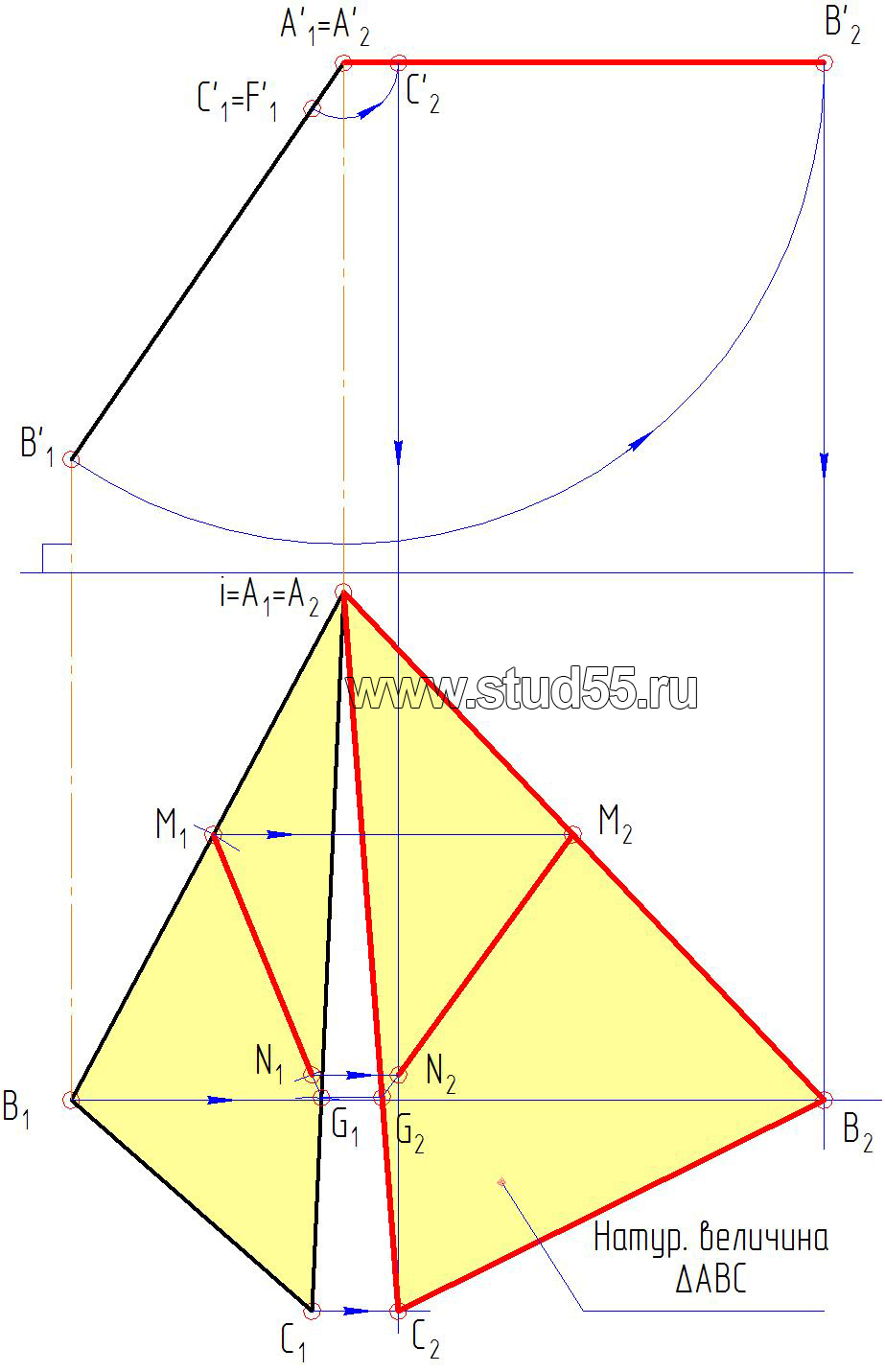
5) тогда для получения натуральной величины треугольника достаточно его фронтальную проекцию развернуть до параллельности с горизонтальной плоскостью. Разворот осуществляем с помощью циркуля через точку А’1, считая ее как центр вращения, ставим треугольник A’1В’1C’1 параллельно оси х, получаем A’2В’2C’2. Как было сказано выше, при вращении точки, на сопряженной (теперь на горизонтальной) проекции они двигаются по прямым параллельным оси х. Опуская перпендикуляры (линии связи) из фронтальных проекций точек A’2 В’2 C’2 пересечения их с соответствующими линиями находим горизонтальную проекцию треугольника ABC (A2В2C2) в натуральную величину (рис.1.7).
Рис. 1.7
У меня есть все готовые решения задач с такими координатами, купить можно >>здесь<<
Цена 55 руб, чертежи по начертательной геометрии из книжки Фролова Вы легко можете скачать сразу после оплаты или я вышлю Вам на почту. Они находятся в ZIP архиве в различных форматах:
*.jpg – обычный цветной рисунок чертежа в масштабе 1 к 1 в хорошем разрешении 300 dpi;
*.cdw – формат программы Компас 12 и выше или версии LT;
*.dwg и .dxf — формат программы AUTOCAD, nanoCAD;
Раздел: Начертательная геометрия /
- Рекомендуем
- Комментарии
- Наши товары