Как найти вершину треугольника?

Для того чтобы найти координаты вершины равностороннего треугольника, если известны координаты двух других его вершин, нужно воспользоваться одним из предложенных способов.
1 способ (графический)

- В системе координат отмечаем две заданные вершины.
- Ставим ножку циркуля в одну из построенных точек.
- Проводим окружность с радиусом, равным расстоянию между отмеченными вершинами.
- Таким же образом чертим вторую окружность с тем же радиусом, но из второй отмеченной точки.
- Точки пересечения проведённых окружностей определяют вершины треугольников (их получится два).
- Определяем координаты полученных точек, исходя из полученного чертежа.
Данный способ позволяет точно построить третью вершину. Однако определение координат является приблизительным. Метод хорошо использовать для иллюстрации.
2 способ (аналитический)
Решение задачи основано на применении формулы нахождения расстояния между двумя точками: d(A(x1;y1);B(x2;y2))=√((x2-x1)^2+(y2-y1)^2)
- Пусть имеются вершины A(x1;y1) и B(x2;y2) треугольника АВС. Обозначим координаты третьей вершины x и y (то есть, С(x;y))
- Составляем соотношения
AC=√((x-x1)^2+(y-y1)^2)
BC=√((x-x2)^2+(y-y2)^2)
AB=√((x2-x1)^2+(y2-y1)^2) - Учитывая, что треугольник равносторонний, составляем систему уравнений:
AC=BC
AC=AB
Или система уравнений:
√((x-x1)^2+(y-y1)^2)= √((x-x2)^2+(y-y2)^2)
√((x-x1)^2+(y-y1)^2)= √((x2-x1)^2+(y2-y1)^2) - Методом подстановки решаем полученную систему.
Теперь вы знаете, как найти вершину треугольника.
Внимание! Оба случая применимы только для равностороннего треугольника.
Для равнобедренного или любого другого произвольного треугольника для нахождения координат третьей вершины требуются дополнительные данные (например, значение некоторых отрезков или углов).
Уравнение описанной окружности
Как составить уравнение описанной около треугольника окружности по координатам его вершин? Как найти координаты центра описанной окружности? Как найти радиус описанной окружности, зная координаты вершин треугольника?
Решение всех этих задач сводится к одной — написать уравнение окружности, проходящей через три данные точки. Для этого достаточно подставить координаты точек (вершин треугольника) в уравнение окружности. Получим систему из трёх уравнений с тремя неизвестными: координатами центра и радиусом окружности.
Составить уравнение описанной окружности для треугольника с вершинами в точках A(2;1), B(6;3), C(9;2).
Подставив координаты вершин треугольника в уравнение окружности
![]()
получим систему уравнений
![[ left{ begin{array}{l} (2 - a)^2 + (1 - b)^2 = R^2 , \ (6 - a)^2 + (3 - b)^2 = R^2 , \ (9 - a)^2 + (2 - b)^2 = R^2 . \ end{array} right. ]](https://www.treugolniki.ru/wp-content/ql-cache/quicklatex.com-82dd95fa041ab9c8ca35f00eaea5d2ba_l3.png)
Вычтем из первого уравнения системы второе:
![]()
![]()
![]()
![]()
Теперь из второго уравнения системы вычтем третье:
![]()
![]()
![]()
Приравняем правые части равенств b=-2a+10 и b=3a-20:
![]()
![]()
![]()
![]()
Подставим в первое уравнение системы a=6 и b=-2:
![]()
![]()
![]()
a и b — координаты центра окружности, R — её радиус. Таким образом, точка (6;-2) — центр описанной около треугольника ABC окружности, радиус R=5, а уравнение описанной окружности
![]()
Для решения аналогичной задачи для четырёхугольника либо многоугольника достаточно знать координаты трёх его вершин.
Прямая на плоскости

Построение графика функции методом дифференциального исчисления
Экстремум функции двух переменных
Пример . В задачах даны координаты точек A , B , C . Требуется: 1) записать векторы AB и AC в системе орт и найти модули этих векторов; 2) найти угол между векторами AB и AC .
Решение.
1) Координаты векторов в системе орт. Координаты векторов находим по формуле:
X=xj-xi; Y=yj-yi
здесь X , Y координаты вектора; xi , yi — координаты точки Аi ; xj , yj — координаты точки Аj
Например, для вектора AB: X=x2-x1=12-7=5 ; Y=y2-y1=-1-(-4)=3
AB(5;3), AC(3;5), BC(-2;2)
2) Длина сторон треугольника. Длина вектора a(X;Y) выражается через его координаты формулой: 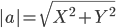
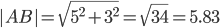
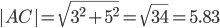
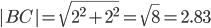
3) Угол между прямыми. Угол между векторами a1(X1;Y1) , a2(X2;Y2) можно найти по формуле: 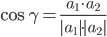
где a1a2=X1X2+Y1Y2
Найдем угол между сторонами AB и AC 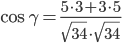
γ = arccos(0.88) = 28.07 0
8) Уравнение прямой. Прямая, проходящая через точки A1(x1; y1) и A2(x2; y2) , представляется уравнениями: 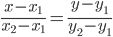
Уравнение прямой AB . Каноническое уравнение прямой: 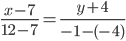 или
или 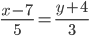
y= 3 /5x- 41 /5 или 5y-3x+41=0
| Автор | Сообщение | ||||
|---|---|---|---|---|---|
|
|||||
|
Здравствуйте, уважаемые форумчане. Помогите пожалуйста с формулой Как найти координаты третьей вершины треугольника по длинам трёх сторон и двум координатам вершин? Известны координаты точек А(x1,y1), С(x2,y2).
Использовать для вычислений Косинус и Синус угла АСВ и смещение прямой АС относительно системы координат нельзя из-за получающейся огромной погрешности при вычислениях. Я про формулу такого вида: x3 = x2 + a*cosС, y3 = y2 + a*sinС
|
||||
| Вернуться к началу |
|
||||
|
Avgust |
|
||
|
Точка А – центр окружности радиусом с Точка С – центр окружности радиусом a Пересечение двух окружностей дадут точку B, то есть ее координаты. Всего-то нужно решить систему относительно [math]x,[/math] и [math]y[/math] [math](y-y_1)^2+(x-x_1)^2=c^2[/math] [math](y-y_2)^2+(x-x_2)^2=a^2[/math] Получим два решения при допустимых соотношениях параметров (при которых треугольник может существовать) Последний раз редактировалось Avgust 26 мар 2013, 09:10, всего редактировалось 1 раз. |
|||
| Вернуться к началу |
|
||
| За это сообщение пользователю Avgust “Спасибо” сказали: panda |
|||
|
panda |
|
||
|
Спасибо за ответ. А не могли бы вы оформить его в виде формулы?
|
|||
| Вернуться к началу |
|
||
|
Avgust |
|
||
|
Формулы я получил. Но они такие громоздкие, что писать полчаса надо. Вот численно элементарно делается. Например, зададим параметры пифагорова треугольника: Тогда по команде Maple solve({(y-y1)^2+(x-x1)^2 = c^2, (y-y2)^2+(x-x2)^2 = a^2}, [x, y]); получим два решения: 1) [math]x=4 , ; , y=0[/math] 2) [math]x=frac{28}{25}, ; , y=frac{96}{25}[/math] Графическое представление этой задачи:
|
|||
| Вернуться к началу |
|
||
| За это сообщение пользователю Avgust “Спасибо” сказали: panda |
|||
|
Avgust |
|
||
|
Я добавил рисунок… x:=(1/2)*((y1-y2)*sqrt(-(-x1^2+2*x2*x1-x2^2+(-c+a-y1+y2)*(-c+a+y1-y2))*(-x1^2+2*x2*x1-x2^2+(c+a-y1+y2)*(c+a+y1-y2))*(x1-x2)^2)+(x1^3-x1^2*x2+(y2^2-2*y1*y2-c^2+y1^2+a^2-x2^2)*x1-x2*(a^2-c^2-x2^2-y2^2+2*y1*y2-y1^2))*(x1-x2))/((x1-x2)*(x1^2-2*x2*x1+x2^2+(y1-y2)^2)); y := (-sqrt(-(-x1^2+2*x2*x1-x2^2+(-c+a-y1+y2)*(-c+a+y1-y2))*(-x1^2+2*x2*x1-x2^2+(c+a-y1+y2)*(c+a+y1-y2))*(x1-x2)^2)+y1^3-y1^2*y2+(a^2+x1^2-c^2+x2^2-2*x2*x1-y2^2)*y1+y2^3+(x2^2-2*x2*x1+c^2-a^2+x1^2)*y2)/(2*y1^2-4*y1*y2+2*y2^2+2*(x1-x2)^2); Второе решение: x := (1/2)*((-y1+y2)*sqrt(-(-x1^2+2*x2*x1-x2^2+(-c+a-y1+y2)*(-c+a+y1-y2))*(x1-x2)^2*(-x1^2+2*x2*x1-x2^2+(c+a-y1+y2)*(c+a+y1-y2)))+(x1-x2)*(x1^3-x1^2*x2+(y1^2-2*y1*y2+y2^2+a^2-c^2-x2^2)*x1-x2*(-c^2-x2^2+a^2-y1^2+2*y1*y2-y2^2)))/((x1^2-2*x2*x1+x2^2+(y1-y2)^2)*(x1-x2)); y := (sqrt(-(x1-x2)^2*(-x1^2+2*x2*x1-x2^2+(c+a+y1-y2)*(c+a-y1+y2))*(-x1^2+2*x2*x1-x2^2+(-c+a+y1-y2)*(-c+a-y1+y2)))+y1^3-y1^2*y2+(a^2+x1^2-c^2+x2^2-2*x2*x1-y2^2)*y1+y2^3+(x2^2-2*x2*x1+c^2-a^2+x1^2)*y2)/(2*y1^2-4*y1*y2+2*y2^2+2*(x1-x2)^2); Формулы проверил – работают отлично. Вот если бы их суметь упростить!
|
|||
| Вернуться к началу |
|
||
| За это сообщение пользователю Avgust “Спасибо” сказали: amjava, panda, Realdreamer |
|||
|
Realdreamer |
|
||
|
Уважаемые математики Пишу программу, но к сожалению не очень силен в математических науках. Нужно как раз вершины треугольника Вообще в итоге мне нужно написать симуляцию работы вентилятора. Крутится то я его заставлю. Пытался сам найти, но видимо не так запрос формирую.
|
|||
| Вернуться к началу |
|
||
|
Realdreamer |
|
||
|
vvvv Координат всего должно быть 9 для каждой оси, но в таблице их 10 В итоге я пошёл по другому пути a = 70 и разделил её пополам. Получил координату по Y в обе стороны y1 = sqrt(a ** 2 – b ** 2) А потом по формуле окружности просто сдвинул на 120 градусов влево и вправо xn1 = sin(120 – 15) * a xn1 = sin(-120 – 15) * a От меня вам всё равно спасибо что откликнулись!
|
|||
| Вернуться к началу |
|
||
|
39 / 28 / 8 Регистрация: 14.04.2012 Сообщений: 249 |
|
|
1 |
|
Как найти координаты третьей вершины треугольника, зная все стороны и две вершины?07.07.2013, 16:27. Показов 97578. Ответов 19
Добрый день, подскажите как найти координаты третьей вершины треугольника?
0 |
|
107 / 102 / 9 Регистрация: 29.06.2013 Сообщений: 369 |
|
|
07.07.2013, 17:10 |
2 |
|
Зная то, что расстояние между двумя точками равно: Откуда и найдем координаты 3-ей точки
2 |
|
39 / 28 / 8 Регистрация: 14.04.2012 Сообщений: 249 |
|
|
07.07.2013, 17:18 [ТС] |
3 |
|
А как вывести из формулы нужную?
0 |
|
107 / 102 / 9 Регистрация: 29.06.2013 Сообщений: 369 |
|
|
07.07.2013, 17:44 |
4 |
|
Например, можно произвести смещение точки А в начало координат.
0 |
|
39 / 28 / 8 Регистрация: 14.04.2012 Сообщений: 249 |
|
|
07.07.2013, 17:46 [ТС] |
5 |
|
Извени, но я не понимаю…
0 |
|
1764 / 968 / 180 Регистрация: 24.02.2013 Сообщений: 2,782 Записей в блоге: 12 |
|
|
07.07.2013, 19:38 |
6 |
|
А так понимаете?
0 |
|
39 / 28 / 8 Регистрация: 14.04.2012 Сообщений: 249 |
|
|
07.07.2013, 20:07 [ТС] |
7 |
|
Рисунок не доступен пишет.
0 |
|
4216 / 3411 / 396 Регистрация: 15.06.2009 Сообщений: 5,818 |
|
|
07.07.2013, 21:35 |
8 |
|
Известны координаты точек А(x1,y1), С(x2,y2). Условие некорректно – переопределено. Две заданных вершины тем самым уже определяют и длину одной стороны.
0 |
|
39 / 28 / 8 Регистрация: 14.04.2012 Сообщений: 249 |
|
|
07.07.2013, 23:27 [ТС] |
9 |
|
Условие некорректно – переопределено. Две заданных вершины тем самым уже определяют и длину одной стороны. Длина и координаты две разные вещи.
0 |
|
2525 / 1751 / 152 Регистрация: 11.08.2012 Сообщений: 3,349 |
|
|
07.07.2013, 23:52 |
10 |
|
Длина и координаты две разные вещи. А Том Ардер другого и не утверждал. Читайте внимательнее.
0 |
|
1764 / 968 / 180 Регистрация: 24.02.2013 Сообщений: 2,782 Записей в блоге: 12 |
|
|
08.07.2013, 11:23 |
11 |
|
Решение
Добрый день, подскажите как найти координаты третьей вершины треугольника? Вот картинка. Миниатюры
3 |
|
39 / 28 / 8 Регистрация: 14.04.2012 Сообщений: 249 |
|
|
08.07.2013, 14:48 [ТС] |
12 |
|
А как вы выделили x и y из формулы?
0 |
|
1764 / 968 / 180 Регистрация: 24.02.2013 Сообщений: 2,782 Записей в блоге: 12 |
|
|
09.07.2013, 09:13 |
13 |
|
Справа на картинке записана система двух уравнениий – уравнений окружностей.Решив систему, получаем координаты двух точек. т.е. точек В может быть две.
0 |
|
39 / 28 / 8 Регистрация: 14.04.2012 Сообщений: 249 |
|
|
09.07.2013, 14:03 [ТС] |
14 |
|
проблема в том, что я не знаю как решить уравнение окружностей(
0 |
|
107 / 102 / 9 Регистрация: 29.06.2013 Сообщений: 369 |
|
|
09.07.2013, 14:11 |
15 |
|
Раскройте скобки, вычтите из 1 уравнения другое. Уйдут квадраты, выразите одну переменную через другую. Подставите в 1 исходное.
0 |
|
1764 / 968 / 180 Регистрация: 24.02.2013 Сообщений: 2,782 Записей в блоге: 12 |
|
|
09.07.2013, 15:16 |
16 |
|
Только проще сначала вычесть из первого уравнение второе, затем воспользоваться формулой разности квадратов.
1 |
|
0 / 0 / 0 Регистрация: 10.04.2016 Сообщений: 7 |
|
|
28.04.2016, 22:07 |
17 |
|
А можно решить как-нибудь без системы уравнений?
0 |
|
0 / 0 / 0 Регистрация: 08.04.2019 Сообщений: 6 |
|
|
10.04.2019, 13:19 |
18 |
|
Я тоже был бы не против без системы уравнений
0 |
|
1471 / 826 / 140 Регистрация: 12.10.2013 Сообщений: 5,456 |
|||||
|
10.04.2019, 21:50 |
19 |
||||
|
del Для чего тут система уравнений?
Нормализуем вектор AC и множим на длину AB стороны и крутим матрицей поворота в 2д на нужный угол. Угол треугольника найти по трем сторонам. Эх раньше бы и рис и формулы кинул…но теперь лень =). Может кто из гуру не полениться…
0 |
|
pro4vayder 1 / 1 / 0 Регистрация: 25.05.2016 Сообщений: 2 |
||||
|
04.11.2020, 09:49 |
20 |
|||
|
Прошу глянуть решение здесь. Ответ выше был близок к ответу, но человеку далекому от математики (мне) – это не особо было понятно. P.S решение выводит 2 ответа точек пересечения Кликните здесь для просмотра всего текста http://algolist.ru/maths/geom/… rcle2d.php
1 |
|
IT_Exp Эксперт 87844 / 49110 / 22898 Регистрация: 17.06.2006 Сообщений: 92,604 |
04.11.2020, 09:49 |
|
20 |
Раз уж вы нашли косинус и синус угла в треугольнике – дальше вы можете просто повернуть на этот угол вектор одной из сторон и получить направление второй стороны, а дальше нужно лишь изменить длину вектора.
Но есть и решение в векторах, вообще без тригонометрии.
Рассмотрим задачу в общем виде: у нас заданы вершины A и B, нам надо найти третью вершину треугольника С зная прилежащие к ней стороны – AC=a и BC=b соответственно. Построим окружности нужных радиусов с центрами в точках A и B, и тогда точка C как раз будет на их пересечении:

Обозначим через rA, rB и rC радиус-векторы точек. Тогда получаем следующую систему уравнений:
(rC-rA)² = a²
(rC-rB)² = b²
Решив её относительно rC можно получить ответ. Для решения первым делом вычтем одно уравнение из другого, чтобы избавиться от квадрата rC:
(rC-rA)² - (rC-rB)² = a² - b²
(rC² - 2rCrA + rA²) - (rC² - 2rCrB + rB²) = a² - b²
2rC(rB-rA) + rA² - rB² = a² - b²
2rC(rB-rA) = a² - b² - (rA² - rB²)
У нас получилось, внезапно или не очень, уравнение прямой в одном из своих форм. Этой прямой по построению принадлежат точки C и C’ – значит, это уравнение прямой CC’. Кстати, разности rB – rA будет в дальнейшем встречаться часто, поэтому обозначим её как AB (потому что это и есть вектор стороны AB).
В принципе, на этом этапе можно перейти от векторного вида к координатному, выразить через это уравнение переменную y через x или наоборот, подставить в любое уравнение окружности и решить обыкновенное квадратное уравнение. Однако, любого кто так попытается сделать, ожидает засада под названием “сингулярность”: если прямая CC’ вертикальная, то при попытке выразить y через x в формуле будет деление на ноль, а если она горизонтальная – деление на ноль будет при попытке выразить x через y.
Можно было бы просто разобрать два случая, но есть вариант лучше. Для этого надо перейти к параметрическому виду уравнения прямой СС’. Напомню, что параметрический вид уравнения прямой выглядит вот так:
r = r0 + t u
Чтобы получить параметрическое уравнение прямой, нужно знать направляющий вектор и любую точку на этой прямой. Точки C и С’ мы узнать не можем (точнее можем, но если узнаем – задача будет уже решена), поэтому попытаемся найти точку пересечения прямых CC’ и AB.
Это сделать не так сложно как кажется, потому что у нас есть уравнение прямой CC’ и мы можем составить параметрическое уравнение прямой AB:
r = rA + tAB
2r·AB = a² - b² - (rA² - rB²)
Подставим первое уравнение во второе и решим его относительно переменной t:
2(rA + tAB)·AB = a² - b² - (rA² - rB²)
2rA·AB + 2t AB² = a² - b² - (rA² - rB²)
t = (a² - b² - rA² + rB² - 2rA·AB) / 2AB²
t = (a² - b² - rA² + rB² + 2rA² - 2rA·rB) / 2AB²
t = (a² - b² + rA² + rB² - 2rA·rB) / 2AB²
t = (a² - b² + (rA - rB)²) / 2AB²
t = (a² - b² + AB²) / 2AB²
Осталось подставить эту переменную обратно в параметрическое уравнение:
t = (a² - b² + AB²) / 2AB²
r0 = rA + tAB
Формула выглядит страшно, но не имеет сингулярностей пока A и B – разные точки. Даже в случае некорректных начальных данных у тут будет какое-то решение.
Кстати, для проверки корректности формулы можно подставить сюда вырожденные треугольники: при a=0, b=AB точка r0 окажется равна rA; а при a=AB, b=0 точка r0 окажется равна rB. Пока всё нормально.
И так, у нас есть точка r0, осталось найти направляющий вектор прямой CC’. Ну, это тоже просто: надо лишь взять вектор AB и повернуть его на прямой угол в любую сторону. Это делается тоже просто, если вектор AB был с координатами (xB – xA, yB – yA) – то повёрнутый будет с координатами (-yB + yA, xB – xA). Почему так – объясняется по ссылке, которую я уже приводил ранее. Обозначим его через AB^.
Ну, теперь у нас есть параметрическое уравнение прямой CC’ и уравнение одной из окружностей, осталось их пересечь и мы найдём точки C и C’.
rC = r0 + k AB^
(rC-rA)² = a²
И снова мы можем просто подставить одно уравнение в другое (вот почему я так люблю параметрические уравнения прямых в задачах на геометрию!):
(r0-rA + k AB^)² = a²
k² AB^² + 2k AB^ (r0-rA) + (r0-rA)² - a² = 0
Тут есть и дальнейшие упрощения: вектор r0–rA сонаправлен AB, а потому при умножении на AB^ будет чистый ноль, можно и не считать. Кстати, длина вектора AB^ равна длине вектора AB, что тоже позволяет чуть упростить формулу.
Суммируя всё что написано выше, получаем следующую систему уравнений:
t = (a² - b² + AB²) / 2AB²
k² AB² = a² - t² AB²
r0 = rA + t AB
rC = r0 + k AB^
Осталось решить примитивное квадратное уравнение:
t = (a² - b² + AB²) / 2AB²
k = ± sqrt(a² / AB² - t²)
rC = rA + t AB + k AB^
Дальше осталось перейти от векторов к координатам и решение готово.
Дано: у нас есть треугольник, нам известны только координаты его вершин. У нас есть точка, нам известны её координаты.
Что нужно узнать: нужно установить принадлежность точки треугольнику.
В данной статье разбирается несколько разных методов определения принадлежности точки треугольнику.
Метод сравнения площадей
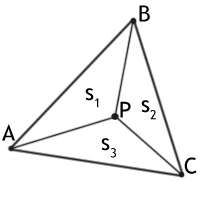
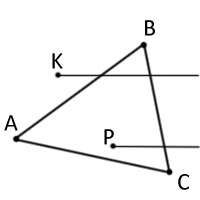
В данном методе сначала находятся площади 3-х треугольников, которые образует данная точка с каждой стороной треугольника. В нашем случае(рис. 1) это треугольники ABP, BCP, CAP и их площади s1, s2, s3 соответственно.
Затем находится площадь самого треугольника ABC.
Найденный площади сравниваются — если сумма 3-х площадей равна площади всего треугольника, то значит точка принадлежит треугольнику. При сравнении, как правило, задаётся погрешность.
Так как у нас известны только координаты точек, то все площади, находятся по формуле Герона, от обильности операций которой становится ясно, почему этот метод очень трудоёмкий.
Простейшая реализация алгоритма:
|
// проверка принадлежности точки треугольнику формулами Герона function IsPointIn_Geron(aAx, aAy, aBx, aBy, aCx, aCy, aPx, aPy: single): boolean; // funcs // площадь треугольника по точкам function Square(aAx, aAy, aBx, aBy, aCx, aCy: single): single; begin Result := abs(aBx*aCy – aCx*aBy – aAx*aCy + aCx*aAy + aAx*aBy – aBx*aAy); end; var s : single; begin s := Square(aPx, aPy, aAx, aAy, aBx, aBy) + Square(aPx, aPy, aBx, aBy, aCx, aCy) + Square(aPx, aPy, aCx, aCy, aAx, aAy); Result := abs(Square(aAx, aAy, aBx, aBy, aCx, aCy) – s) <= 0.01{погрешность}; end; |
Атрибуты функции: aAx, aAy, aBx, aBy, aCx, aCy — координаты точек A, B, C треугольника; aPx, aPy — координаты точки, принадлежность которой надо определить.
Метод относительности
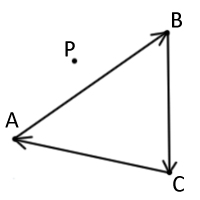
Данный метод заключается в следующем. Сначала выбирается ориентация движения по вершинам треугольника(по часовой или против часовой стрелке). Я выбираю по часовой. На рисунке 2 выбранная ориентация движения(по часовой) показана стрелками. По данной ориентации проходим все стороны треугольника, рассматривая их как прямые, и рассчитываем по какую сторону от текущей прямой лежит наша точка. Не трудно догадаться, что если точка для всех прямых, при нашей ориентации, лежит с правой стороны, то значит точка принадлежит треугольнику, а если хоть для какой-то прямой она лежит с левой стороны, то значит условие принадлежности не выполняется.
На рисунке 2 продемонстрирована ситуация, когда точка только для одной прямой AB лежит по левую сторону, а значит не принадлежит треугольнику.
Реализация алгоритма:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 |
// проверка прин. точки треуг. методом относительности положения function IsPointIn_Relat(aAx, aAy, aBx, aBy, aCx, aCy, aPx, aPy: single): boolean; // funcs function Q(ax, ay, bx, by, atx, aty: single): single; begin Result := atx * (by – ay) + aty * (ax – bx) + ay * bx – ax * by; end; var q1, q2, q3 : single; begin // выбираем определённую ориентацию по вершинам(чтоб было по порядку) // универсальный q1 := Q(aAx, aAy, aBx, aBy, aPx, aPy); q2 := Q(aBx, aBy, aCx, aCy, aPx, aPy); q3 := Q(aCx, aCy, aAx, aAy, aPx, aPy); Result := ((q1 >= 0) and (q2 >= 0) and (q3 >= 0)) or ((q1 < 0) and (q2 < 0) and (q3 < 0)); //} { // для строгой ориентации по часовой Result := (Q(ftx1, fty1, ftx2, fty2, fpx, fpy) >= 0) and (Q(ftx2, fty2, ftx3, fty3, fpx, fpy) >= 0) and (Q(ftx3, fty3, ftx1, fty1, fpx, fpy) >= 0); //} { // для строгой ориентации против часовой Result := (Q(ftx1, fty1, ftx2, fty2, fpx, fpy) <= 0) and (Q(ftx2, fty2, ftx3, fty3, fpx, fpy) <= 0) and (Q(ftx3, fty3, ftx1, fty1, fpx, fpy) <= 0); //} end; |
Всё относительно!
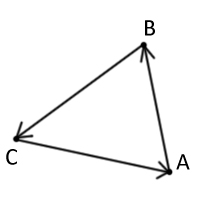
Тут надо кое что пояснить, весьма не маловажное, что может сыграть роль в оптимизации и выборе алгоритма. Обратите внимание, что в приведённом коде есть закомментированные блоки кода с комментариями «для строгой ориентации», в то время как рабочий код универсален — он предназначен для любой ориентации. Т.е. представленный код определит принадлежность точки для любого заданного треугольника. В моей тестирующей программе треугольники как раз таки строятся по random()-у координат вершин, а ориентация идёт по вершинам(A>B>C>A). Для рисунка 2 — это по часовой стрелки, но для рисунка 3 — это против часовой.
Так вот, в случае рисунка 3 точка должна лежать по левую сторону векторов, чтобы принадлежать треугольнику.
Вот тут и получается важный момент! Если вы уверены, что в вашем проекте все треугольники будут ориентированы по часовой стрелке(а т.е. вершина C будет всегда правее вектора AB), то вам можно закомментировать блок универсального решения и раскомментировать блок «для строгой ориентации по часовой» и данный алгоритм упрощается аж на 3 логических операции!
Векторный метод
Третий метод который я освещаю для меня самый интересный.
Идея его применения зарождается если взглянуть на треугольник как на половинку параллелограмма…
Данный метод я сначала проверил на бумаге. После всех оптимизаций формул, как всё сошлось, я реализовал его в коде, где он показал себя вполне успешным и результативным. Аж эффективнее 2-х предыдущих методов :]
Алгоритм такой:
1) одну вершину треугольника помещаем в координаты (0;0);
2) две стороны, выходящие из этой вершины, представляем как вектора.
Таким образом из всего этого появляется система простых условий нахождения точки P между векторами b и c.(рис. 4)

Смотрим код:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
function IsPIn_Vector(aAx, aAy, aBx, aBy, aCx, aCy, aPx, aPy: single): boolean; var Bx, By, Cx, Cy, Px, Py : single; m, l : single; // мю и лямбда begin Result := False; // переносим треугольник точкой А в (0;0). Bx := aBx – aAx; By := aBy – aAy; Cx := aCx – aAx; Cy := aCy – aAy; Px := aPx – aAx; Py := aPy – aAy; // m := (Px*By – Bx*Py) / (Cx*By – Bx*Cy); if (m >= 0) and (m <= 1) then begin l := (Px – m*Cx) / Bx; if (l >= 0) and ((m + l) <= 1) then Result := True; end; end; |
По коду можно увидеть, что находятся новые координаты точек B и C, которые одновременно являются векторами b и c (рис. 4.). А новые координаты точки P являются вектором (Px, Py). Далее идёт формула, которую я предварительно свёл к общему виду и упростил.
Кол-во основных операций получается 13(+4). Совсем не плохо :]
Метод геометрического луча
Это достаточно известный метод, особенно когда определяется принадлежность точки многоугольникам. Часто данный метод называют «трассировка луча», хотя это не совсем правильно, т.к. трассировка луча — это расчёт хода световых лучей в 3D сцене.
Суть в том, что из данной точки пускается луч по какой-либо оси в каком-либо направлении.
Затем проверяются пересечения со сторонами многоугольника и ведётся подсчёт пересечений.
Таким образом если кол-во пересечений чётное, то значит точка лежит вне многоугольника, если же кол-во НЕчётное, то значит точка лежит внутри.
На рисунке 5 изображены две подопытные точки P и K, у луча из точки P одно пересечение со сторонами треугольника, таким образом точка P принадлежит фигуре, а точке K не повезло — у неё два пересечения.
Реализация алгоритма:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 |
function IsPIn_RayCast(aAx, aAy, aBx, aBy, aCx, aCy, aPx, aPy: single): boolean; // funcs // p1 – начало 1ого отрезка, p2 – конец 1ого отрезка, p3 – начало 2ого отрезка, p4 – конец 2ого отрезка function peresechenie(p1, p2, p3, p4: TPoint): boolean; var zn, ua, ub : single; begin // 25 операций zn := (p4.y – p3.y) * (p2.x – p1.x) – (p4.x – p3.x) * (p2.y – p1.y); ua := ((p4.x–p3.x)*(p1.y–p3.y) – (p4.y–p3.y)*(p1.x–p3.x)) / zn; ub := ((p2.x–p1.x)*(p1.y–p3.y) – (p2.y–p1.y)*(p1.x–p3.x)) / zn; // если ‘ua’ и ‘ub’ принадлежат [0,1] то отрезки пересекаются Result := (ua >= 0) and (ua <= 1) and (ub >= 0) and (ub <= 1); end; var cros_cnt : integer; s1, s2 : single; // коэф. begin cros_cnt := 0; // кол-во пересечений граней (лучом из точки) // луч пускаем по оси X вправо // 1-я сторона треугла s2 := (aPy – aAy) / (aBy – aAy); s1 := aAx – aPx + s2 * (aBx – aAx); if (s1 >= 0) and (s2 >= 0) and (s2 <= 1) then inc(cros_cnt); // 2-я сторона треугла s2 := (aPy – aBy) / (aCy – aBy); s1 := aBx – aPx + s2 * (aCx – aBx); if (s1 >= 0) and (s2 >= 0) and (s2 <= 1) then inc(cros_cnt); // 3-я сторона треугла if cros_cnt < 2 then begin s2 := (aPy – aCy) / (aAy – aCy); s1 := aCx – aPx + s2 * (aAx – aCx); if (s1 >= 0) and (s2 >= 0) and (s2 <= 1) then inc(cros_cnt); end; Result := cros_cnt = 1; end; |
Вроде нормально упростил(для треугольника имею ввиду), но что-то мне кажется, что может быть и по круче…
А так, получается примерно 30 операций.
Сравнение скоростей
Ну вот мы и подошли к самому интересному! Кто быстрее и сильнее!? :]
Я провёл тест со следующими параметрами(хотя всё зависит от процессора):
- кол-во повторений алгоритма за 1 имитацию = 4 миллиона.
- кол-во имитаций для каждого алгоритма = 1000.
Таблица результатов:
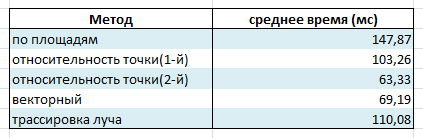
Ну что сказать, векторный метод хорош)
С ним конечно соперничает второй способ относительности точки, но главное отличие в том, что для отн. точки необходима строгая ориентация сторон треугольника, а для векторного это не важно, поэтому он круче)
Так же можно скачать написанную в ходе экспериментов программу: prin_tochki_proga. Программа реализована на Delphi 2007.








 Сообщение было отмечено как решение
Сообщение было отмечено как решение

