Как найти координаты точки в момент времени

Прямолинейное равномерное движение является наиболее простым и понятным типом механического движения. Подробнее узнать про этот вид движения можно здесь.

Для нахождения координаты тела при равномерном прямолинейном движении используется довольно простая формула:

Формула координаты тела при равномерном прямолинейном движении

Таким образом, для того, чтобы найти координату тела при равномерном прямолинейном движении необходимо знать только начальную координату тела, его скорость и время в пути. Вы можете подставить эти значения в наш онлайн калькулятор и получить результат.

Движение материальной точки в пространстве – это изменение ее положения относительно других тел с течением времени.

Имеет смысл говорить только о движении в некоторой системе отсчета.

Система отсчета. Системы координат

Точки, располагаемые в пустом пространстве, не различаются. Поэтому о точке рассуждают при условии нахождения в ней материальной точки. Определить ее положение можно при помощи измерений в системе координат, где и проводится нахождение пространственных координат. Если рассматривать в виде примера поверхность Земли, то следует учитывать широту и долготу располагаемой точки.

В теории используется декартова прямоугольная система координат, где определение точки возможно при наличии радиус-вектора r и трех проекций x, y, z – ее координат. Могут быть применены другие:

• сферическая система с положением точек и ее радиус-вектором, определенных координатами r, υ, φ;
• цилиндрическая система с координатами p, z, α;
• на полярной плоскости с параметрами r, φ.

В теории зачастую не принимают во внимание реальную систему отсчета, а сохраняют только ту, которая представляет собой ее математическую модель, применяемую во время практических измерений.

Кинематическое уравнение движения материальной точки

Любая система отсчета или координат предполагает определение координат материальной точки в любой момент времени.

Аналитически положение точки определяется совокупностью трех независимых между собой чисел. Иначе говоря, свободная точка имеет три степени свободы движения.

Ее перемещение по уравнению (1) определено, если имеется указанное положение в любой момент времени t. Для этого следует задавать декартовы координаты точки в качестве однозначных и непрерывных функций времени:

x(t)=x, y(t)=y, z(t)=z (2).

Прямоугольные декартовы координаты x, y, z – это проекции радиус-вектора r¯, проведенного из начала координат. Очевидно, что длину и направление r¯ можно найти из соотношений, где a, β, γ являются образованными радиус-вектором углами с координатными осями.

Равенства (2) считают кинематическими уравнениями движения материальной точки в декартовых координатах.

Они могут быть записаны в другой системе координат, которая связана с декартовой взаимно однозначным преобразованием. Если движение точки происходит в плоскости Оху, тогда применимы полярные координаты r, φ, относящиеся к декартовым преобразованиям. Данный случай подразумевает использование уравнения движения точки следующего вида:

r=r(t), φ=φ(t) (3).

Кинематическое уравнение движения точки в криволинейных координатах q1, q2, q3, связанных с декартовыми преобразованиями вида x=x(q1, q2, q3), y=y(q1, q2, q3), z=z(q1, q2, q3) (4), записывается как

q1=q1(t), q2=q2(t), q3=q3(t) (5).

Кривая радиус-вектора, описываемая концом вектора r при движении точки, совпадает с ее траекторией. Параметрическое уравнение траектории с t представлено кинематическими уравнениями (2), (5). Чтобы получить координатное уравнение траектории следует исключить время из кинематических уравнений.

Понятия координатного и естественного способа задания движения точки физически эквивалентны. С математической стороны это рассматривают как возможность применения разных методов, исходя из случая математической задачи.

Задание такого закона возможно аналитическим, графическим путем или с использованием таблицы, последние два из которых зачастую рассматривают в виде графиков и расписаний движений поездов.

Уравнение координаты при равноускоренном прямолинейном движении

теория по физике 🧲 кинематика

Уравнение координаты — зависимость координаты тела от времени:

Уравнение координаты при равноускоренном прямолинейном движении:

x₀ — координата тела в начальный момент времени, v_0x —проекция начальной скорости на ось ОХ, a_x —проекция ускорения на ось ОХ, x — координата тела в момент времени t

Зная уравнение координаты, можно определить координату тела в любой момент времени.

Пример №1. Движение автомобиля задано уравнением:

Определить начальное положение автомобиля относительно тела отсчета, его начальную скорость и ускорение. Также найти положение тела относительно тела отсчета в момент времени t = 10 c.

Уравнение координаты — это многочлен. В уравнении выше оно включает в себя только 2 многочлена. Первый — 15 — соответствует начальной координате тела. Поэтому x₀ = 15. Коэффициент перед квадратом времени второго многочлена соответствует ускорению тела. Поэтому a = 5 м/с 2 . Второй многочлен отсутствует. Это значит, что коэффициент перед t равен 0. Поэтому начальная скорость тела равна нулю: v₀ = 0 м/с.

В момент времени t = 10 c координата автомобиля равна:

Совместное движение двух тел

Иногда в одной системе отсчета рассматривается движение сразу двух тел. В этом случае движение каждого тела задается своим уравнением. Эти уравнения используются для нахождения различных параметров движения этих тел. Такой способ решения задач называется аналитическим.

Аналитический способ решения задачи на совместное движение тел

Чтобы найти место встречи двух тел, нужно:

1. Построить уравнения зависимости x(t) обоих тел: x1(t) и x2(t).
2. Построить уравнение вида x₁ = x₂.
3. Найти время встречи двух тел t_встр.
4. Подставить найденной время в любое из уравнений x1(t) или x2(t), чтобы вычислить координату x_встрч.

Пример №2. По одному направлению из одной точки начали двигаться два тела. Первое тело движется прямолинейно и равномерно со скоростью 3 м/с. Второе тело — равноускорено с ускорением 1 м/с 2 без начальной скорости. Определите, через какое время второе тело догонит первое. Вычислите, на каком расстоянии от тела отсчета это произойдет.

Составим уравнения для движения каждого из тел:

Приравняем правые части этих уравнений и найдем время t:

Корень – осевой, обычно подземный вегетативный орган высших сосудистых растений, обладающий неограниченным ростом в длину и положительным геотропизмом. Корень осуществляет закрепление растения в почве и обеспечивает поглощение и проведение воды с растворёнными минеральными веществами к стеблю и листьям.

Чтобы найти, какое расстояние они пройдут за это время, подставим известное время в любое из уравнений:

x = 3t = 3∙6 = 18 (м).

Графический способ решения задачи на совместное движение тел

Существует графический способ решения данной задачи. Для этого нужно:

1. Построить графики x1(t) и x2(t).
2. Найти точку пересечения графиков.
3. Пустить перпендикуляр из этой точки к оси ОХ.
4. Значение точки пересечения — координата места пересечения двух тел.

Таким способом можно определить, в какое время произойдет встреча двух тел. Нужно лишь провести перпендикуляр к оси времени после построения графиков перемещений.

Графический способ решения задач требует высокой точности построения графиков. Поэтому он применяется редко!

Если в одной системе описывается движение двух тел, и одно тело начинает движение с опозданием t_запазд, то его уравнение координаты принимает

Вид — группа особей, сходных по морфолого-анатомическим, физиолого-экологическим, биохимическим и генетическим признакам, занимающих естественный ареал, способных свободно скрещиваться между собой и давать плодовитое потомство.

Пример №3. Мальчики соревнуются в беге. По команде «Старт!» Миша побежал с ускорением 1 м/с 2 и через 4 секунды достиг максимальной скорости, с которой дальше продолжил движение. Саша отреагировал с опозданием и начал движение спустя 1 с после команды с ускорением 1,5 м/с 2 , достигнув максимальной скорости через 3 секунды. Найти время, через которое Саша догонит Мишу.

Если Саша догонит Мишу до того, как мальчики станут двигаться с равномерной скоростью, уравнение движения с равномерной скоростью можно игнорировать. Если это так, то корнем уравнения будет время, не превышающее 4 с (через столько времени оба мальчика начнут двигаться равномерно).

В таком случае составим уравнения только для тех участков пути, на которых мальчики двигались равноускорено:

Приравняем правые части уравнений и вычислим t:

В результате получаем два

Корень – осевой, обычно подземный вегетативный орган высших сосудистых растений, обладающий неограниченным ростом в длину и положительным геотропизмом. Корень осуществляет закрепление растения в почве и обеспечивает поглощение и проведение воды с растворёнными минеральными веществами к стеблю и листьям.

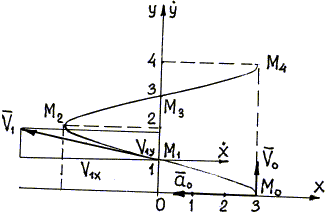
Материальная точка движется прямолинейно с постоянным ускорением. График зависимости её координаты от времени x=x(t) изображён на рисунке.

В момент времени t=0 проекции её скорости υ_x и ускорения a_x на ось Ох удовлетворяют соотношениям:

а)

б)

в)

г)

Алгоритм решения

1. Определить характер движения материальной точки.
2. Записать уравнение координаты материальной точки.
3. С помощью графика зависимости координаты от времени и уравнения координаты определить проекции искомых величин.

Решение Графиком зависимости координаты от времени является парабола. Такой график соответствует равноускоренному прямолинейному движению. Уравнение координаты при равноускоренном прямолинейном движении имеет вид: 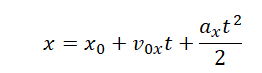Ветви параболы смотрят вверх. Это значит, что коэффициент перед квадратом переменной величины (времени) стоит положительный коэффициент. Следовательно, a_x>0. Поэтому варианты «б» и «г» исключаются. Остается выяснить, чему равна скорость: она равна нулю (как в ответе «а») или меньше нуля (как в ответе «в»)? Моменту времени t=0 соответствует точка, являющая вершиной параболы. Когда ветви параболы смотрят вверх, в ее вершине скорость тела всегда равна нулю, так как эта точка лежит на границе между отрицательной и положительной скоростью. Отсюда делаем вывод, что верный ответ «а».Ответ: а

pазбирался: Алиса Никитина | обсудить разбор | оценить

Алгоритм решения

1. Записать исходные данные.
2. Записать уравнение движения грузовика и преобразовать его с учетом условий задачи.
3. Выразить скорость грузовика из уравнения его движения.
4. Записать уравнение движения мотоциклиста.
5. Найти время встречи мотоциклиста и грузовика из уравнения движения мотоциклиста.
6. Подставить время в формулу скорости грузовика и вычислить ее.

Решение

• Координата встречи грузовика и мотоциклиста: x = 150 м.
• Время запаздывания мотоциклиста: t_запазд = 5 с.
• Ускорение, с которым мотоциклист начал движение: a = 3 м/с 2 .

Запишем уравнение движения грузовика:

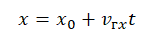
Так как начальная координата равна нулю, это уравнение примет

Вид — группа особей, сходных по морфолого-анатомическим, физиолого-экологическим, биохимическим и генетическим признакам, занимающих естественный ареал, способных свободно скрещиваться между собой и давать плодовитое потомство.

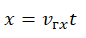
Отсюда скорость движения грузовика равна:

Запишем уравнение движения мотоциклиста:

Так как начальная координата равна нулю, начальная скорость тоже нулевая, и мотоциклист начал движение позже грузовика, это уравнение примет вид:

Найдем время, через которое грузовик и мотоциклист встретились:

Подставим найденное время встречи в формулу для вычисления проекции скорости грузовика:

pазбирался: Алиса Никитина | обсудить разбор | оценить

Уравнение зависимости координаты от времени по графику

1 мин = 60 с; 1 ч = 3600 с; 1 км = 1000 м; 1 м/с = 3,6 км/ч.

ПРИМЕРЫ РЕШЕНИЯ ТИПОВЫХ ЗАДАЧ

Типовая задача «Уравнение координаты (нахождение неизвестной величины)»

Задача № 1. В начальный момент времени тело находилось в точке с координатой 5 м, а через 2 мин от начала движения — в точке с координатой 95 м. Определите скорость тела и его перемещение.

Типовая задача «Уравнение координаты. Движение двух тел»

Задача № 2. Движение двух тел задано уравнениями x₁ = 20 – 8t и х₂ = –16 + 10t (время измеряется в секундах, координата — в метрах). Определите для каждого тела начальную координату, проекцию скорости, направление скорости. Вычислите время и место встречи тел.

Типовая задача «График координаты»

Задача № 3. Движение тела задано графиком координаты (зависимости координаты от времени). По графику определите: а) начальную координату тела; б) проекцию скорости тела; в) направление движения тела (по оси х или против оси х); г) запишите уравнение координаты.

Типовая задача «График координаты. Движение нескольких тел»

Задача № 4. На рисунке изображены графики движения трех тел. Изучив рисунок, для каждого тела определите: а) начальную координату; б) скорость; в) направление движения; г) запишите уравнение координаты.

ЗАДАЧИ ПОСЛОЖНЕЕ

Задача № 5. На рисунке представлены графики зависимости координаты х от времени t для пяти тел. Определите скорости этих тел. Проанализируйте точки пересечения графиков. Постройте графики зависимости скорости от времени.

РЕШЕНИЕ:

Задача № 6. По графикам на рисунке напишите уравнения движения x = x(t) . Из уравнений и графиков найдите координаты тел через 5 с , скорости движения тел, время и место встречи второго и третьего тел.

РЕШЕНИЕ:

Задача № 7. ОГЭ Расстояние ( S ) между городами М и К = 250 км . Одновременно из обоих городов навстречу друг другу выезжают автомашины. Машина из города М движется со скоростью = 60 км/ч , из города К — со скоростью ν₂ = 40 км/ч . Построить график зависимости пути от времени для каждой из машин и по ним определить место встречи и время их движения до встречи.

Задача № 8. ЕГЭ Скорость течения реки v_p = 1 м/с , скорость лодки относительно воды v₀ = 2 м/с . Под каким углом к берегу следует держать курс, чтобы лодка двигалась перпендикулярно берегу? За какое время t она переправится через реку, ширина которой d = 200 м ?

Алгоритм решения ЗАДАЧИ на Прямолинейное равномерное движение.

Задачи, описывающие движение, содержат два типа величин: векторные (имеющие направление) и скалярные (выражающиеся только числом). К векторным величинам при описании равномерного прямолинейного движения относятся скорость и перемещение.

Для перехода от векторов к скалярам выбирают координатную ось и находят проекции векторов на эту ось, руководствуясь следующим правилом: если вектор сонаправлен с осью, то его проекция положительна, если противоположно направлен — отрицательна. (Могут быть и более сложные случаи, когда вектор не параллелен координатной оси, а направлен к ней под некоторым углом.) Поэтому при решении задачи обязательно нужно сделать чертеж, на котором изобразить направления всех векторов и координатную ось. При записи «дано» следует учитывать знаки проекций.

При решении задач все величины должны выражаться в международной системе единиц (СИ), если нет специальных оговорок.

В решении задачи единицы величин не пишутся, а записываются только после найденного значения величины.

Это конспект по теме «ЗАДАЧИ на Прямолинейное равномерное движение с решениями». Выберите дальнейшие действия:

Уравнение движения, графики равномерного прямолинейного движения

п.1. Прямолинейное равномерное движение на координатной прямой

Система отсчета, с помощью которой можно описать прямолинейное движение состоит из:
1) тела отсчета; 2) координатной прямой; 3) часов для отсчета времени.
Пусть телом отсчета будет дом.
В начальный момент времени машина стоит в 20 м справа от дома.

Рассмотрим движение машины со скоростью 10 м/с вправо.
Направим координатную прямую параллельно вектору скорости, вправо.

Составим таблицу перемещений за первые 4 секунды:

t, c	0	1	2	3	4
x, м	20	30	40	50	60

Стартуя с точки x₀=20, машина каждую секунду удаляется от дома еще на 10 м.
Пройденный путь за 2 секунды – 10·2=20 м, за 3 секунды – 10·3=30 м, за t секунд s=vt метров. Значит, для произвольного времени t можем записать координату x в виде: begin x=x_0+s=x_0+vt\ x=20+10t end

Если при тех же начальных условиях и направлении координатной прямой машина будет двигаться влево, получим таблицу:

t, c	0	1	2	3	4
x, м	20	10	0	-10	-20

В этом случае координата x в любой момент времени t имеет вид: begin x=x_0-st=x_0-vt\ x=20-10t end Если же машина никуда не едет, её скорость v=0, и координата x=x₀ в любой момент времени t.

п.2. Уравнение прямолинейного равномерного движения

Зависимость координаты тела от времени в механике называют уравнением движения.
Если уравнение движения известно, то мы можем решить основную задачу механики.

п.3. Удобная система отсчета для решения задачи о прямолинейном движении

При решении задачи можно выбрать различные тела отсчета и связать с ними различные системы координат. Как правило, некоторая система отсчета является наиболее удобной для решения данной задачи в том смысле, что в ней уравнение движения выглядит и решается проще, чем в других системах.

При решении задач на прямолинейное движение телом отсчета может быть неподвижная поверхность (земля, пол, стол и т.п.), само движущееся тело или другое тело.
При этом системой координат является координатная прямая, параллельная направлению движения (вектору перемещения) тела, уравнение движения которого мы хотим получить.

Проекции скорости и перемещения на координатную прямую могут быть положительными, равными нулю или отрицательными. Величины скорости и перемещения будут равны длинам соответствующих проекций.

п.4. График движения x=x(t)

Сравним полученное уравнение движения (x(t)=x_0+v_x t) с уравнением прямой (y(x)=kx+b) (см. §38 справочника по алгебре для 7 класса).

В уравнении движения роль углового коэффициента (k) играет проекция скорости (v_x), а роль свободного члена (b) – начальная координата (x_0).

Построим графики зависимости координаты от времени для нашего примера:

x=20+10t – машина движется вправо (в направлении оси OX)
x=20-10t – машина движется влево (в направлении, противоположном оси OX)
x=20 – машина стоит

п.5. Как найти уравнение движения по графику движения?

п.6. График скорости v_x=v_x(t)

Для рассмотренного примера:

п.7. Как найти путь и перемещение по графику скорости?

Пусть тело движется прямолинейно равномерно, зависимость его координаты от времени описывается уравнением: $$ x(t)=x_0+v_x t $$ Тогда в некоторый момент времени (t_1) координата равна (x_1=x_0+v_x t_1).
Несколько позже, в момент времени (t_2gt t_1) координата равна (x_2=x_0+v_x t_2).
Если (v_xgt 0), то пройденный за промежуток времени (triangle t=t_2-t_1) путь равен разности координат: $$ s=x_2-x_1=(x_0+v_x t_2)-(x_0+v_x t_1)=x_0-x_0+v_x (t_2-t_1)=v_x triangle t $$ В общем случае, т.к. (v_x) может быть и отрицательным, а путь всегда положительный, в формуле нужно поставить модуль: $$ s=|v_x|triangle t $$
Изобразим полученное соотношение на графике скорости:

Проекция скорости (v_x) может быть не только положительной, но и отрицательной.
Если учитывать знак, то произведение: $$ triangle x=v_x triangle t $$ дает проекцию перемещения на ось OX. Знак этого произведения указывает на направление перемещения.

Проекция перемещения может быть как положительной, так и отрицательной или равной 0.

п.8. Задачи

Задача 1. Спортсмен бежит по прямолинейному участку дистанции с постоянной скоростью 8 м/с. Примите (x_0=0) и запишите уравнение движения.
а) Постройте график движения (x=x(t)) и найдите с его помощью, сколько пробежит спортсмен за (t_1=5 с), за (t_2=10 с);
б) постройте график скорости (v=v(t)) и найдите с его помощью, какой путь преодолеет спортсмен за промежуток времени (triangle t=t_2-t_1)?

По условию (x_0=0, v_x=8).
Уравнение движения: (x=x_0+v_x t=0+8t=8t)
а) Строим график прямой (x=8t) по двум точкам:

По графику находим: begin x_1=x(5)=8cdot 5=40 text<(м)>\ x_2=x(10)=8cdot 10=80 text <(м)>end
б) Скорость (v_x=8) м/с – постоянная величина, её график:

$$ t_1=5 с, t_2=10 с $$ Пройденный путь за промежуток времени (triangle t=t_2-t_1) равен площади заштрихованного прямоугольника: $$ s=v_x triangle t=8cdot (10-5)=40 text <(м)>$$ Ответ: а) 40 м и 80 м; б) 40 м

Задача 2. Космический корабль движется прямолинейно с постоянной скоростью.
Известно, что через 1 час после старта корабль находился на расстоянии 38 тыс.км от астероида Веста, а через 2 часа после старта – на расстоянии 56 тыс.км.
а) постройте график движения корабля, найдите по графику уравнение движения.
б) на каком расстоянии от астероида находился корабль в начальный момент времени?
в) на каком расстоянии от астероида будет находиться корабль через 4 часа после старта?
г) чему равна скорость корабля в километрах в секунду?

а) Будем откладывать время в часах, а расстояние в тыс.км
Отмечаем точки A(1;38) и B(2;56), проводим через них прямую.
Полученная прямая и есть график движения (x=x(t)).

Найдем скорость корабля (v_x): $$ v_x=frac=frac<56-38><2-1>=18 (text<тыс.км/ч>) $$ Найдем начальную координату (x_0): $$ x_0=x_1-v_x t_1=38-18cdot v_1=20 (text<тыс.км/ч>) $$ Получаем уравнение движения: $$ x(t)=x_0+v_x t, x(t)=20+18t $$ где (x) – в тыс.км, а (t) – в часах.

б) В начальный момент времени корабль находился на расстоянии (x_0=20) тыс.км от астероида.

в) Через 4 часа после старта корабль будет находиться на расстоянии $$ x(4)=20+18cdot 4=92 (text<тыс.км>) $$
г) Переведем скорость в км/с: $$ 18000frac<text<км>><text<ч>>=frac<18000 text<км>><1 text<ч>>=frac<18000 text<км>><3600 text>=5 text <км/c>$$ Ответ:
а) (x(t)=20+18t) ((x) в тыс.км, (t) в часах); б) 20 тыс.км; в) 92 тыс.км; г) 5 км/с

[spoiler title=”источники:”]

http://reshator.com/sprav/fizika/7-klass/uravnenie-dvizheniya-grafiki-ravnomernogo-pryamolinejnogo-dvizheniya/

[/spoiler]

    В
задачах данного раздела определяются
координаты, скорость, ускорение точки
в любой назначенный момент времени при
различных способах задания движения.
Из всех способов задания движения точки
наибольшее распространение получили
координатный и естественный способы.

    Рассмотрим
вначале координатный способ задания
движения точки. Положение в пространстве
движущейся точки определяется тремя
координатами в декартовой системе
координат. Эти координаты задаются как
функции времени:

                      
(1.1)

    Зависимости
(1.1) называются уравнениями движения
точки в декартовых координатах.

    Если
движение точки происходит в плоскости
ху, то задаются только два уравнения
движения:

x
= x(t);              
y = y (t).

    При
прямолинейном движении точки достаточно
задать одно уравнение движения:

x
= x(t),

если
принять, что ось х совпадает с прямой,
по которой движется точка.

    Скорость
точки представляет собой вектор,
характеризующий быстроту и направление
движения точки в данный момент времени.

    При
задании движения точки уравнениями
(1.1) проекции скорости на оси декартовых
координат равны:

    Модуль
скорости

                               
.
                                         
(1.2)

    Направление
скорости определяется направляющими
косинусами:

.

    Если
движение точки задается в плоскости
ху, то

.

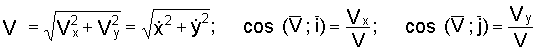    При
прямолинейном движении по оси х:

.

    Характеристикой
быстроты изменения скорости является
ускорение
а.
Ускорение точки равно производной от
вектора скорости по времени:

.

    При
задании движения точки уравнениями
(1.1) проекции ускорения на координатные
оси равны:

    Модуль
ускорения:

                      
.
                                         
(1.3)

    Направление
ускорения определяется направляющими
косинусами

;
;.

    Если
движение точки задается в плоскости
ху, то
;

;
;.

    При
прямолинейном движении по оси х

;
.

    Далее
рассмотрим естественный способ задания
движения точки.

    Считается,
что движение точки задано естественным
способом, если указаны ее траектория и
закон изменения криволинейной координаты
s = s(t). Уравнение s = s(t) называется
законом движения точки по траектории.
При этом на траектории указывается
начало отсчета, а также положительное
направление отсчета координаты s в виде
стрелки
.

    Модуль
скорости точки определяется по формуле

                              
.
                                                                 
(1.4)

    Вектор
скорости
V направлен по касательной к траектории
в сторону стрелки
,
если,
и в противоположную сторону, если.

    Ускорение
точки определяется как векторная сумма
касательного и нормального ускорений
точки:

 а
=
а
+
а_n
.

    Модуль
касательного ускорения определяется
по формуле

                             
.
                                                   
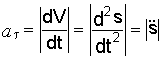(1.5)

    Вектор
касательного ускорения
а
направлен
по касательной к траектории в сторону
стрелки
,
если,
и в противоположную, если.

    Модуль
нормального ускорения определяется по
формуле

                                         
,
                                                            
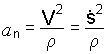(1.6)

где

– радиус кривизны траектории в данной
точке.

    Вектор
нормального ускорения
а_n
всегда направлен по главной нормали в
сторону центра кривизны траектории.

    Модуль
полного ускорения

                                           
.
                                                          
(1.7)

    Если
движение точки задано координатным
способом, то можно определить параметры
движения, характерные для естественного
способа задания движения.

    Так
можно, например, по уравнениям движения
точки (1.1) найти уравнение ее траектории
в форме зависимости между координатами.
Для этого надо из уравнений движения
исключить время t. Затем можно найти
закон движения точки по траектории s =
s(t), используя формулу (1.4). Из этой формулы
следует, что ds = V dt; с учетом формулы
(1.2) имеем
и

                                       
.
                                                
(1.8)

    В
законе движения (1.8) за начало отсчета
координаты s принимается начальное
положение точки, когда t = 0. Знак “плюс”
или “минус” перед интегралом ставится
в зависимости от выбора положительного
направления отсчета координаты s: если
движение точки начинается в сторону
стрелки
,
то следует брать знак “плюс”, в противном
случае – знак “минус”.

    Рассмотрим
вначале методику решения задач, в которых
движение точки задано координатным
способом. Уравнения (1.1) определяются
либо из геометрических условий, либо в
результате интегрирования дифференциальных
уравнений движения точки. Интегрирование
дифференциальных уравнений движения
точки рассматривается в разделе “Динамика
точки”, который не входит в данное
пособие. Получение уравнений (1.1) с
использованием геометрии движения
рассмотрим на примере исследования
движения точки обода колеса.

Задача
1.1 (3)

Задача
1.2 (1)

Задача
1.3 (2)

Задача
1.4 (4)

Задача
1.5 (4)

Задача
1.6 (5)

Задача
1.7 (6)

Задача
1.8 (7)

Задача
1.1 (3)

    Найти
уравнения движения точки М обода колеса
радиуса R вагона, который движется по
прямолинейному участку пути со скоростью
V. Колесо катится без скольжения. Точка
М в начальный момент движения соприкасалась
с рельсом, т.е. занимала положение М₀
(рис. 1.1).

Рис.
1.1

    Решение

    Изобразим
на расчетной схеме (рис. 1.1) оси координат
х и у, начало координат поместим в
начальное положение точки М₀.

    Рассмотрим
два положения колеса: в начальный момент
t = 0 и в текущий момент времени t.

    Отметим
положение точки М на ободе колеса и
положение центра С колеса в момент t,
координаты точки: x_м
= М₀В,
у_м
= МВ.

    Расстояние
от центра колеса до рельса остается
постоянным и равным R; это значит, что
центр C колеса движется по прямой,
параллельной оси х. За время t центр
колеса переместится на расстояние C₀C
= Vt (закон равномерного движения точки
C), одновременно колесо повернется на
угол 
.

    Чтобы
получить уравнения движения точки М,
надо координаты этой точки представить
как функции времени.

    Из
расчетной схемы (рис. 1.1) видно, что

х_м
= C₀C
– ЕС, у_м
= ВЕ – МЕ;

или

х_м
= Vt – ЕС, у_м
= R – МЕ.

    Из
треугольника МЕС имеем;

МЕ
= Rsin (90
– 
) = Rcos
,

ЕC
= Rcos (90
– 
) = Rsin
,

Тогда
х_м
= Vt – Rsin
, (a)

у_м
= R – Rcos
.

    Найдем
зависимость угла 
от времени t: так как колесо катится без
скольжения, то длина дуги АМ окружности
обода колеса (рис.1.1) равна длине отрезка
М₀А.

    При
этом

М₀А
= С₀С
= Vt ,

но
длина дуги АМ равна также произведению
радиуса R на центральный угол 
; поэтому Vt = R
, отсюда
.

    Теперь
уравнения (а) будут иметь вид

;
                
.

    Полученные
уравнения представляют собой уравнения
движения точки М. В аналитической
геометрии показано, что это параметрические
уравнения циклоиды (параметром в данном
случае является время t). Таким образом,
траектория точки обода колеса, движущегося
по прямолинейному участку пути без
проскальзывания, является циклоидой.
Длина одной ветви циклоиды L (рис. 1.1)
равна 2
R, высота – H = 2R.

Задача
1.2 (1)

    Даны
уравнения движения точки:

      
;       
(х,
у – м; t – с).                          
(б)

1. Определить
   уравнение траектории и построить ее.

2. Определить
   начальное положение точки на траектории.

3. Указать
   моменты времени, когда точка пересекает
   оси координат.

4. Найти
   закон движения точки по траектории s =
   s(t), принимая за начало отсчета расстояний
   начальное положение точки.

5. Построить
   график движения точки.

    Решение

    1.
Для получения уравнения траектории
вида F(x, y) = 0 исключим из уравнений
движения (б) время t: из первого уравнения
системы (б) найдем

,

подставляя
это выражение во второе уравнение той
же системы, получим уравнение траектории

y
= x + 5.

Рис. 1.2

Это – уравнение прямой линии. Для построения прямой представим ее уравнение в отрезках , где а– отрезок, отсекаемый прямой на оси х, b – отрезок, отсекаемый прямой на оси у. В данном случаеа= -5 м, b = 5 м. Откладываем на оси х отрезока= -5 м, по оси у – отрезок b = 5 м. Через полученные точки проводим прямую (рис. 1.2).

    2.
Для определения положения точки в
начальный момент времени необходимо
подставить значение t = 0 в уравнения
движения (б)

м;

м.

Точка
при t = 0 занимает положение М₀
(-1;4).

    3.
В момент пересечения точкой оси у
координата х равна нулю, а первое
уравнение системы (б) примет вид:

.

Отсюда

где
n = 0, 1, 2 …

    В
момент пересечения точкой оси х координата
у равна нулю, а второе уравнение системы
(б) примет вид:

или
.

Но
косинус не может быть больше 1.
Следовательно, точка не пересекает ось
х (см. об этом также п. 4 решения задачи).

    4.
Для определения закона движения точки
по траектории воспользуемся формулой
(1.8). За начало отсчета координаты s примем
начальное положение точки М₀.
Подставляя в уравнения (б) значения t >
0, видим, что с выходом из начального
положения М₀
координаты точки х и у увеличиваются.
Это направление движения точки примем
за положительное направление отсчета
координаты s (см. стрелку
на
рис. 1.2), а в формуле (1.8) оставим знак
“плюс”:

.

    Учитывая,
что

получим

или

                                         
.
                                                      
(в)

    Из
закона (в) следует, что координата s не
может быть отрицательной, т.е. точка
движется по полупрямой М₀М
(рис.1.2) и ось х не пересекает (см. по этому
поводу п. 3 решения задачи).

    5.
График движения точки – это графическое
представление зависимости расстояния
s от времени t. Для построения такого
графика по оси абсцисс откладывают
последовательные значения времени t, а
по оси ординат – соответствующие им
значения расстояния s. Построенные точки
соединяют плавной линией. График
зависимости (в) можно построить быстрее,
если воспользоваться известным графиком
косинуса. Для этого вначале построим
график функции
(штриховая
линия на рис. 1.3), затем этот график
сместим вдоль оси s на величинум.

Рис.
1.3.

Задача
1.3 (2)

    Даны
уравнения движения точки:

          
;       
(х,
у – см; t – с ).                            
(г)

1. Определить
   уравнение траектории и построить ее.

2. Определить
   начальное положение точки на ее
   траектории.

3. Найти
   закон движения точки по траектории s =
   s(t), принимая за начало отсчета расстояний
   начальное положение точки.

4. Определить
   время T прохождения точкой полной
   окружности.

    Решение

Рис. 1.4

1. Чтобы найти уравнение траектории точки необходимо из уравнений движения (г) исключить время t. Для этого уравнения движения (г) разрешим относительно ии возведем полученные результаты в квадрат ; ,

    сложим
эти уравнения и после преобразования
получим

.

    Это
уравнение окружности радиуса R = 5 см,
центр окружности расположен в точке
С (-2,5; 5) (рис. 1.4).

    2.
Для определения начального положения
точки подставим значение времени t = 0 в
уравнения (г)

х₀
= 5 соs0 – 2,5 = 2,5 см; у₀
= 5 sin0 – 5 = 5 см;

    Точка
при t = 0 занимает положение М₀
(2,5; 5).

    3.
Для определения закона движения точки
по траектории воспользуемся формулой
(1.8). За начало отсчета координаты s примем
точку M₀.
Из системы уравнений (г) видно, что с
увеличением времени t от нуля x уменьшается,
а y увеличивается.

    Такое
возможно, если после выхода из начального
положения точка будет двигаться по
окружности против часовой стрелки. Это
направление движения точки примем за
положительное направление отсчета
координаты s (см. стрелку
на
рис. 1.4), а в формуле (1.8) перед интегралом
оставим знак “плюс”:

,
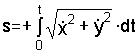где
;.

    Отсюда

                                              
;
.
                                          
(д)

    4.
Определим время Т прохождения точкой
полной окружности.
Т – время, по
истечении которого s в формуле (д) станет
равным длине окружности 2
R:

                                       
.

    Отсюда
с.

Задача
1.4 (4)

    Даны
уравнения движения точки:

                              
;
               
y = t (x, y – м; t – с ).                                
(е)

1. Определить
   уравнение траектории точки.

2. Определить
   скорость и ускорение точки при t = 0 и t
   = 1 с.

3. Построить
   траекторию и указать полученные векторы
   скорости и ускорения на чертеже.

    Решение

    1.
Уравнение траектории получается
подстановкой в первое уравнение системы
(е) величины t = y, полученной из второго
уравнения этой системы:

                                                  
.
                                                            
(ж)

    2.
Модуль скорости точки определяется по
формуле
,
где–
проекции вектора скорости на координатные
оси. Для заданного движения (е) имеем

,
                            
м/c.

    При
t = 0                  
,м/c.

    Модуль
скорости V₀
= 1 м/c.

    При
t = 1 с,          
м/c,м/c.

    Модуль
скорости V₁
= 4,82 м/с.

    Модуль
ускорения точки определяется по формуле
,
где,–
проекции вектора ускорения на координатные
оси. Для заданного движения (е) имеем

                               
,
                          
.

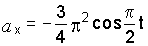    При
t = 0             
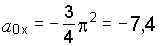м/с²
,
               
.

    Модуль
ускорения a₀
= 7,4 м/с².

    При
t = 1 с                  
,.

    Модуль
ускорения a₁
= 0.

    3.
Траектория точки (ж) представляет собой
косинусоиду.

Рис.1.5

Для построения траектории найдем по уравнению (ж) пять точек, задавшись пятью значениями у: у = 0, 1, 2, 3, 4, М0(3; 0), М1(0; 1), М2(-3; 2), М3(0; 3), М4(3; 4). По этим точкам построена траектория на рис. 1.5.   Определим положение точки в моменты времени t = 0 и t = 1 с, учитывая (е). При t = 0 x0 = 3 м, y0 = 0, точка занимает положение М0(3; 0).

  При
t = 1 с x₁
= 0, y₁ =
1 м, точка занимает положение М₁(0;
1). Для этих положений точки построим
векторы скорости и ускорения. От точки
M₀
отложим проекции скорости V_0x = 0
и V_0y = 1
м/с (см. п.2); направление вектора 
V₀
показано на рис. 1.5. Вектор скорости 
V₁
построим следующим образом: через точку
M₁
проведем оси
и,
осьпараллельна
оси x, а осьсовпадает
с осью y. Вдоль этих осей от точки M₁
отложим отрезки, равные проекциям V_1x
и V_1y
(с
учетом их знаков); затем построим
прямоугольник, диагональ которого есть
вектор 
V₁.
Модуль вектора ускорения
a₀
равен модулю проекции a_0x
(см. п. 2), 
a₀
направлен от точки M₀
в сторону, противоположную положительному
направлению оси x (cкорости 
V₀,

V₁
должны совпадать с касательными к
траектории соответственно в точках M₀
и M₁.
Вектор
a₀
должен быть направлен от точки M₀
внутрь кривой).

Задача
1.5 (4)

    Даны
уравнения движения точки:

                       
;
         
(х,
у – м; t – с ).                     
(з)

1. Определить
   уравнение траектории точки.

2. Определить
   скорость и ускорение точки при t = 1 с.

3. Построить
   траекторию и указать полученные векторы
   скорости и ускорения на чертеже.

    Решение

    1.
Для того чтобы получить уравнение
траектории, необходимо из уравнений
движения (з) исключить время. Запишем
эти уравнения в виде

,
.

    Возведем
оба уравнения в квадрат, вычтем второе
из первого и получим уравнение траектории:

                                                  
x²
– y²
= 4².
                                                              
(и)

    Это
уравнение равнобочной гиперболы, полуось
которой b = 4 м.

    2.
Определим проекции скорости

    В
заданный момент времени t = 1с, V_1x
= 4,68 м/с, V_1у
=
6,16 м/с
модуль скорости
м/с.

    Определим
проекции ускорения

м/с²,
           
м/с²
.

    В
момент времени t = 1с, а_1x
= 6,16 м/с²,
а_1у
=
4,68 м/с²
модуль
ускорения
м/с².

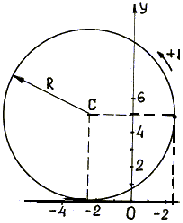
    3.
Построим траекторию точки по уравнению
(и). Действительной осью гиперболы
является ось х (рис. 1.6). На траектории
найдем точку М₁,
соответствующую моменту времени t = 1 с.
Координаты этой точки: x₁ = 2(e +
e^-1)
= 6,16 м; y₁ = 2(e –
e^-1)
= 4,68 м; M₁
(6,16; 4,68).

Рис.
1.6

Вектор
скорости построим следующим образом:
через точку М₁
проведем оси
и,
параллельные соответствующим осям x и
y; вдоль этих осей от точки М₁
отложим отрезки, равные проекциям V_1x
и V_1y
(с учетом их знаков). Диагональ
прямоугольника, построенного на этих
отрезках, есть вектор
V₁.
Вектор ускорения
a₁
строим подобным образом: от точки М₁
вдоль оси
отложим
отрезок, равный проекцииa_1x,
а вдоль оси
отложим
отрезокa_1y.
Затем на этих отрезках строим прямоугольник,
диагональ которого есть вектор
a₁.
Вектор скорости
V₁
должен быть направлен по касательной
к траектории в точке M₁,
а вектор ускорения
a₁
должен быть направлен от точки M₁
внутрь кривой.    
Задача 1.6 (5)

Рис. 1.7

Даны уравнения движения точки М шатуна АВ кривошипно-ползунного механизма (рис. 1.7): (х, у – м; t – с ).         (к) Определить уравнение траектории точки. Определить скорость и ускорение точки в момент, когда она пересечет прямую y = 20 см.

    Решение

1.
Чтобы определить уравнение траектории,
следует исключить время из уравнений
движения (к). Учитывая, что

,

получим
.

Траектория
представляет собой эллипс с полуосями
20 см и 40 см.

    2.
Определим время Т, когда точка пересечет
прямую у = 20 см, первое уравнение системы
(к) в этот момент примет вид:
20 = 40 sin2
t, отсюда следует
с.

    Найдем
величины скорости и ускорения по
значениям их проекций в момент времени
с:

см/с;
               
см/с.

    Модуль
скорости
см/с.

    Проекции
ускорения

см/с²;

см/с².

    Модуль
ускорения

см/с².

Задача
1.7 (6)

    Дан
закон движения точки по окружности
радиуса R = 5 м:

                 
(s
– см; t –с ).                                             
(л)

1. Определить
   скорость и ускорение точки при t = 0 и t₁
   = 10 с.

2. Определить
   моменты остановки точки.

3. Определить
   путь, пройденный точкой за 10 с.

    Решение

Рис. 1.8

1. На траектории отметим точку O – начало отсчета координаты s и укажем положительное направление отсчета этой координаты стрелкой (рис. 1.8). Отметим положение точки в моменты времени t = 0 и t1= 10 с. При t = 0 s0= -15 см; при t1= 10 с s1= 355 см. Положение точек M0и M1указано на рис. 1.8. Проведем из точек M0и M1естественные оси координат0, n0;1, n1.

Определим
проекцию скорости на касательную
,
учитывая (л),

                                          
.
(м)

При
t = 0,                 
V
_o
= 162 см/с             
и t₁
= 10 c                
V
₁
= 12 см/с.

    Теперь
отложим найденные проекции скорости
из точек M₀
и M₁
по соответствующим касательным: V
_o
– по касательной 
_o,
V
₁
– по касательной 
₁.
Векторы 
V_o
и 
V₁
совпадают со своими проекциями V
_o
и V₁.

Определим
проекции ускорения на естественные оси
координат, учитывая (л),

см/с²;
см/с².

    Ускорение
точки
.

При
t = 0                       
см/с²;
                   
см/с²;

см/с².

При
t₁
= 10 с             
см/с²;
                     
см/с²;

см/с².

    Отложим
из точек M₀
и M₁
по естественным осям проекции а_o,
а_no,
а
₁,
а_n1.
Векторы
a₀,
a₁
изображаются диагоналями прямоугольников,
построенных на проекциях ускорений.

    2.
Чтобы найти моменты остановки, необходимо
найти время t*, когда скорость точки
равна нулю. Из уравнения (м) получим

3(t*)²
– 45t* + 162 = 0.

    Решив
это уравнение, будем иметь t₁*
= 6 с, t₂*
= 9 с.

    3.
Поскольку за 10 с точка сделала две
остановки (см. п. 2), пройденный ею путь
за 10 с можно найти как сумму пути,
пройденного точкой от начального
положения до первой остановки, пути,
пройденного точкой от первой до второй
остановки, и пути, пройденного точкой
от второй остановки до момента времени
t₁
= 10 с, т.е.

,

где
s₀
= -15 см;

см;

см;

см.

Путь,
пройденный точкой за 10 с, равен

 см.

Задача
1.8 (7)

    По
заданным уравнениям движения точки:

       
;
               
(х,
у – м; t – с)                         
(н)

найти
ее касательное и нормальное ускорение,
а также радиус кривизны траектории для
заданного момента времени t₁
= 0,5 
с.

    Решение

    Заданные
уравнения движения точки (н) позволяют
найти проекции скорости точки, м/с,

;

.

    Модуль
скорости, м/с,

                                    
.
                                  
(о)

    В
момент времени t₁
= 0,5 
с V₁
= 2 м/с.

    Проекции
ускорения точки, м/с²:

.

    Модуль
полного ускорения, м/с²

                                   
.
                                      
(п)

    В
момент времени t₁
= 0,5 
                        
с_а
= 2 м/с².

    Зная
выражение скорости, как функции времени
t (о), определим модуль касательного
ускорения точки, м/с²,
по формуле (1.5)

                                          
.
                                       
(р)

    В
момент
см/с².

    По
полному ускорению (п) и касательному
ускорению (р) найдем модуль нормального
ускорения точки для
с,
учитывая формулу (1.7)

м/с².

    Нормальное
ускорение а_n1
и радиус кривизны траектории 
₁
связаны зависимостью (1.6), из которой
следует, что при
с

м.