Как найти координаты 4-й вершины параллелограмма, зная координаты трёх других его вершин?
В декартовых координатах эту задачу можно решить, используя свойство диагоналей параллелограмма.
Из трёх известных вершин две являются концами одной диагонали. Находим координаты середины этой диагонали. Точка пересечения диагоналей является серединой каждой из них. Для второй диагонали находим второй конец по известным одному концу и середине.
Примеры.
1)
 Дано: ABCD — параллелограмм,
Дано: ABCD — параллелограмм,
A(-3;11), B(12;-4), C(1;-7)
Найти: D.
Решение:
 1) Найдём координаты точки O — середины диагонали AC.
1) Найдём координаты точки O — середины диагонали AC.
По формуле координат середины отрезка
![]()
![]()
То есть O(-1;2).
2) По свойству диагоналей параллелограмма, точка O также является серединой BD:
![]()
![]()
Ответ: D (-14; 8).
2)
Дано: ABCD — параллелограмм,
B(7;4), C(-5;10), D(-1;-2)
Найти: A.
Решение:
1) Ищем координаты точки O — середины отрезка BD:
![]()
![]()
Итак, O (3;1).
2) Точка O также является серединой AC:
![]()
![]()
Ответ: A (11;-8).
Мастер
(1538),
закрыт
13 лет назад
Татьяна
Просветленный
(40524)
13 лет назад
Найдем координаты т. О – середины ВД, О ( 4; 2)
Т. к. хо=(ха+хс) /2, то (-1+хс) /2=4, откуда хс=9,
уо=(уа+ус) /2, то (1+ус) /2=2, откуда ус=3.
Ответ: С (9;3).
2 способ. АВСД – параллелограмм, значит векторы АВ=ДС, координаты АВ (2;6); ДС (хс-7; ус+3),
откуда хс-7=2; хс=9; ус+3=6; ус=3
С (9;3).
Алина
Гуру
(3220)
13 лет назад
надо исходит из того, что диагонали параллелограмма в точке пересечения делятся пополам. Зная координаты точек B,D, найти координаты точки пересечения диагоналей Е:
Хе= (1+7):2=4 Уе=(7-3):2=2 Теперь зная координаты точки А : (-1+Хс): 2=4
Хс=9. (1+Ус): 2=2. Ус=3
Координаты точки С ( 9; 3 )
Источник: знания
UCHEES.RU – помощь студентам и школьникам
В 19:39 поступил вопрос в раздел ЕГЭ (школьный), который вызвал затруднения у обучающегося.
Вопрос вызвавший трудности
Найдите координаты вершины D параллелограмма ABCD, если А (-2; 3), В (4; 5), С (2; 1).
Ответ подготовленный экспертами Учись.Ru
Для того чтобы дать полноценный ответ, был привлечен специалист, который хорошо разбирается требуемой тематике “ЕГЭ (школьный)”. Ваш вопрос звучал следующим образом: Найдите координаты вершины D параллелограмма ABCD, если А (-2; 3), В (4; 5), С (2; 1).
После проведенного совещания с другими специалистами нашего сервиса, мы склонны полагать, что правильный ответ на заданный вами вопрос будет звучать следующим образом:
решение задания по геометрии
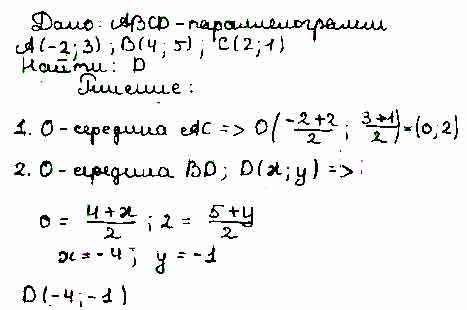
НЕСКОЛЬКО СЛОВ ОБ АВТОРЕ ЭТОГО ОТВЕТА:

Работы, которые я готовлю для студентов, преподаватели всегда оценивают на отлично. Я занимаюсь написанием студенческих работ уже более 4-х лет. За это время, мне еще ни разу не возвращали выполненную работу на доработку! Если вы желаете заказать у меня помощь оставьте заявку на этом сайте. Ознакомиться с отзывами моих клиентов можно на этой странице.
Полякова Ярослава Алексеевна – автор студенческих работ, заработанная сумма за прошлый месяц 63 922 рублей. Её работа началась с того, что она просто откликнулась на эту вакансию
ПОМОГАЕМ УЧИТЬСЯ НА ОТЛИЧНО!
Выполняем ученические работы любой сложности на заказ. Гарантируем низкие цены и высокое качество.

Деятельность компании в цифрах:
Зачтено оказывает услуги помощи студентам с 1999 года. За все время деятельности мы выполнили более 400 тысяч работ. Написанные нами работы все были успешно защищены и сданы. К настоящему моменту наши офисы работают в 40 городах.
РАЗДЕЛЫ САЙТА
Ответы на вопросы – в этот раздел попадают вопросы, которые задают нам посетители нашего сайта. Рубрику ведут эксперты различных научных отраслей.
Полезные статьи – раздел наполняется студенческой информацией, которая может помочь в сдаче экзаменов и сессий, а так же при написании различных учебных работ.
Красивые высказывания – цитаты, афоризмы, статусы для социальных сетей. Мы собрали полный сборник высказываний всех народов мира и отсортировали его по соответствующим рубрикам. Вы можете свободно поделиться любой цитатой с нашего сайта в социальных сетях без предварительного уведомления администрации.
ЗАДАТЬ ВОПРОС
НОВЫЕ ОТВЕТЫ
- Абадзехская стоянка, Даховская пещера. ..
- По закону сохранения заряда каждый шарик после соприкасl..
- 2)прогудел первый мохнатый шмель 3) Зазвенела Прогудел 4) ..
- В мілкій траві ворушаться сліди веселих, сполоханих доще
..
ПОХОЖИЕ ВОПРОСЫ
- В правильном шестиугольнике ABCDEF соединили середины сторон АВ, CD и EF. Найдите сторону правильного треугольника, образовавшегося
- Найдите длину отрезка АВ и координаты его середины, если А (-3;2) и В(1;-5).
Площадка Учись.Ru разработана специально для студентов и школьников. Здесь можно найти ответы на вопросы по гуманитарным, техническим, естественным, общественным, прикладным и прочим наукам. Если же ответ не удается найти, то можно задать свой вопрос экспертам. С нами сотрудничают преподаватели школ, колледжей, университетов, которые с радостью помогут вам. Помощь студентам и школьникам оказывается круглосуточно. С Учись.Ru обучение станет в несколько раз проще, так как здесь можно не только получить ответ на свой вопрос, но расширить свои знания изучая ответы экспертов по различным направлениям науки.
2020 – 2023 – UCHEES.RU
Ответ:
D (-4; -1)
Пошаговое объяснение:
Из названия параллелограмма АВСD следует, что его диагонали – АС и ВД. Они по свойству параллелограмма должны пересекаться в одной точке, назовем ее К, являющейся серединой обеих диагоналей.
Координаты концов для АС даны в условии, а координаты К (как середины отрезка) равны их полусумме:
х(к) = (-2+2)/2 = 0
у(к) = (3+1)/2 = 2
К(0;2) —– координаты точки пересечения диагоналей.
Эти координаты входят в формулы для определения середины диагонали ВD, включающие координаты точки D. И их легко найти, так как координаты точки В известны (4,5), а точки К уже вычислены:
(4+х(D))/2 = 0 ⇒ x(D) = -4
(5+y(D))/2 = 2 ⇒ y(D) = 4 + (-5) = -1
D(-4; -1) —– координаты вершины D параллелограмма
Ответ: D(-4; -1)
Примечание:
координаты четвертой вершины параллелограмма можно найти построением.
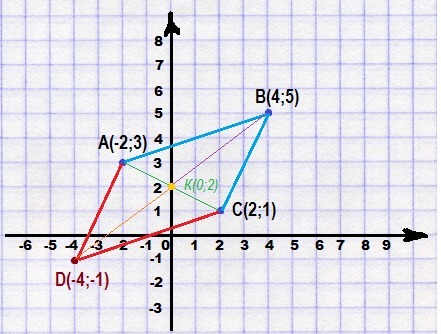
Найти четвертую вершину параллелограмма
Как найти координаты 4-й вершины параллелограмма, зная координаты трёх других его вершин?
В декартовых координатах эту задачу можно решить, используя свойство диагоналей параллелограмма.
Из трёх известных вершин две являются концами одной диагонали. Находим координаты середины этой диагонали. Точка пересечения диагоналей является серединой каждой из них. Для второй диагонали находим второй конец по известным одному концу и середине.
Дано: ABCD — параллелограмм,
1) Найдём координаты точки O — середины диагонали AC.
2) По свойству диагоналей параллелограмма, точка O также является серединой BD:
Дано: ABCD — параллелограмм,
1) Ищем координаты точки O — середины отрезка BD:
2) Точка O также является серединой AC:
2 Comments
А как вы получили -14 в первом примере.
Можно применить основное свойство пропорции: 12+xD=2∙(-1), xD=-2-12=-14.
Дан параллелограмм найти векторы
Задача 1. Дано: АВСD – параллелограмм Найти: а) векторы, коллинеарные вектору ОС; б) векторы, сонаправленные вектору АВ; в) векторы, противоположно направленные. — презентация
Презентация была опубликована 6 лет назад пользователемАльбина Селиванкина
Похожие презентации
Презентация на тему: » Задача 1. Дано: АВСD – параллелограмм Найти: а) векторы, коллинеарные вектору ОС; б) векторы, сонаправленные вектору АВ; в) векторы, противоположно направленные.» — Транскрипт:
2 Задача 1. Дано: АВСD – параллелограмм Найти: а) векторы, коллинеарные вектору ОС; б) векторы, сонаправленные вектору АВ; в) векторы, противоположно направленные вектору ВС; г) векторы, равные вектору ВО; д) ВD, если АВ = 4, ВС = 5, ВАD = 60 0 ; А С В D О е), если АВ = 4, ВС = 5, АС = 6.
3 Задача 2. Дано: АВСD – квадрат. АВ = А В С D O а) ВО; б) угол АВО, угол АОВ; ? ? в) Найти: г)
4 Угол между векторами. О А В
5 Ответьте на вопросы: О 1. Чему равен угол между векторами а и b? 2. Каков угол между векторами b и с? 3. Угол между векторами c и d? 4. Угол между векторами с и f острый или тупой? 5. Определите угол между векторами а и d. 6. Угол между векторами а и f?
6 Угол между векторами не зависит от выбора точки, от которой они откладываются Возьмите на заметку!
7 Скалярное произведение векторов. Скалярным произведением двух векторов называется произведение их длин на косинус угла между ними.
8 Если, то Если, то Если, то Если, то Скалярное произведение называется скалярным квадратом вектора
9 Примечание: В термине «скалярное произведение» первое слово указывает на то, что результат действия есть скаляр, т.е. действительное число. Второе слово подчеркивает, что для этого действия имеют силу основные свойства обычного умножения.
10 Свойства умножения: — переместительное свойство — сочетательное свойство — распределительное свойство
11 Тест: Вставьте пропущенное слово: Скалярным произведением двух векторов называется число, равное произведению модулей этих векторов на __________ угла между ними. косинус
12 Вектор а скалярно умножили на вектор b. Как можно охарактеризовать результат этого действия? 1. Результат действия есть вектор. 2. Результат действия есть скаляр. 3. Результат действия есть скаляр, если векторы а и b коллинеарные, или вектор, если векторы а и b не являются коллинеарными.
13 Какие из представленных на рисунке векторов перпендикулярны? О 1. а и c 2. b и d 3. с и d 4. b и с 5. f и d
14 Сопоставьте углы между векторами и их градусной мерой. О c и f 0 o d и a 45 o a и f 180 o a и b 135 o 45 0
15 Выберите правильный ответ; Известно, что Скалярное произведение векторов равно: а) б) в)
16 Вставьте пропущенное слово: Скалярное произведение называется ____________ квадратом вектора Скалярный ___________ вектора равен квадрату его модуля. скалярным квадрат
17 1. Сформулируйте теорему синусов. 2. Сформулируйте теорему косинусов. 3. Что значит «решить треугольник»? 4. Какое наименьшее число элементов надо знать, что бы «решить треугольник»? 5. Сформулируйте определение скалярного произведения векторов. Математическая разминка.
18 Имя автора теоремы: «Если на сторонах треугольника во внешнюю сторону построить равносторонние треугольники, то их центры будут вершинами равностороннего треугольника» А В С АВС — равносторонний
19 п) Решение треугольника по трем сторонам. л) Решение треугольника по двум сторонам и углу, противолежащему одной из них. о) Решение треугольника по стороне и углам, один из которых лежит против данной стороны. н) Решение треугольника по двум сторонам и углу между ними. о) Решение треугольника по трем углам. е) Решение треугольника не осуществляется. а) Решение треугольника по стороне и прилежащим углам. Определите к какому типу задач «решение треугольника» можно отнести данную модель
20 7) Результатом скалярного произведения векторов является … а) вектор. о) число. л) градус. 8) Скалярный квадрат координатного вектора равен: т) -1. р) 0. н) 1.
21 Теорема Наполеона: «Если на сторонах треугольника во внешнюю сторону построить равносторонние треугольники, то их центры будут вершинами равностороннего треугольника» А В С АВС — равносторонний НАПОЛЕОН
22 Доказательство теоремы Пифагора в 8 классе а) б) c 2 =a 2 +b 2
23 Математический тест Запишите в карточке для ответов свой вариант и Ф.И.
24 Математический тест Внизу под вашими ответами выставьте себе оценку за тест. Обменяйтесь карточками с соседом по парте для взаимопроверки. Таблица правильных ответов: Выставьте оценку по следующим критериям: 0 ошибок – оценка «5» 1 ошибка – оценка «4» 2 ошибки – оценка «3» 3-5 ошибок – оценка «2». Правильные ответы Вариант 1 Вариант 2 1 бф 2 аа 3 вв 4 б 5 вб
25 Новый материал Теорема Скалярное произведение векторов и выражается формулой:
26 Следствие 1. Следствие 2.
27 Свойства скалярного произведение векторов Действия над векторами (свойства), причем при Закон Действия над числами (свойства) a, b и с –любые числа — любые вектора k – любое число 1 переместительный 2 распределительный 3 сочетательный 4
28 «Геометрия является самым могущественным средством для развития наших умственных способностей и дает нам возможность правильно мыслить и рассуждать» Галилео Галилей
Четырехугольник АВСD — параллелограмм , О — точка пересечения его диагоналей?
Математика | 5 — 9 классы
Четырехугольник АВСD — параллелограмм , О — точка пересечения его диагоналей.
Назовите вектор с началом О , равный вектору — OD.

— ОД = ДО и ему равный вектор ОВ в параллелограмме, т.
К. у параллелограмма точка пересечения диагоналей делит их пополам.

Вычислите длины диагоналей параллелограмма, построенного на векторах a = 2m + n и b = m — 2n , где m и n ― единичные векторы, угол между которыми o 60 ?
Вычислите длины диагоналей параллелограмма, построенного на векторах a = 2m + n и b = m — 2n , где m и n ― единичные векторы, угол между которыми o 60 .

Стороны параллелограмма равны 8 и 11?
Стороны параллелограмма равны 8 и 11.
Найдите большую из диагоналей четырехугольника, образованного пересечениями биссектрис внутренних углов параллелограмма.

Вычислить длины диагоналей и площадь параллелограмма, построенного на векторах : Полное решение?
Вычислить длины диагоналей и площадь параллелограмма, построенного на векторах : Полное решение.

Параллелограмм построен на векторах а = (1 ; 2 ; — 3) b = (2 ; — 1 ; — 1), нужно определить косинус угла между диагоналями и найти длину высоты, опущенной на вектор а?
Параллелограмм построен на векторах а = (1 ; 2 ; — 3) b = (2 ; — 1 ; — 1), нужно определить косинус угла между диагоналями и найти длину высоты, опущенной на вектор а.

Диагонали паралеллограмма ABCD пересекаются в точке O?
Диагонали паралеллограмма ABCD пересекаются в точке O.
Какие векторы равны вектору OC.

Назовите вектор, начало и конец котрого я вляются внршинами параллепипеда ABCDA1B1C1D1, равный сумме векторов AB и A1D1?
Назовите вектор, начало и конец котрого я вляются внршинами параллепипеда ABCDA1B1C1D1, равный сумме векторов AB и A1D1.

Дан параллелограмм ABCD?
Дан параллелограмм ABCD.
Найдите сумму векторов вектор АВи АD.

Дана трапеция с основаниями ABCD с основаниями AD = 20 b ВС = 8, O — точка пересечения диагоналей?
Дана трапеция с основаниями ABCD с основаниями AD = 20 b ВС = 8, O — точка пересечения диагоналей.
Разложите вектор DO по векторам AD = a, и AB = b.

Найдите угол между диагоналями параллелограмма построенного на векторах p = 2a — b b q = a + b как на сторонах если a и b единичные векторы и угол между векторами a и b = 60°?
Найдите угол между диагоналями параллелограмма построенного на векторах p = 2a — b b q = a + b как на сторонах если a и b единичные векторы и угол между векторами a и b = 60°.

Дан параллелограмм ABCD?
Дан параллелограмм ABCD.
Выразите вектор ba через векторы bc и ac.
На этой странице сайта вы найдете ответы на вопрос Четырехугольник АВСD — параллелограмм , О — точка пересечения его диагоналей?, относящийся к категории Математика. Сложность вопроса соответствует базовым знаниям учеников 5 — 9 классов. Для получения дополнительной информации найдите другие вопросы, относящимися к данной тематике, с помощью поисковой системы. Или сформулируйте новый вопрос: нажмите кнопку вверху страницы, и задайте нужный запрос с помощью ключевых слов, отвечающих вашим критериям. Общайтесь с посетителями страницы, обсуждайте тему. Возможно, их ответы помогут найти нужную информацию.

20 / 25 = 4 / 5 = 8 / 10 = 0, 8 17 / 34 = 1 / 2 = 5 / 10 = 0, 5 24 / 32 = 3 / 4 = 75 / 100 = 0, 75 39 / 60 = 13 / 20 = 80 / 100 = 8 / 10 = 0, 8 27 / 75 = 9 / 25 = 36 / 100 = 0, 36 15 / 24 = 5 / 8 = 0, 625.

Тут прямая зависимость : Так как муки в 36 раз больше, то и хлеба будет в 36 раз больше = 135 * 36 = 4860%.

36×135 = 4860% хлеба получится.


Составляет уравнение : Ч — чашки чая, П — пирожки, К — конфеты. 2Ч + 1П + 4К = 48 4Ч + 5П + 2К = 66 1Ч + 1П + 1К — ? Если не трудно, пометь мой ответ как лучший, умоляю. Заранее спасибо) СМотри, здесь можно заметить , что если сложить первые 2 ура..

3. а) — 57 + 16 + 57 = — 41 + 57 = 16 в) — 64 + ( — 58) + 64 = — 64 — 58 + 64 = — 122 + 64 = — 58.

Из какого номера а)и в) не знаю, поэтому решила из всех номеров.

В треугольнике АВС примем длину стороны АС = 1, а АВ = 2. Тогда длину стороны ВС определим по теореме косинусов : ВС = √(1² + 2² — 2 * 1 * 2 * cos120°) = √7. ВС : АС = √7 : 1.

4. 3x — 2. 9x = — 4. 8 — 0. 8 1. 4x = — 5. 6 x = — 4.

4, 3х + 4, 8 = 2, 9х — 0, 8 4, 3х — 2, 9х = — 0, 8 — 4, 8 1, 4х = — 5, 6 х = — 5, 6 : 1, 4 х = — 4.
Дан параллелограмм ABCD. Постройте указанные суммы и разности векторов, лежащих на его сторонах.
Ваш ответ
решение вопроса
Похожие вопросы
- Все категории
- экономические 43,277
- гуманитарные 33,618
- юридические 17,900
- школьный раздел 606,845
- разное 16,824
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
Математический портал
Nav view search
Navigation
Search
- Вы здесь:
- Home
Базис линейного пространства. Разложение вектора по базису.
Литература: Сборник задач по математике. Часть 1. Под ред А. В. Ефимова, Б. П. Демидовича.
Упорядоченная тройка некомпланарных векторов $e_1, e_2, e_3$ называется базисом в пространстве всех геометрических векторов. Всякий геометрический вектор $a$ может быть представлен единственным образом в виде $$a=X_1e_1+X_2e_2+X_3e_3.qquadqquadqquadqquadqquad (1)$$ Числа $X_1, X_2, X_3$ называются координатами вектора в базисе $B=.$ Запись (1) называют разложением вектора $a$ по базису $B.$
Аналогично, упорядоченная пара неколлинеарных векторов $e_1, e_2$ называется базисом $B=(e_1, e_2)$ в множестве геометрических векторов, компланарных некоторой плоскости.
Наконец, всякий ненулевой вектор $e$ образует базис $B=(e)$ в множестве геометрических векторов, коллинеарных некоторому направлению.
Если вектор $a$ есть линейная комбинация векторов $a_1, a_2, . a_n$ с коэффициентами $lambda_1, lambda_2, . lambda_n$, то есть $$a=sumlimits_^n lambda_ka_k$$ то каждая координата $X_i(a)$ вектора $a$ равна сумме произведений коэффициентов $lambda_1,lambda_2. lambda_n$ на одноименные координаты векторов $a_1, a_2, . a_n: $ $$X_i(a)=sumlimits_^nlambda_k X_i(a_k),qquad (i=1, 2, 3.)$$
Базис $B=(e_1, e_2, e_3)$ называется прямоугольным, если векторы $e_1, e_2$ и $e_3$ попрано перпендикулярны и имеют единичную длину. В этом случае приняты обозначения $$e_1=i;,, e_2-j;,, e_3=k.$$
Примеры.
2.26. Задан тетраэдр $OABC.$ В базисе из ребер $overline, overline$ и $overline$ найти координаты:
а) вектора $overline,$ где $D$ и $E$ середины ребер $OA$ и $BC.$
б) вектора $overline,$ где $F-$ точка пересечения медиан основания $ABC.$
Решение.
а)
Выразим вектор $overline$ через вектора $overline, overline, overline:$
Из треугольника $ODE$ имеем $overline=overline+overline.qquadqquadqquad (1)$
вектор $overline$ найдем из треугольника $OBE:$
здесь $overline=frac<1><2>overline,$ а вектор $overline$ находим из треугольника $OBC:$
Таким образом, из (2) получаем $overline=overline+frac<1><2>(overline-overline).$
Наконец из (1) имеем $$overline=overline+overline=-frac<1><2>overline+overline+frac<1><2>(overline-overline)=$$ $$=-frac<1><2>overline+frac<1><2>overline+frac<1><2>overline.$$
Таким образом, координаты вектора $overline$ в базисе из ребер $overline, overline, overline:$ $left(-frac<1><2>,frac<1><2>,frac<1><2>right).$
Ответ: $left(-frac<1><2>; frac<1><2>; frac<1><2>right).$
б)
Выразим вектор $overline$ через вектора $overline, overline, overline:$
Из треугольника $OFB$ имеем $overline=overline+overline.qquadqquadqquad (1)$
вектор $overline$ найдем из треугольника $BMC:$
здесь $overline=frac<1><2>overline,$ а вектор $overline$ находим из треугольника $OCA:$
Таким образом, из (2) получаем $$overline=overline+overline=overline-overline+frac<1><2>overline=$$ $$=overline-overline+frac<1><2>(-overline+overline).$$
Наконец из (1) имеем $$overline=overline+overline=overline+frac<2><3>overline=$$ $$=overline+frac<2><3>left(overline-overline+frac<1><2>(-overline+overline)right)=$$ $$=overline+frac<2><3>overline-frac<2><3>overline+frac<1><3>(-overline+overline)=frac<1><3>overline+frac<1><3>overline+frac<1><3>overline.$$
Таким образом, координаты вектора $overline$ в базисе из ребер $overline, overline, overline:$ $left(frac<1><3>; frac<1><3>; frac<1><3>right).$
Ответ: $left(frac<1><3>; frac<1><3>; frac<1><3>right).$
2.27. В тетраэдре $OABC$ медиана $AL$ грани $ABC$ делится точкой $M$ в отношении $|overline|:|overline|=3:7.$ Найти координаты вектора $overline$ в базисе из ребер $overline, overline, overline.$
Решение.
Вектор $overline$ найдем из треугольника $AOM:$ $$overline=overline+overline.qquadqquadqquad (1)$$
Из условия $|overline|:|overline|=3:7$ имеем $overline=frac<3><10>overline.$ Из треугольника $ABL$ находим $overline=overline+overline=overline+frac<1><2>overline.$
Далее, из треугольников $AOB$ и $BOC$ получаем
Отсюда и из (1) получаем $$overline=overline+overline=overline+frac<3><10>overline+frac<3><20>overline+frac<3><20>overline=$$ $$=frac<7><10>overline-frac<3><20>overline+frac<3><20>overline.$$
Ответ: $left(frac<7><10>; frac<3><20>;frac<3><20>right).$
2.29. В трапеции $ABCD$ известно отношение длин оснований $|overline|/|overline|=lambda$ Найти координаты вектора $overline$ в базисе из векторов $overline$ и $overline.$
Решение.
Вектор $overline$ можно найти из треугольника $ABC:$ $overline=overline+overline.$
$overline$ находим из треугольника $ACD:$ $overline=overline+overline=overline-overline.$
Из условия $|overline|/|overline|=lambda$ находим вектор $overline:$ $overline=-overline/lambda.$
Таким образом, $overline=-overline/lambda-overline;$
2.36. Заданы векторы $e(-1, 1, 1/2)$ и $a(2, -2, -1).$ Убедиться, что они коллинеарны и найти разложение вектора $a$ по базису $B(e). $
Решение.
Векторы коллинеарны, если их направления совпадают или противоположны, т.е. тогда и только тогда когда их координаты пропорциональны. Проверим: $$frac<-1><2>=frac<1><-2>=frac<1/2><-1>=-frac<1><2>,$$ то есть векторы $e$ и $a$ коллинеарны.
Найдем разложение вектора $a$ по базису $B(e),$ то есть найдем такое число $lambda$ что $a=lambda e:$
Ответ: $a=-2e.$
Домашнее задание.
2.28. Вне плоскости параллелограмма $ABCD$ взята точка $O.$ В базисе из векторов $overline, overline$ и $overline$ найти координаты:
а) вектора $overline$ , где $M$ точка пересечения диагоналей параллелограмма;
б) вектора $overline,$ где $K$- середина стороны $AD.$
Ответ: а) $(1/2; 0; 1/2);$ б) $(1, -1/2, 1/2).$
2.31. В треугольнике $ABC$ $overline=alphaoverline; overline=betaoverline;$ $overline=gammaoverline.$ Пусть $P, Q$ и $R -$ точки пересечения прямых $BF$ и $CK;$ $CK$ и $AM;$ $AM$ и $BF$ соответственно. В базисе из векторов $overline$ и $overline$ найти координаты векторов $overline,$ $overline$ и $overline.$
2.37. На плоскости заданы векторы $e_1(-1,2),$ $e_2(2,1)$ и $a(0,-2).$ Убедиться, что базис $B=e_1, e_2$ в множестве всех векторов на плоскости Построить заданные веткоры и найти разложение вектора $a$ по базису $B.$
Ответ: $a=-frac<4><5>e_1-frac<2><5>e_2.$
2.38. Показать, что тройка векторов $e_1(1,0,0), e_2(1,1,0)$ и $e_3(1,1,1)$ образуют базис в множестве всех векторов пространства. Вычислить координаты вектора $a=-2i-k$ в базисе $B(e_1, e_2, e_3)$ и написать соответствующее разложение вектора по базису.
[spoiler title=”источники:”]
http://b4.cooksy.ru/articles/dan-parallelogramm-nayti-vektory
http://mathportal.net/index.php/component/content/article/79-visshaya-matematika/121-bazis-linejnogo-prostranstva-razmernost-linejnogo-prostranstva
[/spoiler]
