Как найти координаты на карте видеоурок
Географическая широта и географическая долгота. Географические координаты. Видеоурок по географии
География 5 класс (Урок№12 – Географические координаты.)
Как определить географические координаты
Содержание:
- § 1 Координаты на плоскости
- § 2 Построение точек по их координатам
- § 3 Краткие итоги по теме урока
§ 1 Координаты на плоскости
Практически все люди любят путешествовать. Давайте отправимся на поиски клада. Мы поплывем на корабле по бескрайнему морю, и ориентиром для нас будет карта острова, где спрятаны сокровища. Но, к сожалению, мы не единственные, кто ищет клад. Пираты тоже хотят найти его. Капитан пиратского корабля, знаменитый капитан Флинт, стремится отобрать у нас карту острова сокровищ. Они догоняют наш корабль, и нам придётся принять бой.
Многие хорошо знают игру «Морской бой». Давайте вспомним её правила. В эту игру всегда играют двое. Каждый игрок чертит 2 квадрата со стороной 10 клеток. В первом квадрате игроки располагают свои “корабли”. Во втором квадрате восстанавливают расположение флота противника.
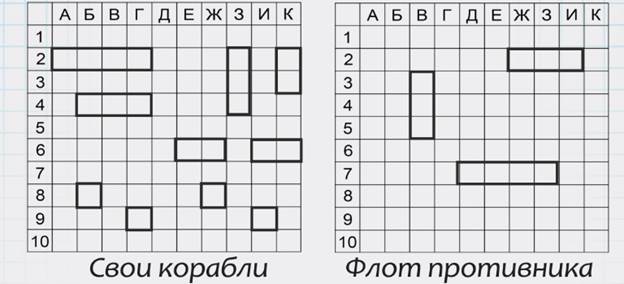
Корабли располагаются произвольно, но не касаются друг друга. Например, так:
Играющий должен суметь объяснить противнику, в какую клетку произведен выстрел. Как это сделать? Для этого столбцы обозначают буквами (слева направо), а строчки – цифрами от 1 до 10 (сверху вниз). Тогда любую клетку можно обозначить соответствующими ей буквой и числом. Первой всегда называется буква, а число стоит на втором месте. Например: “д – семь” или «а – пять». Два элемента, взятые в определенном порядке, называют парой элементов и записывают в круглых скобках (д; 7) или (а; 5) – это координата клетки.
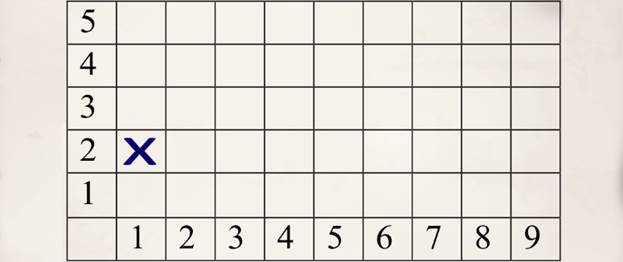
Играя в «Морской бой», мы научились находить нужную клетку по её координатам. Используя этот принцип координат, определим, как будет выглядеть наш остров, к которому мы плывем. Нам даны координаты, по которым нужно восстановить карту нашего острова. Как и в игре «Морской бой», будем ставить крестик в клетке с данной координатой. Возьмём первую координату (1;2) . Это значит, что мы должны найти клетку, которая находится на пересечении столбика под № 1 и строки под №2, ставим там крестик.
Точно так же находим все остальные координаты:
Что же у нас получилось? Наш остров похож на ключ. А мы научились находить координаты на плоскости. В последней клетке значок отмечен другим цветом, это значит, что где-то в этом месте зарыт клад.
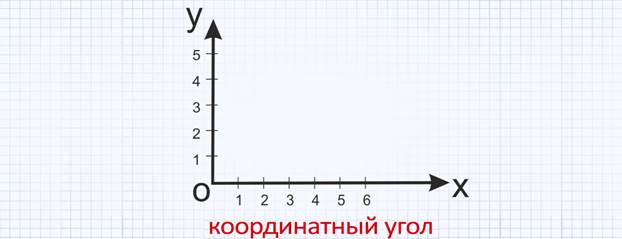
Подобным образом обозначается и положение точек на плоскости. Для этого строят прямой угол, стороны которого являются координатными лучами с общим началом в вершине угла. Такой угол называют координатным углом.
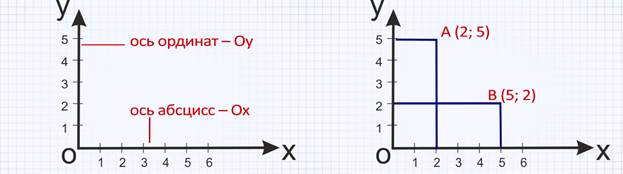
Одну из сторон координатного угла располагают горизонтально и называют осью абсцисс – Ох, а другую сторону – вертикально и называют осью ординат – Оу. Чтобы обозначить числами положение любой точки координатного угла, надо провести перпендикулярные прямые к сторонам угла и назвать сначала абсциссу (координату на оси Ох), а затем ординату (координату на оси Оу). Так, например, точка А имеет абсциссу 2 и ординату 5, значит, координатами точки А является пара чисел (2; 5). Пишут: А (2; 5).
При определении координат точки нельзя путать их порядок. Например, если поменять местами абсциссу и ординату точки А, то получится другая точка В (5; 2), которая показана на рисунке.
Запись А (2; 5) можно прочитать разными способами:
• Точка А с абсциссой 2 и ординатой 5.
• Точка А с координатами 2 и 5.
• Координаты точки А – пара чисел 2 и 5.
Итак, координата – это величина, определяющая положение точки в пространстве.
§ 2 Построение точек по их координатам
Научимся строить точки по их координатам. Чтобы определить положение точки на координатном угле по известным её координатам, можно воспользоваться одним из двух способов.
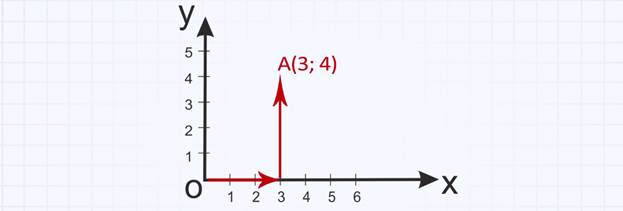
1 способ: сначала нужно пройти необходимое количество единиц по оси х, а потом подняться вверх по оси у.
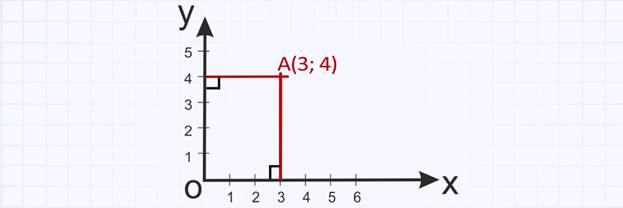
2 способ: нужно найти пересечение прямых, проведённых перпендикулярно осям координат через заданные значения координат точки.
Необходимо также запомнить, что:
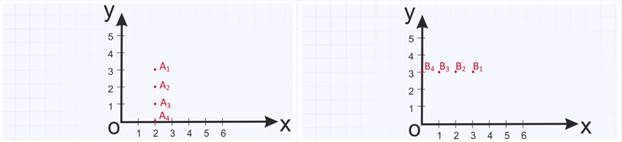
Например: изобразим точки А1( 2;3 ), А2(2;2 ), А3( 2;1 ), А4( 2; 0). Как видно на рисунке, точка А4 лежит на оси абсцисс, её ордината равна нулю. А теперь построим точки B1( 3;3), В2( 2; 3), В3( 1; 3 ), В4( 0 ;3 ). На получившемся рисунке точка В4 принадлежит оси ординат, её абсцисса равна нулю.
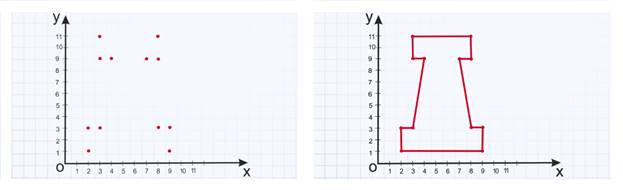
Мы высадились на острове, здесь находится несколько древних статуй. Под одной из них зарыт наш клад. Чтобы определить, какая из статуй нам подходит, нужно, используя данный шифр, построить эту фигуру на координатном угле. Для этого отметим точки по их координатам: (2,1); (2,3);(3,3); (4,9); (3,9); (3,11); (8,11); (8,9); (7,9);(8,3); (9,3); (9,1). Затем соединим их последовательно между собой ломаной линией.
У нас получилась фигура статуи, под которой зарыто сокровище. Мы молодцы! Клад найден. Мы справились со всеми заданиями.
§ 3 Краткие итоги по теме урока
1. Координата – это величина, определяющая положение точки в пространстве.
2. Прямой угол, стороны которого являются координатными лучами с общим началом в вершине угла, называют координатным углом.
3. Одну из сторон координатного угла располагают горизонтально и называют осью абсцисс – Ох, а другую сторону – вертикально и называют осью ординат – Оу.
4. Чтобы определить положение точки на координатном угле по известным её координатам, можно воспользоваться двумя способами:
5. 1 способ: сначала нужно пройти необходимое количество единиц по оси х, а потом подняться вверх по оси у;
6. 2 способ: нужно найти пересечение прямых, проведённых перпендикулярно осям координат через заданные значения координат точки.
7. Если точка принадлежит оси абсцисс, то её ордината равна нулю.
8. Если точка принадлежит оси ординат, то её абсцисса равна нулю.
Список использованной литературы:
- Петерсон Л.Г. Математика. 4 класс. Часть 1. / Л.Г. Петерсон. – М.: Ювента, 2014. – 96 с.: ил.
- Математика. 4 класс. Методические рекомендации к учебнику математики «Учусь учиться» для 4 класса. / Л.Г. Петерсон . – М.: Ювента, 2014. – 280 с.: ил.
- Зак С.М. Все задания к учебнику математики для 4 класса Л.Г. Петерсон и комплекту самостоятельных и контрольных работ. ФГОС. – М.: ЮНВЕС, 2014.
Использованные изображения:
Представим
себе такую историю…
–
Привет, Саша! Мы идём в субботу в кино? Ты купил билеты? – спросил у друга Паша.
–
Купил, – ответил Саша. – У нас 5 и 6
места.
–
А в каком ряду наши места? – снова задал вопрос Паша. – Ведь в кинотеатре много
рядов, и на каждом из них есть и 5,
и 6
место.
–
Наши места в 3 ряду, – уточнил Саша.
–
Вот теперь понятно, – сказал Паша. – Места в зрительном зале кинотеатра всегда
задают двумя числами: первое число – номер ряда, второе число – номер кресла в
этом ряду. А знать только номер ряда или только номер кресла нам будет мало.
–
Можно сказать, что номер ряда и номер кресла в этом ряду – это наши координаты
в зале, – добавил Саша.
–
Саша, а мы ведь на уроках математики не раз встречались с координатами, –
сказал Паша.
–
Точно. На координатной прямой мы отмечали точку, зная её координату, – вспомнил
Саша
–
Да. Но положение точки на координатной прямой определяется одной координатой, а
расположение наших с тобой мест в зале – двумя, – задумался Паша. – Может, Мудряш
поможет нам разобраться в этом.
–
Ребята, прежде чем мы с вами поговорим, давайте немного разомнёмся и выполним
устные задания, – предложил Мудряш.
–
Теперь сверимся! – сказал Мудряш. –
Посмотрите, что у вас должно было получиться!
–
А сейчас вернёмся к вашему вопросу, – начал Мудряш. – Ребята, вы уже знакомы с
координатной прямой. Это прямая, на которой выбрали начало отсчёта, единичный
отрезок и направление. Вы знаете, как найти точку на ней, если известна
координата этой точки. Например, числу соответствует
единственная точка .
Однако,
покупая билеты в кино, вы обратили внимание, чтобы отыскать нужное нам место в
зале, недостаточно знать одну координату, то есть только номер ряда или только
номер кресла.
Чтобы
занять нужное место, нам надо знать и номер кресла, и номер ряда, то есть две
координаты.
Подобным
образом можно обозначить положение точки на плоскости.
Давайте
на плоскости проведём две перпендикулярные координатные прямые таким образом,
чтобы их начала отсчёта совпали. Эти прямые называют осями координат. Обозначим
точку их пересечения точкой О. Точку О
называют началом координат. Горизонтальную ось обозначают буквой и
называют осью абсцисс, или осью ,
а вертикальную ось обозначают буквой и
называют осью ординат, или осью .
Ось
и
ось образуют
прямоугольную систему координат. А плоскость, на которой задана система
координат, называют координатной плоскостью.
Обратите
внимание, что координатные оси разделяют плоскость на четыре части, которые
называют координатными четвертями и нумеруют против часовой стрелки:
первая четверть, вторая четверть, третья четверть, четвёртая четверть.
–
А давайте отметим на координатной плоскости какую-нибудь точку, – предложили
ребята Мудряшу.
–
Давайте отметим точку ,
– начал Мудряш. – Проведём через эту точку прямые, перпендикулярные осям
координат. Пересечение с осью обозначим
точкой ,
а с осью –
точкой .
Посмотрите,
точка на
оси имеет
координату .
–
А точка на
оси имеет
координату ,
– помогли Мудряшу ребята.
–
Верно, – сказал Мудряш. – Число называют
абсциссой точки ,
число –
ординатой точки .
Эти числа определяют положение точки на
координатной прямой.
–
И их называют координатами точки ?
– задали вопрос мальчишки.
–
Да, – ответил Мудряш. – И записывают так: При
этом обратите внимание, что абсциссу всегда ставят на первое место, а ординату
– на второе.
–
А если поменять местами минус и
?
– спросили ребята.
–
Тогда мы получим другую точку. Например, точку ,
– объяснил Мудряш. – Отметим эту точку на координатной плоскости.
Для
этого на оси находим
абсциссу точки .
Она равна .
Проведём через неё прямую, перпендикулярную оси .
Затем на оси находим
ординату точки .
Она равна минус трём. Проведём через неё прямую, перпендикулярную оси .
Точка, в которой пересекаются эти прямые, и есть точка .
–
А какие координаты имеет точка О? – поинтересовался Паша.
–
Абсцисса и ордината у начала координат равны 0.
Записывают это так: .
Ребята,
посмотрите на рисунок. Здесь отмечены точка и
точка .
–
Точка лежит
на оси ,
а точка лежит
на оси ,
– отметили мальчики.
–
И обратите внимание, что у точки ордината
равна ,
а у точки абсцисса
равна ,
– добавил Мудряш. – Запомните! Если точка лежит на оси абсцисс, то её
ордината равна ,
а если точка лежит на оси ординат, то равна
её абсцисса.
Теперь
отметим на координатной плоскости точку и
точку .
–
У этих точек абсцисса и ордината – противоположные числа, – заметил Паша.
–
Правильно, – сказал Мудряш. – И эти точки симметричны относительно точки О,
то есть относительно начала координат. Запомните! Две точки с
противоположными абсциссами и ординатами симметричны относительно начала
координат.
Отметим
на координатной плоскости точку и
точку .
–
У этих точек абсциссы – противоположные числа, а ординаты равны, – заметили
мальчишки.
–
Верно, – сказал Мудряш. – При этом точки и
симметричны
относительно оси .
Запомните! Две точки с равными ординатами и противоположными абсциссами
симметричны относительно оси ординат.
А
теперь давайте отметим точку и
точку .
–
У этих точек, наоборот, абсциссы равны, а ординаты – противоположные числа, – снова
заметили Саша и Паша.
–
При этом точки и
симметричны
относительно оси .
Запомните! Две точки с равными абсциссами и противоположными ординатами
симметричны относительно оси абсцисс.
Ребята,
а сейчас давайте выполним несколько заданий, – предложил Мудряш.
Задание
первое: найдите координаты точек ,
и
,
изображённых на рисунке.
Решение: найдём
координаты точки .
Для этого проведём через неё прямую, перпендикулярную оси ,
и прямую, перпендикулярную оси .
Видим, что точка пересечения прямой, перпендикулярной оси ,
и оси имеет
координату 3, а значит, абсцисса точки равна
3.
Точка пересечения прямой, перпендикулярной оси ,
и оси имеет
координату 4, а значит, ордината точки равна
4.
Найдём
координаты точки .
Проведём через неё прямую, перпендикулярную оси ,
и прямую, перпендикулярную оси .
Точка пересечения прямой, перпендикулярной оси ,
и оси имеет
координату ,
а значит, абсцисса точки равна
.
Точка пересечения прямой, перпендикулярной оси ,
и оси имеет
координату ,
а значит, ордината точки равна
.
И
найдём координаты точки .
Проведём через неё прямые, перпендикулярные осям координат. Видим, что точка
пересечения прямой, перпендикулярной оси ,
и оси имеет
координату ,
а значит, абсцисса точки равна
.
Точка пересечения прямой, перпендикулярной оси ,
и оси имеет
координату ,
а значит, ордината точки равна
.
Второе
задание: отметьте на координатной плоскости точки: ,
,
.
Решение:
отметим точку .
Абсцисса точки равна
.
Проведём через неё прямую, перпендикулярную оси .
Ордината точки равна
.
Проведём через неё прямую, перпендикулярную оси .
Точка, в которой пересекаются эти прямые, и есть точка .
Теперь
отметим точку .
Абсцисса точки равна
.
Проведём через неё прямую, перпендикулярную оси .
Ордината точки БЭ – 1. Проведём через неё
прямую, перпендикулярную оси .
Точка, в которой пересекаются эти прямые, и есть точка .
Осталось
отметить точку .
Абсцисса этой точки равна ,
а значит, точка лежит
на оси ординат. Ордината этой точки равна .
И
ещё одно задание: постройте на координатной плоскости
отрезки и
,
если точка ,
,
,
.
Найдите точку пересечения этих отрезков.
Решение: чтобы
построить отрезки и
,
отметим на координатной плоскости точки ,
,
и
.
Отметим
точку .
Абсцисса этой точки равна ,
а значит, точка лежит
на оси ординат. Ордината этой точки равна .
Отметим
точку .
Абсцисса точки равна
.
Проведём через неё прямую, перпендикулярную оси .
Ордината точки равна
.
Проведём через неё прямую, перпендикулярную оси .
Точка, в которой пересекаются эти прямые, и есть точка .
Отметим
точку .
Ордината этой точки равна ,
а значит, точка лежит
на оси абсцисс. Абсцисса этой точки равна .
Отметим
точку .
Абсцисса точки равна
.
Проведём через неё прямую, перпендикулярную оси .
Ордината точки ДЭ равна .
Проведём через неё прямую, перпендикулярную оси .
Точка, в которой пересекаются эти прямые, и есть точка .
Соединим
точки и
,
и
.
Обозначим точку пересечения отрезков и
точкой
.
Найдём координаты этой точки. Для этого проведём через неё прямую,
перпендикулярную оси ,
и прямую, перпендикулярную оси .
Видим, что точка пересечения прямой, перпендикулярной оси ,
и оси имеет
на оси координату
,
а значит, абсцисса точки равна
.
Точка пересечения прямой, перпендикулярной оси ,
и оси имеет
на оси координату
,
а значит, ордината точки равна
.
Таким
образом, отрезки и
пересекаются
в точке .
В данной публикации мы рассмотрим, что такое точка пересечения двух прямых, и как найти ее координаты разными способами. Также разберем пример решения задачи по этой теме.
- Нахождение координат точки пересечения
-
Пример задачи
Нахождение координат точки пересечения
Пересекающимися называются прямые, которые имеют одну общую точку.
M – точка пересечения прямых. Она принадлежит им обоим, значит ее координаты одновременно должны удовлетворять обоим их уравнениях.
Для нахождения координат этой точки на плоскости можно использовать два способа:
- графический – чертим графики прямых на координатой плоскости и находим их точку пересечения (не всегда применимо);
- аналитический – более универсальный метод. Мы объединяем уравнения прямых в систему. Затем решаем ее и получаем требуемые координаты. От количества решений зависит то, каким образом ведут себя прямые по отношению друг к другу:
- одно решение – пересекаются;
- множество решений – совпадают;
- нет решений – параллельны, т.е. не пересекаются.
Пример задачи
Найдем координаты точки пересечения прямых y = x + 6 и y = 2x – 8.
Решение
Составим систему уравнений и решим ее:
В первом уравнении выразим x через y:
x = y – 6
Теперь подставим полученное выражение во второе уравнение вместо x:
y = 2 (y – 6) – 8
y = 2y – 12 – 8
y – 2y = -12 – 8
-y = -20
y = 20
Значит, x = 20 – 6 = 14
Таким образом, общая точка пересечения заданных прямых имеет координаты (14, 20).
Главная > Алгебра 7 класс > Координатная плоскость
Координатная плоскость – видеоурок
На этом видео уроке по алгебре для 7 класса дается понятие координатной плоскости и объясняется как находить координаты точек на координатной плоскости, решаются задачи из учебника Макарычев, Мордкович и Мерзляк.