Графический метод
довольно прост и нагляден для решения
задач ЛП с двумя переменными. Он основан
на геометрическом
представлении
допустимых решений и ЦФ задачи. Каждое
из неравенств задачи ЛП определяет на
координатной плоскости (x1,
x2
) некоторую полуплоскость, а система
неравенств в целом – пересечение
соответствующих полуплоскостей.
Множество точек пересечения данных
полуплоскостей называется областью
допустимых решений (ОДР).
ОДР всегда представляет собой выпуклую
фигуру, т.е.
обладающую следующим свойством: если
две точки А и В принадлежат этой фигуре,
то и весь отрезок АВ принадлежит ей. ОДР
графически может быть представлена
выпуклым многоугольником, неограниченной
выпуклой многоугольной областью,
отрезком, лучем, одной точкой. В случае
несовместности системы ограничений
задачи ОДР является пустым множеством.
Оптимальное решение
всегда находится на границе ОДР т.е. ЦФ
L(X)=c1x1+c2x2
принимает свое max(min)
значение на границе области, точнее в
ее угловых точках.
При поиске
оптимального решения задач ЛП возможны
следующие ситуации: существует
единственное решение задачи; существует
бесконечное множество решений
(альтернативный
оптиум); ЦФ
не ограничена; область допустимых
решений – единственная точка; задача
не имеет решений.
Методика решения задач лп графическим методом
-
В ограничениях
задачи замените знаки неравенств на
знаки точных равенств и постройте
соответствующие прямые. -
Найдите и заштрихуйте
полуплоскости, разрешенные каждым из
ограничений-неравенств задачи. Для
этого подставьте в конкретное неравенство
координаты какой-либо точки [например,
(0;0)], и проверьте истинность полученного
неравенства.
Если неравенство
истинное, то
надо
заштриховать полуплоскость, содержащую
данную точку; иначе
(неравенство
ложное) надо заштриховать полуплоскость,
не содержащую данную точку.
Поскольку x1
и x2
должны быть неотрицательными, то их
допустимые значения всегда будут
находиться выше оси x1
и правее оси x2
, т.е. в I-м квадранте. Ограничения-равенства
разрешают только те точки, которые лежат
на соответствующей прямой, поэтому
выделите на графике такие прямые.
III. Определите
ОДР как часть плоскости, принадлежащую
одновременно всем разрешенным областям,
и выделите ее. При отсутствии ОДР задача
не имеет
решений,
о чем сделайте соответствующий вывод.
IV. Если
ОДР – не пустое множество, то определите
координаты угловых точке. Определение
координат сводится к решению системы
соответствующих линейных уравнений.
-
Подставьте
координаты угловых точек в уравнение
для Ц.Ф. и найдите max
(min)
значение целевой функции.
Можно вместо
перебора всех угловых точек (пункт
IV,
V)
произвести
следующие действия:
IV.а Провести
вектор координатами которого служат
коэффициенты в уравнении с целевой
функцией. Сдвигать прямую перпендикулярную
построенному вектору, от начала по
направлению вектора, до момента, когда
пресечение сдвигаемой прямой с ОДР
будет составлять одну точку.
V.а Координаты
найденной точки будут являться оптимальным
планом, а если их подставить в уравнение
целевой функции, то получим ее max
(min)
значение.
Задача
Найдем оптимальное
решение задачи о красках, математическая
модель которой имеет вид:
Построим прямые
ограничений (рис. 1).
Рис. 1. Графическое
решение задачи
Определим ОДР.
Например, подставим точку (0;0) в исходное
ограничение (3), получим 0≤1 , что является
истинным неравенством, поэтому стрелкой
(или штрихованием) обозначим полуплоскость,
содержащую
точку
(0;0), т.е. расположенную правее и ниже
прямой (3). Аналогично определим допустимые
полуплоскости для остальных ограничений
и укажем их стрелками у соответствующих
прямых ограничений (см. рис. 1.). Общей
областью, разрешенной всеми ограничениями,
т.е. ОДР является многоугольник ABCDEF.
Найдем координаты
точек пересечения прямых ограничений,
т.е. координаты угловых точек. В некоторых
случаях хороший рисунок позволяет сразу
определять координаты угловых точек.
;
;
;
;
Для определения
координаты точки Е решим систему
уравнений с ограничениями (1) и (2).
Решая данную
систему получаем:
.
Найдем значение
целевой функции в угловых точках, т.е.
подставим их координаты в уравнение
.
Е – это точка
максимума ЦФ.
Таким образом,
наилучшим режимом работы фирмы является
ежесуточное производство краски 1-го
вида в объеме 3 1/3 т. и краски 2-го вида в
объеме 1 1/3 т. Доход от продажи красок
составит 12 2/3 тыс. руб. в сутки.
Решая графическим
методом предполагающим построение
целевого вектора, проводим
вектор координатами которого служат
коэффициенты в уравнении с целевой
функцией
,
сдвигая прямую перпендикулярную
построенному вектору (от начала к концу)
найдем точку, являющуюся последней в
пресечении сдвигаемой прямой сОДР,
(это точка Е) ее координаты найденные
из решении системы соответствующих
уравнений будут являться оптимальным
планом, а значение целевой функции в
ней будет max.
В более общем
случае, разработан и широко применяется
универсальный метод решения любой
задачи ЛП, называемый симплекс-методом.
Симплекс метод,
как метод решения задач ЛП был предложен
в американским математиком-экономистом
Данцигом в 1951 году.
Графически симплекс
метод представляет из себя передвижение
по выпуклому многограннику от вершине
к вершине, при этом значение целевой
функции на каждом шаге улучшается до
тех пор, пока не достигается оптимум.
Идея
симплекс метода состоит в том, чтобы
преобразовать уравнение содержащее
целевую функцию к виду:
,
т.к. в этом случае становиться возможным
выразить
,
а в силу того что перед нами ставится
задача максимизироватьL,
то эта задача достигается в случае когда
все переменные присутствующие в данном
уравнении принимают нулевые значения
(т.к. переменные не отрицательны по
условию).
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Основные определения:
Множество точек называется выпуклым, если оно вместе с любыми
двумя своими точками содержит весь отрезок, соединяющий эти точки.
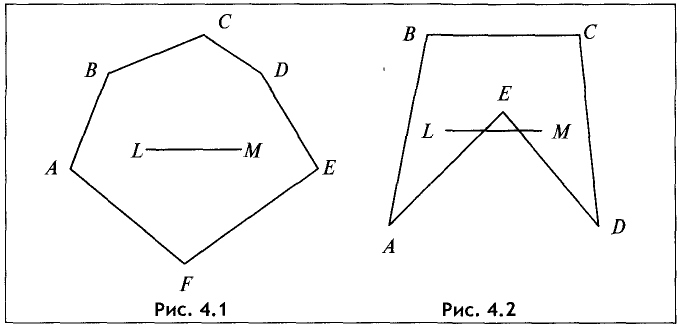
Например, многоугольник, представленный на рис. 4.1,
является выпуклым, а многоугольник на рис.4.2 выпуклым не является.
Выпуклыми множествами могут быть не только многоугольники. Примерами выпуклых множеств являются прямая, круг, куб,
многогранная область, полуплоскость, полупространство и т.д.
Пересечение любого числа выпуклых множеств есть выпуклое
множество.
Точка множества называется внутренней, если в любой ее окрестности (например, круг или шар с центром в этой точке) содержатся точки только данного множества.
Точка множества называется граничной, если в любой ее окрестности содержатся как точки, принадлежащие данному множеству, так и точки, не принадлежащие ему.
Точка множества называется угловой (крайней), если она не является внутренней ни для какого отрезка, целиком принадлежащего данному множеству.
Примеры угловой А, внутренней L и граничной М точек приведены на рис. 4.3.
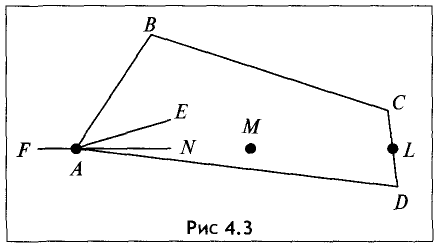
Точка А является угловой, так как для любого отрезка АЕ,
целиком принадлежащего многоугольнику, она не является
внутренней. Точка А — внутренняя для отрезка FN, но этот отрезок не принадлежит целиком множеству.
Для выпуклого множества угловые точки всегда совпадают с вершинами многоугольника (многогранника).
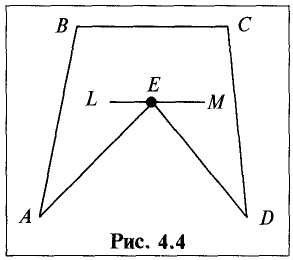
Так, на рис. 4.4 точка Е является вершиной невыпуклого многоугольника, но не является угловой, так как она является внутренней для отрезка LM, целиком принадлежащего этому
многоугольнику.
Множество точек называется замкнутым, если оно включает все свои граничные точки.
Множество точек называется ограниченным, если существует круг (шар) радиуса конечной длины с центром в любой точке множества, который полностью содержит в себе данное множество. В противном случае множество называется неограниченным.
Выпуклое замкнутое множество точек плоскости (пространства), имеющее конечное число угловых точек, называется выпуклым многоугольником (многогранником), если оно ограниченное, и выпуклой многоугольной (многогранной) областью, если оно неограниченное.
Введенные понятия рассматривались для множества точек на
плоскости и в пространстве. Их можно обобщить также на n-мерное
точечное пространство.
Геометрический смысл решений неравенств
Рассмотрим решения неравенств с двумя переменными типа
Теорема:
Множество решений неравенств с двумя переменными (4.1) является одной из двух полуплоскостей, на которые вся плоскость делится прямой
включая и эту прямую, а другая полуплоскость — множеством решений неравенства
Пример:
Построить график множества решений следующих
неравенств:
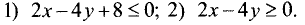
Решение:
В соответствии с теоремой множество решений
приведенных неравенств есть полуплоскость.
1.Границей первой полуплоскости является прямая
2х-4у + 8 = 0.
Представим уравнение этой прямой в виде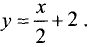 
Ее график представлен на рис. 4.5.
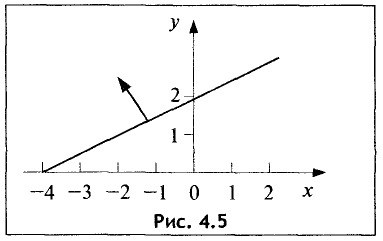
Для определения искомой полуплоскости зададим произвольную контрольную точку, не лежащую на построенной прямой. Проще всего задать точку с координатами (0; 0). Подставив данные
координаты в неравенство
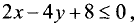
видим, что оно не выполняется, так как 8 > 0. Поэтому искомой является верхняя полуплоскость.
2.Границей второй полуплоскости является прямая
2х-4у = 0.
Представим это уравнение в виде
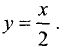
График исследуемой прямой представлен на рис. 4.6.
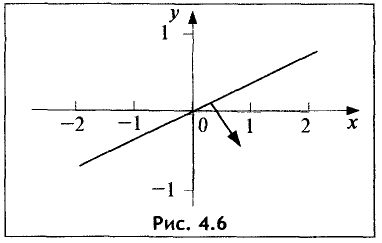
В данном случае точка с координатами (0; 0) лежит на этой
прямой. Поэтому выбираем точку с координатами (0; —1) и подставляем данные координаты в неравенство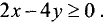 
Так как неравенство выполняется (4 > 0), то искомой является нижняя полуплоскость. ►
Основные свойства выпуклого множества точек
Рассмотрим множество решений совместной системы линейных
неравенств с двумя переменными.
Теорема:
Множество решений совместной системы т линейных
неравенств с двумя переменными
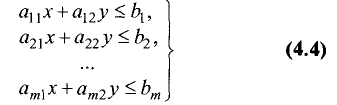
является выпуклым многоугольником (или выпуклой многоугольной областью).
Знаки некоторых или всех неравенств могут быть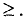 
Эту теорему для n переменных можно сформулировать
следующим образом.
Теорема:
Множество решений совместной системы m линейных
неравенств с n переменными
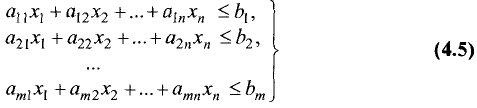
является выпуклым многогранником (или выпуклой многогранной областью) в n-мерном пространстве.
Пересечение полуплоскостей, каждая из которых определяется соответствующим неравенством системы, называется областью решения системы.
Область решений системы, удовлетворяющая условиям неотрицательности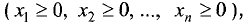 
называется областью неотрицательных (или допустимых) решений.
Пример:
Построить область решений и область допустимых
решений системы неравенств и определить координаты угловых точек области допустимых решений:
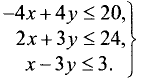
Решение:
Областью решений является треугольник ABC, представленный на рис. 4.7.
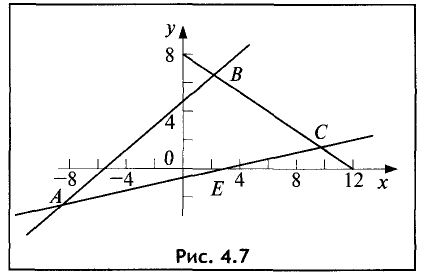
Сторона АВ треугольника, образованная границей первого неравенства системы, определяется уравнением прямой у = х + 5 .
Для нахождения искомой полуплоскости зададим контрольную
точку с координатами (0; 0). Подставив данные координаты в неравенство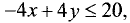 
видим, что оно выполняется, так как 0 < 20 . Поэтому искомой является нижняя полуплоскость.
Сторона ВС треугольника, образованная границей второго неравенства системы, определяется уравнением прямой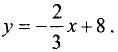 
Для контрольной точки с координатами (0; 0) неравенство 
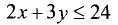выполняется, так как 0 < 24, поэтому искомой также является нижняя полуплоскость.
Сторона CD треугольника, образованная границей третьего неравенства системы, определяется уравнением прямой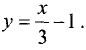 
. Для контрольной точки с координатами (0; 0) неравенство 
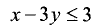выполняется, так как 0 < 3. Поэтому искомой является верхняя полуплоскость.
Областью допустимых решений системы неравенств является пятиугольник ODBCE. Координаты угловых точек (вершин) этого пятиугольника находятся как координаты точек пересечения соответствующих прямых. Например, точка В — точка пересечения первой и второй прямых, т.е. ее координаты являются решением системы двух уравнений:
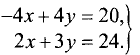
Решив эту систему, получим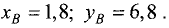 
Аналогично находим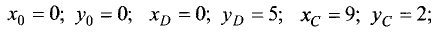 
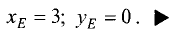
Пример:
Построить область решений и область допустимых решений системы неравенств и определить координаты угловых точек области допустимых решений:
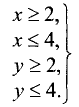
Решение:
Областью решений является квадрат ABCD, представленный на рис. 4.8.
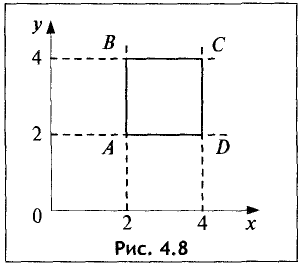
Областью допустимых решений является тот же квадрат ABCD. Координаты угловых точек данного квадрата находятся как координаты точек пересечения соответствующих прямых:
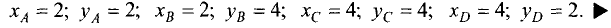
Пример:
Построить область решений и область допустимых решений системы неравенств:
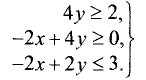
Решение:
Построим прямые и определим решения неравенств.
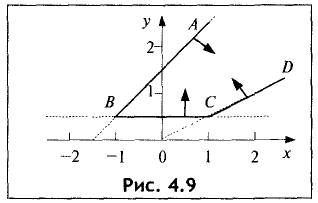
Областью решений является неограниченная многоугольная область
ABCD (рис. 4.9).
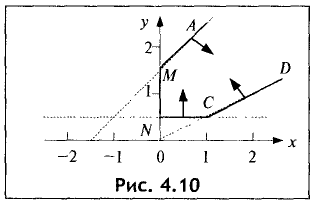
Областью допустимых решений является неограниченная
многоугольная область AMNCD, представленная на рис. 4.10. ►
Решение заданий и задач по предметам:
- Математика
- Высшая математика
- Математический анализ
- Линейная алгебра
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Система координат
В данном случае неравенство 
в контрольной
точке не выполняется. Значит, оно выполняется в противоположной плоскости на
рис.4.1 (заштрихована).
 |
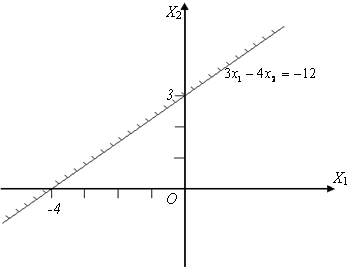Рис. 4.1
2. 
.
Прямая проходит через начало координат. За вторую точку можно взять
любую, лежащую на прямой, например А (2;3)
 |
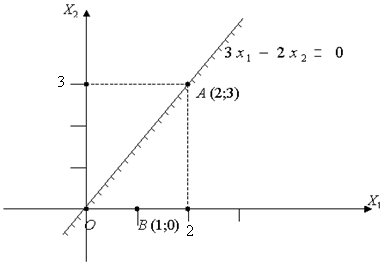Рис.
4.2
В качестве контрольной точки возьмём любую не
лежащую на прямой, Например В(1;0).
В этой точке 3–2∙0 > 0 неравенство выполняется. Значит область решений
неравенства – нижняя полуплоскость (заштрихована, рис.4.2).
Множество точек, удовлетворяющих уравнению 
при
является плоскостью, при 
– гиперплоскостью. В этом случае
теорему о решении неравенства, содержащего n неизвестных можно обобщить
следующим образом.
Теорема.
Область решения неравенства с n переменными 
есть одно из полупространств, на
которые все пространство делится гиперплоскостью ,
включая и эту гиперплоскость.
4.2. Множество решений системы неравенств.
Множеством решений системы линейных неравенств являются точки, которые
принадлежат полуплоскостям решений всех неравенств, т.е. принадлежат их
пересечению.
Рассмотрим конкретный пример.
Пример 4.2.
Построить
множество решений системы неравенств.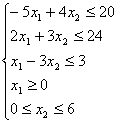
Для
определения множества решений системы неравенств строим последовательно множество
решений каждого неравенства.
 |
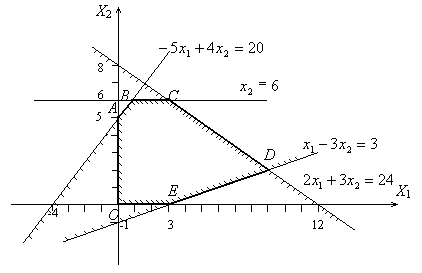Рис.4.3
В рассматриваемом
примере областью решений системы неравенств является так называемый выпуклый
многоугольник.
Выпуклой фигурой
называется фигура, обладающая следующим свойством: если две точки А и В
принадлежат этой фигуре, то и весь отрезок АВ принадлежит ей. Координаты
угловых точек – вершин этого многоугольника найдём как координаты точек
пересечения соответствующих прямых.
Например,
координаты точки D найдём, решая совместно
систему уравнений
При построении
области решений системы неравенств могут встретится и другие случаи:
–
многоугольная область (рис.4.4.)
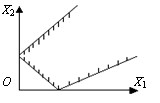
Рис. 4.4
– одна точка
(рис.4.5)
 |
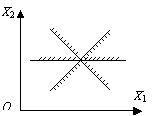Рис.4.5
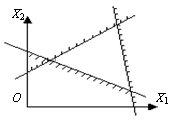
– пустое
множество, когда система неравенств несовместна (рис. 4.6)
Задача 34855 Построить множество решений системы…
Условие
Построить множество решений системы линейных алгебраических неравенств и
найти координаты угловых точек.
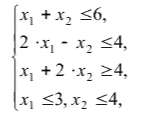
математика 10-11 класс
2317
Решение
★
Граница каждой области -прямая, которая разбивает плоскость x_(1)Ox_(2) на 2 части
Строим прямую x_(1)+x_(2)=6
по двум точкам (0;6) и (6;0)
Выбираем произвольную точку из любой области, например, точку (0;0)
Подставляем в первое неравенство
0+0 ≤ 6 – верно.
Значит первое неравенство задает ту область, которая содержит точку (0;0)
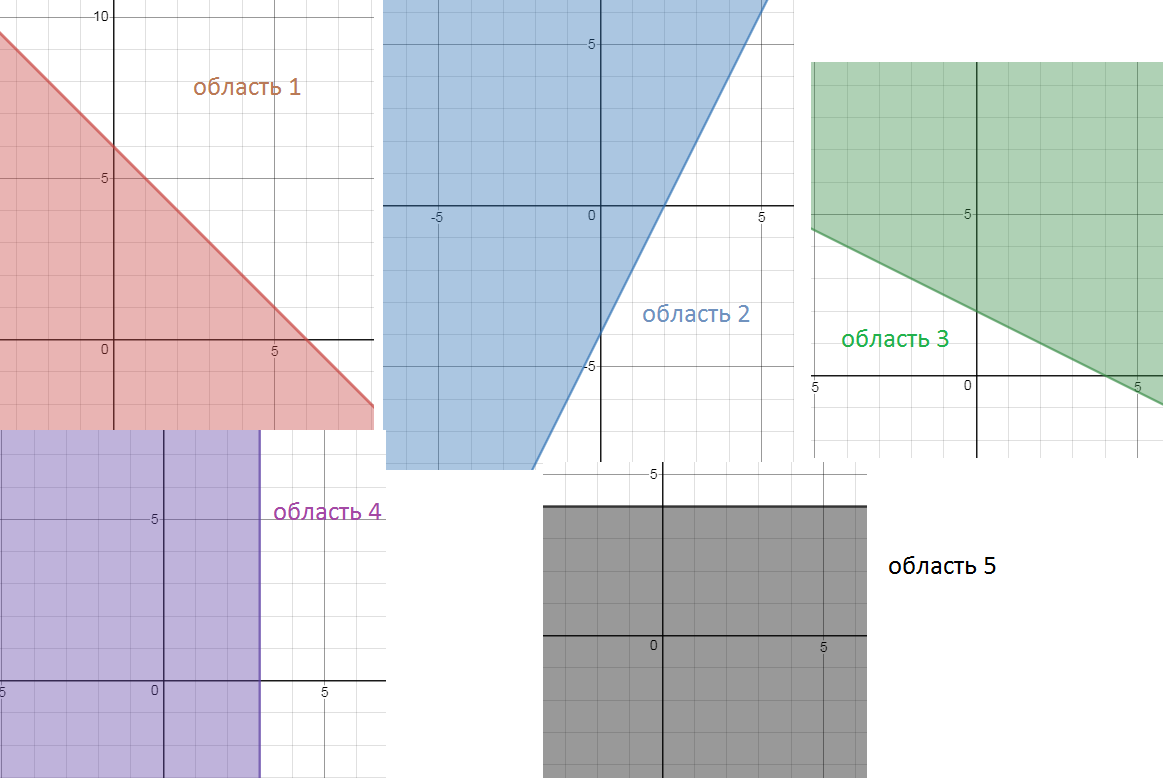
Первое неравенство задает область 1 ( см. рис)
второе – область 2, …
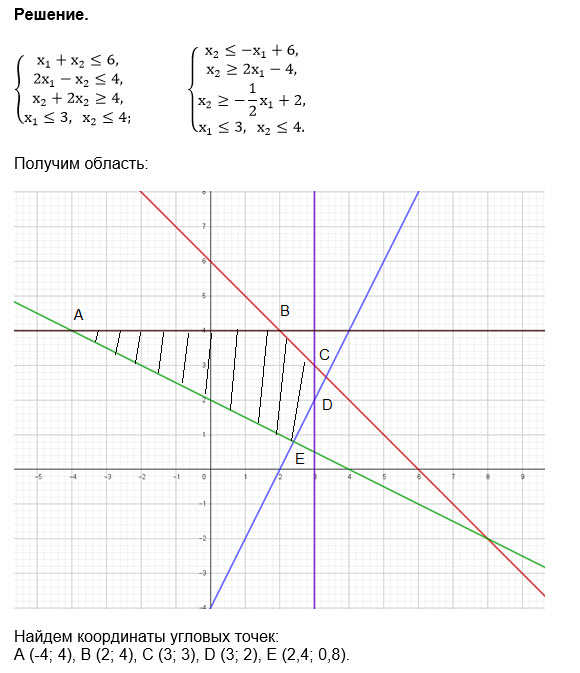
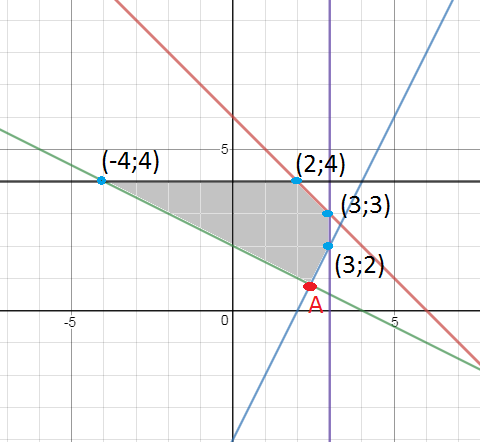
Система неравенств задает область на рис. 6
Координаты угловых точек-координаты границ, задающих неравенство.
Например, координаты точки А находим из системы:
{2x_(1)-x_(2)=4
{x_(1)+2x_(2)=4
Умножаем первое уравнение на 2
{4x_(1)-2x_(2)=8
{x_(1)+2x_(2)=4
и складываем
5x_(1)=12
x_(1)=12/5=2,4
x_(2)=2x_(1)-4=2*2,4-4=0,8
А(2,4;0,8)
Остальные координаты на рисунке ≤
Все решения
