Графический метод
довольно прост и нагляден для решения
задач ЛП с двумя переменными. Он основан
на геометрическом
представлении
допустимых решений и ЦФ задачи. Каждое
из неравенств задачи ЛП определяет на
координатной плоскости (x1,
x2
) некоторую полуплоскость, а система
неравенств в целом – пересечение
соответствующих полуплоскостей.
Множество точек пересечения данных
полуплоскостей называется областью
допустимых решений (ОДР).
ОДР всегда представляет собой выпуклую
фигуру, т.е.
обладающую следующим свойством: если
две точки А и В принадлежат этой фигуре,
то и весь отрезок АВ принадлежит ей. ОДР
графически может быть представлена
выпуклым многоугольником, неограниченной
выпуклой многоугольной областью,
отрезком, лучем, одной точкой. В случае
несовместности системы ограничений
задачи ОДР является пустым множеством.
Оптимальное решение
всегда находится на границе ОДР т.е. ЦФ
L(X)=c1x1+c2x2
принимает свое max(min)
значение на границе области, точнее в
ее угловых точках.
При поиске
оптимального решения задач ЛП возможны
следующие ситуации: существует
единственное решение задачи; существует
бесконечное множество решений
(альтернативный
оптиум); ЦФ
не ограничена; область допустимых
решений – единственная точка; задача
не имеет решений.
Методика решения задач лп графическим методом
-
В ограничениях
задачи замените знаки неравенств на
знаки точных равенств и постройте
соответствующие прямые. -
Найдите и заштрихуйте
полуплоскости, разрешенные каждым из
ограничений-неравенств задачи. Для
этого подставьте в конкретное неравенство
координаты какой-либо точки [например,
(0;0)], и проверьте истинность полученного
неравенства.
Если неравенство
истинное, то
надо
заштриховать полуплоскость, содержащую
данную точку; иначе
(неравенство
ложное) надо заштриховать полуплоскость,
не содержащую данную точку.
Поскольку x1
и x2
должны быть неотрицательными, то их
допустимые значения всегда будут
находиться выше оси x1
и правее оси x2
, т.е. в I-м квадранте. Ограничения-равенства
разрешают только те точки, которые лежат
на соответствующей прямой, поэтому
выделите на графике такие прямые.
III. Определите
ОДР как часть плоскости, принадлежащую
одновременно всем разрешенным областям,
и выделите ее. При отсутствии ОДР задача
не имеет
решений,
о чем сделайте соответствующий вывод.
IV. Если
ОДР – не пустое множество, то определите
координаты угловых точке. Определение
координат сводится к решению системы
соответствующих линейных уравнений.
-
Подставьте
координаты угловых точек в уравнение
для Ц.Ф. и найдите max
(min)
значение целевой функции.
Можно вместо
перебора всех угловых точек (пункт
IV,
V)
произвести
следующие действия:
IV.а Провести
вектор координатами которого служат
коэффициенты в уравнении с целевой
функцией. Сдвигать прямую перпендикулярную
построенному вектору, от начала по
направлению вектора, до момента, когда
пресечение сдвигаемой прямой с ОДР
будет составлять одну точку.
V.а Координаты
найденной точки будут являться оптимальным
планом, а если их подставить в уравнение
целевой функции, то получим ее max
(min)
значение.
Задача
Найдем оптимальное
решение задачи о красках, математическая
модель которой имеет вид:
![]()

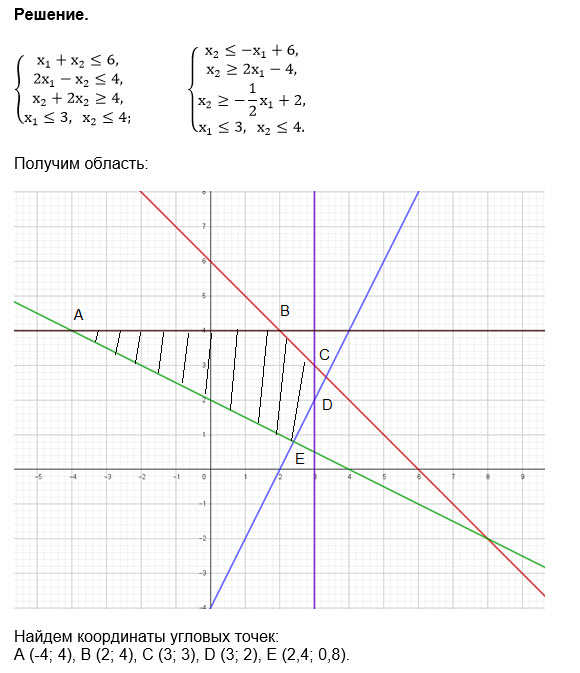
Построим прямые
ограничений (рис. 1).

Рис. 1. Графическое
решение задачи

Определим ОДР.
Например, подставим точку (0;0) в исходное
ограничение (3), получим 0≤1 , что является
истинным неравенством, поэтому стрелкой
(или штрихованием) обозначим полуплоскость,
содержащую
точку
(0;0), т.е. расположенную правее и ниже
прямой (3). Аналогично определим допустимые
полуплоскости для остальных ограничений
и укажем их стрелками у соответствующих
прямых ограничений (см. рис. 1.). Общей
областью, разрешенной всеми ограничениями,
т.е. ОДР является многоугольник ABCDEF.
Найдем координаты
точек пересечения прямых ограничений,
т.е. координаты угловых точек. В некоторых
случаях хороший рисунок позволяет сразу
определять координаты угловых точек.
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
Для определения
координаты точки Е решим систему
уравнений с ограничениями (1) и (2).

Решая данную
систему получаем:

![]()
![]() .
.
Найдем значение
целевой функции в угловых точках, т.е.
подставим их координаты в уравнение
![]() .
.
![]()
![]()
![]()
![]()
![]()
![]()
Е – это точка
максимума ЦФ.
Таким образом,
наилучшим режимом работы фирмы является
ежесуточное производство краски 1-го
вида в объеме 3 1/3 т. и краски 2-го вида в
объеме 1 1/3 т. Доход от продажи красок
составит 12 2/3 тыс. руб. в сутки.
Решая графическим
методом предполагающим построение
целевого вектора, проводим
вектор координатами которого служат
коэффициенты в уравнении с целевой
функцией
![]() ,
,
сдвигая прямую перпендикулярную
построенному вектору (от начала к концу)
найдем точку, являющуюся последней в
пресечении сдвигаемой прямой сОДР,
(это точка Е) ее координаты найденные
из решении системы соответствующих
уравнений будут являться оптимальным
планом, а значение целевой функции в
ней будет max.
В более общем
случае, разработан и широко применяется
универсальный метод решения любой
задачи ЛП, называемый симплекс-методом.
Симплекс метод,
как метод решения задач ЛП был предложен
в американским математиком-экономистом
Данцигом в 1951 году.
Графически симплекс
метод представляет из себя передвижение
по выпуклому многограннику от вершине
к вершине, при этом значение целевой
функции на каждом шаге улучшается до
тех пор, пока не достигается оптимум.
Идея
симплекс метода состоит в том, чтобы
преобразовать уравнение содержащее
целевую функцию к виду:
![]() ,
,
т.к. в этом случае становиться возможным
выразить![]() ,
,
а в силу того что перед нами ставится
задача максимизироватьL,
то эта задача достигается в случае когда
все переменные присутствующие в данном
уравнении принимают нулевые значения
(т.к. переменные не отрицательны по
условию).
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Подробный разбор симплекс-метода
Пролог
Недавно появилась необходимость создать с нуля программу, реализующую алгоритм симплекс-метода. Но в ходе решения я столкнулся с проблемой: в интернете не так уж много ресурсов, на которых можно посмотреть подробный теоретический разбор алгоритма (его обоснование: почему мы делаем те или иные шаги) и советы по практической реализации — непосредственно, алгоритм. Тогда я дал себе обещание — как только завершу задачу, напишу свой пост на эту тему. Об этом, собственно, и поговорим.
Замечание. Пост будет написан достаточно формальным языком, но будет снабжен комментариями, которые должны внести некоторую ясность. Такой формат позволит сохранить научный подход и при этом, возможно, поможет некоторым в изучении данного вопроса.
§1. Постановка задачи линейного программирования
Определение: Линейное программирование – математическая дисциплина, посвященная теории и методам решения экстремальных задач на множествах n- мерного пространства, задаваемых системами линейными уравнений и неравенств.
Общая задача линейного программирования (далее – ЛП) имеет вид:
§2. Каноническая форма задачи ЛП
Каноническая форма задачи ЛП:
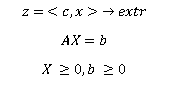
Замечание: Любая задача ЛП сводится к канонической.
Алгоритм перехода от произвольной задачи ЛП к канонической форме:
- Неравенства с отрицательными умножаем на (-1).
- Если неравенство вида (≤), то к левой части добавляем – добавочную переменную, и получаем равенство.
- Если неравенство вида (≥), то из левой части вычитаем , и получаем равенство.
- Делаем замену переменных:
- Если , то
- Если — любой, то , где
Замечание: Будем нумеровать по номеру неравенства, в которое мы его добавили.
Замечание: ≥0.
§3. Угловые точки. Базисные/свободные переменные. Базисные решения
Определение: Точка называется угловой точкой, если представление возможно только при .
Иными словами, невозможно найти две точки в области, интервал проходящий через которые содержит (т.е. – не внутренняя точка).
Графический способ решения задачи ЛП показывает, что нахождение оптимального решения ассоциируется с угловой точкой. Это является основной концепцией при разработке симплекс-метода.
Определение: Пусть есть система m уравнений и n неизвестных (m
Задача 34855 Построить множество решений системы.
Условие
![]()
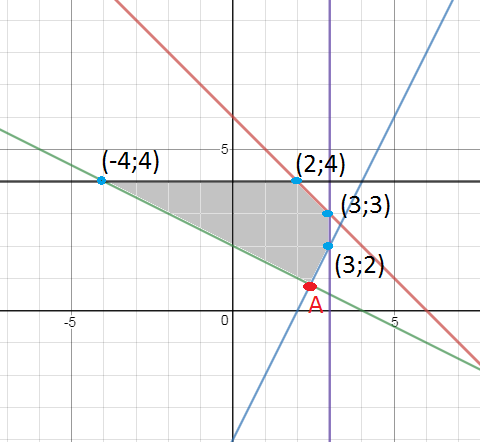
Построить множество решений системы линейных алгебраических неравенств и
найти координаты угловых точек. 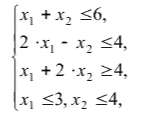
Решение
![]()
Граница каждой области -прямая, которая разбивает плоскость x_(1)Ox_(2) на 2 части
Строим прямую x_(1)+x_(2)=6
по двум точкам (0;6) и (6;0)
Выбираем произвольную точку из любой области, например, точку (0;0)
Подставляем в первое неравенство
0+0 ≤ 6 – верно.
Значит первое неравенство задает ту область, которая содержит точку (0;0)
Первое неравенство задает область 1 ( см. рис)
второе – область 2, .
Система неравенств задает область на рис. 6
Координаты угловых точек-координаты границ, задающих неравенство.
Например, координаты точки А находим из системы:
<2x_(1)-x_(2)=4
Остальные координаты на рисунке ≤ 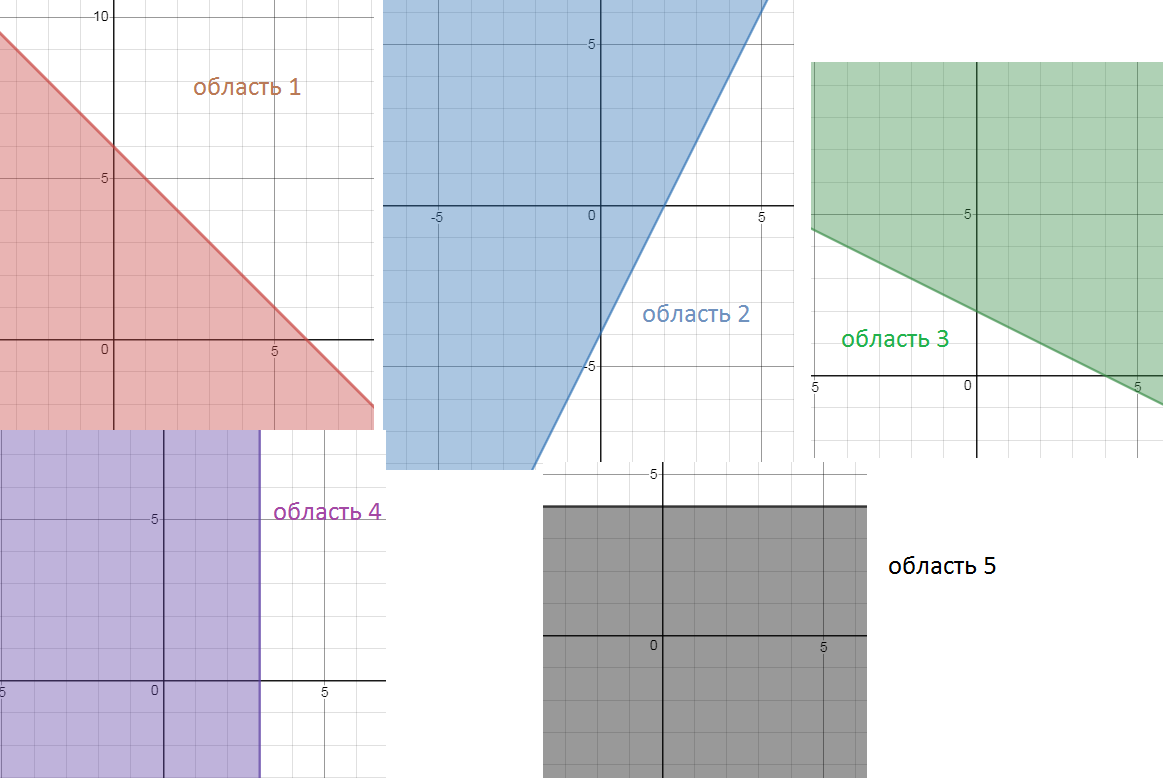
Решение систем уравнений
Содержание:
Графический метод решения систем уравнений
Вспоминаем то, что знаем
Что такое график уравнения с двумя неизвестными?
Что представляет собой график линейного уравнения с двумя неизвестными?
Решите графическим методом систему линейных уравнений:
 Открываем новые знания
Открываем новые знания
Решите графическим методом систему уравнений:

Как можно решить систему двух уравнений с двумя неизвестными с помощью графиков уравнений этой системы? Отвечаем, проверяем себя по тексту
В курсе алгебры 7-го класса вы изучали системы линейных уравнений.
Для их решения вы применяли три метода: графический, метод подстановки и метод алгебраического сложения. Эти же методы служат и для решения других систем двух уравнений с двумя неизвестными, в которых могут содержаться уравнения второй степени или другие рациональные уравнения — как целые, так и дробные.
По этой ссылке вы найдёте полный курс лекций по высшей математике:
Начнём с графического метода
Этот метод основан на том, что каждому уравнению с двумя неизвестными соответствует некоторое множество точек координатной плоскости (график этого уравнения). Построив графики уравнений, мы найдём точки пересечения этих графиков (если они есть), и пары чисел — координаты точек пересечения — будут представлять собой решения системы уравнений.
Найденные решения будут, вообще говоря, приближёнными, в зависимости от точности построений соответствующих графиков.
Таким образом, решить графически систему уравнений — значит найти общие точки графиков уравнений, входящих в систему.
Возможно вам будут полезны данные страницы:
Примеры с решением
Пример 1:
Решим систему уравнений:

Построим графики уравнений 
Графиком первого уравнения является парабола, с вершиной в точке (0; 1) и ветвями, направленными вверх, графиком второго — прямая, проходящая через точки (0; 3) и (-3; 0).
 Парабола и прямая пересекаются в точках А(2; 5) и В(— 1; 2).
Парабола и прямая пересекаются в точках А(2; 5) и В(— 1; 2).
Проверкой убеждаемся, что найденные пары чисел действительно являются решениями системы.
Ответ: (2; 5) и (-1; 2).
Пример 2:
Выясним количество решений системы уравнений:

Построим графики уравнений 
Графики этих уравнений — окружности. Центр первой окружности — начало координат, а её радиус равен 2; центр второй окружности — точка Р(1; — 1), её радиус равен 3.
 Окружности пересекаются в двух точках М и N, координаты которых можно найти приближённо. Поскольку нам нужно определить только количество решений, мы делать этого не будем.
Окружности пересекаются в двух точках М и N, координаты которых можно найти приближённо. Поскольку нам нужно определить только количество решений, мы делать этого не будем.
Ответ: Два решения.
Решение систем уравнений методом подстановки
Вспоминаем то, что знаем
Расскажите, как решить систему двух линейных уравнений с двумя неизвестными методом подстановки.
Решите систему линейных уравнений методом подстановки:

Открываем новые знания
Как вы думаете, можно ли применять метод подстановки при решении систем, где не все уравнения являются линейными? При каком условии это удастся сделать?
Решите систему уравнений методом подстановки:

Как решить систему двух уравнений с двумя неизвестными методом подстановки?
Всякую ли систему двух уравнений с двумя неизвестными можно решить методом подстановки?
Ранее вы решали системы уравнений первой степени.
Теперь познакомимся с системами, в которых хотя бы одно уравнение не является линейным. Как и прежде, распространённым методом решения систем является метод подстановки.
Пример 3:

Пусть (х; у) — решение системы.
Выразим х из уравнения 

Подставим найденное выражение в первое уравнение:

Решим полученное уравнение:


Убедиться, что найденные пары чисел действительно являются решениями системы, можно подстановкой.
Чуть сложнее дело обстоит в следующем примере.
Пример 4:
Решим систему уравнений:

Пусть (х; у) — решение системы.
Выразим у из линейного уравнения:

Подставим найденное выражение в первое уравнение системы:

После преобразований получим:


Ответ: (-0,5; 0,5), (4; 5).
Если это целесообразно, то можно осуществлять подстановку некоторого выражения «в целом».
Пример 5:

Подставим во второе уравнение  тогда его можно переписать в виде:
тогда его можно переписать в виде:

Теперь выразим х через у из первого уравнения системы:

Подставим в полученное ранее уравнение ху = 2:

Корни этого уравнения: 
 .
.
Иногда решить систему можно, используя метод алгебраического сложения.
Пример 6:

Сложим уравнения, предварительно умножив первое уравнение на —1. В результате получим:
 .
.
Корни этого уравнения: 
Подставим найденные значения в первое уравнение. Рассмотрим два случая:
1) 
2)  , получим уравнение
, получим уравнение  корней нет.
корней нет.
Иногда упростить решение удаётся, используя различные варианты замены неизвестных.
Пример 7:
Решим систему уравнений:

Обозначим 
Второе уравнение системы примет вид:

Решим полученное уравнение. Получим, умножая обе части на 2а:


Осталось решить методом подстановки линейные системы:

Ответ: (2; 1), (1; 2). Решение задач с помощью систем уравнений Знакомимся с новыми знаниями
Напомним, что при решении задач обычно действуют следующим образом:
1) обозначают буквами какие-нибудь неизвестные величины, выражают через них другие величины, составляют систему уравнений;
2) решают полученную систему;
3) отвечают на вопрос задачи.
Пример 8:
Периметр прямоугольника равен 34 см, а его диагональ 13 см. Найдите стороны прямоугольника.
Пусть х см — длина, у см — ширина (х у), тогда периметр прямоугольника —  см.
см.
Воспользуемся теоремой Пифагора: 

Решим систему. Выразим из первого уравнения у:

Подставим во второе уравнение:

Корни уравнения: 
Найдём 
С учётом условия  получим ответ: длина — 12 см, ширина — 5 см.
получим ответ: длина — 12 см, ширина — 5 см.
Пример 9:
Если произведение двух положительных чисел увеличить на первое из них, то получится 128. Если это же произведение увеличить на второе из них то получится 135. Найдите эти числа.
Пусть х — первое число, у — второе число.
Тогда:  — произведение, увеличенное на первое число, ху 4-у — произведение, увеличенное на второе число.
— произведение, увеличенное на первое число, ху 4-у — произведение, увеличенное на второе число.

Вычтем из второго уравнения первое. Получим:

Дальше будем решать методом подстановки:

Подставим в первое уравнение выражение для у:

Корни уравнения:  (не подходит по смыслу задачи).
(не подходит по смыслу задачи).
Найдём у из уравнения:

Получим ответ: 16 и 7.
Симметричные системы уравнений с двумя неизвестными
Уравнение с двумя неизвестными называется симметричным, если при перестановке этих неизвестных местами уравнение не меняется. Например, уравнение  симметричное, так как при перестановке входящих в него неизвестных оно приобретает вид
симметричное, так как при перестановке входящих в него неизвестных оно приобретает вид  , то есть не меняется. А вот уравнение
, то есть не меняется. А вот уравнение  не симметричное, так как при перестановке входящих в него неизвестных оно приобретает вид
не симметричное, так как при перестановке входящих в него неизвестных оно приобретает вид  , то есть меняется.
, то есть меняется.
Система двух уравнений с двумя неизвестными называется симметричной, если каждое уравнение этой системы симметричное.
ПРЕДУПРЕЖДЕНИЕ. В определении симметричной системы уравнений требуется, чтобы каждое уравнение в отдельности не менялось.
Например, если в системе уравнений

переставить местами неизвестные х и у, то получим систему:

Видно, что система в целом не изменилась (уравнения поменялись местами по сравнению с первоначальной системой). Но такая система не является симметричной, так как каждое из уравнений в отдельности изменилось.
Убедитесь, что симметричные системы с двумя неизвестными х и у можно решать с помощью замены неизвестных:

Сначала научитесь выражать через неизвестные  выражения:
выражения:



Присылайте задания в любое время дня и ночи в ➔ 
Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.
Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.
Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.
[spoiler title=”источники:”]
http://reshimvse.com/zadacha.php?id=34855
http://natalibrilenova.ru/reshenie-sistem-uravnenij/
[/spoiler]
Пример 1. Найти область решений (ОР) и область допустимых решений (ОДР) системы неравенств и определить координаты угловых точек ОДР
РЕШЕНИЕ. Найдем ОР первого неравенства: X2 + 3X2 ≥ 3.
Построим граничную прямую X1 +3X2 – 3 = 0 (рис. 1).
Подставим координаты точки (0,0) в неравенство: 1∙0 + 3∙0 > 3; так как координаты точки (0,0) не удовлетворяют ему, то решением неравенства (1) является полуплоскость, не содержащая точку (0,0).
Аналогично найдем решения остальных неравенств системы.
Получим, что ОР и ОДР системы неравенств является выпуклый многогранник ABCD.
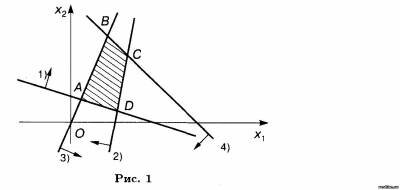
Найдем угловые точки многогранника. Точку А определим как точку пересечения прямых
Решая систему, получим А(3/7, 6/7). Точку В найдем как точку пересечения прямых
Из системы получим B(5/3, 10/3). Аналогично найдем координаты точек С и D: С(11/4; 9/14), D(3/10; 21/10).
Ответ: ОР и ОДР совпадают, является многоугольник ABCD.
Пример 2 Найти ОР и ОДР системы неравенств и определить координаты угловых точек ОДР.
Решение.
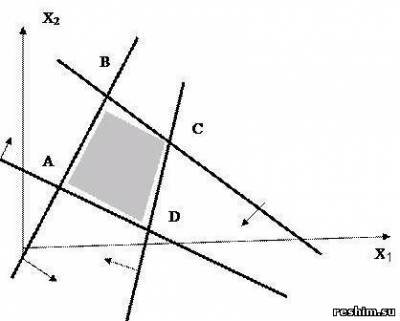
Ответ: А(3/7, 6/7), В(5/3, 10/3), С(11/4, 9/4), D(21/10, 3/10), ОР и ОДР совпадают.
На следующем примере покажем отличие ОР и ОДР
Пример 3. Найти ОР и ОДР системы неравенств
Решение.
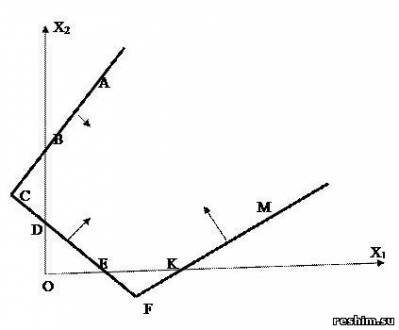
Область решения (ОР) системы, удовлетворяющая условиям неотрицательности (xj ≥ 0, j = 1,n), называется областью неотрицательных, или допустимых, решений (ОДР).
Ответ: ACFM – ОР, ABDEKM – ОДР.
Общее решение и область допустимых значений системы неравенств могут иметь одну общую точку, рассмотрим данный случай на следующем примере.
Пример 4.Найти ОР и ОДР системы неравенств
Решение.
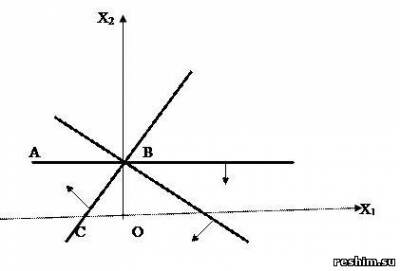
Ответ:ABC – ОР, точка B – ОДР.
ОР и ОДР системы несовместные, смотри следующий пример.
Пример 5.Найти ОР и ОДР системы неравенств
Решение.
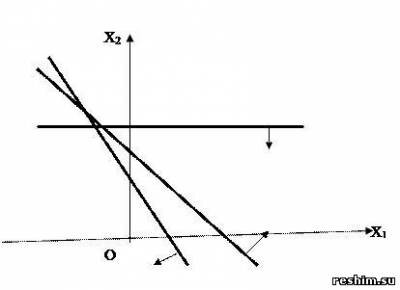
Ответ: ОР и ОДР несовместны.
Для того, чтобы найти угловые точки:
Найти угловые точки графика функции
Онлайн калькулятор поможет вычислить координаты угловых точек (точек излома).
Точка излома или угловая точка — особая точка кривой, обладающая тем свойством, что ветви кривой, на которые эта точка делит исходную кривую, имеют в этой точке различные (односторонние) касательные. Функция не является гладкой в данной точке.
Синтаксис
основных функций:
xa: x^a
|x|: abs(x)
√x: Sqrt[x]
n√x: x^(1/n)
ax: a^x
logax: Log[a, x]
ln x: Log[x]
cos x: cos[x] или Cos[x]
sin x: sin[x] или Sin[x]
tg: tan[x] или Tan[x]
ctg: cot[x] или Cot[x]
sec x: sec[x] или Sec[x]
cosec x: csc[x] или Csc[x]
arccos x: ArcCos[x]
arcsin x: ArcSin[x]
arctg x: ArcTan[x]
arcctg x: ArcCot[x]
arcsec x: ArcSec[x]
arccosec x: ArcCsc[x]
ch x: cosh[x] или Cosh[x]
sh x: sinh[x] или Sinh[x]
th x: tanh[x] или Tanh[x]
cth x: coth[x] или Coth[x]
sech x: sech[x] или Sech[x]
cosech x: csch[x] или Csch[е]
areach x: ArcCosh[x]
areash x: ArcSinh[x]
areath x: ArcTanh[x]
areacth x: ArcCoth[x]
areasech x: ArcSech[x]
areacosech x: ArcCsch[x]
конъюнкция “И” ∧: &&
дизъюнкция “ИЛИ” ∨: ||
отрицание “НЕ” ¬: !
импликация =>
число π pi : Pi
число e: E
бесконечность ∞: Infinity, inf или oo
×
Пожалуйста напишите с чем связна такая низкая оценка:
×
Для установки калькулятора на iPhone – просто добавьте страницу
«На главный экран»

Для установки калькулятора на Android – просто добавьте страницу
«На главный экран»

Задача 34855 Построить множество решений системы…
Условие
![]()
Построить множество решений системы линейных алгебраических неравенств и
найти координаты угловых точек.
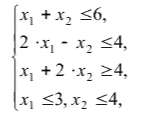
математика 10-11 класс
2330
Решение
![]()
★
Граница каждой области -прямая, которая разбивает плоскость x_(1)Ox_(2) на 2 части
Строим прямую x_(1)+x_(2)=6
по двум точкам (0;6) и (6;0)
Выбираем произвольную точку из любой области, например, точку (0;0)
Подставляем в первое неравенство
0+0 ≤ 6 – верно.
Значит первое неравенство задает ту область, которая содержит точку (0;0)
Первое неравенство задает область 1 ( см. рис)
второе – область 2, …
Система неравенств задает область на рис. 6
Координаты угловых точек-координаты границ, задающих неравенство.
Например, координаты точки А находим из системы:
{2x_(1)-x_(2)=4
{x_(1)+2x_(2)=4
Умножаем первое уравнение на 2
{4x_(1)-2x_(2)=8
{x_(1)+2x_(2)=4
и складываем
5x_(1)=12
x_(1)=12/5=2,4
x_(2)=2x_(1)-4=2*2,4-4=0,8
А(2,4;0,8)
Остальные координаты на рисунке ≤


Все решения
![]()