В данной публикации мы рассмотрим формулы, с помощью которых можно найти координаты вектора, заданного координатами его начальной и конечной точек, а также разберем примеры решения задач по этой теме.
- Нахождение координат вектора
- Примеры задач
Нахождение координат вектора
Для того, чтобы найти координаты вектора AB, нужно из координат его конечной точки (B) вычесть соответствующие координаты начальной точки (A).
Формулы для определения координат вектора
| Для плоских задач | AB = {Bx – Ax; By – Ay} |
| Для трехмерных задач | AB = {Bx – Ax; By – Ay; Bz – Az} |
| Для n-мерных векторов | AB = {B1 – A1; B2 – A2; … Bn – An} |
Примеры задач
Задание 1
Найдем координаты вектора AB, если у его точек следующие координаты: A = (2; 8), B = (5; 12).
Решение:
AB = {5 – 2; 12 – 8} = {3; 4}.
Задание 2
Определим координаты точки B вектора AB = {6; 14}, если координаты точки A = (2; 5).
Решение:
Координаты точки B можно вывести из формулы для расчета координат вектора:
Bx = ABx + Ax = 6 + 2 = 8.
By = ABy + Ay = 14 + 5 = 19.
Таким образом, B = (8; 19).
Вспомним, что при умножении вектора на число
k≠0
мы получаем два коллинеарных (параллельных) вектора, которые или сонаправлены, если
k>0
, или противоположно направлены, если
k<0
. Длины векторов различаются (k) раз.
Справедливо и обратное суждение.
Если ненулевые векторы коллинеарны, то обязательно можно найти число
k≠0
так, что
b→=k⋅a→
.
Для неколлинеарных векторов справедливо суждение, что каждый вектор на плоскости можно представить в виде
c→=k⋅a→+m⋅b→
. Говорят, что вектор
c→
разложен по векторам
a→
и
b→
, а числа (k) и (m) называют коэффициентами разложения.
Это справедливо для любого вектора на плоскости, причём коэффициенты определяются единственным образом.
Выберем два не коллинеарных вектора на осях системы координат. Пусть длина каждого из них будет равна единичному отрезку в этой системе координат. Эти векторы называют координатными векторами и обозначают
i→
и
j→
.
Если от начала координат отложить вектор
a→
, то его можно разложить по векторам
i→
и
j→
следующим образом:
a→=3⋅i→+2⋅j→
.
В этом разложении коэффициенты координатных векторов называют координатами вектора
a→
.
Это записывают как
a→3;2
.
Любой вектор, который равен с вектором
a→
, можно переместить и отложить от начала координат. Следовательно, можем сделать вывод.
Равные векторы имеют равные координаты.
Но в то же время в координатной системе можно переместить векторы
i→
и
j→
, таким образом определить координаты векторов независимо от их места расположения в координатной системе.
Легко понять, что разница между абсциссами (координатами x) конечной и начальной точки вектора и есть абсцисса вектора, а разница между ординатами (координатами y) конечной и начальной точки вектора есть ордината вектора.
Связь между координатами противоположных векторов следует из того, что, если умножить вектор на (-1), результатом будет противоположный вектор.
У противоположных векторов противоположные координаты.
Важно понять ещё несколько интересных связей между координатами векторов одинаковой длины.
Ранее
вы уже сталкивались с координатами, но указывали их для точек. При этом
работали в прямоугольной координатной плоскости, для задания которой необходимо
было провести две взаимно перпендикулярные прямые с выбранными на них
направлениями (их называют координатными осями) и выбрать единицу измерения на
каждой из осей.
Это
и позволяло определить координаты любой точки.
На
этом уроке нам предстоит выяснить, что называют координатами вектора.
С
прошлых занятий вам известно, что любой вектор на плоскости можно разложить по
двум неколлинеарным векторам.
От
точки О начала координат отложим векторы ,
длины которых равны единице (в дальнейшем будем называть такие векторы
единичными), так, чтобы направление вектора совпадало с
направлением оси x, а направление вектора совпадало
с направлением оси y.
Тогда
векторы будем
называть координатными векторами. Понятно, что любой вектор можно разложить по
векторам .
Причём коэффициенты разложения, числа x
и y, определяются единственным образом.
Так
вот коэффициенты разложения вектора по координатным
векторам называют координатами вектора в данной системе
координат.
Координаты
вектора будем записывать в фигурных скобках через точку с
запятой. При этом первым будем записывать коэффициент разложения x,
а вторым — y.
На
одном из прошлых занятий мы разлаживали векторы, изображённые в координатной
плоскости по векторам .
Пользуясь
этими разложениями, запишем координаты данных векторов.
Итак,
вектор имеет
координаты .
Вектор имеет
координаты .
Координатами
вектора являются
числа ..
Ну,
а координатами вектора будут
числа .
Обратите
внимание, что такие координаты данные векторы будут иметь только в конкретной
системе координат и при конкретных координатных векторах .
Коэффициенты
разложения нулевого вектора по векторам равны
нулю. Тогда получаем, что нулевой вектор имеет координаты 0 0, причём в любой
системе координат и при любых координатных векторах.
Если
векторы равны, то их разложения по векторам также
будут равны, а значит, равны будут и коэффициенты разложения. Таким образом,
получаем, что координаты равных векторов соответственно равны.
Рассмотрим
ещё один особенный случай — противоположные векторы.
Их
разложения противоположны. Значит, противоположны будут и соответственные
координаты.
Можем
подытожить, что координаты равных векторов соответственно равны, а координаты
противоположных векторов соответственно противоположны.
Пользуясь
полученными выводами, для каждого из данных векторов запишем противоположный и
укажем его координаты.
;
;
;
;
.
Задача. Разложить векторы по
координатным векторам и
, указать их координаты.
Начнём
с вектора .
Его разложение .
Значит, его координатами будут числа 7 и 2.
Далее
запишем разложение вектора .
Коэффициенты разложения 6 и -1 являются его координатами.
Вектор
. Коэффициенты разложения
равны 0 и 3. Значит, вектор .
Следующим
рассмотрим вектор .
Значит, координаты вектора .
Далее обратим своё внимание на вектор . Тогда
координаты данного вектора .
Запишем разложение вектора . Значит, он
имеет координаты .
Последним рассмотрим вектор . Тогда
получаем, .
Видим, что для определения координат вектора достаточно его
разложения по координатным векторам. Поэтому при наличии разложения вектора
можно сразу назвать его координаты. Главное — помнить, что в качестве первой
координаты записывают коэффициент разложения при координатном векторе,
коллинеарном оси x (в данном случае — это вектор ), а в
качестве второй координаты — коэффициент разложения при координатном векторе,
коллинеарном оси y (в данном случае — это вектор ).
Запишем координаты векторов, пользуясь их разложениями по
координатным векторам .
Из разложения вектора видим, что он имеет координаты
.
, то
;
, то
;
, то
;
, то
.
А
теперь, пользуясь только координатами данных векторов, построим их в
прямоугольной координатной плоскости, откладывая каждый вектор от точки О
начала координат.
Координатами
вектора являются
числа 8 и -1. Значит, чтобы переместиться из точки О на вектор , сначала нужно
переместиться на вектор ,
а затем на вектор .
Соединив точку О с конечной точкой, получим вектор .
Далее
изобразим вектор .
Для этого из точки О переместимся на вектор .
Тем самым получим искомый вектор .
Чтобы
из точки О переместиться на вектор сначала
переместимся на вектор ,,
а затем на вектор .
Проведём вектор из точки О в конечную точку. Так мы получили вектор .
Далее
построим вектор .
Последним
построим вектор .
Перемещение на этот вектор состоит из перемещений на вектор и на вектор
. Перемещение из точки О
в конечную точку и задаёт вектор
Так
мы рассмотрели примеры построения вектора по его координатам.
Далее,
пользуясь приобретёнными знаниями о координатах вектора, получим правила
нахождения координат векторов, полученных уже известными вам действиями:
сложением, вычитанием и умножением вектора на число.
Сначала
рассмотрим сумму двух векторов ,
.
Пользуясь
их координатами, можем записать разложения данных векторов по координатным
векторам ,
.
Сложим
полученные равенства .
Пользуясь свойствами сложения векторов и произведения вектора на число,
получаем, что координаты вектора суммы векторов и
равны
,
.
Можем
записать правило.
Каждая
координата суммы двух и более векторов равна сумме соответствующих координат
этих векторов.
Найдём
координаты векторов суммы, если вектор ,
,
,
.
Координаты
вектора суммы и
равны
.
Координаты
вектора суммы ,
,
равны
.
Теперь
рассмотрим разность векторов –
.
Из
разложения вектора вычтем
разложение вектора .
Получаем,
что координаты вектора разности равны .
Запишем
правило. Каждая координата разности двух векторов равна разности
соответствующих координат данных векторов.
Разность
векторов и
имеет координаты
.
Разность
векторов и
имеет координаты
.
Далее
получим координаты произведения вектора на число k.
Получаем,
что координаты произведения равны .
Запишем
правило. Каждая координата произведения вектора на число равна произведению
соответствующей координаты вектора на это число.
Найдём
координаты вектора 4.
Они равны .
Координаты
вектора 2,5 равны
.
Вектор
3 имеет координаты
.
Ну,
а вектор
имеет
координаты .
Все
три правила, полученные нами, в дальнейшем помогут определять координаты любого
вектора, представленного в виде алгебраической суммы данных векторов с
известными координатами.
Задача.
Найти
координаты векторов и
по координатам
данных векторов ,
,
,
.
Представим
это выражение в виде суммы.
Вектор
имеет координаты
, или
.
Вектор
имеет
координаты ,
или .
Координаты
вектора . А вот координаты
вектора .
Координаты
вектора найдём
как суммы соответствующих координат полученных векторов. В результате получаем,
что имеет
координаты
Далее
найдём координаты вектора .
Запишем второй множитель в виде суммы. Координаты векторов и
. Вектор
имеет координаты
, или
. Вектор
.
Сумма
полученных векторов будет иметь координаты .
Произведение
этого вектора на 3 имеет координаты .
Это и есть координаты вектора .
Подведём
итоги урока. Сегодня, пользуясь уже известным правилом разложения вектора по
двум неколлинеарным векторам, мы ввели понятие координатных векторов и дали
определение координатам вектора. А также получили правила нахождения координат
векторов суммы векторов, разности векторов и произведения вектора на число.
Этих правила позволяют определять координаты векторов, представленных в виде
алгебраической суммы данных векторов с известными координатами.
На
следующем уроке мы найдём связь между координатами вектора и координатами его
начала и конца.
Координаты вектора
Пусть на плоскости задана прямоугольная система координат. Определим понятие координат вектора. Для этого отложим вектор так, чтобы его начало совпало с началом координат. Тогда координаты его конца называются координатами вектора .
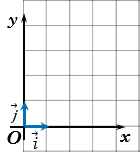
Обозначим векторы с координатами (1, 0), (0, 1) соответственно. Их длины равны единице, а направления совпадают с направлениями соответствующих осей координат. Будем рисовать эти векторы, отложенными от начала координат и называть их координатными векторами .
В режиме слайдов ответы появляются после кликанья мышкой
Теорема
Теорема. Вектор имеет координаты ( x , y ) тогда и только тогда, когда он представим в виде
Доказательство. Отложим вектор от начала координат, и его конец обозначим через А . Имеет место равенство Точка А имеет координаты ( x , y ) тогда и только тогда, когда выполняются равенства и, значит,
В режиме слайдов ответы появляются после кликанья мышкой
2
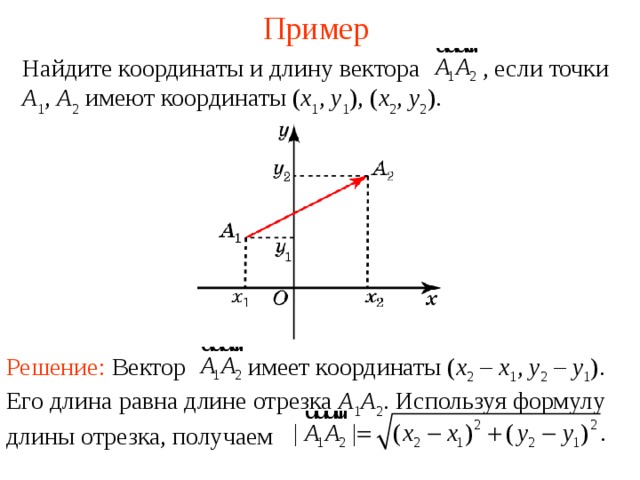
Пример
Найди те координаты и длину вектора , если точки А 1 , А 2 имеют координаты ( x 1 , y 1 ), ( x 2 , y 2 ).
В режиме слайдов ответы появляются после кликанья мышкой
Решение: В ектор имеет координаты ( x 2 – x 1 , y 2 – y 1 ). Его длина равна длине отрезка А 1 А 2 . Используя формулу длины отрезка, получаем
3
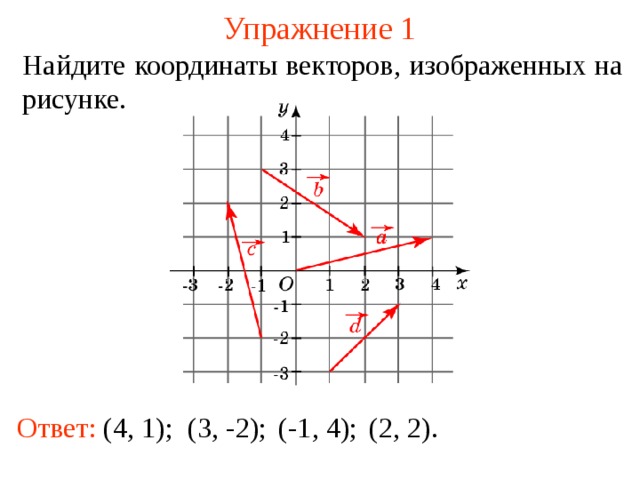
Упражнение 1
На йдите координаты векторов , изображенных на рисунке.
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: ( 4 , 1 );
( 3 , -2 );
( -1 , 4 );
( 2 , 2 ).
Упражнение 2
Назовите координаты векторов:
а)
б)
в)
г)
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: а) (–2, 6);
б) (1, 3);
в) (0, -3);
г) (-5, 0).
Упражнение 3
Найдите координаты вектора , если точки A 1 , A 2 имеют координаты (-3, 5), (2, 3) соответственно.
В режиме слайдов ответы появляются после кликанья мышкой
Ответ: (5, -2).
Упражнение 4
Выразите длину вектора через его координаты ( x , y ).
Ответ:
В режиме слайдов ответы появляются после кликанья мышкой
7
Упражнение 5
Найдите координаты точки N , если вектор имеет координаты (4, -3) и точка M – (1, -3).
Ответ: (5, -6).
В режиме слайдов ответы появляются после кликанья мышкой
Упражнение 6
Найдите координаты вектора , если: а) A (2, -6), B (-5, 3); б) A (1, 3), B (6, -5); в) A (-3, 1), B (5, 1).
Ответ: а) (-7, 9);
б) (5, -8);
в) (8, 0).
В режиме слайдов ответы появляются после кликанья мышкой
Упражнение 7
Вектор имеет координаты ( a , b ). Найдите координаты вектора .
Ответ: (- a , – b ).
В режиме слайдов ответы появляются после кликанья мышкой
Упражнение 8
Даны три точки А (1, 1), В (-1, 0), С (0, 1). Найдите такую точку D ( x , y ), чтобы векторы и были равны.
Ответ: (-2, 0).
В режиме слайдов ответы появляются после кликанья мышкой
Упражнение 9
Найдите координаты векторов и , если (1, 0), (0, 3).
Ответ: (1, 3) и (1, -3).
В режиме слайдов ответы появляются после кликанья мышкой
Упражнение 10
Даны векторы (-1, 2) и (2, -4). Найдите координаты вектора:
а)
б)
в)
Ответ: а) (1, -2);
б) (-1, 2);
в) (11, -22).
В режиме слайдов ответы появляются после кликанья мышкой
Упражнение 1 1
Вершины треугольника имеют координаты A (1, 3 ), B (2, 1) и C (3, 4). Найдите координаты точки M пересечения медиан.
Решение:
В режиме слайдов ответы появляются после кликанья мышкой
Следовательно, имеет координаты
Точка M имеет координаты
14
- Главная
- Справочники
- Справочник по геометрии 7-9 класс
- Метод координат
- Координаты вектора
Прямоугольная система координат (декаротова система координат) — прямолинейная система координат с взаимно перпендикулярными осями на плоскости или в пространстве. Для задания прямоугольной системы координат нужно провести две взаимно перпендикулярные прямые, на каждой из них выбрать направление (оно обозначается стрелкой) и выбрать единицу измерения отрезков.
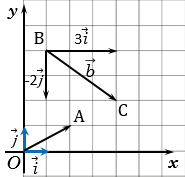
На рисунке выше оси 
Отложим от начала координат О единичные векторы 
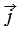
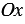
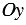
Векторы 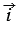
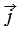
Координатные векторы не коллинеарны, поэтому любой вектор 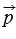
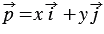
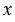
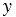
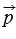
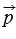
Координаты вектора записывают в фигурных скобках после обозначения вектора: 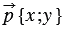
На рисунке выше 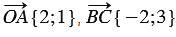
Нулевой вектор можно представить в виде 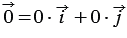
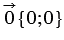
Если векторы 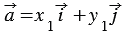
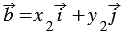
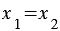
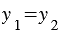
Правила, позволяющие по координатам векторов находить координаты их суммы, разности и произведения вектора на число:
10. Каждая координата суммы двух и более векторов равна сумме соответствующих координат этих векторов.
Доказательство
Дано: 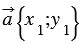
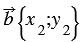
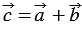
Доказать: 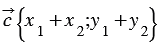
Доказательство:
По условию 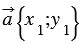
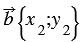
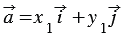
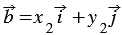
Сложим последние два равенства и применим свойства сложения векторов и умножения вектора на число, получим: 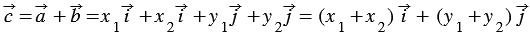
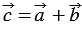

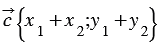
20. Каждая координата разности двух векторов равна разности соответствующих координат этих векторов.
Доказательство
Дано: 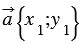
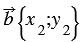
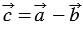
Доказать: 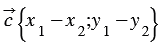
Доказательство:
По условию 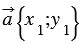
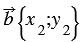
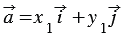
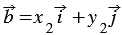
Вычтем из равенства (1) равенство (2) и применим свойства сложения векторов и умножения вектора на число, получим: 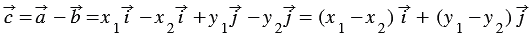
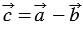
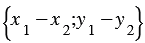
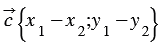
30. Каждая координата произведения вектора на число равна произведению соответствующей координаты вектора на это число.
Доказательство
Дано: 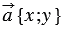
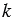
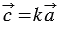
Доказать: 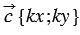
Доказательство:
По условию 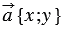
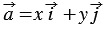
Умножим последнее равенство на число 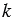
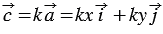
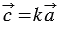
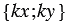
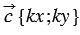
Данные правила позволяют определить координаты любого вектора, представленного в виде алгебраической суммы данных векторов с известными координатами.
Пример
Найти координаты вектора 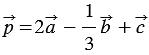
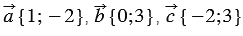
Решение:
По правилу 30 вектор 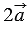
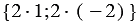
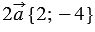
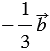
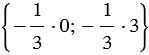
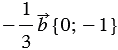
Так как 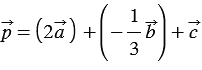
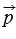
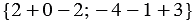
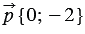
Ответ: 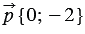
Советуем посмотреть:
Разложение вектора по двум неколлинеарным векторам
Связь между координатами вектора его начала и конца
Простейшие задачи в координатах
Уравнение линии на плоскости
Уравнение окружности
Уравнение прямой
Взаимное расположение двух окружностей
Метод координат
Правило встречается в следующих упражнениях:
7 класс
Задание 916,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 918,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 926,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 943,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 944,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 958,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 6,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 11,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 21,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1066,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник