Отложим от начала координат единичные векторы, то есть векторы, длины которых равны единице. Направление вектора i→ должно совпадать с осью Ox, а направление вектора j→ с осью Oy.
Векторы i→ и j→ называют координатными векторами.
Координатные векторы неколлинеарны. Поэтому любой вектор p→ можно разложить по векторам p→=xi→+yj→. Коэффициенты x и y определяются единственным образом. Коэффициенты разложения вектора p→ по координатным векторам называются координатами вектора p→ в данной системе координат.

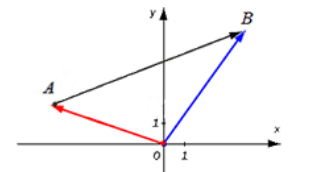
Координаты вектора записываются в фигурных скобках p→x; y. На рисунке вектор OA→ имеет координаты 2; 1, а вектор b→ имеет координаты 3;-2. Нулевой вектор представляется в виде 0→0; 0.
Если векторы a→ и b→ равны, то и y1=y2. Запишем это так: a→=x1i→+y1j→=b→=x2i→+y2j→, значит x1=x2, y1=y2 .
Таким образом, координаты равных векторов соответственно равны.
Если точка координат не совпадает с его началом системы координат, тогда рассмотрим задачу. Пусть в декартовой системе координат на Oxy заданы координаты точек начала и конца AB→: Axa, ya, Bxb, yb. Найти координаты заданного вектора.
Изобразим координатную ось.

Из формулы сложения векторов имеем OA→+AB→=OB→, где O – начало координат. Отсюда следует, что AB→=OB→-OA→.
OA→ и OB→ – это радиус-векторы заданных точек А и В, значит координаты точек имеют значения OA→=xa, ya, OB→=xb, yb.
По правилу операций над векторами найдем AB→=OB→-OA→=xb-xa, yb-ya.

Нахождение в трехмерном пространстве проходит по такому же принципу, только для трех точек.
Для нахождения координат вектора, необходимо найти разность его точек конца и начала.
Найти координаты OA→ и AB→ при значении координат точек A(2,-3), B(-4,-1).
Решение
Для начала определяется радиус-вектор точки A. OA→=(2,-3). Чтобы найти AB→, нужно вычесть значение координат точек начала из координат точек конца.
Получаем: AB→=(-4-2,-1-(-3))=(-6, 2).
Ответ: OA→=(2,-3), AB→=(-6,-2).
Задано трехмерное пространство с точкой A=(3, 5, 7), AB→=(2, 0,-2). Найти координаты конца AB→.
Решение
Подставляем координаты точки A: AB→=(xb-3, yb-5, zb-7).
По условию известно, что AB→=(2, 0,-2).
Известно, что равенство векторов справедливо тогда, когда координаты равны соответственно. Составим систему уравнений: xb-3=2yb-5=0zb-7=-2
Отсюда следует, что координаты точки B AB→равны: xb=5yb=5zb=5
Ответ: B(5, 5, 5).
![]()
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
Определение
Вектор – это направленный отрезок, т.е. отрезок, имеющий длину и определенное направление. Графически вектор изображается в виде направленных отрезков определенной длины.
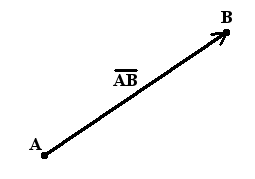
Вектор, имеющий начальную точку А и конечную точку В, обозначается [overrightarrow{A B}](рис. 1).
Определения
Длина направленного отрезка определяет числовое значение вектора и называется длиной вектора [overrightarrow{A B}]. Длина вектора [overrightarrow{A B}] обозначается как: [|overrightarrow{A B}|]
Векторы параллельные одной прямой или лежащие на одной прямой, называются коллинеарными векторами.
Определение
Единичный вектор или орт — это вектор, длина которого равна единице.
Правило нахождения координат вектора
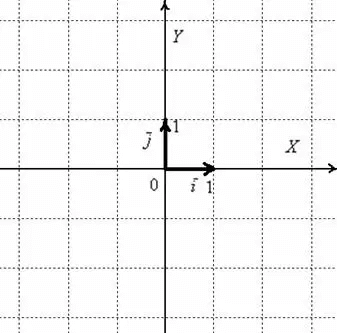
Отложим от начала системы координат два единичных вектора, то есть векторы, длины которых равны единице. Направление вектора [bar{i}] должно совпадать с осью [O x], а направление вектора [bar{j}] с осью [O y].
Векторы [bar{i}, bar{j}] — рассматриваемые векторы называются векторами координат или ортами. Эти векторы образуют базис поверхности. Иногда построенный базис называют ортонормированным базисом плоскости.
Обозначение: базис обычно пишется в круглых скобках, внутри которых в строгом порядке перечисляются векторы.
Любой вектор плоскости выражается по формуле нахождения координат вектора:
[vec{v}=v_{1} cdot vec{i}+v_{2} cdot vec{j}]
Где числа в этом базисе называются векторными координатами. Но само выражение называется векторным разложением.
Как выразить вектор через его координаты
Чтобы выразить вектор [overrightarrow{A B}(a, b)], где [Aleft(x_{1} ; y_{1}right)], а [Bleft(x_{2} ; y_{2}right)], сначала вычислим разницу между абсциссами [x], чтобы получить [a], затем вычислим разницу между ординатами [y], чтобы получить [b]:
[overrightarrow{A B}=left(x_{2}-x_{1} ; y_{2}-y_{1}right)]
Пример 1
Найти координаты [overrightarrow{A B}] при значении координат точек [A(3 ; 2), B(6 ; 9)].
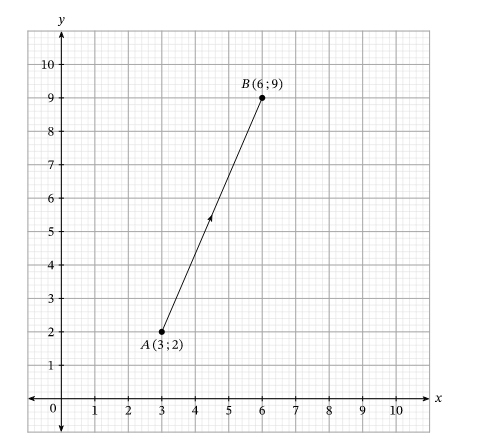
Решение:
Горизонтальное расстояние равно разнице между абсциссами [x], т.е. 6−3=3. Вертикальное расстояние равно разнице между ординатами [y], где 9−2=7.
Поэтому мы можем обозначить вектор от А до В как:
[overrightarrow{A B}=(3 ; 7)]
Нахождение координат вектора в пространстве
Теперь рассмотрим векторы в трехмерном пространстве, здесь все почти так же, как на плоскости, но будет добавлена только одна дополнительная координата.
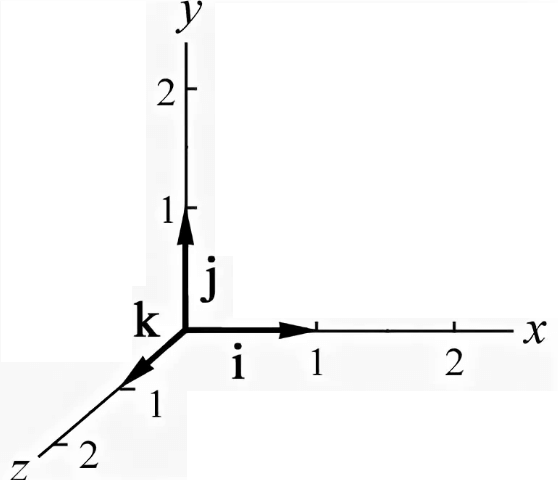
Любой вектор в пространстве выражается следующим образом:
[vec{v}=v_{1} cdot vec{i}+v_{2} cdot vec{j}+v_{3} cdot vec{k}], где координаты вектора (числа) в заданном базисе.
Пример 2
Нужно найти вектор, соединяющий точку А (начало) с координатами (4, 5, 6) с точкой В (конец) с координатами (10, 11, 12).
Решение:
Вектор направлен из точки А в точку В и может быть обозначен как [overrightarrow{A B}]. Таким образом:
[overrightarrow{A B}=(10-4) ;(11-5) ;(12-6)=(6 ; 6 ; 6)]
Нет времени решать самому?
Наши эксперты помогут!
Как записать вектор на основе единичных векторов
Если мы перейдем от начальной точки к конечной точке [Cleft(x_{y} ; y_{1}right) Dleft(x_{2} ; y_{2}right)], это описывает вектор, который представляет собой смещение на расстояние в направлении [overrightarrow{C D}left(x_{2}-x_{1}right) x] затем с расстояния в направлении [left(y_{2}-y_{1}right) y].
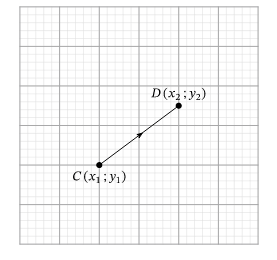
Мы можем обозначить этот вектор двумя способами:
[overrightarrow{C D}=left(x_{2}-x_{1}, y_{2}-y_{1}right)] или [overrightarrow{C D}=left(x_{2}-x_{1}right) i+left(y_{2}-y_{1}right) vec{j}]
Пример 3
Выразить вектор в виде суммы единичных векторов.
Зная, что каждый квадрат сетки имеет длину 1, представим вектор [overrightarrow{A B}] как [a vec{i}+b vec{j}].
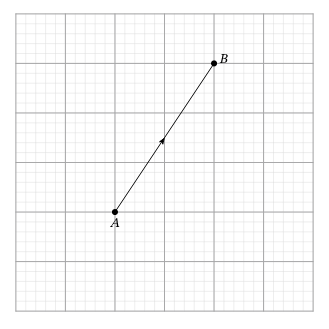
Решение:
Из точки [A](начало), мы перемещаем единицы в горизонтальном направлении (которое представляет собой вектор), затем мы перемещаем единицы в вертикальном направлении (что представляет собой вектор), чтобы перейти к точке [B+2(2 vec{i}) u+3(3 vec{j})].
Вектор [overrightarrow{A B}] что представляет собой прямое движение от [A] к [B] , тогда равна сумме этих единичных векторов.
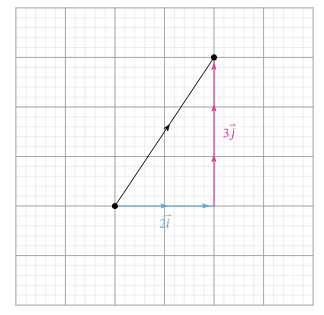
Как результат: [overrightarrow{A B}=2 vec{i}+3 vec{j}=(2,3)].
Использование векторов и позволяет описать вектор в соответствии с количеством шагов по горизонтали и вертикали длиной 1, которые необходимо сделать, чтобы пройти от начала до конца. Обратите внимание, что отрицательные коэффициенты представляют движение влево или вниз соответственно.
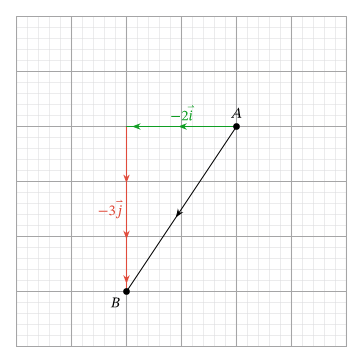
Например, приведенный выше вектор, представляющий смещение на -2 единицы в направлении и на -3 единицы в направлении [overrightarrow{A B}=(-2 ;-3) x y] или [(-2 vec{i})+(-3 vec{j})].
[overrightarrow{A B}=-2 vec{i}-3 vec{j}]
Важно
Следует понимать разницу между координатами точки и векторными координатами:
Координаты точки — это обычные координаты в прямоугольной системе координат. Каждая точка имеет строгое место на карте, и их нельзя никуда перемещать.
Координаты вектора — это его разложение относительно основания.
Любой вектор свободен, поэтому при желании или необходимости мы легко можем отложить его от другой точки плоскости. Записи координат точек и векторных координат выглядят одинаков, а значение координат совсем разные.
Координаты равных векторов соответственно равны.
Если точка начала вектора не совпадает с началом системы координат, тогда рассмотрим задачу. На оси [O_{x y}] заданы координаты точек вектора, где [Aleft(x_{a} ; y_{a}right)] и [Bleft(x_{b} y_{b}right)]. Найти координаты [overrightarrow{A B}].
Зная формулу сложения векторов, имеем [overrightarrow{O A}+overrightarrow{A B}=overrightarrow{O B}], следует: [overrightarrow{A B}=overrightarrow{O B}-overrightarrow{O A}].
[overrightarrow{O A}] и [overrightarrow{O B}] радиус-векторы точек А и В, следовательно, координаты точек: [overrightarrow{O A}=left(x_{a}, y_{a}right), overrightarrow{O B}=left(x_{b} ; y_{b}right)].
В данной публикации мы рассмотрим формулы, с помощью которых можно найти координаты вектора, заданного координатами его начальной и конечной точек, а также разберем примеры решения задач по этой теме.
- Нахождение координат вектора
- Примеры задач
Нахождение координат вектора
Для того, чтобы найти координаты вектора AB, нужно из координат его конечной точки (B) вычесть соответствующие координаты начальной точки (A).

Формулы для определения координат вектора
| Для плоских задач | AB = {Bx – Ax; By – Ay} |
| Для трехмерных задач | AB = {Bx – Ax; By – Ay; Bz – Az} |
| Для n-мерных векторов | AB = {B1 – A1; B2 – A2; … Bn – An} |
Примеры задач
Задание 1
Найдем координаты вектора AB, если у его точек следующие координаты: A = (2; 8), B = (5; 12).
Решение:
AB = {5 – 2; 12 – 8} = {3; 4}.
Задание 2
Определим координаты точки B вектора AB = {6; 14}, если координаты точки A = (2; 5).
Решение:
Координаты точки B можно вывести из формулы для расчета координат вектора:
Bx = ABx + Ax = 6 + 2 = 8.
By = ABy + Ay = 14 + 5 = 19.
Таким образом, B = (8; 19).
Как найти вектор по точкам
ФОРМУЛА
Чтобы найти координаты вектора (
overline{A B}
)на плоскости, если он задан координатами его начала (
Aleft(x_{1} ; y_{1}right)
) и (
Bleft(x_{2} ; y_{2}right)
) конца, необходимо вычесть соответствующие координаты начала из координат конца, то есть
(
overline{A B}=left(x_{2}-x_{1} ; y_{2}-y_{1}right)
)
Чтобы найти координаты вектора (
overline{A B}
), заданного в пространстве по координатам (
Aleft(x_{1} ; y_{1} ; z_{1}right)
) и (
Bleft(x_{2} ; y_{2} ; z_{2}right)
), необходимо, по аналогии с плоским случаем, вычесть координаты начала из координат конца:
(
overline{A B}=left(x_{2}-x_{1} ; y_{2}-y_{1} ; z_{2}-z_{1}right)
)
ПРИМЕРЫ НАХОЖДЕНИЯ КООРДИНАТ ВЕКТОРА ПО ТОЧКАМ
ПРИМЕР
A(4 ;-1)
) и (
B(2 ; 1)
). Найти координаты векторов (
overline{A B}
) и (
overline{B A}
)
overline{A B}
) точка (
mathrm{A}
) является началом, а точка (
B
) – концом. Тогда координаты вектора (
overline{B A}
)равны
(
overline{A B}=(2-4 ; 1-(-1))=(-2 ; 2)
)
Для вектора (
overline{B A}
) точка (
B
) является началом, а точка (
mathrm{A}
) – концом. Тогда координаты вектора (
overline{B A}
)равны
(
overline{B A}=(4-2 ;-1-1)=(2 ;-2)
)
overline{A B}=(-2 ; 2)
)
(
overline{B A}=(2 ;-2)
)
ПРИМЕР
A(1 ;-2 ; 0,5)
) , (
B(3 ; 2 ; 1,5)
) и (
C(0 ;-1 ; 1)
). Найти координаты векторов (
overline{A B}, overline{A C}, overline{B C}
)
overline{A B}
) точка (
mathrm{A}
) является началом, а точка (
B
) – концом. Тогда координаты вектора (
overline{A B}
)соответственно равны:
(
overline{A B}=(3-1 ; 2-(-2) ; 1,5-0,5)=(2 ; 4 ; 1)
)
Для вектора (
overline{A C}
)точка (
mathrm{A}
) является началом, а точка (
mathrm{C}
) – концом. Тогда его координаты соответственно равны
(
overline{A C}=(0-1 ;-1-(-2) ; 1-0,5)=(-1 ; 1 ; 0,5)
)
Для вектора (
overline{B C}
) точка (
B
) является началом, а точка (
mathrm{C}
) – концом. Его координаты равны
(
overline{B C}=(0-3 ;-1-2 ; 1-1,5)=(-3 ;-3 ;-0,5)
)
overline{A B}=(2 ; 4 ; 1)
)
(
overline{A C}=(-1 ; 1 ; 0,5)
)
(
overline{B C}=(-3 ;-3 ;-0,5)
)
Нахождение координат вектора через координаты точек
Отложим от начала координат единичные векторы, то есть векторы, длины которых равны единице. Направление вектора i → должно совпадать с осью O x , а направление вектора j → с осью O y .
Векторы i → и j → называют координатными векторами.
Координатные векторы неколлинеарны. Поэтому любой вектор p → можно разложить по векторам p → = x i → + y j → . Коэффициенты x и y определяются единственным образом. Коэффициенты разложения вектора p → по координатным векторам называются координатами вектора p → в данной системе координат.

Координаты вектора записываются в фигурных скобках p → x ; y . На рисунке вектор O A → имеет координаты 2 ; 1 , а вектор b → имеет координаты 3 ; – 2 . Нулевой вектор представляется в виде 0 → 0 ; 0 .
Если векторы a → и b → равны, то и y 1 = y 2 . Запишем это так: a → = x 1 i → + y 1 j → = b → = x 2 i → + y 2 j → , значит x 1 = x 2 , y 1 = y 2 .
Таким образом, координаты равных векторов соответственно равны.
Если точка координат не совпадает с его началом системы координат, тогда рассмотрим задачу. Пусть в декартовой системе координат на O x y заданы координаты точек начала и конца A B → : A x a , y a , B x b , y b . Найти координаты заданного вектора.
Изобразим координатную ось.

Из формулы сложения векторов имеем O A → + A B → = O B → , где O – начало координат. Отсюда следует, что A B → = O B → – O A → .
O A → и O B → – это радиус-векторы заданных точек А и В, значит координаты точек имеют значения O A → = x a , y a , O B → = x b , y b .
По правилу операций над векторами найдем A B → = O B → – O A → = x b – x a , y b – y a .

Нахождение в трехмерном пространстве проходит по такому же принципу, только для трех точек.
Для нахождения координат вектора, необходимо найти разность его точек конца и начала.
Найти координаты O A → и A B → при значении координат точек A ( 2 , – 3 ) , B ( – 4 , – 1 ) .
Для начала определяется радиус-вектор точки A . O A → = ( 2 , – 3 ) . Чтобы найти A B → , нужно вычесть значение координат точек начала из координат точек конца.
Получаем: A B → = ( – 4 – 2 , – 1 – ( – 3 ) ) = ( – 6 , 2 ) .
Ответ: O A → = ( 2 , – 3 ) , A B → = ( – 6 , – 2 ) .
Задано трехмерное пространство с точкой A = ( 3 , 5 , 7 ) , A B → = ( 2 , 0 , – 2 ) . Найти координаты конца A B → .
Подставляем координаты точки A : A B → = ( x b – 3 , y b – 5 , z b – 7 ) .
По условию известно, что A B → = ( 2 , 0 , – 2 ) .
Известно, что равенство векторов справедливо тогда, когда координаты равны соответственно. Составим систему уравнений: x b – 3 = 2 y b – 5 = 0 z b – 7 = – 2
Отсюда следует, что координаты точки B A B → равны: x b = 5 y b = 5 z b = 5
Ответ: B ( 5 , 5 , 5 ) .
Нахождение координат вектора
В данной публикации мы рассмотрим формулы, с помощью которых можно найти координаты вектора, заданного координатами его начальной и конечной точек, а также разберем примеры решения задач по этой теме.
Нахождение координат вектора
Для того, чтобы найти координаты вектора AB , нужно из координат его конечной точки (B) вычесть соответствующие координаты начальной точки (A).

Формулы для определения координат вектора
” data-lang=”default” data-override=”<“emptyTable”:””,”info”:””,”infoEmpty”:””,”infoFiltered”:””,”lengthMenu”:””,”search”:””,”zeroRecords”:””,”exportLabel”:””,”file”:”default”>” data-merged=”[]” data-responsive-mode=”2″ data-from-history=”0″>
| Для плоских задач | AB = x – Ax; By – Ay> |
| Для трехмерных задач | AB = x – Ax; By – Ay; Bz – Az> |
| Для n-мерных векторов | AB = 1 – A1; B2 – A2; . Bn – An> |
Примеры задач
Задание 1
Найдем координаты вектора AB , если у его точек следующие координаты: , .
Задание 2
Определим координаты точки B вектора , если координаты точки .
Решение:
Координаты точки B можно вывести из формулы для расчета координат вектора:
Bx = AB x + Ax = 6 + 2 = 8.
By = AB y + Ay = 14 + 5 = 19.
Как найти вектор по точкам
Формула
Чтобы найти координаты вектора $overline$ на плоскости, если он задан координатами своих начала $Aleft(x_ <1>; y_<1>right)$ и конца $Bleft(x_ <2>; y_<2>right)$, необходимо от координат конца отнять соответствующие координаты начала, то есть
Чтобы найти координаты вектора $overline$, заданного в пространстве координатами $Aleft(x_ <1>; y_ <1>; z_<1>right)$ и $Bleft(x_ <2>; y_ <2>; z_<2>right)$, необходимо, по аналогии с плоским случаем, из координат конца вычесть координаты начала:
Примеры нахождения координат вектора по точкам
Задание. Даны точки $A(4;-1)$ и $B(2;1)$. Найти координаты векторов $overline$ и $overline$
Решение. Для вектора $overline$ точка $A$ является началом, а точка $B$ – концом. Тогда координаты вектора $overline$ равны
Для вектора  точка $B$ является началом, а точка $A$ – концом. Тогда координаты вектора $overline$ равны
точка $B$ является началом, а точка $A$ – концом. Тогда координаты вектора $overline$ равны
Ответ. $overline=(-2 ; 2), overline=(2 ;-2)$
Задание. Даны три точки в пространстве точки $A(1;-2;0,5)$, $B(3;2;1,5)$ и $C(0;-1;1)$. Найти координаты векторов $overline$, $overline$, $overline$
Решение. Для искомого вектора $overline$ точка $A$ является началом, а точка $B$ – концом. Тогда координаты вектора $overline$ соответственно равны:
$$overline=(3-1 ; 2-(-2) ; 1,5-0,5)=(2 ; 4 ; 1)$$
Для вектора $overline$ точка $A$ является началом, а точка $C$ – концом. Тогда его координаты соответственно равны
Для вектора $overline$ точка $B$ является началом, а точка $C$ – концом. Его координаты равны
Ответ. $overline=(2 ; 4 ; 1), overline=(-1 ; 1 ; 0,5), overline=(-3 ;-3 ;-0,5)$
[spoiler title=”источники:”]
http://www.webmath.ru/poleznoe/formules_13_0.php
[/spoiler]

