Как найти координаты вектора в другом базисе

Матрица перехода

3 июля 2022

Матрица перехода — это просто квадратная матрица, в столбцах которой записаны координаты новых базисных векторов. У такой матрицы много важных свойств, которые сформулированы и доказаны в первой части урока — теоретической. Этой теории хватит для любого экзамена или коллоквиума.

Вторая часть урока — практическая. В ней разобраны все типовые задачи, которые встречаются на контрольных, зачётах и экзаменах.

Содержание

1. Определение матрицы перехода
2. Свойства матрицы перехода
3. Теорема о замене координат
4. Задача 1. Базисы трёхмерного пространства
5. Задача 2. Базисы в поле вычетов
6. Задача 3. Пространство многочленов
7. Задача 4. Матрица перехода при симметрии
8. Задача 5. Матрица поворота

Если вы учитесь в серьёзном университете (МГУ, Бауманка и т.д.), то обязательно изучите первые три пункта. А если вам нужны только задачи, сразу переходите к пункта 4—6.

1. Определение матрицы перехода

Пусть дано $n$-мерное линейное пространство $L$. Пусть также $left{ {{e}_{1}},ldots ,{{e}_{n}} right}$ и $left{ {{f}_{1}},ldots ,{{f}_{n}} right}$ — два базиса в $L$.

Определение. Матрица перехода ${{T}_{eto f}}$ от базиса $e=left{ {{e}_{1}},ldots ,{{e}_{n}} right}$ к базису $f=left{ {{f}_{1}},ldots ,{{f}_{n}} right}$ — это квадратная матрица порядка $n$, где по столбцам записаны координаты нового базиса $f$ в старом базисе $e$:

[{{T}_{eto f}}=left[ begin{array}{c|c|c|c}{{t}_{1,1}} & {{t}_{2,1}} & cdots & {{t}_{n,1}} \{{t}_{1,2}} & {{t}_{2,2}} & cdots & {{t}_{n,1}} \cdots & cdots & cdots & cdots \{{t}_{1,n}} & {{t}_{2,n}} & cdots & {{t}_{n,n}} \end{array} right]]

Обратите внимание на нумерацию элементов ${{t}_{i,j}}$: первый индекс обозначает номер столбца, т.е. номер нового базисного вектора, а второй отвечает за координаты этого вектора в старом базисе. Так, во втором столбце записаны координаты вектора ${{f}_{2}}$:

[{{f}_{2}}={{left[ {{t}_{2,1}},{{t}_{2,2}},ldots ,{{t}_{2,n}} right]}^{T}}]

Или, что то же самое, разложение вектора ${{f}_{2}}$ по базису $left{ {{e}_{1}},ldots ,{{e}_{n}} right}$:

[{{f}_{2}}={{t}_{2,1}}{{e}_{1}}+{{t}_{2,2}}{{e}_{2}}+ldots +{{t}_{2,n}}{{e}_{n}}]

Да, такая нумерация не является обязательной. Но она очень распространена именно в записи матриц перехода: первый индекс отвечает за номер базисного вектора, второй — за номер координаты этого вектора.

Пример 1. В некотором базисе $e=left{ {{e}_{1}},{{e}_{2}},{{e}_{3}} right}$ векторного пространства ${{mathbb{R}}^{3}}$ даны три вектора:

[{{f}_{1}}={{left( 1,0,1 right)}^{T}},quad {{f}_{2}}={{left( 2,1,0 right)}^{T}},quad {{f}_{3}}={{left( 0,3,1 right)}^{T}}]

[begin{align}{{f}_{1}} &={{left( 1,0,1 right)}^{T}}, \ {{f}_{2}} &={{left( 2,1,0 right)}^{T}}, \ {{f}_{3}} &={{left( 0,3,1 right)}^{T}} \ end{align}]

Убедитесь, что система векторов $f=left{ {{f}_{1}},{{f}_{2}},{{f}_{3}} right}$ образует базис в ${{mathbb{R}}^{3}}$, найдите матрицу перехода ${{T}_{eto f}}$.

Решение. Система векторов будет базисом, если эти векторы линейно независимы, а их количество совпадает с размерностью пространства. Поскольку у нас три вектора и $dim{{mathbb{R}}^{3}}=3$, осталось проверить линейную независимость. Составим матрицу из столбцов с координатами векторов ${{f}_{1}}$, ${{f}_{2}}$ и ${{f}_{3}}$:

[left[ begin{matrix}1 & 2 & 0 \ 0 & 1 & 3 \ 1 & 0 & 1 \ end{matrix} right]]

Вообще-то это и есть матрица перехода ${{T}_{eto f}}$, но сначала надо установить линейную независимость. Поэтому выполним элементарные преобразования строк:

[left[ begin{matrix} 1 & 2 & 0 \ 0 & 1 & 3 \ 1 & 0 & 1 \ end{matrix} right]begin{matrix} \ \ -1cdot left[ 1 right] \ end{matrix}sim left[ begin{array}{crc} 1 & 2 & 0 \ 0 & 1 & 3 \ 0 & -2 & 1 \ end{array} right]begin{matrix} -2cdot left[ 2 right] \ \ +2cdot left[ 2 right] \ end{matrix}sim left[ begin{array}{ccr} 1 & 0 & -6 \ 0 & 1 & 3 \ 0 & 0 & 7 \ end{array} right]]

[begin{align} & left[ begin{matrix} 1 & 2 & 0 \ 0 & 1 & 3 \ 1 & 0 & 1 \ end{matrix} right]begin{matrix} \ \ -1cdot left[ 1 right] \ end{matrix} \ & left[ begin{array}{crc} 1 & 2 & 0 \ 0 & 1 & 3 \ 0 & -2 & 1 \ end{array} right]begin{matrix} -2cdot left[ 2 right] \ \ +2cdot left[ 2 right] \ end{matrix} \ & left[ begin{array}{ccr} 1 & 0 & -6 \ 0 & 1 & 3 \ 0 & 0 & 7 \ end{array} right] \ end{align}]

Получили верхнетреугольную матрицу без нулей на главной диагонали. Ранг такой матрицы равен 3, поэтому система $left{ {{f}_{1}},{{f}_{2}},{{f}_{3}} right}$ линейно независима и образует базис. Матрица перехода от базиса $e$ к базису $f$ уже известна:

[{{T}_{eto f}}=left[ begin{matrix} 1 & 2 & 0 \ 0 & 1 & 3 \ 1 & 0 & 1 \ end{matrix} right]]

1.1. Зачем нужна матрица перехода

Матрица перехода нужна для того, чтобы компактно и наглядно выражать новый базис через старый. В самом деле, разложим векторы $left{ {{f}_{1}},ldots ,{{f}_{n}} right}$ нового базиса по старому базису $left{ {{e}_{1}},ldots ,{{e}_{n}} right}$:

[begin{align}{{f}_{1}} &={{x}_{1,1}}{{e}_{1}}+{{x}_{2,1}}{{e}_{2}}+ldots +{{x}_{n,1}}{{e}_{n}} \ {{f}_{2}} &={{x}_{1,2}}{{e}_{1}}+{{x}_{2,2}}{{e}_{2}}+ldots +{{x}_{n,2}}{{e}_{n}} \ & cdots \ {{f}_{n}} &={{x}_{1,n}}{{e}_{1}}+{{x}_{2,n}}{{e}_{2}}+ldots +{{x}_{n,n}}{{e}_{n}} \ end{align}]

Получили систему из $n$ уравнений, которые в матричном виде можно представить так:

[left[ begin{matrix} {{f}_{1}} & cdots & {{f}_{n}} \ end{matrix} right]=left[ begin{matrix} {{e}_{1}} & cdots & {{e}_{n}} \ end{matrix} right]cdot left[ begin{matrix} {{x}_{1,1}} & cdots & {{x}_{1,n}} \ cdots & cdots & cdots \ {{x}_{n,1}} & cdots & {{x}_{n,n}} \ end{matrix} right]]

[left[ {{f}_{1}} cdots {{f}_{n}} right]=left[ {{e}_{1}} cdots {{e}_{n}} right]cdot left[ begin{matrix} {{x}_{1,1}} & cdots & {{x}_{1,n}} \ cdots & cdots & cdots \ {{x}_{n,1}} & cdots & {{x}_{n,n}} \ end{matrix} right]]

Обратите внимание: ${{f}_{1}},ldots ,{{f}_{n}}$ и ${{e}_{1}},ldots ,{{e}_{n}}$ — это именно векторы, а не числа. Такие наборы принято записывать строками — в отличие от вектор-столбцов, элементами которых как раз выступают обычные числа.

Последний множитель — это и есть матрица перехода ${{T}_{eto f}}$, поэтому всё произведение можно записать более компактно:

[left[ begin{matrix} {{f}_{1}} & cdots & {{f}_{n}} \ end{matrix} right]=left[ begin{matrix} {{e}_{1}} & cdots & {{e}_{n}} \ end{matrix} right]cdot {{T}_{eto f}}]

2. Свойства матрицы перехода

Мы разберём три простых свойства, а далее отдельным разделом будет ещё одно — уже более серьёзное.

2.1. Переход от базиса к этому же базису

Свойство 1. При переходе от базиса $e$ к этому же базису $e$ матрица перехода ${{T}_{eto e}}=E$.

Для доказательства достаточно рассмотреть формулы

[begin{align}{{f}_{1}} &={{x}_{1,1}}{{e}_{1}}+{{x}_{2,1}}{{e}_{2}}+ldots +{{x}_{n,1}}{{e}_{n}} \ {{f}_{2}} &={{x}_{1,2}}{{e}_{1}}+{{x}_{2,2}}{{e}_{2}}+ldots +{{x}_{n,2}}{{e}_{n}} \ &cdots \ {{f}_{n}} &={{x}_{1,n}}{{e}_{1}}+{{x}_{2,n}}{{e}_{2}}+ldots +{{x}_{n,n}}{{e}_{n}} \ end{align}]

А затем положить ${{f}_{1}}={{e}_{1}}$, ${{f}_{2}}={{e}_{2}}$, …, ${{f}_{n}}={{e}_{n}}$. Тогда:

[begin{align} {{f}_{1}} &={{e}_{1}}=1cdot {{e}_{1}}+0cdot {{e}_{2}}+ldots +0cdot {{e}_{n}} \ {{f}_{2}} &={{e}_{2}}=0cdot {{e}_{1}}+1cdot {{e}_{2}}+ldots +0cdot {{e}_{n}} \ &cdots \ {{f}_{n}} &={{e}_{n}}=0cdot {{e}_{1}}+0cdot {{e}_{2}}+ldots +1cdot {{e}_{n}} \ end{align}]

Указанное выражение однозначно, поскольку $e$ — базис. Следовательно, матрица перехода равна

[{{T}_{eto f}}=left[ begin{array}{c|c|c|c} 1 & 0 & cdots& 0 \ 0 & 1 & cdots& 0 \ cdots& cdots& cdots& cdots \ 0 & 0 & cdots& 1 \ end{array} right]=E]

Итак, ${{T}_{eto f}}=E$, что и требовалось доказать.

2.2. Обратный переход

Свойство 2. Если ${{T}_{eto f}}$ — матрица перехода от базиса $e$ к базису $f$, то ${{T}_{fto e}}={{left( {{T}_{eto f}} right)}^{-1}}$ матрица обратного перехода, от базиса $f$ к базису $e$.

В самом деле, базисы $e$ и $f$ связаны с матрицей перехода по формуле

[left[ {{f}_{1}},ldots ,{{f}_{n}} right]=left[ {{e}_{1}},ldots ,{{e}_{n}} right]cdot {{T}_{eto f}}]

Поскольку матрица ${{T}_{eto f}}$ невырожденная, существует обратная к ней матрица ${{left( {{T}_{eto f}} right)}^{-1}}$. Домножим на эту матрицу обе части формулы, связывающей базисы $e$ и $f$:

[left[ {{f}_{1}},ldots ,{{f}_{n}} right]cdot {{left( {{T}_{eto f}} right)}^{-1}}=left[ {{e}_{1}},ldots ,{{e}_{n}} right]cdot {{T}_{eto f}}cdot {{left( {{T}_{eto f}} right)}^{-1}}]

[begin{align}left[ {{f}_{1}},ldots ,{{f}_{n}} right] &cdot {{left( {{T}_{eto f}} right)}^{-1}}= \ &=left[ {{e}_{1}},ldots ,{{e}_{n}} right]cdot {{T}_{eto f}}cdot {{left( {{T}_{eto f}} right)}^{-1}} \ end{align}]

Упрощаем эту формулу и получаем

[left[ {{e}_{1}},ldots ,{{e}_{n}} right]=left[ {{f}_{1}},ldots ,{{f}_{n}} right]cdot {{left( {{T}_{eto f}} right)}^{-1}}]

Итак, мы получили формулу перехода от базиса $f$ к базису $e$. Следовательно, ${{left( {{T}_{eto f}} right)}^{-1}}$ — матрица такого перехода, что и требовалось доказать.

2.3. Переход через транзитный базис

Пусть ${{T}_{eto f}}$ — матрица перехода от базиса $e$ к базису $f$ линейного пространства $L$, а ${{T}_{fto g}}$ — матрица перехода от базиса $f$ к базису $g$ того же линейного пространства $L$.

Тогда матрица перехода ${{T}_{eto g}}$ от базиса $e$ к базису $g$ находится по формуле

[{{T}_{eto g}}={{T}_{eto f}}cdot {{T}_{fto g}}]

Для доказательства достаточно записать формулы для выражения базисов $f$ и $g$, а затем подставить одну формулу в другую. По условию теоремы, базис $f$ выражается через базис $e$ по формуле

[left[ {{f}_{1}},ldots ,{{f}_{n}} right]=left[ {{e}_{1}},ldots ,{{e}_{n}} right]cdot {{T}_{eto f}}]

Кроме того, базис $g$ выражается через базис $f$ по формуле

[left[ {{g}_{1}},ldots ,{{g}_{n}} right]=left[ {{f}_{1}},ldots ,{{f}_{n}} right]cdot {{T}_{fto g}}]

Подставим первое выражение во второе и получим

[begin{align}left[ {{g}_{1}},ldots ,{{g}_{n}} right] &=left[ {{f}_{1}},ldots ,{{f}_{n}} right]cdot {{T}_{fto g}}= \ &=left( left[ {{e}_{1}},ldots ,{{e}_{n}} right]cdot {{T}_{eto f}} right)cdot {{T}_{fto g}}= \ & =left[ {{e}_{1}},ldots ,{{e}_{n}} right]cdot left( {{T}_{eto f}}cdot {{T}_{fto g}} right) end{align}]

[begin{align}& left[ {{g}_{1}},ldots ,{{g}_{n}} right]= \ =& left[ {{f}_{1}},ldots ,{{f}_{n}} right]cdot {{T}_{fto g}}= \ =& left( left[ {{e}_{1}},ldots ,{{e}_{n}} right]cdot {{T}_{eto f}} right)cdot {{T}_{fto g}}= \ =& left[ {{e}_{1}},ldots ,{{e}_{n}} right]cdot left( {{T}_{eto f}}cdot {{T}_{fto g}} right) end{align}]

Мы получили прямое выражение базиса $g$ через базис $e$, причём матрица перехода равна

[{{T}_{eto g}}={{T}_{eto f}}cdot {{T}_{fto g}}]

Это именно та формула, которую и требовалось доказать.

2.4. Невырожденные матрицы

И ещё одно важное свойство:

Свойство 4. Пусть дана произвольная квадратная невырожденная матрица

[T=left[ begin{matrix}{{a}_{1,1}} & {{a}_{1,2}} & cdots & {{a}_{1,n}} \ {{a}_{2,1}} & {{a}_{2,2}} & cdots & {{a}_{2,n}} \ cdots & cdots & cdots & cdots \ {{a}_{n,1}} & {{a}_{n,2}} & cdots & {{a}_{n,n}} \ end{matrix} right]]

Пусть $left{ {{e}_{1}},ldots ,{{e}_{n}} right}$ — произвольный базис линейного пространства $L$. Тогда система векторов $left{ {{f}_{1}},ldots ,{{f}_{n}} right}$, полученных по формуле

[begin{align}{{f}_{1}}&={{a}_{1,1}}{{e}_{1}}+{{a}_{2,1}}{{e}_{2}}+ldots +{{a}_{n,1}}{{e}_{n}} \ {{f}_{2}}&={{a}_{1,2}}{{e}_{1}}+{{a}_{2,2}}{{e}_{2}}+ldots +{{a}_{n,2}}{{e}_{n}} \ & cdots \ {{f}_{n}}&={{a}_{1,n}}{{e}_{1}}+{{a}_{2,n}}{{e}_{2}}+ldots +{{a}_{n,n}}{{e}_{n}} \ end{align}]

тоже будет базисом $L$.

Иначе говоря, всякая квадратная невырожденная матрица $T$ является матрицей перехода от данного базиса $left{ {{e}_{1}},ldots ,{{e}_{n}} right}$ к некоторому новому базису $left{ {{f}_{1}},ldots ,{{f}_{n}} right}$ линейного пространства $L$.

Обратите внимание: поскольку изначально мы не знаем, что $T$ — матрица перехода, её элементы пронумерованы стандартным образом: первый индекс отвечает за строку, а второй — за столбец. Однако это нисколько не помешает нам доказать теорему.

Для доказательства того, что $left{ {{f}_{1}},ldots ,{{f}_{n}} right}$ — базис линейного пространства $L$, нужно доказать два утверждения:

• 1.Система векторов $left{ {{f}_{1}},ldots ,{{f}_{n}} right}$ — линейно независима.
• 2.Ранг этой системы векторов совпадает с размерностью пространства $L$.

Поскольку количество векторов в системе $left{ {{f}_{1}},ldots ,{{f}_{n}} right}$ совпадает с количеством базисных векторов $left{ {{e}_{1}},ldots ,{{e}_{n}} right}$, т.е. равно $n=dim L$, достаточно лишь проверить линейную независимость.

Рассмотрим линейную комбинацию векторов $left{ {{f}_{1}},ldots ,{{f}_{n}} right}$ и предположим, что она равна нулю:

[{{lambda }_{1}}{{f}_{1}}+{{lambda }_{2}}{{f}_{2}}+ldots +{{lambda }_{n}}{{f}_{n}}=0]

В матричном виде это выглядит так:

[left[ {{f}_{1}},ldots ,{{f}_{n}} right]cdot left[ begin{align}& {{lambda }_{1}} \ & cdots\ & {{lambda }_{n}} \ end{align} right]=0]

По условию теоремы векторы $left{ {{f}_{1}},ldots ,{{f}_{n}} right}$ раскладываются по базису $left{ {{e}_{1}},ldots ,{{e}_{n}} right}$ с коэффициентами, записанными в столбцах матрицы $T$. В матричном виде это выглядит так:

[left[ {{f}_{1}},ldots ,{{f}_{n}} right]=left[ {{e}_{1}},ldots ,{{e}_{n}} right]cdot T]

Подставляем полученное выражение для $left{ {{f}_{1}},ldots ,{{f}_{n}} right}$ в предыдущее матричное уравнение и получаем

[left[ {{e}_{1}},ldots ,{{e}_{n}} right]cdot Tcdot left[ begin{align}& {{lambda }_{1}} \ & cdots \ & {{lambda }_{n}} \ end{align} right]=0]

Поскольку $left{ {{e}_{1}},ldots ,{{e}_{n}} right}$ — базис линейного пространства $L$, такое равенство возможно лишь при условии

[Tcdot left[ begin{matrix} {{lambda }_{1}} \ cdots \ {{lambda }_{n}} \ end{matrix} right]=left[ begin{matrix} 0 \ cdots \ 0 \ end{matrix} right]]

Это матричное уравнение можно рассматривать как систему из $n$ однородных уравнений относительно переменных ${{lambda }_{1}},ldots ,{{lambda }_{n}}$. И поскольку по условию теоремы матрица $T$ невырожденная, это СЛАУ имеет лишь одно решение — тривиальное:

[{{lambda }_{1}}={{lambda }_{2}}=ldots ={{lambda }_{n}}=0]

Получаем, что система векторов $left{ {{f}_{1}},ldots ,{{f}_{n}} right}$ линейно независима, а количество векторов совпадает с размерностью линейного пространства $L$. Следовательно, эта система — базис, что и требовалось доказать.

3. Замена координат в новом базисе

До сих пор мы рассуждали лишь о том, как координаты новых базисных векторов $left{ {{f}_{1}},ldots ,{{f}_{n}} right}$ выражаются через координаты старых базисных векторов $left{ {{e}_{1}},ldots ,{{e}_{n}} right}$. Но что будет с координатами одного и того же вектора линейного пространства $L$ при переходе от одного базиса к другому?

Ответ даёт следующая теорема.

3.1. Формулировка теоремы

Теорема. Пусть $e=left{ {{e}_{1}},ldots ,{{e}_{n}} right}$ и $f=left{ {{f}_{1}},ldots ,{{f}_{n}} right}$ — базисы линейного пространства $L$ над полем $K$. Пусть ${{T}_{eto f}}$ — матрица перехода от базиса $e$ к $f$:

[{{T}_{eto f}}=left[ begin{matrix}{{a}_{1,1}} & cdots& {{a}_{1,n}} \ cdots& cdots& cdots \ {{a}_{n,1}} & cdots & {{a}_{n,n}} \ end{matrix} right]]

Тогда координаты произвольного вектора $hin L$ пересчитываются по формуле

[{{left[ begin{matrix} {{x}_{1}} \ cdots \ {{x}_{n}} \ end{matrix} right]}_{e}}={{T}_{eto f}}cdot {{left[ begin{matrix} {{y}_{1}} \ cdots \ {{y}_{n}} \ end{matrix} right]}_{f}}]

Ещё раз: если произвольный вектор $hin L$ в новом базисе $f$ имеет координаты

[{{left[ h right]}_{f}}=left[ begin{matrix} {{y}_{1}} \ cdots \ {{y}_{n}} \ end{matrix} right]]

то в старом базисе $e$ этот же вектор $hin L$ имеет координаты

[{{left[ h right]}_{e}}=left[ begin{matrix} {{x}_{1}} \ cdots \ {{x}_{n}} \ end{matrix} right]={{T}_{eto f}}cdot left[ begin{matrix} {{y}_{1}} \ cdots \ {{y}_{n}} \ end{matrix} right]]

Т.е. для векторов всё наоборот: не новые координаты выражаются через старые, а старые — через новые. Впрочем, никто не мешает найти матрицу $T_{eto f}^{-1}$ и записать

[left[ begin{matrix} {{y}_{1}} \ cdots \ {{y}_{n}} \ end{matrix} right]=T_{eto f}^{-1}cdot left[ begin{matrix} {{x}_{1}} \ cdots \ {{x}_{n}} \ end{matrix} right]]

Но такая запись предполагает дополнительное действие — нахождение обратной матрицы.

3.2. Доказательство

Сначала «соберём» матрицу ${{T}_{eto f}}$. Для этого разложим векторы $left{ {{f}_{1}},ldots ,{{f}_{n}} right}$ по базису $left{ {{e}_{1}},ldots ,{{e}_{n}} right}$:

[left{ begin{align}{{f}_{1}} &={{a}_{1,1}}{{e}_{1}}+{{a}_{2,1}}{{e}_{2}}+ldots +{{a}_{n,1}}{{e}_{n}} \ {{f}_{2}} &={{a}_{1,2}}{{e}_{1}}+{{a}_{2,2}}{{e}_{2}}+ldots +{{a}_{n,2}}{{e}_{n}} \ & cdots \ {{f}_{n}} &={{a}_{1,n}}{{e}_{1}} +{{a}_{2,n}}{{e}_{2}}+ldots +{{a}_{n,n}}{{e}_{n}} \ end{align} right.]

В матричной форме эту систему линейных уравнений можно записать так:

[left[ begin{matrix} {{f}_{1}} \ {{f}_{2}} \ cdots \ {{f}_{n}} \ end{matrix} right]=left[ begin{matrix} {{a}_{1,1}} & {{a}_{2,1}} & cdots & {{a}_{n,1}} \ {{a}_{1,2}} & {{a}_{2,2}} & cdots & {{a}_{n,2}} \ cdots & cdots & cdots & cdots \ {{a}_{1,n}} & {{a}_{2,n}} & cdots & {{a}_{n,n}} \ end{matrix} right]cdot left[ begin{matrix} {{e}_{1}} \ {{e}_{2}} \ cdots \ {{e}_{n}} \ end{matrix} right]]

Транспонируем обе стороны равенства, учитывая, что произведение справа транспонируется по правилу ${{left( Acdot B right)}^{T}}={{B}^{T}}cdot {{A}^{T}}$:

[left[ begin{matrix}{{f}_{1}} & cdots & {{f}_{n}} \ end{matrix} right]=left[ begin{matrix} {{e}_{1}} & cdots & {{e}_{n}} \ end{matrix} right]cdot left[ begin{matrix} {{a}_{1,1}} & {{a}_{1,2}} & cdots & {{a}_{1,n}} \ {{a}_{2,1}} & {{a}_{2,2}} & cdots & {{a}_{2,n}} \ cdots & cdots & cdots & cdots \ {{a}_{n,1}} & {{a}_{n,2}} & cdots & {{a}_{n,n}} \ end{matrix} right]]

[left[ {{f}_{1}} cdots {{f}_{n}} right]=left[ {{e}_{1}} cdots {{e}_{n}} right]cdot left[ begin{matrix} {{a}_{1,1}} & cdots & {{a}_{1,n}} \ cdots & cdots & cdots \ {{a}_{n,1}} & cdots & {{a}_{n,n}} \ end{matrix} right]]

Квадратная матрица справа — это и есть матрица перехода ${{T}_{eto f}}$. Поэтому матричное уравнение можно переписать так:

[left[ begin{matrix}{{f}_{1}} & cdots& {{f}_{n}} \ end{matrix} right]=left[ begin{matrix}{{e}_{1}} & cdots& {{e}_{n}} \ end{matrix} right]cdot {{T}_{eto f}}]

Теперь возьмём произвольный вектор $hin L$ и разложим его по базисам $left{ {{e}_{1}},ldots ,{{e}_{n}} right}$ и $left{ {{f}_{1}},ldots ,{{f}_{n}} right}$:

[begin{align}h &={{x}_{1}}{{e}_{1}}+{{x}_{2}}{{e}_{2}}+ldots +{{x}_{n}}{{e}_{n}}= \ &={{y}_{1}}{{f}_{1}}+{{y}_{2}}{{f}_{2}}+ldots +{{y}_{n}}{{f}_{n}} end{align}]

Вновь перейдём к матричной форме. Сначала учтём, что координаты векторов принято записывать в виде вектор-столбцов:

[{{left[ h right]}_{e}}=left[ begin{matrix} {{x}_{1}} \ {{x}_{2}} \ cdots \ {{x}_{n}} \ end{matrix} right]quad {{left[ h right]}_{f}}=left[ begin{matrix} {{y}_{1}} \ {{y}_{2}} \ cdots \ {{y}_{n}} \ end{matrix} right]]

Тогда левую и правую часть уравнения можно представить как произведение строк с базисными векторами и указанных вектор-столбцов с координатами:

[left[ begin{matrix} {{e}_{1}} & cdots & {{e}_{n}} \ end{matrix} right]cdot left[ begin{matrix} {{x}_{1}} \ cdots \ {{x}_{n}} \ end{matrix} right]=left[ begin{matrix} {{f}_{1}} & cdots & {{f}_{n}} \ end{matrix} right]cdot left[ begin{matrix} {{y}_{1}} \ cdots \ {{y}_{n}} \ end{matrix} right]]

[left[ {{e}_{1}} cdots {{e}_{n}} right]cdot left[ begin{matrix} {{x}_{1}} \ cdots \ {{x}_{n}} \ end{matrix} right]=left[ {{f}_{1}} cdots {{f}_{n}} right]cdot left[ begin{matrix} {{y}_{1}} \ cdots \ {{y}_{n}} \ end{matrix} right]]

Но выше мы выражали строку векторов $left[ {{f}_{1}},ldots ,{{f}_{n}} right]$ через строку $left[ {{e}_{1}},ldots ,{{e}_{n}} right]$ и матрицу перехода ${{T}_{eto f}}$. Подставим это выражение в наше матричное уравнение:

[left[ begin{matrix} {{e}_{1}} & cdots & {{e}_{n}} \ end{matrix} right]cdot left[ begin{matrix} {{x}_{1}} \ cdots \ {{x}_{n}} \ end{matrix} right]=left[ begin{matrix} {{e}_{1}} & cdots & {{e}_{n}} \ end{matrix} right]cdot {{T}_{eto f}}cdot left[ begin{matrix} {{y}_{1}} \ cdots \ {{y}_{n}} \ end{matrix} right]]

[left[ {{e}_{1}} cdots {{e}_{n}} right]cdot left[ begin{matrix} {{x}_{1}} \ cdots \ {{x}_{n}} \ end{matrix} right]=left[ {{e}_{1}} cdots {{e}_{n}} right]cdot {{T}_{eto f}}cdot left[ begin{matrix} {{y}_{1}} \ cdots \ {{y}_{n}} \ end{matrix} right]]

Уберём слева и справа первый множитель — строку $left[ {{e}_{1}},ldots ,{{e}_{n}} right]$. Получим уравнение, связывающее координаты вектора в разных базисах:

[left[ begin{matrix} {{x}_{1}} \ cdots \ {{x}_{n}} \ end{matrix} right]={{T}_{eto f}}cdot left[ begin{matrix} {{y}_{1}} \ cdots \ {{y}_{n}} \ end{matrix} right]]

Это именно та формула, которую и требовалось доказать.

Задача 1. Базисы трёхмерного пространства

Задача. Убедитесь, что системы векторов

[{{a}_{1}}={{left( 1,2,1 right)}^{T}},quad {{a}_{2}}={{left( 2,3,2 right)}^{T}},quad {{a}_{3}}={{left( 1,-1,2 right)}^{T}}]

[begin{align}{{a}_{1}} &={{left( 1,2,1 right)}^{T}}, \ {{a}_{2}} &={{left( 2,3,2 right)}^{T}}, \ {{a}_{3}} &={{left( 1,-1,2 right)}^{T}} \ end{align}]

и

[{{b}_{1}}={{left( 1,3,1 right)}^{T}},quad {{b}_{2}}={{left( 1,-1,3 right)}^{T}},quad {{b}_{3}}={{left( 2,2,1 right)}^{T}}]

[begin{align}{{b}_{1}} &={{left( 1,3,1 right)}^{T}}, \ {{b}_{2}} &={{left( 1,-1,3 right)}^{T}}, \ {{b}_{3}} &={{left( 2,2,1 right)}^{T}} \ end{align}]

являются базисами в векторном пространстве ${{mathbb{R}}^{3}}$. Найдите матрицу перехода ${{T}_{ato b}}$. Найдите координаты в базисе $a$ вектора $x$, который в базисе $b$ имеет координаты ${{left( 0,3,2 right)}^{T}}$.

Решение

Чтобы доказать, что система векторов образует базис, достаточно составить матрицу $A$ из координат этих векторов, а затем вычислить её определитель $det A$. И если $det Ane 0$, то векторы линейно независимы. А поскольку их количество совпадает с размерностью линейного пространства, такие векторы образуют базис.

Рассмотрим систему векторов $a=left{ {{a}_{1}},{{a}_{2}},{{a}_{3}} right}$. Составим из них матрицу, расположив координаты по столбцам. Получим матрицу перехода ${{T}_{eto a}}$ от некого исходного базиса $e$ (в котором как раз и даны координаты векторов ${{a}_{i}}$ и ${{b}_{i}}$ в условии задачи) к базису $a$:

[{{T}_{eto a}}=left[ begin{array}{ccr} 1 & 2 & 1 \ 2 & 3 & -1 \ 1 & 2 & 2 \ end{array} right]]

Определитель этой матрицы отличен от нуля:

[det {{T}_{eto a}}=-1ne 0]

Следовательно, $left{ {{a}_{1}},{{a}_{2}},{{a}_{3}} right}$ — базис пространства ${{mathbb{R}}^{3}}$.

Теперь составим матрицу из векторов $b=left{ {{b}_{1}},{{b}_{2}},{{b}_{3}} right}$. Получим матрицу перехода ${{T}_{eto b}}$:

[{{T}_{eto b}}=left[ begin{array}{crc} 1 & 1 & 2 \ 3 & -1 & 2 \ 1 & 3 & 1 \ end{array} right]]

Определитель этой матрицы вновь отличен от нуля:

[det {{T}_{eto b}}=12ne 0]

Следовательно, $left{ {{b}_{1}},{{b}_{2}},{{b}_{3}} right}$ — тоже базис пространства ${{mathbb{R}}^{3}}$.

Осталось найти матрицу перехода ${{T}_{ato b}}$. Заметим, что эту матрицу можно выразить так:

[begin{align}{{T}_{ato b}} &={{T}_{ato e}}cdot {{T}_{eto b}}= \ &={{left( {{T}_{eto a}} right)}^{-1}}cdot {{T}_{eto b}}end{align}]

Мы внедрили «транзитный» базис $e$ и вместо прямого перехода $ato b$ рассмотрели цепочку $ato eto b$. Это стандартный и очень распространённый приём, но из-за этого появился новый элемент $T_{eto a}^{-1}$ — матрица, обратная к ${{T}_{eto a}}$. Найдём $T_{eto a}^{-1}$ методом присоединённой матрицы:

[left[ {{T}_{eto a}}|E right]sim ldots sim left[ E|T_{eto a}^{-1} right]]

Напомню, что элементарные преобразования в присоединённых матрицах выполняются только над строками. Если вы забыли, как всё это работает, см. урок «Обратная матрица». В нашем случае получим:

[left[ begin{array}{ccr|ccc}1 & 2 & 1 & 1 & 0 & 0 \ 2 & 3 & -1 & 0 & 1 & 0 \ 1 & 2 & 2 & 0 & 0 & 1 \end{array} right]begin{matrix} , \ -2cdot left[ 1 right] \ -1cdot left[ 1 right] \ end{matrix}]

Мы «зачистили» первый столбец. Теперь «зачистим» последний:

[left[ begin{array}{crr|rcc} 1 & 2 & 1 & 1 & 0 & 0 \ 0 & -1 & -3 & -2 & 1 & 0 \ 0 & 0 & 1 & -1 & 0 & 1 \ end{array} right]begin{matrix} -1cdot left[ 3 right] \ +3cdot left[ 3 right] \ , \ end{matrix}]

Остался лишь средний. Разберёмся и с ним:

[left[ begin{array}{crc|rcr} 1 & 2 & 0 & 2 & 0 & -1 \ 0 & -1 & 0 & -5 & 1 & 3 \ 0 & 0 & 1 & -1 & 0 & 1 \ end{array} right]begin{matrix} +2cdot left[ 2 right] \ |cdot left( -1 right) \ , \ end{matrix}]

Получили единичную матрицу слева от вертикальной черты. Значит, справа стоит искомая матрица $T_{eto a}^{-1}$:

[left[ begin{array}{ccc|rrr} 1 & 0 & 0 & -8 & 2 & 5 \ 0 & 1 & 0 & 5 & -1 & -3 \ 0 & 0 & 1 & -1 & 0 & 1 \ end{array} right]]

Теперь у нас есть всё, чтобы найти матрицу перехода ${{T}_{ato b}}$:

[{{T}_{ato b}}={{left( {{T}_{eto a}} right)}^{-1}}cdot {{T}_{eto b}}=left[ begin{array}{rrr} -8 & 2 & 5 \ 5 & -1 & -3 \ -1 & 0 & 1 \ end{array} right]cdot left[ begin{array}{crc} 1 & 1 & 2 \ 3 & -1 & 2 \ 1 & 3 & 1 \ end{array} right]]

[begin{align}{{T}_{ato b}} &={{left( {{T}_{eto a}} right)}^{-1}}cdot {{T}_{eto b}}= \ &=left[ begin{array}{rrr} -8 & 2 & 5 \ 5 & -1 & -3 \ -1 & 0 & 1 \ end{array} right]cdot left[ begin{array}{crc} 1 & 1 & 2 \ 3 & -1 & 2 \ 1 & 3 & 1 \ end{array} right] end{align}]

После несложных вычислений получаем матрицу перехода от базиса $a$ к базису $b$:

[{{T}_{ato b}}=left[ begin{array}{rrr} 3 & 5 & -7 \ -1 & -3 & 5 \ 0 & 2 & -1 \ end{array} right]]

Осталось найти координаты вектора $x$, который в базисе $b$ имеет координаты ${{left( 0,3,2 right)}^{T}}$. Вспомним формулу, выражающую координаты в старом базисе через координаты в новом базисе:

[{{left[ x right]}_{a}}={{T}_{ato b}}cdot {{left[ x right]}_{b}}]

Подставляем в эту формулу матрицу ${{T}_{ato b}}$ и вектор-столбец ${{left[ x right]}_{b}}={{left[ 0,3,2 right]}^{T}}$:

[{{left[ x right]}_{a}}=left[ begin{array}{rrr} 3 & 5 & -7 \ -1 & -3 & 5 \ 0 & 2 & -1 \ end{array} right]cdot left[ begin{matrix} 0 \ 3 \ 2 \ end{matrix} right]=left[ begin{matrix} 1 \ 1 \ 4 \ end{matrix} right]]

Итак, вектор $x$ в базисе $a$ имеет координаты ${{left( 1,1,4 right)}^{T}}$. Задача решена.

Альтернативное решение

Можно найти матрицу ${{T}_{ato b}}$ заметно быстрее, если использовать алгоритм решения матричных уравнений. Заметим, что нам требуется найти произведение

[{{T}_{ato b}}={{A}^{-1}}cdot B]

С другой стороны, для нахождения такого произведения достаточно составить присоединённую матрицу вида $left[ A|B right]$ и цепочкой элементарных преобразований свести её к виду

[left[ A|B right]sim ldots sim left[ E|{{A}^{-1}}cdot B right]]

Другими словами, справа от вертикальной черты мы получим искомую матрицу перехода ${{T}_{ato b}}$!

На практике это выглядит так. Записываем присоединённую матрицу $left[ A|B right]$:

[left[ begin{array}{ccr|crc} 1 & 2 & 1 & 1 & 1 & 2 \ 2 & 3 & -1 & 3 & -1 & 2 \ 1 & 2 & 2 & 1 & 2 & 1 \ end{array} right]]

И после элементарных преобразований получим

[left[ begin{array}{ccc|rrr} 1 & 0 & 0 & 3 & 5 & -7 \ 0 & 1 & 0 & -1 & -3 & 5 \ 0 & 0 & 1 & 0 & 2 & -1 \ end{array} right]]

Для экономии места я пропустил промежуточные шаги. Попробуйте сделать их самостоятельно — это очень полезная практика.

Если же вы хотите разобраться, как это работает (и почему вдруг справа возникает матрица вида ${{A}^{-1}}cdot B$), см. урок «Матричные уравнения». А мы идём дальше.

Задача 2. Базисы в поле вычетов

Найдите матрицу перехода от базиса

[{{a}_{1}}={{left( 1,1,1 right)}^{T}},quad {{a}_{2}}={{left( 2,1,1 right)}^{T}},quad {{a}_{3}}={{left( 3,2,1 right)}^{T}}]

[begin{align}{{a}_{1}} &={{left( 1,1,1 right)}^{T}}, \ {{a}_{2}} &={{left( 2,1,1 right)}^{T}}, \ {{a}_{3}} &={{left( 3,2,1 right)}^{T}} \ end{align}]

к базису

[{{b}_{1}}={{left( 0,4,3 right)}^{T}},quad {{b}_{2}}={{left( 3,3,2 right)}^{T}},quad {{b}_{3}}={{left( 2,2,1 right)}^{T}}]

[begin{align}{{b}_{1}} &={{left( 0,4,3 right)}^{T}}, \ {{b}_{2}} &={{left( 3,3,2 right)}^{T}}, \ {{b}_{3}} &={{left( 2,2,1 right)}^{T}} \ end{align}]

арифметического линейного пространства $mathbb{Z}_{5}^{3}$.

Решение

Эта задача проще предыдущей, поскольку поле вычетов ${{mathbb{Z}}_{5}}$ является конечным и состоит всего из пяти элементов — представителей смежных классов:

[{{mathbb{Z}}_{5}}=left{ 0,1,2,3,4 right}]

Как и в предыдущей задаче, рассмотрим систему векторов $a=left{ {{a}_{1}},{{a}_{2}},{{a}_{3}} right}$ и составим из них матрицу ${{T}_{eto a}}$:

[{{T}_{eto a}}=left[ begin{matrix} 1 & 2 & 3 \ 1 & 1 & 2 \ 1 & 1 & 1 \ end{matrix} right]]

Определитель $det {{T}_{eto a}}=1ne 0$, поэтому $left{ {{a}_{1}},{{a}_{2}},{{a}_{3}} right}$ — базис.

Аналогично, рассмотрим систему $b=left{ {{b}_{1}},{{b}_{2}},{{b}_{3}} right}$ и составим матрицу ${{T}_{eto b}}$:

[{{T}_{eto b}}=left[ begin{matrix} 0 & 3 & 2 \ 4 & 3 & 2 \ 3 & 2 & 1 \ end{matrix} right]]

Определитель $det {{T}_{eto b}}=4ne 0$, поэтому $left{ {{b}_{1}},{{b}_{2}},{{b}_{3}} right}$ — базис.

Выразим искомую матрицу ${{T}_{ato b}}$ через «транзитный» базис $e$:

[begin{align}{{T}_{ato b}} &={{T}_{ato e}}cdot {{T}_{eto b}}= \ &={{left( {{T}_{eto a}} right)}^{-1}}cdot {{T}_{eto b}} end{align}]

Найдём $T_{eto a}^{-1}$ через присоединённую матрицу:

[left[ begin{array}{ccc|ccc} 1 & 2 & 3 & 1 & 0 & 0 \ 1 & 1 & 2 & 0 & 1 & 0 \ 1 & 1 & 1 & 0 & 0 & 1 \ end{array} right]]

После цепочки элементарных преобразований над строками (попробуйте выполнить их самостоятельно!) получим

[left[ begin{array}{ccc|ccc} 1 & 0 & 0 & 4 & 1 & 1 \ 0 & 1 & 0 & 1 & 3 & 1 \ 0 & 0 & 1 & 0 & 1 & 4 \ end{array} right]]

Итак, мы нашли матрицу $T_{eto a}^{-1}$:

[T_{eto a}^{-1}=left[ begin{matrix} 4 & 1 & 1 \ 1 & 3 & 1 \ 0 & 1 & 4 \ end{matrix} right]]

Осталось вычислить искомую матрицу перехода ${{T}_{ato b}}$:

[{{T}_{ato b}}={{left( {{T}_{eto a}} right)}^{-1}}cdot {{T}_{eto b}}=left[ begin{matrix} 4 & 1 & 1 \ 1 & 3 & 1 \ 0 & 1 & 4 \ end{matrix} right]cdot left[ begin{matrix} 0 & 3 & 2 \ 4 & 3 & 2 \ 3 & 2 & 1 \ end{matrix} right]=left[ begin{matrix} 2 & 2 & 1 \ 0 & 4 & 4 \ 1 & 1 & 1 \ end{matrix} right]]

[begin{align}{{T}_{ato b}} &={{left( {{T}_{eto a}} right)}^{-1}}cdot {{T}_{eto b}}= \ &=left[ begin{matrix} 4 & 1 & 1 \ 1 & 3 & 1 \ 0 & 1 & 4 \ end{matrix} right]cdot left[ begin{matrix} 0 & 3 & 2 \ 4 & 3 & 2 \ 3 & 2 & 1 \ end{matrix} right]= \ &=left[ begin{matrix} 2 & 2 & 1 \ 0 & 4 & 4 \ 1 & 1 & 1 \ end{matrix} right] end{align}]

По аналогии с предыдущей задачей, матрицу ${{T}_{ato b}}$ можно найти и через элементарные преобразования присоединённой матрицы $left[ A|B right]$. Результат будет точно такой же, но мы сэкономим пару строк вычислений и несколько минут времени.

Задача 3. Пространство многочленов

Убедитесь, что системы многочленов

[begin{align}e &=left{ 1,t-1,{{left( t-1 right)}^{2}} right} \ f &=left( 1,t+1,{{left( t+1 right)}^{2}} right) \ end{align}]

являются базисами в пространстве ${{P}_{3}}$ многочленов степени не выше 2. Найдите матрицу перехода ${{T}_{eto f}}$. Разложите по степеням $left( t-1 right)$ многочлен ${{left( t+1 right)}^{2}}+left( t+1 right)+1$.

Решение

Стандартным базисом в пространстве многочленов является система многочленов $p=left{ {{p}_{1}},{{p}_{2}},{{p}_{3}} right}$, где

[{{p}_{1}}=1quad {{p}_{2}}=tquad {{p}_{3}}={{t}^{2}}]

Выразим через базис $p$ многочлены из системы $e$:

[begin{align} & {{e}_{1}}=1={{p}_{1}} \ & {{e}_{2}}=t-1={{p}_{2}}-{{p}_{1}} \ & {{e}_{3}}={{left( t-1 right)}^{2}}={{t}^{2}}-2t+1={{p}_{3}}-2{{p}_{2}}+{{p}_{1}} end{align}]

[begin{align}{{e}_{1}} &=1={{p}_{1}} \ {{e}_{2}} &=t-1={{p}_{2}}-{{p}_{1}} \ {{e}_{3}} &={{left( t-1 right)}^{2}}= \ &={{t}^{2}}-2t+1= \ &={{p}_{3}}-2{{p}_{2}}+{{p}_{1}} end{align}]

Следовательно, матрица перехода ${{T}_{pto e}}$ выглядит так:

[{{T}_{pto e}}=left[ begin{array}{crr} 1 & -1 & 1 \ 0 & 1 & -2 \ 0 & 0 & 1 \ end{array} right]]

Аналогично, выразим через базис $p$ многочлены из системы $f$:

[begin{align} & {{f}_{1}}=1={{p}_{1}} \ & {{f}_{2}}=t+1={{p}_{2}}+{{p}_{1}} \ & {{f}_{3}}={{left( t+1 right)}^{2}}={{t}^{2}}+2t+1={{p}_{3}}+2{{p}_{2}}+{{p}_{1}} end{align}]

[begin{align}{{f}_{1}} &=1={{p}_{1}} \ {{f}_{2}} &=t+1={{p}_{2}}+{{p}_{1}} \ {{f}_{3}} &={{left( t+1 right)}^{2}}= \ &={{t}^{2}}+2t+1= \ &={{p}_{3}}+2{{p}_{2}}+{{p}_{1}} end{align}]

Получим матрицу перехода ${{T}_{pto f}}$:

[{{T}_{pto f}}=left[ begin{matrix} 1 & 1 & 1 \ 0 & 1 & 2 \ 0 & 0 & 1 \ end{matrix} right]]

Обе матрицы оказались верхнетреугольными, их определители отличны от нуля:

[begin{align} det {{T}_{pto e}} &=1cdot 1cdot 1=1 \ det {{T}_{pto f}} &=1cdot 1cdot 1=1 \ end{align}]

Следовательно системы многочленов $e$ и $f$ действительно являются базисами пространства ${{P}_{3}}$.

Теперь найдём матрицу перехода ${{T}_{eto f}}$. Для этого нам даже не потребуется искать обратную матрицу. Достаточно заметить, что векторы ${{f}_{1}}$ и ${{f}_{2}}$ легко раскладываются по базису $e$:

[begin{align}{{f}_{1}} &=1={{e}_{1}} \ {{f}_{2}} &=t+1=left( t-1 right)+2={{e}_{2}}+2{{e}_{1}} \ end{align}]

С вектором ${{f}_{3}}$ вычислений будет чуть больше:

[begin{align}{{f}_{3}} &={{left( t+1 right)}^{2}}= \ &={{left( t-1 right)}^{2}}+4t= \ &={{left( t-1 right)}^{2}}+4left( t-1 right)+4= \ &={{e}_{3}}+4{{e}_{2}}+4{{e}_{1}} end{align}]

Итого матрица перехода ${{T}_{eto f}}$ примет вид

[{{T}_{eto f}}=left[ begin{matrix} 1 & 2 & 4 \ 0 & 1 & 4 \ 0 & 0 & 1 \ end{matrix} right]]

Теперь разложим многочлен ${{left( t+1 right)}^{2}}+left( t+1 right)+1$ по базису $e$. Сначала перепишем этот многочлен так:

[begin{align}hleft( t right) &=1+left( t+1 right)+{{left( t+1 right)}^{2}}= \ &={{f}_{1}}+{{f}_{2}}+{{f}_{3}} end{align}]

Следовательно, в базисе $f$ многочлен $hleft( t right)$ имеет координаты ${{left( 1,1,1 right)}^{T}}$. Но тогда по теореме о замене координат этот же многочлен в базисе $e$ имеет координаты

[{{left[ h right]}_{e}}={{T}_{eto f}}cdot {{left[ h right]}_{f}}=left[ begin{matrix} 1 & 2 & 4 \ 0 & 1 & 4 \ 0 & 0 & 1 \ end{matrix} right]cdot left[ begin{matrix} 1 \ 1 \ 1 \ end{matrix} right]=left[ begin{matrix} 7 \ 5 \ 1 \ end{matrix} right]]

[begin{align}{{left[ h right]}_{e}} &={{T}_{eto f}}cdot {{left[ h right]}_{f}}= \ &=left[ begin{matrix} 1 & 2 & 4 \ 0 & 1 & 4 \ 0 & 0 & 1 \ end{matrix} right]cdot left[ begin{matrix} 1 \ 1 \ 1 \ end{matrix} right]=left[ begin{matrix} 7 \ 5 \ 1 \ end{matrix} right] end{align}]

Другими словами, многочлен $hleft( t right)$ имеет вид

[hleft( t right)={{left( t-1 right)}^{2}}+5left( t-1 right)+7]

Это и есть искомое разложение многочлена ${{left( t+1 right)}^{2}}+left( t+1 right)+1$ по степеням $left( t-1 right)$.

Альтернативное решение

Искомое разложение можно получить и без привлечения матриц перехода. Достаточно применить схему Горнера или выделить нужные степени напрямую:

[begin{align}hleft( t right) &={{left( t+1 right)}^{2}}+left( t+1 right)+1= \ &={{left( t-1 right)}^{2}}+4t+t+1+1= \ &={{left( t-1 right)}^{2}}+5left( t-1 right)+5+2= \ &={{left( t-1 right)}^{2}}+5left( t-1 right)+7 end{align}]

Как видим, результат получился тем же самым, а времени потрачено меньше. Однако уже в пространстве ${{P}_{4}}$ многочленов степени не выше 4 сложность решения через матрицы и через выделение степеней будет сопоставимой. А дальше матрицы начнут выигрывать.

Смысл линейной алгебры — дать универсальные алгоритмы, которые работают с объектами любой природы, если эти объекты подчиняются аксиомам линейного пространства.

Задача 4. Матрица перехода при симметрии

Базис $b$получается из базиса

[{{a}_{1}}={{left( 2,1,3 right)}^{T}},quad {{a}_{2}}={{left( 1,1,-1 right)}^{T}},quad {{a}_{3}}={{left( 2,-1,-1 right)}^{T}}]

[begin{align}{{a}_{1}} &={{left( 2,1,3 right)}^{T}}, \ {{a}_{2}} &={{left( 1,1,-1 right)}^{T}}, \ {{a}_{3}} &={{left( 2,-1,-1 right)}^{T}} \ end{align}]

пространства ${{V}_{3}}$ симметрией относительно плоскости $2x+y+3z=0$. Найти матрицу перехода ${{T}_{ato b}}$.

Решение

Из курса аналитической геометрии мы знаем, что если плоскость задана уравнением

[ax+by+cz+d=0]

то вектор-нормаль $n$ имеет координаты

[n=left( a,b,c right)]

Тогда для плоскости $2x+y+3z=0$ нормаль имеет координаты $n=left( 2,1,3 right)$, что в точности совпадает с вектором ${{a}_{1}}$. Следовательно, при симметрии относительно плоскости этот вектор просто перейдёт в противоположный: ${{b}_{1}}=-{{a}_{1}}$.

Далее заметим, что векторы ${{a}_{2}}$ и ${{a}_{3}}$ лежат в плоскости симметрии, поскольку при подстановке их координат уравнение плоскости обращается в верное числовое равенство:

[begin{align}{{a}_{2}}={{left( 1,1,-1 right)}^{T}} &Rightarrow 2cdot 1+1+3cdot left( -1 right)=0 \ {{a}_{3}}={{left( 2,-1,-1 right)}^{T}} &Rightarrow 2cdot 2-1+3cdot left( -1 right)=0 \ end{align}]

[begin{align}{{a}_{2}}=&{{left( 1,1,-1 right)}^{T}}Rightarrow \ & Rightarrow 2cdot 1+1+3cdot left( -1 right)=0 \ {{a}_{3}}=&{{left( 2,-1,-1 right)}^{T}}Rightarrow \ & Rightarrow 2cdot 2-1+3cdot left( -1 right)=0 \ end{align}]

Следовательно, при симметрии эти векторы переходят сами в себя: ${{b}_{2}}={{a}_{2}}$, ${{b}_{3}}={{a}_{3}}$. Матрица перехода имеет вид

[{{T}_{ato b}}=left[ begin{array}{rcc} -1 & 0 & 0 \ 0 & 1 & 0 \ 0 & 0 & 1 \ end{array} right]]

Важное замечание. симметрия предполагает использование проекций и углов, что в конечном счёте сводится к скалярному произведению. Однако мы пока не знаем, что такое скалярное произведение в линейном пространстве.

Полноценное определение скалярного произведения будет намного позже — см. урок «Евклидово пространство». А пока будем считать, что скалярное произведение векторов $a$ и $b$ определено стандартным образом:

[left( a,b right)=left| a right|cdot left| b right|cdot cos alpha ]

Геометрическая интерпретация

Симметрию на плоскости и в пространстве удобно представлять графически. Пусть $alpha $ — плоскость, относительно которой выполняется симметрия. Тогда векторы $left{ {{a}_{1}},{{a}_{2}},{{a}_{3}} right}$ будут выглядеть так:

Из приведённого рисунка сразу видно, что при симметрии вектор ${{a}_{1}}$ перейдёт в противоположный, а векторы ${{a}_{2}}$ и ${{a}_{3}}$ останутся на месте.

Задача 5. Матрица поворота

Базис $e=left{ i,j,k right}$ пространства ${{V}_{3}}$ поворачивается на 180° вокруг прямой $l$, заданной системой

[left{ begin{align}x-y &=0 \ z &=0 \ end{align} right.]

Затем полученный базис $f$ поворачивается на 90° в отрицательном направлении вокруг нового положения вектора $j$. В результате получается базис $g=left{ {{i}_{2}},{{j}_{2}},{{k}_{2}} right}$.

Найдите матрицу перехода ${{T}_{eto g}}$. Найдите в базисе $e$ координаты вектора $h$, который в новом базисе $g$ имеет координаты $left( 1,1,1 right)$.

Решение

Вращение базиса и матрица поворота — это очень важная тема, по которой есть отдельный урок — «Матрица поворота». Но сейчас вращение совсем простое, поэтому обойдёмся без специальных матриц.

Вновь обратимся к геометрической интерпретации. Рассмотрим исходный базис $e=left{ i,j,k right}$ трёхмерного пространства:

Также на этом рисунке изображена прямая $l$, которая задаётся требованиями $z=0$ и $x=y$. Эта лежит в плоскости $Oxy$ и является биссектрисой первой координатной четверти.

Очевидно, что при повороте пространства на 180° относительно прямой $l$ базисные векторы $i$ и $j$ просто поменяются местами, а вектор $k$ перейдёт в противоположный:

Другими словами, ${{i}_{1}}=j$, ${{j}_{1}}=i$, ${{k}_{1}}=-k$, поэтому матрица перехода от базиса $e=left{ i,j,k right}$ к базису $f=left{ {{i}_{1}},{{j}_{1}},{{k}_{1}} right}$ примет вид

[{{T}_{eto f}}=left[ begin{array}{ccr} 0 & 1 & 0 \ 1 & 0 & 0 \ 0 & 0 & -1 \ end{array} right]]

Далее поворот осуществляется вокруг нового положения вектора $j$, т.е. вокруг вектора ${{j}_{1}}$. Вновь обратимся к чертежу. В этот раз нам уже не нужны координатные оси — нас интересуют лишь векторы ${{i}_{1}}$, ${{j}_{1}}$ и ${{k}_{1}}$, а также ось вращения:

Обратите внимание: в задаче сказано, что базис вращается на 90° в отрицательном направлении. Если мы смотрим на плоскость, образованную векторами ${{i}_{1}}$ и ${{k}_{1}}$, с вершины вектора ${{j}_{1}}$ (как на картинке), то отрицательное направление — это по часовой стрелке (отмечено зелёным), а положительное —против часовой стрелки (отмечено красным).

Все эти тонкости (положительное и отрицательное направление, правые и левые тройки векторов) детально описаны в уроке про матрицы поворота. Сейчас не будем подробно разбираться в них, а просто нарисуем результат:

Итак, ${{i}_{2}}={{k}_{1}}$, ${{j}_{2}}={{j}_{1}}$ и ${{k}_{2}}=-{{i}_{1}}$, поэтому матрица перехода от базиса $f=left{ {{i}_{1}},{{j}_{1}},{{k}_{1}} right}$ к базису $g=left{ {{i}_{2}},{{j}_{2}},{{k}_{2}} right}$ имеет вид

[{{T}_{fto g}}=left[ begin{array}{ccr} 0 & 0 & -1 \ 0 & 1 & 0 \ 1 & 0 & 0 \ end{array} right]]

Теперь мы можем найти матрицу ${{T}_{eto g}}$ через транзитный базис $f$:

[{{T}_{eto g}}={{T}_{eto f}}cdot {{T}_{fto g}}=left[ begin{array}{ccr} 0 & 1 & 0 \ 1 & 0 & 0 \ 0 & 0 & -1 \ end{array} right]cdot left[ begin{array}{ccr} 0 & 0 & -1 \ 0 & 1 & 0 \ 1 & 0 & 0 \ end{array} right]=left[ begin{array}{rcr} 0 & 1 & 0 \ 0 & 0 & -1 \ -1 & 0 & 0 \ end{array} right]]

[begin{align}{{T}_{eto g}} &={{T}_{eto f}}cdot {{T}_{fto g}}= \ &=left[ begin{array}{ccr} 0 & 1 & 0 \ 1 & 0 & 0 \ 0 & 0 & -1 \ end{array} right]cdot left[ begin{array}{ccr} 0 & 0 & -1 \ 0 & 1 & 0 \ 1 & 0 & 0 \ end{array} right]= \ &=left[ begin{array}{rcr} 0 & 1 & 0 \ 0 & 0 & -1 \ -1 & 0 & 0 \ end{array} right] end{align}]

Кроме того, нам известны координаты вектора $h$ в базисе $g$:

[h={{left( 1,1,1 right)}^{T}}]

Тогда в базисе $e$ координаты этого же вектора равны

[{{left[ h right]}_{e}}={{T}_{eto g}}cdot {{left[ h right]}_{g}}=left[ begin{array}{rcr} 0 & 1 & 0 \ 0 & 0 & -1 \ -1 & 0 & 0 \ end{array} right].left[ begin{matrix} 1 \ 1 \ 1 \ end{matrix} right]=left[ begin{array}{r} 1 \ -1 \ -1 \ end{array} right]]

[begin{align}{{left[ h right]}_{e}} &={{T}_{eto g}}cdot {{left[ h right]}_{g}}= \ &=left[ begin{array}{rcr} 0 & 1 & 0 \ 0 & 0 & -1 \ -1 & 0 & 0 \ end{array} right].left[ begin{matrix} 1 \ 1 \ 1 \ end{matrix} right]=left[ begin{array}{r} 1 \ -1 \ -1 \ end{array} right] end{align}]

Итак, мы нашли матрицу перехода ${{T}_{eto g}}$ и координаты вектора $h$ в исходном базисе. Задача решена.

Смотрите также:

1. Критерий Сильвестра для квадратичных функций
2. Работа с формулами в задаче B12
3. Тест к уроку «Площади многоугольников на координатной сетке» (легкий)
4. Показательные функции в задаче B15
5. Задача B5: площадь кольца
6. Случай четырехугольной пирамиды

Координаты вектора в базисе

В системе векторов a₁, a₂, a₃, a₄ найти любую подсистему векторов, которые образуют базис, разложить векторы по базису, перейти к другому базису, найти коэффициенты разложения векторов во втором базисе; в обоих случаях определить обратные матрицы, соответствующие векторам базиса. Правильность вычисления в каждом случае проверить с помощью умножения вектора слева на матрицу, обратную матрице вектора базиса.

Пример №2 . В системе векторов a₁, a₂, a₃, a₄ найти любую подсистему векторов, которые образуют базис, разложить векторы по базису, перейти к другому базису, найти коэффициенты разложения векторов во втором базисе; в обоих случаях определить обратные матрицы, соответствующие векторам базиса. Правильность вычисления в каждом случае проверить с помощью умножения вектора слева на матрицу, обратную матрице вектора базиса.
a₁=(1;5;3), a₂=(2;1;-1), a₃=(4;2;1), a₄=(17;13;4).

4.3.3 Формулы перехода от одного базиса к другому

Очевидно, что в одном и том же пространстве можно выбрать множество базисов. Пусть в выбрано два базиса и .

Векторы базиса 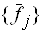могут быть выражены через векторы базиса :

(4)

Матрица называется матрицей перехода от базиса к базису 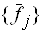. В ее столбцах записаны координаты векторов относительно базиса .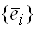

Соотношения (4) называются формулами перехода от базиса 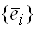к базису 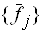. Их можно записать в матричной форме:

, отсюда .

Пусть вектор 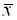задан своими координатами относи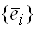тельно базиса – , а относительно базиса 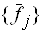– . Тогда

и . (5)

Пример 4. Относительно базиса 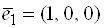, , 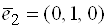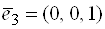даны четыре вектора , , и . Векторы 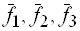можно принять за базис в 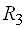. Найти координаты вектора 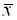в базисе .

Решение. Матрица перехода от базиса к базису имеет вид . Обозначим координаты вектора 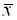в базисе через 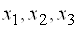. Согласно формулам (5), имеем:

. Находим : ;

; ; ;

; ; ;

; ; ;

.

Проверка: ;

;

или .

Анал_Геом / Изменение координат вектора при изменении базиса

Пусть в -мерном линейном пространстве выбран базис , который мы будем для удобства называть «старый» и другой базис , который мы будем называть «новый». Возьмем призвольный вектор из 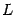. Его координатный столбец в старом базисе обозначим , а в новом — . Нам нужно выяснить, как связаны друг с другом координаты в старом и в новом базисе. Для этого нам сначала нужно «связать» друг с другом старый и новый базисы. Запишем разложения новых базисных векторов по старому базису

Составим матрицу, столбцами которой служат координатные столбцы векторов нового базиса

Эта матрица называется матрицей перехода от старого базиса к новому.

Замечание 18.1 Матрица перехода всегда невырождена, то есть .

Предложение 18.5 Координатные столбцы в старом базисе и в новом базисе связаны формулой

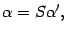
где справа стоит произведение матрицы перехода на матрицу-столбец.

Доказательство. Так как — координатный столбец вектора в новом базисе, то

Заменив векторы 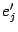их разложениями по старому базису, получим

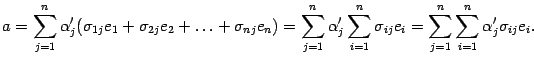
В силу предложения 14.3 изменим порядок суммирования

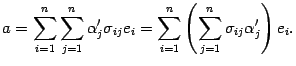
Здесь мы получили разложение вектора по старому базису, причем координата вектора с номером равна . Элемент с номером столбца 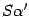будет иметь такой же вид. Следовательно, формула (18.1) доказана.

Пример 18.4 Пусть , то есть — трехмерное векторное пространство. Пусть задан ортонормированный базис i, j, k. Выберем другой (новый) базис

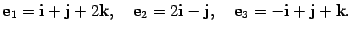
Возьмем вектор . Найдем его координаты в новом базисе.

Выпишем матрицу перехода, ее столбцы — это координаты новых базисных векторов

Пусть — координатный столбец вектора в новом базисе. Тогда

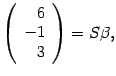
Найдем матрицу по формуле (14.14). Находим определитель

Находим алгебраические дополнения

Находим координаты вектора

Таким образом, новые координаты вектора : , , , .

Тот же самый результат можно было получить, записав формулу (18.2) в виде системы уравнений

Решив эту систему, например, методом Гаусса, найдем новые координаты , , .

Тут вы можете оставить комментарий к выбранному абзацу или сообщить об ошибке.

Рассмотрим произвольный элемент и запишем его разложение в двух заданных базисах и :

Перепишем равенства (3) в матричной форме:

То есть , откуда с учётом формулы (2), получим:

, (4)

Где – матрица перехода от базиса к базису .

Пример 9. В заданы два базиса: и Найти матрицу перехода от базиса к базису . Координаты базисных векторов заданы в ОНБ .

Решение. Из формулы (2) имеем: , значит, . Составим матрицы и : .

Так как , то

Следовательно, .

Ответ: .

Пример 10. В вектор задан в базисе . Найти координаты в базисе , если задана матрица перехода от базиса к базису .

Решение. Связь между координатами вектора в разных базисах выражается формулой (4):

, откуда .

По условию Найдём : значит,

, тогда , т. е.

,

значит,

Ответ:

Пример 11. В вектор – матрица перехода от базиса к базису . Найти разложение в базисе .

Решение. Связь между координатами вектора в разных базисах выражается формулой: , откуда .

Найдём :

Так как , то , значит, Т. е.

Ответ:

Пример 12. В заданы два базиса: и Известно, что Найти разложение в базисе . Координаты базисных векторов заданы в ОНБ .

Решение. Связь между координатами вектора в разных базисах выражается формулой: откуда , где – матрица перехода от базиса к базису , а и – координаты в этих базисах, то есть и

Матрицу найдём из формулы (2): , то есть , где

.

Так как , то

Откуда Таким образом,

Проверку Правильности выполненных действий сделаем, переходя к ОНБ . Так, в базисе : с другой стороны, в базисе : .

Литература: [4, 5, 11].

< Предыдущая		Следующая >

Как найти координаты вектора в базисе

Решение:
Записываем матрицу перехода А:

и находим ее определитель
<>0
Видим, что ранг матрицы С равен трем. Из теоремы о базисном миноре векторы f₁ , f₂ , f₃ линейно независимы, а поэтому могут быть приняты в качестве базиса пространства R 3 .
Находим обратную матрицу А -1 .
Транспонированная матрица:

Обратная матрица А -1

Находим координаты вектора х относительно нового базиса.

Пример №1 . Даны векторы a<1;2;1>, b<2;-2;1>, c <1;-2;0>и d <0;3;1>. Установить, что векторы a , b , c образуют базис, и найти координаты вектора d в этом базисе.
Решение:
Соотношение, записанное для векторов d = αa + βb + γc, справедливо для каждой из проекций:
α*1 + β*2 + γ*1 = 0
α*2 – β*2 – γ*2 = 3
α*1 + β*1 + γ0 = 1 т.е. получена алгебраическая система трёх уравнений с тремя неизвестными. Решение системы удобнее вычислять методом Крамера или методом обратной матрицы:
α = 1/2; β = 1/2; γ = -3/2
следовательно, и вектор d имеет разложение в базисе a, b, c :
d = 1/2a + 1/2b – 3/2c

Пример №2 . Даны векторы . Показать, что векторы образуют базис трехмерного пространства и найти координаты вектора в этом базисе:

Пример №3 . Даны два линейных преобразования:
х’₁ = a₁₁x₁ + a₁₂x₂ + a₁₃x₃, х”₁ = b₁₁x’₁ + b₁₂x’₂ + b₁₃x’₃,
х’₂ = a21x1 + a22x2 + a23x3, х”₂ = b₂₁x’1 + b₂₂x’₂ + b₂₃x’₃,
х’₃ = a₃₁x₁ + a₃₂x₂ + a₃₃x₃, х”₃ = b₃₁x’₁ + b₃₂x’₂ + b₃₃x’₃,
Средствами матричного исчисления найти преобразование, выражающее х”₁, x”₂, x”₃ через х₁, х₂, х₃.
х’₁ = 4x₁ + 3x₂ + 5x₃, х”₁ = – x’₁ + 3x’₂ – 2x’₃,
х’₂ = 6x₁ + 7x₂ + x₃, х”₂ = – 4x’₁ + x’₂ + 2x’₃,
х’₃ = 9x₁ + x₂ + 8x₃, х”₃ = 3x’₁ – 4x’₂ + 5x’₃,
Решение. Используя калькулятор, получаем:
Обозначим:

Тогда матричное уравнение запишется в виде: A·X = B.
Вычислим определитель матрицы А:
∆ = 4*(7*8 – 1*1) – 6*(3*8 – 1*5) + 9*(3*1 – 7*5) = -182
Определитель матрицы А равен detA=-182
Так как A невырожденная матрица, то существует обратная матрица A -1 . Умножим слева обе части уравнения на A -1 : A -1 ·A·X = A -1 ·B, тогда получим E·X = A -1 ·B, или X = A -1 ·B.
Найдем обратную матрицу A -1 .

A -1 = -1/182

55 -19 -32 -39 -13 26 -57 23 10

Матрицу Х ищем по формуле:

X = A -1 ·B = -1/182

55 -19 -32 -39 -13 26 -57 23 10

*

=

75 /182 -1 46 /91 1 9 /13 -13 /14 1 2 /7 -1 5 /182 1 3 /91 -1 2 /13

Пример №4 . В декартовой прямой системе координат даны вершины пирамиды A(3,0,-1), B(-1,-2,-4), C(-1,2,4), D(7,-3,1). Найдите:
а) длину ребра AB;
б) косинус угла между векторами AB и AC ;
в) уравнение ребра AB;
г) уравнение грани ABC;
д) уравнение высоты, опущенной из вершины D на грань ABC;
е) координаты векторов e ₁= AB , e ₂= AC , e ₃= AD и докажите, что они образуют линейную независимую систему;
ж) координаты вектора MN , где M и N – середины ребер AD и DC соответственно;
з) разложение вектора MN по базису ( e ₁, e ₂, e ₃)

Решение. Пункты (а-д) решаются через онлайн калькулятор.

Задание 1 . Разложить вектор d =(8;-5) по векторам a =(1;-2) и b =(2;3).
Решение. Векторы a и b образуют базис на плоскости, так как они не коллинеарны (, то есть соответствующие координаты этих векторов не пропорциональны).
Следовательно, вектор d = α a +β b , где α и β – коэффициенты, которые надо найти.
Таким образом, имеем равенство
8i-5j=α(i-2j)+β(2i+3j)=(α+2β)i+ (-2α+3β)j.
В координатной форме это равенство примет вид
Решим полученную систему уравнений.

Алгоритм нахождения базиса системы векторов

Для того чтобы найти базис системы векторов A_v А₂. А , необходимо:

1) составить соответствующую системе векторов однородную систему уравнений

2) привести эту систему к равносильной разрешенной системе вида

• 3) записать базис системы векторов Б = (А_рА₂, . А ), включив в него векторы, соответствующие разрешенным неизвестным;
• 4) записать разложения векторов по базису; коэффициентами разложения вектора А. по этому базису являются координаты соответствующего вектора

в разрешенной системе уравнений, т.е.

Система векторов, состоящая из п векторов, ранг которой равен г, может иметь несколько базисов. Число возможных базисов системы векторов определяется как число меньшее или равное числу сочетаний из п по г.

Пример 3.3. Найти ранг и базис системы векторов

разложения векторов по базису, перейти к новому базису и найти число возможных базисов системы.

Решение. Составим систему уравнений A _t ay + А₂х₂ + . + А„х_п = 0, которая в координатной записи имеет вид

Приведение данной системы уравнений с помощью преобразований Жордана к равносильной разрешенной приведено в ниже следующей таблице.

Разрешенная система имеет вид

В базис системы векторов включаем 1-й и 2-й векторы Б_: = (A_VA₂), которые соответствуют разрешенным неизвестным х₁ и х₂. Ранг системы векторов равен числу векторов, вошедших в базис, т.е. г = 2.

Запишем разложения векторов по базису. Коэффициентами разложения вектора А₃ являются координаты вектора А’₃ = (3, -2), т.е. коэффициенты при х₃ в разрешенной системе уравнений (в последних трех строках таблицы), они образуют столбец, расположенный под х₃ А₃ = ЗЛ₁ – 2А_г Аналогично, коэффициентами разложения вектора А₄ являются координаты вектора А’₄ = (4, 1) А₄ = 4А_у + 1 А_т

Для нахождения нового базиса необходимо выбрать новый разрешающий элемент. Пусть этим элементом будет элемент я₉₄ = 1.

Векторное пространство: размерность и базис, разложение вектора по базису

В статье о n -мерных векторах мы пришли к понятию линейного пространства, порождаемого множеством n -мерных векторов. Теперь нам предстоит рассмотреть не менее важные понятия, такие как размерность и базис векторного пространства. Они напрямую связаны с понятием линейно независимой системы векторов, так что дополнительно рекомендуется напомнить себе основы и этой темы.

Введем некоторые определения.

Размерность векторного пространства – число, соответствующее максимальному количеству линейно независимых векторов в этом пространстве.

Базис векторного пространства – совокупность линейно независимых векторов, упорядоченная и в своей численности равная размерности пространства.

Рассмотрим некое пространство n -векторов. Размерность его соответственно равна n . Возьмем систему из n -единичных векторов:

e ( 1 ) = ( 1 , 0 , . . . , 0 ) e ( 2 ) = ( 0 , 1 , . . . , 0 ) e ( n ) = ( 0 , 0 , . . . , 1 )

Используем эти векторы в качестве составляющих матрицы A : она будет являться единичной с размерностью n на n . Ранг этой матрицы равен n . Следовательно, векторная система e ( 1 ) , e ( 2 ) , . . . , e ( n ) является линейно независимой. При этом к системе невозможно добавить ни одного вектора, не нарушив ее линейной независимости.

Так как число векторов в системе равно n , то размерность пространства n -мерных векторов равна n , а единичные векторы e ( 1 ) , e ( 2 ) , . . . , e ( n ) являются базисом указанного пространства.

Из полученного определения сделаем вывод: любая система n -мерных векторов, в которой число векторов меньше n , не является базисом пространства.

Если мы поменяем местами первый и второй вектор, получим систему векторов e ( 2 ) , e ( 1 ) , . . . , e ( n ) . Она также будет являться базисом n -мерного векторного пространства. Составим матрицу, взяв за ее строки векторы полученной системы. Матрица может быть получена из единичной матрицы перестановкой местами первых двух строк, ранг ее будет равен n . Система e ( 2 ) , e ( 1 ) , . . . , e ( n ) линейно независима и является базисом n -мерного векторного пространства.

Переставив местами в исходной системе другие векторы, получим еще один базис.

Мы можем взять линейно независимую систему неединичных векторов, и она также будет представлять собой базис n -мерного векторного пространства.

Векторное пространство с размерностью n имеет столько базисов, сколько существует линейно независимых систем из n -мерных векторов числом n.

Плоскость является двумерным пространством – ее базисом будут два любых неколлинеарных вектора. Базисом трехмерного пространства послужат три любых некомпланарных вектора.

Рассмотрим применение данной теории на конкретных примерах.

Исходные данные: векторы

a = ( 3 , – 2 , 1 ) b = ( 2 , 1 , 2 ) c = ( 3 , – 1 , – 2 )

Необходимо определить, являются ли указанные векторы базисом трехмерного векторного пространства.

Решение

Для решения поставленной задачи исследуем заданную систему векторов на линейную зависимость. Составим матрицу, где строки – координаты векторов. Определим ранг матрицы.

A = 3 2 3 – 2 1 – 1 1 2 – 2 A = 3 – 2 1 2 1 2 3 – 1 – 2 = 3 · 1 · ( – 2 ) + ( – 2 ) · 2 · 3 + 1 · 2 · ( – 1 ) – 1 · 1 · 3 – ( – 2 ) · 2 · ( – 2 ) – 3 · 2 · ( – 1 ) = = – 25 ≠ 0 ⇒ R a n k ( A ) = 3

Следовательно, заданные условием задачи векторы линейно независимы, и их численность равна размерности векторного пространства – они являются базисом векторного пространства.

Ответ: указанные векторы являются базисом векторного пространства.

Исходные данные: векторы

a = ( 3 , – 2 , 1 ) b = ( 2 , 1 , 2 ) c = ( 3 , – 1 , – 2 ) d = ( 0 , 1 , 2 )

Необходимо определить, может ли указанная система векторов являться базисом трехмерного пространства.

Решение

Указанная в условии задачи система векторов является линейно зависимой, т.к. максимальное число линейно независимых векторов равно 3. Таким образом, указанная система векторов не может служить базисом трехмерного векторного пространства. Но стоит отметить, что подсистема исходной системы a = ( 3 , – 2 , 1 ) , b = ( 2 , 1 , 2 ) , c = ( 3 , – 1 , – 2 ) является базисом.

Ответ: указанная система векторов не является базисом.

Исходные данные: векторы

a = ( 1 , 2 , 3 , 3 ) b = ( 2 , 5 , 6 , 8 ) c = ( 1 , 3 , 2 , 4 ) d = ( 2 , 5 , 4 , 7 )

Могут ли они являться базисом четырехмерного пространства?

Решение

Cоставим матрицу, используя в качестве строк координаты заданных векторов

A = 1 2 3 3 2 5 6 8 1 3 2 4 2 5 4 7

По методу Гаусса определим ранг матрицы:

A = 1 2 3 3 2 5 6 8 1 3 2 4 2 5 4 7

1 2 3 3 0 1 0 2 0 1 – 1 1 0 1 – 2 1

1 2 3 3 0 1 0 2 0 0 – 1 – 1 0 0 – 2 – 1

1 2 3 3 0 1 0 2 0 0 – 1 – 1 0 0 0 1 ⇒ ⇒ R a n k ( A ) = 4

Следовательно, система заданных векторов линейно независима и их численность равна размерности векторного пространства – они являются базисом четырехмерного векторного пространства.

Ответ: заданные векторы являются базисом четырехмерного пространства.

Исходные данные: векторы

a ( 1 ) = ( 1 , 2 , – 1 , – 2 ) a ( 2 ) = ( 0 , 2 , 1 , – 3 ) a ( 3 ) = ( 1 , 0 , 0 , 5 )

Составляют ли они базис пространства размерностью 4?

Решение

Исходная система векторов линейно независима, но численность векторов в ней недостаточна, чтобы стать базисом четырехмерного пространства.

Ответ: нет, не составляют.

Разложение вектора по базису

Примем, что произвольные векторы e ( 1 ) , e ( 2 ) , . . . , e ( n ) являются базисом векторного n-мерного пространства. Добавим к ним некий n -мерный вектор x → : полученная система векторов станет линейно зависимой. Свойства линейной зависимости гласят, что хотя бы один из векторов такой системы может линейно выражаться через остальные. Переформулируя это утверждение, можно говорить о том, что хотя бы один из векторов линейно зависимой системы может раскладываться по остальным векторам.

Таким образом, мы пришли к формулировке важнейшей теоремы:

Любой вектор n -мерного векторного пространства единственным образом раскладывается по базису.

Докажем эту теорему:

зададим базис n -мерного векторного пространства – e ( 1 ) , e ( 2 ) , . . . , e ( n ) . Сделаем систему линейно зависимой, добавив к ней n -мерный вектор x → . Этот вектор может быть линейно выражен через исходные векторы e :

x = x 1 · e ( 1 ) + x 2 · e ( 2 ) + . . . + x n · e ( n ) , где x 1 , x 2 , . . . , x n – некоторые числа.

Теперь докажем, что такое разложение является единственным. Предположим, что это не так и существует еще одно подобное разложение:

Отнимем от левой и правой частей этого равенства соответственно левую и правую части равенства x = x 1 · e ( 1 ) + x 2 · e ( 2 ) + . . . + x n · e ( n ) . Получим:

1 – x 1 ) · e ( 1 ) + ( x

2 – x 2 ) · e ( 2 ) + . . . ( x

Система базисных векторов e ( 1 ) , e ( 2 ) , . . . , e ( n ) линейно независима; по определению линейной независимости системы векторов равенство выше возможно только тогда, когда все коэффициенты ( x

2 – x 2 ) , . . . , ( x

n – x n ) будут равны нулю. Из чего справедливым будет: x 1 = x

n . И это доказывает единственный вариант разложения вектора по базису.

При этом коэффициенты x 1 , x 2 , . . . , x n называются координатами вектора x → в базисе e ( 1 ) , e ( 2 ) , . . . , e ( n ) .

Доказанная теория делает понятным выражение «задан n -мерный вектор x = ( x 1 , x 2 , . . . , x n ) »: рассматривается вектор x → n -мерного векторного пространства, и его координаты заданы в некотором базисе. При этом также понятно, что этот же вектор в другом базисе n -мерного пространства будет иметь другие координаты.

Рассмотрим следующий пример: допустим, что в некотором базисе n -мерного векторного пространства задана система из n линейно независимых векторов

e ( 1 ) = ( e 1 ( 1 ) , e 2 ( 1 ) , . . . , e n ( 1 ) ) e ( 2 ) = ( e 1 ( 2 ) , e 2 ( 2 ) , . . . , e n ( 2 ) ) ⋮ e ( n ) = ( e 1 ( n ) , e 2 ( n ) , . . . , e n ( n ) )

а также задан вектор x = ( x 1 , x 2 , . . . , x n ) .

Векторы e 1 ( 1 ) , e 2 ( 2 ) , . . . , e n ( n ) в этом случае также являются базисом этого векторного пространства.

Предположим, что необходимо определить координаты вектора x → в базисе e 1 ( 1 ) , e 2 ( 2 ) , . . . , e n ( n ) , обозначаемые как x

Вектор x → будет представлен следующим образом:

2 · e ( 2 ) + . . . + x

Запишем это выражение в координатной форме:

( x 1 , x 2 , . . . , x n ) = x

1 · ( e ( 1 ) 1 , e ( 1 ) 2 , . . . , e ( 1 ) n ) + x

2 · ( e ( 2 ) 1 , e ( 2 ) 2 , . . . , e ( 2 ) n ) + . . . + + x

n · ( e ( n ) 1 , e ( n ) 2 , . . . , e ( n ) n ) = = ( x

2 e 1 ( 2 ) + . . . + x

2 e 2 ( 2 ) + + . . . + x

n e 2 ( n ) , . . . , x

2 e n ( 2 ) + . . . + x

Полученное равенство равносильно системе из n линейных алгебраических выражений с n неизвестными линейными переменными x

n e 2 n ⋮ x n = x

Матрица этой системы будет иметь следующий вид:

e 1 ( 1 ) e 1 ( 2 ) ⋯ e 1 ( n ) e 2 ( 1 ) e 2 ( 2 ) ⋯ e 2 ( n ) ⋮ ⋮ ⋮ ⋮ e n ( 1 ) e n ( 2 ) ⋯ e n ( n )

Пусть это будет матрица A , и ее столбцы – векторы линейно независимой системы векторов e 1 ( 1 ) , e 2 ( 2 ) , . . . , e n ( n ) . Ранг матрицы – n , и ее определитель отличен от нуля. Это свидетельствует о том, что система уравнений имеет единственное решение, определяемое любым удобным способом: к примеру, методом Крамера или матричным методом. Таким образом мы сможем определить координаты x

n вектора x → в базисе e 1 ( 1 ) , e 2 ( 2 ) , . . . , e n ( n ) .

Применим рассмотренную теорию на конкретном примере.

Исходные данные: в базисе трехмерного пространства заданы векторы

e ( 1 ) = ( 1 , – 1 , 1 ) e ( 2 ) = ( 3 , 2 , – 5 ) e ( 3 ) = ( 2 , 1 , – 3 ) x = ( 6 , 2 , – 7 )

Необходимо подтвердить факт, что система векторов e ( 1 ) , e ( 2 ) , e ( 3 ) также служит базисом заданного пространства, а также определить координаты вектора х в заданном базисе.

Решение

Система векторов e ( 1 ) , e ( 2 ) , e ( 3 ) будет являться базисом трехмерного пространства, если она линейно независима. Выясним эту возможность, определив ранг матрицы A , строки которой – заданные векторы e ( 1 ) , e ( 2 ) , e ( 3 ) .

Используем метод Гаусса:

A = 1 – 1 1 3 2 – 5 2 1 – 3

1 – 1 1 0 5 – 8 0 3 – 5

1 – 1 1 0 5 – 8 0 0 – 1 5

R a n k ( A ) = 3 . Таким образом, система векторов e ( 1 ) , e ( 2 ) , e ( 3 ) линейно независима и является базисом.

Пусть в базисе вектор x → имеет координаты x

3 . Связь этих координат определяется уравнением:

3 e 1 ( 3 ) x 2 = x

3 e 2 ( 3 ) x 3 = x

Применим значения согласно условиям задачи:

Решим систему уравнений методом Крамера:

∆ = 1 3 2 – 1 2 1 1 – 5 – 3 = – 1 ∆ x

1 = 6 3 2 2 2 1 – 7 – 5 – 3 = – 1 , x

1 ∆ = – 1 – 1 = 1 ∆ x

2 = 1 6 2 – 1 2 1 1 – 7 – 3 = – 1 , x

2 ∆ = – 1 – 1 = 1 ∆ x

3 = 1 3 6 – 1 2 2 1 – 5 – 7 = – 1 , x

Так, вектор x → в базисе e ( 1 ) , e ( 2 ) , e ( 3 ) имеет координаты x

Ответ: x = ( 1 , 1 , 1 )

Связь между базисами

Предположим, что в некотором базисе n-мерного векторного пространства даны две линейно независимые системы векторов:

c ( 1 ) = ( c 1 ( 1 ) , c 2 ( 1 ) , . . . , c n ( 1 ) ) c ( 2 ) = ( c 1 ( 2 ) , c 2 ( 2 ) , . . . , c n ( 2 ) ) ⋮ c ( n ) = ( c 1 ( n ) , e 2 ( n ) , . . . , c n ( n ) )

e ( 1 ) = ( e 1 ( 1 ) , e 2 ( 1 ) , . . . , e n ( 1 ) ) e ( 2 ) = ( e 1 ( 2 ) , e 2 ( 2 ) , . . . , e n ( 2 ) ) ⋮ e ( n ) = ( e 1 ( n ) , e 2 ( n ) , . . . , e n ( n ) )

Указанные системы являются также базисами заданного пространства.

n ( 1 ) – координаты вектора c ( 1 ) в базисе e ( 1 ) , e ( 2 ) , . . . , e ( 3 ) , тогда связь координат будет задаваться системой линейных уравнений:

1 ( 1 ) e 1 ( 1 ) + c

2 ( 1 ) e 1 ( 2 ) + . . . + c

n ( 1 ) e 1 ( n ) с 2 ( 1 ) = c

1 ( 1 ) e 2 ( 1 ) + c

2 ( 1 ) e 2 ( 2 ) + . . . + c

n ( 1 ) e 2 ( n ) ⋮ с n ( 1 ) = c

1 ( 1 ) e n ( 1 ) + c

2 ( 1 ) e n ( 2 ) + . . . + c

В виде матрицы систему можно отобразить так:

( c 1 ( 1 ) , c 2 ( 1 ) , . . . , c n ( 1 ) ) = ( c

n ( 1 ) ) · e 1 ( 1 ) e 2 ( 1 ) … e n ( 1 ) e 1 ( 2 ) e 2 ( 2 ) … e n ( 2 ) ⋮ ⋮ ⋮ ⋮ e 1 ( n ) e 2 ( n ) … e n ( n )

Сделаем по аналогии такую же запись для вектора c ( 2 ) :

( c 1 ( 2 ) , c 2 ( 2 ) , . . . , c n ( 2 ) ) = ( c

n ( 2 ) ) · e 1 ( 1 ) e 2 ( 1 ) … e n ( 1 ) e 1 ( 2 ) e 2 ( 2 ) … e n ( 2 ) ⋮ ⋮ ⋮ ⋮ e 1 ( n ) e 2 ( n ) … e n ( n )

И, далее действуя по тому же принципу, получаем:

( c 1 ( n ) , c 2 ( n ) , . . . , c n ( n ) ) = ( c

n ( n ) ) · e 1 ( 1 ) e 2 ( 1 ) … e n ( 1 ) e 1 ( 2 ) e 2 ( 2 ) … e n ( 2 ) ⋮ ⋮ ⋮ ⋮ e 1 ( n ) e 2 ( n ) … e n ( n )

Матричные равенства объединим в одно выражение:

c 1 ( 1 ) c 2 ( 1 ) ⋯ c n ( 1 ) c 1 ( 2 ) c 2 ( 2 ) ⋯ c n ( 2 ) ⋮ ⋮ ⋮ ⋮ c 1 ( n ) c 2 ( n ) ⋯ c n ( n ) = c

n ( n ) · e 1 ( 1 ) e 2 ( 1 ) ⋯ e n ( 1 ) e 1 ( 2 ) e 2 ( 2 ) ⋯ e n ( 2 ) ⋮ ⋮ ⋮ ⋮ e 1 ( n ) e 2 ( n ) ⋯ e n ( n )

Оно и будет определять связь векторов двух различных базисов.

Используя тот же принцип, возможно выразить все векторы базиса e ( 1 ) , e ( 2 ) , . . . , e ( 3 ) через базис c ( 1 ) , c ( 2 ) , . . . , c ( n ) :

e 1 ( 1 ) e 2 ( 1 ) ⋯ e n ( 1 ) e 1 ( 2 ) e 2 ( 2 ) ⋯ e n ( 2 ) ⋮ ⋮ ⋮ ⋮ e 1 ( n ) e 2 ( n ) ⋯ e n ( n ) = e

n ( n ) · c 1 ( 1 ) c 2 ( 1 ) ⋯ c n ( 1 ) c 1 ( 2 ) c 2 ( 2 ) ⋯ c n ( 2 ) ⋮ ⋮ ⋮ ⋮ c 1 ( n ) c 2 ( n ) ⋯ c n ( n )

Дадим следующие определения:

n ( n ) является матрицей перехода от базиса e ( 1 ) , e ( 2 ) , . . . , e ( 3 )

к базису c ( 1 ) , c ( 2 ) , . . . , c ( n ) .

n ( n ) является матрицей перехода от базиса c ( 1 ) , c ( 2 ) , . . . , c ( n )

к базису e ( 1 ) , e ( 2 ) , . . . , e ( 3 ) .

[spoiler title=”источники:”]

http://bstudy.net/719717/estestvoznanie/algoritm_nahozhdeniya_bazisa_sistemy_vektorov

http://zaochnik.com/spravochnik/matematika/vektory/vektornoe-prostranstvo/

[/spoiler]

В линейной алгебре базис векторного пространства размерности  — это последовательность из векторов , таких, что любой вектор пространства может быть представлен единственным образом в виде линейной комбинации базисных векторов. При заданном базисе операторы представляются в виде квадратных матриц. Так как часто необходимо работать с несколькими базисами в одном и том же векторном пространстве, необходимо иметь правило перевода координат векторов и операторов из базиса в базис. Такой переход осуществляется с помощью матрицы перехода.

Определение[править | править код]

Если векторы выражаются через векторы как:

.

.

.

.

то матрица перехода от базиса к базису ) будет:

Использование[править | править код]

При умножении матрицы, обратной к матрице перехода, на столбец, составленный из коэффициентов разложения вектора по базису , мы получаем тот же вектор, выраженный через базис .

Пример[править | править код]

Для того, чтобы повернуть вектор на угол θ против часовой стрелки, можно умножить матрицу поворота на него:

Матрицы наиболее распространённых преобразований
	В двумерных координатах	В однородных двумерных координатах	В однородных трёхмерных координатах
Масштабирование При a, b и c — коэффициенты масштабирования соответственно по осям OX, OY и OZ:
Поворот При φ — угол поворота изображения в двухмерном пространстве	По часовой стрелке		Относительно OX на угол φ	Относительно OY на угол ψ
Против часовой стрелки	Относительно OZ на угол χ
Перемещение При a, b и c — смещение соответственно по осям OX, OY и OZ.	В неоднородных координатах не имеет матричного представления.

Свойства[править | править код]

• Матрица перехода является невырожденной. То есть определитель этой матрицы не равен нулю.
• 

Пример поиска матрицы[править | править код]

Найдём матрицу перехода от базиса к единичному базису
путём элементарных преобразований

следовательно

См. также[править | править код]

• Цепи Маркова
• Стохастическая матрица
• Матрица поворота

Ссылки[править | править код]

• Матрицы перехода от базиса к базису