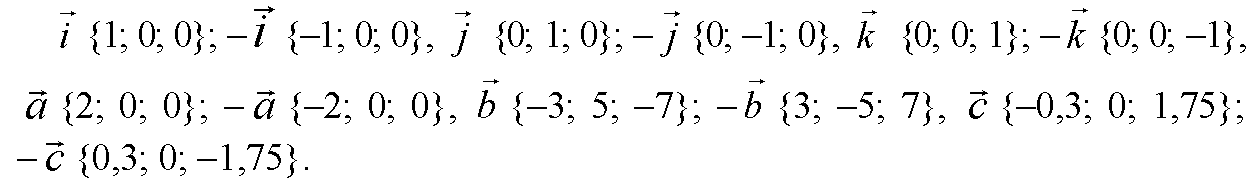Как найти координаты векторов противоположных следующим векторам

Глава V. Метод координат в пространстве. § 1. Координаты точки и координаты вектора. → номер 412

Для вектора i противоположным будет вектор с обратным знаком: (- i), для j — вектор (- j) и т. д.

Источник

Помогите решить, а главное объясните как это решить. (Геометрия)

Дарья

Знаток

(424),
закрыт

11 лет назад

Татьяна Егорова

Мудрец

(17066)

11 лет назад

Ты же уже все сделала, остадись только единичные векторы; -i(-1:0;0), – j(0;-1:0), -к (0;0;-1)

ДарьяЗнаток (424)

11 лет назад

А как эти векторы узнаются?

Дарья
Знаток
(424)
а… всё извиняюсь, всё поняла. Просто сразу не сообразила, что они всегда такие только положительные… Ох… ну я и ступила…

Источник

Вспомним, как мы находили координаты вектора на
плоскости.

Пользуясь тем, что любой вектор можно разложить по
двум неколлинеарным векторам, на осях мы задавали единичные векторы. Таким
образом, любой вектор можно разложить по данным единичным векторам, а
координатами вектора являются коэффициенты этого разложения.

Так же вам уже известно, что любой вектор пространства
можно выразить через 3 некомпланарных вектора, то есть векторы, не лежащие в
одной плоскости.

Изобразим прямоугольную систему координат Охуz.
На каждой из положительных осей от начала координат отложим единичные векторы.

Буквой i
обозначим единичный вектор оси Оx,
буквой j — единичный вектор оси Оy,
буквой k — единичный вектор оси Оz.

Определение:

Векторы i,
j, k
будем называть координатными векторами.

Понятно, что они являются некомпланарными. И
поэтому любой вектор пространства можно разложить по единичным векторам i,
j, k.
Причём коэффициенты разложения х, у и z
определяются единственным образом.

Коэффициенты х, у и z
называют
координатами вектора р в данной системе координат. Координаты
вектора будем записывать в фигурных скобках в последовательности х, у, z.

Задание: Пользуясь
разложениями векторов по координатным векторам, записать их координаты.

Решение:

Задание: пользуясь
координатами векторов, запишем их разложения по координатным векторам i,
j, k.

Решение:

Задача: В
прямоугольном параллелепипеде 𝑂𝐴 =
2, 𝑂𝐵 =
3, а ОО₁ = 2. Найти координаты векторов 𝑂𝐴₁,
𝑂𝐵₁,
𝑂𝑂₁,
𝑂𝐶,
𝑂𝐶₁,
𝐵𝐶₁,
𝐴𝐶₁
и 𝑂₁ 𝐶.

Решение:

После выполнения этого задания можно сделать вывод
о том, что если вектор лежит в некоторой из координатных плоскостей или
параллелен ей, а также лежит или параллелен некоторой из координатных осей, то
его соответствующие координаты равны нулю.

Если вектор лежит в координатной плоскости Оху или
параллелен ей, то его аппликата равна нулю. Если вектор принадлежит или
параллелен координатной плоскости Охz,
то его ордината равна нулю. Если же вектор принадлежит или параллелен
координатной плоскости Оyz,
то его абсцисса равна нулю.

В случае, когда вектор лежит на оси координат Оx
или параллелен ей, то ордината и аппликата равны нулю. Если вектор принадлежит
или параллелен оси Оy, то абсцисса и
аппликата равны нулю. И если вектор принадлежит или параллелен оси Оz,
то абсцисса и ордината равны нулю.

А сейчас поговорим о противоположных векторах. Из
планиметрии известно, что координаты противоположных векторов
противоположны. Это утверждение верно и для векторов в пространстве.

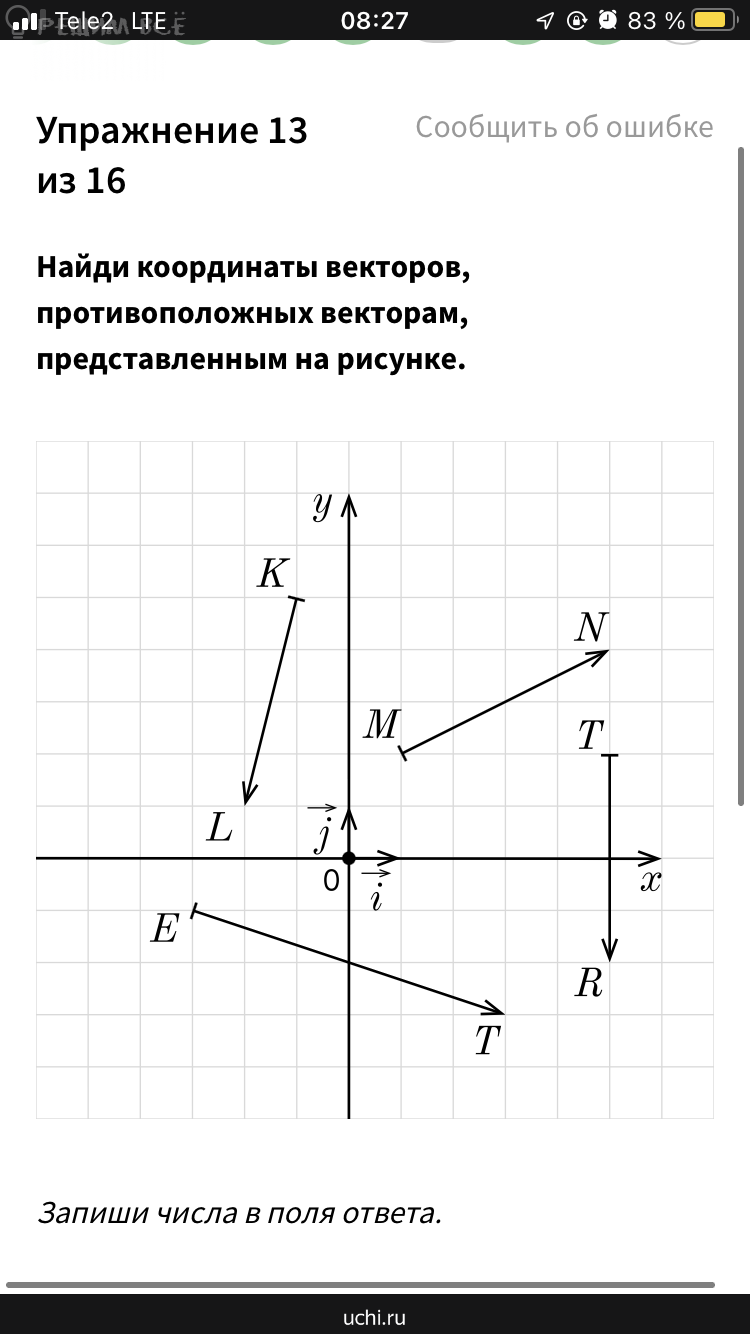
Задание: найти
координаты векторов противоположных данным векторам.

Решение:

Также из курса планиметрии вам известны правила
определения координат вектора суммы, вектора разности и произведения
вектора на число.

Такие же правила действую и для координат векторов в
пространстве.

Задание: 𝑎 ⃗{−1;0;3},
𝑏 ⃗{5;−2;1}
и 𝑐 ⃗{1;7;−2}.
Определить координаты векторов:

1) 𝑎 ⃗+𝑐 ⃗;
2) 𝑏 ⃗−𝑎 ⃗;
3) 2𝑎 ⃗+𝑏 ⃗;
4) 1/2 𝑎 ⃗−2𝑏 ⃗+𝑐 ⃗.

Решение:

Так, используя правила определения координат вектора
суммы, разности и произведения вектора на число, мы определили координаты
данных векторов.

Итоги:

Сегодня мы ввели понятие координатных векторов i,
j, k.
И, пользуясь тем, что любой вектор пространства можно выразить через 3
некомпланарных вектора, записали, что коэффициенты х, у и z
называют координатами вектора p
в данной системе координат.

Мы отметили, что все координаты нулевого вектора равны
нулю. Равные векторы имеют равные координаты, а координаты противоположных
векторов противоположны.

Также мы записали правила, которые позволяют находить
координаты любого вектора, представленного в виде алгебраической суммы данных
векторов, координаты которых известны.

Источник

§ 1. Векторы.

.
Векторы. Основные понятия. Правила
действия с векторами.

Основные
понятия, связанные с векторами, в
стереометрии те же, что и в планиметрии.

Определение.
Вектором
называется направленный отрезок, т.е.
вектор однозначно определяется
направлением и длиной.

Любая
точка пространства может рассматриваться
как нулевой
вектор.

Определение.
Длиной
вектора
называется расстояние от начала вектора
до его конца

Определение.
Два ненулевых вектора называются
коллинеарными,
если они лежат на одной прямой или на
параллельных прямых. Коллинеарные
векторы могут быть сонаправленными
или противоположно
направленными.

Теорема.
Если векторы
и
коллинеарны и вектор
– ненулевой, то существует число k
такое, что .

Определение.
Два ненулевых вектора называются
противоположными,
если их длины равны и они противоположно
направлены.

Определение.
Векторы называются равными,
если они сонаправлены и их длины равны.

Определение.
Векторы называются взаимно
перпендикулярными
(ортогональными),
если угол между ними равен 90°.

К
известным правилам сложения векторов
(правила треугольника, параллелограмма,
многоугольника (или ломаной)) в пространстве
добавляется правило
параллелепипеда:
.

Правила
сложения векторов:

① ;

② ;

③ .

Вычитание
векторов .

Правила
умножения вектора на число:

① β
· (λ
·
)
= (β
· λ)
·;

② 1
·
= ;

③ -1
·
= ;

④ (β
+ λ)·

= β
·
+ λ
· ;

⑤ λ
· ()
= λ
·
+ λ
· .

Теорема.
Любой вектор на плоскости можно разложить
единственным образом по двум неколлинеарным
векторам.

;
числа x,
y
называют коэффициентами разложения.

.
Компланарные векторы.

Определение.
Векторы называются компланарными,
если они параллельны одной плоскости
или лежат в одной плоскости. Другими
словами, векторы компланарны, если при
откладывании их от одной точки они будут
лежать в одной плоскости.

Очевидно,
что любые два вектора компланарны; три
вектора, два из которых коллинеарны,
также компланарны.

Векторы
,

и
компланарны.

Векторы
,

и
не компланарны.

A₁

C₁

B₁

Теорема.
Любой вектор можно разложить по трём
данным некомпланарным векторам, причём
коэффициенты разложения определяются
единственным образом.

.
Скалярное произведение векторов.
Основные формулы.

Скалярное
произведение векторов вычисляется по
формуле

, где φ – угол между векторами
и .

Законы
скалярного произведения:

① ;

;

③;

④

и
перпендикулярны.

Из
определения скалярного произведения
получаем формулу для нахождения косинуса
угла между векторами:

Если
,
то угол φ
– острый;

Если
,
то угол φ
– тупой;

Если
,
то угол φ
– прямой.

§ 2. Координаты в пространстве.

.
Прямоугольная система координат в
пространстве.

Если
через точку пространства проведены три
попарно перпендикулярные прямые, на
каждой из которых выбрано направление
и выбрана единица измерения отрезков,
то говорят, что задана прямоугольная
система координат
в пространстве.

Оси
координат:

Ox
– ось абсцисс;

Oy
– ось ординат;

Oz
– ось аппликат.

Координатные
плоскости: Oxy,
Oxz,
Oyz.

Вся
система координат обозначается Oxyz.

Каждой
точке М
пространства сопоставляется тройка
чисел, которые называются её координатами.

Координатные
(базисные) векторы:

единичный
вектор оси абсцисс;

единичный
вектор оси ординат;

единичный
вектор оси аппликат.

Очевидно,
что координатные векторы не коллинеарны,
поэтому любой вектор

можно разложить по координатным векторам:
,
причём коэффициенты разложения x,
y,
z
определяются единственным образом и
называются координатами вектора.

Применяют
запись: .

Каждая
координата вектора равна разности
соответствующих координат его конца и
начала.

.
Правила
действий с векторами в координатах.
Основные формулы.

– Каждая
координата суммы двух или более векторов
равна сумме соответствующих координат
этих векторов.

– Каждая
координата разности двух векторов равна
разности соответствующих координат
этих векторов.

– Каждая
координата произведения вектора на
число равна произведению соответствующей
координаты вектора на это число.

Длина
вектора :

Скалярное
произведение
векторов
и :

Косинус
угла
между векторами
и :

Условие
перпендикулярности
(ортогональности) векторов
и :

Условие
коллинеарности
векторов
и :

Расстояние
между точками
М₁
и М₂
:

|M₁M₂|
= .

Пусть
С
(x;
y;
z)
– середина
отрезка
M₁M₂.
Тогда координаты точки С:

;
;
.

Вопросы
и задачи

Точки
М
и К
– середины рёбер В₁С₁
и А₁D₁
параллелепипеда ABCDA₁B₁C₁D₁
соответственно. Укажите все пары:

а)
сонаправленных векторов;

б)
противоположно направленных векторов;

в)
равных векторов.

На
плоскости даны векторы и
.
Построить векторы: 3,

+ ,
.
ABCD
– параллелограмм, ,
.
Выразить через
и
векторы ,
,
,
.
Упростите
выражение: а) ;
б) ;
в) ;
г) .
Даны
точки А, В, С и D.
Представьте вектор
в виде алгебраической суммы следующих
векторов: а) ,
,
;
б),
,
;
в) ,
,
.
Упростите
выражение: а) ;б);в).
Упростите:
а) ;
б).
Докажите,
что в параллелепипедеABCDA₁B₁C₁D₁+

= 2.
Дан
параллелепипед ABCDA₁B₁C₁D₁.
Какие из следующих трёх векторов
компланарны: а) ;
б) ,
,
;
в) ;
г),
?
Дан
параллелепипед ABCDA₁B₁C₁D₁.
а) Разложите вектор
по векторам .
б) Разложите вектор по
векторам ,

и .
Докажите,
что если М – точка пересечения медиан
треугольника АВС,
а О
– произвольная точка пространства, то
.
Даны
точки А (3; -1; 0), В (0; 0; -7), С (2; 0; 0), D(-
4; 0; 3), E
(0; -1; 0), F(1;
2; 3), G
(0; 5; -7), H
(-;
;
0). Какие из этих точек лежат на: а) оси
абсцисс; б) оси ординат; в) оси аппликат;
г) плоскости Oxy;
д) плоскости Оyz;
е) плоскости Оxz?
Найдите
координаты проекций точек А (2; -3; 5), В
(3; -5; )
и С ()
на: а) координатные плоскости Оxz,
Oxy
и Oyz;
б) оси координат Ох,
Оу
и Оz.
Даны
координаты четырёх вершин куба
ABCDA₁B₁C₁D₁:
А (0; 0; 0), В (0; 0; 1), D
(0; 1; 0) и А₁
(1; 0; 0). Найдите координаты остальных
вершин куба.
В
кубе ABCDA₁B₁C₁D₁D
(0; 0; 0), C
(2; 0; 0), A₁
(0; 2; 2). Найдите координаты остальных
вершин куба.
Даны
точки А (1; 4; -3), В (-1; 0; -2). Найдите координаты
вектора и
его длину.
Даны
три точки А (1; 0; 2), В (-1; -1; 0), С (1; 2; 0). Найти
векторы ,
,,
.
Даны
три точки А (2; 1; 0), В (-1; 3; 1), С (-1; 3; -4). Найти
векторы ,,
.
Даны
векторы
(5; 1; -1) и
(9; 0; -4). Найти вектор
и его длину.
Даны
векторы
(5; 0; 1) и
(-7; 4; -2). Найти вектор
и его длину.
Запишите
координаты векторов: ,
,
,
,
,
.
Даны
векторы ,
,
,
.
Запишите разложения этих векторов по
координатным векторам ,
,
.
Даны
векторы
и .
Найти векторы ;
;
;
.
Даны
векторы
и .
Найти векторы ;
;
;
.
Даны
векторы ,
,

и .
Найдите координаты векторов: а) ;
б) ;
в) ;
г) ;
д) ;
е) ;
ж) ;
з) .
Даны
векторы (5;
-1; 1),
(-2; 1; 0), (0;
0,2; 0) и
().
Найдите координаты векторов: а) ;
б) ;
в) ;
г) ;
д) ;
е) ;
ж) ;
з) 2;
и) -3;
к) -6;
л) ;
м) 0,2.
Даны
векторы ,
и
.
Найдите координаты векторов и
.
Найдите
координаты векторов, противоположных
следующим векторам: ,
,
,
,
,
).
Коллинеарны
ли векторы: а)
и
;
б)

и
;
в)

и
;
г)

и
;
д)

и
?
Найдите
значения m
и n,
при которых следующие векторы коллинеарны:
а)
и ;
б)

и .
Даны
два вектора
и .
Найти x
и z,
если
|| .
Даны
два вектора
и .
Найти k
и m,
если
|| .
Определить,
при каких значениях х
векторы (х³
– 1)·
и 2х
являются сонаправленными, если .
Определить,
при каких значениях m
векторы (m²
– m
– 2)·
и m³·
противоположно направлены, если .
Даны
три последовательные вершины
параллелограмма: А (3; -1; 4), В (0; -2; 5) и
С (1; 2; 2). Найти четвёртую вершину
параллелограмма.
Даны
три последовательные вершины
параллелограмма: А (2; 3; 4), В (1; -3; 7) и
С (4; 3; 7). Найти четвёртую вершину
параллелограмма.
Даны
точки А (3; -1; 2), В (1; 2; -1), С (-1; 1; -3) и D
(3; -5; 3). Доказать, что ABCD
– трапеция.
Найти
такое число m,
при котором векторы ,

и
являются
компланарными.
Установить,
являются ли компланарными следующие
векторы:

а)

(2; 3; -1); (1;
-1; 3); (1;
9; -11);

б)

(3; -2; 1);
(2; 1; 2);
(3; -1; -2);

в)

(2; -1; 2);
(1; 2; -3);
(3; -4; 7).

Компланарны
ли векторы: а) ,

и
;
б) ,

и
;
в)
,

и
;
г) ,

и
;
д) ,

и

(-1; 2; 4);
е) ,
и
?
Дан
куб ABCDA₁B₁C₁D₁.
Найдите угол между векторами: а) и
;
б)
и
;
в)
и
;
г)
и
;
д)
и
;
е) и
;
ж)
и
;
з)
и
.
Даны
векторы
(1; -1; 2),
(-1; 1; 1) и
(5; 6; 2). Вычислите ,
,
,
,
.
Даны
векторы
(3; -1; 1),
(-5; 1; 0) и
(-1; -2; 1).Выясните, какой угол (острый,
прямой или тупой между векторами: а)

и ;
б)
и ;
в)
и .
Даны
векторы
и .
При каком значении mвекторы
и

перпендикулярны?
Даны
точки А (0; 1; 2), В (;
1; 2), С (;
2; 1) и D
(0; 2; 1). Докажите, что ABCD
– квадрат.
Вычислите
углы между вектором
и координатными векторами.
Даны
точки А (1; 3; 0), В (2; 3; -1) и С (1; 2; -1). Вычислите
угол между векторами
и .
Найдите
углы, периметр и площадь треугольника,
вершинами которого являются точки А
(1; -1; 3), В (3; -1; 1) и С (-1; 1; 3).
Найти
,
если ||
= 3; ||
= 4 и угол между
и
равен .
Найти
,
если ||
= 1; ||
= 2 и угол между
и
равен .
Найти
,
если ||
= 2; ||
= 3 и вектор .
Найти
,
если ||
= 3; ||
= 4; угол между
и
равен .
Найти
угол между векторами
и .
Дан
треугольник с вершинами в точках А (3;
-2; 1), В (3; 0; 2) и С (1; 2; 5). Найти угол,
образованный медианой BD
и стороной АС.
Даны
вектора
и .
Найти угол, образованный векторами
и .
Найти
площадь параллелограмма, построенного
на векторах и
,
если векторы и

составляют угол 30° и .
Найти
площадь треугольника с вершинами А (2;
3; 1), В (4; 4; 0) и С (3; 1; -1).
Точки
А (4; -3; 7), В (5; 3; 8) и D
(10; -4; 6) являются вершинами ромба ABCD.
Найти длину диагонали АС.

РИЛОЖЕНИЕ

Греческий
алфавит.

Α	α	альфа	Ι	ι	йота	Ρ	ρ	ро
Β	β	бета	Κ	κ	каппа	Σ	σ	сигма
Γ	γ	гамма	Λ	λ	лямбда	Τ	τ	тау
Δ	δ	дельта	Μ	μ	мю	Υ	υ	ипсилон
Ε	ε	эпсилон	Ν	ν	ню	Φ	φ	фи
Ζ	ζ	дзета	Ξ	ξ	кси	Χ	χ	хи
Η	η	эта	Ο	ο	омикрон	Ψ	ψ	пси
Θ	θ	тета	Π	π	пи	Ω	ω	омега

Латинский
алфавит.

A	a	а	J	j	жи	S	s	эс
B	b	бе	K	k	ка	T	t	тэ
C	c	це	L	l	эль	U	u	у
D	d	де	M	m	эм	V	v	вэ
E	e	э	N	n	эн	W	w	дубль-вэ
F	f	эф	O	o	о	X	x	икс
G	g	же	P	p	пэ	Y	y	игрек
H	h	аш	Q	q	ку	Z	z	зет
I	i	и	R	r	эр

Квадраты
натуральных чисел от 11 до 99.

	1	2	3	4	5	6	7	8	9
1	121	144	169	196	225	256	289	324	361
2	441	484	529	576	625	676	729	784	841
3	961	1024	1089	1156	1225	1296	1369	1444	1521
4	1681	1764	1849	1936	2025	2116	2209	2304	2401
5	2601	2704	2809	2916	3025	3136	3249	3364	3481
6	3721	3844	3969	4096	4225	4356	4489	4624	4761
7	5041	5184	5329	5476	5625	5776	5929	6084	6241
8	6561	6724	6889	7056	7225	7396	7569	7744	7921
9	8281	8464	8649	8836	9025	9216	9409	9604	9801

Факториалы.

n	0	1	2	3	4	5	6	7	8	9	10
n!	1	1	2	6	24	120	720	5040	40320	362880	3628800

Степени.

n	2ⁿ	3ⁿ	4ⁿ	5ⁿ	6ⁿ	7ⁿ	8ⁿ	9ⁿ
0	1	1	1	1	1	1	1	1
1	2	3	4	5	6	7	8	9
2	4	9	16	25	36	49	64	81
3	8	27	64	125	216	343	512	729
4	16	81	256	625	1296	2401	4096	6561
5	32	243	1024	3125	7776	16807	32768	59049
6	64	729	4096	15625	46656	117649	262144	531441
7	128	2187	16384	78125	279936	823543	2097152	4782969
8	256	6561	65536	390625	1679616	5764801	16777216	43046721
9	512	19683	262144	1953125	10077696	40353607	134217728	387420489
10	1028	59049	1048576	9765625	60466176	282475249	1073741824	3486784401

Некоторые
сведения из курса планиметрии.

.
Площади
фигур.

Площадь
треугольника.

Следствия
из формулы (1):

(
h_a–
высота, проведённая к стороне a)

Площадь
квадрата со стороной a:

Площадь
прямоугольника со сторонами a
и b:

Площадь
параллелограмма.

h_b

h_a



Площадь
ромба со стороной a
и углом .



Площадь
трапеции с основаниями a
и b
высотой h.

Площадь
круга радиуса R:

Длина
окружности радиуса R:

Площади
подобных фигур относятся как квадрат
коэффициента подобия.

.
Теорема косинусов.

.
Теорема синусов.

V.
Четыре
замечательных точки треугольника.

Медианы
треугольника пересекаются в одной
точке (центр тяжести) и делятся в
отношении 2 : 1, считая от вершины.

Медиана
делит треугольник на два равновеликих.
Три медианы делят треугольник на
шесть равновеликих треугольников.

A₁

C₁

B₁

Высоты
треугольника пересекаются в одной точке
( ортоцентр).

Биссектрисы
треугольника
пересекаются в одной точке, которая
является центром окружности, вписанной
в данный треугольник.

Серединные
перпендикуляры к
сторонам треугольника пересекаются в
одной точке, которая является центром
окружности, описанной около данного
треугольника.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Задать свой вопрос

*более 50 000 пользователей получили ответ на «Решим всё»

Задача 66517 Найди координаты векторов,…

Условие

635a14eeaf70910651f83229

27.10.2022 08:28:23

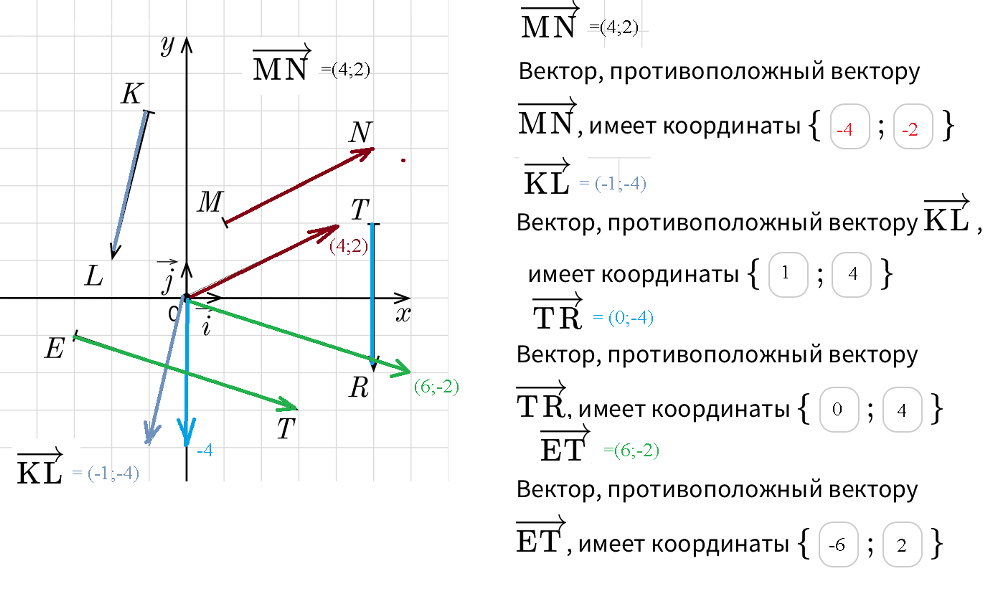
Найди координаты векторов, противоположных векторам, представленным на рисунке

математика 8-9 класс
321

Решение

5f3ea7e3faf909182968ddd9

27.10.2022 10:17:40

★

Равные векторы имеют равные координаты.

Строим вектор, равный требуемому, так, чтобы он выходил из начала координат.

Тогда координаты конечной точки совпадают с координатами вектора, потому что вычитаем координаты О(0;0)

Написать комментарий

Присоединяйся в ВК

Источник