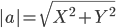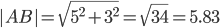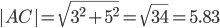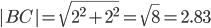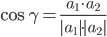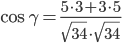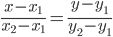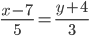Как определить координаты вершин по уравнению
Стороны треугольника заданы уравнениями:
Найти координаты вершин треугольника.
Координаты вершины A найдем, решая систему, составленную из уравнений сторон AB и AC:
Систему двух линейных уравнений с двумя неизвестными решаем способами, известными из элементарной алгебры, и получаем
Вершина A имеет координаты
Координаты вершины B найдем, решая систему из уравнений сторон AB и BC:
получаем .
Координаты вершины C получим, решая систему из уравнений сторон BC и AC:
Вершина C имеет координаты .
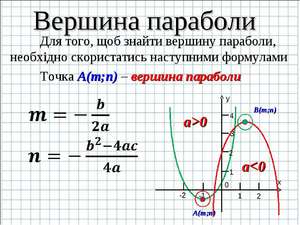
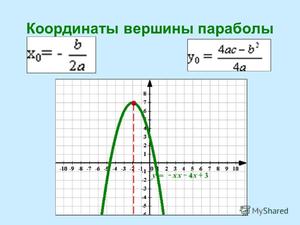
Как найти вершину параболы: три формулы
Парабола присутствует в мире математики, физики и других наук. По траектории параболы передвигаются искусственные спутники, которые стремятся покинуть пределы Солнечной системы, мяч при игре в волейбол тоже описывает её траекторию. Нужно уметь строить параболу. А чтобы это не составляло труда, надо знать, как найти вершину параболы.
Нахождение вершины параболы: способы, примеры, советы
График функции y = ax 2 + bx + c, где a — первый коэффициент, b – второй коэффициент, c – свободный член, называется параболой. Но обратите внимание на тот факт, что a ≠0.
У каждой точки параболы есть симметричная ей, кроме одной точки, и эта точка называется вершиной. Для того чтобы найти точку, которая является вершиной, нужно определиться, что такое точка на графике. Точка на графике – это определённая координата по оси абсцисс и по оси ординат. Она обозначается как (x; y). Давайте разбираться, как найти заветные числа.
Первый способ
Если вы хотите знать, как необходимо правильно вычислять координаты вершины, то нужно только выучить формулу x0 = -b/2a. Подставляя полученное число в функцию, получим y0.
Например, y =x 2 –8 x +15;
находим первый, второй коэффициенты и свободный член;
подставляем значения a и b в формулу;
вычисляем значения y;
Значит, вершина находится в точке (4;-1).
Ветви параболы симметричны относительно оси симметрии, которая идёт через вершину параболы. Зная корни уравнения, можно без особых трудностей посчитать абсциссу вершины параболы. Предположим, что k и n – корни квадратичного уравнения. Тогда точка x0 равноудалена от точек k и n, и её можно вычислить по формуле: x0 = (k + n)/2.
Рассмотрим на примере y =x 2 –6x+5
1) Приравниваем к нулю:
2) Находим дискриминант, используя формулу: D = b 2 –4 ac:
3) Находим корни уравнения по формуле (-b±√ D)/2a:
- 1 – первый корень;
- 5 – второй корень.
Второй способ
Дополнение до полного квадрата – отличный способ узнать, где располагается вершина. Используя этот способ, вы сможете вычислить точки x и y одновременно, без нужды подставлять x в начальный пример. Рассмотрим этот метод на примере функции: y=x 2 +8 x +10.
1. Сначала нужно приравнять выражение с переменной к 0. Потом перенести c в правую сторону с противоположным знаком, то есть у нас получается выражение x 2 + 8x = -10.
2. Теперь в левой части нужно сделать полный квадрат. Для этого посчитайте (b/2) 2 и увеличьте обе части уравнения результат. В этом случае нужно подставит 8 вместо b.
У нас получается 16. Теперь прибавьте это число к обеим частям уравнения:
3. Видно, что полученное выражение – полный квадрат. Его можно представить в форме: (x + 4) 2 = 6.
4. Используйте это выражение для поиска координат вершины параболы. Чтобы посчитать x, нужно приравнять его к 0. Получаем, x =-4. Координата y равна тому, что находится в правой части, то есть y =6. Вершина параболы этого уравнения (-4, 6).
Третий способ
Если вы знаете, что такое производная, то для вас есть другая формула. Несмотря на то, куда смотрят «рога» параболы, её вершина — точка экстремума. Для этого способа надо применить следующий алгоритм:
1. Нахождение первой производной по формуле f'(x) = (ax² + bx + c)’ = 2ax + b.
2. Приравнивание производной к 0. В итоге вы получите 0 = 2ax + b, отсюда можно найти то, что нас интересует.
Рассмотрим этот способ подробнее.
Дана функция y = 4x²+16x-17;
- Записываем производную и приравниваем к нулю.
f'(x) = (4x²+16x-17)’ = 8x+16 =0
Построение параболы
Самое трудное при построении – это верно найти точки функции. Для подробного построения нужно просчитать 5–7 точек (для школьного курса хватит этого). Для этого выбираем какое-либо значение x и подставляем его в данную функцию. Итогом подсчётов будет число точки по оси ординат. После этого ставим на координатную плоскость полученные нами точки. В итоге у нас получается парабола.
Рассмотрим подробнее вопрос о нахождении точек, которые нужно отметить. Для примера возьмём функцию y =-x 2 +11 x -24 с вершиной в точке (5,5;-6,25).
1) Строим таблицу
2) Заполняем таблицу
Так как парабола имеет осевую симметрию, то можно считать только значения справа или слева от вершины. Лучше считать те значения, которые ближе к 0, так удобнее. В нашем случае эти значения 4 и 5.
| X | 4 | 5 | 5,5 | 6 | 7 |
| Y | -4 | -6 | -6,25 | -6 | -4 |
Советы
Правильно находите коэффициенты.
Пишите промежуточные вычисления на бумаге. Это не только облегчит нахождение вершины, но и поможет найти свои ошибки.
Делайте всё поэтапно. Следуйте алгоритму.
Обратите ваше внимание на то, что:
- Нужно проверять правильно ли ваше решение.
- Необходимо успокоиться. Решение любых задач по математике требует опыта. Просто нужно отработать данную тему, и тогда непременно у вас всё получится.
Видео
Это видео поможет вам научиться находить вершину параболы
Формула нахождения вершины параболы
Вы будете перенаправлены на Автор24
Парабола – это геометрическое множество точек, равноудалённых от точки F, не лежащей на параболе, и прямой $d$, не проходящей через точку $F$.
Что значит вершина параболы
Вершина параболы – это точка, ближайшая к директрисе параболы. Она является центром отрезка, ограниченного точкой фокуса параболы $F$ и директрисой $d$.
Производная в вершине квадратичной параболы равна нулю.
Каноническое уравнение параболы $y^2 = 2px$ справедливо для параболы, вершина которой находится в центре осей.
Для того, чтобы определить, принадлежит ли точка графику заданной параболы, необходимо подставить её координаты в формулу $y = ax^2 + bx + c$.
Если равенство выполняется — точка принадлежит графику.
Как найти вершины параболы, задающейся квадратичной функцией
Рисунок 1. Пример уравнения и графика квадратичной параболы
Довольно часто парабола задаётся квадратичной функцией вида $y = ax^2 + bx + c$, вершина такой параболы находится в произвольной точке.
Какой-то единой формулы для нахождения сразу обеих координат вершины параболы нет, но при этом определить координаты вершины параболы по уравнению довольно просто.
Алгоритм для нахождения вершины параболы такой:
- Запишите коэффициенты $a, b, c$ из уравнения. Если коэффициент $a$ при $y$ положительный, то ветви параболы будут смотреть вверх, а если отрицательный, то вниз.
- Найдите абсциссу вершины параболы ($x$ вершины) по формуле $x = – frac<2a>$, для этого воспользуйтесь коэффициентами $a, b, c$ из уравнения.
- Подставьте найденный $x$ в уравнение параболы и вычислите ординату вершины параболы $y$.
- Запишите полученные координаты x и y вершины параболы в форме точки $(x; y)$.
Рассмотрим уравнение параболы $y = x^2 – 5x + 7$
- Коэффициенты этой параболы $a = 1$, $b = -5$, $c = 7$.
- Для вычисления x вершины параболы подставьте $a = 1$ и $b = -5$ в формулу $x = – frac<2a>= frac<5><2>=2.5$
- Подставьте найденный $x$ в исходное уравнение:
- $y = 2,5^2 – 5 cdot 2.5 + 7$
- $y = 0,75$
- Координаты вершины этой параболы $(2.5;0.75)$.
Вершина кубической параболы
Чтобы найти вершины (точки локальных минимумов и максимумов) кубической параболы, необходимо найти её производную, приравнять её к нулю и затем вычислить $x$ и $y$.
Если же необходимо найти точку перегиба кубической параболы, необходимо найти вторую производную и также приравнять её к нулю.
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 04 12 2021
[spoiler title=”источники:”]
http://liveposts.ru/articles/education-articles/matematika/kak-najti-vershinu-paraboly-tri-formuly
http://spravochnick.ru/matematika/parabola/formula_nahozhdeniya_vershiny_paraboly/
[/spoiler]
Найти координаты вершин треугольника,
если стороны заданы уравнениями:
x – 2y + 3 = 0;
2x – y – 3 = 0;
x + y – 3 = 0;
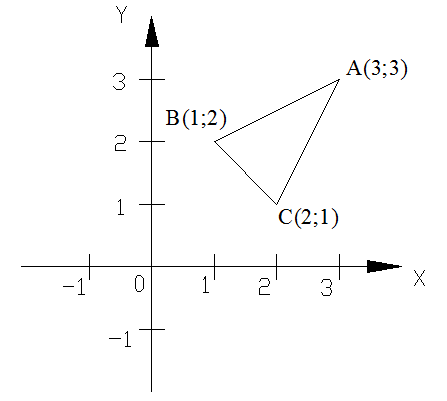
Дано: АВ: х-2у+3=0, АС: 2х-у-3=0, ВС: х+у-3=0
Найти: А,В и С.
Решение.
Найдем вершины треугольника АВС, как
точки пересечения сторон треугольника.
т.А:
3у=-9 у=3,
x-2*3+3=0, у=3, х=3
имеем: A(3;3)
т. В:
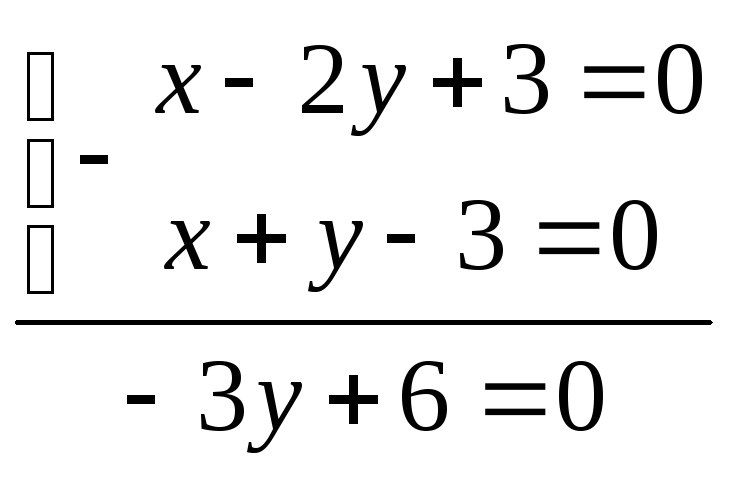
х-2*2+3=0,
у=2, х=1
имеем: т. B(1;2)
т.С :
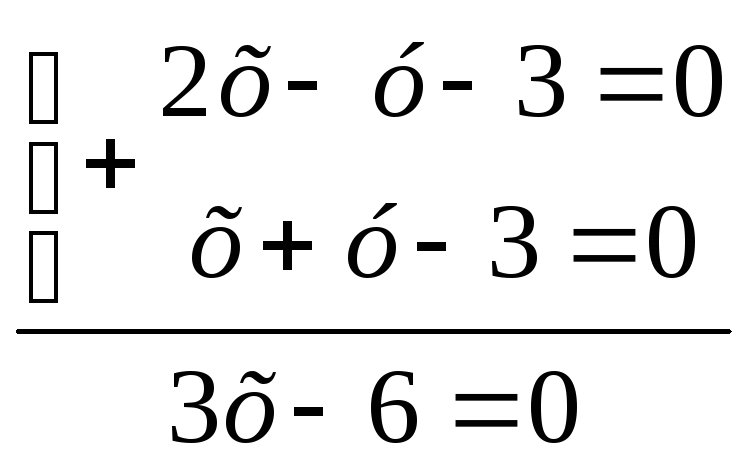
3х=6 х=2, 2+y-3=0,
х=3, y=1
имеем: т. C(2;1)
Ответ: координаты вершин треугольника:
А (3;3); В(1;2); С(2;1).
Задача №2
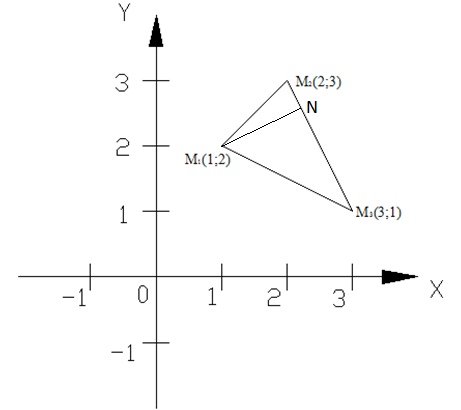
Даны вершины треугольника:;2);
;3);
;1).
Написать уравнение высоты, опущенной
из точки
Решение
Дано:
(1;2);
(2;3);
(3;1)
– вершины треугольника
Решение: проведем из точки
высоту
к стороне
запишем уравнение стороны
откуда имеем
-2х+4-у+2=0,
у+2х-6=0, у = -2х+6, т.е. угловой коэффициент
прямой k= -2. Тогда, угловой
коэффициент перпендикулярной прямой
(высоты
)
будет
.
Найдем уравнение высоты, как уравнение
прямой, проходящей через одну точку:
y-y1
=k(x-x1),
Где x1 и y1
– координаты точки .
y-2=
(x-1), откуда имеем 2y-x-3=0
.
откуда, преобразовав, получим
2у-х-3=0
Ответ: уравнение высоты 2у-х-3=0
Задача №3.
Даны
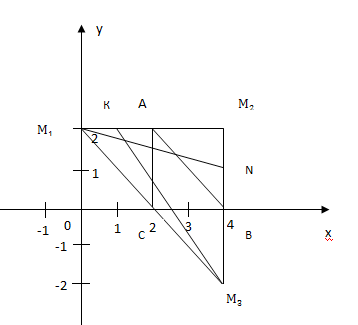
вершины треугольника M1M2M3:
М1(-3;0), M2(2;5),
M3(3;2).
а)
Найти периметр треугольника, вершинами
которого служат середины сторон.
б)
Найти периметр треугольника, вершинами
которого служат основания высот,
проведенных из вершин M1
M2 M3
к противоположным сторонам.
в)
Найти периметр треугольника, вершинами
которого служат основания биссектрис,
проведенных из вершин M1
M2 M3
к противоположным сторонам.
Решение.
а)
Построение:
К, Е,
F – середины соответствующих
сторон М1М3, М1М2,
М2М3.
F
E
K
M1
M2
M3
К –
середина М1М3, тогда координаты
середины стороны будут:
Тогда К(0;1).
Е –
середина М1М2, тогда координаты
середины стороны будут:
тогда Е(-0,5; 2,5).
F
– середина М2М3, тогда
координаты середины стороны будут:
.
тогда
F(2,5; 3,5).
KF=
Аналогично: EF=;
EK=.
Тогда периметр
треугольника будет:
б)
M1
M2
M3=N=M
K

М1 ?
Покажем,
что треугольник прямоугольный и его
три высоты не могут составить замкнутую
фигуру.
Найдем
уравнение стороны М1М2:
откуда имеем
5x+15=5y;
y=x+3. Хорошо
видно, что угловой коэффициент этой
прямой k1=1, а
т. к. высота М3К перпендикулярна
стороне М1М2, то k2
Используя уравнение прямой через точку:
у-y1=k(x-x1)
имеем
M3K:
y-2=-1(x-3),
y-2=-x+3
откуда получаем y+x-5=0.
Уравнение
пучка прямых:
.
2y=8,
y=4,
то x=1, тогда М3КМ1М2=К(1;4).
Найдем
уравнение стороны М2М3:
.
-3x+6=y-5,
y=-3x+11, откуда
видно что угловой коэффициент этой
прямой k1=-3,
т. к. М1N
перпендикуляреныМ2М3, k2
тогда уравнение стороны М2М3
будет
,
3y-x-3=0
Уравнение
пучка прямых:
.
у=11-3x,
33-9x-x-3=0.
x=3 y=2, то
x=3,
тогда
М1NМ2М3=N(3;2).
Найдем
уравнение стороны М1М3:
.
2x+6=6y,
3x-x-3=0,
y=x+1,
k1=,
то k2
т. к. М2M перпендикулярна
М1М3, k2=.
Найдем уравнение
стороны М1N:
y-5=-3(x-2),
y-5=-3x+6,
y+3x-11=0.
Уравнение
пучка прямых:
.
y=2,
то x=3,
тогда М2MМ1М3=N(3;2).
Имеем:
KN=;
КM=;
NM=0; т.е. мы доказали, что
ΔКNM не существует
в)Построение:
М1А, М2В и М3С –
биссектрисы углов при вершинах М1М2
М3
A
C
B
M3
M2
M1
Найти
периметр треугольника АВС
1)
.
(у-х-3)=3у-х-3;
у-
х-3
=3у-х-3;
у(-3)+х(-
+1)+(3-3
)=0
– уравнение биссектрисы
2)
.
(у-х-3)=у+3х+11;
у-
х-3
=у+3х+11;
у(-1)+х(-
-3)+(-3
+11)=0
– уравнение биссектрисы
3)
.
3у-х-3=у+3х-11;
2у-4х+8=0 – уравнение
биссектрисы
Найдем основания биссектрис, как точки
пересечения сторон треугольника и с
ответствующей биссектрисы :
1)
=-4
;
=-20
+20;
=
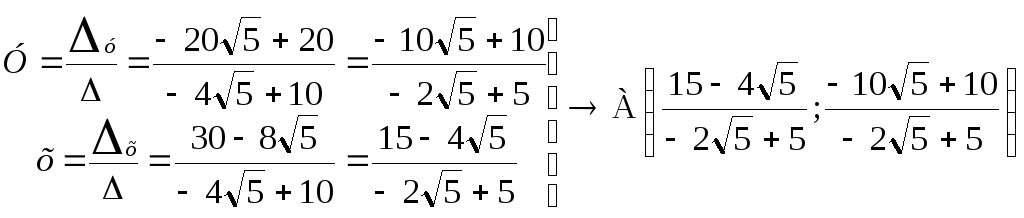
2)
;
;
.
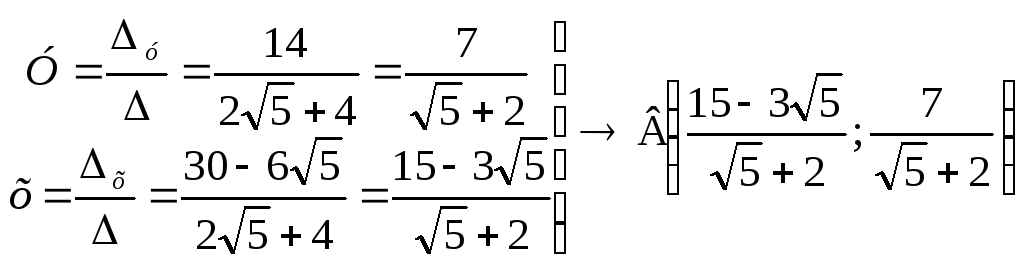
3)
.
у =10,
х=7 Следовательно С(7,0)
Найдем
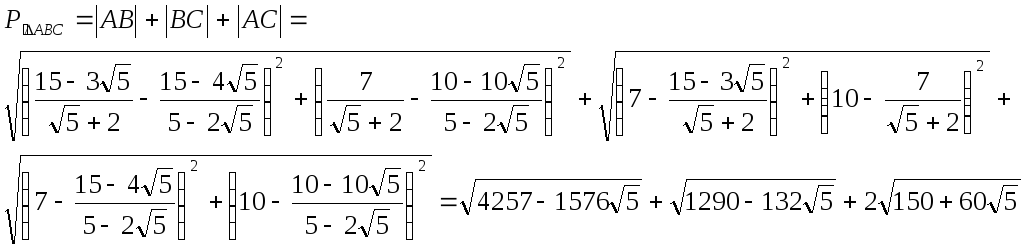
Задача №4
Даны вершины равнобедренного треугольника
а)Доказать, что середины сторон
равнобедренного треугольника являются
также вершинами равнобедренного
треугольника.
б) Доказать, что биссектриса, проведенная
из вершины при основании равны.
в) Медианы, проведенные из вершин при
основании равны.
а)Дано: ΔАВС
Доказать, что середины сторон
равнобедренного треугольника являются
также вершинами равнобедренного
треугольника.
Доказательство.
Найдем середины сторон треугольника
1) Найдём середину отрезка A
А(2;
2)
2) Найдём середину отрезка B
В(4;0)
3) Найдём середину отрезка C(
С(2;0)
4)
АС=CB
треугольник
АВС – равнобедренный, что и
требовалось доказать
б)Дано:
Доказать, что биссектриса, проведенная
из вершины при основании равны.
Доказательство.
1)
Найдём каноническое уравнение 2-ух точек
M3, M1
4-x=y+2,
x+y-2=0
x-4=0
Найдём каноническое уравнение 2-ух точек
y+x-3=
у+(1-
у=2,
y-2=0
.
Составим систему уравнения из
K
Найдем длину.
2) Найдём каноническое уравнение 2-ух
точек
у
Составим систему уравнения из
Найдем длину
что и требовалось доказать
в)Дано: ΔАВС и
оказать,
что медианы, проведенные из вершин при
основании равны.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Лучший ответ
|
|
 |
|
Как найти вершину треугольника?
Для того чтобы найти координаты вершины равностороннего треугольника, если известны координаты двух других его вершин, нужно воспользоваться одним из предложенных способов.
1 способ (графический)
- В системе координат отмечаем две заданные вершины.
- Ставим ножку циркуля в одну из построенных точек.
- Проводим окружность с радиусом, равным расстоянию между отмеченными вершинами.
- Таким же образом чертим вторую окружность с тем же радиусом, но из второй отмеченной точки.
- Точки пересечения проведённых окружностей определяют вершины треугольников (их получится два).
- Определяем координаты полученных точек, исходя из полученного чертежа.
Данный способ позволяет точно построить третью вершину. Однако определение координат является приблизительным. Метод хорошо использовать для иллюстрации.
2 способ (аналитический)
Решение задачи основано на применении формулы нахождения расстояния между двумя точками: d(A(x1;y1);B(x2;y2))=√((x2-x1)^2+(y2-y1)^2)
- Пусть имеются вершины A(x1;y1) и B(x2;y2) треугольника АВС. Обозначим координаты третьей вершины x и y (то есть, С(x;y))
- Составляем соотношения
AC=√((x-x1)^2+(y-y1)^2)
BC=√((x-x2)^2+(y-y2)^2)
AB=√((x2-x1)^2+(y2-y1)^2) - Учитывая, что треугольник равносторонний, составляем систему уравнений:
AC=BC
AC=AB
Или система уравнений:
√((x-x1)^2+(y-y1)^2)= √((x-x2)^2+(y-y2)^2)
√((x-x1)^2+(y-y1)^2)= √((x2-x1)^2+(y2-y1)^2) - Методом подстановки решаем полученную систему.
Теперь вы знаете, как найти вершину треугольника.
Внимание! Оба случая применимы только для равностороннего треугольника.
Для равнобедренного или любого другого произвольного треугольника для нахождения координат третьей вершины требуются дополнительные данные (например, значение некоторых отрезков или углов).
Уравнение описанной окружности
Как составить уравнение описанной около треугольника окружности по координатам его вершин? Как найти координаты центра описанной окружности? Как найти радиус описанной окружности, зная координаты вершин треугольника?
Решение всех этих задач сводится к одной — написать уравнение окружности, проходящей через три данные точки. Для этого достаточно подставить координаты точек (вершин треугольника) в уравнение окружности. Получим систему из трёх уравнений с тремя неизвестными: координатами центра и радиусом окружности.
Составить уравнение описанной окружности для треугольника с вершинами в точках A(2;1), B(6;3), C(9;2).
Подставив координаты вершин треугольника в уравнение окружности
получим систему уравнений
Вычтем из первого уравнения системы второе:
Теперь из второго уравнения системы вычтем третье:
Приравняем правые части равенств b=-2a+10 и b=3a-20:
Подставим в первое уравнение системы a=6 и b=-2:
a и b — координаты центра окружности, R — её радиус. Таким образом, точка (6;-2) — центр описанной около треугольника ABC окружности, радиус R=5, а уравнение описанной окружности
Для решения аналогичной задачи для четырёхугольника либо многоугольника достаточно знать координаты трёх его вершин.
Прямая на плоскости
Построение графика функции методом дифференциального исчисления
Экстремум функции двух переменных
Пример . В задачах даны координаты точек A , B , C . Требуется: 1) записать векторы AB и AC в системе орт и найти модули этих векторов; 2) найти угол между векторами AB и AC .
Решение.
1) Координаты векторов в системе орт. Координаты векторов находим по формуле:
X=xj-xi; Y=yj-yi
здесь X , Y координаты вектора; xi , yi — координаты точки Аi ; xj , yj — координаты точки Аj
Например, для вектора AB: X=x2-x1=12-7=5 ; Y=y2-y1=-1-(-4)=3
AB(5;3), AC(3;5), BC(-2;2)
2) Длина сторон треугольника. Длина вектора a(X;Y) выражается через его координаты формулой:
3) Угол между прямыми. Угол между векторами a1(X1;Y1) , a2(X2;Y2) можно найти по формуле:
где a1a2=X1X2+Y1Y2
Найдем угол между сторонами AB и AC
γ = arccos(0.88) = 28.07 0
8) Уравнение прямой. Прямая, проходящая через точки A1(x1; y1) и A2(x2; y2) , представляется уравнениями:
Уравнение прямой AB . Каноническое уравнение прямой: 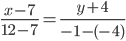
y= 3 /5x- 41 /5 или 5y-3x+41=0
Примеры решений по аналитической геометрии на плоскости
В этом разделе вы найдете бесплатные примеры решений задач по аналитической геометрии на плоскости об исследовании треугольника (заданного вершинами или сторонами): уравнения сторон, углы, площадь, уравнения и длины высот, медиан, биссектрис и т.п.
Другие решения по аналитической геометрии на плоскости
Лучшее спасибо – порекомендовать эту страницу
Решения задач о треугольнике онлайн
Задача 1. Даны вершины треугольника $A (-2, 1), B (3, 3), С (1, 0)$. Найти:
а) длину стороны $AB$;
б) уравнение медианы $BM$;
в) $cos$ угла $BCA$;
г) уравнение высоты $CD$;
д) длину высоты $СD$;
е) площадь треугольника $АВС$.
Задача 2. Найти длину высоты $AD$ в треугольнике с вершинами $A(3,2), B(2,-5), C(-6,-1)$ и написать уравнение перпендикуляра, опущенного из точки $C$ на прямую $AB$.
Задача 3. Даны вершины $A(1,1), B(7,5), C(4,5)$ треугольника. Найти:
1) длину стороны $AB$;
2) внутренний угол $A$ в радианах с точностью до 0,01;
3) уравнение высоты, проведенной через вершину $C$;
4) уравнение медианы, проведенной через вершину $C$;
5) точку пересечения высот треугольника;
6) длину высоты, опущенной из вершины $C$;
7) систему линейных неравенств, определяющую внутреннюю область треугольника.
Сделать чертеж.
Задача 4. Даны уравнения двух сторон треугольника $4x-5y+9=0$ и $x+4y-3=0$. Найти уравнение третьей стороны, если известно, что медианы этого треугольника пересекаются в точке $P(3,1)$.
Задача 5. Даны две вершины $A(-3,3)$, $B(5,-1)$ и точка $D(4,3)$ пересечения высот треугольника. Составить уравнения его сторон.
Задача 6. Найти углы и площадь треугольника, образованного прямыми $у = 2х$, $y = -2х$ и $у = х + 6$.
Задача 7. Найти точку пересечения медиан и точку пересечения высот треугольника: $А(0, – 4)$, $В(3, 0)$ и $С(0, 6)$.
Задача 8. Вычислить координаты точек середины отрезков, являющихся медианами треугольника $ABC$, если $A(-6;1)$, $B(4;3)$, $C(10;8)$.
Не получаются задачи? Решим быстро и подробно!

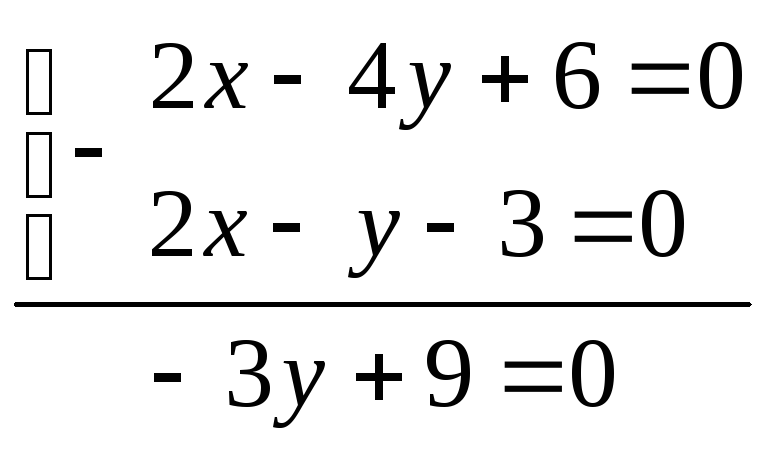








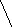




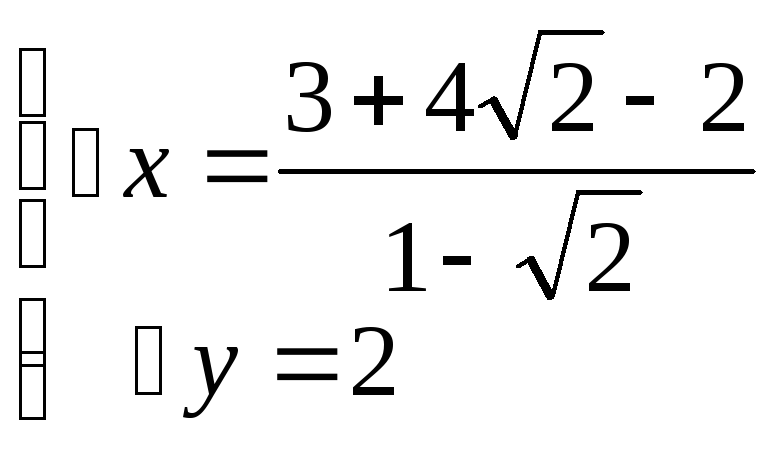
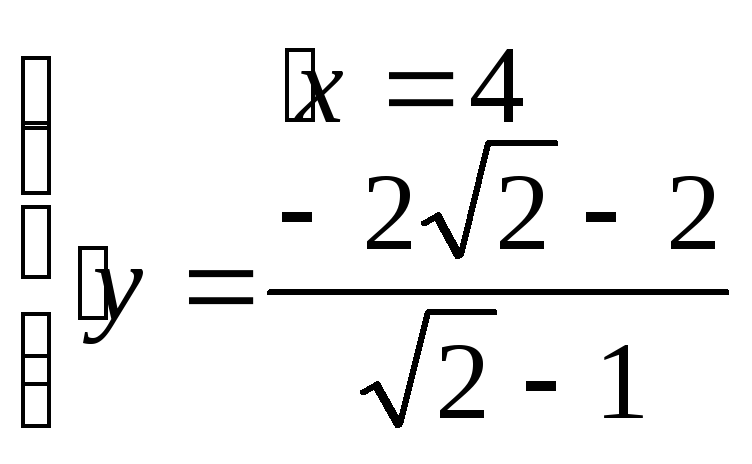




![[ left{ begin{array}{l} (2 - a)^2 + (1 - b)^2 = R^2 , \ (6 - a)^2 + (3 - b)^2 = R^2 , \ (9 - a)^2 + (2 - b)^2 = R^2 . \ end{array} right. ]](https://www.treugolniki.ru/wp-content/ql-cache/quicklatex.com-82dd95fa041ab9c8ca35f00eaea5d2ba_l3.png)