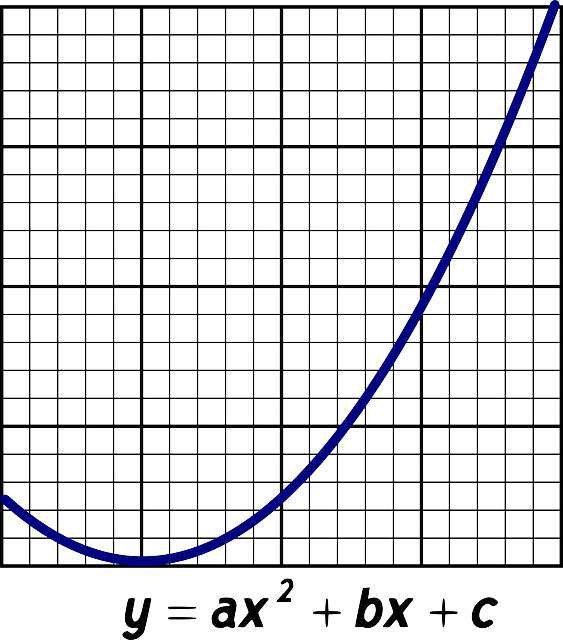
Парабола – это функция, заданная уравнением:
Её график имеет следующий вид:
Причем, в зависимости от знака коэффициента
, ветви параболы направлены вверх (если
) или вниз (если
).
В школьном курсе алгебры возникает задача нахождения
координат вершины параболы.
Их можно найти по формулам:
Вершина параболы, отмечена оранжевой точкой на приведённом выше графике.
Наш онлайн калькулятор позволяет найти координаты вершины параболы с описанием подробного хода решения на русском языке. Для работы калькулятора, необходимо ввести уравнение параболы и указать её переменную. Уравнение параболы можно вводить в различных форматах, а коэффициентами могут быть не только числа или дроби, но и параметры. Нажмите на кнопку “Примеры”, расположенную на панели калькулятора, чтобы посмотреть различные форматы ввода.
y=x2+x+
Правила ввода
Если вы хотите ввести неполную квадратичную параболу y=ax², y=ax²+bx или y=ax²+c вам нужно вместо соответствующих коэффициентов вписать 0. Если поля останутся пустыми программа впишет 1.
Вводить можно целые(1, 2, 3, -7), десятичные(0.25, -1.15), дробные(-1/8, 32/9). Если необходимо ввести смешанное число, то нужно перед вводом перевести его в неправильную обыкновенную дробь. Т.е. 1 целая 1/2 вводить нужно будет как 3/2.
Формулы вычисления координат вершины параболы
Графиком квадратичной функции является парабола
[large y=ax^2+bx+c, ane0]
[large x_0=-frac{b}{2a}]
[large y_0=frac{4ac-b^2}{4a}]
Вывод формул вычисления координат вершины параболы
Для того, чтобы вывести формулу вершины параболы необходимо из квадратного трёхчлена выделить полный квадрат по формуле
[large (a+b)^2=a^2+2ab+b^2]
Возьмём формулу квадратного трёхчлена
[large y=ax^2+bx+c, ane0]
Вынесем коэффициент a за скобку
[large y=a(x^2+frac{b}{a}x)+c]
Прибавим и вычтем второе слагаемое квадрата суммы
[large y=aBig(x^2+2frac{b}{2a}x+Big(frac{b}{2a}Big)^2-Big(frac{b}{2a}Big)^2Big)+c]
Выделим квадрат суммы
[large y=aBig(x+frac{b}{2a}Big)^2 + frac{4ac-b^2}{4a}]
По сути у нас получается функция вида (y=a(x+l)^2+m) которая отличается от функции (y=ax^2) смещением по оси абцисс на (-l), а по оси ординат на m
[large l=x_0=-frac{b}{2a}]
[large m=y_0=frac{4ac-b^2}{4a}]
Способы вычисления координат вершины параболы
1) Если дискриминант равен 0 то уравнение будет иметь один корень. Другими словами вершина параболы будет лежать на оси абцисс. Соответственно корень уравнения и будет координатой вершины параболы. Координату по оси ординат можно будет найти подставив найденный корень в уравнение.
Разберём пример
Найдём координаты вершины параболы x²+2x+1=y
D=2²-4×1×1=0
x=(-2)/(2×1)=-1
Подставим в наше уравнение -1
y=(-1)²+2×(-1)+1=0
Соответственно координаты вершины параболы будут в точке (-1, 0)
2) Если дискриминант больше 0 то уравнение имеет 2 корня. Парабола симметрична относительно вертикали проходящей через её вершину. Соответственно координата x0 равна среднему арифметическому его корней т.е x0=(x1+x2)/2.
Разберём пример
Найдём координаты вершины параболы 2x²+3x-5=y
D=3²-4×2×(-5)=49
x1=(-3+7)/(2×2)=1
x2=(-3-7)/(2×2)=-2.5
x0=(1+(-2.5))/2=-0.75
Подставим в наше уравнение -0.75
y=2×(-0.75)²+3×(-0.75)-5=-6.125
Соответственно координаты вершины параболы будут в точке (-0.75, -6.125)
3) Если квадратный трёхчлен привести к виду y=a(x+l)²+m то координаты вершины параболы будут в точке (-l,m)
Разберём пример
Найдём координаты вершины параболы y=2x²-20x+54
Вынесем 2 за скобку
y=2(x²-10x)+54
Прибавим и отнимем 25
y=2(x²-10x+25-25)+54
y=2(x²-2×5x+5²-25)+54
y=2((x-5)²-25)+54
y=2(x-5)²-50+54
y=2(x-5)²+4
Соответственно координаты вершины параболы будут в точке (5, 4)
| bold{mathrm{Basic}} | bold{alphabetagamma} | bold{mathrm{ABGamma}} | bold{sincos} | bold{gedivrightarrow} | bold{overline{x}spacemathbb{C}forall} | bold{sumspaceintspaceproduct} | bold{begin{pmatrix}square&square\square&squareend{pmatrix}} | bold{H_{2}O} | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Подпишитесь, чтобы подтвердить свой ответ
Подписаться
Войдите, чтобы сохранять заметки
Войти
Номер Строки
Примеры
-
вершина:(y-2)=3(x-5)^2
-
вершина:3x^2+2x+5y-6=0
-
вершина:x=y^2
-
вершина:(y-3)^2=8(x-5)
-
вершина:(x+3)^2=-20(y-1)
- Показать больше
Описание
Пошаговый расчет вершины параболы по заданному уравнению
parabola-vertex-calculator
ru
Блог-сообщения, имеющие отношение к Symbolab
Practice Makes Perfect
Learning math takes practice, lots of practice. Just like running, it takes practice and dedication. If you want…
Read More
Введите Задачу
Сохранить в блокнот!
Войти
Калькулятор онлайн.
Построение графика квадратичной функции.
Если вам нужно просто построить график любой функции, то для этого у нас есть отдельная программа.
Эта математическая программа для построения графика квадратичной функции сначала делает преобразование вида
( y=ax^2+cx+b ;; rightarrow ;; y=a(x+p)^2+q )
а затем последовательно строит графики функций:
$$ y=ax^2 $$
$$ y=a(x+p)^2+q $$
Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и
экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре.
А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее
сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным
решением.
Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень
образования в области решаемых задач повышается.
Если вы не знакомы с правилами ввода квадратного многочлена, рекомендуем с ними ознакомиться.
Правила ввода квадратного многочлена
В качестве переменной может выступать любая латинсая буква.
Например: ( x, y, z, a, b, c, o, p, q ) и т.д.
Числа можно вводить целые или дробные.
Причём, дробные числа можно вводить не только в виде десятичной, но и в виде обыкновенной дроби.
Правила ввода десятичных дробей.
В десятичных дробях дробная часть от целой может отделяться как точкой так и запятой.
Например, можно вводить десятичные дроби так: 2.5x – 3,5x^2
Правила ввода обыкновенных дробей.
В качестве числителя, знаменателя и целой части дроби может выступать только целое число.
Знаменатель не может быть отрицательным.
При вводе числовой дроби числитель отделяется от знаменателя знаком деления: /
Целая часть отделяется от дроби знаком амперсанд: &
Ввод: 3&1/3 – 5&6/5x +1/7x^2
Результат: ( 3frac{1}{3} – 5frac{6}{5} x + frac{1}{7}x^2 )
При вводе выражения можно использовать скобки. В этом случае при решении введённое выражение сначала упрощается.
Например: 1/2(x-1)(x+1)-(5x-10&1/2)
Наши игры, головоломки, эмуляторы:
Немного теории.
Построение графика квадратичной функции
Теорема
Любую квадратичную функцию у = ax2 + bx + c с помощью выделения полного квадрата можно записать в виде
$$ y = a left( x+frac{b}{2a} right)^2 – frac{b^2-4ac}{4a}, $$
т.е. в виде ( y=a(x-x_0)^2 +y_0), где ( x_0=-frac{b}{2a}, quad y_0=-frac{b^2-4ac}{4a} )
Теорема
Графиком функции ( y=a(x-x_0)^2+y_0 ) является парабола, получаемая сдвигом параболы ( y=ax^2):
вдоль оси абсцисс вправо на x0, если х0 > 0, влево на |х0|, если х0 < 0;
вдоль оси ординат вверх на y0, если y0 > 0, вниз на |y0|, если y0<0.
Таким образом, графиком функции у = ax2 + bx + c является парабола, получаемая сдвигом параболы у = ax2 вдоль
координатных осей. Равенство у = ax2 + bx + c называют уравнением параболы.
Координаты (x0; y0) вершины параболы у = ax2 + bx + c можно найти по формулам
$$ x_0=-frac{b}{2a}, quad y_0=ax_0^2+bx_0+c $$
Ось симметрии параболы у = ax2 + bx + c – прямая, параллельная оси ординат и проходящая через вершину параболы.
Ветви параболы у = ax2 + bx + c направлены вверх, если a>0, и направлены вниз, если a<0.
Инструкции:
Используйте этот калькулятор для выражения квадратичной функции, представленной в виде вершины. Пожалуйста, введите правильное квадратичное выражение в x в поле формы ниже.
Подробнее об этом вершинном калькуляторе
Этот калькулятор позволит вам получить квадратичную функцию, которую вы вводите в
Вершинная форма
, показывая все шаги. Вам необходимо предоставить действительное квадратное выражение в x. Любая допустимая квадратичная функция будет работать.
Например, вы можете предоставить что-то вроде x^2 + 3x + 4, или, возможно, вы можете предоставить выражение, которое не упрощается, например, x^2 + 3x – 1/2 x + 3x^2 – 3.
Как только вы зададите действительную квадратичную функцию, просто нажмите кнопку “Вычислить”, и вам будет показано вычисление вершинной формы со всеми шагами, предусмотренными этим
Калькулятор параболы
.
Каждая квадратичная функция, которая достоверно определена, имеет форму вершины, из которой можно непосредственно получить координаты вершины, а также то, открывается ли парабола “вверх” или “вниз”.
Как найти форму вершины параболы?
Все квадратичные функции графически изображаются параболой. Эта парабола будет раскрываться вверх или вниз в зависимости от знака ведущего коэффициента.
В конечном итоге, получение параболы в виде вершины сводится к нахождению вершины квадратичной функции, что достигается следующим образом
Завершение квадрата
.
Каковы этапы вычисления вершинной формы?
Так,
как найти форму вершины
? Вы можете выполнить следующие действия:
- Шаг 1: Определите квадратичную функцию. Выражение должно иметь степень 2, а ведущий коэффициент умножения x² должен быть отличен от нуля
- Шаг 2: Если ведущий коэффициент, умножающий x², положительный, парабола раскрывается вверх, а если отрицательный – вниз
- Шаг 3: Заполните квадраты, обратите внимание на член в скобках с x, так как он определяет x-координату вершины
- Шаг 4: После заполнения квадратов, константа вне скобок (она может быть нулевой) соответствует y-координате вершины
Таким образом, мы видим, что общий процесс вычисления формы вершины тесно связан с процессом заполнения квадратов.
Существует ли формула вершины?
Собственно говоря, да, есть. Обычно завершение процесса квадратов — это долгий путь. Предположим, у вас есть
квадратичная функция
, выраженный:
[ f(x) = a x^2 + b x + c]
Итак, у вас уже есть упрощенная квадратичная функция. Координата x вершины вычисляется по следующей формуле:
[ x_v = displaystyle frac{-b}{2a} ]
Очень просто, правда? Да. Но как тогда получить координату y вершины? Вы берете значение (x_v) и подставляете его в квадратичную функцию. Итак, мы получаем
[ y_v = f(x_v) = a x_v^2 + b x_v + c ]
Естественно, эта формула может быть намного быстрее, чем процесс заполнения квадратов, но каждый метод имеет свое применение, и обстоятельства конкретной задачи подскажут вам, какую форму использовать. .
Квадратичная форма к вершинной?
Почему вы хотите перейти от квадратичной формы к вершинной? Есть много причин: с геометрической точки зрения, вершинная форма позволяет рассматривать данную квадратичную функцию как перевод и масштабирование элементарной параболы, где перевод определяется вершиной, а масштабирование – ведущим коэффициентом.
Расчет может быть трудоемким, но это
Калькулятор параболы
сделает всю работу за вас.
Стандартная форма вершины?
Обычно с этим возникает некоторая путаница. Поясню, вершинная форма — это другое название стандартной формы. Итак, стандартная форма квадратичной функции (y = a(x-h)^2 + k) совпадает с формой вершины.
Путаница возникает из-за того, что иногда люди используют общую форму квадратичного числа, когда ссылаются на стандартную форму. Общая форма – (y = ax^2 + bx + c).
Таким образом, вопрос, который имеет смысл, заключается в том, как перейти от общей формы к вершинной форме, что равносильно вопросу о том, как перейти от общей формы к стандартной форме. Ответ прост: начните с общей формы, а затем
Заполните квадраты
чтобы получить стандартную форму.
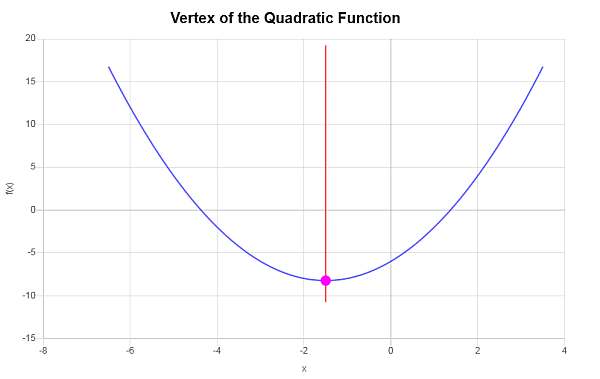
Пример: как найти форму вершины
Найдите вершину следующего квадратного выражения (f(x) = x^2 + 3x – 6), используя формулу вершины
Отвечать:
Нам нужно найти форму вершины квадратичной функции (displaystyle f(x)=x^2+3x-6).
Сначала мы вычисляем координаты вершины параболы, связанной с данной квадратичной функцией.
Для квадратичной функции вида (f(x) = a x^2 + bx + c) координата x вершины вычисляется по следующей формуле:
[x_V = displaystyle -frac{b}{2a}]
В этом случае мы имеем, что функция, для которой нам нужно найти вершину, является (f(x) = displaystyle x^2+3x-6), что подразумевает, что соответствующие коэффициенты равны:
[a = 1]
[b = 3]
[c = -6]
Подставляя известные значения (a) и (b) в формулу координаты x вершины, получаем:
[x_V = displaystyle -frac{b}{2a} = displaystyle -frac{3}{2 cdot 1} = -frac{3}{2}]
Теперь нам нужно подставить значение (x_V = displaystyle -frac{3}{2}) в квадратичную функцию, так что мы получим:
[y_V = f(x_V)]
[ = 1cdot left(-frac{3}{2}right)^2+3cdot left(-frac{3}{2}right)-6=1cdotfrac{9}{4}+3cdot left(-frac{3}{2}right)-6=frac{9}{4}+3cdot left(-frac{3}{2}right)-6=frac{9}{4}-frac{9}{2}-6=-frac{33}{4}]
Следовательно, координата x вершины равна (x_V = displaystyle -frac{3}{2}), а координата y вершины равна (y_V = displaystyle -frac{33}{4}). Это указывает на то, что точкой, представляющей вершину, является ( displaystyle left(-frac{3}{2}, -frac{33}{4}right)).
Графически получается следующее:
Нам нужно заполнить квадрат квадратного выражения (displaystyle x^2+6x-2).
Для завершения квадрата необходимо выполнить следующие шаги:
Шаг 1:
В этом случае, поскольку ведущая константа, член, который умножает (x^2) в данном многочлене, равен (a = 1), поэтому мы не должны его выносить на множитель.
Шаг 2:
Мы добавим “2” перед членом (x), заметив, что член порядка 1 в данном квадратном выражении можно переписать: (displaystyle 6 x = 2 cdot left(3right) x), тогда мы получим [ x^2+6x-2 = x^2+2 cdot left(3right) x-2 ]
Шаг 3:
Член, умножающий на 2, в данном случае — это (displaystyle 3), поэтому, чтобы использовать биномиальное уравнение, нам нужно, чтобы его квадрат (displaystyle left(3right)^2) присутствовал в выражении.
Чтобы добиться этого, мы теперь добавляем и вычитаем член (displaystyle left(3right)^2 = 9), чтобы завершить квадрат. Добавление и вычитание одного и того же члена аналогично добавлению нуля, поэтому это не влияет на выражение: [ begin{array}{ccl} displaystyle x^2+6x-2 & = & displaystyle x^2+2 cdot left(3right) x-2 \\ \\ & = & displaystyle x^2+2 cdot left(3right) x-2+9-9 end{array}]
Шаг 4:
Завершаем квадрат и упрощаем константы: [ begin{array}{ccl} x^2+6x-2 & = & displaystyle x^2+2 cdot left(3right) x-2 \\ \\ & = & displaystyle x^2+2 cdot left(3right) x-2+9-9 \\ \\ & = & displaystyle x^2+2 cdot left(3right) x+9-2-9 \\ \\ & = & displaystyle left[x^2+2 cdot left(3right) x+left(3right)^2right]-2-9 \\ \\ & = & displaystyle left( x+3 right)^2-11 end{array}]
Заключение:
Следовательно, мы находим, что функция в вершинной форме имеет вид (displaystyle f(x) = left( x+3 right)^2-11), что завершает расчет.
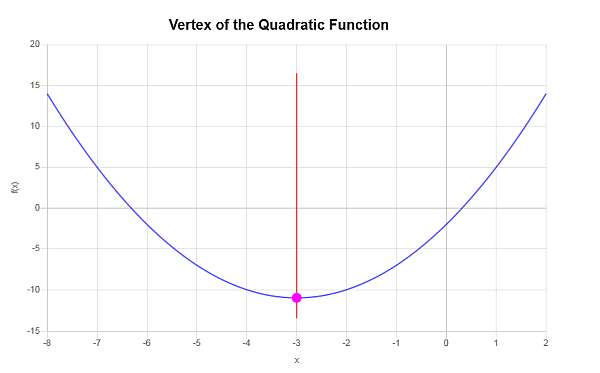
Пример: приведение квадратичной формы к вершинной
Преобразуйте следующую квадратичную форму (f(x) = x^2 + 6x – 2) в вершинную форму. Каковы координаты вершины? Парабола направлена вверх или вниз?
Решение:
Нам нужно найти форму вершины квадратичной функции (displaystyle f(x)=x^2+6x-2).
Сначала мы вычисляем координаты вершины параболы, связанной с данной квадратичной функцией.
Для квадратичной функции вида (f(x) = a x^2 + bx + c) координата x вершины вычисляется по следующей формуле:
[x_V = displaystyle -frac{b}{2a}]
В этом случае мы имеем, что функция, для которой нам нужно найти вершину, является (f(x) = displaystyle x^2+6x-2), что подразумевает, что соответствующие коэффициенты равны:
[a = 1] [b = 6] [c = -2]
Подставляя известные значения (a) и (b) в формулу координаты x вершины, получаем:
[x_V = displaystyle -frac{b}{2a} = displaystyle -frac{6}{2 cdot 1} = -3]
Теперь нам нужно подставить значение (x_V = displaystyle -3) в квадратичную функцию, так что мы получим:
[y_V = f(x_V)] [ = 1cdot left(-3right)^2+6cdot left(-3right)-2=1cdot left(-3right)^2+6cdot left(-3right)-2=-3^2+6cdot left(-3right)-2=9-18-2=-11]
Следовательно, координата x вершины равна (x_V = displaystyle -3), а координата y вершины равна (y_V = displaystyle -11). Это указывает на то, что точкой, представляющей вершину, является ( displaystyle left(-3, -11right)).
Нам нужно заполнить квадрат квадратного выражения (displaystyle x^2+6x-2).
Для завершения квадрата необходимо выполнить следующие шаги:
Шаг 1:
В этом случае, поскольку ведущая константа, член, который умножает (x^2) в данном многочлене, равен (a = 1), поэтому мы не должны его выносить на множитель.
Шаг 2:
Мы добавим “2” перед членом (x), заметив, что член порядка 1 в данном квадратном выражении можно переписать: (displaystyle 6 x = 2 cdot left(3right) x), тогда мы получим [ x^2+6x-2 = x^2+2 cdot left(3right) x-2 ]
Шаг 3:
Член, умножающий на 2, в данном случае — это (displaystyle 3), поэтому, чтобы использовать биномиальное уравнение, нам нужно, чтобы его квадрат (displaystyle left(3right)^2) присутствовал в выражении.
Чтобы добиться этого, мы теперь добавляем и вычитаем член (displaystyle left(3right)^2 = 9), чтобы завершить квадрат. Добавление и вычитание одного и того же члена аналогично добавлению нуля, поэтому это не влияет на выражение: [ begin{array}{ccl} displaystyle x^2+6x-2 & = & displaystyle x^2+2 cdot left(3right) x-2 \\ \\ & = & displaystyle x^2+2 cdot left(3right) x-2+9-9 end{array}]
Шаг 4:
Завершаем квадрат и упрощаем константы: [ begin{array}{ccl} x^2+6x-2 & = & displaystyle x^2+2 cdot left(3right) x-2 \\ \\ & = & displaystyle x^2+2 cdot left(3right) x-2+9-9 \\ \\ & = & displaystyle x^2+2 cdot left(3right) x+9-2-9 \\ \\ & = & displaystyle left[x^2+2 cdot left(3right) x+left(3right)^2right]-2-9 \\ \\ & = & displaystyle left( x+3 right)^2-11 end{array}]
Заключение:
Следовательно, мы находим, что функция в вершинной форме имеет вид (displaystyle f(x) = left( x+3 right)^2-11), что завершает расчет.
Другие квадратичные калькуляторы
Большинство из
квадратичные калькуляторы
в той или иной степени зависят от процесса
квадрат
, который позволяет группировать внутри круглых скобок то, что возведено в квадрат.
Как мы видим в формуле вершины, расчет вершины тесно связан с
квадратичная формула
а также
вычисление корней квадратного уравнения
. .