Сущность метода координат, как метода решения задач состоит в том, что задавая фигуры уравнениями и выражая в координатах различной геометрические соотношения мы можем решать геометрическую задачу средствами, алгебры метод координат – это универсальный метод. Он обеспечивает тесную связь между алгеброй и геометрией которой дают богатые плоды. Какие они не могли бы дать, оставаясь разделёнными.
В некоторых случаях метод координат даёт возможность строить доказательства и решать многие задачи более рационально красиво, чем чисто геометрическими способами. Координатно- векторный способ позволяет без особого труда решить стереометрическую задачу из курса ЕГЭ профильной математики.
Вспомним теорию и ответим на вопросы – интерактивный кроссворд.
Решение задач на нахождение элементов в правильных многоугольниках.
Видеоролик: Выбор системы координат в правильных призмах и пирамидах.
Интерактивное приложение: Нахождение координат вершин в правильных призмах и пирамидах.
Задача
Веб-квест “Нахождение вершин правильных призм и пирамид”
Буду рада вам! Подписывайтесь на мои каналы!
https://www.youtube.com/channel/UCrrze24VyUrfKKfpoa9uL1Q
I. Основные формулы:
1. Расстояние между точками А (![]() ,
, ![]() ), В
), В ![]() ,
, ![]() ) равно
) равно ![]() =
=![]() .
.
2. Угол между плоскостями. Если β – угол между плоскостями, заданными уравнениями ![]() х+
х+![]() z+
z+![]() =0 и
=0 и ![]() х+
х+![]() z+
z+![]() =0, то
=0, то
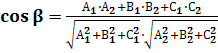 .
.
3. Расстояние от точки до плоскости. Если ρ – расстояние от точки ![]() (
(![]() ,
, ![]() ), до плоскости
), до плоскости ![]() х+
х+![]() z+D =0, то
z+D =0, то
ρ=![]() .
.
4. Уравнение плоскости, проходящей через три заданные точки ![]() (
(![]() ,
, ![]() ),
),![]() (
(![]() ,
, ![]() ),
),![]() (
(![]() ,
, ![]() ), в координатной форме:
), в координатной форме:
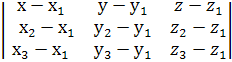 =0;
=0;
5. Если отрезок, концами которого служат точки А (![]() ,
, ![]() ), В
), В ![]() ,
, ![]() ) разделен точкой С (х, у,
) разделен точкой С (х, у,![]() ) в отношении λ, то координаты точки С определяются по формулам
) в отношении λ, то координаты точки С определяются по формулам
Х = ![]() ; у=
; у=![]() ; z=
; z=![]() .
.
II. Координаты вершин многогранников.
Определите координаты вершин многогранников:
1. Единичный куб A…D1
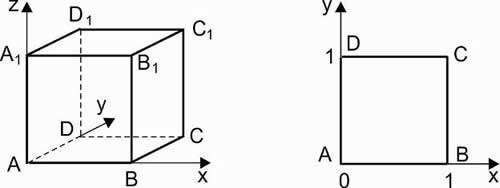
Решение: координаты вершин А (0, 0, 0), А1 (0, 0, 1), В (1, 0, 0), В1 (1, 0, 1), D (0, 1, 0), D1 (0, 1, 1), С (1, 1, 0), С1 (1, 1, 1).
2. Правильная треугольная призма A…C1 , все ребра, которой равны 1.
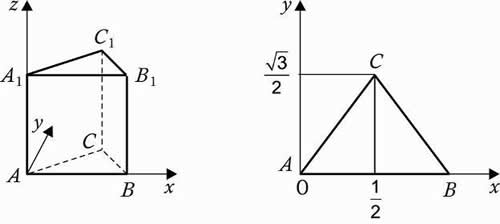
Решение: координаты вершин: А (0, 0, 0), А1 (0, 0, 1), В (1, 0, 0), В1 (1, 0, 1), С (0,5; ![]() , 0), С1 (0,5;
, 0), С1 (0,5; ![]() , 1).
, 1).
3. Правильная шестиугольная призма A…F1, все ребра которой равны 1.
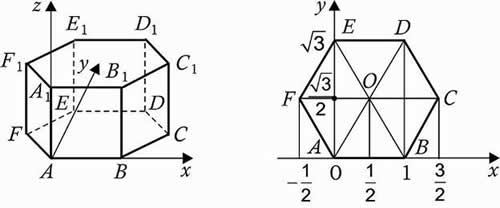
Решение: координаты вершин: А (0, 0, 0), А1 (0, 0, 1), В (1, 0, 0), В1 (1, 0, 1), С (1,5; ![]() , 0), С1 (1,5;
, 0), С1 (1,5; ![]() , 1), D (1,
, 1), D (1, ![]() (1,
(1, ![]() Е (0,
Е (0, ![]() ,
, ![]() (0,
(0, ![]() ,
,
F(-0,5 , ![]() 0),
0), ![]() (-0,5,
(-0,5, ![]() 1).
1).
4. Правильная треугольная пирамида (тетраэдр) ABCD все ребра которой равны 1.
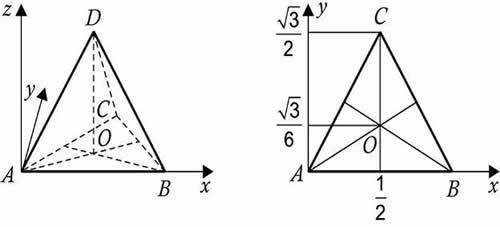
Решение: координаты вершин: А (0, 0, 0), В (1, 0, 0), С (0,5; ![]() , 0), D (0,5,
, 0), D (0,5, ![]()
5. Правильная четырехугольная пирамида SABCD, все ребра которой равны 1.
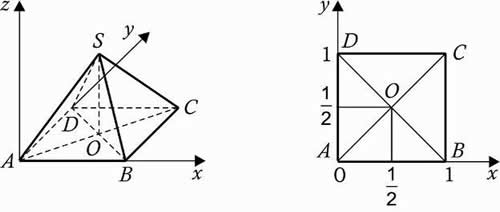
Решение: координаты вершин: А (0, 0, 0), В (1, 0, 0), С (1, 1, 0), D (0, 1, 0![]() S (0,5; 0,5;
S (0,5; 0,5; ![]() ).
).
6. Правильная шестиугольная пирамида SABCDEF, стороны основания которой равны 1, а боковые ребра равны 2.
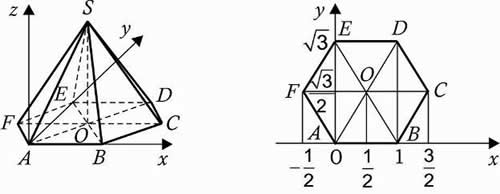
III. Решение задач.
Решение: координаты вершин: А (0, 0, 0), В (1, 0, 0), С (1,5; ![]() , 0), D (1,
, 0), D (1, ![]() Е (0,
Е (0, ![]() , F (-05,
, F (-05, ![]() 0), S (0,5;
0), S (0,5; ![]() ).
).
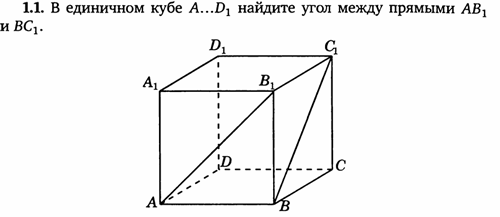
Решение:
- А (0, 0, 0), А1 (0, 0, 1), В (1, 0, 0), В1 (1, 0, 1), D (0, 1, 0), D1 (0, 1, 1), С (1, 1, 0), С1 (1, 1, 1).
- Найдем координаты векторов
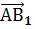 (1, 0, 1) и
(1, 0, 1) и 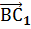 = (0, 1, 1)
= (0, 1, 1) - Найдем косинус угла между векторами
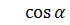 =
=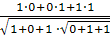 =
= ; α=60.
; α=60.
Ответ: 60.
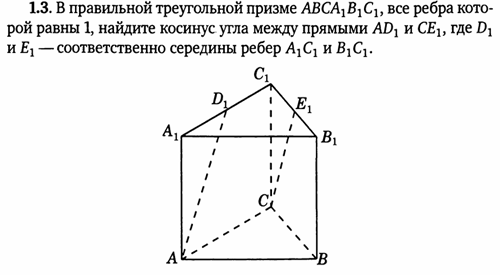
Решение:
- координаты вершин А (0, 0, 0), D1 (
 ,
, 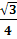 , 1), С (0,5;
, 1), С (0,5; 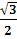 , 0), Е1 (
, 0), Е1 ( ;
; 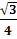 , 1).
, 1). - Найдем координаты векторов:
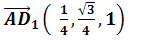 и
и 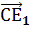 (
( ,
, 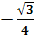 , 1)
, 1) - Найдем косинус угла между векторами
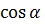 =
=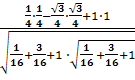 =0,7;
=0,7;
Ответ: 0,7.
Полностью текст работы приведен в Приложении.
1. Система координат в пространстве.
Выберем начало координат. Проведем три взаимно перпендикулярные оси х, y и z . Выберем масштаб.

Получилась система координат в трехмерном пространстве.
Каждая точка характеризуется тремя числами – координатами по x, y и z. Запись M(−1;
3;
2)
означает,
что координата точки M по
x (абсцисса) равна −1, координата
по y (ордината) равна 3, а координата по z (аппликата) равна 2.
Векторы в пространстве определяются так же, как и на плоскости.
Это направленные отрезки, имеющие начало и конец. Только в пространстве вектор задается тремя координатами
x, y и z:
ﺂ؟![]() (xa; ya; za)
(xa; ya; za)
Чтобы найти
координаты
вектора, так же, как и на плоскости, из
координаты конца надо вычесть координату начала.
1.![]()
![]()
2.![]()
![]()
Если точка M – середина отрезка AB,
то ее координаты находятся по формуле:
3. ![]()
![]()
![]()
4. 
 – сумма векторов.
– сумма векторов.
5. ![]() – разность векторов.
– разность векторов.
6. ![]() – произведение вектора на число.
– произведение вектора на число.
7. ![]() – скалярное произведение векторов
– скалярное произведение векторов
8.  – косинус угла между
– косинус угла между
векторами.
2. Введение системы координат.
Метод
координат – это, конечно, очень хорошо, но в настоящих задачах C2
никаких координат и векторов нет, поэтому их надо вводить.
Самое
замечательное свойство заключается в том, что не имеет никакого значения как
именно вводить систему координат. Если все вычисления будут правильными, то и
ответ будет правильным.

2.1
Координаты куба.
Система координат вводится очень просто:
1. Начало
координат – в точке A
2. Если
ребро куба не указано, то принимаем его за единичный отрезок;
3. Ось
x
направляем по ребру АВ, у – по ребру АD, а
ось z
– по ребру AA1 .
Теперь
у каждой вершины куба есть координаты:
A
(0; 0; 0), B (1; 0; 0), C
(1; 1; 0), D (0; 1; 0),
A1 (0; 0;1) B
(1; 0; 1) C1
(1; 1; 1), D1
(0; 1; 1).
2.2 Координаты
правильной треугольной призмы


A
(1; 0; 0), B![]() , C
, C
(0; 0; 0), A1 (1;
0; 1), B1 ![]() , C1 (0; 0; 1).
, C1 (0; 0; 1).
2.3
Координаты правильной шестиугольной призмы


, , , ,
, , ,
, , ,
, .
2.4 Координаты
правильной четырехугольной пирамиды

Введем
систему координат с началом в точке А
A (0; 0; 0), B (1;
0; 0), C (1; 1; 0), D (0; 1; 0), H (0,5;
0,5; 0).
Найдем
координаты точки S. Рассмотрим треугольники ASH и ABH
1. AS = AB =
1 по условию;
2. Угол AHS = AHB =
90°, поскольку SH — высота, а AH ⊥ HB как диагонали
квадрата;
3. Сторона AH — общая.
Следовательно,
прямоугольные треугольники ASH и ABH равны по одному
катету и гипотенузе. Значит, SH = BH =
0,5 · BD. Но BD — диагональ квадрата
со стороной 1. Поэтому имеем:
![]()
Итак,
координаты точки S:

 Рассмотрим
Рассмотрим
случай, если боковые ребра пирамиды не равны ребрам основания.
В этом случае рассмотрим треугольник AHS:
Треугольник AHS — прямоугольный,
причем гипотенуза AS — это одновременно и боковое
ребро исходной пирамиды SABCD. Катет: AH =
0,5 · AC. Оставшийся катет SH найдем по теореме
Пифагора. Это и будет координата z для
точки S.
3. Матрицы и
определители второго и третьего порядка.
Определение:
Таблица, составленная из четырёх чисел ![]() называется
называется
квадратной матрицей второго порядка. Числа ![]() называют
называют
элементами матрицы.
Определение:
Число ∆ называется определителем или детерминантом матрицы.
∆=
Определитель третьего порядка можно вычислить так:

4. Метод
координат в пространстве
4.1 Угол
между прямыми.
Вычисление
направляющих векторов для прямых.
В задаче С2
прямые всегда задаются парой точек. Если ввести систему координат и рассмотреть
вектор с началом и концом в этих точках, получим направляющий вектор для
прямой.


α-угол
между прямыми
3.1 Угол
между двумя прямыми – это угол между их направляющими векторами.
 Задача 1.
Задача 1.
В единичном
кубе ABCDA1B1C1D1
найдите угол между прямыми AE и BF, где E –
середина ребра A1B1,
где Е – середина ребра А1В1 а F –
середина ребра B1C1.
Решение
(1 способ)
K–
середина A1D1 AK║BF
угол KAE = φ
По теореме
Пифагора

По
теореме косинусов для ∆ AKE
KE² = AE²
+ AK²
– 2 * AE
*AK
* cos φ
cos φ=0,8
φ=arccos0.8
Решение
(2 способ)
С
помощью векторов и координат легко найти угол между прямыми.
 |
А
если требуется найти угол между плоскостями или между прямой и плоскостью, то
для этого нам понадобится уравнение плоскости в пространстве.
4.2
Плоскость в пространстве задается уравнением.
Ax+By+Cz+D=0,
где A,
B
и С – координаты вектора, перпендикулярного этой плоскости. Его называют
нормалью к плоскости.
Чтобы
написать уравнение плоскости, берем координаты трех принадлежащих ей точек.
Подставляем их по очереди в уравнение плоскости. Решаем полученную систему.
Напишем
уравнение плоскости, проходящей через точки M (1;
0; 1), N(2;
-2; 0) и К (4; 1; 2)
Уравнение
плоскости выглядит так:
Ax+By+Cz+D=0
Получим
систему из трех уравнений:

В ней
четыре неизвестных: A, B,
С и D.
Поэтому одну из них мы выберем сами, а другие выразим через нее. Правило –
простое вместо одной из переменных можно взять любое число, не равное нулю.
Решив систему, получим:
A=-![]() B=-
B=-![]() C=
C=![]()
Уравнение
плоскости MNK имеет вид:
![]()
Умножим
обе части уравнения на -3. Тогда коэффициенты станут целыми:
x+4y+7z+6-0
Вектор
![]() (1; 4; -7) – это нормаль к плоскости MNK.
(1; 4; -7) – это нормаль к плоскости MNK.
Если
плоскость проходит через начало координат, то D=0
(так как D≠0 не позволит получить верное числовое
равенство).
Уравнение
плоскости, проходящей, через заданную точку ![]() имеет
имеет
вид:
![]()
Уравнение плоскости можно составить и с помощью определителя третьего
порядка :
Пусть имеем точки
![]()
![]()
![]() ,
,
Тогда уравнение плоскости, проходящей через эти
три точки ,будет иметь вид:
 =0
=0
4.3
Угол между плоскостями равен углу между нормалями к
этим плоскостям:
cos φ=
![]()
При
пересечении двух плоскостей образуется четыре угла . Мы
берем меньший из них. Поэтому в формуле стоит модуль скалярного произведения –
чтобы косинус угла был неотрицателен.
Задача
2
В кубе ABCDA1B1C1D1 точки E и F с
середины ребер соответственно A1B1 и
A1D1. Найдите косинус угла между плоскостями AEF и BDD1.

Видно, что плоскости AEF и BDD1 пересекаются где-то вне куба. В классическом решении пришлось бы
строить пересечения. Но координатный метод значительно всё
упрощает. Достаточно отметить координаты нужных точек и найти
угол между нормалями
к плоскостям
AEF и BDD1.
A(0;
0; 0), C(1; 1; 0)
Сначала
– нормаль к плоскости BDD1.
Мы можем подставить координаты точек B, D
и D1 в уравнение плоскости и найти координаты
вектора нормали. А можно увидеть нужную нормаль на чертеже. Ведь плоскость BDD1 – это диагональное сечение куба. Вектор ![]() перпендикулярен этой плоскости.
перпендикулярен этой плоскости.
Итак,
первый вектор нормали у нас уже есть: ![]()
Напишем
уравнение плоскости AEF.
A![]() E
E![]() F
F![]()
Составим уравнение плоскости:


![]()
Уравнение
плоскости AEF: 2x+2y–z=0
Нормаль
к плоскости AEF: ![]() (2;
(2;
2; -1)
Найдем
угол между плоскостями: ![]()
 4.4
4.4
Угол между прямой и плоскостью
![]()

![]()
Задача
3.
В
правильной четырехугольной пирамиде SABCD, все
ребра которой равны 1, найдите угол между прямой DE, где E-середина
апофемы SF
грани ASB
грани и плоскостью ASC

![]()
![]()
![]()
![]()
![]()
![]()

![]()
OB –
вектор нормали плоскости ASC
DE –
направляющий вектор прямой
OB – ![]() – вектор нормали
– вектор нормали
плоскости ASC
DE – ![]() – вектор направляющей
– вектор направляющей
вектор прямой DE
 |
![]()
 Ответ:
Ответ:
4.5
Расстояние от точки до плоскости


Задача
4
В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1
, все рёбра которой равны 1, найдите расстояние от точки E
до прямой B1C1.

Решение
(1 способ)
1) Рассмотрим ΔCDE:
по теореме косинусов:
СЕ2 = 2СD2
– 2CD2 cos120° = 2 + 2*1/2 = 3 =>
CE = ![]()
2) Рассмотрим ΔС1СЕ: он
прямоугольный, т.к. С1С перпендикулярна плоскости нижнего основания
=> CC1
перпендикулярна СЕ.
По теореме Пифагора:
С1Е2 = (![]() )2 + 12
)2 + 12
= 4, С1Е = 2
3) Рассмотрим ΔBCE:
он прямоугольный , т.к. 120° – 60°:2 = 90° (из ΔCDE)
ВЕ2 = (![]() )2 + 12
)2 + 12
= 4, ВЕ = 2
4) Рассмотрим ΔВВ1Е: он прямоугольный,
т.к. ВВ1 перпендикулярна ВЕ,
по теореме Пифагора:
В1Е2 = В1В2
+ ВЕ2 = 4 + 1 = 5, ВЕ = ![]()
5) Рассмотрим ΔВ1С1Е:
С1Е = 2, С1В1
= 1, В1Е = ![]() , т.е. 22 + 12
, т.е. 22 + 12
= (![]() )2. Таким образом,
)2. Таким образом,
по теореме обратной теореме Пифагора, ΔВ1С1Е –
прямоугольный, угол В1С1Е = 90°
 6) Искомое расстояние от точки Е до прямой В1С1
6) Искомое расстояние от точки Е до прямой В1С1
– это длина С1Е = 2
2
способ
1)
Поместим призму в прямоугольную систему координат, расположив координатные оси,
как показано на рисунке. СС1, СВ и СЕ попарно перпендикулярны,
поэтому можно направить вдоль них координатные оси. Получаем координаты:
С1 (0;0;1),
Е (![]() ;0;0), В1 (0;1;1)
;0;0), В1 (0;1;1)
2) Найдем координаты
векторов С1В1 и С1Е:
С1В1
(0;1;0), С1Е (![]() ;0;-1).
;0;-1).
3) Найдем косинус угла
между С1В1 и С1Е, используя скалярное
произведение векторов С1В1 и С1Е:
cosβ = ![]() = 0 => β
= 0 => β
= 90° => C1E
– искомое расстояние.
4) С1Е = ![]() =2
=2
4.6 Расстояние между скрещивающимися прямыми
в пространстве — это длина их общего перпендикуляра. Общий перпендикуляр скрещивающихся прямых — отрезок с
концами на этих прямых, перпендикулярный обеим этим прямым.
Если прямые в пространстве пересекаются, расстояние между ними считается равным
0.
Пусть есть не
пересекающиеся в пространстве прямые a и b.
Построим плоскости α и β так, чтобы эти плоскости были
параллельны, плоскость α содержала в себе прямую a, плоскость β содержала в себе прямую b.
Расстоянием между прямыми a и b будет расстояние между плоскостями α и β.




СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до
Готовые ключевые этапы урока всегда будут у вас под рукой

Была в сети 17.05.2023 23:42

Медведева Ирина Викторовна
учитель математики
50 лет
![]() 4 307
4 307
![]() 8 153
8 153 ![]()
Местоположение
Россия, Калининградская область
Координаты вершин многогранников
13.10.2017 01:02

Сопровождение к уроку геометрии в 11 классе по теме “Координаты вершин многогранников”. Рекомендуется использовать при изученни координатного метода решения задач и при поготовке к ЕГЭ
Просмотр содержимого документа
«Координаты вершин многогранников»
Рекомендуем курсы ПК и ППК для учителей
Похожие файлы
Введение системы координат
30 мая 2011
Метод координат — это, конечно, очень хорошо, но в настоящих задачах C2 никаких координат и векторов нет. Поэтому их придется вводить. Да-да, вот так взять и ввести: указать начало отсчета, единичный отрезок и направление осей x, y и z.
Самое замечательное свойство этого метода заключается в том, что не имеет никакого значения, как именно вводить систему координат. Если все вычисления будут правильными, то и ответ будет правильным.
Тем не менее, приведу некоторые рекомендации, как лучше ввести систему координат для самых часто встречающихся в задаче C2 многогранников. С указанием конкретных точек. Во всех случаях упор делается на минимизацию объема вычислений.
Координаты куба
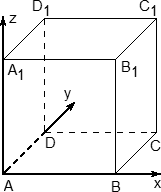
Если в задаче C2 будет куб — считайте, что вам повезло. Это самый простой многогранник, все двугранные углы которого равны 90°.
Система координат также вводится очень просто:
- Начало координат — в точке A;
- Чаще всего ребро куба не указано, поэтому принимаем его за единичный отрезок;
- Ось x направляем по ребру AB, y — по ребру AD, а ось z — по ребру AA1.
Обратите внимание: ось z направляется вверх! После двумерной системы координат это несколько непривычно, но на самом деле очень логично.
Итак, теперь у каждой вершины куба есть координаты. Соберем их в таблицу — отдельно для нижней плоскости куба:
| Точка | A | B | C | D |
| Координаты | (0; 0; 0) | (1; 0; 0) | (1; 1; 0) | (0; 1; 0) |
И для верхней:
| Точка | A1 | B1 | C1 | D1 |
| Координаты | (0; 0; 1) | (1; 0; 1) | (1; 1; 1) | (0; 1; 1) |
Несложно заметить, что точки верхней плоскости отличаются соответствующих точек нижней только координатой z. Например, B = (1; 0; 0), B1 = (1; 0; 1). Главное — не запутаться!
Координаты трехгранной призмы
Призма — это уже намного веселее. При правильном подходе достаточно знать координаты только нижнего основания — верхнее будет считаться автоматически.
В задачах C2 встречаются исключительно правильные трехгранные призмы (прямые призмы, в основании которых лежит правильный треугольник). Для них система координат вводится почти так же, как и для куба. Кстати, если кто не в курсе, куб — это тоже призма, только четырехгранная.
Итак, поехали! Вводим систему координат:
- Начало координат — в точке A;
- Сторону призмы принимаем за единичный отрезок, если иное не указано в условии задачи;
- Ось x направляем по ребру AB, z — по ребру AA1, а ось y расположим так, чтобы плоскость OXY совпадала с плоскостью основания ABC.
Здесь требуются некоторые пояснения. Дело в том, что ось y НЕ совпадает с ребром AC, как многие считают. А почему не совпадает? Подумайте сами: треугольник ABC — равносторонний, в нем все углы по 60°. А углы между осями координат должны быть по 90°, поэтому сверху картинка будет выглядеть так:

Надеюсь, теперь понятно, почему ось y не пойдет вдоль AC. Проведем в этом треугольнике высоту CH. Треугольник ACH — прямоугольный, причем AC = 1, поэтому AH = 1 · cos A = cos 60°; CH = 1 · sin A = sin 60°. Эти факты нужны для вычисления координат точки C.
Теперь взглянем на всю призму вместе с построенной системой координат:
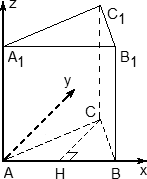
Получаем следующие координаты точек:
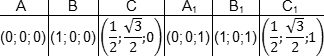
Как видим, точки верхнего основания призмы снова отличаются от соответствующих точек нижнего лишь координатой z. Основная проблема — это точки C и C1. У них есть иррациональные координаты, которые надо просто запомнить. Ну, или понять, откуда они возникают.
Координаты шестигранной призмы
Шестигранная призма — это «клонированная» трехгранная. Можно понять, как это происходит, если взглянуть на нижнее основание — обозначим его ABCDEF. Проведем дополнительные построения: отрезки AD, BE и CF. Получилось шесть треугольников, каждый из которых (например, треугольник ABO) является основанием для трехгранной призмы.
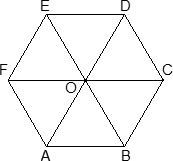
Теперь введем собственно систему координат. Начало координат — точку O — поместим в центр симметрии шестиугольника ABCDEF. Ось x пойдет вдоль FC, а ось y — через середины отрезков AB и DE. Получим такую картинку:
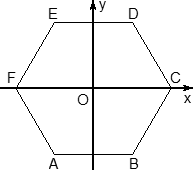
Обратите внимание: начало координат НЕ совпадает с вершиной многогранника! На самом деле, при решении настоящих задач вы обнаружите, что это очень удобно, поскольку позволяет значительно уменьшить объем вычислений.
Осталось добавить ось z. По традиции, проводим ее перпендикулярно плоскости OXY и направляем вертикально вверх. Получим итоговую картинку:
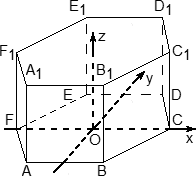
Запишем теперь координаты точек. Предположим, что все ребра нашей правильной шестигранной призмы равны 1. Итак, координаты нижнего основания:
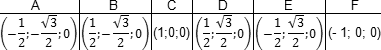
Координаты верхнего основания сдвинуты на единицу по оси z:
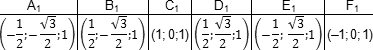
Координаты четырехугольной пирамиды
Пирамида — это вообще очень сурово. Мы разберем только самый простой случай — правильную четырехугольную пирамиду, все ребра которой равны единице. Однако в настоящих задачах C2 длины ребер могут отличаться, поэтому ниже приведена и общая схема вычисления координат.
Итак, правильная четырехугольная пирамида. Это такая же, как у Хеопса, только чуть поменьше. Обозначим ее SABCD, где S — вершина. Введем систему координат: начало в точке A, единичный отрезок AB = 1, ось x направим вдоль AB, ось y — вдоль AD, а ось z — вверх, перпендикулярно плоскости OXY. Для дальнейших вычислений нам потребуется высота SH — вот и построим ее. Получим следующую картинку:
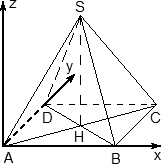
Теперь найдем координаты точек. Для начала рассмотрим плоскость OXY. Здесь все просто: в основании лежит квадрат, его координаты известны. Проблемы возникают с точкой S. Поскольку SH — высота к плоскости OXY, точки S и H отличаются лишь координатой z. Собственно, длина отрезка SH — это и есть координата z для точки S, поскольку H = (0,5; 0,5; 0).
Заметим, что треугольники ABC и ASC равны по трем сторонам (AS = CS = AB = CB = 1, а сторона AC — общая). Следовательно, SH = BH. Но BH — половина диагонали квадрата ABCD, т.е. BH = AB · sin 45°. Получаем координаты всех точек:
![]()
Вот и все с координатами пирамиды. Но не с координатами вообще. Мы рассмотрели лишь самые распространенные многогранники, однако этих примеров достаточно, чтобы самостоятельно вычислить координаты любых других фигур. Поэтому можно приступать, собственно, к методам решения конкретных задач C2.
Смотрите также:
- Четырехугольная пирамида в задаче C2

- Метод координат в пространстве

- Сложение и вычитание дробей

- Не пишите единицы измерения в задаче B12

- Как решать простейшие логарифмические уравнения

- Задача B4: транзит нефти

