Решить треугольник Онлайн по координатам
Данный онлайн-сервис вычисляет (показываются промежуточные расчёты) следующие параметры треугольника:
1) длины и уравнения сторон, медиан, средних линий, высот, серединных перпендикуляров, биссектрис;
2) система линейных неравенств, определяющих треугольник;
2) уравнения прямых, проходящих через вершины параллельно противолежащим сторонам;
3) внутренние углы по теореме косинусов;
4) площадь треугольника;
5) точка пересечения медиан (центроид) и точки пересечения медиан со сторонами;
10) параметры вписанной и описанной окружностей и их уравнения.
Внимание! Этот сервис не работает в браузере IE (Internet Explorer).
Запишите координаты вершин треугольника и нажмите кнопку.
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
Решить треугольник Онлайн по координатам
1) длины и уравнения сторон, медиан, средних линий, высот, серединных перпендикуляров, биссектрис;
2) система линейных неравенств, определяющих треугольник;
2) уравнения прямых, проходящих через вершины параллельно противолежащим сторонам;
3) внутренние углы по теореме косинусов;
4) площадь треугольника;
5) точка пересечения медиан (центроид) и точки пересечения медиан со сторонами;
10) параметры вписанной и описанной окружностей и их уравнения.
Внимание! Этот сервис не работает в браузере IE (Internet Explorer).
Запишите координаты вершин треугольника и нажмите кнопку.
//mailru,yandex,google,vkontakte,odnoklassniki,instagram,wargaming,facebook,twitter,liveid,steam,soundcloud,lastfm, // echo( ‘
Калькулятор онлайн.
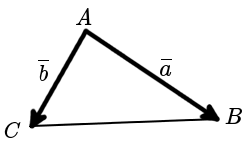
Вычисление площади треугольника построенного на векторах.
Этот калькулятор онлайн вычисляет площадь треугольника построенного на векторах. Треугольник может быть задан координатами двух векторов или координатами трех вершин треугольника.
Онлайн калькулятор для вычисления площади треугольника построенного на векторах не просто даёт ответ задачи, он приводит подробное решение с пояснениями, т.е. отображает процесс решения для того чтобы проконтролировать знания по математике и/или алгебре.
Этот калькулятор онлайн может быть полезен учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.
Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.
Если вы не знакомы с правилами ввода чисел, рекомендуем с ними ознакомиться.
Числа можно вводить целые или дробные.
Причём, дробные числа можно вводить не только в виде десятичной, но и в виде обыкновенной дроби.
Правила ввода десятичных дробей.
В десятичных дробях дробная часть от целой может отделяться как точкой так и запятой.
Например, можно вводить десятичные дроби так: 2.5 или так 1,3
Правила ввода обыкновенных дробей.
В качестве числителя, знаменателя и целой части дроби может выступать только целое число.
Знаменатель не может быть отрицательным.
При вводе числовой дроби числитель отделяется от знаменателя знаком деления: /
Ввод: -2/3
Результат: ( -frac<2> <3>)
Целая часть отделяется от дроби знаком амперсанд: &
Ввод: -1&5/7
Результат: ( -1frac<5> <7>)
[spoiler title=”источники:”]
http://ru.onlinemschool.com/math/assistance/vector/triangle_area/
http://www.math-solution.ru/math-task/vect-area-triangle
[/spoiler]
| A ( ; ), B ( ; ), C ( ; ) |
Примечание: дробные числа записывайте Округлять до -го знака после запятой. Онлайн калькулятор. Площадь треугольника построенного на векторах.Этот онлайн калькулятор позволит вам очень просто найти площадь треугольника построенного на векторах. Воспользовавшись онлайн калькулятором, вы получите детальное решение вашей задачи, которое позволит понять алгоритм решения задач на вычисление площади треугольника построенного на векторах и закрепить пройденый материал. Калькулятор для вычисления площади треугольника построенного на векторахВыберите каким образом задается треугольник: Введите значения векторов: Введите координаты точек: Инструкция использования калькулятора для вычисления площади треугольника построенного на векторахВвод данных в калькулятор для вычисления площади треугольника построенного на векторахВ онлайн калькулятор вводить можно числа или дроби. Более подробно читайте в правилах ввода чисел. Дополнительные возможности калькулятора вычисления площади треугольника построенного на векторах
Теория. Площадь треугольника построенного на векторахОпределение Площадь треугольника образованного векторами a и b равна половине модуля векторного произведения этих векторов: Вводить можно числа или дроби (-2.4, 5/7, . ). Более подробно читайте в правилах ввода чисел. Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список! Добро пожаловать на OnlineMSchool. Решение задач по математике онлайн |
Треугольник на плоскости по трем вершинам
Введите координаты трех вершин A,B,C треугольника и нажмите “Ok”. Будет построен треугольник по трем вашим точкам, вычислены длины его сторон (edge lengths), вычислена его площадь (area), его периметр (perimeter), а также углы (interor angles) и другие параметры.
2010-09-03 • Просмотров [ 8431 ]
|
Порядок вывода комментариев: Найти периметр треугольника по вершинам А(4;1;-1), В(2;-2;4), С(2;-4;3) найти вектор медианы АМ |
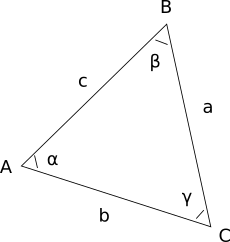
Этот онлайн калькулятор предназначен для быстрого вычисления ряда характеристик треугольника по координатам его вершин. Вы вводите координаты вершин A, B и C. Калькулятор рассчитывает по координатам следующие величины:
- длину стороны a – стороны, противолежащей вершине А
- длину стороны b – стороны, противолежащей вершине B
- длину стороны c – стороны, противолежащей вершине C
- значение угла α при вершине A
- значение угла β при вершине B
- значение угла γ при вершине C
- периметр треугольника
- площадь треугольника
Если нужно что-то еще, пишите в комментариях, добавим. Формулы расчета значений треугольника описаны под калькулятором.
Параметры треугольника по координатам вершин
Вершина А
Вершина B
Вершина C
Точность вычисления
Знаков после запятой: 2
Расчет треугольника по координатам вершин
Длины сторон находятся по формуле вычисления расстояния между точками в декартовых координатах
Углы – из формул скалярного произведения векторов при вершинах.
Периметр находится простым суммированием длин сторон.
Площадь треугольника находится через определитель
Произвольный треугольник по заданным параметрам
| Введите известные даные треугольника |
| Сторона а |
| Сторона b |
| Сторона c |
| Угол А в градусах |
| Угол B в градусах |
| Угол C в градусах |
| Медиана на сторону а |
| Медиана на сторону b |
| Медиана на сторону c |
| Высота на сторону a |
| Высота на сторону b |
| Высота на сторону c |
| Координаты вершины А |
| X
Y |
| Координаты вершины B |
| X
Y |
| Координаты вершины C |
| X
Y |
| Площадь треугольника S |
| Полупериметр сторон треугольника p |
| Результат расчета параметров заданного треугольника |
Представляем Вам калькулятор, который позволял рассчитывать все возможные параметры треугольника по заданным параметрам.
Хотелось бы обратить Ваше внимание именно на то, что это универсальный бот. Он рассчитывает все параметры произвольного треугольника, при произвольно заданных параметрах. Такого бота вы не найдете нигде.
Вам известна сторона и две высоты? или две стороны и медиана? Или биссектриса два угла и основание треугольника?
По любым запросам, мы можем получить правильный расчет параметров треугольника.
Вам нет необходимости искать формулы и делать расчет самостоятельно. За вас уже все сделано.
Создайте запрос и получите точный ответ.
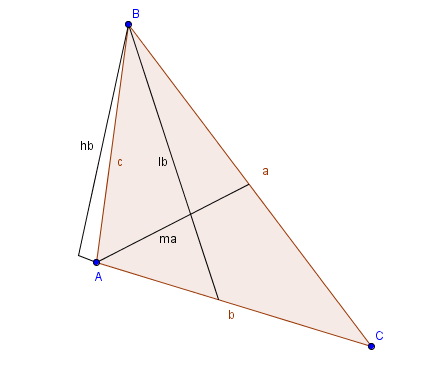
Показан произвольный треугольник. Сразу оговоримся как и что обозначается, дабы в дальнейшем не было путаницы и ошибок в расчетах.
Стороны противоположные любому углу называются так же только маленькой буквой. То есть напротив угла А лежит сторона треугольника а, стороне с противостоит угол С.
ma – это медина, падающая на сторону а, соответственно есть еще медианы mb и mc падающие на соответствующие стороны.
lb – это биссектриса , падающая на сторону b, соответственно есть еще биссектрисы la и lc падающие на соответствующие стороны.
hb – это высота, падающая на сторону b, соответственно есть еще высоты ha и hc падающие на соответствующие стороны.
Ну и второе, помните что треугольником является фигура в которой присутствует фундаментальное правило:
Сумма любых(!) двух сторон должна быть больше третьей.
Поэтому не удивляйтесь если получите ошибку При таких данных треугольника не существует при попытке рассчитатать параметры треугольника со сторонами 3, 3 и 7.
Синтаксис
Для позволяателей XMPP клиентов запрос вот такой treug <список параметров>
Для пользователй сайта, все сделано на этой странице.
Список параметров – параметры которые известны, разделенные точкой с запятой
параметр записываетя как параметр=значение
Например если известна сторона а с значением 10, то так и записываем a=10
Более того, значения могут быть не только в виде вещественного числа, но и например как результат какого то выражения
Например если нам нужно посчитать площадь треугольника с сторонами 1, 3, 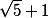
А вот и сам список парметров которые могут фигурировать в расчетах.
Сторона a
Сторона b
Сторона c
Полупериметр p
Угол А
Угол B
Угол C
Площадь треугольника S
Высота ha на сторону a
Высота hb на сторону b
Высота hc на сторону c
Медиана ma на сторону a
Медиана mb на сторону b
Медиана mc на сторону c
Координаты вершин (xa,ya) (xb,yb) (xc,yc)
Примеры
Рассчитать параметры треугольника если известны сторона = 8, угол прилежащей к этой стороне =70 градусов и высота, падающая на эту сторону =2
пишем treug a=8;C=70;ha=2
Параметры треугольника по заданным параметрам
Сторона a = 8
Сторона b = 2.1283555449519
Сторона c = 7.5420719851515
Полупериметр p = 8.8352137650517
Угол А = 2.1882518638666 в градусах 125.37759631119
Угол B = 2.873202966917 в градусах 164.62240368881
Угол C = 1.221730476396 в градусах 70
Площадь треугольника S = 8
Высота ha на сторону a = 2
Высота hb на сторону b = 7.5175409662872
Высота hc на сторону c = 2.1214329472723
Медиана ma на сторону a = 3.8348889915443
Медиана mb на сторону b = 7.7012304590352
Медиана mc на сторону c = 4.4770789813853
Вот и все, все параметры треугольника.
Вопрос, почему мы сторону назвали а, а не в или с? Это не влияет на решение. Главное выдержать условие о котором я уже сказал “Стороны противоположные любому углу называются так же, только маленькой буквой.” А далее нарисовать в уме треугольник, и применить к заданному вопросу.
Можно было бы взять вместо а в, но тогда прилежащий угол будет не С а А ну и высота будет hb. Результат если вы проверите, будет один и тот же.
Как рассчитать треугольник если известны координаты его вершин?
Например вот такими (xa,ya) =3,4 (xb,yb) =-6,14 (xc,yc)=-6,-3
пишем запрос treug xa=3;ya=4;xb=-6;yb=14;xc=-6;yc=-3
и получаем
Параметры треугольника по заданным параметрам
Сторона a = 17
Сторона b = 11.401754250991
Сторона c = 13.453624047073
Полупериметр p = 20.927689149032
Угол А = 1.4990243938603 в градусах 85.887771155351
Угол B = 0.73281510178655 в градусах 41.987212495819
Угол C = 0.90975315794426 в градусах 52.125016348905
Площадь треугольника S = 76.5
Высота ha на сторону a = 9
Высота hb на сторону b = 13.418987695398
Высота hc на сторону c = 11.372400437582
Медиана ma на сторону a = 9.1241437954466
Медиана mb на сторону b = 14.230249470757
Медиана mc на сторону c = 12.816005617976
Удачных расчетов!!