Как найти координаты вершины параллелограмма если известны

Как найти координаты вершины параллелограмма если известны

Как найти координаты 4-й вершины параллелограмма, зная координаты трёх других его вершин?

В декартовых координатах эту задачу можно решить, используя свойство диагоналей параллелограмма.

Из трёх известных вершин две являются концами одной диагонали. Находим координаты середины этой диагонали. Точка пересечения диагоналей является серединой каждой из них. Для второй диагонали находим второй конец по известным одному концу и середине.

Примеры.

1)

najti-koordinaty-vershiny-parallelogramma Дано: ABCD — параллелограмм,

A(-3;11), B(12;-4), C(1;-7)

Найти: D.

Решение:

najti-4-vershinu-parallelogramma1) Найдём координаты точки O — середины диагонали AC.

По формуле координат середины отрезка

    [x_O = frac{{x_A + x_C }}{2} = frac{{ - 3 + 1}}{2} = - 1;]

    [y_O = frac{{y_A + y_C }}{2} = frac{{11 + ( - 7)}}{2} = 2.]

То есть O(-1;2).

2) По свойству диагоналей параллелограмма, точка O также является серединой BD:

    [x_O = frac{{x_B + x_D }}{2}; - 1 = frac{{12 + x_D }}{2};x_D = - 14;]

    [y_O = frac{{y_B + y_D }}{2};2 = frac{{ - 4 + y_D }}{2};y_D = 8.]

Ответ: D (-14; 8).

2)

Дано: ABCD — параллелограмм,

B(7;4), C(-5;10), D(-1;-2)

Найти: A.

Решение:

1) Ищем координаты точки O — середины отрезка BD:

    [x_O = frac{{x_B + x_D }}{2};x_O = frac{{7 + ( - 1)}}{2} = 3;]

    [y_O = frac{{y_B + y_D }}{2};x_O = frac{{4 + ( - 2)}}{2} = 1.]

Итак, O (3;1).

2) Точка O также является серединой AC:

    [x_O = frac{{x_A + x_C }}{2};3 = frac{{x_A + ( - 5)}}{2};x_A = 11;]

    [y_O = frac{{y_A + y_C }}{2};1 = frac{{y_A + 10}}{2};y_A = - 8.]

Ответ: A (11;-8).

Источник

Найдите координаты всех вершин параллелограмма, если известны координаты одной вершины А(1;0) и уравнения двух его сторон: – 3x+7y-5=0 и 5x-9y+3=0

математика ВУЗ
1113

★

Точка А не принадлежит ни одной из данных прямых, так как

при подстановке координат точки А в данные уравнения не получается верных равенств:

-3*1+7*0-5=0 – неверно
5*1-9*0+3=0 – неверно

Найдем точку пересечения двух сторон, заданных уравнениями:

[m]left{begin{matrix}-3x+7y-5=0\5x-9y+3=0 end{matrix}right.[/m].

Умножаем первое уравнение на 5, второе на 3
[m]left{begin{matrix}-15x+35y-25=0\15x-27y+9=0 end{matrix}right.[/m].

Складываем, т. е одно из данных уравнений оставляем без изменения, а вместо второго
– сумму двух последних
[m]left{begin{matrix}-3x+7y-5=0\7y-16=0 end{matrix}right.[/m].

[m]left{begin{matrix}3x=7cdotfrac{16}{7} -5 \y=frac{16}{7} end{matrix}right.[/m].

Пусть это точка С ([m]frac{11}{3}[/m];[m]frac{16}{9}[/m])

Тогда составляем уравнение сторон, параллельных данным и проходящих через точку А:

( см. решение аналогичной задачи https://reshimvse.com/question/5fad897f322e6f41f4eb6685 )

-3x+7y-5=0 ⇒ Семейство параллельных ей прямых -3x+7y+m=0 ⇒ -3*1+7*0+m=0 ⇒ m=3

[b]-3x+7y+3=0 [/b]

5x-9y+3=0⇒ Семейство параллельных ей прямых 5x-9y+n=0 ⇒5*1-9*0+n=0 ⇒n=-5

[b]5x-9y-5=0[/b]

Находим двух других вершин как точки пересечения прямых:
[m]left{begin{matrix}-3x+7y-5=0\5x-9y-5=0 end{matrix}right.[/m] и [m]left{begin{matrix}-3x+7y+3=0\5x-9y+3=0 end{matrix}right.[/m].

Решаем самстоятельно ….

Источник

ГДЗ (готовое домашние задание из решебника) на Задача №13, § 4 по учебнику Геометрия. 10-11 классы. Учебник для общеобразовательных учреждений / А. В. Погорелов – 13-е издание. Просвещение, 2014-2017г.

Условие

Найдите координаты вершины D параллелограмма ABCD, если координаты трех других вершин известны: 1) A(2;3;2), B(0;2;4), C(4;1;0); 2) A(1;-1;0), B(0;1;-1), C(-1;0;1); 3) A(4;2;-1), B(1;-3;2), C(-4;2;1).

Решение 1

Фото решения 1: Задача №13, Параграф 4 из ГДЗ по Геометрии 10-11 класс: Погорелов А.В. г.

Популярные решебники

Ваше сообщение отправлено
и скоро будет рассмотрено

Источник

   1. Поскольку координаты точки A не удовлетворяют двум уравнениям, то они соответствуют сторонам CB и CD параллелограмма:

  • {3x + 6y = -69;
    {-6x + 9y + 30 = 0;
  • {y = -0,5x – 11,5; //BC
    {y = 2/3 * x – 10/3; //CD
  • k1 = -0,5;
  • k2 = 2/3.

   2. Уравнение AB:

  • y + 5 = 2/3 * (x – 8);
  • y = 2/3 * x – 16/3 – 15/3;
  • y = 2/3 * x – 31/3.

   3. Уравнение AD:

  • y + 5 = -0,5 * (x – 8);
  • y = -0,5x + 4 – 5;
  • y = -0,5x – 1.

   4. Решив систему каждой пары уравнений, найдем координаты вершин параллелограмма (http://bit.ly/2ODBDXk):

   1)

  • {y = -0,5x – 11,5; //BC
    {y = 2/3 * x – 10/3; //CD
  • С(-7; -8).

   2)

  • {y = 2/3 * x – 31/3; //AB
    {y = -0,5x – 11,5; //BC
  • B(-1; -11).

   3)

  • {y = -0,5x – 1; //AD
    {y = 2/3 * x – 10/3; //CD
  • D(2; -2).

   Ответ: A(8; -5), B(-1; -11), С(-7; -8), D(2; -2).

Источник

Ответ:

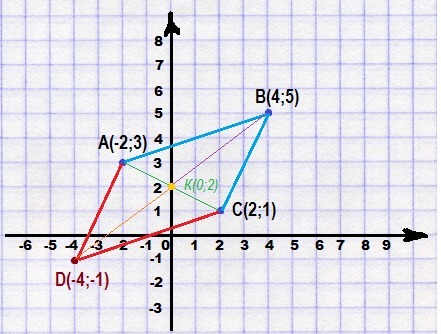
D (-4; -1)

Пошаговое объяснение:
Из названия параллелограмма АВСD следует, что его диагонали – АС и ВД. Они по свойству параллелограмма должны пересекаться в одной точке, назовем ее К, являющейся серединой обеих диагоналей.
Координаты концов для АС даны в условии, а координаты К (как середины отрезка) равны их полусумме:
х(к) = (-2+2)/2 = 0
у(к) = (3+1)/2 = 2
К(0;2) —– координаты точки пересечения диагоналей.
Эти координаты входят в формулы для определения середины диагонали ВD, включающие координаты точки D. И их легко найти, так как координаты точки В известны (4,5), а точки К уже вычислены:
(4+х(D))/2 = 0 ⇒ x(D) = -4
(5+y(D))/2 = 2 ⇒ y(D) = 4 + (-5) = -1
D(-4; -1) —– координаты вершины D параллелограмма
Ответ: D(-4; -1)

Примечание:

координаты четвертой вершины параллелограмма можно найти построением.

image

Источник

Добавить комментарий