Представьте, перед вам нарисованный куб с осями координат, направленным по трем ребрам, выходящим из одной вершины. За единицу масштаба берем ребро куба и обозначим вершины буквами $%A$%, $%B$%, $%C$%, $%D$%, $%A_1$%, $%B_1$%, $%C_1$% и $%D_1$%. Нужно:
- Найти координаты всех вершин куба.
- Найти координаты середины ребра $%CC_1$%.
- Найти, чему равно расстояние от вершины $%(0;0;0)$% куба до точки пересечения диагоналей грани $%BB_1C_1C$%.
Здесь не сказано, какая из вершин принята за начало координат а также не указан порядок выбора осей, что создаёт неоднозначность в ответах на некоторые из пунктов. Координаты вершин всегда имеют вид 000, 001, 010, 011, 100, 101, 110, 111 (пишу для простоты без скобок и промежуточных запятых). Для всего остального требуются уточнения, хотя там всё в принципе просто.
(15 Мар ’15 12:02)
falcao
@falcao, начало координат-точка А. Оси x,y,z соответствуют ребрам AB, AD, AA1
1
Тогда все координаты непосредственно видны из рисунка: B(1;0;0), D(0;1;0), C(1;1;0), C1(1;1;1). Середина ребра соответствует полусумме координат: (1;1;1/2). В пункте 3 берётся середина грани, координаты (1;1/2;1/2). Расстояние до нуля — корень из суммы квадратов, то есть $%sqrt{3/2}=sqrt6/2$%.
(15 Мар ’15 12:34)
falcao
Как определить вершины куба?
Вершина куба— это точка, где сходятся три грани или точка, в которой сходятся три ребра куба.
Сколько вершин у куба?
| Куб | |
|---|---|
| Элементы | 6 граней 12 рёбер 8 вершин Χ = 2 |
| Грани | квадраты |
| Конфигурация вершины | 4.4.4 |
| Двойственный многогранник | правильный октаэдр |
Как узнать площадь грани куба?
Вычислим площадь одной грани куба. Так как гранью куба является квадрат, то площадь грани равна площади квадрата, то есть длине ребра куба в квадрате. Например: длина ребра куба равна 5, тогда площадь его грани 5*5=25.
Сколько ребер сходятся в одной вершине куба?
У куба 8 вершин, 6 граней и 12 ребер. В одной вершине куба сходится 3 ребра.
Что является вершиной многоугольника?
Вершина — это угловая точка многоугольника или многогранника (любой размерности), иначе говоря его 0-мерная граней. В многоугольнике вершина называется «выпуклой», если внутренний угол многоугольника меньше π радиан (180° — два прямых угла).
Сколько вершин у 4 кубиков?
У каждого кубика 8 вершин , поэтому у четырёх кубиков их 32.
Сколько граней у 7 угольной призмы?
6 6 6 6 боковых граней + грань основания = 7 = 7 = 7 =7 граней всего.
Как найти площадь грани куба Зная объем?
Формула площади поверхности куба имеет вид: S = 6∙(³√V)². Когда задана длина диагонали гексаэдра (L), тогда длину одной грани можно легко вычислить, а вместе с ней и площадь фигуры. Диагональ определяют так: L/v3.
Как можно вычислить куб?
Вычислить объем куба легко — нужно перемножить длину, ширину и высоту. Так как у куба длина равна ширине и равна высоте, то объем куба равен s3, где s — длина одного (любого) ребра куба.
Сколько углов может быть у многоугольника?
Любой многоугольник, правильный или неправильный имеет столько углов, сколько сторон. или 180n−360 градусам, где n– вершина многоугольника. Это связано с тем, что любой простой N-угольник можно считать состоящим из (n−2) треугольников, каждый из которых имеет сумму углов π радианов или 180 градусов.
Какие многоугольники называются равными?
Многоугольники, имеющие равные площади, называют равновеликими. Если один из многоугольников можно разрезать на несколько частей, из которых можно сложить другой, то эти многоугольники называются равносоставленными. Очевидно, что любые равносоставленные многоугольники являются равновеликими.
Как узнать сколько вершин у призмы?
Граф треугольной призмы — 6 вершин, 9 рёбер Кубический граф — 8 вершин, 12 рёбер Граф пятиугольной призмы — 10 вершин, 15 рёбер Граф шестиугольной призмы — 12 вершин, 18 рёбер
Сколько ребер р вершин В и граней Г у 7 угольной призмы?
Граф семиугольной призмы — 14 вершин, 21 рёбер
Сколько граней у девяти угольный призмы?
Восьмиугольная призма
| Однородная восьмиугольная призма | |
|---|---|
| Свойства | выпуклый, зоноэдр |
| Комбинаторика | |
| Элементы | 24 ребра 16 вершин Χ = 2 |
| Грани | 8 квадратов 2 восьмиугольника |
Как найти площадь куба зная сторону?
Если вы знаете длину одной из сторон Площадь куба — это сумма площади всех шести его сторон. Вот формула: 6 x s2, где «s» — это сторона куба. Найдите площадь одной из сторон куба, то есть «s», длину стороны куба, а затем нужно найти s2.
Как найти площадь если знаешь объем?
площадь (S) — это произведение длинны и ширины (S= l*b), а объем – произведение длины, ширины и высоты. Подставьте в формулу вычисления объема вместо l*b площадь. Вы получите выражение V=S*h.
Как найти объем по длине ширине и высоте?
Как уже упоминалось, формула расчета объема выглядит следующим образом: V = Длина x Ширина x Высота; поэтому для получения объема необходимо просто перемножить все три стороны.
Введение системы координат
30 мая 2011
Метод координат — это, конечно, очень хорошо, но в настоящих задачах C2 никаких координат и векторов нет. Поэтому их придется вводить. Да-да, вот так взять и ввести: указать начало отсчета, единичный отрезок и направление осей x, y и z.
Самое замечательное свойство этого метода заключается в том, что не имеет никакого значения, как именно вводить систему координат. Если все вычисления будут правильными, то и ответ будет правильным.
Тем не менее, приведу некоторые рекомендации, как лучше ввести систему координат для самых часто встречающихся в задаче C2 многогранников. С указанием конкретных точек. Во всех случаях упор делается на минимизацию объема вычислений.
Координаты куба
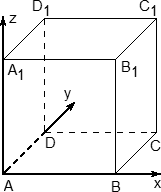
Если в задаче C2 будет куб — считайте, что вам повезло. Это самый простой многогранник, все двугранные углы которого равны 90°.
Система координат также вводится очень просто:
- Начало координат — в точке A;
- Чаще всего ребро куба не указано, поэтому принимаем его за единичный отрезок;
- Ось x направляем по ребру AB, y — по ребру AD, а ось z — по ребру AA1.
Обратите внимание: ось z направляется вверх! После двумерной системы координат это несколько непривычно, но на самом деле очень логично.
Итак, теперь у каждой вершины куба есть координаты. Соберем их в таблицу — отдельно для нижней плоскости куба:
| Точка | A | B | C | D |
| Координаты | (0; 0; 0) | (1; 0; 0) | (1; 1; 0) | (0; 1; 0) |
И для верхней:
| Точка | A1 | B1 | C1 | D1 |
| Координаты | (0; 0; 1) | (1; 0; 1) | (1; 1; 1) | (0; 1; 1) |
Несложно заметить, что точки верхней плоскости отличаются соответствующих точек нижней только координатой z. Например, B = (1; 0; 0), B1 = (1; 0; 1). Главное — не запутаться!
Координаты трехгранной призмы
Призма — это уже намного веселее. При правильном подходе достаточно знать координаты только нижнего основания — верхнее будет считаться автоматически.
В задачах C2 встречаются исключительно правильные трехгранные призмы (прямые призмы, в основании которых лежит правильный треугольник). Для них система координат вводится почти так же, как и для куба. Кстати, если кто не в курсе, куб — это тоже призма, только четырехгранная.
Итак, поехали! Вводим систему координат:
- Начало координат — в точке A;
- Сторону призмы принимаем за единичный отрезок, если иное не указано в условии задачи;
- Ось x направляем по ребру AB, z — по ребру AA1, а ось y расположим так, чтобы плоскость OXY совпадала с плоскостью основания ABC.
Здесь требуются некоторые пояснения. Дело в том, что ось y НЕ совпадает с ребром AC, как многие считают. А почему не совпадает? Подумайте сами: треугольник ABC — равносторонний, в нем все углы по 60°. А углы между осями координат должны быть по 90°, поэтому сверху картинка будет выглядеть так:

Надеюсь, теперь понятно, почему ось y не пойдет вдоль AC. Проведем в этом треугольнике высоту CH. Треугольник ACH — прямоугольный, причем AC = 1, поэтому AH = 1 · cos A = cos 60°; CH = 1 · sin A = sin 60°. Эти факты нужны для вычисления координат точки C.
Теперь взглянем на всю призму вместе с построенной системой координат:
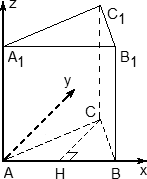
Получаем следующие координаты точек:
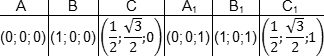
Как видим, точки верхнего основания призмы снова отличаются от соответствующих точек нижнего лишь координатой z. Основная проблема — это точки C и C1. У них есть иррациональные координаты, которые надо просто запомнить. Ну, или понять, откуда они возникают.
Координаты шестигранной призмы
Шестигранная призма — это «клонированная» трехгранная. Можно понять, как это происходит, если взглянуть на нижнее основание — обозначим его ABCDEF. Проведем дополнительные построения: отрезки AD, BE и CF. Получилось шесть треугольников, каждый из которых (например, треугольник ABO) является основанием для трехгранной призмы.
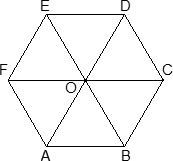
Теперь введем собственно систему координат. Начало координат — точку O — поместим в центр симметрии шестиугольника ABCDEF. Ось x пойдет вдоль FC, а ось y — через середины отрезков AB и DE. Получим такую картинку:
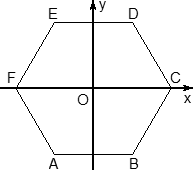
Обратите внимание: начало координат НЕ совпадает с вершиной многогранника! На самом деле, при решении настоящих задач вы обнаружите, что это очень удобно, поскольку позволяет значительно уменьшить объем вычислений.
Осталось добавить ось z. По традиции, проводим ее перпендикулярно плоскости OXY и направляем вертикально вверх. Получим итоговую картинку:
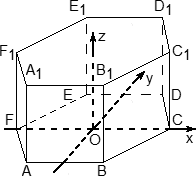
Запишем теперь координаты точек. Предположим, что все ребра нашей правильной шестигранной призмы равны 1. Итак, координаты нижнего основания:
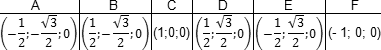
Координаты верхнего основания сдвинуты на единицу по оси z:
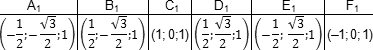
Координаты четырехугольной пирамиды
Пирамида — это вообще очень сурово. Мы разберем только самый простой случай — правильную четырехугольную пирамиду, все ребра которой равны единице. Однако в настоящих задачах C2 длины ребер могут отличаться, поэтому ниже приведена и общая схема вычисления координат.
Итак, правильная четырехугольная пирамида. Это такая же, как у Хеопса, только чуть поменьше. Обозначим ее SABCD, где S — вершина. Введем систему координат: начало в точке A, единичный отрезок AB = 1, ось x направим вдоль AB, ось y — вдоль AD, а ось z — вверх, перпендикулярно плоскости OXY. Для дальнейших вычислений нам потребуется высота SH — вот и построим ее. Получим следующую картинку:
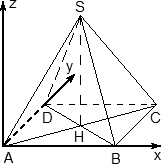
Теперь найдем координаты точек. Для начала рассмотрим плоскость OXY. Здесь все просто: в основании лежит квадрат, его координаты известны. Проблемы возникают с точкой S. Поскольку SH — высота к плоскости OXY, точки S и H отличаются лишь координатой z. Собственно, длина отрезка SH — это и есть координата z для точки S, поскольку H = (0,5; 0,5; 0).
Заметим, что треугольники ABC и ASC равны по трем сторонам (AS = CS = AB = CB = 1, а сторона AC — общая). Следовательно, SH = BH. Но BH — половина диагонали квадрата ABCD, т.е. BH = AB · sin 45°. Получаем координаты всех точек:
![]()
Вот и все с координатами пирамиды. Но не с координатами вообще. Мы рассмотрели лишь самые распространенные многогранники, однако этих примеров достаточно, чтобы самостоятельно вычислить координаты любых других фигур. Поэтому можно приступать, собственно, к методам решения конкретных задач C2.
Смотрите также:
- Четырехугольная пирамида в задаче C2

- Метод координат в пространстве

- Сложение и вычитание дробей

- Не пишите единицы измерения в задаче B12

- Как решать простейшие логарифмические уравнения

- Задача B4: транзит нефти

1) Из условия C (-2; 4; 0) вытекает, что длина ребра куба равна 4, отсюда получаем координаты:
A (2; 0; 0) B (-2; 0; 0) D (2; 4; 0) A1 (2, 0, 4) B1 (-2, 0, 4) C1 (-2, 4, 4) D1 (2, 4, 4)
Допустим у Вас точка О — является началом координат (откуда точка К что она такое и ее расположение, к сожалению вы не указали.)
(Правило, для справки: Чтобы вычислить координаты вектора, зная координаты (x1; y1) его начала A и координаты (x2; y2) его конца B, нужно из координат конца вычесть координаты начала: (x2 – x1; y2 – y1). )
Имеем точки с координатами О(0;0;0), С (-2;4;0), В1(-2;0;4). Из этого следует:
Вектор ОС=(-2-0;4-0;0-0), вектор ОС=(-2;4;0).
Вектор ОВ1=(-2-0;0-0;4-0), вектор ОВ1=(-2;0;4)

ДАЮ 70 БАЛОВ ЗА ПРАВИЛЬНЫЙ ОТВЕТ!!!! куб abcda1b1c1d1 помещен в прямоугольную систему координат с -2 4 0 .найдите координаты всех остальных вершин куба , найдите координаты векторов OC , OB1 ,OK

Светило науки – 12834 ответа – 102068 раз оказано помощи
А(-6;0;0) В(-6;4;0) Д(-2;0;0)
А₁(-6;0;4) В₁(-6;4;4) С₁(-2;4;4) Д₁(2;0;4)
см рисунок.
На рисунке изображено основание куба – квадрат АВСD (зеленым контуром)
возможны другие ответы ( см квадраты с вершиной С красного контура и синего)
вектор OC будет иметь такие же координаты как и точка С
вектор OB1 будет иметь такие же координаты как и точка В₁
про вектор OK ничего нельзя сказать, так как ничего не известно про точку К

